Clustering Analysis for the Pareto Optimal Front in Multi-Objective Optimization

Abstract

Bio-inspired algorithms are a suitable alternative for solving multi-objective optimization problems. Among different proposals, a widely used approach is based on the Pareto front. In this document, a proposal is made for the analysis of the optimal front for multi-objective optimization problems using clustering techniques. With this approach, an alternative is sought for further use and improvement of multi-objective optimization algorithms considering solutions and clusters found. To carry out the clustering, the methods k-means and fuzzy c-means are employed, in such a way that there are two alternatives to generate the possible clusters. Regarding the results, it is observed that both clustering algorithms perform an adequate separation of the optimal Pareto continuous fronts; for discontinuous fronts, k-means and fuzzy c-means obtain results that complement each other (there is no superior algorithm). In terms of processing time, k-means presents less execution time than fuzzy c-means.

1. Introduction

Many multi-objective optimization algorithms are the bio-inspired type; in the same way, a wide number of these are based on the Pareto optimal front (POF). The main difficulty of these approaches is presented with discontinuous Pareto optimal fronts; therefore, the optimization algorithm can remain performing the search process in a single sector of the Pareto front. Considering the above, in this document, a proposal is made for clustering analysis of the Pareto front solutions in such a way that it can be taken as a reference to improve multi-objective optimization algorithms.

In order to contextualize the proposal made in this document, the following subsections review the related topics seen in Figure 1, presenting the most well-known multi-objective optimization algorithms, and the approaches that can be taken using clustering to improve algorithms.

1.1. Multi-Objective Optimization

Bio-inspired multi-objective optimization algorithms have proven to be a suitable tool for solving problems with different objective functions [1]. Among the most representative algorithms, there are those based on evolution and also on swarms of particles. In relation to the characteristics of the evolutionary strategy, a suitable approach to obtain the entire Pareto front is achieved but requires many generations; on the other hand, algorithms based on swarms of particles present a high rate of convergence; however, their main disadvantage is to achieve an adequate diversity management [1,2].

According to [3], the optimal solutions of a multi-objective optimization problem correspond to a non-dominated front that is characterized by a compromise solution between the objectives. A “knee” region on this Pareto front, which visually is a convex bulge at the front, is important for decision-making, and it often constitutes the optimum in equilibrium.

As a first approximation of genetic algorithms, the following approaches are presented: Multi-Objective Genetic Algorithm (MOGA), Non-Dominated Sorting Genetic Algorithm (NSGA), Niched Pareto Genetic Algorithm (NPGA), Niched Pareto Genetic Algorithm II (NPGA-II). A second group of representative algorithms are: Strength Pareto Evolutionary Algorithm (SPEA) [4,5], Pareto Archived Evolution Strategy (PAES) [6], Envelope-Based Selection Algorithm (PESA) [7], Non-Dominated Sorting Genetic Algorithm II (NSGA-II) [8] and SPEA-II [9], Pareto Adaptive Algorithm (APA) [10].

Regarding recent developments, in [11], there is a proposal combining the Whale Optimization Algorithm (WOA) with Tabu Search (TS) for multi-objective problems called MOWOATS. This algorithm uses TS to store in elite lists the non-dominated solutions to drive the swarm. The crossover is used in MOWOATS during intensification and diversification phases to enhance the population diversity. An improvement of the SPEA-II algorithm applied to the multi-objective decision-making of investment is presented in [12]. In this case, an external archive is employed separately for local search after the genetic operation to achieve global and local ability. In addition, a crossover operator and individual update strategy are used to enhance the convergence, maintaining the population diversity. Meanwhile, in [13], the authors presented a development based on Chaotic Search (CS), where different Tchebychev scalarization strategies are considered.

According to [14], GA implementations must find a compromise to prevent being trapped into local minima and to avoid a poor approximation to the optimal solution. Commonly, GA algorithms use elitism to preserve some of the current best solutions. When the initial population is randomly selected, as in many GA implementations, the elite can be concentrated in a limited sector in the Pareto front. The authors in [14] show that a full view of the Pareto front is possible by solving the single-objective problems (associated with the extremes of the Pareto boundary), and then employing these solutions as the elite members for the initial population.

A proposal of the Harmony Search (HS) algorithm with pitch adjustment using genotype is described in [15]. The approach consists of adjusting the pitch and employing the crowding distance (in the search space). This adjustment regulates the exploration and exploitation process, considering the distribution of the harmonies in the search space during the calculation of Pareto front. In this way, the algorithm avoids the use of dynamic parameters or a static bandwidth, since, for its operation, it only requires presetting the pitch adjustment rate and the harmony memory accepting rate.

Meanwhile, in [16], a random strategy and second-order difference strategy were used in the NSGA-III, given the algorithm SDNSGA-III. In cases when the environment changes in SDNSGA-III, the aforementioned strategies are used to improve the individuals in the next generation. Tests were performed using the metric values: Mean Generational Distance (MGD), Mean Inverted Generational Distance (MIGD), and Mean Hyper Volume (MHV).

According to [17], the Lebesgue measure is one of the most relevant indicators in evolutionary algorithms given the Pareto compliance characteristic. However, the main deficiency in using the Lebesgue measure is the computational cost, which increases with the number of objective functions associated with the problem. In this regard, in [17], to deal with box-constrained continuous multi-objective optimization problems, an evolutionary algorithm based on the Lebesgue measure is introduced. This algorithm includes a survival selection mechanism that considers the local property of the Lebesgue measure to reduce the computational time.

1.2. Multi-Objective Particle Swarm Optimization

In this regard, Ref. [2] proposed the Multi-Objective Particle Swarm Optimization (MOPSO), one of the first Pareto-based PSO approaches, where the non-dominated solutions detected by the particles are stored in a repository. This approach uses the Pareto dominance concept to determine the best positions (particle leaders) that will guide the swarm in the search process. The search space is divided into hypercubes, and for each hypercube is assigned a fitness value inversely proportional to the number of particles that it contains. The algorithm employs a classic roulette wheel to select a hypercube and a leader. The best position is updated at each iteration, based on the dominance relationship between the particle’s best existing position and its new position. The record is limited in size and new positions are inserted based on retention criteria that prioritize solutions located in the less populated areas of the target space.

An alternative to achieve a better exploration of the entire Pareto front is to use multiple populations. Regarding the development of algorithms that use several populations, in [18], an algorithm is developed based on the concept of the coevolution of a family of preferences together with a population of candidate solutions.

Meanwhile, in [19], a multi-objective evolutionary algorithm based on the parallel evolution of multiple populations and a population from the Pareto file is proposed. For each population, an evolutionary algorithm is used to separately optimize each of the functions, where the individuals are generated by selection (tournament type) of the union of a population associated with a goal and the population of the Pareto file. At each iteration, a population of finite size from the Pareto file is iteratively updated and trimmed using a comparison operation.

Regarding approaches that employ several groups of individuals, in [20], an algorithm with multiple swarms called Distance Sorting Multi-Objective Particle Swarm Optimization (DSMOPSO) is proposed, where the number of swarms is dynamically adjusted. The authors propose a dynamic swarm strategy to assign an appropriate number of swarms, as needed. A modified mechanism for PSO update is also employed to better manage convergence and communication between and within swarms. The compression of the target space and the expansion strategy are proposed progressively to exploit the target space during the different stages of the search process.

Other related work can be seen in [21], where a multi-objective optimization algorithm with multiple swarms is developed proposing that the number of swarms is adaptively adjusted during the search process. The strategy assigns an appropriate number of swarms to improve convergence and diversity among the swarms. A PSO update mechanism is included to better manage intra-swarm and inter-swarm communication and space compression. An expansion of the search space is also carried out for a progressive exploration of it.

In [22], a coevolutionary technique is proposed using several populations for multiple objectives. This approach provides a way to solve the multi-objective problem by letting each population correspond to a single objective. In this way, the fitness assignment problem can be addressed since the fitness of the individuals in each population can be assigned by the corresponding objective. In this way, the Coevolutionary Multiswarm Particle Swarm Optimization (CMPSO) algorithm is proposed, which uses an external shared file for different populations to exchange the required information, incorporating two mechanisms. The first consists of modifying the speed equation using the information found by different populations. The other mechanism is the use of an elitist learning strategy for shared file updating.

According to [23], optimization problems with more than one objective, where at least one objective changes in time, are defined as dynamic multi-objective optimization problems. In the case when at least two objectives are in conflict, there is no single solution and therefore the task of a dynamic multi-objective optimization algorithm is to follow the set of optimal solutions through time. In addition, one of the main problems in solving optimization problems is balancing exploitation and exploration during the search process. In [23], the performance of the dynamic evaluated vector particle swarm optimization algorithm is investigated using a heterogeneous swarm, where each particle exhibits a different behavior; that is, there are specialized particles in separated exploration and exploitation.

In order to obtain the balance between convergence and diversity, in [24], the Clone Immunity Chaotic Multi-Objective Particle Swarm Optimization (CICMOPSO) is proposed, where the points in a non-dominated solution are mapped to a parallel-cell coordinate system. In order to maintain and change the external archive, logistic mapping and a neighboring immune operator are employed. In the CICMOPSO algorithm, the status of the particles is evaluated using the Pareto entropy and difference entropy.

Meanwhile, in [25], the hybridization of two multi-objective derivative-free global and local algorithms is presented. In this proposal, the global exploration capability of the deterministic MPOS is enhanced via the local search accuracy of a derivative-free line-search method (multi-objective). The algorithm develops the global and local searches considering the hypervolume metric. In order to control the local search activation, the hybridization scheme employs two parameters.

Additionally, in [26], the Quantum-Behaved Particle Swarm Optimization (QPSO) algorithm is integrated with the Decomposition-Based Multi-Objective Evolutionary Algorithm (MOEA/D) to allow the QPSO to solve multi-objective optimization problems effectively. In this algorithm, to avoid premature convergence, a diversity controlling mechanism is employed, and also nondominated solutions are used to generate the global best for driving the swarm.

Finally, regarding previous works related to this paper, the Multi-Objective Vortex Particle Swarm Optimization (MOVPSO) algorithm is presented in [27,28]. This algorithm employs vortex behavior to enhance the exploratory process to find the optimal Pareto front. The algorithm uses convergence and dispersion processes iteratively. In the convergence phase, particles are grouped in the vortex. Then, in the next stage, the particles are dispersed through the vorticity behavior characterized by circular movements.

1.3. Clustering Techniques and Multi-Objective Optimization

Clustering of numerical data is used for system modeling and classification. The goal of clustering is to identify natural groups of data to produce a concise representation of the behavior of a data system. Fuzzy logic (FL) provides some techniques to find clusters for training data. In this way, it can use the cluster information to make a Sugeno fuzzy inference system that models the data behavior using a minimal number of rules. The partition rules are determined according to the fuzzy qualities associated with each of the data groups [29,30]. A widely used clustering algorithm based on fuzzy logic corresponds to c-means, which uses the membership values to generate the clusters.

Another useful clustering algorithm corresponds to k-means, which is an unsupervised algorithm that determines clusters of objects into k groups based on the characteristics of the data. The clusters are determined by minimizing the sum of the distances between each object and the cluster centroid, where the quadratic distance is often used [31,32].

An attempt to enhance a multi-objective optimization algorithm using clustering is presented in [33], developing a two-phase PSO strategy based on clustering. The initial population is built according to the distribution of the particles. The subpopulations representing the specialized niche clusters of particles are dynamically identified employing density-based clustering algorithms. The evolution of the particles is restricted in each niche; in the same way, information is not exchanged between the different niches.

Regarding clustering proposals to improve the Pareto set in multi-objective optimization problems, a development is presented in [34] applying clustering with a flexible similarity metric. Meanwhile, in [35], a clustering strategy is employed to guide the search in evolutionary multi-objective optimization.

On the other hand, considering applications of data clustering, in [36], a cluster-based strategy is applied for solution selection in a multi-objective evolutionary algorithm based on decomposition using particle swarm optimization. In this proposal, a clustering of the Pareto solutions is performed for evaluating new candidates. In this way, a local search strategy is introduced in the solution selection process. According to the authors, this technique can be effective on datasets presenting highly overlapping clusters.

Regarding the clustering process for improving the optimization techniques, in [37], the concept of the Pareto region is presented, which provides the points beyond the Pareto front. The region is determined using a Fisher–Snedecor test over an augmented Lagrangian function. In this way, a Constrained Sliding Particle Swarm Optimizer (CSPSO) is applied to obtain the Pareto regions. Over these Pareto regions, a clustering strategy is applied to define sub-regions to prioritize one of the objectives and an intermediary region that allows one to establish a balance between objectives.

1.4. Article Approach and Document Organization

This article proposes a study based on clustering analysis using k-means and fuzzy c-means with the purpose of identifying the characteristics to incorporate the clustering process in a multi-objective optimization algorithm that allows us to improve the solutions in the Pareto front. In particular, it is considered how the clustering process can be incorporated to improve the Multi-Objective Vortex Particle Swarm Optimization (MOVPSO) algorithm described in [27,28]. Mainly, clustering can be used to determine the vortex used to carry out the dispersion of the particles in the MOVPSO algorithm.

The originality is focused on observing the characteristics that clustering has to improve in the multi-objective optimization algorithms, mainly observing the clusters formed for continuous and discontinuous Pareto optimal fronts, and the processing time.

The article is organized as follows. In the first part, Section 2, the concepts associated with multi-objective optimization are reviewed, particularly describing the concept associated with the Pareto optimal front, and then the clustering techniques of k-means and fuzzy c-means are reviewed in Section 3 and Section 4; later, the Pareto fronts and associated multi-objective functions are described in Section 5. With the data of the Pareto fronts, the clustering process and analysis are carried out considering different cases in Section 6. Finally, in Section 7 and Section 8, the discussion and conclusions of the work are established.

2. Multi-Objective Optimization

Multi-objective optimization is relevant in engineering when there must be a balance in various objective functions associated with the design processes. Considering the literature [1] the Multi-Objective Optimization Problem (MOP) corresponds to the following task: Find a vector of decision variables that satisfies some constraints and optimizes a vector function whose elements represent the objective functions.

The formulation of the multi-objective optimization problem implies determining a vector of variables ${\overrightarrow{x}}^{*}={[x_1^{*},x_2^{*},...,x_n^{*}]}^T$ that optimizes the vector objective function given by Equation (1), and satisfies the m inequality constraints given in Equation (2) and the p equality constraints in Equation (3).

$$\overrightarrow{f}\left(\overrightarrow{x}\right)={[{\overrightarrow{f}}_1\left(\overrightarrow{x}\right),{\overrightarrow{f}}_2\left(\overrightarrow{x}\right),...,{\overrightarrow{f}}_k\left(\overrightarrow{x}\right)]}^T$$

(1)

$$g_i\left(\overrightarrow{x}\right)\le 0\mathrm{for}i=1,2,...,m$$

(2)

$$h_i\left(\overrightarrow{x}\right)\le 0\mathrm{for}i=1,2,...,p$$

(3)

A vector ${\overrightarrow{x}}^{*}\in \Omega$ corresponds to a feasible solution, and the set of constraints given by Equations (2) and (3) defines the feasible region $\Omega$. As shown in Figure 2, the vector of functions $\overrightarrow{f}\left(\overrightarrow{x}\right)$ maps the set $\Omega$ to the set $\Lambda$ that contains the possible values of the objective functions [1].

Pareto Optimality

The multi-objective optimization seeks to determine the best value in the objective functions; nevertheless, an increase in the performance of a function is not possible without a decrease in the rest of the objective functions.

According to [1], Pareto dominance establishes that if one solution dominates over another, this function needs to be necessarily better in at least one objective and never show worse/lower performance than the others. In Figure 3, it is observed that solution $P_1$ dominates solution $P_2$ since it is better in both $f_1$ and $f_2$; however, it does not dominate $P_3$ or $P_4$ [38].

A Pareto optimum means having a vector with independent variables ${\overrightarrow{x}}^{*}\in \Omega$ and another $\overrightarrow{x}\in \Omega$ in such a way that $f_i\left({\overrightarrow{x}}^{*}\right)\le f_i\left(\overrightarrow{x}\right)$ for all $i=1,...,k$ and $f_j\left({\overrightarrow{x}}^{*}\right)<f_j\left(\overrightarrow{x}\right)$ for at least one j; thus, the set of vectors ${\overrightarrow{x}}^{*}$ linked to the solutions for the Pareto optimal are non-dominating; moreover, the set of $f_i\left({\overrightarrow{x}}^{*}\right)$ corresponds to the Pareto front [1].

In many cases, it is difficult to obtain an analytical expression for the Pareto front; then, a set of feasible points in $\Omega$ to calculate the values of $\overrightarrow{f}\left({\overrightarrow{x}}^{*}\right)$ for all ${\overrightarrow{x}}^{*}\in \Omega$ is considered as the standard procedure in the generation of the Pareto front. In this way, the non-dominated points in the Pareto front are achievable by having a sufficient number of points in $\Lambda$ [1].

3. K-Means Clustering Algorithm

The k-means clustering algorithm is a method to carry out separations in data observations into K exclusive groups to establish vector indices to show the K cluster associated with each observation [31,32].

The k-means clustering algorithm takes each observation in the data as a point in a Euclidean space. A partition is determined considering that the objects within each group are close to each other, and far away from objects in other groups. Depending on the data type to group, clustering employs various measures to minimize the sum of the distances. In the partition, each cluster consists of the points and the center (centroid) [31,32].

Implementing the clustering includes the use of an iterative algorithm to reduce the sum of distances from each object to its own centroid group, regarding all groups until no further sums are possible to obtain the set of clusters [31,32].

Considering a set of observations $(x_1,x_2,...,x_n)$, where each observation corresponds to a vector of d dimensions, the algorithm makes a partition of the observations into K sets $C_i=\{C_1,C_2,...,C_K\}$, where $(K\le n)$. The steps of the k-means algorithm are as follows.

• Establish a group of K centroids in the represented space.
• Calculate the distance of each object with each of the centroids of K and assign it to the centroid for which its distance is the smallest.
• When all objects are assigned, recalculate the position of the centroids.
• Terminate the algorithm if the stop criterion is met; otherwise, return to step 2.

Equation (4) shows a usual similarity measure based on the squared error, where x is one of the elements and $r_i$ the midpoint of the cluster $C_i$.

$$J_E=\sum _{i=1}^K\sum _{x\in C_i}{\parallel x-r_i\parallel }^2$$

(4)

The first part of the algorithm includes using a statistical measure such as the mean or median to determine the initial value of the centroids. During the second step, any distance metric can be used, where each object is compared to all centroids, assigning the centroid with the smallest distance. In the third instance, some heuristics are usually used to modify the centroids; the mean or median position of the objects is usually employed to calculate the position of the new centroids. Lastly, under some conditions, the algorithm stops in the fourth step due to the number of iterations, or in cases when no variation is present in the sum of the shortest distances; otherwise, the algorithm returns to step 2.

4. C-Means Clustering Algorithm

The fuzzy c-means algorithm is a data clustering technique where each data point belongs to a group to a certain extent specified by a membership degree. This technique offers a method to group larger sets of data in multidimensional space into a specific number of distinct groups [39,40].

Using the groups generated by the fuzzy c-means algorithm, a fuzzy inference system can be built by creating membership functions to represent the linguistic labels of each group, employing the concept fuzzy partition.

A fuzzy partition characterizes the separation of each sample in all groups using membership functions that take values between zero and one, where, for each sample, the sum of the membership is one. In this way, it is possible to translate the fuzzy clustering problem to meet an optimal fuzzy partition [29,30,40,41].

Given that $c>1$ a positive integer, and a subset $X=(x_1,...,x_n)$ of dimension d (in a Euclidean space), then a fuzzy partition of X in c groups is a list of c membership functions $\mu =({\mu }_1,\dots ,{\mu }_c)$ that accomplish Equations (5)–(7).

$$\sum _{i=1}^c{\mu }_i\left(x_j\right)=1,\forall j=1,\dots ,c$$

(5)

$$0\le {\mu }_i\left(x\right)\le 1,\forall i=1,\dots ,c$$

(6)

$$0<\sum _{j=1}^n{\mu }_i\left(x_j\right)<1,\forall i=1,\dots ,c$$

(7)

In this way, the fuzzy partitions are represented as ${\mu }_{ik}$, where i corresponds to the cluster and k the data. Fuzzy c-means algorithms employ a clustering criterion given by an objective function that depends on the fuzzy partition. The procedure consists of iteratively minimizing this function until obtaining an optimal fuzzy partition [29,30,40,41].

Different clustering criteria can be used to determine the optimal fuzzy partition for X; the most widely used is associated with the least squares error function given in Equation (8).

$$J_m=\sum _{k=1}^n\sum _{i=1}^c{\left({\mu }_{ik}\right)}^m{\parallel x_k-r_i\parallel }_A^2$$

(8)

The value $\parallel x_k-r_i{\parallel }_A^2$ corresponds to the square distance between the elements of X and the centers of the groups, given by Equation (9), where $(x_1,x_2,\dots ,x_n)$ are the data, $r_i=(r_{i1},r_{i2},\dots ,r_{ic})$ is the center vector of the group i, and finally ${\parallel ·\parallel }_A$ is the norm induced by A that is a $n\times n$ positive definite weight matrix; when A is the identity matrix, the square of the Euclidean distance is obtained.

$$\parallel x_k-v_i{\parallel }_A^2={(x_k-r_i)}^{T}A(x_k-r_i)$$

(9)

Considering the k-th data in the i-th cluster, the factor ${\left({\mu }_{ik}\right)}^m$ corresponds to the m-th power of the respective membership value, where $m>1$ controls the fuzzy overlap corresponding to the amount of data having significant membership in different clusters [29,30,40,41]. The general procedure of the fuzzy c-means algorithm is as follows.

• Set c, m, A, ${\parallel ·\parallel }_A$ and determine an initial matrix of fuzzy partitions.
• Calculate the centers of the groups.
• Update the fuzzy partition matrix.
• Finish if stop criterion is met; otherwise, return to step 2.

The first part of the process is to set the parameters of the algorithm. The second part includes an approximation toward the center of the clusters to mark the average location of each group. Then, the fuzzy c-means algorithm for each group and datum assigns an associating degree of membership. Updating for each data point the cluster centers and membership degrees, the algorithm iteratively adjusts the cluster centers. This process is performed until a stop criterion is met [29,30,40].

5. Test Functions Employed

Ideally, the test functions chosen to evaluate an MOEA should contain characteristics similar to the real-world problem to be solved [1]. The specialized literature proposes to employ artificial functions to describe different levels of difficulty to test multi-objective evolutionary algorithms [1].

Among different multi-objective test functions, the functions used were chosen considering the number of segments that compose the optimal Pareto front. In this way, different cases that arise when executing multi-objective optimization algorithms are considered, especially those functions that allow the observation of features to enhance the exploration of the optimization algorithms via the clustering process. Figure 4 displays the Pareto fronts for the test functions considered, which are described below.

$F_1$: Binh1

• Number of variables: $n=2$.
• Limits of the variables: $[-5,10]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& x_1^2+x_2^2\hfill \\ \hfill f_2& =& {(x_1-5)}^2+{(x_2-5)}^2\hfill \end{array}$$

$F_2$: Fonseca1

• Number of variables: $n=2$.
• Limits of the variables: $[-1,1]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& 1-exp\left(-{(x_1-1)}^2-{(x_2+1)}^2\right)\hfill \\ \hfill f_2& =& 1-exp\left(-{(x_1+1)}^2-{(x_2-1)}^2\right)\hfill \end{array}$$

$F_3$: Fonseca2

• Number of variables: $n=3$.
• Limits of the variables: $[-4,4]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& 1-exp\left(-\sum _{i=1}^n{\left(x_i-\frac{1}{\sqrt{n}}\right)}^2\right)\hfill \\ \hfill f_2& =& 1-exp\left(-\sum _{i=1}^n{\left(x_i+\frac{1}{\sqrt{n}}\right)}^2\right)\hfill \end{array}$$

$F_4$: Schaffer1

• Number of variables: $n=1$.
• Limits of the variables: $[0,2]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& x^2\hfill \\ \hfill f_2& =& {(x-2)}^2\hfill \end{array}$$

$F_5$: Schaffer2

• Number of variables: $n=1$.
• Limits of the variables: $[-5,10]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& \left\{\begin{array}{cc}-x,\hfill & \mathrm{if}x\le 1,\hfill \\ -2+x,\hfill & \mathrm{if}1<x\le 3,\hfill \\ 4-x,\hfill & \mathrm{if}3<x\le 4,\hfill \\ -4+x,\hfill & \mathrm{if}x>4,\hfill \end{array}\right.\hfill \\ \hfill f_2& =& {(x-5)}^2\hfill \end{array}$$

$F_6$: Deb2

• Number of variables: $n=2$.
• Limits of the variables: $[0,1]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& x_1\hfill \\ \hfill f_2& =& g·h\hfill \end{array}$$

$$\begin{array}{ccc}\hfill g& =& 1+10x_2\hfill \\ \hfill h& =& 1-{\left(\frac{f_1}{g}\right)}^2-\frac{f_1}{g}sin\left(12\pi f_1\right)\hfill \end{array}$$

$F_7$: Kursawe

• Number of variables: $n=3$.
• Limits of the variables: $[-5,5]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& \sum _{i=1}^{n-1}\left(-10exp\left(-0.2\sqrt{x_i^2+x_{i+1}^2}\right)\right)\hfill \\ \hfill f_2& =& \sum _{i=1}^{n-1}\left(|x_i{|}^{0.8}+5sin\left(x_i^3\right)\right)\hfill \end{array}$$

$F_8$: Poloni

• Number of variables: $n=2$.
• Limits of the variables: $[-3,3]$.
• Objective functions:

  $$\begin{array}{ccc}\hfill f_1& =& -[1+{(A_1-B_1)}^2+{(A_2-B_2)}^2]\hfill \\ \hfill f_2& =& -[{(x_1+3)}^2+{(x_2+1)}^2]\hfill \end{array}$$

  $$\begin{array}{ccc}\hfill A_1& =& 0.5sin\left(1\right)-2cos\left(1\right)+sin\left(2\right)-1.5cos\left(2\right)\hfill \\ \hfill A_2& =& 1.5sin\left(1\right)-cos\left(1\right)+2sin\left(2\right)-0.5cos\left(2\right)\hfill \\ \hfill B_1& =& 0.5sin\left(x_1\right)-2cos\left(x_1\right)+sin\left(x_2\right)-1.5cos\left(x_2\right)\hfill \\ \hfill B_2& =& 1.5sin\left(x_1\right)-cos\left(x_1\right)+2sin\left(x_2\right)-0.5cos\left(x_2\right)\hfill \end{array}$$

Function selection is made to have different characteristics of the Pareto optimal fronts. Functions $F_1$, $F_2$, $F_3$, and $F_4$ are characterized by presenting continuous POFs; it is expected that clustering algorithms perform an equal division of these POFs. Meanwhile, functions $F_5$, $F_6$, $F_7$, and $F_8$ have non-continuous POFs, for which it is expected the formation of groups for each segment of the POF. As seen, there are 2, 3, and 6 segments.

With these test functions, the purpose is to observe if the clustering process allows the establishment of mechanisms to improve the exploration process of multi-objective optimization algorithms. Regarding some strategies, swarms can be formed considering the identified clusters, or the center of the cluster can be used to carry out a dispersion process that allows the determination of additional and more suitable solutions of the Pareto optimal front.

In Figure 4, $F_1$, $F_2$, $F_3$, and $F_4$ show continuous POFs; that is, they are not divided into segments, for which it is expected that the clustering algorithms perform a uniform segmentation of POFs. Moreover, in this figure, it seems that $F_5$, $F_6$, $F_7$, and $F_8$ present discontinuous POFs, where there are different segments that do not have the same amount of data, for which it is expected that the algorithms will be able to make the groups for each segment.

The number of data used for each Pareto front shown in Figure 4 is presented in

Table 1. Amount of data used for each Pareto optimal front.

Function	Amount of Data	Function	Amount of Data
$F_1$	670	$F_5$	200
$F_2$	200	$F_6$	660
$F_3$	435	$F_7$	875
$F_4$	200	$F_8$	1100

, where the largest amount of data is for $F_8$ with 1100 points and the smallest for $F_2$, $F_4$ and $F_5$ with 200 points.

It should be noted that, in this work, no multi-objective optimization algorithm is employed to determine the Pareto front, for which Pareto front data reported in the literature as in [42] are used.

6. Clustering Analysis

This section presents the results obtained first for the k-means algorithm and then for fuzzy c-means. It is noticeable that the clusters obtained their centers and the separation seeking to cover the data associated with the Pareto optimal front. Also presented is the processing time used in the clustering process for each optimal Pareto front.

Regarding implementation, the experiments were carried out with PC Intel i5-3230M 2.60 GHz and RAM of 6.00 GB using software MATLAB 2017a for the implementation of k-means [43,44] and fuzzy c-means [45,46].

The results using k-means can be seen in Figure 5; the groups obtained for each Pareto front are shown taking $K=2,3,4,5,6$ clusters. In the experiments, the maximum clusters taken are 6 since it is the maximum number of segments in the POFs (case of $F_6$).

Additionally, in

Table 2. Performance index using k-means (best values in blue).

	$\mathit{K}=2$	$\mathit{K}=3$	$\mathit{K}=4$	$\mathit{K}=5$	$\mathit{K}=6$
$F_1$	8391.7500	5594.5500	4196.1000	3357.9000	2798.5500
$F_2$	56.9314	34.9253	25.6418	20.2137	16.6845
$F_3$	112.4049	71.5409	52.4383	41.3160	34.2348
$F_4$	198.0000	132.0400	99.0800	79.2400	66.0800
$F_5$	251.2500	151.0000	117.6820	101.1522	75.2619
$F_6$	207.9879	135.8786	100.9513	73.6020	67.0604
$F_7$	1374.4139	1038.9623	843.0882	654.9459	516.1611
$F_8$	3381.1151	1938.7807	1436.3547	1241.3337	877.1011

, one can see the sum of the total distances obtained ($L_1$ distance) given in Equation (10), where $x_j$ is the j-th data point (observation) and $c_j$ is the j-th centroid (a row vector). Each centroid corresponds to the median of the points in the respective cluster [44,47].

$$J_E=\sum _{j=1}^p\parallel x_j-c_j\parallel$$

(10)

In order to show the results graphically, an array is made in Figure 5, where the rows correspond to the POFs (from $F_1$ to $F_8$), and the columns show the number of clusters used (from $K=2$ to $K=6$). In this group of figures, the clusters are depicted using different colors and the center of each cluster with the symbol ◇. It is noteworthy that the first four rows correspond to continuous POFs while the last four rows to discontinuous POFs.

According to Figure 5, for the continuous POFs, an adequate clustering distribution of the POF is observed, which can be used to improve the exploitation by improving each segment separately using a multi-objective optimization algorithm. On the other hand, for discontinuous POFs, it is sought that the number of segments be equal to the number of clusters. In the case of two segments, there is a correct segmentation of the POF; for three segments, it is not achieved correctly, and for six, it is achieved in most segments; however, there are three segments that share a few data in the clusters.

Based on Table 2 for all cases, by increasing the number of clusters, an improvement in the objective function is obtained; however, for the case when the POFs are discontinuous, the best value is not obtained when the number of clusters coincides with the number of segments. This feature must be considered when including the clustering process in the optimization algorithm, since a procedure must be established to determine the appropriate number of clusters.

An interesting comparison can be made among test functions considering the performance index; nevertheless, the POFs do not have the same range values and the amount of data; for example, the POF for $F_2$ and $F_3$ has the same range values; however, the amount of data is different.

Observing

Table 3. Processing time in seconds using k-means (best values in blue).

	$\mathit{K}=2$	$\mathit{K}=3$	$\mathit{K}=4$	$\mathit{K}=5$	$\mathit{K}=6$
$F_1$	0.2348700	0.0432130	0.0389430	0.0199730	0.0519910
$F_2$	0.0055761	0.0047870	0.0063644	0.0054241	0.0056799
$F_3$	0.0047795	0.0063817	0.0071171	0.0117810	0.0080207
$F_4$	0.0040129	0.0060577	0.0056353	0.0056906	0.0068515
$F_5$	0.0039584	0.0050692	0.0051604	0.0042107	0.0053566
$F_6$	0.0040619	0.0047554	0.0052575	0.0054063	0.0054762
$F_7$	0.0044325	0.0075443	0.0072893	0.0086594	0.0124490
$F_8$	0.0034583	0.0048920	0.0051983	0.0052315	0.0087573

, the processing time tends to increase when increasing the number of clusters. However, there are a few cases where the processing time decreases. Considering the functions with continuous POF, for $F_1$, the shortest time is with $K=5$, for $F_2$ with $K=3$, for $F_3$ and $F_4$ with $K=2$; meanwhile, taking the functions with continuous POFs, $F_5$, $F_6$, $F_7$, and $F_8$, the shortest time is obtained with $K=2$. It should also be noted that although the POF of $F_8$ is the one with the most data, the processing time is not the longest found in the experiments carried out.

In addition, considering functions $F_2$ and $F_3$ with continuous POFs in the range $[0,1]$, where $F_2$ has 200 points and $F_3$ 435 points, in Table 3, it is observed that the shortest time is obtained for $F_3$ with $K=2$.

On the other hand, the results using fuzzy c-means are depicted in Figure 6; the groups for each Pareto front are obtained taking $C=2,3,4,5,6$ clusters. Furthermore, in

Table 4. Performance index using fuzzy c-means (best values in blue).

	$\mathit{C}=2$	$\mathit{C}=3$	$\mathit{C}=4$	$\mathit{C}=5$	$\mathit{C}=6$
$F_1$	72003.2367	30109.4874	16353.9897	10222.6895	6979.9672
$F_2$	13.3770	4.5067	2.4794	1.4929	1.0136
$F_3$	17.6615	6.7323	3.4962	2.1238	1.4304
$F_4$	134.3028	56.1533	30.4953	19.0607	13.0137
$F_5$	413.3438	101.7896	52.3381	38.2433	29.1930
$F_6$	42.6418	17.1626	9.4975	5.5728	2.8960
$F_7$	1875.8525	1027.1601	430.1388	272.0026	196.7863
$F_8$	12851.3018	2986.7051	2350.5175	1178.4914	577.2411

, one can see the performance index used by the fuzzy c-means algorithm to establish the clusters. The objective function used is given by Equation (11), where $x_i$ represents the i-th observation (data point), $c_j$ corresponds to the j-th cluster center, D is the total number of data points, and N is the amount of clusters; meanwhile, $m>1$ is the fuzzy partition exponent employed for controlling the degree of fuzzy overlap; finally, ${\mu }_{ij}$ corresponds to the membership value of $x_i$ in the respective j-th cluster [46,48].

$$J_m=\sum _{i=1}^D\sum _{j=1}^N{\left({\mu }_{ij}\right)}^m{\parallel x_i-c_j\parallel }^2$$

(11)

Figure 6 shows the clusters formed with the elements having the highest membership value associated with each cluster. In this figure, the results are organized in an array where functions $F_1$ to $F_8$ are found in the rows and number of clusters used from $C=2$ to $C=6$ in the columns. In these results, the symbol ◇ represents the center of each cluster depicted using different colors.

From Figure 6, for the continuous POFs, an adequate distribution of the POF is observed since it tends to generate equitable groups in the Pareto optimal front. On the other hand, for discontinuous POFs, it is sought to have the number of POF segments equal to the number of clusters. For the case of two segments, there is a correct segmentation of the POF; for six segments, it is not achieved correctly, and for three, it is achieved in most segments.

Based on Table 4, for all cases, by increasing the number of clusters, an improvement in the objective function is obtained; however, when the POFs are discontinuous, the best value is not obtained when the number of clusters coincides with the number of segments.

Considering

Table 5. Processing time in seconds using fuzzy c-means (best values in blue).

	$\mathit{C}=2$	$\mathit{C}=3$	$\mathit{C}=4$	$\mathit{C}=5$	$\mathit{C}=6$
$F_1$	0.0260160	0.0150030	0.0293120	0.0471320	0.062578
$F_2$	0.0018817	0.0021549	0.0088161	0.0052173	0.014639
$F_3$	0.0018079	0.0039356	0.0081450	0.0171960	0.021882
$F_4$	0.0016741	0.0034390	0.0087518	0.0090822	0.018726
$F_5$	0.0011365	0.0027533	0.0052488	0.0061023	0.013021
$F_6$	0.0041349	0.0079623	0.0190770	0.0531580	0.010667
$F_7$	0.0048490	0.0370210	0.0170500	0.0261660	0.044281
$F_8$	0.0039849	0.0096585	0.0126120	0.0378470	0.043933

, it is observed that the processing time increases when increasing the number of clusters; nonetheless, there are a few cases where the processing time decreases. Considering the functions with continuous POF for $F_1$, the shortest time is with $C=3$, and for $F_2$, $F_3$, and $F_4$ with $C=2$. Meanwhile, taking the functions with continuous POFs, $F_5$, $F_6$, $F_7$, and $F_8$, the shortest time is with $C=2$. It should also be noted that although the POF of $F_8$ is the one with the most data, the processing time is not the longest obtained in the experiments carried out. In addition, considering $F_2$, $F_4$, and $F_5$ that present 200 points in the POF, the shortest processing time is for $F_5$.

Regarding general observations of clustering analysis, as can be seen in Table 2 and Table 4, as the number of clusters increases, the performance index decreases for both k-means and fuzzy c-means. For continuous POF, it is sought that the clusters are well distributed along the POF, while, for discontinuous POFs, it is expected that the clusters will be generated for each segment of the POF.

For functions $F_1$, $F_2$, $F_3$, and $F_4$, the clustering algorithms perform a balanced segmentation of these POFs. Meanwhile, for discontinuous POFs using k-means and fuzzy c-means, a correct clustering for $F_5$ and $F_8$ is achieved; meanwhile, a suitable clustering for $F_6$ is obtained using k-means, and for $F_7$ using fuzzy c-means. Figure 5 and Figure 6 allow us to observe the cluster formation in a qualitative way.

Considering the above results, an important aspect when incorporating the clustering process into the multi-objective optimization algorithm is the mechanism to determine the appropriate number of clusters, which can be done iteratively; however, it also increases the computational time.

In addition, a combination of k-means and c-means allows an appropriate clustering of POFs; therefore, these clustering algorithms are suitable to use in the VMPSO algorithm. The clusters can be calculated after obtaining a certain number of solutions of the Pareto front. Then, with the clusters, the vortices of the VMPSO algorithm can be established to refine the solutions.

It should be noted that the performance index used for k-means is different from the one used with fuzzy c-means; therefore, a comparison of Table 2 (for k-means) and Table 4 (for fuzzy c-means) is not possible directly. Considering the above, the performance index $J_E$ is calculated using the results of fuzzy c-means, obtaining

Table 6. Performance index $J_E$ using clusters obtained via fuzzy c-means (best values in blue).

	$\mathit{C}=2$	$\mathit{C}=3$	$\mathit{C}=4$	$\mathit{C}=5$	$\mathit{C}=6$
$F_1$	8485.8217	5678.6370	4252.2398	3399.8150	2830.6087
$F_2$	57.7005	35.7828	25.8042	20.4484	16.7659
$F_3$	112.8745	71.7645	52.5503	41.3734	34.2655
$F_4$	200.1859	133.9046	100.2882	80.2219	66.7837
$F_5$	252.6031	152.0242	125.6948	92.1816	91.7635
$F_6$	211.8209	145.6224	108.1482	78.8322	49.8207
$F_7$	1433.0815	1175.4328	767.0160	613.8347	534.0547
$F_8$	3416.8323	1961.6507	1590.9511	1082.4891	978.9860

, observing that, in most cases, a better value is obtained with k-means since $J_E$ is used as the performance index in k-means; however, a better value was obtained using fuzzy c-means for the cases of $F_7$ with $C=4$, and also for $F_5$, $F_7$, and $F_8$ with $C=5$, and finally for $F_6$ with $C=6$.

Table 7. Difference in processing time between k-means and fuzzy c-means.

	2 Clusters	3 Clusters	4 Clusters	5 Clusters	6 Clusters
$F_1$	0.2089	0.0282	0.0096	−0.0272	−0.0106
$F_2$	0.0037	0.0026	−0.0025	0.0002	−0.0090
$F_3$	0.0030	0.0024	−0.0010	−0.0054	−0.0139
$F_4$	0.0023	0.0026	−0.0031	−0.0034	−0.0119
$F_5$	0.0028	0.0023	−0.0001	−0.0019	−0.0077
$F_6$	−0.0001	−0.0032	−0.0138	−0.0478	−0.0052
$F_7$	−0.0004	−0.0295	−0.0098	−0.0175	−0.0318
$F_8$	−0.0005	−0.0048	−0.0074	−0.0326	−0.0352

displays the difference in processing time between k-means and fuzzy c-means. In these results, the higher difference is for k-means (case $F_1$ with 2 clusters); it is also observed that in 12 of the 40 implementations, the k-means algorithm required more time than fuzzy c-means; meanwhile, 28 implementations using fuzzy c-means required more time than k-means.

7. Discussion

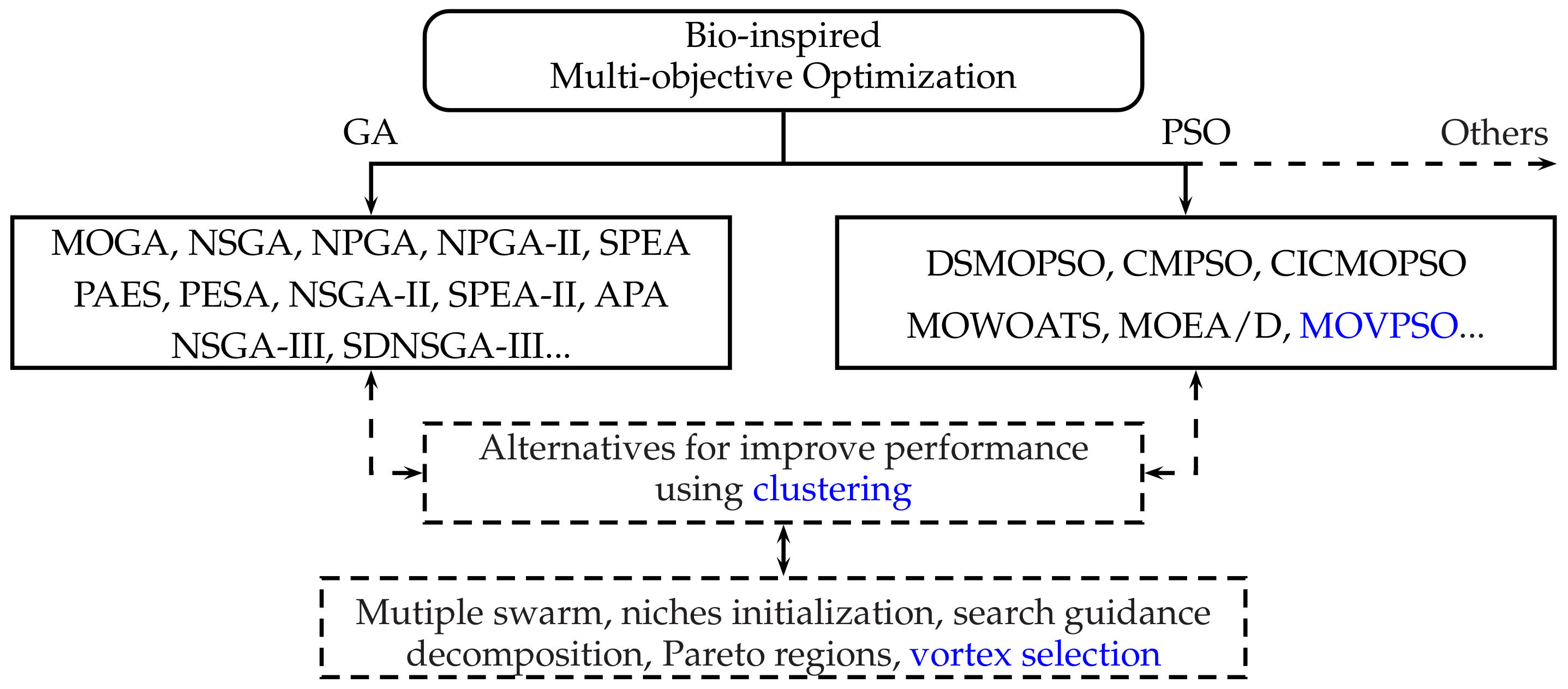
The present work is of an exploratory type to observe the characteristics that can be obtained with the clustering process to improve multi-objective optimization algorithms, particularly MOVPSO. A comparison with other proposals is expected to be made when the algorithm is implemented using clustering.

The originality is focused on establishing the characteristics that clustering has to improve in the multi-objective optimization algorithms, mainly observing the clusters for continuous and discontinuous Pareto optimal fronts. For continuous POFs, it is sought to have a suitable distribution of clusters, while for discontinuous POFs, it is necessary that the clusters coincide with the segments. As another important aspect, the processing time is also considered.

In this document, we present a clustering analysis that can be used to formulate alternatives to better explore the solutions of a Pareto front; however, it should be considered that this work presents the limitation of using the optimal points of the Pareto front. In the first place, it must be borne in mind that a multi-objective optimization algorithm constructs this front iteratively; therefore, it must be determined when to use the data obtained to establish the clusters. Second, from the perspective of the algorithm to improve the solutions, it must be locked with the decision variables, which is why it must be possible to establish the equivalent clusters in this domain.

For a multi-objective optimization algorithm that uses particle swarms, the found centers of each cluster can be used to create individual swarms. In particular, for the Multi-Objective Vortex Particle Swarm Optimization (MOVPSO) algorithm described in [27,28], where it is required to establish the vortex over which the particles will move, the center of each cluster can be used to determine the vortex point. In this way, it is sought to improve the solutions close to the established vortices. Figure 7 displays the flow chart for MOVPSO, including the clustering process; it is observed that clustering is used in an iterative way after the algorithm performs a convergence or a dispersion process. In this order, the clustering is used to determine the vortex point where the swarm congregates in the convergence phase and then carries out the dispersion process.

Additionally, the computational complexity that the clustering technique adds to the optimization algorithm must be considered; for example, if the clustering technique is used in each iteration, it may increase the computation time. For the MOVPSO algorithm, the clustering process can be used when determining a set of solutions; then, the calculation required for the clustering technique is not extensive. When the total computational complexity of both the clustering and optimization processes is included together, the validity of the approach becomes meaningful in the context of performance and computational time. It is expected to evaluate this aspect when the optimization algorithm and the clustering processes will be implemented.

Moreover, when including clustering techniques in the multi-objective optimization algorithms, the mechanism to obtain the number of suitable clusters must be considered, which can influence the performance and computational complexity of the algorithm.

8. Conclusions

The k-means and fuzzy c-means algorithms achieve an adequate segmentation of the continuous POFs. In the case of discontinuous POFs, these algorithms can be complementary to find the appropriate groups for each POF segment.

Regarding the processing time, it is observed that the k-means algorithm has a lower processing time than fuzzy c-means. Time is a critical factor when using clustering algorithms in each iteration of the optimization algorithms; however, clustering algorithms can be used after having defined several solutions of the Pareto front.

The clustering analysis of the solutions from the Pareto optimal front presented in this paper can be used for the formulation of strategies to improve the quality of the solutions found. In this way, it is important to establish a mechanism to determine the suitable number of clusters.

A possible strategy to carry out considering the cluster analysis consists of the formation of multiple populations that improve the solutions associated with each group found. For MOVPSO, the clustering can be used for determining the vortex used in this algorithm.

The main disadvantage of including a clustering analysis in a multi-objective optimization algorithm is the additional calculations associated with the clustering algorithm used. Therefore, a strategy must also be implemented to determine the appropriate time to perform a clustering analysis during the execution of the multi-objective algorithm.

Including the clustering process in the multi-objective optimization algorithm can improve its performance; however, it can also significantly increase the computation time, which becomes relevant when researching the appropriate strategy to incorporate the clustering process.

Once the implementation of the clustering process is carried out in the optimization algorithm, it is expected to perform the comparison of results with other algorithms in further works.