Next Article in Journal
Estimation Parameters of Dependence Meta-Analytic Model: New Techniques for the Hierarchical Bayesian Model
Next Article in Special Issue
Influence of the Chemical Pressure on the Magnetic Properties of the Mixed Anion Cuprates Cu2OX2 (X = Cl, Br, I)
Previous Article in Journal
In Silico Analysis of Peptide-Based Derivatives Containing Bifunctional Warheads Engaging Prime and Non-Prime Subsites to Covalent Binding SARS-CoV-2 Main Protease (Mpro)
Previous Article in Special Issue
Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Computation
Volume 10
Issue 5
10.3390/computation10050070
computation-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

LFDFT—A Practical Tool for Coordination Chemistry

by
Harry Ramanantoanina
Department Chemie, Johannes Gutenberg-Universität Mainz, Fritz-Strassmann Weg 2, 55128 Mainz, Germany
Computation 2022, 10(5), 70; https://doi.org/10.3390/computation10050070
Submission received: 31 March 2022 / Revised: 28 April 2022 / Accepted: 28 April 2022 / Published: 2 May 2022
(This article belongs to the Special Issue Commemorative Issue in Honor of Professor Karlheinz Schwarz on the Occasion of his 80th Birthday)
Browse Figures
Review Reports Versions Notes

Abstract

:
The electronic structure of coordination compounds with lanthanide ions is studied by means of density functional theory (DFT) calculations. This work deals with the electronic structure and properties of open-shell systems based on the calculation of multiplet structure and ligand-field interaction, within the framework of the Ligand–Field Density-Functional Theory (LFDFT) method. Using effective Hamiltonian in conjunction with the DFT, we are able to reasonably calculate the low-lying excited states of the molecular [Eu(NO 3 ) 3 (phenanthroline) 2 ] complex, subjected to the Eu 3 + configuration 4f 6 . The results are compared with available experimental data, revealing relative uncertainties of less than 5% for many energy levels. We also demonstrate the ability of the LFDFT method to simulate absorption spectrum, considering cerocene as an example. Ce M 4 , 5 X-ray absorption spectra are simulated for the complexes [Ce( η 8 − C 8 H 8 ) 2 ] and [Ce( η 8 − C 8 H 8 ) 2 ][Li(tetrahydrofurane) 4 ], which are approximated by the Ce oxidation states 4 + and 3 + , respectively. The results showed a very good agreement with the experimental data for the Ce 3 + compound, unlike for the Ce 4 + one, where charge transfer electronic structure is still missing in the theoretical model. Therefore this presentation reports the benefits of having a theoretical method that is primarily dedicated to coordination chemistry, but it also outlines limitations and places the ongoing developmental efforts in the broader context of treating complex molecular systems.

1. Introduction

Coordination compounds play an important role in modern chemistry, as they are involved in many fields of research: for example in catalysis [1,2], optics [3,4], magnetism [5,6,7], etc. The electronic structures of coordination compounds of metal ions (including transition metals, lanthanide, and actinide elements) exhibit open-shell species and near-degeneracy correlation [8,9,10]. Low-lying excited states are often very challenging to identify from the experiments, and to calculate from theoretical modeling. In particular, the latter is not possible unless a proper treatment of the multi-electronic system is taken into consideration [11,12,13]. Post Hartree–Fock methods, including many-body treatment of electron correlation effects, have been extensively developed to deal with coordination compounds. For instance, complete active space self-consistent field (CASSCF) and related methodologies [14,15,16] are currently enjoying wide popularity in the community of computational chemists. However, because the configuration interaction expansion increases exponentially with the number of active orbitals, the calculations of large systems becoming difficult.
Kohn–Sham Density Functional Theory (DFT), on the other hand, is generally applied to ground state electronic structure [17,18,19]. Its scope includes calculation of large size molecules as well as condensed matter [20]. In DFT, excited states are often approached via linear response theory as it is implemented in the time-dependent DFT (TDDFT) formalism [21,22,23]. The disadvantage of TDDFT, however, is that it lacks computational protocols for addressing highly correlated electrons, and multiplet structures, which interactions are very relevant in coordination chemistry [24,25]. Therefore, new developments in DFT encompass a methodology to incorporate many-body corrections and configuration interaction models [11,13,26], in order to solve open-shell electronic structures and strongly correlated materials.
We developed LFDFT, Ligand–Field Density Functional Theory [27,28,29,30], to bring a methodological concept for calculating multiplet structures and properties of coordination compounds with metal ions across the periodic table of elements. In this work, we demonstrate how LFDFT can be applied to solve electronic structure problems and to provide rapid estimation of spectroscopic properties at low computational cost. We use selective applications that consist in: (1) calculating the ground and low-lying excited states of the molecular [Eu(NO 3 ) 3 (phenanthroline) 2 ] complex in order to understand the luminescence properties of the Eu 3 + 4f 6 ⟶ 4f 6 transitions; and (2) calculating the core-electron excitation in cerocene in order to simulate the X-ray absorption spectral profiles of the Ce M 4 , 5 -edge that corresponds to the 4f n ⟶ 3d 9 4f n + 1 transitions, with n = 0, and 1.

2. Theory

2.1. General

The concept of ligand-field and its theoretical foundation have been extensively described and can be found elsewhere [31,32,33,34]. Hereafter, we are giving a more practical view of the LFDFT methodology with recent calculation possibilities and technical development. LFDFT is now available in the Amsterdam Density Functional (ADF) code that is part of the Amsterdam Modeling Suite (AMS2021 onwards) [35,36]. In LFDFT, near-degeneracy correlation is explicitly treated using ad hoc full-configuration interaction algorithm within an active subspace of the Kohn–Sham molecular orbitals [27,28,29,30]. Kohn–Sham molecular orbitals are occupied with fractional electrons to build a statistically averaged electron density that is isomorphic with the basis of a model Hamiltonian for a configuration system with open-shell d or f electrons. The model Hamiltonian is defined so that the most relevant quantum–chemical interactions are taken into consideration. These include inter-electron repulsion, relativistic spin-orbit coupling and ligand-field potential. LFDFT uses a parameterization scheme, but it does not rely upon empiricism [30]. In practice, the parameters (Slater–Condon integrals, spin-orbit coupling constants and ligand-field potential) are derived from the DFT calculation [30], therefore LFDFT has a good predictive power.

2.2. Computational Details

The main results reported in this presentation have been carried out by means of the AMS2021 code [35,36]. To perform geometries and vibrational analysis, we used DFT functional based on the generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) [37]. To calculate the electronic structure, we used DFT functional based on the GGA PBE [37], as well as hybrid functional following the B3LYP, [38], PBE0 [39,40] and KMLYP parameterization [41]. Molecular orbitals were expanded by means of the Slater-type Orbital (STO) functions for all elements at the triple-zeta plus polarization extra functions (TZ2P) level [42]. Relativistic corrections were added by using the Zeroth-Order Regular Approximation (ZORA) of the Dirac-equation method [43,44,45]. All electronic structures were done at the scalar ZORA relativistic level of theory, and spin-orbit coupling interaction was included by using the spin-orbit ZORA method. The self-consistent field (SCF) was set up to take into account all electrons.

2.3. Methodology

First of all, the definition of the structural inputs is described as follows. We have defined three structures for this presentation: [Eu(NO 3 ) 3 (phenanthroline) 2 ] as well as cerocene [Ce( η 8 − C 8 H 8 ) 2 ] and [Ce( η 8 − C 8 H 8 ) 2 ][Li(tetrahydrofurane) 4 ]. For simplicity, we will denominate the two cerocene molecules by the following: [Ce(COT) 2 ] and [Ce(COT) 2 ] − , respectively. We have built the molecular complexes with the help of the graphical user-interface “AMSINPUT” of the AMS2021 program [35,36], where prototypes for possible coordination compounds were available. Then we relaxed the molecular structures with DFT by using the GGA PBE functional [37]: the total energies were minimized and the symmetry was restricted to the point groups that represented the experimental structures (i.e., C 2 [46], D 8 h [47] and C 1 [47] for [Eu(NO 3 ) 3 (phenanthroline) 2 ], [Ce(COT) 2 ] and [Ce(COT) 2 ] − , respectively). We note that the [Ce(COT) 2 ] − unit had intrinsically high symmetry D 8 h , but the descent in symmetry to C 1 resulted from the presence of the counterion [Li(tetrahydrofurane) 4 ] + . The optimized structures were confirmed by vibrational analysis, and no imaginary frequencies have been computed. Schematic representations of the structures are given in Figure 1. For [Eu(NO 3 ) 3 (phenanthroline) 2 ], the average Eu-N and Eu-O optimized bond lengths were 2.588 Å, and 2.559 Å, respectively, close to the experimental data (2.566 Å, and 2.510 Å) [46,48]. For [Ce(COT) 2 ], the average Ce-C bond lengths was 2.703 Å, in agreement with the experimental data (2.675 Å) [47]. For [Ce(COT) 2 ] − , the average Ce-C bond lengths was 2.733 Å, also in agreement with the experimental data (2.741 Å) [47].
The procedural steps for computing the electronic structure are described as follows. Based on the geometrical data given by the previous step, we performed single-point DFT calculations. We used the keyword “IRREPOCCUPATIONS” in ADF [35,36] to set fractional electron occupations of the molecular orbitals. For [Eu(NO 3 ) 3 (phenanthroline) 2 ], seven molecular orbitals were occupied with fractional 6/7 electrons. These molecular orbitals were identified with large atomic 4f characters, and therefore constituted the active subspace of the ligand-field calculation. Figure 2 shows a section of the ADF output file [35,36] depicting this active subspace of the Kohn–Sham orbitals that were used to calculate the multiplet structures of Eu configuration 4f 6 . For the cerocene molecules, the calculations were done in two steps. First, we calculated the system with Ce 3 + configuration 4f 1 (and subsequently Ce 4 + 4f 0 ), which represented the ground state multiplet structure of the systems. Seven molecular orbitals with large atomic 4f parentage are populated with fractional electrons following similar procedure as above. Then, we calculated the systems with a core-hole, i.e., Ce 3 + configuration 3d 9 4f 2 (and subsequently Ce 4 + configuration 3d 9 4f 1 ), which represented the XAS electronic state. For that, three core-orbitals were occupied with fractional 9/5 electrons. These orbitals were identified with 100% atomic 3d characters. Additionally, as previously, seven orbitals that have larger atomic 4f characters were occupied with fractional electrons.
Finally, the ligand-field analyses are performed based on the single-point DFT calculation. We use the ADF keyword “LFDFT” [35,36] to set up the calculation of the multiplet energies. In the output of the LFDFT calculation, we obtained the parameters including the Slater–Condon integrals, the spin-orbit coupling constants and the matrix elements of the ligand-field potential without empirical corrections [30]. We also obtained the calculated multiplet energies and projection analysis of all the energy levels on to the atomic configuration. For the X-ray Absorption calculations, we use the keyword “LFDFT_TDM” to compute the matrix elements of the transition dipole moment that correspond to the 4f n ⟶ 3d 9 4f n + 1 , with n = 0, 1.

3. Results and Discussion

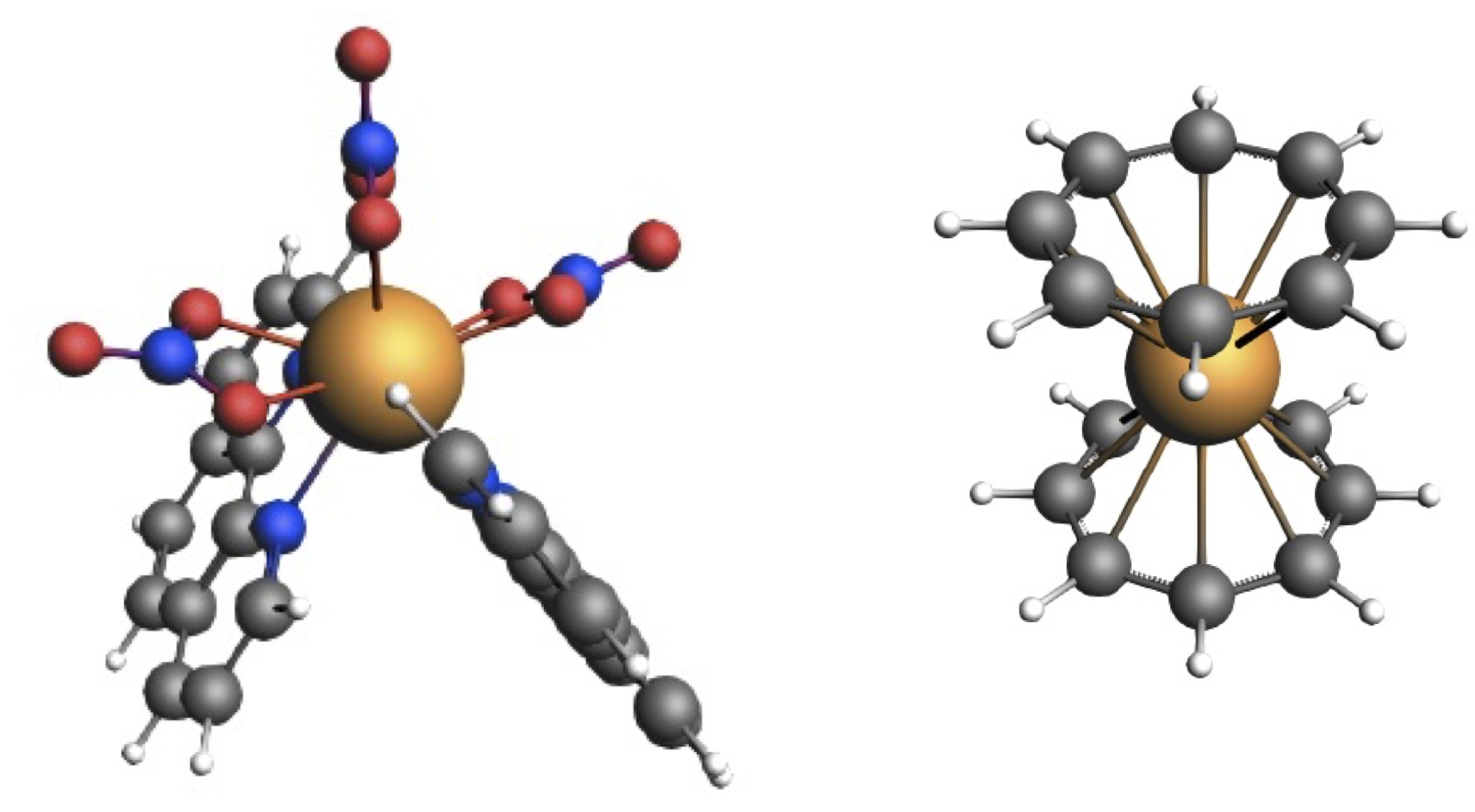
3.1. Low-Lying Excited States of [Eu(NO 3 ) 3 (phenanthroline) 2 ]

Eu 3 + compounds are often used in trichromatic phosphors for lighting purposes [49,50], where they are known for red-color emission. The red emission results from the 4f 6 ⟶ 4f 6 transitions involving ground states 7 F J (with J designating spin-orbit components, i.e., 0, 1, 2, …, 6), and low-lying excited states 5 D 0 [51]. In order to understand the mechanism of the electron transition process, it is necessary to calculate these energy levels, and to assess the effect of the ligand-field interaction on to the atomic multiplets. The luminescence properties of [Eu(NO 3 ) 3 (phenanthroline) 2 ] have been experimentally reported [48,52], together with analysis of the electron transition process, including the energy values at the ligand-field level [52]. We therefore choose this system as testbed for the theoretical method.
Table 1 shows the tabulated energy levels of the Eu 3 + configuration 4f 6 in [Eu(NO 3 ) 3 (phenanthroline) 2 ], which are obtained from the LFDFT calculations at different levels of DFT function. Results are shown for the calculated vertical excitation energies from the ground state (zero of energy) for 28 low-lying excited states that arise from the 7 F and 5 D atomic spectral terms We note that there is no influence of geometrical changes in the energy levels since the four sets of theoretical calculations in Table 1 come from the same atomic configuration of [Eu(NO 3 ) 3 (phenanthroline) 2 ] (see the Methodology section). The energy levels are also compared with the experiments [52], which correspond to photophysical measurement at low temperature. The calculated energies agree within a few hundreds of cm − 1 with the experimental data [52] (see Table 1), although larger discrepancies are more likely observed for certain levels. To assess the accuracy of theoretical results, we also list in Table 1 the calculated percent error for each level with respect to the reference energies. The percent error is calculated as 100 * (theoretical values − reference values)/reference values: a positive value indicating overestimation of the energy levels, and a negative value indicating underestimation. In terms of absolute value, the percent errors decrease from the GGA results to the hybrid ones, which can be attributed to the self-interaction error in DFT. Self-interaction error can, in part, be corrected by the inclusion of Hartree–Fock exchange as it is in the formulation of the DFT hybrid functional [53,54,55]. More particularly, the higher the percentage of the Hartree–Fock exchange, the more accurate are the predicted energy levels, as per the default values of the Hartree–Fock exchange in B3LYP [38] PBE0 [39,40], and KMLYP [41] equal 20.0%, 25.0% and 55.7%, respectively. We could not modulate the hybrid functional to include larger percentage of Hartree–Fock exchange, since we observe that although this helps improve higher-energy excited states, this also makes the prediction of the lower-energy ones poorer (see Table 1).
At this point, it is worth stressing the following: (1) the energy levels are reasonably predicted by the LFDFT calculations, the uncertainties vis-à-vis the experiments are relatively small independent of the choice of the DFT functional. (2) We primarily observe overestimation of the energy levels (many numbers in the percent error columns of Table 1 have positive sign) that can be attributed to the self-consistent error in DFT. (3) The inconsistency with experiments may be removed by using hybrid functional that reduces largely the percent error for many levels. (4) The inconsistency with experiments can also be removed by different starting geometries of the molecular complex, by using, for instance, the experimental structure from X-ray diffraction or other techniques as input.
Table 2 lists the values for the energy parameters obtained for Eu 3 + ion configuration 4f 6 in [Eu(NO 3 ) 3 (phenanthroline) 2 ]. These parameters refer to the three Slater–Condon F k (4f,4f) integrals, with k = 2, 4 and 6, the spin-orbit coupling constant ζ (4f) [30], and the ligand-field potential in the form of the Wybourne-normalized crystal-field parameters [56,57]. For comparison, the reference data in Table 2 are drawn from earlier reports of the average free ion parameters [51] and theoretical CASSCF/NEVPT2 computation of the free ion [58]. In Table 2, the parameters values that are reported in the experimental work [52] are also listed for comparison. We note that changes in the parameters values from free ions to molecular complexes are expected, in terms of a reduction of the values as results of covalence and the nephelauxetic effect [59,60,61]. Therefore the comparison of the values in Table 2 is qualitative. For the spin-orbit coupling constant, the agreement with reference values is almost perfect. For the Slater–Condon integrals, on the other hand, our F 2 (4f,4f) parameters are overestimated, whereas F 4 (4f,4f) and F 6 (4f,4f) are underestimated (see Table 2). In Table 2, the Wybourne parameters [56,57] are only part of the multipole expansion of the ligand-field potential, but allow us to compare the theoretical values with the only two values reported in the experiments. Overall the ligand-field potential varies strongly upon the choice of the DFT functional. However, we also see that the LFDFT calculation with hybrid functional yields relatively adequate values.

3.2. X-ray Absorption Spectra of Cerocene

Core-electron excitation has been exploited for decades to understand the properties and chemistry of materials with various techniques: X-ray absorption, X-ray emission, X-ray magnetic circular dichroism, electron energy loss spectroscopy, resonant inelastic scattering, etc. [63,64]. X-ray Absorption Spectroscopy (XAS) has many advantages, most importantly, its element specificity and local electronic and atomic structures probing [63,64]. Lanthanide compounds are often studied at the M 4 , 5 -edge XAS [65], which correspond to the process in which incident photons are absorbed by promoting one electron from the core 3d orbitals to the valence 4f. In the absorption spectra, strong features appeared representing the 4f n ⟶ 3d 9 4f n + 1 transitions governed by the electric-dipole mechanism [30].
Cerocene has been extensively studied in terms of the molecular orbital diagram and ground state electronic structure [47,66,67,68]. The Ce 4f orbitals split in energy into four molecular orbitals within the approximate D 8 h symmetry. The molecular orbital with a 1 u representation (with predominant 4f z 3 ) has the lowest energy, followed by the two-fold degenerate e 3 u (4f x ( x 2 − 3 y 2 ) and 4f y ( 3 x 2 − y 2 ) ), e 1 u (4f z 2 x and 4f z 2 y ) and e 2 u (4f z ( x 2 − y 2 ) and 4f x y z ). Mulliken population analysis of the [Ce(COT) 2 ] shows that the a 1 u , e 3 u and e 1 u are principally metallic orbitals with 4f parentage coefficients greater than 95%. e 2 u has stronger interaction with the C 2p orbitals, with a reduced 4f parentage of 74% only. The Mulliken population analysis of [Ce(COT) 2 ] − shows similar behavior, except that all the molecular orbitals are now relatively localized with 4f parentage coefficients greater than 90%. The molecular orbital diagrams are very similar to other theoretical results [47,66,67,68], so that we use these orbitals as the active subspace of the LFDFT calculation.
Table 3 lists the theoretical values for the energy parameters obtained for Ce ions with configurations 3d 9 4f 1 and 3d 9 4f 2 in [Ce(COT) 2 ] and [Ce(COT) 2 ] − , respectively. These parameters refer to the the Slater–Condon integrals: F k (4f,4f), with k = 2, 4 and 6; F k (3d,4f), with k = 2, and 4; and G k (3d,4f), with k = 1, 3 and 5; the spin-orbit coupling constant ζ (3d), and ζ (4f); and the ligand-field potential in the form of Wybourne parameters [56,57]. For comparison, the reference data in Table 3 correspond to the free ion parameter values for La 3 + , which is iso-electronic to Ce 4 + , and Ce 3 + [65]. In case of the Slater–Condon integrals and spin-orbit coupling constants, the parameters are reduced vis-à-vis the reference free ion values, which shows the decrease of the electron density on the central metal ions via the nephelauxetic effect [59,60,61]. The ligand-field parameters also shows that GGA functional slight overestimates the metal–ligand interaction, as it is also obtained for the Eu 3 + complex (see above).
Figure 3 shows the calculated spectral profiles of [Ce(COT) 2 ] and [Ce(COT) 2 ] − obtained from the LFDFT calculations by using the PBE [37] and PBE0 DFT functional [39,40]. The calculated oscillator strengths of the electric-dipole 4f n ⟶ 3d 9 4f n + 1 transitions, with n = 0, and 1 are represented in bar diagrams. The colorful curves represent the broadening of all the oscillator strengths with a Lorentzian function with a constant half-width-at-half-maximum parameter of 0.25 eV to mimic the core-hole lifetime [30]. The calculated spectra of [Ce(COT) 2 ] are relatively simple, with two sharp peaks and fine structures, resulting from the large spin-orbit coupling of the 3d electrons (see Table 3. The spectra in (Figure 3a) and in (Figure 3c) exhibit similar profiles, except for the excitation energies, where the hybrid functional shifts the energy to higher values, which is already observed in earlier studies [26,30]. To validate the results, we use the experimental spectrum of [Ce(COT) 2 ] in ref. [68] The two sharp peaks are also present in the experiment [68], but additional features appeared also in the form of satellites indicating the mixing between pure metallic Ce 4 + 4f 0 and ligand-to-metal charge transfer (LMCT) C 2p⟶ Ce 4f electronic states. Besides, it has been demonstrated that the ground state of [Ce(COT) 2 ] is, in fact, multiconfigurational [69], limiting then the use of LFDFT in this context. Thus, the treatment of LMCT, which is not yet possible with LFDFT, will constitute the next step methodological development.
The calculated spectra of [Ce(COT) 2 ] − present more complex features. The two strong absorption bands are due to the large spin-orbit coupling of the 3d electrons, and the fine structures results from the multipet levels of the 3d 9 4f 2 configuration (see Figure 3b,d). The first absorption band is characterized by two peaks with small pre-edge shoulders, which is also observed in the experiment [68]. The second absorption band is characterized by three peaks with small post-edge shoulder, that can also be seen in the experimental data [68].

4. Conclusions

The present work is aimed at describing the Ligand-Field Density-Functional Theory (LFDFT) method with practical examples that are chosen from current coordination chemistry topics. Open-shell f electrons still constitute a great challenge for computational chemists owing to strong electron-correlation effects within valence orbitals. Density Functional Theory (DFT) is nowadays very powerful for dealing with molecular and solid-state systems, and the ligand-field concept brings a suitable approach to treat multi-electronic interaction. It is shown here that LFDFT can be used to reasonably perform accurate calculations of coordination compounds with lanthanide elements. The energy levels of Eu 3 + are calculated with reasonable uncertainties, showing also the influence of the choice of the DFT functional on the multiplet energies. The Ce M 4 , 5 -edge XAS spectra of Ce 3 + and Ce 4 + are simulated with good agreement with the experimental data.
With this paper, we also want to state future developments in the LFDFT code. These developments will include: (1) the simulation of the 4f ⟶ 4f absorption and emission spectra, which on top of the energy levels will bring more complete understanding of the luminescence process; (2) the consideration of charge transfer model to take into account ligand orbitals in the active space of the LFDFT calculation; and (3) the development of a ligand-field concept for coordination compounds with two or multiple metallic centers. That is, in the perspective of elaborating more complete and user-friendly theoretical models for complex electronic structure problems.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Acknowledgments

The author gratefully acknowledges high performance computing (HPC) support, time and infrastructure from the Johannes Gutenberg University of Mainz (Mogon), and the HPC-Europa3 program. The author also recognizes support from the Software for Chemistry and Materials (www.scm.com (accessed on 31 March 2022)), namely for providing the ADF developper license file. The author also wishes to thank Claude Daul (University of Fribourg in Switzerland) for his constant support and for useful discussion. Finally, the author wishes to thank the editor for the invitation to this Special Issue.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shibasaki, M.; Yoshikawa, N. Lanthanide Complexes in Multifunctional Asymmetric Catalysis. Chem. Rev. 2002, 102, 2187–2210. [Google Scholar] [CrossRef] [PubMed]
  2. Trummer, D.; Searles, K.; Algasov, A.; Guda, S.A.; Soldatov, A.V.; Ramanantoanina, H.; Safonova, O.V.; Guda, A.A.; Copéret, C. Deciphering the Phillips Catalyst by Orbital Analysis and Supervised Machine Learning from Cr Pre-edge XANES of Molecular Libraries. J. Am. Chem. Soc. 2021, 143, 7326–7341. [Google Scholar] [CrossRef] [PubMed]
  3. Bünzli, J.C.G. Benefiting from the Unique Properties of Lanthanide Ions. Accounts Chem. Res. 2006, 39, 53–61. [Google Scholar] [CrossRef] [PubMed]
  4. Poe, T.N.; Molinari, S.; Beltran-Leiva, M.J.; Celis-Barros, C.; Ramanantoanina, H.; Albrecht-Schönzart, T.E. Influence of Outer-Sphere Anions on the Photoluminescence from Samarium(II) Crown Complexes. Inorg. Chem. 2021, 60, 15196–15207. [Google Scholar] [CrossRef] [PubMed]
  5. Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
  6. Dreiser, J. Molecular lanthanide single-ion magnets: From bulk to submonolayers. J. Phys. Condens. Matter 2015, 27, 183203. [Google Scholar] [CrossRef]
  7. Ramanantoanina, H.; Studniarek, M.; Daffé, N.; Dreiser, J. Non-empirical calculation of X-ray magnetic circular dichroism in lanthanide compounds. Chem. Commun. 2019, 55, 2988–2991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Daul, C. Density functional theory applied to the excited states of coordination compounds. Int. J. Quantum Chem. 1994, 52, 867–877. [Google Scholar] [CrossRef]
  9. Chermette, H. Density functional theory: A powerful tool for theoretical studies in coordination chemistry. Coord. Chem. Rev. 1998, 178–180, 699–721. [Google Scholar] [CrossRef]
  10. Schwarz, K. DFT calculations of solids with LAPW and WIEN2k. J. Solid State Chem. 2003, 176, 319–328. [Google Scholar] [CrossRef]
  11. Grimme, S.; Waletzke, M. A combination of Kohn–Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 1999, 111, 5645–5655. [Google Scholar] [CrossRef]
  12. Szalay, P.G.; Müller, T.; Gidofalvi, G.; Lischka, H.; Shepard, R. Multiconfiguration Self-Consistent Field and Multireference Configuration Interaction Methods and Applications. Chem. Rev. 2012, 112, 108–181. [Google Scholar] [CrossRef] [PubMed]
  13. Ghosh, S.; Verma, P.; Cramer, C.J.; Gagliardi, L.; Truhlar, D.G. Combining Wave Function Methods with Density Functional Theory for Excited States. Chem. Rev. 2018, 118, 7249–7292. [Google Scholar] [CrossRef] [PubMed]
  14. Van den Heuvel, W.; Calvello, S.; Soncini, A. Configuration-averaged 4f orbitals in ab initio calculations of low-lying crystal field levels in lanthanide(iii) complexes. Phys. Chem. Chem. Phys. 2016, 18, 15807–15814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Pathak, S.; Lang, L.; Neese, F. A dynamic correlation dressed complete active space method: Theory, implementation, and preliminary applications. J. Chem. Phys. 2017, 147, 234109. [Google Scholar] [CrossRef]
  16. Singh, S.K.; Atanasov, M.; Neese, F. Challenges in Multireference Perturbation Theory for the Calculations of the g-Tensor of First-Row Transition-Metal Complexes. J. Chem. Theory Comput. 2018, 14, 4662–4677. [Google Scholar] [CrossRef]
  17. Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
  18. Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef]
  19. Verma, P.; Truhlar, D.G. Status and Challenges of Density Functional Theory. Trends Chem. 2020, 2, 302–318. [Google Scholar] [CrossRef]
  20. Schwarz, K.; Blaha, P. Solid state calculations using WIEN2k. Comput. Mater. Sci. 2003, 28, 259–273. [Google Scholar] [CrossRef]
  21. Casida, M.; Huix-Rotllant, M. Progress in Time-Dependent Density-Functional Theory. Annu. Rev. Phys. Chem. 2012, 63, 287–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Adamo, C.; Jacquemin, D. The calculations of excited-state properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [Google Scholar] [CrossRef] [PubMed]
  23. Hannachi, D.; Haroun, M.F.; Khireddine, A.; Chermette, H. Optical and nonlinear optical properties of Ln(Tp)2, where Ln = La,…,Lu and Tp = tris(pyrazolyl)borate: A DFT + TD-DFT study. New J. Chem. 2019, 43, 14377–14389. [Google Scholar] [CrossRef]
  24. Gutierrez, F.; Rabbe, C.; Poteau, R.; Daudey, J.P. Theoretical Study of Ln(III) Complexes with Polyaza-Aromatic Ligands: Geometries of [LnL(H2O)n]3+ Complexes and Successes and Failures of TD-DFT. J. Phys. Chem. A 2005, 109, 4325–4330. [Google Scholar] [CrossRef] [PubMed]
  25. Momeni, M.R.; Brown, A. Why Do TD-DFT Excitation Energies of BODIPY/Aza-BODIPY Families Largely Deviate from Experiment? Answers from Electron Correlated and Multireference Methods. J. Chem. Theory Comput. 2015, 11, 2619–2632. [Google Scholar] [CrossRef]
  26. Ramanantoanina, H.; Daul, C. A non-empirical calculation of 2p core-electron excitation in compounds with 3d transition metal ions using ligand-field and density functional theory (LFDFT). Phys. Chem. Chem. Phys. 2017, 19, 20919–20929. [Google Scholar] [CrossRef] [Green Version]
  27. Atanasov, M.; Daul, C.; Rauzy, C. New insights into the effects of covalency on the ligand field parameters: A DFT study. Chem. Phys. Lett. 2003, 367, 737–746. [Google Scholar] [CrossRef]
  28. Ramanantoanina, H.; Sahnoun, M.; Barbiero, A.; Ferbinteanu, M.; Cimpoesu, F. Development and applications of the LFDFT: The non-empirical account of ligand field and the simulation of the f–d transitions by density functional theory. Phys. Chem. Chem. Phys. 2015, 17, 18547–18557. [Google Scholar] [CrossRef] [Green Version]
  29. Vlahović, F.; Perić, M.; Gruden-Pavlović, M.; Zlatar, M. Assessment of TD-DFT and LF-DFT for study of d– d transitions in first row transition metal hexaaqua complexes. J. Chem. Phys. 2015, 142, 214111. [Google Scholar] [CrossRef] [Green Version]
  30. Ramanantoanina, H. A DFT-based theoretical model for the calculation of spectral profiles of lanthanide M4,5-edge X-ray absorption. J. Chem. Phys. 2018, 149, 054104. [Google Scholar] [CrossRef] [Green Version]
  31. Vanquickenborne, L.; Ceulemans, A. Ligand-field models and the photochemistry of coordination compounds. Coord. Chem. Rev. 1983, 48, 157–202. [Google Scholar] [CrossRef]
  32. Gerloch, M.; Harding, J.H.; Woolley, R.G. The context and application of ligand field theory. In Inorganic Chemistry; Springer: Berlin/Heidelberg, Germany, 1981; pp. 1–46. [Google Scholar]
  33. Woolley, R.G. Ligand-field analysis of transition-metal complexes. Int. Rev. Phys. Chem. 1987, 6, 93–141. [Google Scholar] [CrossRef]
  34. Hoffmann, R.; Alvarez, S.; Mealli, C.; Falceto, A.; Cahill, T.J.; Zeng, T.; Manca, G. From Widely Accepted Concepts in Coordination Chemistry to Inverted Ligand Fields. Chem. Rev. 2016, 116, 8173–8192. [Google Scholar] [CrossRef] [PubMed]
  35. Baerends, E.; Ziegler, T.; Atkins, A.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.; Bo, C.; Boerrigter, P.; et al. ADF 2021.1, SCM; Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2021. [Google Scholar]
  36. te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
  37. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  38. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  39. Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
  40. Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
  41. Kang, J.K.; Musgrave, C.B. Prediction of transition state barriers and enthalpies of reaction by a new hybrid density-functional approximation. J. Chem. Phys. 2001, 115, 11040–11051. [Google Scholar] [CrossRef]
  42. Lenthe, E.V.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
  43. Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
  44. van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
  45. van Lenthe, E.; Ehlers, A.; Baerends, E.J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef] [Green Version]
  46. Singh, U.P.; Goel, N.; Singh, G.; Srivastava, P. Syntheses, structural and thermal studies of Eu(III) and Gd(III) complexes with 2, 6-dinitrophenol and 1, 10-phenanthroline/2, 2′-bipyridine ligands. Inorganica Chim. Acta 2012, 387, 294–307. [Google Scholar] [CrossRef]
  47. Walter, M.D.; Booth, C.H.; Lukens, W.W.; Andersen, R.A. Cerocene Revisited: The Electronic Structure of and Interconversion Between Ce2(C8H8)3 and Ce(C8H8)2. Organometallics 2009, 28, 698–707. [Google Scholar] [CrossRef] [Green Version]
  48. Georgieva, I.; Trendafilova, N.; Zahariev, T.; Danchova, N.; Gutzov, S. Theoretical insight in highly luminescent properties of Eu(III) complex with phenanthroline. J. Lumin. 2018, 202, 192–205. [Google Scholar] [CrossRef]
  49. Bünzli, J.C.G.; Piguet, C. Taking advantage of luminescent lanthanide ions. Chem. Soc. Rev. 2005, 34, 1048. [Google Scholar] [CrossRef]
  50. Thejo Kalyani, N.; Dhoble, S. Organic light emitting diodes: Energy saving lighting technology—A review. Renew. Sustain. Energy Rev. 2012, 16, 2696–2723. [Google Scholar] [CrossRef]
  51. Binnemans, K. Interpretation of europium(III) spectra. Coord. Chem. Rev. 2015, 295, 1–45. [Google Scholar] [CrossRef] [Green Version]
  52. Pan, Z.; Jia, G.; Duan, C.K.; Wong, W.Y.; Wong, W.T.; Tanner, P.A. Crystal Structure, Spectroscopy and Crystal Field Analysis of Substituted 1, 10-Phenanthroline–Europium Complexes. Eur. J. Inorg. Chem. 2011, 2011, 637–646. [Google Scholar] [CrossRef]
  53. Zhang, Y.; Yang, W. A challenge for density functionals: Self-interaction error increases for systems with a noninteger number of electrons. J. Chem. Phys. 1998, 109, 2604–2608. [Google Scholar] [CrossRef]
  54. de Silva, P.; Corminboeuf, C. Local hybrid functionals with orbital-free mixing functions and balanced elimination of self-interaction error. J. Chem. Phys. 2015, 142, 074112. [Google Scholar] [CrossRef] [PubMed]
  55. Schwarz, K. Challenges for Theory and Computation. Computation 2017, 5, 49. [Google Scholar] [CrossRef] [Green Version]
  56. Hüfner. Optical Spectra of Transparent Rare Earth Compounds; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
  57. Newman, D.J.; Ng, B. (Eds.) Crystal Field Handbook; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
  58. Aravena, D.; Atanasov, M.; Neese, F. Periodic Trends in Lanthanide Compounds through the Eyes of Multireference ab Initio Theory. Inorg. Chem. 2016, 55, 4457–4469. [Google Scholar] [CrossRef]
  59. Tchougréeff, A.L.; Dronskowski, R. Nephelauxetic effect revisited. Int. J. Quantum Chem. 2009, 109, 2606–2621. [Google Scholar] [CrossRef]
  60. Tanner, P.A.; Yeung, Y.Y.; Ning, L. What Factors Affect the 5D0 Energy of Eu3+? An Investigation of Nephelauxetic Effects. J. Phys. Chem. A 2013, 117, 2771–2781. [Google Scholar] [CrossRef]
  61. Dorenbos, P. Lanthanide 4f-electron binding energies and the nephelauxetic effect in wide band gap compounds. J. Lumin. 2013, 136, 122–129. [Google Scholar] [CrossRef]
  62. Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Oakland, CA, USA, 1981. [Google Scholar]
  63. de Groot, F. Multiplet effects in X-ray spectroscopy. Coord. Chem. Rev. 2005, 249, 31–63. [Google Scholar] [CrossRef]
  64. de Groot, F.; Kotani, A. Core Level Spectroscopy of Solids; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
  65. Thole, B.T.; van der Laan, G.; Fuggle, J.C.; Sawatzky, G.A.; Karnatak, R.C.; Esteva, J.M. 3d X-ray-absorption lines and the 3d94fn+1 multiplets of the lanthanides. Phys. Rev. B 1985, 32, 5107–5118. [Google Scholar] [CrossRef]
  66. Edelstein, N.M.; Allen, P.G.; Bucher, J.J.; Shuh, D.K.; Sofield, C.D.; Kaltsoyannis, N.; Maunder, G.H.; Russo, M.R.; Sella, A. The Oxidation State of Ce in the Sandwich Molecule Cerocene. J. Am. Chem. Soc. 1996, 118, 13115–13116. [Google Scholar] [CrossRef] [Green Version]
  67. Mooßen, O.; Dolg, M. Two interpretations of the cerocene electronic ground state. Chem. Phys. Lett. 2014, 594, 47–50. [Google Scholar] [CrossRef]
  68. Smiles, D.E.; Batista, E.R.; Booth, C.H.; Clark, D.L.; Keith, J.M.; Kozimor, S.A.; Martin, R.L.; Minasian, S.G.; Shuh, D.K.; Stieber, S.C.E.; et al. The duality of electron localization and covalency in lanthanide and actinide metallocenes. Chem. Sci. 2020, 11, 2796–2809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Kerridge, A.; Coates, R.; Kaltsoyannis, N. Is Cerocene Really a Ce(III) Compound? All-Electron Spin–Orbit Coupled CASPT2 Calculations on M(η8-C8H8)2 (M = Th, Pa, Ce). J. Phys. Chem. A 2009, 113, 2896–2905. [Google Scholar] [CrossRef] [PubMed]
Computation 10 00070 g001 550
Figure 1. Ball-and-stick molecular model of the structures of [Eu(NO 3 ) 3 (phenanthroline) 2 ] (left-hand-side) and cerocene (right-hand-side). Color code: grey (carbon), red (oygen), white (hydrogen), blue (nitrogen), and Orange (Europium and Cerium).
Figure 1. Ball-and-stick molecular model of the structures of [Eu(NO 3 ) 3 (phenanthroline) 2 ] (left-hand-side) and cerocene (right-hand-side). Color code: grey (carbon), red (oygen), white (hydrogen), blue (nitrogen), and Orange (Europium and Cerium).
Computation 10 00070 g001
Computation 10 00070 g002 550
Figure 2. Selective section of the ADF output for the calculation of [Eu(NO 3 ) 3 (phenanthroline) 2 ] by using DFT with the hybrid PBE0 functional, showing the energy of the seven MOs in eV (in blue) that have larger atomic Eu 4f parentage together with the electron occupation number (in yellow) that are assigned with the MOs. The right-hand-side of the figure shows the percentage characters of the MOs based on Mulliken population analysis.
Figure 2. Selective section of the ADF output for the calculation of [Eu(NO 3 ) 3 (phenanthroline) 2 ] by using DFT with the hybrid PBE0 functional, showing the energy of the seven MOs in eV (in blue) that have larger atomic Eu 4f parentage together with the electron occupation number (in yellow) that are assigned with the MOs. The right-hand-side of the figure shows the percentage characters of the MOs based on Mulliken population analysis.
Computation 10 00070 g002
Computation 10 00070 g003 550
Figure 3. Calculated spectral profiles of the Ce M 4 , 5 -edge XAS of [Ce(COT) 2 ] (left) and [Ce(COT) 2 ] − (right), obtained from the LFDFT calculations using the PBE [37] (a,b) and PBE0 [39,40] (c,d) DFT functional. The light orange and green color bars represent the oscillator strengths of the electric-dipole 4f n ⟵ 3d 9 4f n + 1 , with n = 0, and 1. The Darker orange and green curves represent the broadening of the oscillator strengths with Lorentzian function with half-width at half maximum parameter of 0.25 eV.
Figure 3. Calculated spectral profiles of the Ce M 4 , 5 -edge XAS of [Ce(COT) 2 ] (left) and [Ce(COT) 2 ] − (right), obtained from the LFDFT calculations using the PBE [37] (a,b) and PBE0 [39,40] (c,d) DFT functional. The light orange and green color bars represent the oscillator strengths of the electric-dipole 4f n ⟵ 3d 9 4f n + 1 , with n = 0, and 1. The Darker orange and green curves represent the broadening of the oscillator strengths with Lorentzian function with half-width at half maximum parameter of 0.25 eV.
Computation 10 00070 g003
Table
Table 1. Selective energy values of the multiplet states of Eu 2 + configuration 4f 6 (in cm − 1 ) in the system [Eu(NO 3 ) 3 (phenanthroline) 2 ] obtained from LFDFT using the PBE (1) [37], B3LYP (2) [38], PBE0 (3) [39,40] and KMLYP (4) [41] functional, together with the calculated Percent Error (in%) with respect to the experimental data (Exp.)
Table 1. Selective energy values of the multiplet states of Eu 2 + configuration 4f 6 (in cm − 1 ) in the system [Eu(NO 3 ) 3 (phenanthroline) 2 ] obtained from LFDFT using the PBE (1) [37], B3LYP (2) [38], PBE0 (3) [39,40] and KMLYP (4) [41] functional, together with the calculated Percent Error (in%) with respect to the experimental data (Exp.)
LevelsLFDFTExp. a Percent Error
StateI(1)(2)(3)(4) (1)(2)(3)(4)
7 F 0 A00000----
7 F 1 A214261273349295−27.46−11.53−7.4618.31
B3933963923683677.087.906.810.27
B70052349838944457.6617.7912.16−12.39
7 F 2 B946971974986947−0.112.532.854.12
B102097598010229813.98−0.61-0.104.18
A104711171108102310163.059.949.060.69
A1288113411091027108019.265.002.69−4.91
A1323113511121039111119.082.160.09−6.48
7 F 3 B1882188418741839 ----
A1909189418821852 ----
B195219191905185918087.966.145.372.82
A201119261910186518468.944.333.471.03
B202719321913187018579.154.043.020.70
B203219321921187318937.342.061.48−1.06
A2137198519621874 ----
7 F 4 B22442742276427712587−13.265.996.847.11
A24732812281827802603−4.998.038.266.80
A269828342834279926332.477.637.636.30
B279028902876280126485.369.148.615.78
A286628972885281227354.795.925.482.82
A294529132888283828722.541.430.56−1.18
A307229152898284329464.28−1.05−1.63−3.50
B317929832945285029677.150.54−0.74−3.94
B324529872950288630865.15−3.21−4.41−6.48
5 D 0 A16,08116,51716,53516,87417,241−6.73−4.20−4.09−2.13
5 D 1 A17,70518,12818,14318,48518,945−6.55−4.31−4.23−2.43
B17,71618,16418,17618,488 ----
B17,80618,19918,20618,493 ----
a taken from ref. [52].
Table
Table 2. Calculated parameters of the ligand-field Hamiltonian: Slater–Condon integrals, spin-orbit coupling constant and the ligand-field potential in terms of the Wybourne-normalized crystal-field parameters (in eV) obtained from LFDFT using the PBE (1) [37], B3LYP (2) [38], PBE0 (3) [39,40] and KMLYP (4) [41] functional, compared with reference data taken from the literature: experimental parameters (a), average free-ion parameter (a) and other theoretical model (c).
Table 2. Calculated parameters of the ligand-field Hamiltonian: Slater–Condon integrals, spin-orbit coupling constant and the ligand-field potential in terms of the Wybourne-normalized crystal-field parameters (in eV) obtained from LFDFT using the PBE (1) [37], B3LYP (2) [38], PBE0 (3) [39,40] and KMLYP (4) [41] functional, compared with reference data taken from the literature: experimental parameters (a), average free-ion parameter (a) and other theoretical model (c).
LFDFTReference
(1)(2)(3)(4)(a) a (b) b (c) c
F 2 (4f,4f)11.424411.721611.733411.94648.716410.264810.7841
F 4 (4f,4f)7.12007.30527.31267.4444 7.36527.4879
F 6 (4f,4f)5.10855.24135.24665.3410 5.28755.6741
ζ (4f)0.16040.16100.16070.1600 0.16520.1731
B 2 2 (4f,4f)−0.0519−0.0245−0.01880.0172−0.0196
B 0 2 (4f,4f)−0.2515−0.1332−0.1147−0.0217−0.0471
a taken from ref. [52]; b taken from ref. [51]; c these values are derived from the Racah parameters in ref. [58] using conversion factor in ref. [62].
Table
Table 3. Calculated parameters of the ligand-field Hamiltonian for the [Ce(COT) 2 ] and [Ce(COT) 2 ] − systems: Slater–Condon integrals, spin-orbit coupling constant and the ligand-field potential in terms of the Wybourne-normalized crystal-field parameters (in eV) obtained from LFDFT using the PBE (1) [37], and PBE0 (2) [39,40] functional, compared with reference data taken from the litterature: average free-ion parameter for La 3 + (iso-electronic to Ce 4 + ) (a) and Ce 3 + (b).
Table 3. Calculated parameters of the ligand-field Hamiltonian for the [Ce(COT) 2 ] and [Ce(COT) 2 ] − systems: Slater–Condon integrals, spin-orbit coupling constant and the ligand-field potential in terms of the Wybourne-normalized crystal-field parameters (in eV) obtained from LFDFT using the PBE (1) [37], and PBE0 (2) [39,40] functional, compared with reference data taken from the litterature: average free-ion parameter for La 3 + (iso-electronic to Ce 4 + ) (a) and Ce 3 + (b).
LFDFTReference
[Ce(COT) 2 ][Ce(COT) 2 ] −
(1)(2)(1)(2)(a) a (b) b
F 2 (4f,4f)--9.02598.5968-10.01
F 4 (4f,4f)--5.61265.3400-6.35
F 6 (4f,4f)--4.02343.8265-4.57
G 1 (3d,4f)3.47833.29303.78903.60823.784.06
G 3 (3d,4f)2.05951.94952.24322.13592.212.37
G 5 (3d,4f)1.42871.35241.55601.48161.521.64
F 2 (3d,4f)5.44115.19625.95285.71405.655.99
F 4 (3d,4f)2.42192.30102.64212.52432.532.71
ζ (3d)7.53447.53317.53577.53436.807.45
ζ (4f)0.07810.07420.08520.08140.0860.106
B 0 2 (4f,4f)−0.0523−0.0460−0.0350−0.0058
B 0 4 (4f,4f)−3.00900.9311−1.5888−0.3282
B 0 6 (4f,4f)0.3738−0.91370.1651−0.2111
a taken from ref. [65]; b taken from ref. [65].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ramanantoanina, H. LFDFT—A Practical Tool for Coordination Chemistry. Computation 2022, 10, 70. https://doi.org/10.3390/computation10050070

AMA Style

Ramanantoanina H. LFDFT—A Practical Tool for Coordination Chemistry. Computation. 2022; 10(5):70. https://doi.org/10.3390/computation10050070

Chicago/Turabian Style

Ramanantoanina, Harry. 2022. "LFDFT—A Practical Tool for Coordination Chemistry" Computation 10, no. 5: 70. https://doi.org/10.3390/computation10050070

APA Style

Ramanantoanina, H. (2022). LFDFT—A Practical Tool for Coordination Chemistry. Computation, 10(5), 70. https://doi.org/10.3390/computation10050070

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop