Adaptive Control of Photovoltaic Systems Based on Dual Active Bridge Converters
Abstract
:1. Introduction
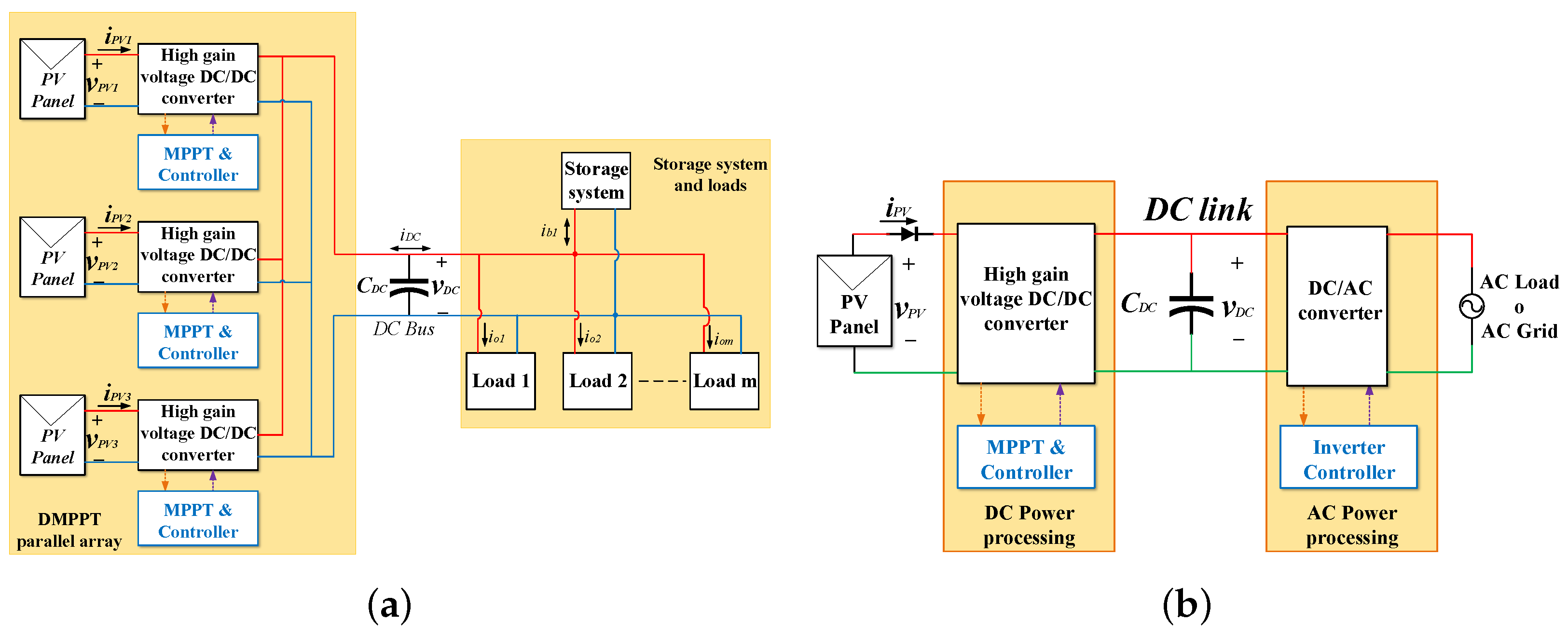
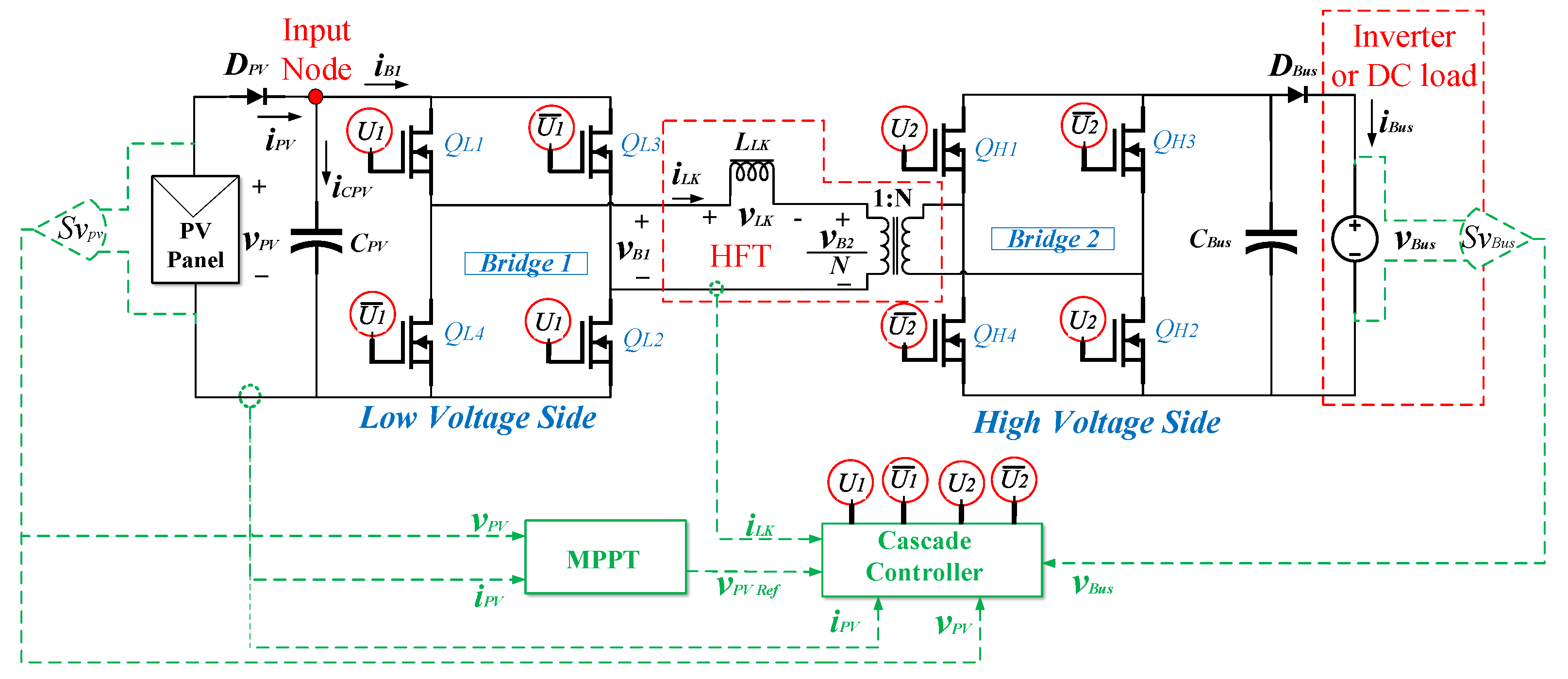
2. PV System Based on the DAB Converter
3. Model of the PV System
3.1. Analysis of Peak Current
3.2. Analysis of Relation between and
4. PV System Control Design
4.1. Design of the Current Controller
- The value does not exceed the positive and negative values defined by the hysteresis band.
- The average value of is equal to zero, thus avoiding core saturation in the HFT.
- The phase shift is lower than 0.5, thus ensuring an efficient operation of the DAB converter.
4.2. Design of an Adaptive PI Control of
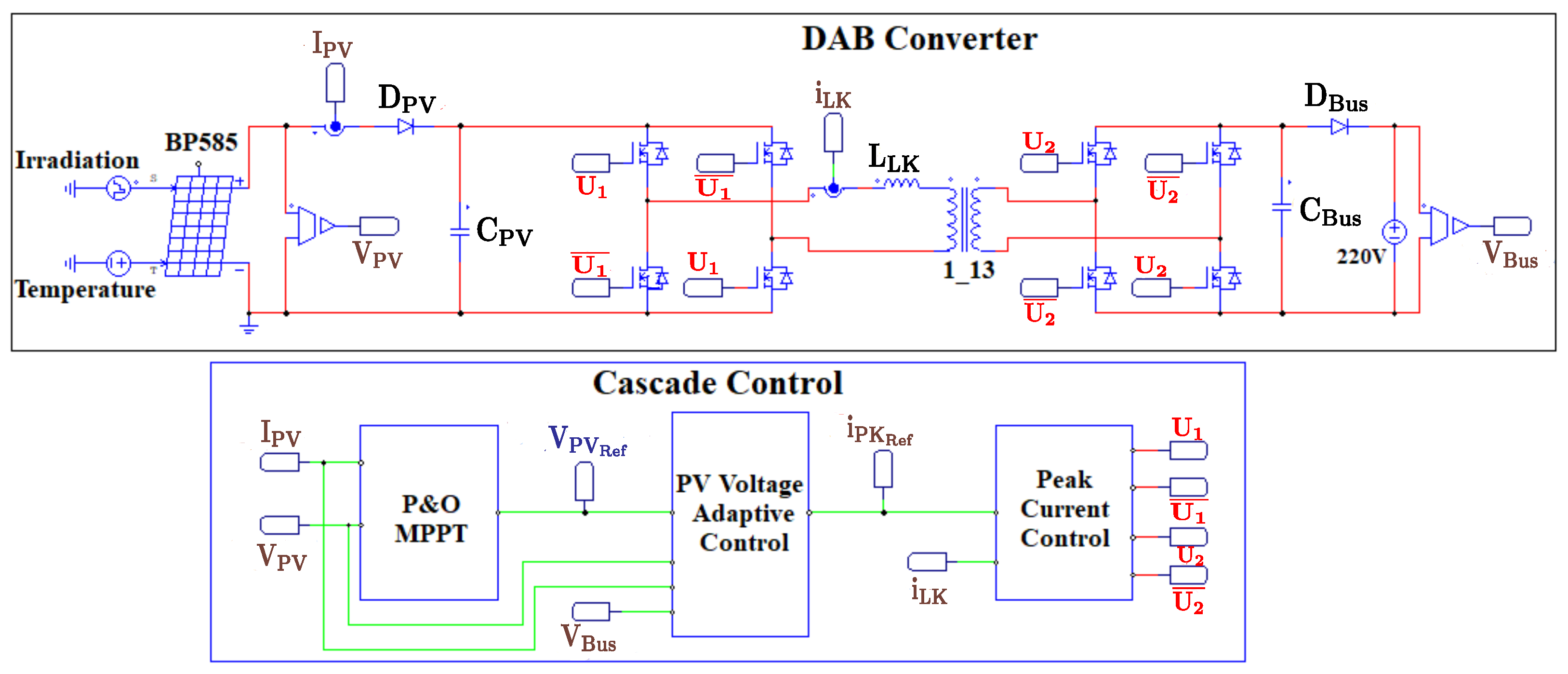
5. Circuital Implementation and Application Example
5.1. Implementation of the Peak Current Controller
5.2. Implementation of the Adaptive PV Voltage Controller
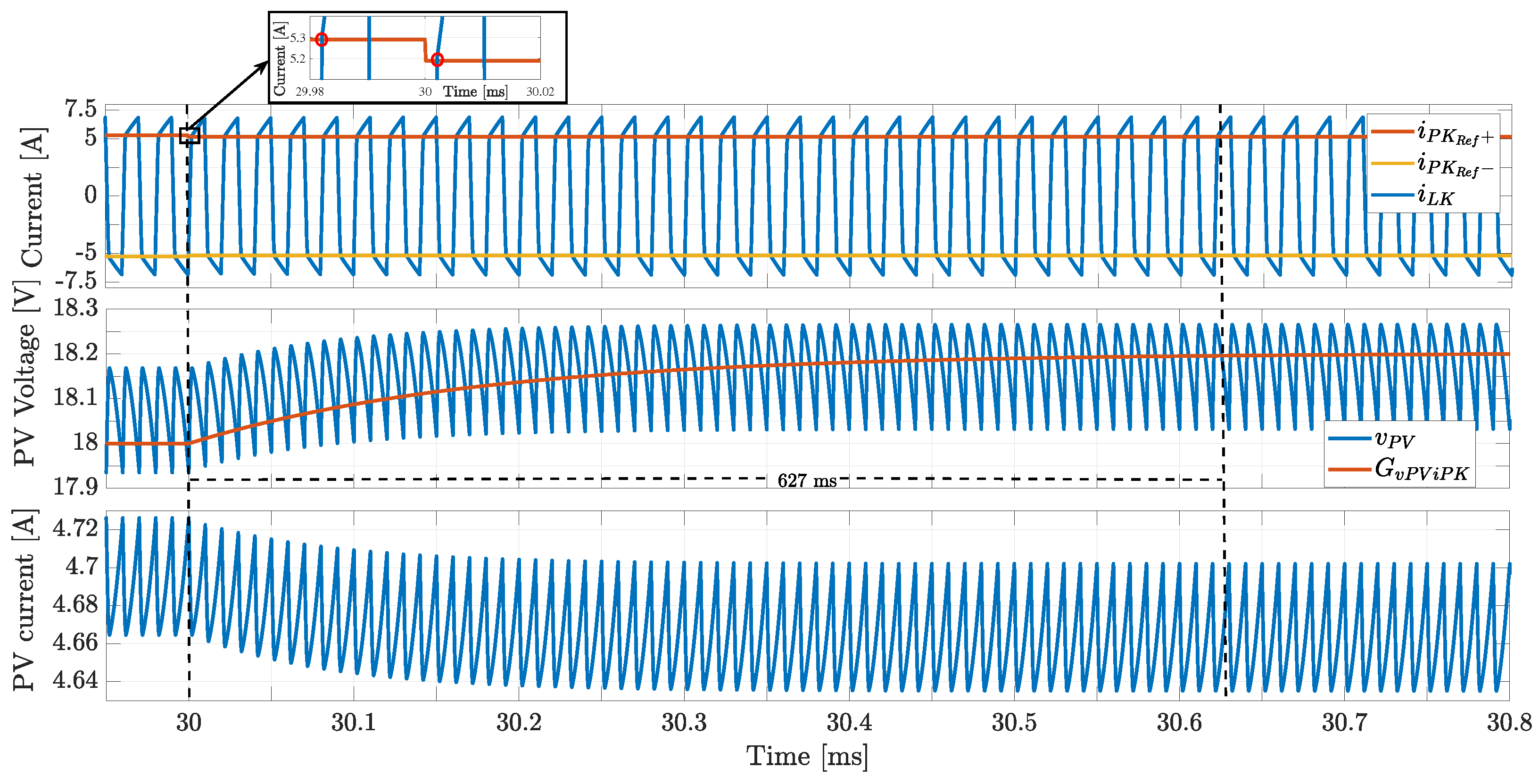
5.3. Performance of the Complete Control System
- Evaluate the settling time of the PV voltage to changes on the reference value ;
- Evaluate the robustness of the PV voltage controller to perturbations on the bus voltage ;
- Evaluate the performance of the PV voltage under the action of the MPPT () algorithm.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- REN21 Secretariat. Renewables 2021 Global Status Report; Technical report; REN21 Secretariat: Paris, France, 2021. [Google Scholar]
- IEA. World Energy Outlook 2021; Technical report; International Energy Agency: Paris, France, 2021. [Google Scholar]
- Wang, Y.; Wang, B.; Chu, C.C.; Pota, H.; Gadh, R. Energy management for a commercial building microgrid with stationary and mobile battery storage. Energy Build. 2016, 116, 141–150. [Google Scholar] [CrossRef] [Green Version]
- García, E.E.G.; Trujillo, C.L.R.; Cubides, H.E.R. Infraestructura De Comunicaciones En Microrredes Eléctricas. Redes Ing. 2015, 5, 28–38. [Google Scholar] [CrossRef]
- Messenger, R.A.; Ventre, J. Photovoltaic Systems Engineering, 2nd ed.; Taylor & Francis e-Library: Boca Raton, FL, USA, 2003; p. 480. [Google Scholar]
- Bastidas-Rodriguez, J.D.; Franco, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Maximum power point tracking architectures for photovoltaic systems in mismatching conditions: A review. IET Power Electron. 2014, 7, 1396–1413. [Google Scholar] [CrossRef]
- Olalla, C.; Deline, C.; Maksimovic, D. Performance of mismatched PV systems with submodule integrated converters. IEEE J. Photovoltaics 2014, 4, 396–404. [Google Scholar] [CrossRef]
- Ramli, M.Z.; Salam, Z. Performance evaluation of dc power optimizer (DCPO) for photovoltaic (PV) system during partial shading. Renew. Energy 2019, 139, 1336–1354. [Google Scholar] [CrossRef]
- Abdelkarim, R.H.M. Cascaded Voltage Step-up Canonical Elements for Power Processing in PV Applications. Ph.D. Thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2014. [Google Scholar]
- Abdelkarim, R.H.M.; El Aroudi, A.; Cid-Pastor, A.; Martinez-Salamero, L. Sliding Mode Control of output-parallel-connected two-stage boost converters for PV systems. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Tofoli, F.L.; Pereira, D.d.C.; de Paula, W.J.; Júnior, D.d.S.O. Survey on non-isolated high-voltage step-up dc–dc topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef] [Green Version]
- Shaneh, M.; Niroomand, M.; Adib, E. Ultrahigh-Step-Up Nonisolated Interleaved Boost Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2747–2758. [Google Scholar] [CrossRef]
- Abbaszadeh, M.A.; Monfared, M.; Heydari-doostabad, H. High Buck in Buck and High Boost in Boost Dual-Mode Inverter (Hb 2 DMI). IEEE Trans. Ind. Electron. 2021, 68, 4838–4847. [Google Scholar] [CrossRef]
- Saadat, P.; Abbaszadeh, K. A Single-Switch High Step-Up DC–DC Converter Based on Quadratic Boost. IEEE Trans. Ind. Electron. 2016, 63, 7733–7742. [Google Scholar] [CrossRef]
- Saadatizadeh, Z.; Babaei, E.; Blaabjerg, F.; Cecati, C. Three-Port High Step-Up and High Step-Down DC-DC Converter With Zero Input Current Ripple. IEEE Trans. Power Electron. 2021, 36, 1804–1813. [Google Scholar] [CrossRef]
- Navamani, J.D.; Vijayakumar, K.; Jegatheesan, R. Reliability and performance analysis of a high step-up DC–DC converter with a coupled inductor for standalone PV application. Int. J. Ambient Energy 2020, 41, 1327–1335. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Wu, H.; Xing, Y.; Batarseh, I. Overview of High-Step-Up Coupled-Inductor Boost Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 689–704. [Google Scholar] [CrossRef]
- Trujillo, C.; Santamaría, F.; Gaona, E. Modeling and testing of two-stage grid-connected photovoltaic micro-inverters. Renew. Energy 2016, 99, 533–542. [Google Scholar] [CrossRef]
- Özgür, Ç.; Teke, A.; Tan, A. Overview of micro-inverters as a challenging technology in photovoltaic applications. Renew. Sustain. Energy Rev. 2018, 82, 3191–3206. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Liu, G.; Zhao, Y. Universal High-Frequency-Link Characterization and Practical Fundamental-Optimal Strategy for Dual-Active-Bridge DC-DC Converter under PWM Plus Phase-Shift Control. IEEE Trans. Power Electron. 2015, 30, 6488–6494. [Google Scholar] [CrossRef]
- Rí os, S.J.; Pagano, D.J.; Lucas, K.E. Bidirectional Power Sharing for DC Microgrid Enabled by Dual Active Bridge DC-DC Converter. Energies 2021, 14, 404. [Google Scholar] [CrossRef]
- Everts, J. Design and Optimization of an Efficient and Compact (2 kW/dm3) Bidirectional Isolated Single-Phase Dual Active Bridge AC-DC Converter. Energies 2016, 9, 799. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Loo, K.H.; Lai, Y.M. Output-Impedance Shaping of Bidirectional DAB DC–DC Converter Using Double-Proportional-Integral Feedback for Near-Ripple-Free DC Bus Voltage Regulation in Renewable Energy Systems. IEEE Trans. Power Electron. 2016, 31, 2187–2199. [Google Scholar] [CrossRef]
- Sharma, R.; Sharma, S.K. Solar Photovoltaic Supply System Integrated with Solid State Transformer. In Proceedings of the 2021 IEEE 4th International Conference on Computing, Power and Communication Technologies (GUCON), Kuala Lumpur, Malaysia, 24–26 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Krishna, B.; Bheemraj, T.S.; Karthikeyan, V. Optimized Active Power Management in Solar PV-Fed Transformerless Grid-Connected System for Rural Electrified Microgrid. J. Circuits. Syst. Comput. 2021, 30, 2150039. [Google Scholar] [CrossRef]
- You, J.; Xia, J.; Jia, H. Analysis and control of DAB based DC-AC multiport converter with small DC link capacitor. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 823–828. [Google Scholar] [CrossRef]
- Kurm, S.; Agarwal, V. Dual Active Bridge Based Reduced Stage Multiport DC/AC Converter for PV-Battery Systems. IEEE Trans. Ind. Appl. 2022, 58, 2341–2351. [Google Scholar] [CrossRef]
- Shah, S.S.; Bhattacharya, S. Control of active component of current in dual active bridge converter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 323–330. [Google Scholar] [CrossRef]
- Jeung, Y.C.; Lee, D.C. Voltage and Current Regulations of Bidirectional Isolated Dual-Active-Bridge DC–DC Converters Based on a Double-Integral Sliding Mode Control. IEEE Trans. Power Electron. 2019, 34, 6937–6946. [Google Scholar] [CrossRef]
- Liu, B.; Zha, Y.; Zhang, T.; Chen, S. Fuzzy logic control of dual active bridge in solid state transformer applications. In Proceedings of the 2016 Tsinghua University-IET Electrical Engineering Academic Forum, Beijing, China, 13–15 May 2016; Institution of Engineering and Technology: Beijing, China, 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Herrera-Jaramillo, D.A.; González Montoya, D.; Henao-Bravo, E.E.; Ramos-Paja, C.A.; Saavedra-Montes, A.J. Systematic analysis of control techniques for the dual active bridge converter in photovoltaic applications. Int. J. Circuit Theory Appl. 2021, 49, 3031–3052. [Google Scholar] [CrossRef]
- Vazquez, N.; Liserre, M. Peak Current Control and Feed-Forward Compensation of a DAB Converter. IEEE Trans. Ind. Electron. 2020, 67, 8381–8391. [Google Scholar] [CrossRef]
- Arredondo, J.; Quispe, M.; Valencia, M. Particle Swarm Optimization MPPT algorithm in a Dual Active Bridge Series-Resonant DC-DC Converter for Partial Shading Conditions. In Proceedings of the 2021 IEEE 5th Colombian Conference on Automatic Control (CCAC), Ibague, Colombia, 19–22 October 2021; pp. 274–279. [Google Scholar] [CrossRef]
- Herrera-Jaramillo, D.A.; Henao-Bravo, E.E.; González Montoya, D.; Ramos-Paja, C.A.; Saavedra-Montes, A.J. Control-Oriented Model of Photovoltaic Systems Based on a Dual Active Bridge Converter. Sustainability 2021, 13, 7689. [Google Scholar] [CrossRef]
- Henao-Bravo, E.E.; Ramos-Paja, C.A.; Saavedra-Montes, A.J.; González-Montoya, D.; Sierra-Pérez, J. Design method of dual active bridge converters for photovoltaic systems with high voltage gain. Energies 2020, 13, 1711. [Google Scholar] [CrossRef] [Green Version]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Ogata, K. Modern Control Engineering; Instrumentation and Controls Series; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. A Technique for Improving P&O MPPT Performances of Double-Stage Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2009, 56, 4473–4482. [Google Scholar] [CrossRef]
- Powersim Inc. PSIM: Unbeatable Power Electronics Software; Powersim, Inc.: Rockville, MD, USA, 2021. [Google Scholar]
- BP Solar. BP585 Solar Modules; BP Solar: Madrid, Spain, 2003. [Google Scholar]
- Batzelis, E.I.; Anagnostou, G.; Chakraborty, C.; Pal, B.C. Computation of the lambert W function in photovoltaic modeling. In ELECTRIMACS 2019; Lecture Notes in Electrical Engineering; Springer: Salerno, Italy, 2020; Volume 615, pp. 583–595. [Google Scholar] [CrossRef]
- Abouchabana, N.; Haddadi, M.; Rabhi, A.; Grasso, A.D.; Tina, G.M. Power Efficiency Improvement of a Boost Converter Using a Coupled Inductor with a Fuzzy Logic Controller: Application to a Photovoltaic System. Appl. Sci. 2021, 11, 980. [Google Scholar] [CrossRef]
- Green, M.A.; Hishikawa, Y.; Dunlop, E.D.; Levi, D.H.; Hohl-Ebinger, J.; Ho-Baillie, A.W. Solar cell efficiency tables (version 52). Prog. Photovoltaics: Res. Appl. 2018, 26, 427–436. [Google Scholar] [CrossRef]
- Torabi, N.; Behjat, A.; Zhou, Y.; Docampo, P.; Stoddard, R.J.; Hillhouse, H.W.; Ameri, T. Progress and challenges in perovskite photovoltaics from single- to multi-junction cells. Mater. Today Energy 2019, 12, 70–94. [Google Scholar] [CrossRef]
















| Solution | Controlled Variables | Damping Factor | High Efficiency Operation | Stability Analysis | Zero DC Offset in | Reach the MPP | Rejection of DC Bus Disturbances |
|---|---|---|---|---|---|---|---|
| [34] | Not reported | Not guaranteed | Not reported | Not guaranteed | Yes | No | |
| [35] | or | Designed for 0.707 but not guaranteed | Guaranteed a duty cycle and shows values lower than 0.5 | Not reported | Not guaranteed | Yes | Yes, step disturbances |
| Proposed | and | Designed and guaranteed for 1 | Guaranteed duty cycle and values lower than 0.5 | If K is negative then and must be negative for global stability | Guaranteed with the peak current control | Yes | Yes, sinusoidal disturbances |
| Solar Panel Parameters at STC | ||
|---|---|---|
| Maximum power | 85 W | |
| Voltage at | 18 V | |
| Current at | 4.72 A | |
| Short-circuit current | 5 A | |
| Open-circuit voltage | 22.1 V | |
| DAB Converter parameters | ||
| Input capacitor | F | |
| Output capacitor | F | |
| Leakage inductor | H | |
| Transformer turns ratio | 1:N | 1:13 |
| Switching frequency | 50 kHz | |
| DC Bus parameters | ||
| DC Bus voltage | 220 V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henao-Bravo, E.E.; Ramos-Paja, C.A.; Saavedra-Montes, A.J. Adaptive Control of Photovoltaic Systems Based on Dual Active Bridge Converters. Computation 2022, 10, 89. https://doi.org/10.3390/computation10060089
Henao-Bravo EE, Ramos-Paja CA, Saavedra-Montes AJ. Adaptive Control of Photovoltaic Systems Based on Dual Active Bridge Converters. Computation. 2022; 10(6):89. https://doi.org/10.3390/computation10060089
Chicago/Turabian StyleHenao-Bravo, Elkin Edilberto, Carlos Andrés Ramos-Paja, and Andrés Julián Saavedra-Montes. 2022. "Adaptive Control of Photovoltaic Systems Based on Dual Active Bridge Converters" Computation 10, no. 6: 89. https://doi.org/10.3390/computation10060089
APA StyleHenao-Bravo, E. E., Ramos-Paja, C. A., & Saavedra-Montes, A. J. (2022). Adaptive Control of Photovoltaic Systems Based on Dual Active Bridge Converters. Computation, 10(6), 89. https://doi.org/10.3390/computation10060089






