Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs

Abstract

I present two novel thread-safe in-place streaming schemes for the lattice Boltzmann method (LBM) on graphics processing units (GPUs), termed Esoteric Pull and Esoteric Push, that result in the LBM only requiring one copy of the density distribution functions (DDFs) instead of two, greatly reducing memory demand. These build upon the idea of the existing Esoteric Twist scheme, to stream half of the DDFs at the end of one stream-collide kernel and the remaining half at the beginning of the next, and offer the same beneficial properties over the AA-Pattern scheme—reduced memory bandwidth due to implicit bounce-back boundaries and the possibility of swapping pointers between even and odd time steps. However, the streaming directions are chosen in a way that allows the algorithm to be implemented in about one tenth the amount of code, as two simple loops, and is compatible with all velocity sets and suitable for automatic code-generation. The performance of the new streaming schemes is slightly increased over Esoteric Twist due to better memory coalescence. Benchmarks across a large variety of GPUs and CPUs show that for most dedicated GPUs, performance differs only insignificantly from the One-Step Pull scheme; however, for integrated GPUs and CPUs, performance is significantly improved. The two proposed algorithms greatly facilitate modifying existing code to in-place streaming, even with extensions already in place, such as demonstrated here for the Free Surface LBM implementation FluidX3D. Their simplicity, together with their ideal performance characteristics, may enable more widespread adoption of in-place streaming across LBM GPU codes.

1. Introduction

The lattice Boltzmann method (LBM) [1] is a type of direct numerical simulation (DNS) to model fluid flow in a physically accurate manner. Its explicit algorithmic structure makes it ideal for parallelization on graphics processing units (GPUs) [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. The LBM works on a mesoscopic scale, representing quantities of fluid molecules by density distribution functions (DDFs) that are exchanged (streamed) between neighboring points on a Cartesian lattice. These DDFs are represented as floating-point numbers, and the streaming consists of copying them to the memory locations associated with neighboring lattice points. So, the LBM algorithm, at its core, copies floating-point numbers in memory with little arithmetic computation in between, meaning its performance is bound by memory bandwidth [3,4,5,6,7,8,9,10,13,14,15,16,17,18,19,20,21,22,33,34,35,36,37,38,39,40,41,42,43,44,45,46,59,60,61,62,63,64,65].

Since each lattice point holds the same number of DDFs and they need to be exchanged between one another at every time step, a strategy for avoiding data dependencies on parallel hardware is needed. The most straightforward and most common approach [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] is to have two copies, A and B, of the DDFs residing in memory; the algorithms reads from A and writes to B in even steps and in odd steps vice versa. With two copies of the DDFs, the memory access can even be configured to result in only partially misaligned reads and only coalesced writes (the One-Step-Pull scheme), enabling peak memory efficiency on modern GPUs [13,14,15,16,17,18,19,20,21,22,23]. This solves the data dependencies but comes at the cost of almost doubling memory demand. Unfortunately, memory capacity is the largest constraint on GPUs [58], limiting the maximum possible lattice resolution. To eliminate the higher memory demand and at the same time resolve data dependencies, a class of thread-safe in-place streaming algorithms have been developed. The first of these is termed the AA-Pattern [3], as it reads from A and at the same time writes to A in a special manner that does not violate data dependencies. The algorithm, however, is asymmetric for even and odd time steps, so it has not been widely adopted. A later variant of AA-Pattern is the Shift-and-Swap-Streaming method [4]. Geier and Schönherr recently found a more intricate solution, termed Esoteric Twist [2], that is symmetric for even and odd time steps and, moreover, has the advantage of slightly reduced memory bandwidth and thus higher performance compared to AA-Pattern; however, its implementation is very complicated, hindering widespread adoption. Few works have thus far considered in-place streaming on GPUs [2,3,4,5,6,7,8,9,10,11,12], and apart from the works introducing the methods [2,3,4,5,66], only a few have adopted in-place streaming in their code [6,7,8,11].

This work introduces two new thread-safe in-place streaming schemes, termed Esoteric Pull and Esoteric Push, that are suitable for GPU implementation. They build upon the same idea as Esoteric Twist and offer ideal performance characteristics while at the same time significantly simplifying implementation and allowing for automatic code generation. The very simple and modular implementation is especially well suited to modifying existing LBM implementations, even if various extensions, such as Free Surface LBM, are already in place.

2. Naive Implementation—One-Step Pull and One-Step Push

The most common LBM implementation uses two copies of the DDFs in memory to resolve data dependencies in a parallel environment [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. There are two variants, namely One-Step Pull (Figure 1, Listing A1) and One-Step Push (Figure 2, Listing A2). The pull variant is generally preferred on GPUs because the penalty for non-coalesced reads is smaller than that for non-coalesced writes [13,14,15,16,17,18,19,20,21,22,23]. The coloring introduced in Figure 1 and Figure 2 illustrates how loading/storing patterns compare to the regular DDF sequence during collision in registers, in other words, where exactly each DDF is loaded and stored in memory. This makes the more recently introduced, more sophisticated streaming patterns more comprehensible. In the One-Step-Pull scheme, DDFs are pulled in from neighbors (copy A of the DDFs), collided, and stored at the center node (copy B of the DDFs). In the One-Step-Push scheme, DDFs are loaded from the center node (copy A of the DDFs), collided, and then pushed out to neighbors (copy B of the DDFs). For both schemes, after every time step, the pointers to A and B are swapped.

3. State-of-the-Art Methods for In-Place Streaming on GPUs

The data dependency problem with in-place streaming on parallel hardware has already been solved by two major approaches, termed AA-Pattern and Esoteric Twist. Both provide the great advantage of significantly reducing memory demand for the LBM; however, both also pose various difficulties in GPU implementation, hindering widespread adoption.

3.1. AA-Pattern

When performing the LBM streaming step on parallel hardware, the issue arises that neighboring lattice points may be processed in parallel, and the exact order of execution is random. One or more threads may not write an updated value to a memory address from which another concurrent thread is reading, because then either the old or the new value may be used by the reading thread. This error is known as a race condition. To perform the LBM streaming step in parallel with only a single buffer for the DDFs, one must write updated values only to the same memory addresses that one thread has previously read the values from. Then, no two threads access the same memory addresses. Bailey et al. [3] have found that this is possible if, for even time steps combining one streaming step, the collision and a second streaming step are performed, and for odd time steps, only the collision step is performed. This makes the processed DDFs always end up in the same locations as they were read from, resolving data dependencies on concurrent hardware with only one copy of the DDFs in memory. To make the DDFs actually stream through memory locations, in even time steps, the DDFs are stored at the neighbor nodes in opposite orientation after the collision, and in odd time steps, before the collision, the DDFs are loaded from the center node in opposite orientation. The resulting algorithm reads the DDFs from copy A of the DDFs and writes to the same copy A in place, so it was termed AA-Pattern (Figure 3, Listing A3). It is a popular but mistaken belief that the different even and odd time steps require duplicate implementation of the stream_collide kernel because the pointers to the DDFs cannot be swapped in between time steps. The loading and storing of the DDFs before and after collision can be placed in functions, and when the LBM time step is passed as a parameter, these functions then switch between loading/storing the DDFs from/to neighbors or at the center point (see Listing A3). The stream_collide kernel then contains calls to these two functions before and after collision, and no duplicate implementation is required. Note that there are also two more modern variants of the AA-Pattern, termed Shift-and-Swap Streaming (SSS) [4] and Periodic Shift (PS) [5], offering benefits in programming languages where pointer arithmetic is available.

3.2. Esoteric Twist

The idea of the Esoteric Twist in-place streaming scheme (Figure 4, Listing A4) is to pull only DDFs for negative directions, execute the collision, and then push only DDFs for positive directions [2]. To resolve data dependencies on concurrent hardware, in even steps, the DDFs are stored in opposite orientation after the collision, and in odd time steps, before the collision, the DDFs are loaded in opposite orientation.

Esoteric Twist resembles a criss-cross access pattern shifted north-east by half a node, accessing the DDFs at a total of 4 nodes (in the 2D case) or up to 8 nodes (in 3D). For certain implementations, this reduces the number of ghost nodes required, but it makes the implementation of the index calculation tedious as it requires manually writing the indices, which are different across velocity sets. On top of this, for some velocity sets such as D3Q15, additional streaming directions must be computed beyond the streaming directions of the velocity set (see Listing A4), making the already tedious implementation even more cumbersome. This is an obstacle to implementing different velocity sets in a modular manner or with code generation. With some LBM extensions such as Volume-of-Fluid, duplicate (inverse) implementation of the streaming is required, so Esoteric Twist becomes very impractical.

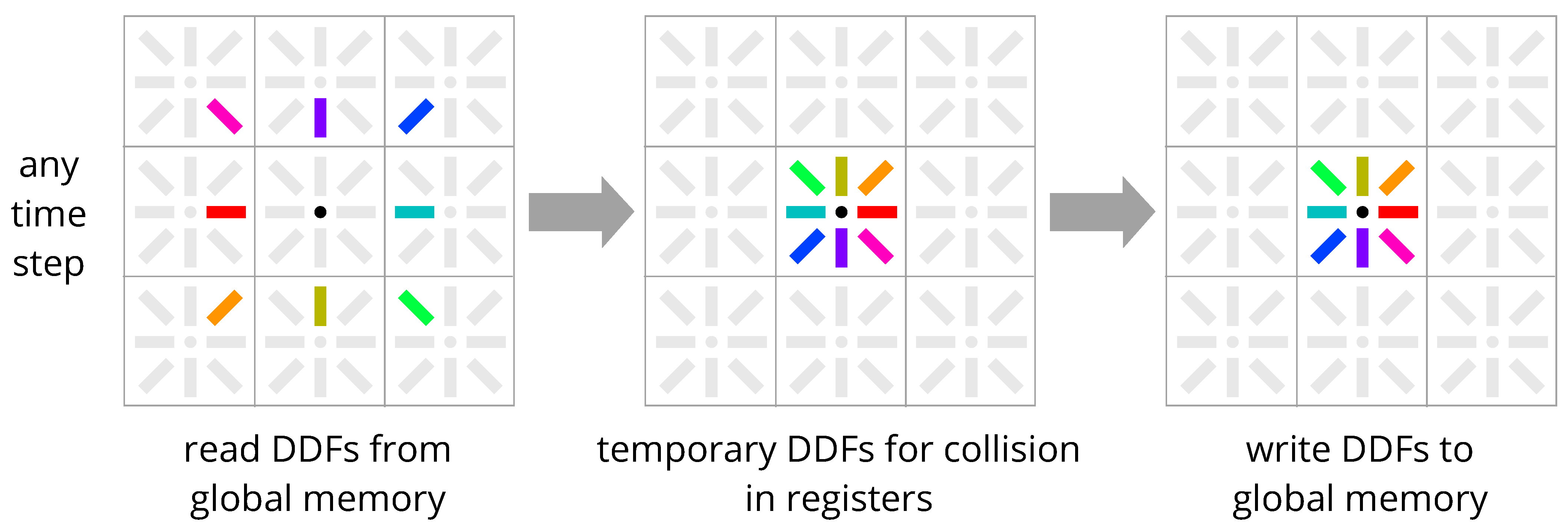
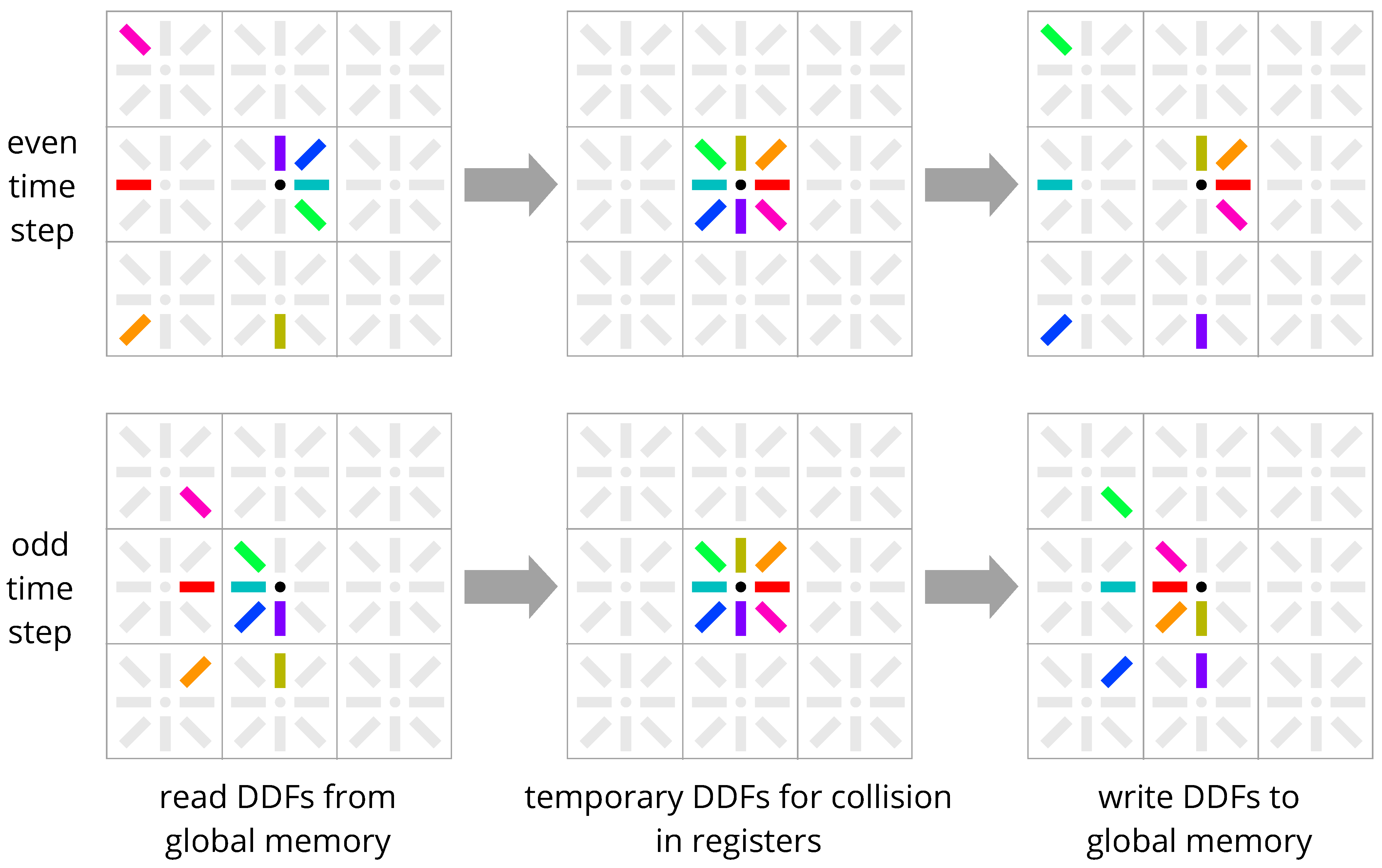
4. New Methods: Esoteric Pull and Esoteric Push

My two novel in-place streaming algorithms are based on the same idea as the Esoteric Twist scheme, namely that only DDFs in negative directions are pulled before collision, and that after collision only DDFs in positive directions are pushed. Thus, half of the DDFs are streamed at the end of one stream_collide kernel and the other half at the beginning of the next.

The important observation I made is that the shifted criss-cross pattern of Esoteric Twist is not essential for the swap algorithm to work. I waive shifting the north-west to south-east DDFs north by one node in 2D, and waive shifting other diagonal directions in 3D, abandoning the shifted criss-cross pattern. Instead, the regular streaming direction neighbors are used. This enables a trivial index calculation in two four-line loops (unrolled by the compiler) for loading and storing in a way that works with all velocity sets out of the box. This also makes the implementation less redundant and much less prone to errors, and it further enables automatic code generation.

The Esoteric Pull scheme (Figure 5, Listing A5) in 2D differs from Esoteric Twist (Figure 4) only in the positions of the DDFs for the north-west to south-east directions, which are loaded/stored in their regular locations instead of shifted north by one node. In 3D, other diagonal directions are also not shifted, and their regular streaming directions are used instead to determine the streaming neighbor nodes. This has not only the advantage of trivial index calculation, but also improves memory coalescence for the DDFs in these diagonal directions that would be otherwise shifted by one lattice point with Esoteric Twist, leading to slightly higher performance demands.

The Esoteric Push scheme (Figure 6, Listing A6) is essentially Figure 5 flipped by 180 degrees (except for the temporary DDFs in registers), highlighting two distinct symmetry flips that can be performed independently of each other: a) switching streaming for positive/negative directions, and b) switching even/odd time steps.

Both schemes yield simulations that are bitwise identical to Esoteric Twist. If pointer arithmetic is available, the pointers of DDFs in positive and negative directions can be swapped in between time steps such that memory addressing is the same for all time steps, in the very same manner as for Esoteric Twist.

4.1. Implicit Bounce-Back

In the very same manner as for the Esoteric Twist scheme [2], both Esoteric Pull and Esoteric Push offer the benefits of the ingeniously emerging implicit bounce-back boundaries. Due to the way the DDFs are flipped in orientation for regular fluid nodes, and because boundary nodes are not processed at all (with a guard clause at the very beginning of the stream_collide kernel), the DDFs of boundary nodes are not flipped in memory, so for neighboring fluid nodes, it appears as if their DDFs are already correctly flipped such that bounce-back boundaries automatically apply.

There are three distinct benefits to this side-effect of the Esoteric streaming schemes: (a) fluid nodes do not have to check the flags of their neighbors at all to apply bounce-back boundaries, reducing overall memory bandwidth and increasing performance slightly, (b) memory access is more coalesced, and (c) the implementation is simplified.

4.2. Comparison with Existing Streaming Schemes

When comparing the different streaming algorithms in

Table 1. Comparing memory storage (Bytes/node) and bandwidth (Bytes/node per time step) requirements of the different GPU-compatible streaming algorithms for DdQq LBM with FP32 arithmetic precision and eight available flag bits per node. With the in-place streaming and implicit bounce-back of the Esoteric schemes, and with FP32/16-bit mixed precision as proposed in [13], memory demands and bandwidth are significantly reduced.

Algorithm	Storage	Bandwidth
One-Step Pull	$8q+4d+5$	$9q$
One-Step Push	$8q+4d+5$	$9q$
AA-Pattern	$4q+4d+5$	$9q$
Esoteric Twist	$4q+4d+5$	$8q+1$
Esoteric Pull	$4q+4d+5$	$8q+1$
Esoteric Push	$4q+4d+5$	$8q+1$
OSP + FP32/16-bit	$4q+4d+5$	$5q$
AA + FP32/16-bit	$2q+4d+5$	$5q$
ET/EP + FP32/16-bit	$2q+4d+5$	$4q+1$

for DdQq LBM, the advantages of in-place streaming become evident, such as reduced storage and, for the Esoteric algorithms, also reduced bandwidth. In-place streaming reduces memory demand by $4q$ Bytes/node. The Esoteric algorithms further reduce memory bandwidth by $q-1$ Byte/node per time step, as neighbor flags do not have to be checked for implicit bounce-back boundaries. Based on their storage and performance properties, Esoteric Pull/Push appear identical to Esoteric Twist, apart from slightly improved memory coalescence for the DDFs in some of the diagonal directions. The main improvements of Esoteric Pull/Push are located in the much more straightforward implementation that is compatible with all velocity sets. Instead of having to manually unroll the loops over the streaming directions and make sure that all indices are typed correctly for each velocity set, the streaming can now be written in a generic way as two short loops that are unrolled by the compiler (compare Listing A4 and Listing A5). This also allows for automatic code generation that many LBM implementations heavily rely on and significantly improves code maintainability.

A recently proposed method for reducing storage and bandwidth by resorting to FP32/16-bit mixed precision [13] makes in-place streaming with the Esoteric schemes even more compelling, reducing memory storage from 169 to 55 Bytes/node—less than one third—and reducing bandwidth from 171 to 77 Bytes/node per time step for D3Q19. Less memory demand per node enables much larger lattice resolutions.

When comparing D3Q19 SRT performance of the different streaming algorithms on the Nvidia A100 40GB GPU with a FP32 single-precision floating-point, One-Step Pull serves as the baseline at $8816\mathrm{MLUPs}/\mathrm{s}$ ($100\%$). One-Step Push is slightly slower at $8675\mathrm{MLUPs}/\mathrm{s}$ ($98\%$). The AA-Pattern runs with $8269\mathrm{MLUPs}/\mathrm{s}$ ($94\%$), Esoteric Twist mitigates the efficiency losses with reduced bandwidth due to implicit bounce-back at $8483\mathrm{MLUPs}/\mathrm{s}$ ($96\%$), and Esoteric Pull/Push offer even slightly higher performance at $8522\mathrm{MLUPs}/\mathrm{s}$ ($97\%$), due to better memory coalescence for the diagonals that are shifted by one lattice point for Esoteric Twist. Looking at additional performance benchmarks across different hardware configurations (Figure 7), the benefit of less memory bandwidth usage due to implicit bounce-back approximately cancels out the drawback of more inefficient, partially misaligned writes due to the inherent symmetry of the memory access. In comparison with the One-Step-Pull streaming scheme [13], although memory efficiency is lower, performance changes only insignificantly on most dedicated GPUs, with some performance increase for FP32/FP16 mixed precision. On integrated GPUs and on CPUs, however, there is a significant increase in performance due to more efficient use of on-chip cache with in-place memory access. The benchmark case used is an empty box with a default size of ${256}^3$, with no extensions enabled except bounce-back boundaries, following [13]. For devices where not enough memory was available, the box size was reduced, and for the AMD Radeon VII, the box size was increased to ${464}^3$.

5. Esoteric Pull for Free Surface LBM on GPUs

Here, to further underline the substantial perks of the added simplicity of Esoteric Pull over Esoteric Twist, the modification of existing Free Surface LBM (FSLBM) code from One-Step Pull to Esoteric Pull in-place streaming is briefly discussed using the example of FluidX3D [14].

Although the One-Step-Pull scheme makes an FSLBM implementation the simplest and most efficient, it can easily be modified to the Esoteric Pull in-place streaming scheme. FSLBM on a GPU requires three more kernels in addition to the stream_collide kernel. To distinguish between node types, three flag bits are required and can be represented as follows: fluid (001, F), interface (010, I), gas (100, G), interface→fluid (011, IF), interface→gas (110), and gas→interface (111, GI). These kernels are first introduced for the implementation of One-Step Pull:

• stream_collide: Immediately return for G nodes. Stream in DDFs from neighbors, but for F and I nodes also load outgoing DDFs from the center node to compute the mass transfer for Volume-of-Fluid [67]. Apply excess mass for F or I nodes by summing it from all neighboring F and I nodes. Compute the local surface curvature with PLIC [26] and reconstruct DDFs from neighboring G nodes. After collision, compare mass m and post-collision density $\rho$; along with neighboring flags, mark whether the center node should remain I or change to IF or IG. Store post-collision DDFs at the local node.
• surface_1: Prevent neighbors of IF nodes from becoming/being G nodes; update flags of such neighbors to either I (from IF) or GI (from G).
• surface_2: For GI nodes, reconstruct and store DDFs based on the average density and velocity of all neighboring F, I, or IF nodes. For IG nodes, turn all neighboring F or IF nodes to I.
• surface_3: Change IF nodes to F, IG nodes to G, and GI nodes to I. Compute excess mass for each case separately as well as for F, I, and G nodes, then divide the local excess mass by the number of neighboring F, I, IF, and GI nodes and store the excess mass on the local node.

After modifying the streaming scheme from One-Step Pull to Esoteric Pull, a fifth kernel must be added preceding the stream_collide kernel because in the stream_collide kernel, the outgoing DDFs cannot be loaded as neighboring nodes may overwrite them in memory within the same time step (race condition):

• surface_0: Immediately return for G nodes. Stream in DDFs as in Figure 5 (incoming DDFs), but also load outgoing DDFs in opposite directions to compute the mass transfer for Volume-of-Fluid. For I nodes, compute the local surface curvature with PLIC and reconstruct DDFs for neighboring G nodes; store these reconstructed DDFs in the locations at the neighbors from which they will be streamed in in the following stream_collide kernel. Apply excess mass for F or I nodes by summing from all neighboring F and I nodes.
• stream_collide: Immediately return for G nodes. Stream in DDFs as in Figure 5 and execute collision. For I nodes, compare mass m and post-collision density $\rho$; along with neighboring flags, mark whether the center node should remain I or change to IF or IG. Stream out the DDFs as in Figure 5.
• surface_1, surface_2, surface_3: unchanged

In the surface_0 kernel, additional streaming in inverted directions is necessary to load outgoing DDFs and store reconstructed DDFs for neighboring G nodes. Having to perform manual index calculations here, as with Esoteric Twist, would vastly elongate and over-complicate the code and reduce maintainability. With the Esoteric Pull/Push variants, only two simple loops of four lines of code each are required. The full FSLBM OpenCL C implementation with Esoteric Pull is provided in the Appendix B in Listing A7.

The change to the Esoteric Pull in-place streaming algorithm reduces the memory demand for FSLBM from 181 to 105 Bytes/node while only decreasing performance by approximately $20\%$ due to the duplicate loading of incoming DDFs and having to store reconstructed DDFs for G nodes. When combined with FP32/16-bit mixed precision [13], the memory demand is further reduced to 67 Bytes/node or about $\frac{1}{3}$ of vanilla FSLBM, comparable to or even less than the memory requirements of other (Navier–)Stokes solvers [68,69,70,71].

This, in turn, enables colossal lattice resolutions as illustrated by an example in Figure 8: a $7\mathrm{mm}$ (188 lattice point) diameter raindrop, $1.5\mathrm{ms}$ (7700 time steps) after impacting a deep pool at $9.55\frac{\mathrm{m}}{\mathrm{s}}$ [24] and ${20}^{\circ }$ inclination, was simulated with the FluidX3D implementation with FP32/FP16C mixed precision [13]. Lattice resolution is $940\times 940\times 800$ or 707 million lattice points. The simulation was conducted on an Nvidia Quadro RTX 8000 GPU with $48\mathrm{GB}$ video memory and took 27 min, including the rendering of the image. The code for this setup is provided in Appendix C in Listing A8.

6. Conclusions

In-place streaming is essential for any LBM GPU implementation as it significantly reduces memory demand and increases the maximum lattice resolution. However, existing thread-safe solutions for GPUs, such as AA-Pattern and Esoteric Twist, never gained widespread adoption due to the difficulty of implementation. The new Esoteric Pull and Esoteric Push schemes presented in this work should change that. They build upon the same idea as the Esoteric Twist scheme—streaming half of the DDFs at the end of one stream_collide kernel and the other half at the beginning of the next—but greatly simplify the implementation because of their trivial index calculations, even allowing for automatic code generation. For existing GPU implementations of the common One-Step-Pull scheme, the switch to Esoteric Pull requires only moderate modifications to the code, even if several extensions are already implemented, as demonstrated herein with Free Surface LBM. In contrast, the implementation of Esoteric Twist would be much more difficult and error-prone in such a case, as the index calculation has to be implemented twice in different variations for regular LBM streaming and for FSLBM mass exchange.

The Esoteric Pull and Esoteric Push schemes share the same performance advantage as Esoteric Twist over AA-Pattern: slightly reduced bandwidth due to implicit bounce-back. Moreover, compared to Esoteric Twist, memory coalescence is slightly improved on the otherwise shifted diagonal directions. This allows the Esoteric Pull/Push schemes, with only one DDF buffer, to provide GPU performance on par with the One-Step-Pull scheme with double DDF buffers, despite requiring less efficient misaligned writes. In addition, on integrated GPUs and CPUs, performance is significantly increased.