On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology
Abstract
:1. Introduction
2. Preliminaries
- ,
- .
3. Stability of FDEs with the GHF Derivative
- (i)
- The equilibrium point is said to be stable if, for any , there exists a such that for each initial condition satisfying , the solution of (6) satisfies for all . Otherwise, we say that is unstable.
- (ii)
- The equilibrium point is said to be asymptotically stable if it is stable and .
- (i)
- and for all ;
- (ii)
- for all .
4. Numerical Scheme
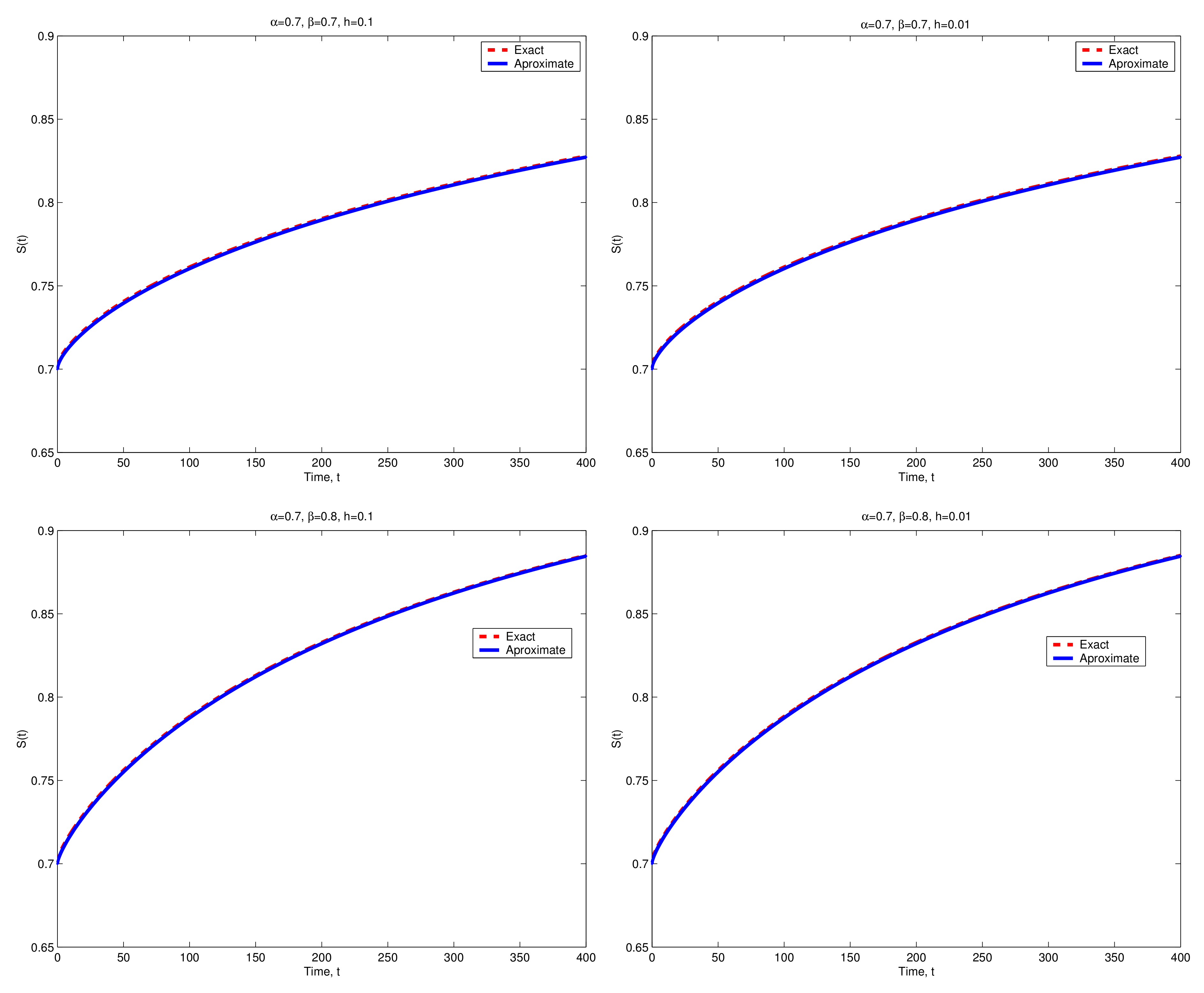
5. Application to Biology
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hattaf, K.; Yousfi, N. Global stability for fractional diffusion equations in biological systems. Complexity 2020, 2020, 5476842. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef] [Green Version]
- Cheneke, K.R.; Rao, K.P.; Edessa, G.K. Application of a new generalized fractional derivative and rank of control measures on Cholera transmission dynamics. Int. J. Math. Math. Sci. 2021, 2021, 2104051. [Google Scholar] [CrossRef]
- Qu, H.; Rahman, M.U.; Ahmad, S.; Riazd, M.B.; Ibrahim, M.; Saeed, T. Investigation of fractional order bacteria dependent disease with the effects of different contact rates. Chaos Solitons Fractals 2022, 159, 112169. [Google Scholar] [CrossRef]
- Zhang, L.; Rahman, M.U.; Ahmad, S.; Riaz, M.B.; Jarad, F. Dynamics of fractional order delay model of coronavirus disease. Aims Math. 2021, 7, 4211–4232. [Google Scholar] [CrossRef]
- Naji, F.A.; Al-Sharaa, I. Controllability of impulsive fractional nonlinear control system with Mittag–Leffler kernel in Banach space. Int. J. Nonlinear Anal. Appl. 2022, 13, 3257–3280. [Google Scholar]
- Meral, F.C.; Royston, T.J.; Magin, R.L. Fractional calculus in viscoelasticity: An experimental study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Pinar, Z. On the explicit solutions of fractional Bagley-Torvik equation arises in engineering. Int. J. Optim. Control Theor. Appl. 2019, 9, 52–58. [Google Scholar] [CrossRef] [Green Version]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Danbury, CT, USA, 2006. [Google Scholar]
- Cao, X.; Lin, Y.-H.; Liu, H. Simultaneously recovering potentials and embedded obstacles for anisotropic fractional Schrödinger operators. Inverse Probl. Imaging 2019, 13, 197–210. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Liu, H. Determining a fractional Helmholtz equation with unknown source and scattering potential. Commun. Math. Sci. 2019, 17, 1861–1876. [Google Scholar] [CrossRef]
- Lai, R.-Y.; Lin, Y.-H. Inverse problems for fractional semilinear elliptic equations. Nonlinear Anal. 2022, 216, 112699. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Sahoo, S.K.; Mohammed, P.O.; Baleanu, D.; Kodamasingh, B. Hermite–Hadamard Type Inequalities for Interval-Valued Preinvex Functions via Fractional Integral Operators. Int. J. Comput. Intell. Syst. 2022, 15, 8. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Y.; Liu, H.; Wang, C. Numerical methods for semilinear fractional diffusion equations with time delay. Adv. Appl. Math. Mech. 2022, 14, 56–78. [Google Scholar]
- Butt, A.I.K.; Ahmad, W.; Rafiq, M.; Baleanu, D. Numerical analysis of Atangana–Baleanu fractional model to understand the propagation of a novel corona virus pandemic. Alex. Eng. J. 2022, 61, 7007–7027. [Google Scholar] [CrossRef]
- Rahman, M.U.; Arfan, M.; Deebani, W.; Kumam, P.; Shah, Z. Analysis of time-fractional Kawahara equation under Mittag–Leffler Power Law. Fractals 2022, 30, 2240021. [Google Scholar] [CrossRef]
- Odabasi, M.; Pinar, Z.; Kocak, H. Analytical solutions of some nonlinear fractional-order differential equations by different methods. Math. Methods Appl. Sci. 2021, 44, 7526–7537. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Dal, F.; Pinar, Z. A note on the fractional hyperbolic differential and difference equations. Appl. Math. Comput. 2011, 217, 4654–4664. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Dal, F.; Pinar, Z. On the numerical solution of fractional hyperbolic partial differential equations. Math. Probl. Eng. 2009, 2009, 730465. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Mathematics in Science and Engineering. In Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Delavari, H.; Baleanu, D.; Sadati, J. Stability analysis of Caputo fractional-order nonlinear systems revisited. Nonlinear Dyn. 2012, 67, 2433–2439. [Google Scholar] [CrossRef]
- Rao, M.R. Ordinary Differential Equations; East-West Press: Minneapolis, MN, USA, 1980. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wang, G.; Pei, K.; Chen, Y.Q. Stability analysis of nonlinear Hadamard fractional differential system. J. Frankl. Inst. 2019, 356, 6538–6546. [Google Scholar] [CrossRef]
- Brzdek, J.; Eghbali, N.; Kalvandi, V. On Ulam stability of a generalized delayed differential equation of fractional order. Results Math. 2022, 77, 26. [Google Scholar] [CrossRef]
- Hattaf, K. Stability of fractional differential equations with new generalized Hattaf fractional derivative. Math. Probl. Eng. 2021, 2021, 8608447. [Google Scholar] [CrossRef]
- Hattaf, K. A new generalized definition of fractional derivative with non-singular kernel. Computation 2020, 8, 49. [Google Scholar] [CrossRef]
- Caputo, A.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Al-Refai, M. On weighted Atangana–Baleanu fractional operators. Adv. Differ. Equ. 2020, 2020, 3. [Google Scholar] [CrossRef] [Green Version]
- Hattaf, K.; Mohsen, A.A.; Al-Husseiny, H.F. Gronwall inequality and existence of solutions for differential equations with generalized Hattaf fractional derivative. Math. Comput. Sci. 2022, 27, 18–27. [Google Scholar] [CrossRef]
- Hattaf, K. On some properties of the new generalized fractional derivative with non-singular kernel. Math. Probl. Eng. 2021, 2021, 1580396. [Google Scholar] [CrossRef]
- Djida, J.D.; Atangana, A.; Area, I. Numerical Computation of a Fractional Derivative with Non-Local and Non-Singular Kernel. Math. Model. Nat. Phenom. 2017, 12, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Fernandez, A. On some new properties of fractional derivatives with Mittag–Leffler kernel. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 444–462. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Li, C.; Chen, Y.Q. Asymptotical stability of nonlinear fractional differential system with Caputo derivative. Int. J. Differ. Equ. 2011, 2011, 635165. [Google Scholar] [CrossRef]

| Parameter | Biological Meaning |
|---|---|
| A | Natality or recruitment rate |
| Natural death rate | |
| Transmission rate of disease | |
| Transfer rate from class E to class I | |
| r | Recovery rate of the infectious individuals |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hattaf, K. On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology. Computation 2022, 10, 97. https://doi.org/10.3390/computation10060097
Hattaf K. On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology. Computation. 2022; 10(6):97. https://doi.org/10.3390/computation10060097
Chicago/Turabian StyleHattaf, Khalid. 2022. "On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology" Computation 10, no. 6: 97. https://doi.org/10.3390/computation10060097
APA StyleHattaf, K. (2022). On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology. Computation, 10(6), 97. https://doi.org/10.3390/computation10060097






