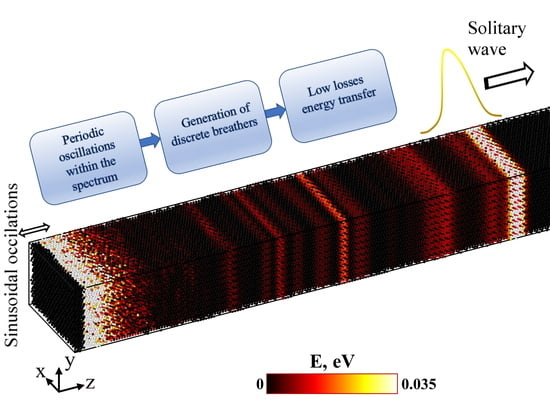
The Influence of Crystal Anisotropy on the Characteristics of Solitary Waves in the Nonlinear Supratransmission Effect: Molecular Dynamic Modeling
Abstract
:1. Introduction
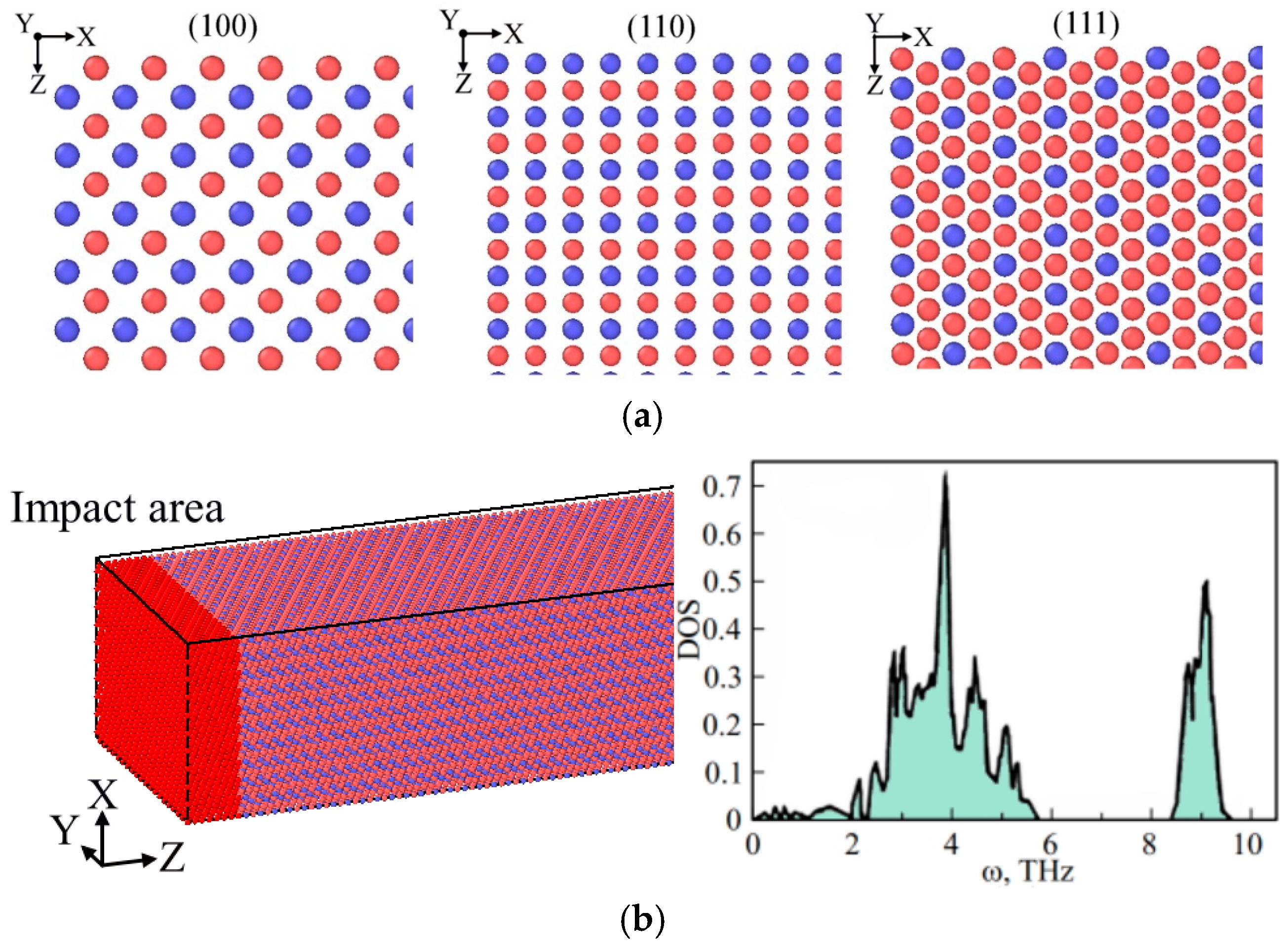
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geniet, F.; Leon, J. Energy transmission in the forbidden band gap of a nonlinear chain. Phys. Rev. Lett. 2002, 89, 134102. [Google Scholar] [CrossRef] [PubMed]
- Caputo, J.-G.; Leon, J.S. Nonlinear energy transmission in the gap. Phys. Lett. A 2001, 283, 129–135. [Google Scholar] [CrossRef]
- Evazzade, I.; Lobzenko, I.P.; Korznikova, E.A.; Ovid’ko, I.A.; Roknabadi, M.R.; Dmitriev, S.V. Energy transfer in strained graphene assisted by discrete breathers excited by external ac driving. Phys. Rev. B 2017, 95, 035423. [Google Scholar] [CrossRef]
- Frazier, M.J.; Kochmann, D.M. Band gap transmission in periodic bistable mechanical systems. J. Sound Vib. 2017, 388, 315–326. [Google Scholar] [CrossRef]
- Macías-Díaz, J.; Bountis, T. Nonlinear Supratransmission in Quartic Hamiltonian Lattices with Globally Interacting Particles and On-Site Potentials. J. Comput. Nonlinear Dyn. 2021, 16, 021001. [Google Scholar] [CrossRef]
- Leon, J.; Spire, A. Gap soliton formation by nonlinear supratransmission in Bragg media. Phys. Lett. A 2004, 327, 474–480. [Google Scholar] [CrossRef]
- Flach, S.; Willis, C.R. Discrete Breathers. Phys. Rep. 1998, 295, 181–264. [Google Scholar] [CrossRef]
- MacKay, R.S.; Aubry, S. Proof of existence of breathers for time-reversible or Hamiltonian networks of weakly coupled oscillators. Nonlinearity 1994, 7, 1623–1643. [Google Scholar] [CrossRef]
- Flach, S.; Gorbach, A.V. Discrete breathers—Advances in theory and applications. Phys. Rep. 2008, 467, 1–116. [Google Scholar] [CrossRef]
- Manley, M.E. Impact of intrinsic localized modes of atomic motion on materials properties. Acta Mater. 2010, 58, 2926–2935. [Google Scholar] [CrossRef]
- Cuevas-Maraver, J.; Chacon, R.; Palmero, F. Impulse-induced generation of stationary and moving discrete breathers in nonlinear oscillator networks. Phys. Rev. E 2016, 94, 062206. [Google Scholar] [CrossRef]
- Upadhyaya, A.; Semenova, M.N.; Kudreyko, A.A.; Dmitriev, S.V. Chaotic discrete breathers and their effect on macroscopic properties of triangular lattice. Commun. Nonlinear Sci. Numer. Simul. 2022, 112, 106541. [Google Scholar] [CrossRef]
- Singh, M.; Morkina, A.Y.; Korznikova, E.A.; Dubinko, V.I.; Terentiev, D.A.; Xiong, D.; Naimark, O.B.; Gani, V.A.; Dmitriev, S.V. Effect of Discrete Breathers on the Specific Heat of a Nonlinear Chain. J. Nonlinear Sci. 2021, 31, 12. [Google Scholar] [CrossRef]
- Chechin, G.M.; Dzhelauhova, G.S.; Mehonoshina, E.A. Quasibreathers as a generalization of the concept of discrete breathers. Phys. Rev. E 2006, 74, 036608. [Google Scholar] [CrossRef] [PubMed]
- Ryabov, D.S.; Chechin, G.M.; Upadhyaya, A.; Korznikova, E.A.; Dubinko, V.I.; Dmitriev, S.V. Delocalized nonlinear vibrational modes of triangular lattices. Nonlinear Dyn. 2020, 102, 2793–2810. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Chetverikov, A.P.; Dmitriev, S.V.; Korznikova, E.A. Shock waves in graphene and boron nitride. Comput. Mater. Sci. 2020, 177, 109549. [Google Scholar] [CrossRef]
- Sato, M.; Hubbard, B.E.; Sievers, A.T. Nonlinear energy localization and its manipulation in micromechanical oscillator arrays. Rev. Mod. Phys. 2006, 78, 13. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Evazzade, I.; Korznikova, E.A.; Shepelev, I.A.; Zhou, K.; Dmitriev, S.V. Low-energy channel for mass transfer in Pt crystal initiated by molecule impact. Comput. Mater. Sci. 2019, 163, 248–255. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Dmitriev, S.V.; Kudreyko, A.A.; Velarde, M.G.; Korznikova, E.A. Supersonic voidions in 2D Morse lattice. Chaos Solitons Fractals 2020, 140, 110217. [Google Scholar] [CrossRef]
- Krylova, K.A.; Baimova, J.A.; Murzaev, R.T.; Mulyukov, R.R. Energy exchange between discrete breathers in graphane in thermal equilibrium. Phys. Lett. A 2019, 383, 1583–1588. [Google Scholar] [CrossRef]
- Kikot, I.K.; Rayzan, N.B.; Kovaleva, M.; Starosvetsky, Y. Discrete breathers and discrete oscillating kink solution in the mass-in-mass chain in the state of acoustic vacuum. Commun. Nonlinear Sci. Numer. Simul. 2020, 107, 106020. [Google Scholar] [CrossRef]
- Korznikova, E.A.; Shcherbinin, S.A.; Ryabov, D.S.; Chechin, G.M.; Ekomasov, E.G.; Barani, E.; Zhou, K.; Dmitriev, S.V. Delocalized Nonlinear Vibrational Modes in Graphene: Second Harmonic Generation and Negative Pressure. Phys. Status Solidi B Basic Res. 2019, 256, 1800061. [Google Scholar] [CrossRef]
- Geniet, F.; Leon, J. Nonlinear supratransmission. J. Condens. Matter Phys. 2003, 15, 2933–2949. [Google Scholar] [CrossRef]
- Leon, J. Nonlinear supratransmission as a fundamental instability. Phys. Lett. A 2003, 319, 130–136. [Google Scholar] [CrossRef]
- Leon, J. Slow-light solitons in two-level media generated by evanescent fields. Phys. Rev. A 2007, 75, 063811. [Google Scholar] [CrossRef]
- Anghel-Vasilescu, P.; Dorignac, J.; Geniet, F.; Leon, J.; Taki, M. Nonlinear supratransmission in multicomponent systems. Phys. Rev. Lett. 2010, 105, 074101. [Google Scholar] [CrossRef]
- Anghel-Vasilescu, P.; Dorignac, J.; Geniet, F.; Leon, J.; Taki, A. Generation and dynamics of quadratic birefringent spatial gap solitons. Phys. Rev. A 2011, 834, 043836. [Google Scholar] [CrossRef]
- Yu, G.; Wang, X.; Tao, Z. Resonant emission of solitons from impurity-induced localized waves in nonlinear lattices. Phys. Rev. E 2011, 83, 026605. [Google Scholar] [CrossRef]
- Togueu Motcheyo, A.B.; Tchinang Tchameu, J.D.; Siewe, S.M.; Tchawoua, C. Homoclinic nonlinear band gap transmission threshold in discrete optical waveguide arrays. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 29–34. [Google Scholar] [CrossRef]
- Togueu Motcheyo, A.B.; Kimura, M.; Doi, Y.; Tchawoua, C. Supratransmission in discrete one-dimensional lattices with the cubic–quintic nonlinearity. Nonlinear Dyn. 2019, 95, 2461–2468. [Google Scholar] [CrossRef]
- Ai, B.Q.; He, D.; Hu, B. Heat conduction in driven Frenkel-Kontorova lattices: Thermal pumping and resonance. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 031124. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.G.; Yang, T.; Niu, M.-Q.; Chen, L.-Q. Interaction effects of driving amplitudes and frequencies on transitivity in a granular chain. J. Sound Vib. 2022, 529, 116966. [Google Scholar] [CrossRef]
- Kamdoum Kuitche, A.; Togueu Motcheyo, A.B.; Kanaa, T.; Tchawoua, C. Modulational instability in transversely connected nonlinear pendulum pairs. Eur. Phys. J. Plus 2023, 138, 142. [Google Scholar] [CrossRef]
- Adile, A.D.; Kenmogne, F.; Tewa, A.K.S.; Simo, H.; Tahir, A.M.; Kumar, S. Dynamics of a mechanical network consisting of discontinuous coupled system oscillators with strong irrational nonlinearities: Resonant states and bursting waves. Int. J. Non-Linear Mech. 2021, 137, 103812. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, K.W. On the wave propagation analysis and supratransmission prediction of a metastable modular metastructure for non-reciprocal energy transmission. J. Sound Vib. 2019, 458, 389–406. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, K.W. Supratransmission in a metastable modular metastructure for tunable non-reciprocal wave transmission. Proc. SPIE—Int. Soc. Opt. Eng. 2018, 10595, 1059514. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, H.; Xu, J. Programmable stopbands and supratransmission effects in a stacked Miura-origami metastructure. Phys. Rev. E 2020, 101, 042206. [Google Scholar] [CrossRef]
- Liu, X.; Cai, G.; Wang, K.W. Nonreciprocal wave transmission in metastable modular metastructures utilizing asymmetric dual-threshold snap-through. In Proceedings of the Conference on Smart Materials, Adaptive Structures and Intelligent Systems: SMASIS 2019, Louisville, KY, USA, 9–11 September 2019; p. V001T03A007. [Google Scholar] [CrossRef]
- Bountis, A. Complex dynamics and statistics of 1-d hamiltonian lattices: Long range interactions and supratransmission. Nonlinear Phenom. Complex Syst. 2020, 23, 133–148. [Google Scholar] [CrossRef]
- Zakharov, P.V. The effect of nonlinear supratransmission in discrete structures: A review. Comput. Res. Model. 2023, 15, 599–617. [Google Scholar] [CrossRef]
- Bountis, T.; Macías-Díaz, J.-E. The Effect of On-Site Potentials on Supratransmission in One-Dimensional Hamiltonian Lattices. Entropy 2023, 25, 423. [Google Scholar] [CrossRef]
- Pechac, J.E.; Frazier, M.J. Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions. Crystals 2021, 11, 94. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Starostenkov, M.D.; Lucenko, I.S.; Kochkin, A.S. Interaction of a soliton wave with nanopores in stoichiometry crystals A3B. J. Phys. Conf. Ser. 2020, 1697, 012076. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Dmitriev, S.V.; Korznikova, E.A. Molecular dynamic analysis of energy transport in a Pt3Al crystal under the impact in the spectrum gap frequency. Lett. Mater. 2021, 11, 338–344. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Cherednichenko, A.I.; Zakharov, P.V. Modulation of oscillations of nonlinear modes on the cylindrical surface of A3B crystal. Mater. Technol. Des. 2022, 4, 60–65. [Google Scholar] [CrossRef]
- Kolesnikov, I.D.; Shepelev, I.A. Excitation and Propagation of I-crowdion in BCC Niobium lattice. Mater. Technol. Des. 2022, 4, 5–10. [Google Scholar] [CrossRef]
- Xiaoxia, L. Investigation on the Mechanical Properties of Polycrystalline Mg Using Molecular Dynamics Simulation. Comput. Model. Eng. Sci. 2022, 131, 919–927. [Google Scholar] [CrossRef]
- Matsumoto, R.; Nakagaki, M.; Nakatani, A.; Kitagawa, H. Molecular-dynamics Study on Crack Growth Behavior Relevant to Crystal Nucleation in Amorphous Metal. Comput. Model. Eng. Sci. 2005, 9, 75–84. [Google Scholar] [CrossRef]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Cherednichenko, A.I.; Zakharov, P.V.; Starostenkov, M.D.; Eremin, A.M.; Dong, G. Analysis of eam and meam potentials for modeling localized states of Ni3Al and Pt3Al crystals. Basic Probl. Mater. Sci. 2021, 2, 188–195. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Eremin, A.M.; Starostenkov, M.D.; Lutsenko, I.S.; Zakhakova, E.A.; Dmitriev, S.V. Excitation of soliton-type waves in crystals of the A3B stoichiometry. Phys. Solid State 2019, 61, 2160–2166. [Google Scholar] [CrossRef]
- Fu, C.L.; Yoo, M.H. Electronic structure and mechanical behavior of transition-metal aluminides: A first-principles total-energy investigation. Mater. Chem. Phys. 1992, 32, 25–36. [Google Scholar] [CrossRef]
- Shcherbinin, S.A.; Krylova, K.A.; Chechin, G.M.; Soboleva, E.G.; Dmitriev, S.V. Delocalized nonlinear vibrational modes in fcc metals. Commun. Nonlinear Sci. Numer. Simul. 2022, 104, 106039. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Chen, C.Q. Amplitude-dependent boundary modes in topological mechanical lattices. J. Mech. Phys. Solids 2021, 153, 104482. [Google Scholar] [CrossRef]
- Smirnov, V.V.; Manevitch, L.I. Large-amplitude nonlinear normal modes of the discrete sine lattices. Phys. Rev. E 2017, 95, 022212. [Google Scholar] [CrossRef] [PubMed]
- Aero, E.L.; Budygin, A.N. Theory of nonlinear waves in solids undergoing a radical rearrangement of the crystal structure. Vychisl. Mekh. Splosh. Sred. 2009, 2, 19–43. [Google Scholar] [CrossRef]
- Kamdoum Kuitche, A.; Togueu Motcheyo, A.B.; Kanaa, T.; Tchawoua, C. Supratransmission in transversely connected nonlinear pendulum pairs. Chaos Solitons Fractals 2022, 160, 112196. [Google Scholar] [CrossRef]
- Born, M.; Kun, H. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1955; 432p. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakharov, P.V.; Korznikova, E.A.; Izosimov, A.A.; Kochkin, A.S. The Influence of Crystal Anisotropy on the Characteristics of Solitary Waves in the Nonlinear Supratransmission Effect: Molecular Dynamic Modeling. Computation 2023, 11, 193. https://doi.org/10.3390/computation11100193
Zakharov PV, Korznikova EA, Izosimov AA, Kochkin AS. The Influence of Crystal Anisotropy on the Characteristics of Solitary Waves in the Nonlinear Supratransmission Effect: Molecular Dynamic Modeling. Computation. 2023; 11(10):193. https://doi.org/10.3390/computation11100193
Chicago/Turabian StyleZakharov, Pavel V., Elena A. Korznikova, Artem A. Izosimov, and Andrey S. Kochkin. 2023. "The Influence of Crystal Anisotropy on the Characteristics of Solitary Waves in the Nonlinear Supratransmission Effect: Molecular Dynamic Modeling" Computation 11, no. 10: 193. https://doi.org/10.3390/computation11100193