Passive Control of Boundary Layer on Wing: Numerical and Experimental Study of Two Configurations of Wing Surface Modification in Cruise and Landing Speed

Abstract

Minimizing the carbon footprint of the aviation industry is of critical importance for the forthcoming years, allowing the mitigation of climate change through fossil fuel economy. Significant progress toward this goal can be achieved through the aerodynamic optimization of wing surfaces. In a previous study, a custom-designed wing equipped with an Eppler 420 airfoil, including an appendant custom-designed blended winglet, was developed and studied in flight conditions. The present paper researches potential improvements to the aerodynamic behavior of this wing by attempting to regenerate the boundary layer. The main goal was to achieve passive control of the boundary layer, which would be approached by means of two different configurations. In the first case, dimples were added at the points where the separation of the boundary layer was expected, for the majority of the wing surface; in the second case, bumps of the same diameter were added at the same points. Both wings were studied in two different Reynolds (Re) numbers and five angles of attack (AoA). The computational fluid dynamics (CFD) simulations were implemented using a pressure-based solver, the spatial discretization was conducted with a second-order upwind scheme, and the k-omega SST (k-ω SST) turbulence model was applied by utilizing the pseudo-transient method. The experimental procedure was conducted in an open-type subsonic flow wind tunnel, for Reynolds 86,000, with 3D-printed models of the wings having undergone suitable surface treatment. The numerical and experimental results converged, showing a degradation in the wing’s aerodynamic performance when bumps were implemented, as well as a slight improvement for the configuration with dimples.

1. Introduction

Over the past century, the aviation industry has been feverishly working to improve the aerodynamic performance of aerial vehicles. Especially in recent years, with the imminent threat of climate change, the need to improve aircraft performance has become increasingly urgent. In this general effort, recent years have seen the introduction of efforts to improve wing configurations, which in turn will lead to a demand for less fuel, thus reducing carbon dioxide emissions and electrical energy overconsumption. The present study presents an attempt to investigate the variation in the behavior of the boundary layer developed on the suction side of a wing. More specifically, an attempt was made to intervene in the initial design of a previously studied wing. This intervention involved the addition of outward bumps and inward dimples at specific points on the wing. These additions were expected to affect the boundary layer by amending its development and delaying its separation through its re-energization. The original wing was designed and studied by Karkoulias et al. [1], with the intention of using it in an unmanned aerial vehicle (UAV) for firefighting purposes.

Since the early decades of fluid mechanics application in industry, researchers have tried to optimize fluid flows around aerodynamic bodies and boundary layer control. The first forms of flow control regarded passive flow control. These efforts mainly focused on the geometry of the bodies (e.g., the development of airfoils), aiming to control the flow field, developing pressure and stress zones. Some examples include vortex generators, fixed slats, boundary layer fences, winglets, fixed flow vanes, and roughness strips. The principle of passive control is associated with structures that are stable and do not require the consumption of external energy to improve the flow, aiming at passive guidance of the flow. These methods, although they are functional, have a limit regarding their efficiency and, as a consequence, active flow control was developed. This control method involves mechanisms and devices that require external energy to be implemented. Examples of such mechanisms include moving slats/flaps of aircraft wings, boundary layer blowing or absorption, controlled flow oscillation (acoustic excitation and plasma actuators), and flexible airfoils. The disadvantage of these methods is the requirement of external energy from the system, and this can be an inhibiting factor in their application.

Passive flow control devices affect the flow mainly by creating small vortices that intensify the mixing of slower streams that are close to the wall, with faster streams further away. The absence of added sensitive electronics seen in passive methods automatically makes this method of control more robust compared to active flow control methods. Over the last decades, a considerable volume of research has been conducted in the development and optimization of the passive boundary layer control methods. Throughout the international literature regarding intentional surface roughness affection, the effort to find suitable positions, shapes, and sizes of those configurations has been intensified in order to validate their positive effect on the aerodynamic performance of an airfoil or wing.

Bons [2], in his study on surface roughness effects, concludes that laminar separation bubbles can be eliminated with the presence of surface roughness at low Re, thus reducing loss. On the contrary, at high Re, when the flow has already transformed to turbulent, tiny surface roughness is capable of thickening the boundary layer, to the extent of causing separation. Bocanegra et al. [3], in their numerical and experimental study, suggest the functionality of a bio-inspired surface coating. This micro-scale surface coating consists of uniformly distributed cylindrical pillars with diverging tips that mitigate flow separation by shifting the separation point downstream and reducing the area of negative flow.

Choi et al. [4], in their experimental study, clarify the way the dimples are responsible for local flow separation and trigger shear layer instability along the separating shear layer, resulting in the generation of high turbulence intensity. With this increased turbulence, a reattachment of the flow on the sphere surface is observed, along with a high momentum near to the wall, overcoming a strong adverse pressure gradient that is formed in the aft side of the sphere surface. Tay et al. [5] investigated the way that arrays of shallow dimples with depth-to-diameter ratios of 1.5% and 5% in a turbulent channel flow affect drag. Their measurements showed that a drag reduction of up to 3% can be achieved by actually reducing the skin friction drag. Song et al. [6] designed orifice plates on centrifugal pumps acting as bumps in order to decrease the negative effects of the backflow vortices.

Shan et al. [7] investigated the subsonic flow separation over the NACA0012 airfoil at an AoA of 6° and the way passive vortex generators are responsible for the reattachment of the separated shear layer to the surface, succeeding to partially eliminate the separation. Zhen et al. [8] studied, both in simulations and in experiments, the effects of an array of vortex generators on the wing of a UAV. They concluded that a higher maximum lift is obtained when the generators are placed nearer to the separation point. Moreover, considering their shape, they concluded that rectangular and curved-edge vortex generators improve the aerodynamic efficiency of the wing compared to triangular ones.

In the current study, a custom-designed wing based on the Eppler 420 airfoil was selected to be studied. This study was divided into three separate stages. In the first stage, external bumps were implemented at the suction side of the wing at 40% of the chord along its semi-wingspan. This wing was studied at five AoA, from 0° to 16°, and at landing and cruise speeds, at Re = 86,000 (9 m/s) and Re = 258,000 (27 m/s), respectively. In the second stage of this study, internal dimples were applied to the same wing at the same points. Similarly, a numerical simulation of the flow around the wing was performed for the aforementioned angles and velocities.

After the completion of the numerical simulations, all three of the wing models were constructed using additive manufacturing. The manufacturing options were configured in such a way that the maximum quality and detail was achieved to require minimum machining on the models. The models were used to perform the experiments in the wind tunnel, simulating the flow velocity with a Reynolds number of 86,000.

At the conclusion of the research, the numerical results for all three of the wings were compared. The results were extracted regarding the aerodynamic coefficients and distributions of aerodynamic quantities on the suction side of the wing and the boundary layer configurations were compared. Furthermore, the results of the aerodynamic coefficients of the numerical simulations were compared with those of the experimental procedure under Re 86,000.

2. Materials and Methods

2.1. Theoretical Background and Modeling

All of the flows involved in the field of engineering, from the simplest ones, such as the two-dimensional flow in pipelines or in a flat plate, to the most complex ones, such as the three-dimensional flows, occur over a certain Reynolds number, which is defined as follows:

$$Re=\frac{VL}{v}$$

(1)

where, V is the velocity of the main flow, L is the characteristic length, and v is the kinematic viscosity. The Reynolds number is an important dimensionless quantity, as it indicates the relationship between the inertia forces and the viscous forces and characterizes the turbulence level of the flow.

The Navier–Stokes equations are a non-linear system of partial differential equations (PDE) that fully describe any flow condition and are expressed based on the principles of the conservation of mass, momentum, and energy. The analytical solution of the equations can only be achieved for very simplified systems, such as fluid flow over a flat plate. The analytical solution of the Navier–Stokes equations for more complex problems is considered impossible and, therefore, the equations are solved by numerical methods of computational fluid dynamics.

By introducing the average values of the fluid properties into the Navier–Stokes equations, a new set of equations is obtained, the so-called Reynolds-averaged Navier–Stokes (RANS) equations. Additional unknown properties appear in these equations, which are called Reynolds stresses. For these stresses, no precise mathematical relations can be derived that can calculate them. For this reason, these stresses have to be modelled appropriately. So-called turbulence models are used to model these stresses. A turbulence model is a computational procedure used to approximate the problem created by the unknown Reynolds stresses. For most engineering applications, it is not necessary to solve and model the details of the variations of the fluid properties. What fundamentally matters is the effect of the time-averaged values of the properties in the problem.

For this purpose, several turbulence models were developed to model and solve the RANS equations. This technique focuses on solving the time-averaged values of the flow properties, in which various turbulence models are solved to include the influence of the turbulence. This method calculates the effects of turbulence, rather than the turbulence itself. In essence, the turbulence effect is studied on a larger time scale than that which occurs, ignoring the variations in velocities over short periods of time, since they do not offer significant changes in the results.

The k-omega (k-ω) turbulence model [9,10] is one of the models most used to capture the effect of turbulent flow conditions. In addition to the conservation equations, it solves two transport equations (PDEs), which account for the history effects, such as convection and diffusion of turbulent energy. The two transported variables are turbulent kinetic energy (k), which determines the energy in turbulence, and the specific turbulent dissipation rate (ω), which determines the rate of dissipation per unit of turbulent kinetic energy. Its main advantages include its best application for near-wall treatment, as well as its superior performance for complex boundary layer flows under adverse pressure gradients and separations (e.g., external aerodynamics and turbomachinery). Furthermore, this model has also been shown to predict excessive and early separations.

The k-omega shear-stress transport (k-ω SST) turbulence model [11,12] combines the advantages of the two-equation k-epsilon (k-ε) and k-ω models. It utilizes the k-ω model in the inner part of the boundary layer, which results in its direct utilization up to the flow wall, below the viscous substrate. Therefore, the k-ω SST model can be used as a low-Re viscosity model without additional equations. It is also converted to a k-ε model in the free-flow region, thus avoiding the common problem of k-ω models, which are very sensitive to the turbulent properties of free flow at the inlet. In addition, it has a much better behavior in flows involving large negative pressure gradients and detachments. However, the k-ω SST model produces slightly higher turbulence levels in regions where strong horizontal forces act, such as stall points and places where there is strong flow acceleration. It is also able to account for the transport of the principal shear stress in adverse pressure gradient boundary layers [13]. It is the most used model in the industry, given its high accuracy to expense ratio. The equations used by k-ω SST to model the turbulence are presented below:

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left({\Gamma }_k\frac{\partial k}{\partial x_j}\right)+{\tilde{G}}_k-Y_k+S_K$$

(2)

where ${\tilde{G}}_k$ represents the generation of turbulent kinetic energy due to the mean velocity gradients, ${\Gamma }_k$ represents the effective diffusivity of k, $Y_k$ represents the dissipation of k due to turbulence, and $S_K$ is a user-defined term.

$$\frac{\partial }{\partial t}\left(\rho \omega \right)+\frac{\partial }{\partial x_i}\left(\rho \omega u_i\right)=\frac{\partial }{\partial x_j}\left({\Gamma }_{\omega }\frac{\partial \omega }{\partial x_j}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }$$

(3)

where $G_{\omega }$ represents the generation of $\omega$,${\Gamma }_{\omega }$ represents the effective diffusivity of $\omega$, $Y_{\omega }$ represents the dissipation of $\omega$ due to turbulence,$D_{\omega }$ represents the cross-diffusion term, and $S_{\omega }$ is a user-defined term.

The boundary layer was first introduced by Prandtl in 1904. With this invention, Prandtl was able to link the frictionless flow with the flow of real fluids. According to Prandtl, in the case of fluids of relatively low viscosity moving over solids, the effect of internal friction is limited only to a very thin layer of fluid near to the surface of the solid, which is known as the boundary layer. Thus, the flow field can be divided into two distinct regions, the boundary layer and the region outside of it, in which the viscosity ceases to be a significant factor in the flow configuration [14]. Referring to a two-dimensional domain (x-y) with a flow parallel to the x-axis, the thin layer beside the body where the velocity (u) gradient perpendicular to the x-axis is greater than zero is called the boundary layer.

$$\frac{\partial }{\partial y}\left(u\right)>0$$

(4)

In the present simulation, a custom-designed wing with a high curvature airfoil—Eppler 420—including an appendant custom-designed blended winglet, was studied. The wing section that was selected to be studied resulted from a preliminary study and conceptual design of a UAV. Thus, it is a custom-designed wing that was produced by using computer-aided design (CAD) software from scratch, attempting to fulfil the flight requirements of the aircraft. The main aerodynamic characteristics of the wing are that it is based on the Eppler 420 airfoil, with a sweep angle of 25 degrees, a twist angle of 5 degrees, and a dihedral angle of 2 degrees, while the wingtip has been replaced by a custom-designed blended winglet.

A thorough perspective of the designed wing section is illustrated in Figure 1 and Figure 2, while the values of the aerodynamic features are presented in

Table 1. Features of the designed wing.

Feature	Value
Airfoil	Eppler 420
Semi-wingspan	0.65 m
Root chord	0.18 m
Tip chord	0.09 m
Sweep angle	25°
Twist angle	5°
Dihedral Angle	2°

. The geometric features of the winglet are presented in

Table 2. Features of the designed winglet.

Feature	Value
Cant angle	70°
Sweep angle	55°
Twist angle	10°
Height	0.06 m
Radius	0.06 m
Outer tip chord	0.02 m

.

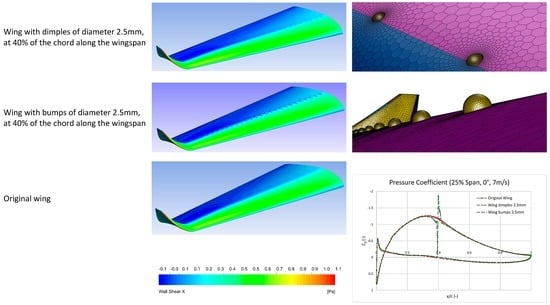
Two modified configurations of the original wing were designed afterwards. Specifically, the first configuration regarded the application of hemispherical bumps measuring 2.5 mm in diameter. These were placed along the entire length of the semi-wingspan in an imaginary straight line, joining the wing root to the wingtip, and intersecting the airfoils’ chords at 40% of their length, as illustrated in Figure 3a. In regard to the second configuration, the construction of inward dimples was selected, again of a hemispherical shape measuring 2.5 mm in diameter. These were placed at exactly the same points that the bumps had been implemented in the first configuration, as illustrated in Figure 3b.

The above referred configurations were exhibited in a macroscopic scale. Examining these on a more microscopic scale, the geometry of both the bumps and dimples can be observed in Figure 4. Specifically, Figure 4a shows the geometry of the first configuration, with 2.5 mm diameter bumps, whereas Figure 4b shows the geometry of the second configuration, with 2.5 mm diameter dimples.

After the completion of the CAD design, this study involved the utilization of the commercial CFD ANSYS FLUENT code to execute the numerical simulations. A three-dimensional domain was created, in which the designed wing would be contained, and the RANS equations would be solved. Due to its reliability, and the reasonable time needed for the simulation’s execution, a mosaic poly-hexcore mesh was developed. This mesh configuration was based on the connection of high-quality octree hexahedra in the bulk region and isotropic poly-prisms in the boundary layer with the mosaic polyhedral elements. Three mesh-independence studies were carried out, each concerning a different configuration of the wing, and are exhibited in Figure 5 for all three of the different wing configurations. For the original wing, 4 meshes were created with cells ranging from 1,722,541 to 5,864,829. For the wing with dimples, similarly, 4 meshes were created with cell numbers ranging from 2,164,941 to 6,612,759, while for the wing with the bumps, the corresponding meshes consisted of a cell count ranging from 2,360,756 to 7,221,884. The meshes selected for the simulations appear in

Table 3. Number of cells and orthogonal quality of the developed grids for each configuration.

Wing Configuration	Cells	Orthogonal Quality
Original Wing	4,444,373	0.9566
Wing with Dimples	5,134,003	0.9597
Wing with Bumps	5,446,729	0.9594

and provide satisfactory solutions, independent of the number of cells. It should be noted that the mesh study was conducted for both velocities, 9 m/s and 27 m/s, leading to the same result concerning the suitability of the mesh selected.

The computational domain was a rectangular parallelepiped, as shown in Figure 6, and the dimensions of the domain are expressed in units of the mean aerodynamic chord (MAC). The inlet and outward surfaces of the domain consisted of a square measuring 20 MAC × 20 MAC, while the remaining four side surfaces consisted of a parallelogram measuring 50 MAC × 20 MAC.

It should be mentioned that bodies of influence were applied around the wing and the added configurations on the suction side as well. This led the simulations to yield more accurate results, without increasing the number of domain cells to a prohibitive and unreasonable number. The final meshes exported after the independence study are exhibited in Figure 7a–c for the original wing, the wing with dimples, and the wing with bumps, respectively. Moreover, the volumetric meshes of the wings’ configurations with dimples and bumps are exhibited in Figure 7d,e.

Following the completion of the mesh development and the independence study, the next step was to define the numerical simulation parameters. As mentioned previously, the selected turbulence model for this case was k-ω SST. Its ability to provide better prediction of flow separation compared to most RANS models, in conjunction with its improved behavior in adverse pressure gradients, were catalytic parameters for this choice. Taking into consideration that Eppler 420 airfoil is characterized by a relatively high camber, along with the fact that it will be studied in high angles of attack up to 16°, explains its suitability as a turbulence model.

For the numerical simulations, the solver utilized in the FLUENT code was the pressure-based solver, considering a time-steady airflow, since the flow field conditions can be considered time-independent. The pseudo-transient approach was utilized to reassure the case stability and time reasonable convergence of the solution. Regarding pressure–velocity coupling, the pressure-based coupled algorithm was used to enable it in full. The second-order upwind scheme decreases the numerical discretization error; therefore, it was applied to the spatial discretization from the start of the calculations. This was mandated by the need for higher accuracy in the results, since the final comparison among the solutions was expected to yield minor deviations, and because of the mesh cell geometries. Regarding the boundary conditions, these are presented in

Table 4. Boundary conditions of the numerical simulation.

Feature	Value
Temperature (T)	288 K
Air density (ρ)	1.225 kg/m3
Dynamic viscosity (μ)	1.7894 × 10−5 kg/(ms)
Convergence criteria	1 × 10−6

.

After the completion of the setup of the solver and the simulation parameters, the numerical simulations were ready for execution. In total, 30 simulations were performed and gathered and are presented in

Table 5. Cases of the numerical simulation.

Inlet Velocity (Re)	Angle of Attack	Wing Formation
9 m/s (86,000)	0°	Original Wing	Wing with Dimples	Wing with Bumps
	4°
	8°
	12°
	16°
27 m/s (258,000)	0°	Original Wing	Wing with Dimples	Wing with Bumps
	4°
	8°
	12°
	16°

.

2.2. Experimental Procedure

For the purposes of the experiments of the present research, the open-type wind tunnel of the Fluid Mechanics and Applications Laboratory (Patras University, Greece) was used, in which the models of the wings were installed and tested. This is an open-type wind tunnel, in which the air flow is discharged into the atmosphere directly after the measurement chamber and the maximum velocity achieved in the measurement chamber is 33 m/s. This configuration has the advantage that the models are directly accessible and the pressure in the measurement chamber is very close to the atmospheric pressure. The measuring chamber has dimensions of 1.7 × 0.65 × 0.65 m and is equipped with three Plexiglas windows with removable frames. A restraint mechanism is used to affix the model and permits a free rotation of 360°. To derive the coefficients of lift and drag of the experimental model, the three-component AFA3 aerodynamic balance from TQ Education and Training Ltd. was used, as shown in Figure 8a. It is a device that measures two forces (lift and drag) and a moment (pitching moment), with capacities of 100 N, 50 N, and 2.5 Nm respectively.

As mentioned in the previous chapter, three models were constructed, one for the original wing, and two others with bumps and dimples (Figure 8b). These were used to perform the experiment, as shown in Figure 8c, and to collect the necessary results for comparison with the numerical simulations. For every angle of attack examined, a set of force measurements was collected. Through the software, a time interval of 0.2 s was set to record the values. It was chosen to keep each angle of attack constant for at least 300 s during the operation of the wind tunnel in order to reduce the margin of error during the recording of the values. After each period of 5 min, more than 1500 values were recorded. These were collected for each angle of attack and were first checked for possible outliers that might affect the mean value, before calculating the mean values of forces for every case.

3. Results

The results section is divided into three subsections. In the first subsection, the results of the lift and drag coefficients of each configuration for both of the flow velocities and the aerodynamic performance will be presented and analyzed, as derived from the numerical simulations. In the second subsection, the pressure distribution on the wings and the selected airfoils will be analyzed in specific cases and angles. In addition, other aerodynamic parameters and the configuration of the boundary layer will be discussed. In the third and final subsection, the results obtained from the experimental procedure will be presented and compared to those that were obtained from the numerical simulations.

3.1. Lift and Drag Coefficients—Numerical Simulations

The numerical simulations yielded the results of the forces acting on the wing, as well as the corresponding coefficients, which are presented in

Table 6. Lift and drag coefficient for each wing configuration in all simulations.

Inlet Velocity (Re)	Angle of Attack	Original Wing		Wing with Dimples		Wing with Bumps
		CL	CD	CL	CD	CL	CD
9 m/s (86,000)	0°	0.30128	0.030140	0.30812	0.029679	0.28865	0.031424
	4°	0.39878	0.041451	0.40448	0.040448	0.38696	0.041830
	8°	0.47363	0.065200	0.48089	0.064995	0.47335	0.065868
	12°	0.52266	0.092223	0.52671	0.090494	0.52313	0.091002
	16°	0.54815	0.122009	0.55396	0.121635	0.55383	0.121757
27 m/s (258,000)	0°	0.41811	0.021423	0.41795	0.021445	0.41031	0.021877
	4°	0.54164	0.033451	0.54197	0.033448	0.52568	0.034730
	8°	0.58346	0.052045	0.58751	0.052125	0.57280	0.053623
	12°	0.61844	0.075248	0.62178	0.075466	0.61474	0.076327
	16°	0.64893	0.103667	0.65431	0.103775	0.65095	0.104327

. It is easily observed that, for both of the airflow velocity assumptions, the wing with bumps on the suction side presents a degradation in the lift coefficient, as compared to the original wing, for all of the angles of attack, with the exception of two cases. When simulating landing speed, at 12° and 16°, there is a slight improvement in the coefficient for the wing with bumps, measured at approximately 1%.

On the contrary, the wing with dimples on its suction side yields a more distinct improvement regarding the lift coefficient for both of the velocity assumptions and at all of the angles of attack. It is noteworthy that the lower the Reynolds number, the more positively the dimples appear to affect the coefficient. Concerning the cruise speed, the maximum improvement is observed at 16°, with a percentage increase of the order of 0.72%, followed by the case of 8°, where the corresponding increase is little more than 0.5%. Concurrently, regarding the lift coefficient at landing speed, an improvement of 2.3% is observed at 0°, while an improvement of 1.5% occurs at 8°. This verifies the above statement that at a lower Reynolds number the positive effect of the dimples is more intense. The diagrams of the lift coefficients for the three wings for both of the velocity assumptions are presented in Figure 9.

Concurrently, the results regarding the drag coefficient show a similar behavior, as illustrated in Figure 10. There is an overall degradation of the drag coefficient due to the presence of the bumps. The mean increase in the coefficient is measured at 2.23% and 0.93% for cruise speed and landing speed, respectively. Again, the configuration with the bumps fails to improve the aerodynamic characteristics by actually increasing drag in all of the simulations. Notably, the increase in the drag coefficient follows an inversely proportional trend in relation to the angle of attack, leading to the conclusion that bumps are likely to reduce static pressure locally, but, at the same time, increase form drag and, therefore, parasite drag, to a disproportionate degree. It is also observed that their negative effect on drag increases with an increasing Reynolds number.

On the contrary, the wing with dimples appears to improve drag, even if marginally, and in any event does not deteriorate it. More specifically, for Re = 258,000, a slight reduction in the drag coefficient appears, averaging 0.13%. Correspondingly, for Re = 86,000, there is an average improvement of 1.3%, with the highest occurring at an AoA of 4°, where it reaches 2.42%. Regarding drag, as before with lift, the same tendency appears: the existence of dimples has more of an influential affect at a lower Reynolds number.

To conclude this first subsection, the final assessment of each configuration should be defined by comparing the lift-to-drag ratios in all of the above cases. The aerodynamic efficiency was exported for each configuration and compared to the results of the original wing. This comparison is presented in Figure 11. In complete accordance with what has been described earlier in this section, the wing with the bumps showed a general degradation of aerodynamic efficiency, with the exception of the aforementioned cases: 12° and 16°, at landing speed. The presence of bumps appeared to deteriorate the lift and drag of the wing, rendering it less aerodynamically efficient compared to the original wing. On the contrary, the wing with dimples appears to be more aerodynamically efficient in the entire range of cases, except for 0° at 27 m/s, where it appears to have a slight reduction of 0.14%. In all of the other cases, it exhibits improved aerodynamic behavior, reaching a maximum improvement of 4% in angles 0° and 4°, at the lower Reynolds number. According to Figure 12, their presence on the suction side has an even greater effect in improving the wing’s aerodynamic behavior at low Reynolds numbers.

3.2. Pressure Distribution and Boundary Layer Configuration

The velocity vectors of the flow around the wings demonstrate more efficiently how the velocity profile is affected by the presence of bumps and dimples. Figure 13 presents the distribution of the velocity vectors at 0° and Re = 86,000 around the airfoils of the wings located at approximately 25% of the wingspan. These airfoils were selected in such a way as to cross a bump and dimple at this location, at its highest dimension.

After analyzing the diagrams, it is observed that the presence of surface anomalies affects the velocity profiles in both cases, not only directly upstream of them, but also a short distance before and after. In the case of bumps, it is observed that the velocity directly above them appears slightly higher in relation to the original wing, due to Bernoulli’s law and the inertia of the air. Locally, the surface irregularity ruins part of the boundary layer, forcing a small quantity of air to acquire a negative velocity, due to direct impact on the bump. The presence of the bump locally increases the flow velocity, seeming to provide energy to the boundary layer. However, it eventually leads to earlier adverse pressure gradients and reverse flow. The result is earlier separation of the boundary layer and the degradation of the aerodynamic coefficients.

In the case of the dimples, the creation of a recirculation bubble is triggered. Observing Figure 13c carefully, it can be seen that air from the bottom of the boundary layer enters the dimple at the point of its end and, after creating a recirculation bubble below the boundary layer, exits the dimple accelerated. The consequence of this is that the velocity profile locally appears richer compared to the original wing. At the same time, the absence of material for a distance equal to the dimple’s diameter could be considered to contribute to the local reduction in surface drag. Further away from the local surface irregularity, the velocity profile appears to be stronger, demonstrating the success in boundary layer re-energizing. However, it has been shown that adverse pressure gradients appear slightly earlier, resulting in the final detachment of the boundary layer taking place earlier. Nevertheless, the boundary layer re-energizing was to such an extent that it was able to improve the aerodynamic coefficients.

A more thorough look at the diagram of Figure 14 explains the conclusions that were developed earlier. By reviewing the diagrams showing the pressure coefficient distribution on the airfoils, the two main conclusions are shown for the specific velocity and angle chosen.

Firstly, in the case of the wing with bumps, the velocity is instantaneously zeroed when the air impacts the front surface of the bump. Simultaneously, there is a drastic local increase in the absolute value of the pressure coefficient on the suction side as the air passes over the top of the bump. Then, in the region of 45–50% of the chord, a drop in pressure compared to the original wing occurs. Moreover, the curve shows an earlier leveling towards the trailing edge of the airfoil, explaining the earlier separation of the boundary layer. Overall, the pressure coefficient distribution justifies the aerodynamic efficiency degradation.

Secondly, in the case of the wing with dimples, the distribution of the pressure coefficient around the airfoil does not show the drastic changes that occurred in the wing with bumps. In the dimple region, and until about 10% afterwards, it is observed that the pressure coefficient of this wing is slightly higher than that of the original wing. Beyond this point, they follow a parallel curve up to the detachment point where the curve of the wing with dimples levels off slightly earlier.

Referring back to the cases where the wings were tested at a velocity of 27 m/s, and choosing to analyze the simulation under 8° AoA, the contours of the velocity variation in the horizontal axis, with respect to the vertical axis, are shown below in Figure 15. In this case, in deference to standard practice demonstrating the velocity gradient by $\frac{\partial }{\partial y}\left(u\right)$, it is shown as “dx velocity dz”, since the vertical axis was chosen to be z for the domain development. In the airfoil with the bump, from the top of the bump up to a region at about 45% of the chord, there is a negative gradient. In this region, a separation of flow occurs, a separation bubble is created, and then a reattachment of the boundary layer occurs. Towards the trailing edge, and at a position of about 80% of the chord, we again have zero gradient and thus a definite detachment of the flow. Compared to the original wing, the final detachment occurs earlier. However, in the case of the wing with bumps, the phenomenon of the boundary layer having higher energy for a longer distance than in the original wing is observed. Despite that, this factor is not enough to guarantee better aerodynamic behavior.

In analyzing the velocity gradient on the wing with the dimples, it is observed that a local detachment inside of the dimple is caused in the corresponding airfoil. From the end of the dimple to toward the trailing edge the boundary layer there is normal contact with the wing surface. Furthermore, after observing Figure 15f more closely, the flow appears to maintain its momentum for a greater distance compared to the original wing (yellow and green color). For both of the airfoils, separation occurs at a point that is located at approximately 85% of the chord. This indicates that this wing has a slightly improved aerodynamic performance compared to the original wing.

At the same velocity and angle of attack, Figure 16 shows a visualization of the x-component of the wall shear stress. The regions in dark blue are the flow separation regions. As mentioned earlier, the wing with dimples exhibits similar behavior to the original wing with respect to the separation region. In contrast, and mainly due to the presence of the surface anomalies, the wing with bumps exhibits a repetitive pattern of separation in the path of the airflow as it passes through them and moves towards the trailing edge.

Looking more closely at the dimples in the region where detachment occurs at the points where the dimples are located, the presence of the dimples appears to slightly delay detachment, creating a short region just after them where shear stress again shows values greater than zero until the final detachment occurs.

Finally, the case of the pressure coefficient distribution at 1/4 of the semi-wingspan, with Re = 258,000 and 4° AoA, was selected to be exhibited in Figure 17 Although the simulation was carried out at a different velocity and angle, the distributions display general similarities with the distribution that is presented in Figure 14. At the airfoil with the bump, at the point of the bump, a drastic zeroing of the pressure coefficient appears, and this phenomenon is instantaneously reversed after that. Moreover, the boundary layer detachment appears to occur at a point of approximately 90% of the chord, which is slightly earlier than that of the original wing.

Observing the diagram of the airfoil with the dimple, at the point where it is located, there are two small peaks of the coefficient at its beginning and end, and between them there is a dip, as an effect of the recirculation bubble and the tendency of the velocity to reach zero at the maximum depth of the dimple. Again, the detachment of the boundary layer occurs at approximately the same point as the original wing, substantially affecting the detachment point neither positively nor negatively.

3.3. Experimental Procedure Results

During the experimental procedure, the values of the lift and drag coefficients were derived for the three wings’ configurations, at angles of attack from 0° to 16°, and with a freestream velocity under a Reynolds number of 86,000. The results are summarized in

Table 7. Experimental lift and drag coefficients for each wing configuration.

Inlet Velocity (Re)	Angle of Attack	Original Wing		Wing with Dimples		Wing with Bumps
		CL	CD	CL	CD	CL	CD
9 m/s (86,000)	0°	0.2932	0.03154	0.3012	0.03112	0.2840	0.03310
	4°	0.3885	0.04387	0.3981	0.04214	0.3758	0.04414
	8°	0.4622	0.06890	0.4714	0.06780	0.4569	0.07110
	12°	0.5097	0.09747	0.5193	0.09525	0.4974	0.10020
	16°	0.5324	0.12953	0.5429	0.12758	0.5247	0.13512

.

Firstly, it was confirmed that the results of the numerical simulations were verified by the experimental procedure. For this purpose, the coefficients were compared in each case. Then, we extracted the deviation between the numerical and the experimental values for each wing configuration, and we calculated the average deviation for each one of the coefficients. These are illustrated more graphically in Figure 18 It is worth noting that the experimental procedure on all three of the wings produced results that were slightly aerodynamically pessimistic compared to those of the numerical simulations. The lift coefficient appeared to be slightly reduced, while the drag coefficient increased to a slightly higher degree.

For the drag coefficient in particular, this can be explained by two reasons. On the one hand, the existence of the restraint shaft does not produce lift, but it does contribute to the increase in drag. Furthermore, the finishing treatment of the wings, no matter how perfectly it is executed, is unable to reflect the ideal aluminum surface that is simulated by the simulation software. It is therefore expected that the skin friction drag, and therefore the parasitic drag of the manufactured wings, will be slightly increased compared to the wings in the numerical simulations. This explains the fact that the drag coefficients have a higher deviation compared to the lift coefficients, in absolute terms.

The average values of the deviations for the lift coefficient range from 2% to 4%. Similarly, the average values of the divergences for the drag coefficient range from 4% to 8%. A variation in these values can therefore be observed, but in no case does this deviation exceed 10%. On this basis, it is estimated that the numerical data are verified by the experimental data to a very significant extent.

A comparison of the experimental results was then conducted among them for the three configuration cases, as illustrated in Figure 19. These showed an almost similar behavior to that of the numerical results. In particular, the wing with bumps has a worse aerodynamic performance compared to the original wing. For all of the angles of attack, the lift coefficient appears lower, while the drag coefficient appears higher. The opposite phenomenon is observed in the wing with dimples, where the lift coefficient appears higher and the drag coefficient lower compared to the original wing. This result becomes clearer when the average aerodynamic efficiency of each wing is compared for a range of angles from 0° to 16°. The average value for the original wing is 6.84, while for the wings with bumps and dimples it is 6.47 and 7.16, respectively.

4. Discussion and Conclusions

In the present research, an attempt was made to simulate the passive control of the boundary layer of a wing and to analyze its effect on a three-dimensional wing. The investigation included a custom-designed wing based on the Eppler 420 airfoil, and two control techniques were investigated. Based on the international literature, one wing was selected to have bumps on the suction side of its surface and the other dimples.

Both of the surface interferences would be of the same shape (hemispherical), of the same diameter (2.5 mm), and would be placed in a straight line, intersecting the wing root and the wingtip at the same chord proportion (40%). The investigation was carried out by means of numerical simulations in a commercial code. Initially, the original wing was studied. Based on the regions where the separation of the boundary layer occurred, the placement of the configurations was selected in a region that could possibly affect an important part of the boundary layer. Then, the flows on the two new wings were simulated at two Reynolds numbers and five angles of attack. After the completion of the numerical simulations, an experiment was conducted in order to validate the results. The experimental procedure involved the investigation of the three wings in a flow of Re = 86,000 and was executed in an open-type subsonic wind tunnel.

The results of the numerical simulations showed that the presence of bumps has a catalytic effect on the boundary layer, but mainly in a negative way. There are points where it re-energizes the flow by locally increasing its momentum; however, its effect is considered to be negative since, in most cases, it increases the parasite drag and causes an earlier detachment of the boundary layer.

The presence of dimples clearly has a more positive effect on the wing than that of the bumps. It re-energizes the boundary layer locally and does not cause early detachment of the boundary layer. In most cases, the dimples increase the lift, and decrease, or have no effect on, the drag. This leads to it being considered to be a successful intervention, through increasing the aerodynamic performance of the wing by a percentage of 0.3% to 3%, depending on the Reynolds number.

What was also observed in both of the configurations is the fact that the aerodynamic performance of the wings is more sensitive to the effect of the modifications at lower Reynolds numbers.

Similar conclusions were derived from the experimental study. Initially, the numerical results showed acceptable deviations in comparison with the experimental results, in a range from 2% to 8%. The behavior of the wings appeared similar inside of the wind tunnel. The wing with dimples showed the best aerodynamic behavior, improving the aerodynamic performance of the original wing by about 4% on average. Conversely, the wing with bumps had a worse aerodynamic performance by an average of 5%. In this way, the initial conclusion that was drawn from the numerical simulations was confirmed.

As regards future research, it is proposed that, in addition to the extraction of the coefficient results, the experimental procedure should be used to visualize the formed boundary layer by means of a ‘Flow Viz’ type procedure.

It is also proposed to test the placement of dimples and bumps at a different point and not necessarily in a straight line from the wing root to the wingtip. Possibly, following the profile of the boundary layer detachment could be important research. Finally, more than one passive control method could be combined on the same wing, which is barely found in the international literature.