Diabetes Classification Using Machine Learning Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Data Preprocessing
2.3. Feature Selection and Construction
2.4. Classification Methods
2.4.1. Decision Tree
2.4.2. Random Forest
2.4.3. Support Vector Machine
2.4.4. K-Nearest Neighbor
2.5. Software Tool
3. Results
3.1. Hyperparameters for Machine Learning Techniques
3.1.1. Decision Tree
- ConfidenceFactor refers to the confidence intervals used in branching.
- MinNumObj refers to the minimum amount of learned information in the leaf node.
3.1.2. Random Forest
- NumIterations refers to the total number of trees to be built.
- MaxDepth refers to the maximum depth of the trees.
3.1.3. Support Vector Machine
- C refers to the regularization parameter.
- Kernel refers to the different types of mathematical functions, such as linear, polynomial, and RBF (radial basis function).
- Exponent refers to the exponent of the polykernel.
- Gamma refers to the hyperparameter that influences the learning dataset of the RBF kernel.
- kernel = polykernel (exponent = 1); C = 5.
- kernel = polykernel (exponent = 2); C = 5.
- kernel = RBF, C = 10, gamma = 0.1.
3.1.4. K-Nearest Neighbor
- K refers to the number of neighbor points used.
- distanceFunction refers to the distance function for finding neighbors. DistanceWeighting refers to the weighting function.
- distanceFunction = Euclidean, DistanceWeighting = Weight by 1/distance, K = 17.
- distanceFunction = Manhattan, DistanceWeighting = Weight by 1/distance, K = 21.
- distanceFunction = Euclidean, DistanceWeighting = Weight by 1/distance, K = 11.
- distanceFunction = Manhattan, DistanceWeighting = Weight by 1/distance, K = 13.
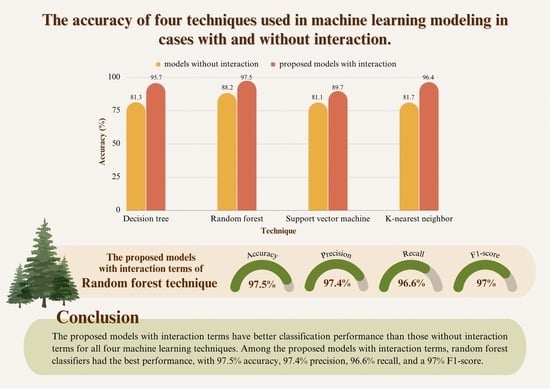
3.2. Comparison of the Efficiency of the Four Techniques
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Available online: https://www.who.int/news-room/fact-sheets/detail/diabetes (accessed on 29 April 2023).
- Available online: https://www.cdc.gov/diabetes/library/spotlights/diabetes-facts-stats.html (accessed on 29 April 2023).
- Griffin, P.; Rodgers, M.D. Type 1 Diabetes. National Institute of Diabetes and Digestive and Kidney Diseases. Available online: https://www.niddk.nih.gov/health-information/diabetes/overview/what-is-diabetes/type-1-diabetes (accessed on 14 April 2023).
- Griffin, P.; Rodgers, M.D. Risk Factors for Type 2 Diabetes. National Institute of Diabetes and Digestive and Kidney Diseases. Available online: https://www.niddk.nih.gov/health-information/diabetes/overview/risk-factors-type-2-diabetes (accessed on 14 April 2023).
- Available online: https://www.cdc.gov/diabetes/basics/risk-factors.html (accessed on 29 April 2023).
- Pacharawongsakda, E. An Introduction to Data Mining Techniques; Pearson Education: London, UK, 2014. [Google Scholar]
- Wei, S.; Zhao, X.; Miao, C. A comprehensive exploration to the machine learning techniques for diabetes identification. In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018; pp. 291–295. [Google Scholar] [CrossRef]
- Zou, Q.; Qu, K.; Luo, Y.; Yin, D.; Ju, Y.; Tang, H. Predicting Diabetes Mellitus with Machine Learning Techniques. Front Genet. 2018, 9, 515. [Google Scholar] [CrossRef] [PubMed]
- Sneha, N.; Tarun, G. Analysis of diabetes mellitus for early prediction using optimal features selection. J. Big Data 2019, 6, 13. [Google Scholar] [CrossRef]
- International Statistical Classification of Diseases and Related Health Problems 10th Revision. Available online: https://icd.who.int/browse10/2019/en#/E10-E14 (accessed on 29 April 2023).
- Available online: https://en.wikipedia.org/wiki/Information_gain_ratio#References (accessed on 29 April 2023).
- Changpetch, P.; Pitpeng, A.; Hiriote, S.; Yuangyai, C. Integrating Data Mining Techniques for Naïve Bayes Classification: Applications to Medical Datasets. Computation 2021, 9, 99. [Google Scholar] [CrossRef]
- Laiteerapong, N.; Karter, A.J.; Liu, J.Y.; Moffet, H.H.; Sudore, R.; Schillinger, D.; John, P.M.; Huang, E.S. Correlates of quality of life in older adults with diabetes: The Diabetes & Aging Study. Diabetes Care 2011, 34, 1749–1753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davidson, K.W.; Barry, M.J.; Mangione, C.M.; Cabana, M.; Caughey, A.B.; Davis, E.M.; Donahue, K.E.; Doubeni, C.A.; Krist, A.H.; Kubik, M.; et al. Screening for Prediabetes and Type 2 Diabetes: US Preventive Services Task Force Recommendation Stateme. JAMA 2021, 326, 736–743. [Google Scholar] [CrossRef] [PubMed]
- Deepti, S.; Dilip, S.S. Prediction of Diabetes using Classification Algorithms. In Proceedings of the International Conference on Computational Intelligence and Data Science (ICCIDS 2018), Gurugram, India, 7–8 April 2018; pp. 1578–1585. [Google Scholar] [CrossRef]
- Hafeez, M.A.; Rashid, M.; Tariq, H.; Abideen, Z.U.; Alotaibi, S.S.; Sinky, M.H. Performance Improvement of Decision Tree: A Robust Classifier Using Tabu Search Algorithm. Appl. Sci. 2021, 11, 6728. [Google Scholar] [CrossRef]
- Dimas, A.A.; Naqshauliza, D.K. Comparison of Accuracy Level of Support Vector Machine (SVM) and K-Nearest Neighbors (KNN) Algorithms in Predicting Heart Disease. Int. J. Emerg. Trends Eng. Res. 2020, 8, 1689–1694. [Google Scholar]
- Maneerat, P. WEKA Data Mining Program. 2012. Available online: https://maneerat-paranan.blogspot.com/2012/02/weka.html (accessed on 14 April 2023).
- Yang, H.; Luo, Y.; Ren, X.; Wu, M.; He, X.; Peng, B.; Deng, K. Risk Prediction of Diabetes: Big data mining with fusion of multifarious physical examination indicators. Inf. Fusion 2021, 75, 140–149. [Google Scholar] [CrossRef]
- Guasch-Ferre, M.; Hruby, A.; Toledo, E.; Clish, C.B.; Martínez-González, M.A.; Salas-Salvado, J.; Hu, F.B. Metabolomics in Prediabetes and Diabetes: A Systematic Review and Meta-analysis. Diabetes Care 2016, 39, 833–846. [Google Scholar] [CrossRef] [PubMed] [Green Version]











| Predicted | |||
|---|---|---|---|
| No | Yes | ||
| Actual | No Yes | TN FN | FP TP |
| Attribute | Measure |
|---|---|
| Diabetes diagnosis results | 0 = non-diabetes 1 = diabetes |
| Sex | 0 = male 1 = female |
| Age | year |
| Weight | kg |
| Height | cm. |
| Body mass index | kg/ |
| Diastolic blood pressure | mmHg |
| Systolic blood pressure | mmHg |
| Resting heart rate | bpm |
| Family history of diabetes | 0 = no 1 = yes |
| Attribute | Diabetes | Non-Diabetes | ||||
|---|---|---|---|---|---|---|
| Mean ± S.D. | Min | Max | Mean ± S.D. | Min | Max | |
| Age | 64 ± 10.96 | 31 | 94 | 62 ± 12.33 | 31 | 97 |
| Weight | 67 ± 14.71 | 31 | 167 | 62 ± 13.69 | 30 | 167 |
| Height | 159 ± 8.46 | 136 | 195 | 158 ± 8.49 | 100 | 195 |
| Body mass index | 26.16 ± 4.97 | 12.66 | 45.79 | 24.69 ± 4.75 | 12.49 | 45.18 |
| Diastolic blood pressure | 71.83 ± 12.49 | 35 | 150 | 73.90 ± 11.86 | 37 | 128 |
| Systolic blood pressure | 135.56 ± 18.33 | 80 | 237 | 132.51 ± 17.70 | 77 | 198 |
| Resting heart rate | 83.20 ± 14.09 | 36 | 151 | 82.43 ± 13.59 | 36 | 161 |
| Attribute | Details |
|---|---|
| Sex () | = 0 if sex = male = 1 if sex = female |
| Age () | = 0 if age < 60 = 1 if age ≥ 60 |
| Body mass index () | = 0 if body mass index < 23 = 1 if body mass index ≥ 23 |
| Diastolic blood pressure () | = 0 if diastolic blood pressure < 90 = 1 if diastolic blood pressure ≥ 90 |
| Systolic blood pressure () | = 0 if systolic blood pressure < 140 = 1 if systolic blood pressure ≥ 140 |
| Resting heart rate () | = 0 if 60 ≤ resting heart rate ≤ 100 = 1 if resting heart rate < 140 or resting heart rate > 100 |
| Family history of diabetes () | = 0 if family history of diabetes = no = 1 if family history of diabetes = yes |
| Interaction Variable | Generated Interactions |
|---|---|
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| and , then | if = 0 and = 0 , otherwise |
| and , then | if = 0 and = 1 , otherwise |
| and , then | if = 1 and = 0 , otherwise |
| and , then | if = 1 and = 1 , otherwise |
| Hyperparameter | Hyperparameter Value |
|---|---|
| confidenceFactor | 0.25, 0.5, 0.75 |
| minNumObj | 1, 3, 5, 7, 9 |
| Hyperparameter | Hyperparameter Value |
|---|---|
| numIterations | 10, 20, ..., 100 |
| maxDepth | 3, 5, 10, 20, none |
| Hyperparameter | Hyperparameter Value |
|---|---|
| C | 5, 10, 15, ..., 50 |
| kernel | polykernel (exponent = 1), polykernel (exponent = 2, …, 5), RBF |
| exponent | 2, 3, 4, 5 |
| gamma | 0.05, 0.1, 0.2, 0.5, 1 |
| Hyperparameter | Hyperparameter Value |
|---|---|
| K | 1, 3, ..., 31 |
| distanceFunction | Euclidean, Manhattan |
| DistanceWeighting | No distance weighting, Weight by 1/distance |
| Model | Technique | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| The models without interaction terms | Decision tree | 0.813 | 0.797 | 0.777 | 0.783 |
| Random forest | 0.882 | 0.922 | 0.893 | 0.907 | |
| Support vector machine | 0.811 | 0.764 | 0.774 | 0.769 | |
| K-nearest neighbor | 0.817 | 0.784 | 0.781 | 0.787 | |
| The proposed models with interaction terms | Decision tree | 0.957 | 0.949 | 0.945 | 0.949 |
| Random forest | 0.975 | 0.974 | 0.966 | 0.970 | |
| Support vector machine | 0.897 | 0.870 | 0.895 | 0.882 | |
| K-nearest neighbor | 0.964 | 0.962 | 0.949 | 0.956 |
| Hypotheses | t | Sig. |
|---|---|---|
| No difference in accuracy b/w random forest and decision tree. Random forest has more accuracy than decision tree. | −14.797 | 0.001 * |
| No difference in accuracy b/w random forest and support vector machine. Random forest has more accuracy than support vector machine. | −11.911 | 0.001 * |
| No difference in accuracy b/w random forest and K-nearest neighbor. Random forest has more accuracy than K-nearest neighbor. | −10.205 | 0.02 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phongying, M.; Hiriote, S. Diabetes Classification Using Machine Learning Techniques. Computation 2023, 11, 96. https://doi.org/10.3390/computation11050096
Phongying M, Hiriote S. Diabetes Classification Using Machine Learning Techniques. Computation. 2023; 11(5):96. https://doi.org/10.3390/computation11050096
Chicago/Turabian StylePhongying, Methaporn, and Sasiprapa Hiriote. 2023. "Diabetes Classification Using Machine Learning Techniques" Computation 11, no. 5: 96. https://doi.org/10.3390/computation11050096
APA StylePhongying, M., & Hiriote, S. (2023). Diabetes Classification Using Machine Learning Techniques. Computation, 11(5), 96. https://doi.org/10.3390/computation11050096