Comparative Study of Deflector Configurations under Variable Vertical Angle of Incidence and Wind Speed through Transient 3D CFD Modeling of Savonius Turbine
Abstract
:1. Introduction
2. Methodology
2.1. Flow Parameters
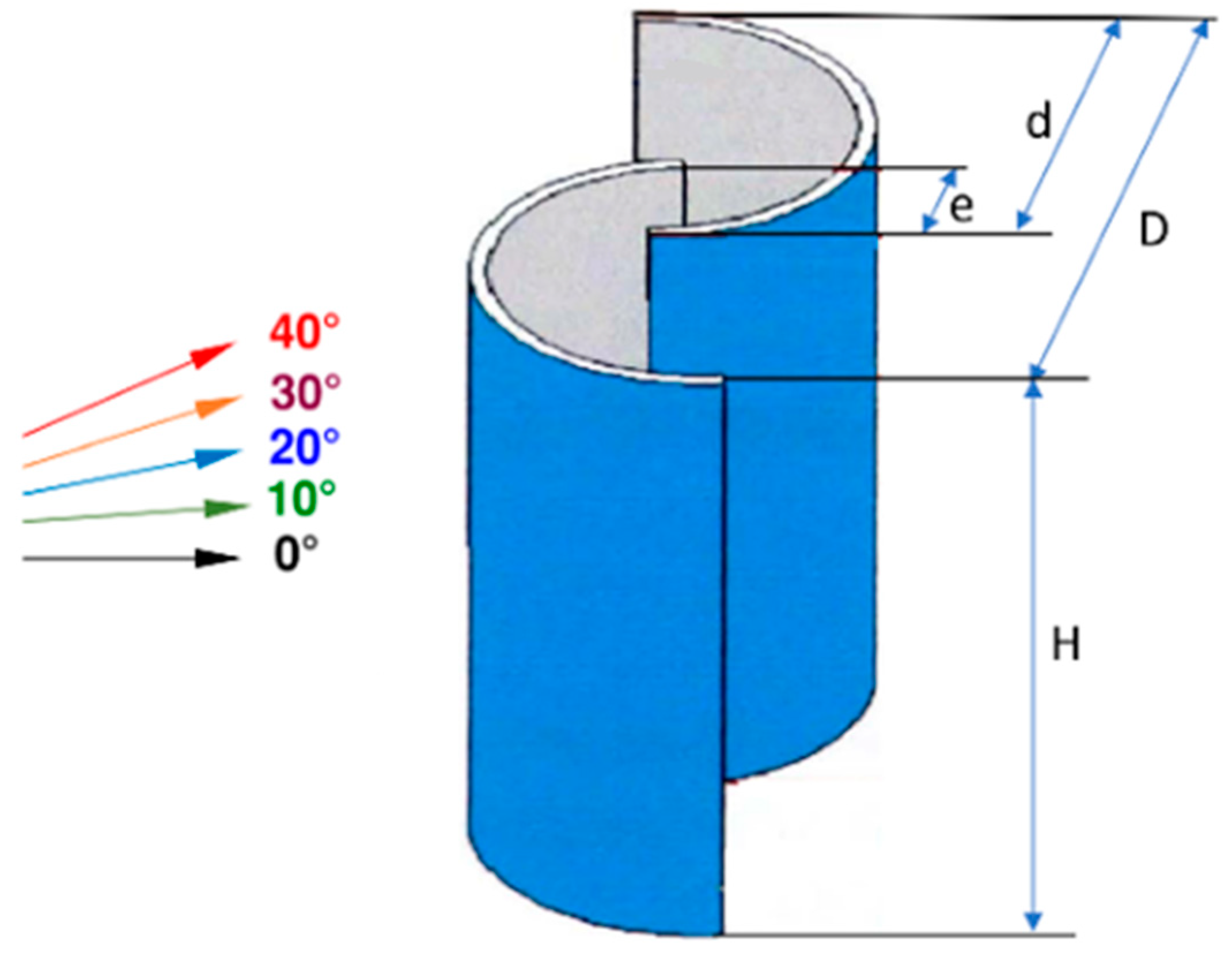
2.2. Geometric Details of the Standard Savonius Turbine (STD)
2.3. Geometric Details of Axisymetric Omnidirectional Deflector (AOD1) and (AOD2)
2.4. Computational Domain and Mesh
2.5. Governing Equations and Turbulence Models
2.6. Solver Settings
3. Results
3.1. Mesh and Timestep Sensitivity Analysis
3.2. Incidence Angle Effect on Power Coefficient on Various Configurations at a Wind Speed of 7 m·s−1
3.2.1. Power Coefficient
3.2.2. Pressure Contours and Streamlines
3.3. Effect of Different Incoming Wind Speed on the Turbine Performance for Different Incidence Angles
4. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alexander, A.; Holownia, B. Wind tunnel tests on a savonius rotor. J. Ind. Aerodyn. 1978, 3, 343–351. [Google Scholar] [CrossRef]
- Blackwell, B.F.; Sheldahl, R.E.; Feltz, L.V. Wind Tunnel Performance Data for Two and Three Bucket Savonius Rotor; Sandia National Laboratories Report, SAND76-0l30; Sandia Laboratories: Springfield, VA, USA, 1977. [Google Scholar]
- El-Askary, W.A.; Nasef, M.H.; Abdelhamid, A.A.; Gad, H.E. Harvesting wind energy for improving performance of Savonius rotor. J. Wind Eng. Ind. Aerodyn. 2015, 139, 8–15. [Google Scholar] [CrossRef]
- Ferrari, G.; Federici, D.; Schito, P.; Inzoli, F.; Mereu, R. CFD study of Savonius wind turbine: 3D model validation and parametric analysis. Renew. Energy 2017, 105, 722–734. [Google Scholar] [CrossRef]
- Renato, R.; Roberto, R.; Sergio, M.; Daniele, V. Experimental study on a Savonius wind rotor for street lighting systems. Appl. Energy 2016, 161, 143–152. [Google Scholar] [CrossRef]
- Fujisawa, N. On the torque mechanism of Savonius rotors. J. Wind. Eng. Ind. Aerodyn. 1991, 40, 277–292. [Google Scholar] [CrossRef]
- Frederikus, W.; Andy, S.; Hadi, S. An Experimental Study on the Performance of Savonius Wind Turbines Related With The Number Of Blades. Energy Procedia 2015, 68, 297–304. [Google Scholar] [CrossRef]
- Thiyagaraj, J.; Rahamathullah, I.; Anbuchezhiyan, G.; Barathiraja, R.; Ponshanmugakumar, A. Influence of blade numbers, overlap ratio and modified blades on performance characteristics of the savonius hydro-kinetic turbine. Mater. Today Proc. 2021, 46, 4047–4053. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Amir, F.; Franco, M. Investigation of deflector geometry and turbine aspect ratio effect on 3D modified in-pipe hydro Savonius turbine: Parametric study. Renew. Energy 2020, 148, 44–59. [Google Scholar] [CrossRef]
- Jeon, K.S.; Jeong, J.I.; Pan, J.-K.; Ryu, K.-W. Effects of end plates with various shapes and sizes on helical Savonius wind turbines. Renew. Energy 2015, 79, 167–176. [Google Scholar] [CrossRef]
- Akwa, J.V.; Vielmo, H.A.; Petry, A.P. A review on the performance of Savonius wind turbines. Renew. Sustai. Energy Rev. 2012, 16, 3054–3064. [Google Scholar] [CrossRef]
- Sobczak, K. Numerical investigations of an influence of the aspect ratio on the Savonius rotor performance. J. Phys. Conf. Ser. 2018, 1101, 012034. [Google Scholar] [CrossRef]
- Tong, Z.; Dietmar, R. Numerical study of detailed flow field and performance of Savonius wind turbines. Renew. Energy 2013, 51, 373–381. [Google Scholar] [CrossRef]
- Al Absi, S.M.; Jabbar, A.H.; Mezan, S.O.; Al-Rawi, B.A.; Al_Attabi, S.T. An experimental test of the performance enhancement of a Savonius turbine by modifying the inner surface of a blade. Mater. Today Proc. 2021, 42, 2233–2240. [Google Scholar] [CrossRef]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage modified Savonius rotor. Appl. Energy 2009, 86, 1064–1073. [Google Scholar] [CrossRef]
- Morcos, S.; Khalafallah, M.; Heikel, H. The effect of sheilding on the aerodynamic performance of Savonius wind turbines. ASME 1981, 2, 2037–2040. [Google Scholar]
- Shaughnessy, B.M.; Probert, S.D. Partially-Blocked Savonius Rotor. Appl. Energ. 1992, 43, 239–249. [Google Scholar] [CrossRef]
- Yonghai, H.; Zhengmin, T.; Shanshan, W. A new type of VAWT and blade optimization. In Proceedings of the International Technology and Innovation Conference 2009 (ITIC 2009), Xi’an, China, 12–14 October 2009. [Google Scholar]
- Burçin, D.A.; Mehmet, A. The use of a curtain design to increase the performance level of a Savonius wind rotors. Renew. Energy 2010, 35, 821–829. [Google Scholar] [CrossRef]
- Tartuferi, M.; Alessandro, V.; Montelpare, S.; Ricci, R. Enhancement of Savonius wind rotor aerodynamic performance: A computational study of new blade shapes and curtain systems. Energy 2015, 79, 371–384. [Google Scholar] [CrossRef]
- Aboujaoude, H.; Bogard, F.; Beaumont, F.; Murer, S.; Polidori, G. Aerodynamic Performance Enhancement of an Axisymmetric Deflector Applied to Savonius Wind Turbine Using Novel Transient 3D CFD Simulation Techniques. Energies 2023, 16, 909. [Google Scholar] [CrossRef]
- Aboujaoude, H.; Beaumont, F.; Murer, S.; Polidori, G.; Bogard, F. Aerodynamic performance enhancement of a Savonius wind turbine using an axisymmetric deflector. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104882. [Google Scholar] [CrossRef]
- Ross, I.; Altman, A. Wind tunnel blockage corrections: Review and application to Savonius vertical-axis wind turbines. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 523–538. [Google Scholar] [CrossRef]
- Saha, U.K.; Thotla, S.; Maity, D. Optimum design configuration of Savonius rotor through wind tunnel experiments. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1359–1375. [Google Scholar] [CrossRef]
- Svetlana, M. Performance of a Savonius Wind Turbine in Urban Sites Using CFD Analysis. Thesis, University of VAASA, Vaasa, Finland, 2016. [Google Scholar]
- Modi, V.J.; Fernando, M.S.U.K. On the performance of the Savonius wind turbine. J. Sol. Energy Eng. 1989, 111, 71–81. [Google Scholar] [CrossRef]
- Duc, M.B.; The, H.T.; Van, K.P.; Le, A.D. Predicting aerodynamic performance of savonius wind turbine: An application of generalized k-ω turbulence model. Ocean. Eng. 2023, 286, 115690. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. On the accuracy of turbulence models for CFD simulations of vertical axis wind turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K.; Dean, A. In the quest of an appropriate turbulence model for analyzing the aerodynamics of a conventional Savonius (S-type) wind rotor. J. Renew. Sustain. Energy 2021, 13, 023313. [Google Scholar] [CrossRef]







| Authors | Design | Reported CPmax | Study | Wind Concentrator |
|---|---|---|---|---|
| El-Askary et al., 2015 [3] | Curtain design | >0.5 | Numerical—2D CFD | Unidirectional |
| Burçin et al., 2010 [20] | Curtain design | 0.38 | Experimental—Wind tunnel | Unidirectional |
| Morcos et al., 1981 [17] | Flat plate shield | 0.34 | Experimental—Wind tunnel | Unidirectional |
| Aboujaoude et al., 2022 [21] | Axisymmetric deflector | 0.31 | Numerical—3D CFD | Axisymmetric multidirectional |
| Tartuferi et al., 2015 [22] | Curtain design | 0.3 | Numerical—2D CFD | Self-rotating |
| Yonghai et al., 2009 [19] | Deflector plate | 0.28 * | Numerical—2D CFD | Unidirectional |
| Alexander et Holownia, 1978 [1] | Flat plate shield | 0.24 | Experimental—Wind tunnel | Unidirectional |
| Shaughnessy et Probert, 1992 [18] | V-shaped deflector | <0.12 * | Experimental—Wind tunnel | Unidirectional |
| Parameters | Description | Unit | Values |
|---|---|---|---|
| λ | Tip speed ratio | Dimensionless | 0.2; 0.4; 0.6; 0.8; 1.0 |
| θ | Vertical wind incident angle | Degree | 0°; 10°; 20°; 30°; 40° |
| Freestream air speed | m/s | 3.5; 7.0; 14.0 |
| Number of Blades | Blade Diameter | Turbine Height | Endplate Diameter | Endplate Height | Dimensionless Gap Width e/d |
|---|---|---|---|---|---|
| 2 | 0.5 m | 1.5 m | 1.0 m | 0.01 m | 0.15 |
| Parameters | Method or Specification |
|---|---|
| Solver Type | Transient |
| Turbulence Model | kw-SST |
| Solution Method | Hybrid solver using Pressure Coupled and Simple Algorithms |
| Timestep | 1° |
| Residual Criteria | 10–4 for the continuity and 10–6 for all the other parameters |
| Rotational Model | Sliding mesh technique |
| Spatial discretization: Gradient | Least square cell based |
| Spatial discretization: Pressure | Second order |
| Momentum, Turbulence Kinetic Energy & Specific Dissipation Rate | Second order upwind |
| Transient Formulation | Second order implicit |
| Rotation Angle per Time Step | Cp at λ = 1.0 |
|---|---|
| 0.5° | 0.2307 |
| 1° | 0.2305 |
| 2° | 0.225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboujaoude, H.; Polidori, G.; Beaumont, F.; Murer, S.; Toumi, Y.; Bogard, F. Comparative Study of Deflector Configurations under Variable Vertical Angle of Incidence and Wind Speed through Transient 3D CFD Modeling of Savonius Turbine. Computation 2024, 12, 204. https://doi.org/10.3390/computation12100204
Aboujaoude H, Polidori G, Beaumont F, Murer S, Toumi Y, Bogard F. Comparative Study of Deflector Configurations under Variable Vertical Angle of Incidence and Wind Speed through Transient 3D CFD Modeling of Savonius Turbine. Computation. 2024; 12(10):204. https://doi.org/10.3390/computation12100204
Chicago/Turabian StyleAboujaoude, Hady, Guillaume Polidori, Fabien Beaumont, Sébastien Murer, Yessine Toumi, and Fabien Bogard. 2024. "Comparative Study of Deflector Configurations under Variable Vertical Angle of Incidence and Wind Speed through Transient 3D CFD Modeling of Savonius Turbine" Computation 12, no. 10: 204. https://doi.org/10.3390/computation12100204
APA StyleAboujaoude, H., Polidori, G., Beaumont, F., Murer, S., Toumi, Y., & Bogard, F. (2024). Comparative Study of Deflector Configurations under Variable Vertical Angle of Incidence and Wind Speed through Transient 3D CFD Modeling of Savonius Turbine. Computation, 12(10), 204. https://doi.org/10.3390/computation12100204












