Classical Chaos in a Driven One-Dimensional Quartic Anharmonic Oscillator
Abstract
1. Introduction
2. One-Dimensional Quartic Anharmonic Oscillator Driven by a Time-Dependent External Square-Wave Force
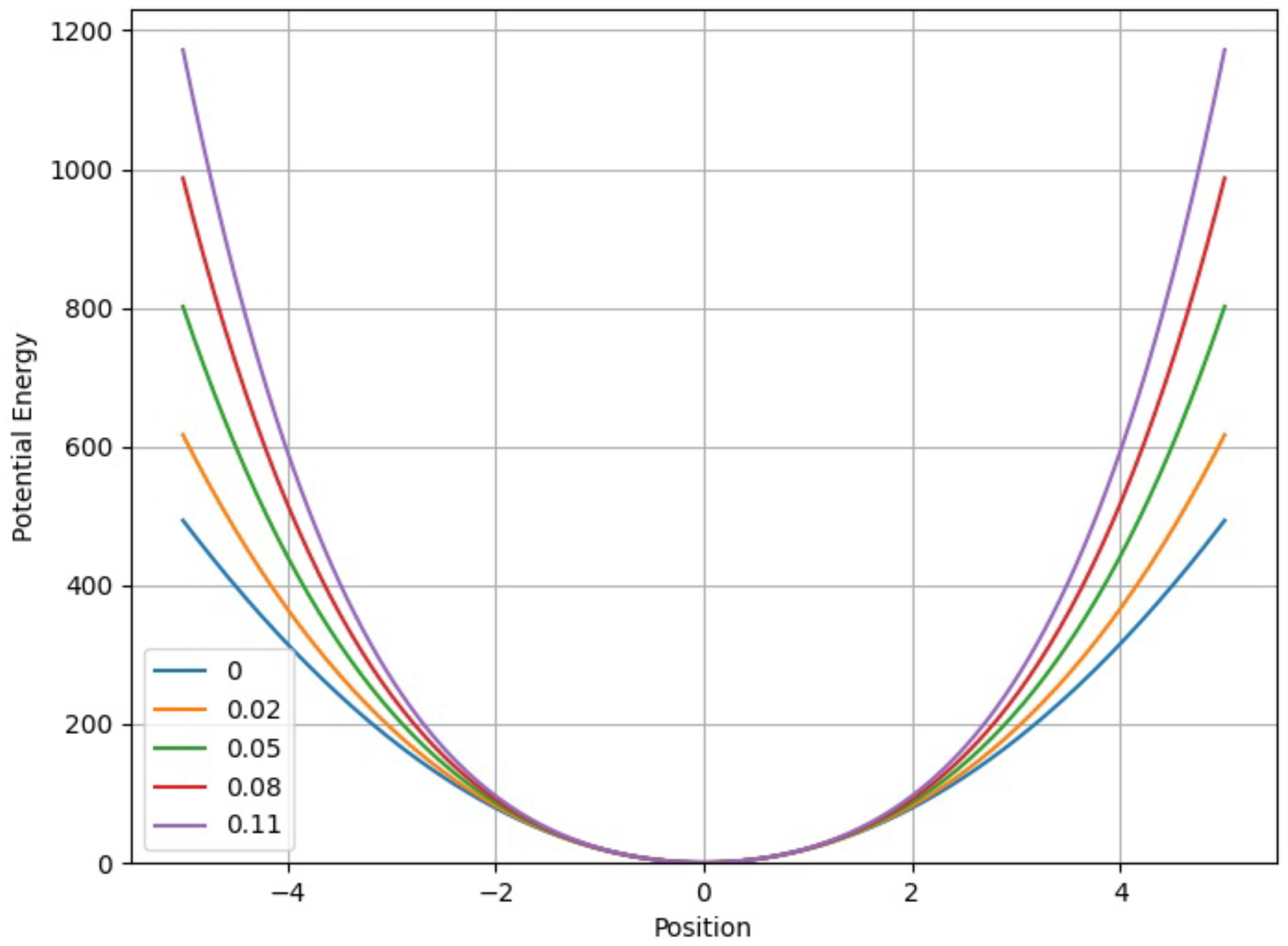
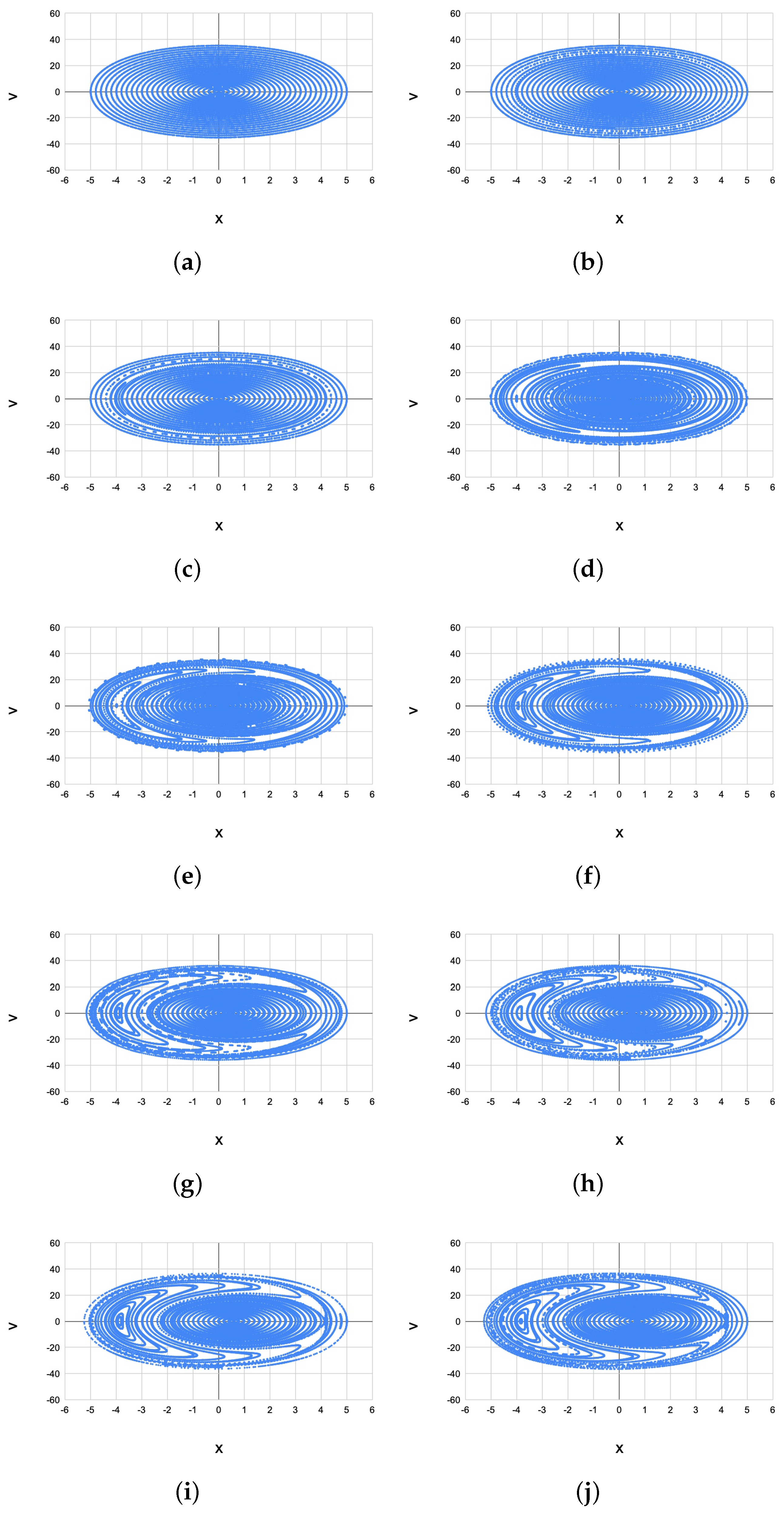
3. Results and Discussion
3.1.
3.2.
3.3. and
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lichtenberg, A.J.; Lieberman, M.A. Regular and Stochastic Motion; Springer: New York, NY, USA, 1983. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Bolotin, Y.; Tur, A.; Yanovsky, V. Chaos: Concepts, Control and Constructive Use; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Atlas, R. Three kinds of butterfly effects within Lorenz models. Encyclopedia 2022, 2, 1250–1259. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263–379. [Google Scholar] [CrossRef]
- Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Ueda, Y. Survey of regular and chaotic phenomena in the forced Duffing oscillator. Chaos Solitons Fractals 1991, 1, 199–231. [Google Scholar] [CrossRef]
- Lee, S.-W.; Lee, H.-W. Chaotic one-dimensional harmonic oscillator. Phys. Rev. E 1997, 56, 5245–5250. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Rajasekar, S. Nonlinear Dynamics: Integrability, Chaos and Patterns; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Mandal, S. The approximate solution of a classical quartic anharmonic oscillator with periodic force: A simple analytical approach. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 341–352. [Google Scholar] [CrossRef]
- Butikov, E.I. Square-wave excitation of a linear oscillator. Am. J. Phys. 2004, 72, 469–476. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; Wiley: Chichester, UK, 2008. [Google Scholar]
- Feigenbaum, M.J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 1978, 19, 25–52. [Google Scholar] [CrossRef]
- Saiki, Y.; Yorke, J.A. Can the flap of a butterfly’s wings shift a tornado into Texas–without chaos? Atmosphere 2023, 14, 821. [Google Scholar] [CrossRef]
- Elwakil, A.S. Nonautonomous pulse-driven chaotic oscillator based on Chua’s circuit. Microelectron. J. 2002, 33, 479–486. [Google Scholar] [CrossRef]
- Gandhimathi, V.M.; Murali, K.; Rajasekar, S. Stochastic resonance with different periodic forces in overdamped two coupled anharmonic oscillators. Chaos Solitons Fractals 2006, 30, 1034–1047. [Google Scholar] [CrossRef]
- Duffing, G. Erzwungene Schwingungen bei Veränderlicher Eigenfrequenz und Ihre Technische Bedeutung; Vieweg: Braunschweig, Germany, 1918. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and their Behaviour; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Blanchard, P.; Devaney, R.L.; Hall, G.R. Differential Equations; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Shen, B.-W. Homoclinic orbits and solitary waves within the nondissipative Lorenz model and KdV equation. Int. J. Bifurc. Chaos 2020, 30, 2050257. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N. Modern Analysis; Cambridge University Press: Cambridge, UK, 1947. [Google Scholar]
- Hsu, C.S. On the application of elliptic functions in non-linear forced oscillations. Q. Appl. Math. 1960, 17, 393–407. [Google Scholar] [CrossRef]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2014. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-H.; Chai, J.-D. Classical Chaos in a Driven One-Dimensional Quartic Anharmonic Oscillator. Computation 2024, 12, 246. https://doi.org/10.3390/computation12120246
Lin Y-H, Chai J-D. Classical Chaos in a Driven One-Dimensional Quartic Anharmonic Oscillator. Computation. 2024; 12(12):246. https://doi.org/10.3390/computation12120246
Chicago/Turabian StyleLin, Yun-Hsi, and Jeng-Da Chai. 2024. "Classical Chaos in a Driven One-Dimensional Quartic Anharmonic Oscillator" Computation 12, no. 12: 246. https://doi.org/10.3390/computation12120246
APA StyleLin, Y.-H., & Chai, J.-D. (2024). Classical Chaos in a Driven One-Dimensional Quartic Anharmonic Oscillator. Computation, 12(12), 246. https://doi.org/10.3390/computation12120246






