A Weighted and Epsilon-Constraint Biased-Randomized Algorithm for the Biobjective TOP with Prioritized Nodes
Abstract
:1. Introduction
2. Related Work
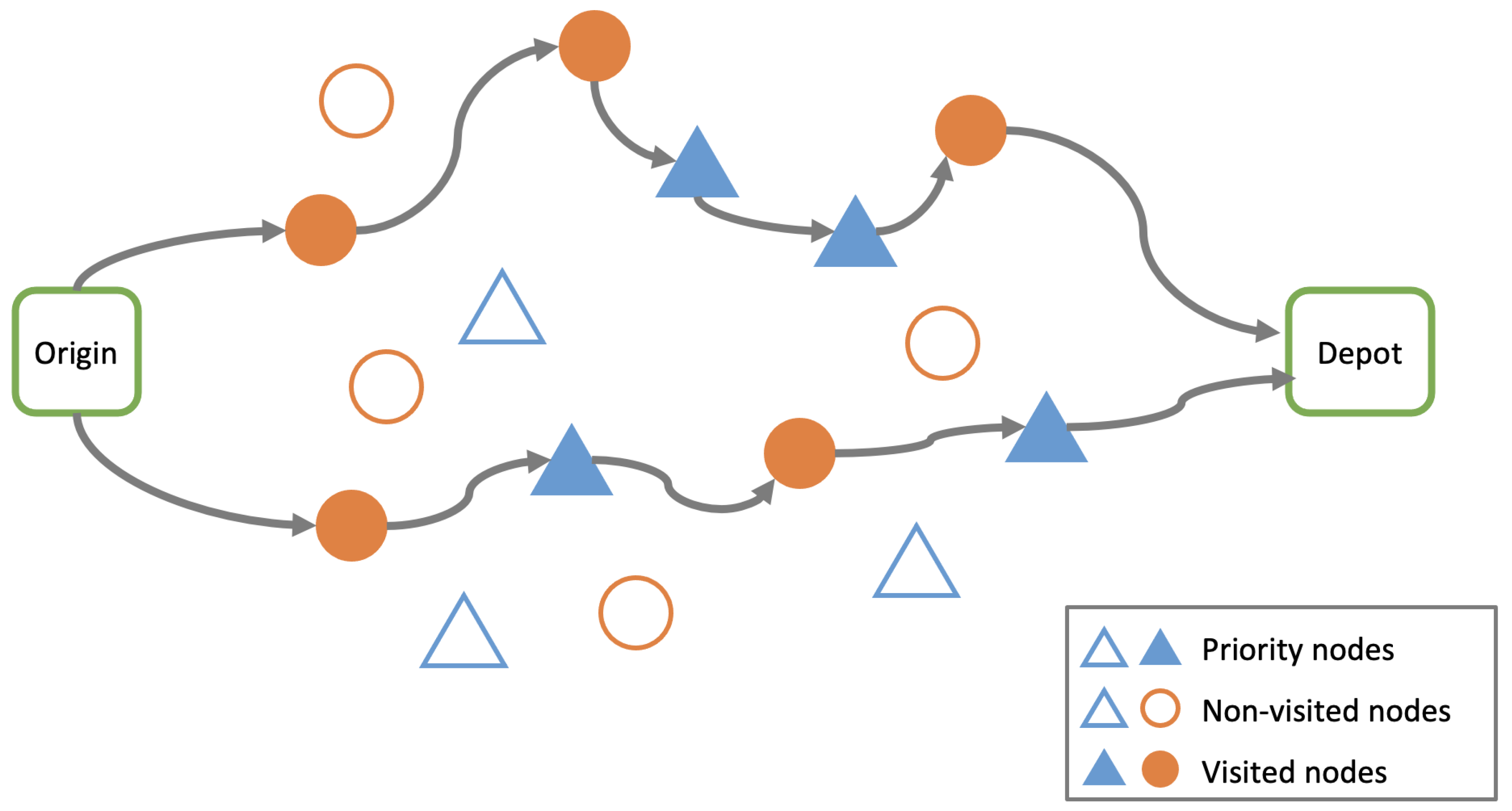
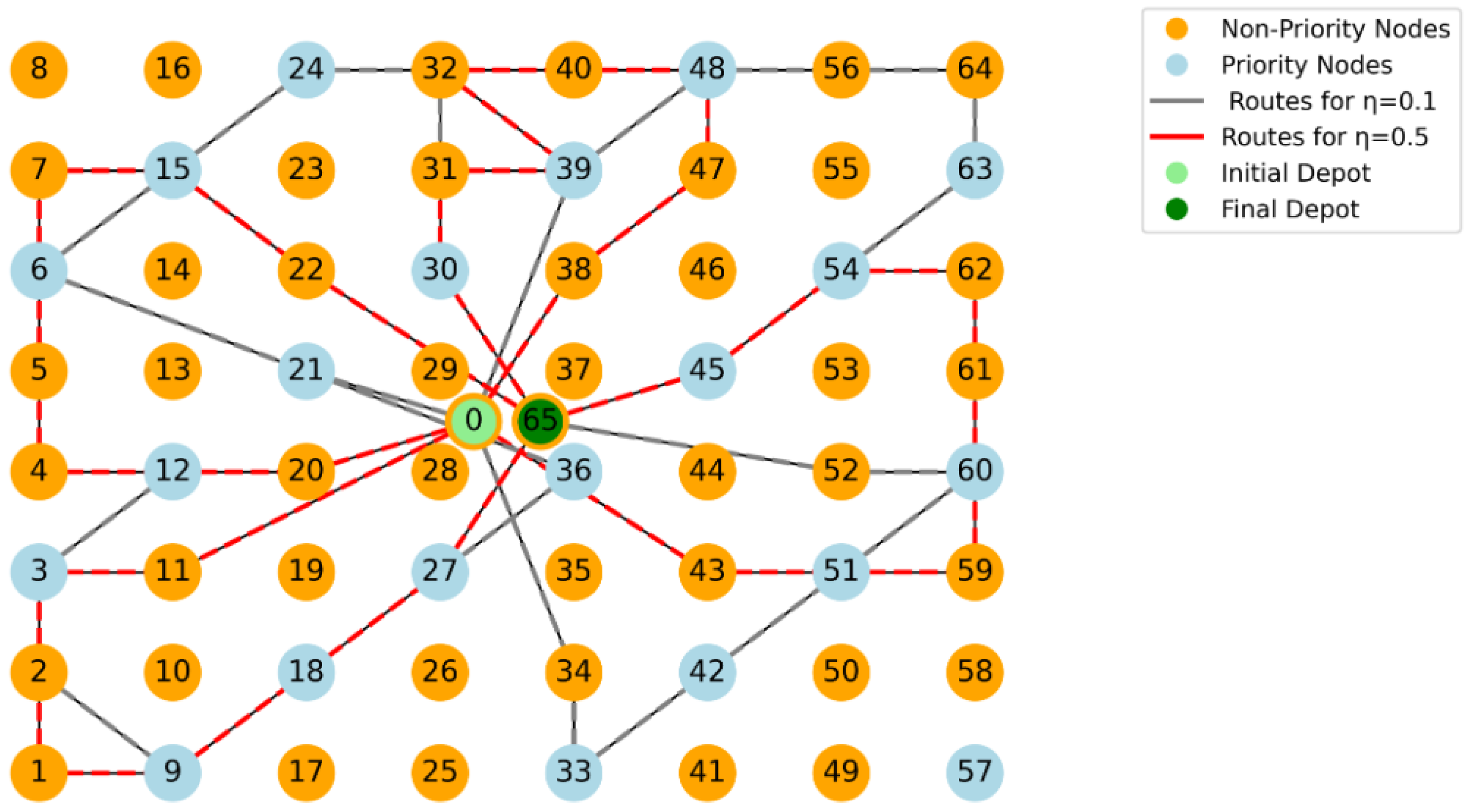
3. Formal Description of the MultiObjective TOP
4. Alternative Approaches for Solving the MO-TOP
4.1. The Weighted Average Method and the Ponderate Weighted Average Method
| Algorithm 1 WAM/POWAM |
Input: Data Output: Best_Sol
|
4.2. The Epsilon-Constraint Method
| Algorithm 2 ECM |
Input: Data Output: Best_Sol
|
- Epsilon-Constraint Positional Method (ECPM): The procedure to generate a solution that satisfies the new constraint where is involved starts by constructing a list of routes ordered by reward. Then, the list is separated into two: one auxiliary solution of the fleet size and the other with the rest of the routes. The auxiliary solution will be the solution of the problem in case it verifies the constraint. Otherwise, the one with the lowest reward is replaced by one of the rest that has a higher PN than it. Recursively, all the positions of the auxiliary solution are run through until a solution is found or the list has been completed.
- Epsilon-Constraint Sublists Method (ECSM): In this other implementation, once the above list of routes has been constructed, the possible sublists of fleet size are generated. Of all of them, the one with the highest reward that verifies the restriction is chosen.
4.3. The Epsilon-Modified Method
| Algorithm 3 EMM |
Input: Data Output: Best_Sol
|
5. Computational Experiments
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| N | Set of intermediate nodes: |
| Set of nodes including the initial and final depots: | |
| E | Set of edges connecting the nodes: |
| G | Graph of the network, |
| D | Set of homogeneous vehicles |
| Travel time for each edge, | |
| Maximum travel time for each vehicle or route | |
| Reward of the node | |
| Binary variable whose value is equal to 1 if vehicle d traverses edge | |
| Position of the node i in the tour made for the vehicle d | |
| Binary variable whose value is equal to 1 if node i is priority | |
| Weight for pondering the rewards in the biobjective function | |
| Convex linear combination constant in the efficiency value | |
| Convex linear combination constant in the biefficiency value | |
| Convex linear combination constant in the biobjective function | |
| Time-based savings associated to the edge , | |
| Efficiency value associated to the edge , | |
| Biefficiency value associated to the edge , | |
| Deviation from the optimal value for the secondary objectives, | |
| Total number of priority nodes being visited |
References
- Chao, I.M.; Golden, B.L.; Wasil, E.A. The team orienteering problem. Eur. J. Oper. Res. 1996, 88, 464–474. [Google Scholar] [CrossRef]
- Golden, B.L.; Levy, L.; Vohra, R. The orienteering problem. Nav. Res. Logist. 1987, 34, 307–318. [Google Scholar] [CrossRef]
- Gunawan, A.; Lau, H.C.; Vansteenwegen, P. Orienteering Problem: A survey of recent variants, solution approaches and applications. Eur. J. Oper. Res. 2016, 255, 315–332. [Google Scholar] [CrossRef]
- Gunawan, A.; Ng, K.M.; Kendall, G.; Lai, J. An iterated local search algorithm for the team orienteering problem with variable profits. Eng. Optim. 2018, 0273, 1–16. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Van Oudheusden, D. The orienteering problem: A survey. Eur. J. Oper. Res. 2011, 209, 1–10. [Google Scholar] [CrossRef]
- Panadero, J.; Juan, A.A.; Bayliss, C.; Currie, C. Maximising reward from a team of surveillance drones: A simheuristic approach to the stochastic team orienteering problem. Eur. J. Ind. Eng. 2020, 14, 485–516. [Google Scholar] [CrossRef]
- Gosavi, A. Simulation-Based Optimization; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Archetti, C.; Hertz, A.; Speranza, M.G. Metaheuristics for the team orienteering problem. J. Heuristics 2007, 13, 49–76. [Google Scholar] [CrossRef]
- Ke, L.; Archetti, C.; Feng, Z. Ants can solve the team orienteering problem. Comput. Ind. Eng. 2008, 54, 648–665. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Berghe, G.V.; Van Oudheusden, D. A guided local search metaheuristic for the team orienteering problem. Eur. J. Oper. Res. 2009, 196, 118–127. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Berghe, G.V.; Van Oudheusden, D. Iterated local search for the team orienteering problem with time windows. Comput. Oper. Res. 2009, 36, 3281–3290. [Google Scholar] [CrossRef]
- Souffriau, W.; Vansteenwegen, P.; Berghe, G.V.; Van Oudheusden, D. A path relinking approach for the team orienteering problem. Comput. Oper. Res. 2010, 37, 1853–1859. [Google Scholar] [CrossRef]
- Tricoire, F.; Romauch, M.; Doerner, K.F.; Hartl, R.F. Heuristics for the multi-period orienteering problem with multiple time windows. Comput. Oper. Res. 2010, 37, 351–367. [Google Scholar] [CrossRef]
- Souffriau, W.; Vansteenwegen, P.; Vanden Berghe, G.; Van Oudheusden, D. The multiconstraint team orienteering problem with multiple time windows. Transp. Sci. 2013, 47, 53–63. [Google Scholar] [CrossRef]
- Verbeeck, C.; Sörensen, K.; Aghezzaf, E.H.; Vansteenwegen, P. A fast solution method for the time-dependent orienteering problem. Eur. J. Oper. Res. 2014, 236, 419–432. [Google Scholar] [CrossRef]
- Vidal, T.; Maculan, N.; Ochi, L.S.; Vaz Penna, P.H. Large neighborhoods with implicit customer selection for vehicle routing problems with profits. Transp. Sci. 2016, 50, 720–734. [Google Scholar] [CrossRef]
- Paolucci, M.; Anghinolfi, D.; Tonelli, F. Field services design and management of natural gas distribution networks: A class of vehicle routing problem with time windows approach. Int. J. Prod. Res. 2018, 56, 1154–1170. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Ferrer, A.; Juan, A.A.; Panadero, J.; Bagirov, A. The Non-Smooth and Bi-Objective Team Orienteering Problem with Soft Constraints. Mathematics 2020, 8, 1461. [Google Scholar] [CrossRef]
- Ruiz-Meza, J.; Brito, J.; Montoya-Torres, J.R. A GRASP to solve the multi-constraints multi-modal team orienteering problem with time windows for groups with heterogeneous preferences. Comput. Ind. Eng. 2021, 162, 107776. [Google Scholar] [CrossRef]
- Sankaran, P.; McConky, K.; Sudit, M.; Ortiz-Peña, H. GAMMA: Graph attention model for multiple agents to Solve team orienteering problem With multiple depots. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9412–9423. [Google Scholar] [CrossRef]
- Panadero, J.; Juan, A.A.; Ghorbani, E.; Faulin, J.; Pagès-Bernaus, A. Solving the stochastic team orienteering problem: Comparing simheuristics with the sample average approximation method. Int. Trans. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Wattanasaeng, N.; Ransikarbum, K. Model and Analysis of Economic- and Risk-Based Objective Optimization Problem for Plant Location within Industrial Estates Using Epsilon-Constraint Algorithms. Computation 2021, 9, 46. [Google Scholar] [CrossRef]
- Mohammadi, T.; Sajadi, S.M.; Najafi, S.E.; Taghizadeh-Yazdi, M. Multi Objective and Multi-Product Perishable Supply Chain with Vendor-Managed Inventory and IoT-Related Technologies. Mathematics 2024, 12, 679. [Google Scholar] [CrossRef]
- Nikoubin, A.; Mahnam, M.; Moslehi, G. A relax-and-fix Pareto-based algorithm for a bi-objective vaccine distribution network considering a mix-and-match strategy in pandemics. Appl. Soft Comput. 2023, 132, 109862. [Google Scholar] [CrossRef]
- Shojatalab, G.; Nasseri, S.H.; Mahdavi, I. New multi-objective optimization model for tourism systems with fuzzy data and new algorithm for solving this model. Oper. Res. Soc. India 2022, 59, 1018–1037. [Google Scholar] [CrossRef]
- Elmi, Z.; Li, B.; Liang, B.; Lau, Y.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. An epsilon-constraint-based exact multi-objective optimization approach for the ship schedule recovery problem in liner shipping. Comput. Ind. Eng. 2023, 183, 109472. [Google Scholar] [CrossRef]
- Banerjee, A.; Pradhan, S.; Misra, B.; Chakraborty, S. A Guide to Meta-Heuristic Algorithms for Multi-objective Optimization: Concepts and Approaches. In Applied Multi-Objective Optimization; Springer Nature: Singapore, 2024; pp. 1–19. [Google Scholar]
- Memarian, S.; Behmanesh-Fard, N.; Aryai, P.; Shokouhifar, M.; Mirjalili, S.; Romero-Ternero, M. TSFIS-GWO: Metaheuristic-driven takagi-sugeno fuzzy system for adaptive real-time routing in WBANs. Appl. Soft Comput. 2024, 155, 111427. [Google Scholar] [CrossRef]
- Evers, L.; Glorie, K.; van der Ster, S.; Barros, A.I.; Monsuur, H. A two-stage approach to the orienteering problem with stochastic weights. Comput. Oper. Res. 2014, 43, 248–260. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Savelsbergh, M.; Juan, A.A.; Panadero, J. Biased-randomized iterated local search for a multiperiod vehicle routing problem with price discounts for delivery flexibility. Int. Trans. Oper. Res. 2019, 26, 1293–1314. [Google Scholar] [CrossRef]
- Panadero, J.; de Armas, J.; Currie, C.S.; Juan, A.A. A simheuristic approach for the stochastic team orienteering problem. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 3208–3217. [Google Scholar]

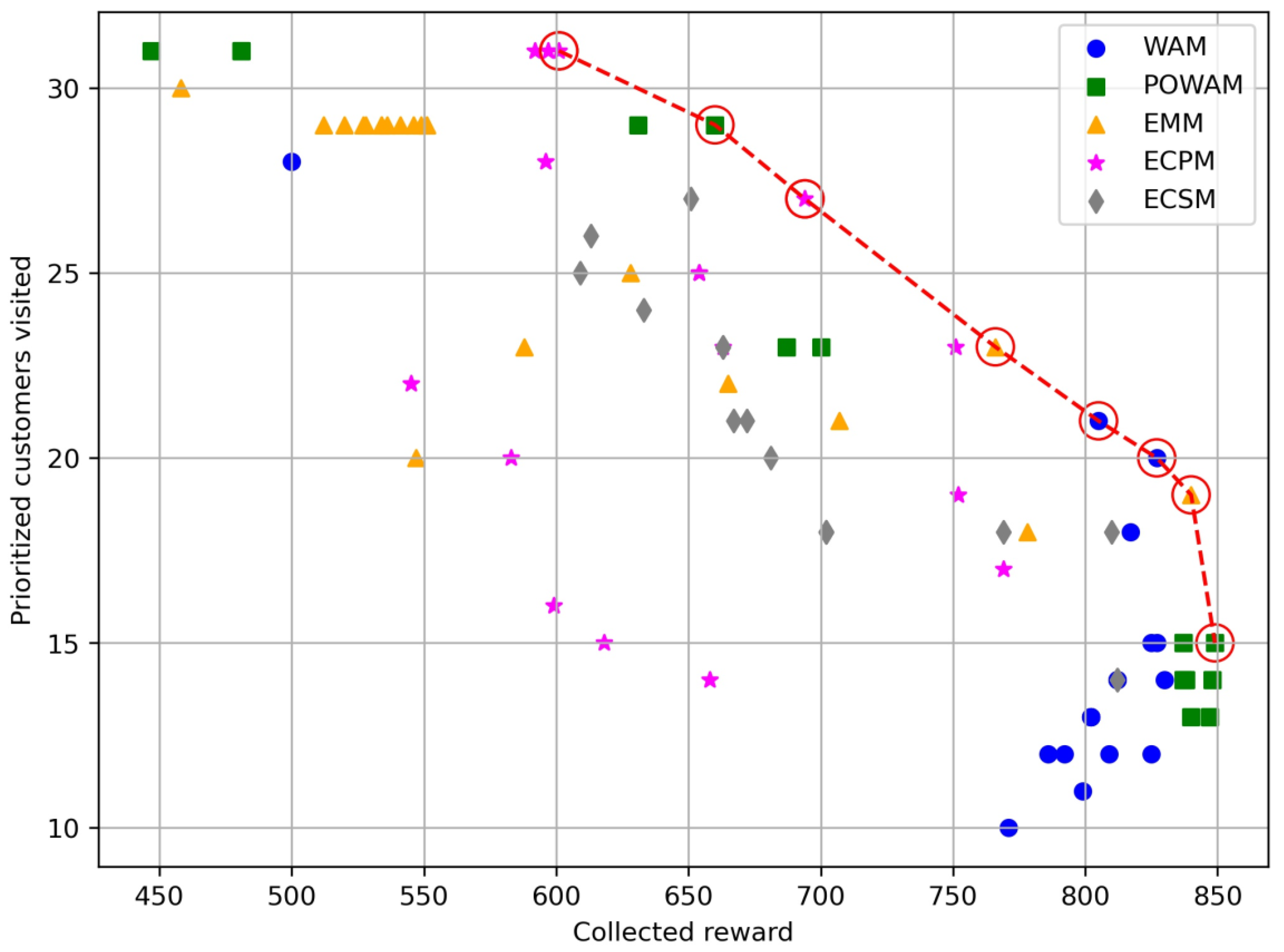


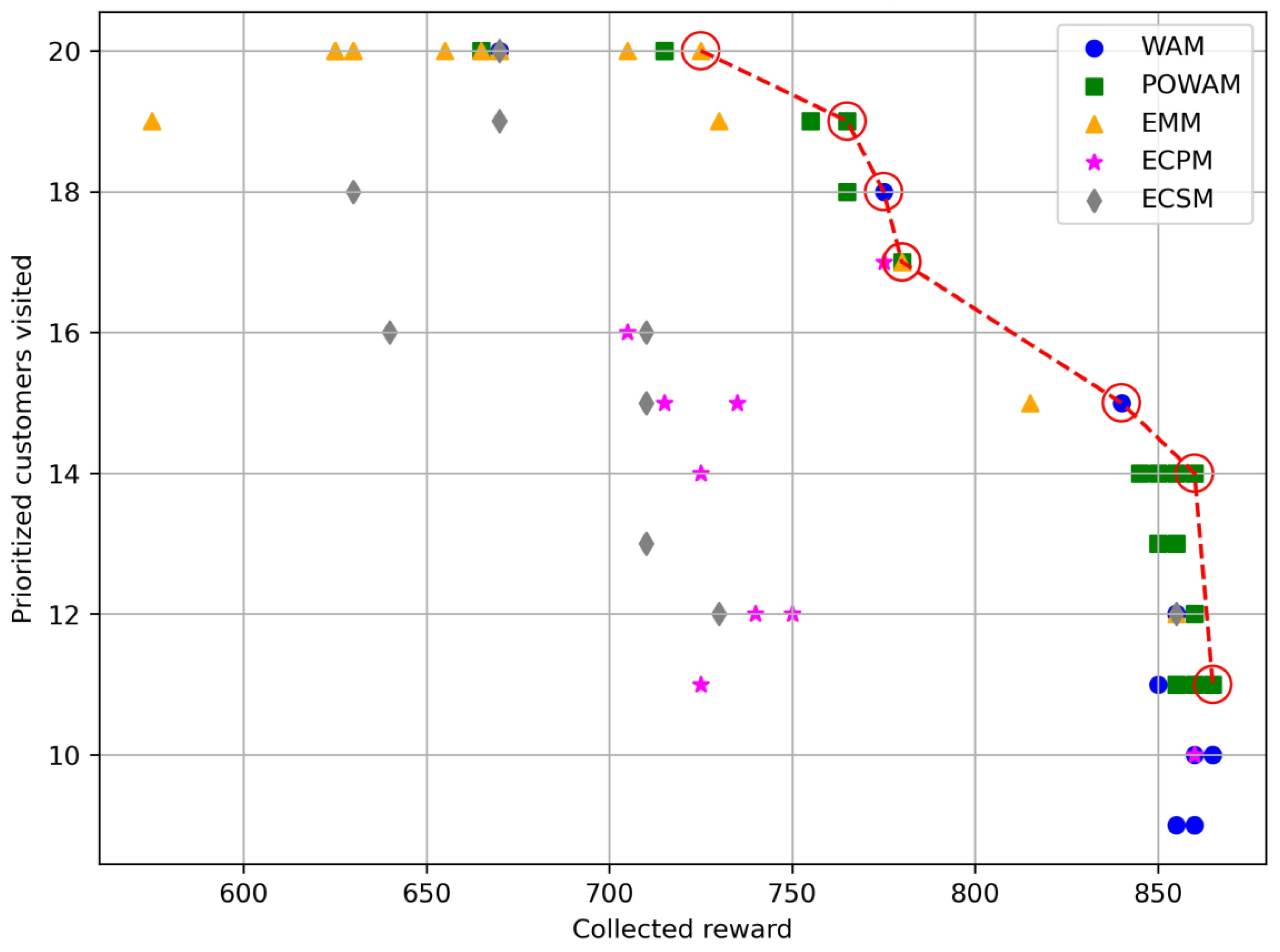

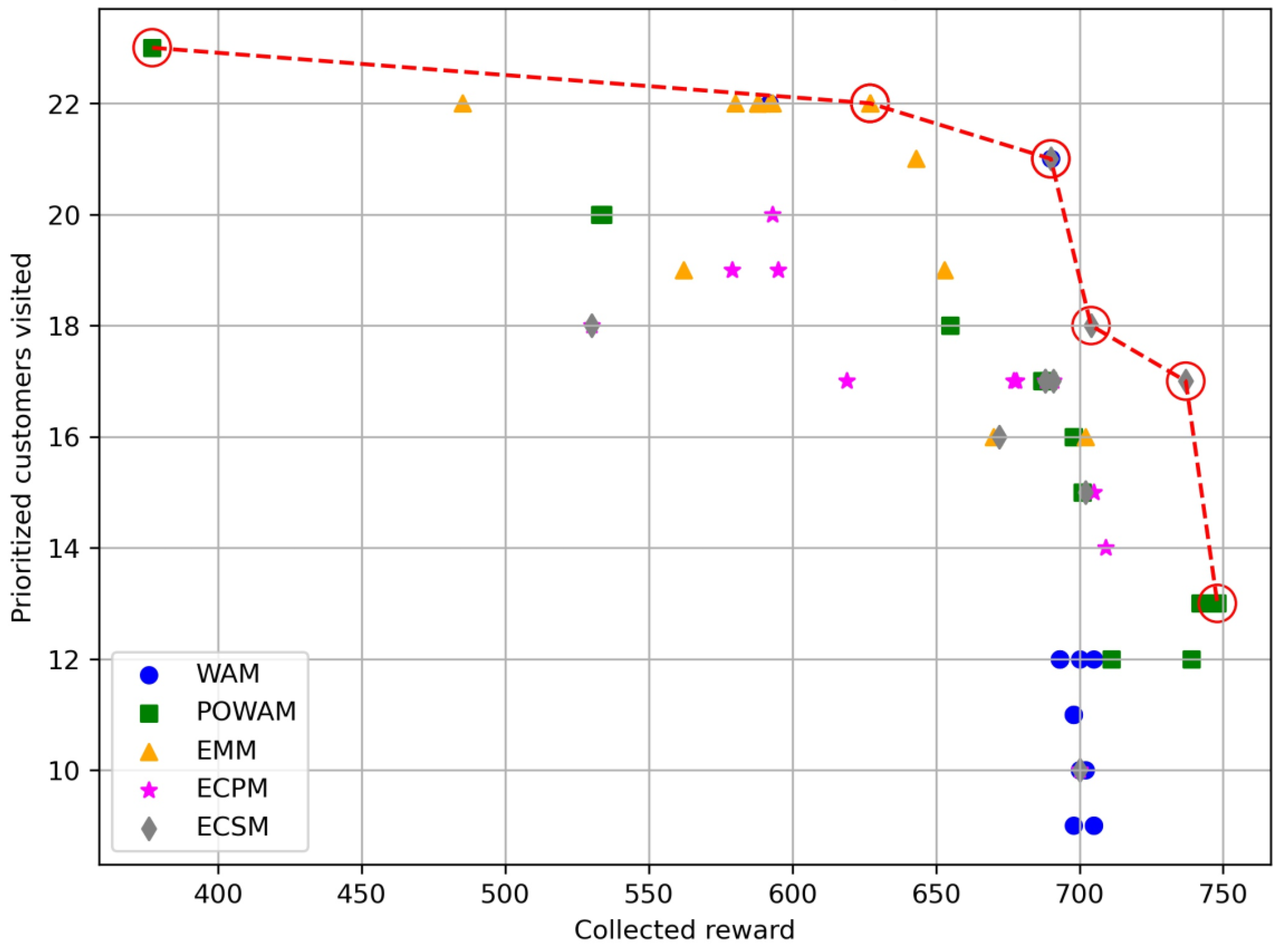

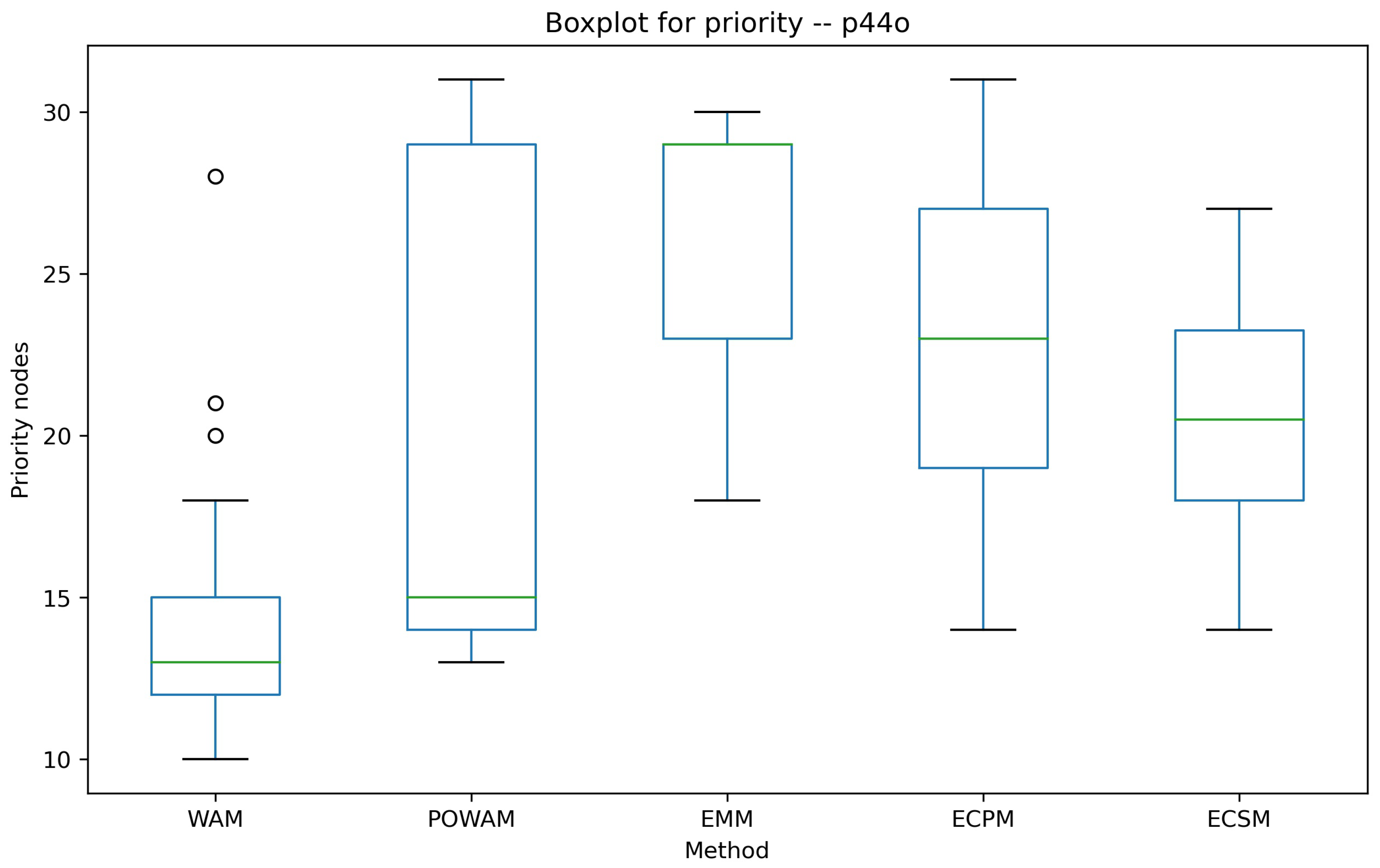
| Instance p44o | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 500 | 28 | 447 | 31 | 840 | 19 | 650 | 14 | 702 | 18 |
| 805 | 21 | 481 | 31 | 778 | 18 | 608 | 16 | 702 | 18 |
| 827 | 20 | 481 | 31 | 766 | 23 | 599 | 16 | 702 | 18 |
| 817 | 18 | 481 | 31 | 707 | 21 | 744 | 17 | 810 | 18 |
| 827 | 15 | 660 | 29 | 665 | 22 | 739 | 19 | 769 | 18 |
| 825 | 15 | 631 | 29 | 628 | 25 | 672 | 21 | 672 | 21 |
| 830 | 14 | 687 | 23 | 588 | 23 | 562 | 20 | 681 | 20 |
| 812 | 14 | 700 | 23 | 536 | 29 | 531 | 21 | 667 | 21 |
| 799 | 11 | 687 | 23 | 520 | 29 | 708 | 23 | 663 | 23 |
| 771 | 10 | 837 | 15 | 551 | 29 | 687 | 24 | 663 | 23 |
| 802 | 13 | 849 | 15 | 528 | 29 | 654 | 25 | 633 | 24 |
| 786 | 12 | 837 | 15 | 547 | 20 | 667 | 25 | 609 | 25 |
| 802 | 13 | 848 | 14 | 549 | 29 | 614 | 31 | 613 | 26 |
| 792 | 12 | 837 | 14 | 534 | 29 | 600 | 31 | 651 | 27 |
| 812 | 14 | 838 | 14 | 551 | 29 | 597 | 31 | 812 | 14 |
| 809 | 12 | 837 | 15 | 527 | 29 | 600 | 31 | 812 | 14 |
| 802 | 13 | 847 | 13 | 458 | 30 | ||||
| 825 | 12 | 847 | 13 | 534 | 29 | ||||
| 802 | 13 | 847 | 13 | 546 | 29 | ||||
| 802 | 13 | 840 | 13 | 512 | 29 | ||||
| 812 | 14 | 837 | 14 | 541 | 29 | ||||
| Instance p44r | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 604 | 31 | 570 | 31 | 989 | 22 | 572 | 18 | 861 | 23 |
| 887 | 27 | 636 | 31 | 918 | 23 | 901 | 21 | 861 | 23 |
| 887 | 27 | 636 | 31 | 871 | 28 | 902 | 22 | 861 | 23 |
| 903 | 28 | 613 | 33 | 830 | 29 | 901 | 21 | 861 | 23 |
| 943 | 20 | 825 | 29 | 777 | 30 | 900 | 22 | 861 | 23 |
| 948 | 21 | 833 | 29 | 759 | 29 | 748 | 24 | 918 | 22 |
| 965 | 21 | 900 | 26 | 735 | 29 | 719 | 25 | 744 | 26 |
| 947 | 17 | 833 | 29 | 680 | 28 | 751 | 29 | 734 | 24 |
| 947 | 22 | 900 | 26 | 592 | 31 | 819 | 30 | 796 | 26 |
| 946 | 18 | 900 | 26 | 545 | 31 | 819 | 30 | 788 | 26 |
| 951 | 16 | 894 | 23 | 587 | 31 | 867 | 28 | 751 | 27 |
| 947 | 17 | 902 | 24 | 594 | 31 | 888 | 31 | 703 | 28 |
| 951 | 16 | 881 | 24 | 561 | 31 | 863 | 30 | 732 | 29 |
| 947 | 17 | 930 | 17 | 532 | 31 | 834 | 21 | 649 | 30 |
| 972 | 17 | 931 | 19 | 576 | 31 | 947 | 17 | ||
| 947 | 17 | 933 | 22 | 647 | 31 | ||||
| 947 | 17 | 909 | 21 | 625 | 31 | ||||
| 947 | 17 | 916 | 20 | 641 | 31 | ||||
| 954 | 17 | 918 | 19 | 579 | 31 | ||||
| 947 | 17 | 900 | 23 | 625 | 31 | ||||
| 947 | 17 | 923 | 17 | 513 | 31 | ||||
| Instance p54q | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 535 | 19 | 535 | 19 | 795 | 12 | 645 | 14 | 640 | 13 |
| 795 | 12 | 580 | 19 | 795 | 12 | 695 | 13 | 635 | 13 |
| 795 | 12 | 570 | 19 | 725 | 14 | 690 | 14 | 630 | 14 |
| 795 | 12 | 580 | 19 | 740 | 14 | 675 | 15 | 620 | 15 |
| 795 | 12 | 580 | 19 | 645 | 15 | 650 | 18 | 590 | 16 |
| 795 | 12 | 580 | 19 | 600 | 16 | 650 | 18 | 595 | 17 |
| 790 | 12 | 680 | 16 | 570 | 19 | 650 | 18 | 595 | 18 |
| 795 | 12 | 755 | 14 | 535 | 19 | 600 | 20 | 580 | 19 |
| 795 | 12 | 785 | 12 | 535 | 19 | ||||
| 780 | 11 | 795 | 12 | 535 | 19 | ||||
| 795 | 12 | 785 | 12 | 535 | 19 | ||||
| 795 | 12 | 785 | 12 | 535 | 19 | ||||
| 775 | 11 | 785 | 11 | 535 | 19 | ||||
| 795 | 12 | 785 | 12 | 535 | 19 | ||||
| 770 | 12 | 785 | 12 | 535 | 19 | ||||
| 770 | 12 | 770 | 12 | 535 | 19 | ||||
| 795 | 12 | 770 | 12 | 535 | 19 | ||||
| 770 | 10 | 785 | 11 | 535 | 19 | ||||
| 770 | 10 | 780 | 10 | 535 | 19 | ||||
| 795 | 12 | 780 | 11 | 535 | 19 | ||||
| 795 | 12 | 785 | 12 | 535 | 19 | ||||
| Instance p54r | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 670 | 20 | 665 | 20 | 855 | 12 | 750 | 12 | 730 | 12 |
| 775 | 18 | 715 | 20 | 815 | 15 | 725 | 11 | 710 | 13 |
| 840 | 15 | 715 | 20 | 780 | 17 | 740 | 12 | 710 | 15 |
| 850 | 14 | 715 | 20 | 730 | 19 | 725 | 14 | 710 | 16 |
| 860 | 11 | 715 | 20 | 725 | 20 | 735 | 15 | 640 | 16 |
| 855 | 12 | 755 | 19 | 665 | 20 | 715 | 15 | 630 | 18 |
| 860 | 11 | 755 | 19 | 705 | 20 | 705 | 16 | 670 | 19 |
| 855 | 12 | 765 | 18 | 575 | 19 | 775 | 17 | 670 | 20 |
| 855 | 13 | 765 | 19 | 625 | 20 | 860 | 10 | 855 | 12 |
| 860 | 9 | 780 | 17 | 625 | 20 | 860 | 10 | ||
| 865 | 10 | 860 | 14 | 630 | 20 | 860 | 10 | ||
| 855 | 12 | 855 | 14 | 655 | 20 | ||||
| 865 | 10 | 845 | 14 | 670 | 20 | ||||
| 860 | 11 | 860 | 12 | 630 | 20 | ||||
| 860 | 11 | 850 | 13 | 670 | 20 | ||||
| 855 | 12 | 850 | 14 | 625 | 20 | ||||
| 860 | 10 | 855 | 11 | 630 | 20 | ||||
| 850 | 11 | 860 | 11 | 625 | 20 | ||||
| 855 | 9 | 855 | 11 | 625 | 20 | ||||
| 860 | 9 | 855 | 13 | 670 | 20 | ||||
| 865 | 10 | 865 | 11 | 625 | 20 | ||||
| Instance p74q | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 496 | 20 | 377 | 23 | 742 | 15 | 708 | 17 | 699 | 17 |
| 704 | 16 | 533 | 20 | 702 | 16 | 708 | 17 | 699 | 17 |
| 700 | 14 | 534 | 20 | 685 | 17 | 689 | 15 | 699 | 17 |
| 700 | 14 | 655 | 18 | 630 | 17 | 632 | 17 | 699 | 17 |
| 700 | 14 | 655 | 18 | 628 | 18 | 653 | 19 | 699 | 17 |
| 697 | 14 | 687 | 17 | 591 | 20 | 638 | 18 | 675 | 18 |
| 733 | 13 | 655 | 18 | 591 | 20 | 626 | 19 | 665 | 19 |
| 733 | 13 | 689 | 17 | 584 | 20 | 640 | 20 | 733 | 13 |
| 733 | 13 | 687 | 17 | 619 | 20 | ||||
| 733 | 13 | 687 | 17 | 607 | 20 | ||||
| 733 | 13 | 689 | 17 | 607 | 20 | ||||
| 733 | 13 | 698 | 16 | 607 | 20 | ||||
| 733 | 13 | 698 | 16 | 591 | 20 | ||||
| 733 | 13 | 701 | 15 | 607 | 20 | ||||
| 733 | 13 | 701 | 15 | 607 | 20 | ||||
| 733 | 13 | 711 | 12 | 607 | 20 | ||||
| 733 | 13 | 748 | 13 | 607 | 20 | ||||
| 733 | 13 | 739 | 12 | 607 | 20 | ||||
| 733 | 13 | 742 | 13 | 607 | 20 | ||||
| 733 | 13 | 747 | 13 | 584 | 20 | ||||
| Instance p74r | |||||||||
| Reward_WAM | P_nodes_WAM | Reward_POWAM | P_nodes_POWAM | Reward_EMM | P_nodes_EMM | Reward_ECPM | P_nodes_ECPM | Reward_ECSM | P_nodes_ECSM |
| 592 | 22 | 377 | 23 | 702 | 16 | 705 | 15 | 672 | 16 |
| 690 | 21 | 533 | 20 | 670 | 16 | 688 | 17 | 702 | 15 |
| 693 | 12 | 534 | 20 | 643 | 21 | 709 | 14 | 688 | 17 |
| 693 | 12 | 655 | 18 | 653 | 19 | 678 | 17 | 688 | 17 |
| 693 | 12 | 655 | 18 | 562 | 19 | 677 | 17 | 688 | 17 |
| 698 | 11 | 687 | 17 | 627 | 22 | 691 | 17 | 691 | 17 |
| 698 | 11 | 655 | 18 | 627 | 22 | 530 | 18 | 530 | 18 |
| 698 | 11 | 689 | 17 | 593 | 22 | 619 | 17 | 737 | 17 |
| 700 | 10 | 687 | 17 | 580 | 22 | 595 | 19 | 704 | 18 |
| 698 | 9 | 687 | 17 | 588 | 22 | 579 | 19 | 690 | 21 |
| 705 | 12 | 689 | 17 | 588 | 22 | 593 | 20 | 700 | 10 |
| 700 | 10 | 698 | 16 | 627 | 22 | 700 | 10 | 700 | 10 |
| 700 | 12 | 698 | 16 | 592 | 22 | 700 | 10 | 700 | 10 |
| 700 | 10 | 698 | 16 | 588 | 22 | ||||
| 693 | 12 | 701 | 15 | 588 | 22 | ||||
| 702 | 10 | 701 | 15 | 588 | 22 | ||||
| 700 | 10 | 711 | 12 | 588 | 22 | ||||
| 700 | 10 | 748 | 13 | 588 | 22 | ||||
| 705 | 9 | 739 | 12 | 588 | 22 | ||||
| 705 | 9 | 742 | 13 | 485 | 22 | ||||
| 700 | 10 | 747 | 13 | 588 | 22 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agud-Albesa, L.; Garrido, N.; Juan, A.A.; Llorens, A.; Oltra-Crespo, S. A Weighted and Epsilon-Constraint Biased-Randomized Algorithm for the Biobjective TOP with Prioritized Nodes. Computation 2024, 12, 84. https://doi.org/10.3390/computation12040084
Agud-Albesa L, Garrido N, Juan AA, Llorens A, Oltra-Crespo S. A Weighted and Epsilon-Constraint Biased-Randomized Algorithm for the Biobjective TOP with Prioritized Nodes. Computation. 2024; 12(4):84. https://doi.org/10.3390/computation12040084
Chicago/Turabian StyleAgud-Albesa, Lucia, Neus Garrido, Angel A. Juan, Almudena Llorens, and Sandra Oltra-Crespo. 2024. "A Weighted and Epsilon-Constraint Biased-Randomized Algorithm for the Biobjective TOP with Prioritized Nodes" Computation 12, no. 4: 84. https://doi.org/10.3390/computation12040084
APA StyleAgud-Albesa, L., Garrido, N., Juan, A. A., Llorens, A., & Oltra-Crespo, S. (2024). A Weighted and Epsilon-Constraint Biased-Randomized Algorithm for the Biobjective TOP with Prioritized Nodes. Computation, 12(4), 84. https://doi.org/10.3390/computation12040084








