Computational Fluid Dynamics-Based Systems Engineering for Ground-Based Astronomy
Abstract
:1. Introduction
2. Integrated Modeling Synergy
2.1. Performance Metrics and Requirement Validation
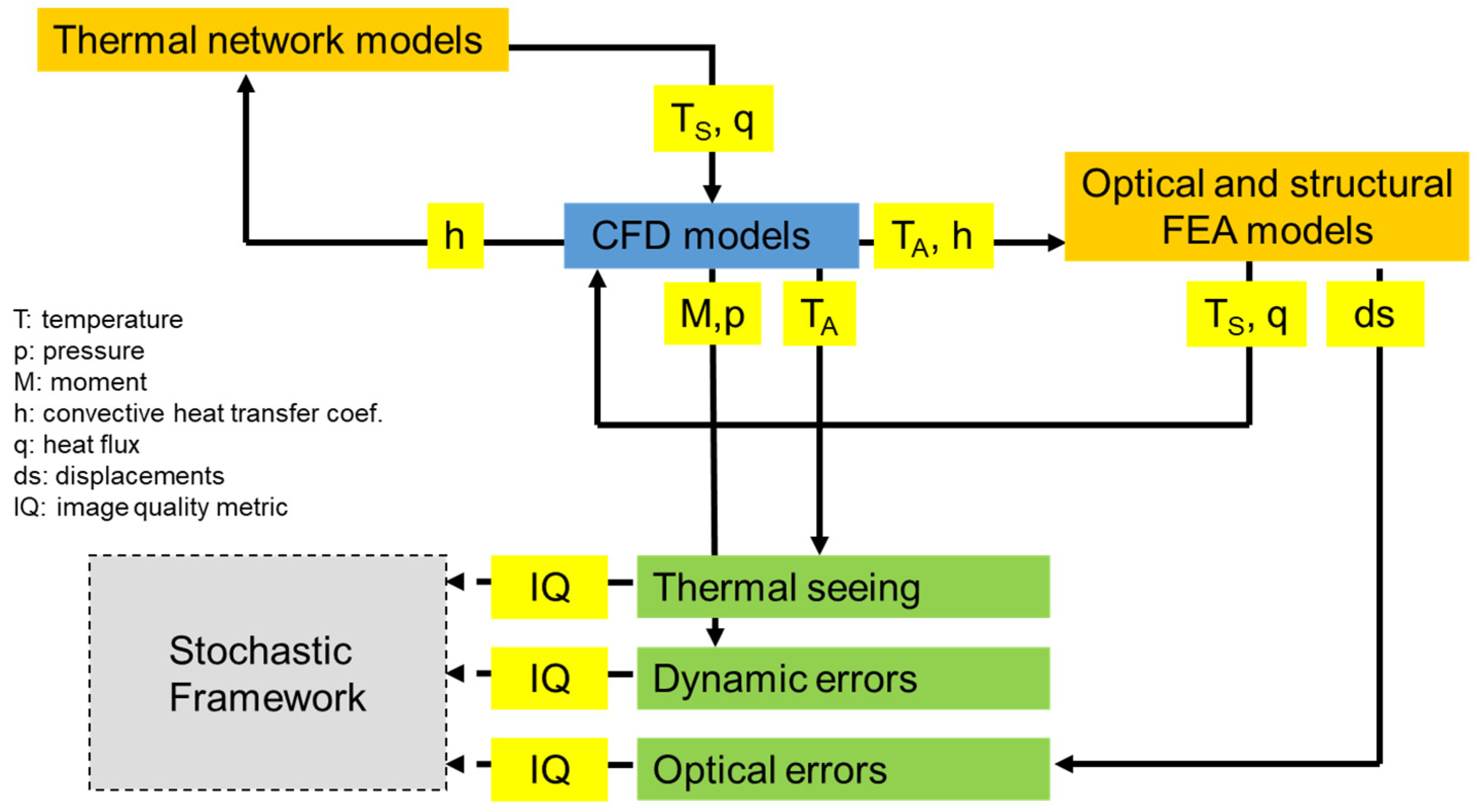
2.2. Integrated Modeling Framework
2.3. Stochastic Framework
- Allows the statistical representation of errors that are randomized by environmental and operating conditions;
- Allows the statistical representation of errors that depend on previous temporal states of the system;
- Allows the combined representation of errors that are correlated and cannot be assessed independently;
- Allows the combined representation of errors that exhibit disparate time and spatial scales;
- Provides probability distributions of errors to denote the range of expected performance under various seeing conditions, knowledge particularly useful to queue observing;
- Allows the investigation of observatory behavior on different candidate sites;
- Allows the optimization of certain operating strategies, such as venting, daytime thermal treatment, and calibration measurement frequency;
- Unveils the true impact of a particular design decision on the expected observatory performance and subsequent science productivity, enabling cost-effective trade-offs.
3. Aerothermal Modeling Synergy
- Thermal network models;
- CFD models;
- Conjugate heat transfer models.
3.1. Thermal Network Models
3.2. Computational Fluid Dynamics Models
3.3. Solid and Conjugate Heat Transfer Models
3.4. Post-Processing Tools
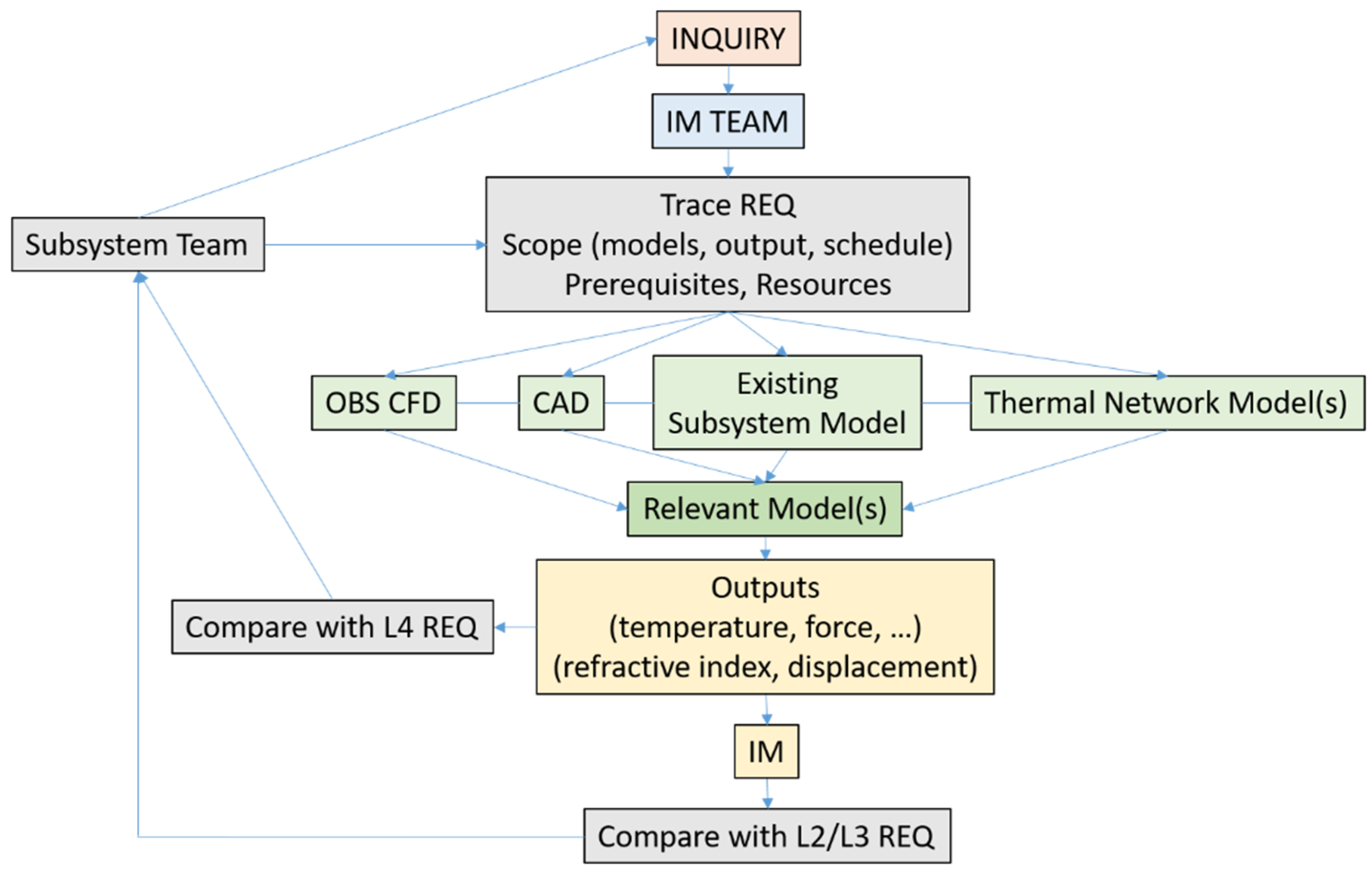
3.5. Subsystem-Level Inquiry Processing
4. Thermal Network Modeling
- Ambient temperature drift since last telescope alignment, used by the telescope/mirror thermal deformation models;
- Temperature differential between sunrise and a particular time of night or mean of night, used for enclosure AHU sizing and to determine supply temperature;
- Temperature differential between daytime external ambient and interior temperatures, using the air conditioning model results, used in combination with external wind speed to determine the enclosure infiltration load.
4.1. Enclosure
- Provides Cumulative Distribution Functions of component temperatures and fluxes: exterior skin, enclosure structure, interior insulation, observing floor, enclosure interior air, and interstitial space air;
- Requirements validation: exterior paint and insulation emissivity;
- Provides maximum expected temperature in interstitial space;
- Provides heat dissipation statistics through insulation and observatory floor;
- Provides input boundary conditions to observatory performance CFD simulations.
4.2. Optics
- Provides glass temperature differential from ambient under various environmental conditions;
- Validation/modification of thermal specifications for primary and secondary mirror systems.
5. Astronomical Site CFD Modeling
5.1. Site Selection
- Upwind wind and temperature conditions, which, along with topography temperature, result in a realistic GL profile between 7 m and 400 m from the ground. The only variables are wind speed and direction. The ground temperature was chosen to be a calculated quantity rather than input, either by imposing the expected net heat flux or by invoking a gray thermal radiation model with an emissivity of 0.8 and appropriate effective sky temperature. The reference location was that of the corresponding site monitoring system.
- Single reference pressure, reflecting the average site altitude. A user-defined function was used for the corresponding density vertical profile, which resulted in the expected reference density at the average site altitude.
- Primary candidate ELT site selection;
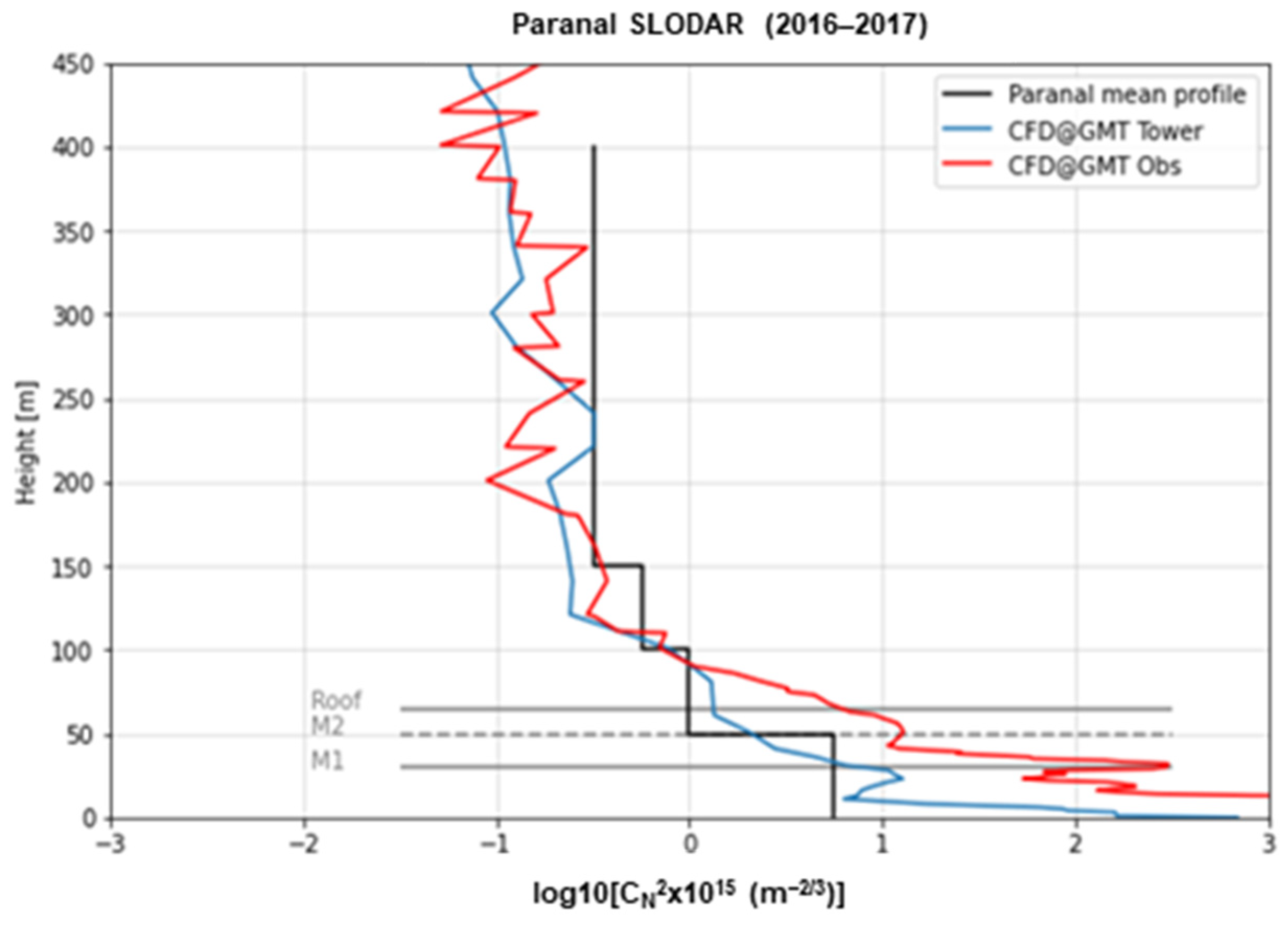
- Risk reduction: validation of GL modeling (comparison with measurements where available);
- Given the appropriate inputs, modeled GL profiles are realistic, while measurement and modeling uncertainties for optical turbulence proved comparable, making the use of thermal modeling an economic and flexible alternative to experiments and in some cases the only option.
5.2. Ground Layer
5.2.1. Maunakea, 13N
5.2.2. Las Campanas
5.2.3. La Palma, ORM
- Alternate candidate TIO site location selection;
- Evaluation of interaction between the TIO and existing observatories, required by Instituto de Astrofisica de Canarias.
6. Observatory CFD Modeling
- The geometries are updated to reflect the latest designs and increased fidelity.
- The heat dissipation budgets are similarly updated, and additional boundaries are created to accommodate the resolved heat sources.
- Advances in meshing methodologies, solver development, and computational power are considered both for simulation setup and output post-processing.
- Upwind domain inputs have been revised to reflect more realistic GL conditions.
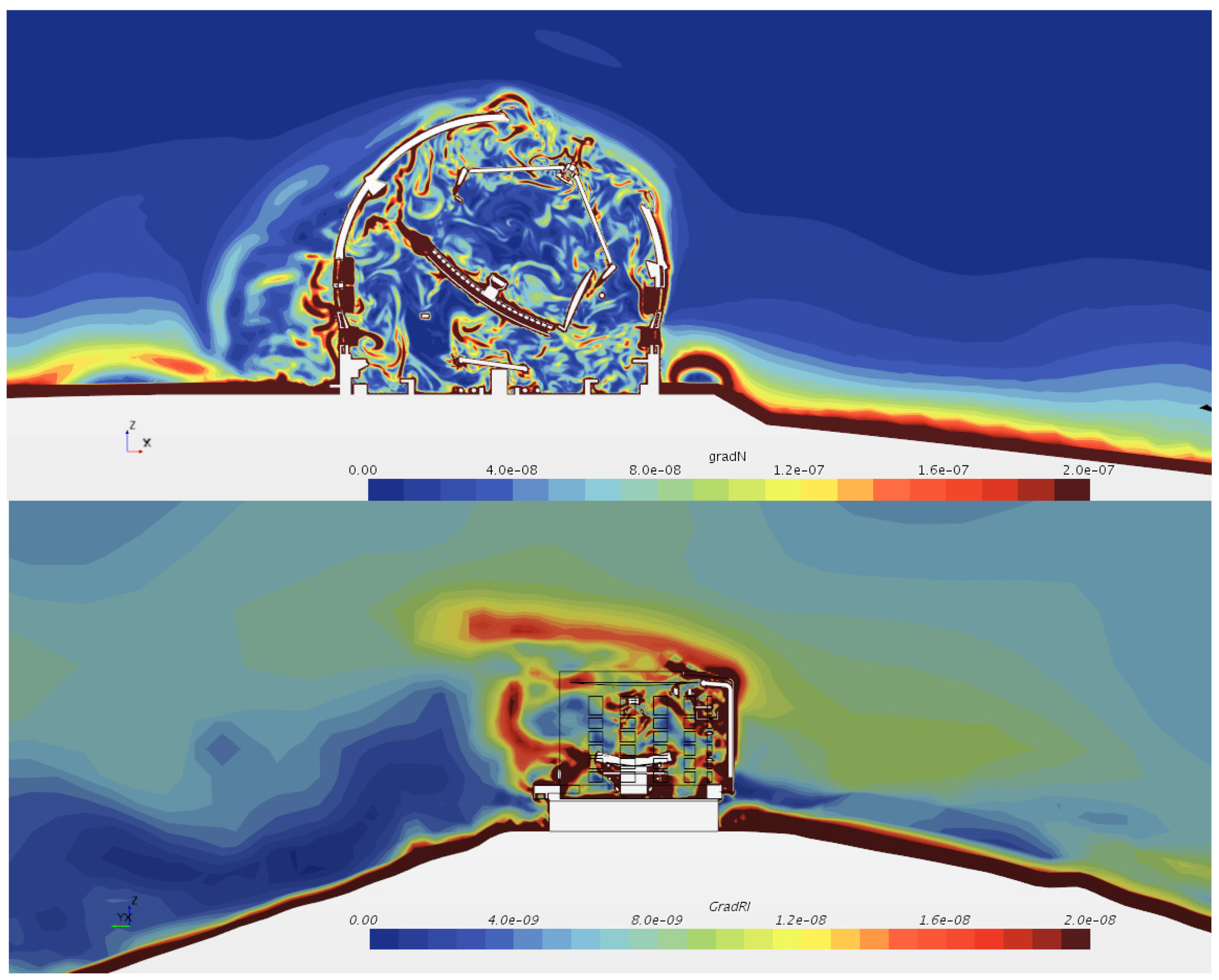
- The models retain the relative motion between tessellated parts and the corresponding local coordinates systems to support it. This way, the boundary conditions can be only applied once, and the model templates can be used for multiple orientations and wind speeds. However, for volume meshing, the parts are combined to minimize numerical errors generated at the volume interfaces, to which thermal seeing PSSn calculation is very sensitive. The procedure can still be automated through scripting, if desired.
6.1. Daytime (Air Conditioning)
- Time records of enclosure air temperatures at various heights from the observatory floor and temperature vertical profiles at specified times during the day;
- Validation/verification of HVAC design (max flow rate capacity, split between primary supply and recirculation rates, nozzle location, operating strategy);
- Optimum HVAC nozzle temperature as a function of target temperature to meet performance requirements;
- Provides heat transfer coefficients for convection calculations to component thermal models.
6.2. Nighttime
- Current thermal boundary conditions on observatory surfaces. The values are grouped into three categories: standard (such as adiabatic, symmetry, etc.), estimated, and assumed. Estimated values are a result of modeling. Assumed values are for components that are either temperature-controlled and have a requirement specification or have insufficient information for accurate thermal modeling. Very few boundaries fall in this category since at least a thermal network model can provide some estimate for most components. For many subsystems, there already exist conjugate heat transfer models that provide surface temperatures. These include optical assemblies, adaptive optics facilities, and some “first light” instruments, with mature enough design. Most boundary conditions are applied as temperature differentials from the ambient reference temperature. In some cases, equilibrium is assumed between convection and radiation, ignoring conduction. These correspond mainly to low-thermal-inertia components, such as the secondary mirror assembly support structure and top end, enclosure and facilities building exterior, and interior surface cladding. Higher thermal inertia component temperatures, such as the enclosure concrete components and telescope lower structure, are given by the corresponding models. Note that proper boundary condition implementation ultimately requires knowledge of the heat balance of the observatory [48].
- Three-dimensional temperature fields inside the optical volume from the M1 vertex until the end of the enclosure boundary layer at a specified temporal sampling rate. These are used as inputs in the thermal seeing post-processor [49,50]. Hence, a byproduct of these simulations is also a time record of Optical Path Difference (OPD) maps. For a historical overview of early thermal seeing modeling, the reader may consult [51,52].
- Convective heat transfer coefficients on selected surfaces for use as inputs in solid and conjugate heat transfer models of components.
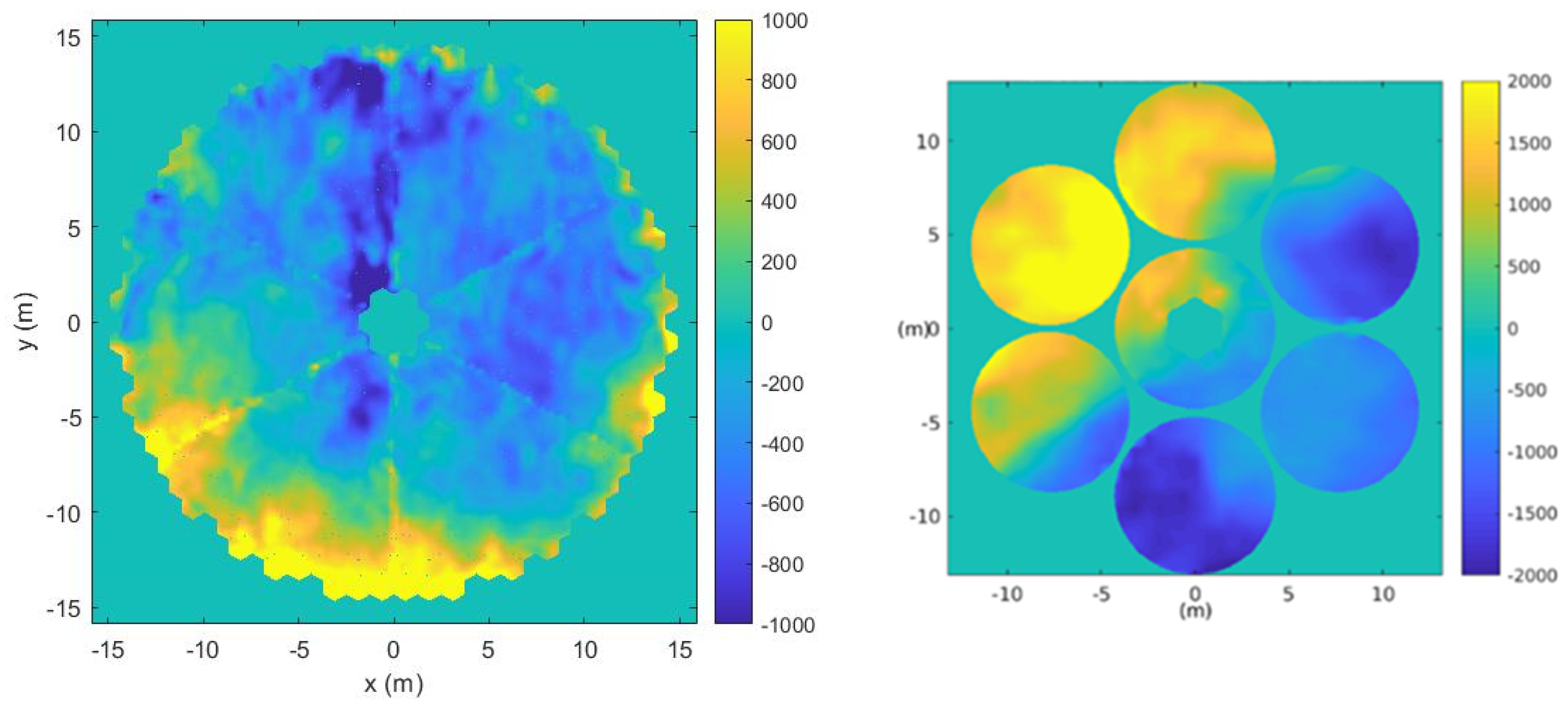
- Observatory-wide aerodynamic optimization and enclosure operating strategy development through a trade-off between wind jitter and thermal seeing;
- Observatory performance and error budget terms estimate: thermal seeing, image jitter, and wind-induced image blur;
- Provides thermal seeing sensitivity to heat sources: heat dissipation budget update and design choices;
- Provides metrology system sensitivity to enclosure environment: expected measurement error;
- Provides heat transfer coefficients for convection and component view factors for radiation calculations to component thermal models.
6.3. Daytime (Solar)
6.4. Validation
- Refractive index variance along the scintillometer path, integrated Cn2: reasonable agreement with measurements;
- Turbulent energy dissipation rate and inner scale: reasonable agreement with measurements;
- Integral length scale: matched aperture width as expected;
- Matched behavior of Cn2 vs. external wind speed;
- Matched behavior of Cn2 vs. fan speed;
- Identified optimal fan speed; half of what Keck was previously using.
- Point Spread Function (PSF) of dome seeing along optical path, PSF Full Width Half Maximum (FWHM): reasonable agreement with measurements;
- Significant reduction in dome seeing FWHM with passive ventilation: at least 25% without including surface temperature differential improvement (it proved to be closer to 50%).
- Risk reduction: validation of dome seeing modeling;
- Optimal Keck fan speed selection: operational cost reduction;
- Support of recommendation to ventilate the CFHT dome: differential IQ improvement;
- Overall comment as in the case of site CFD: modeling and measured uncertainties were comparable.
7. Conjugate Heat Transfer and Solid Thermal Modeling
- Material and thermal properties of components, including emissivity;
- Ambient temperature profile (either user-defined typical diurnal or subsets of the stochastic framework);
- Active heat loads (component-generated, temporal records if possible);
- Convective heat transfer coefficients (from CFD) for surfaces in contact with air volumes not modeled;
- Thermal resistance between conducting components.
- Time (and space if desired) records of bulk and/or surface temperature differential from ambient for each assembly component;
- Time and space records of node displacements from a reference geometry.
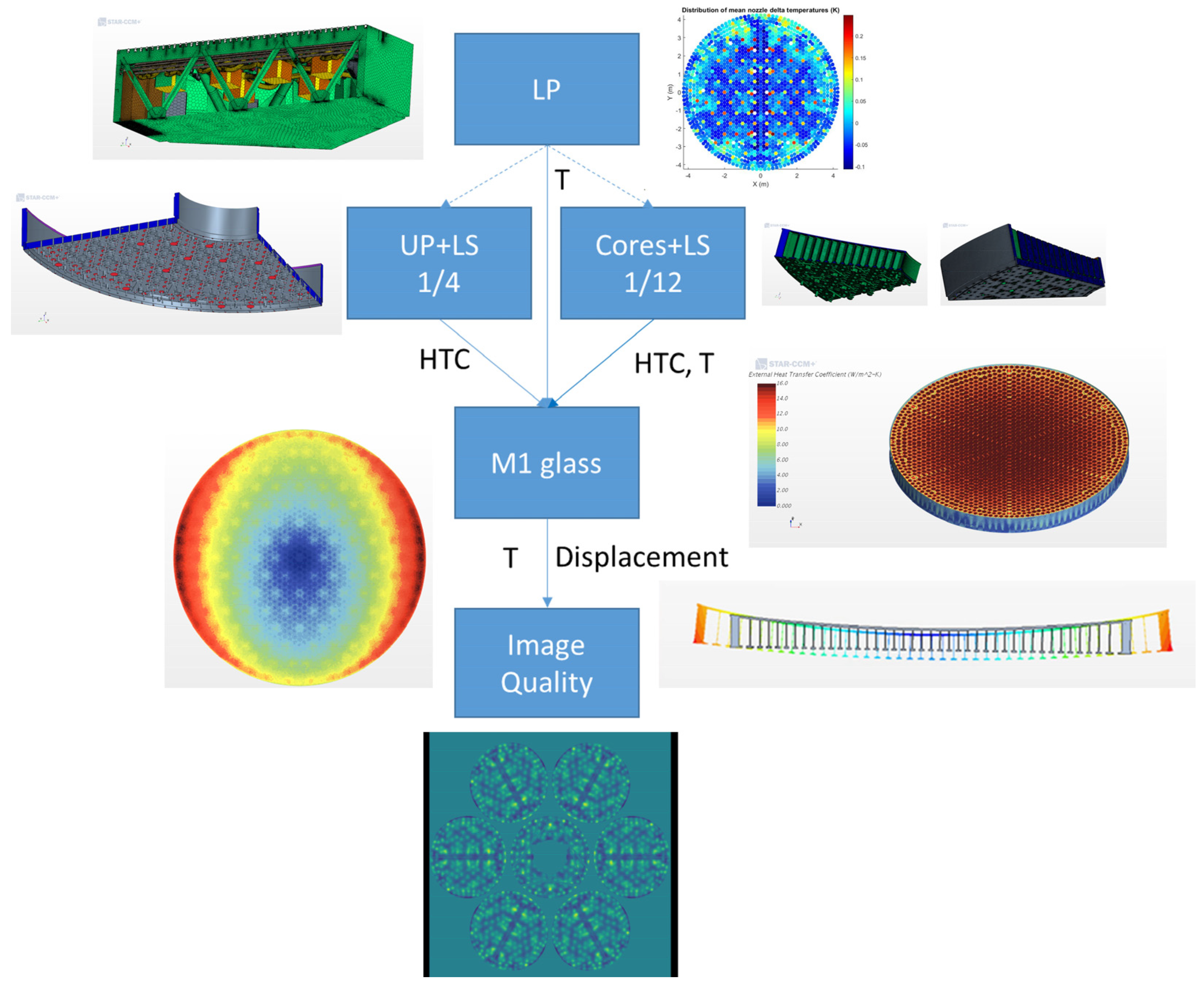
7.1. Mirror Assemblies
- Validation of thermal requirements on optical assemblies;
- Error budget terms estimate: mirror seeing, segment thermal deformation, and dome seeing;
- Provides realistic expected mirror shapes (thermal, pressure-induced deformation) for actuator correction and phasing.
7.2. Enclosure Systems
- Validation of enclosure heat dissipation requirements and insulation performance;
- Design choice: enclosure drives’ and electrical cabinets’ active/passive cooling option and flow rate.
7.3. Telescope Structure
- Requirement verification: minimum segment gap distance, residual on-sky tracking error, telescope pointing error, maximum actuator stroke, and maximum back focal distance shift;
- Provides realistic expected thermal misalignments for correction strategy testing;
- Provides input boundary conditions to observatory performance CFD simulations.
7.4. Subsystems/Components
7.4.1. Elevation Drives
- Validation of EL drives’ cooling flow rate and max coil temperature requirements;
- Provides input boundary conditions to observatory performance CFD simulations.
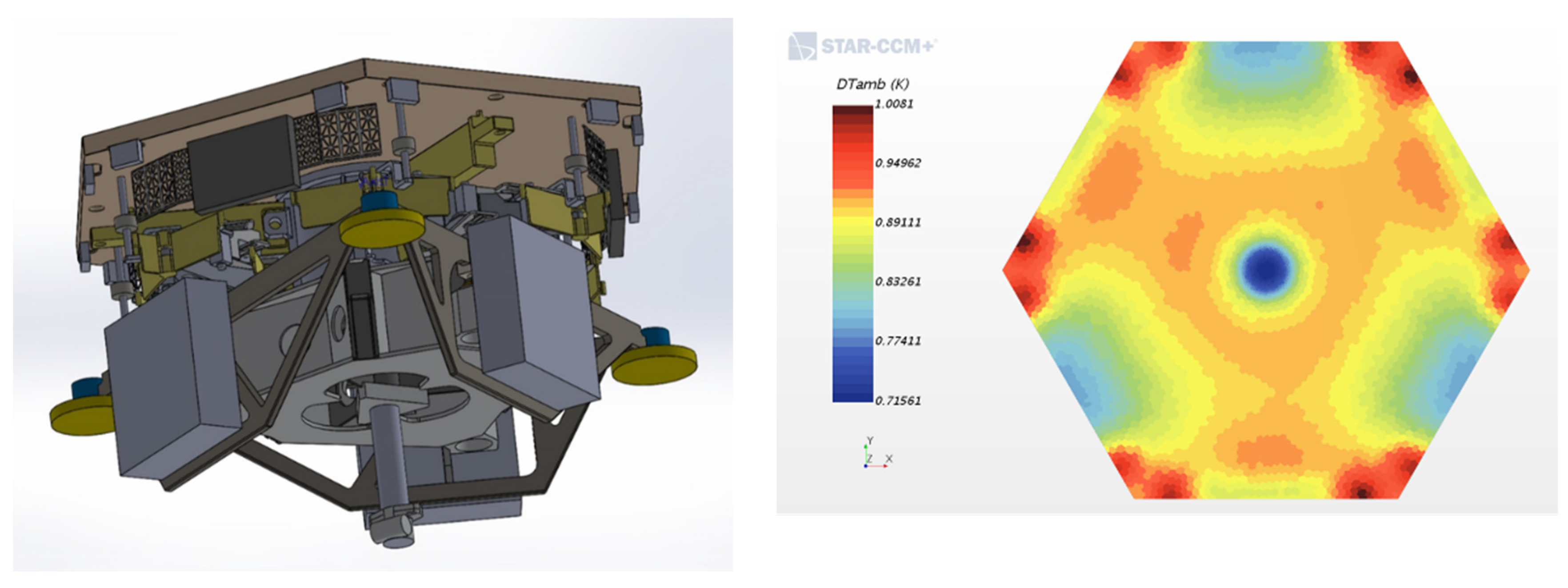
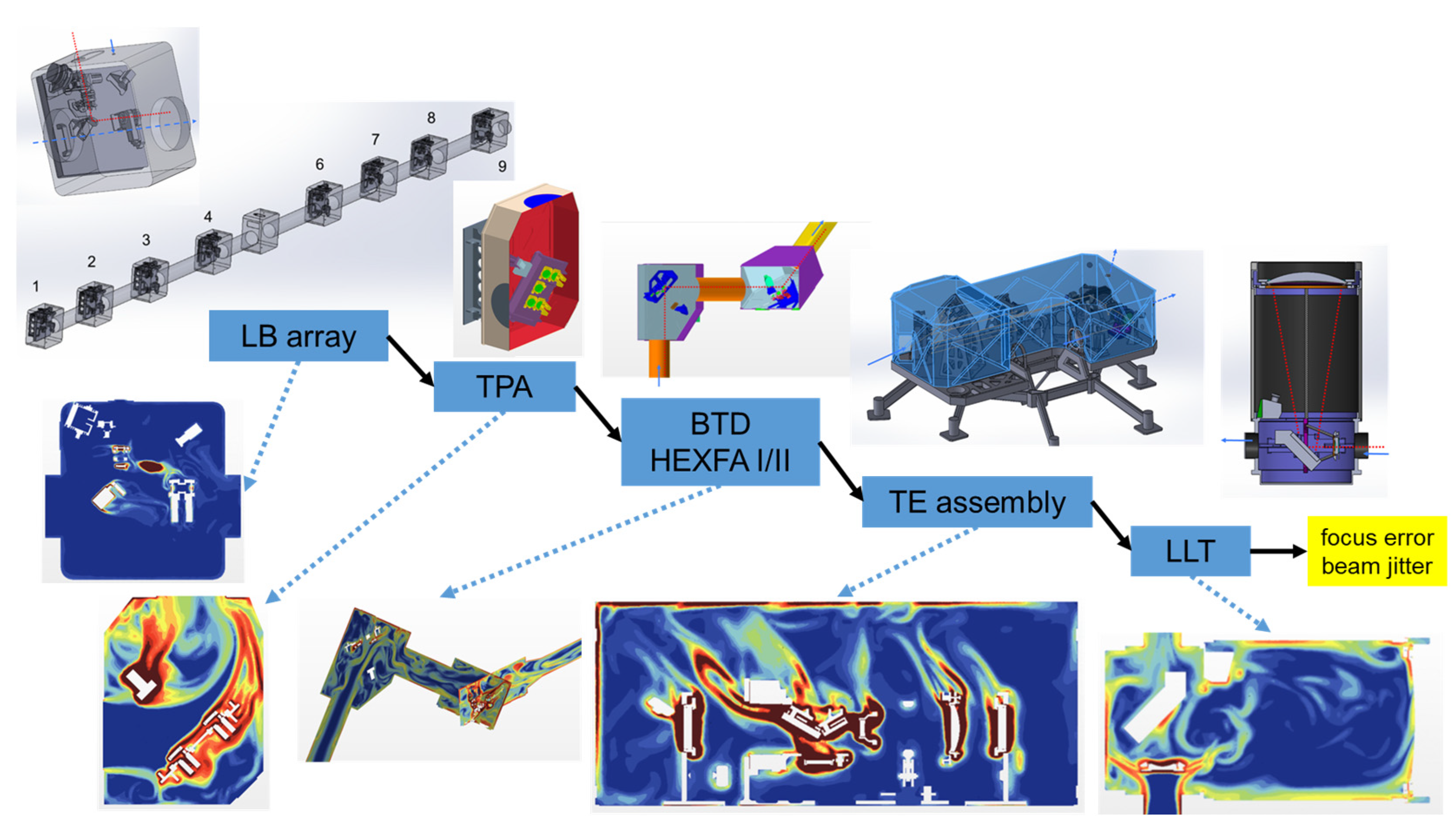
7.4.2. TIO Laser Guide Star Facility (LGSF)
- Design modifications to minimize path turbulence and enhance lens cooling;
- Estimates of beam jitter and focus error budget terms.
7.4.3. Electronic/Electrical Cabinets
8. Support CFD Modeling
8.1. TIO Enclosure Aperture Deflectors
8.2. Spider Beams
8.3. Flow-Induced Pipe Vibration
8.4. Summit Facilities’ Exhaust
- Requirements validation: chiller exhaust temperature differential from ambient, flow rate, orientation, and potential geometric modifications near the facilities’ exhaust area.
8.5. TIO Mechanical Room and Utility Tunnel
- Requirements validation: flow sign at cable wrap opening, tunnel fan and utility exhaust flow rates, tunnel gas discharge location, mechanical room exhaust temperature, and temperature environment around equipment.
8.6. Segment Ion Beam Figuring
8.7. Hexagonal Segment Profilometer
8.8. Factory Acceptance Tests
9. CFD Vision 2030
9.1. Geometry and Mesh Generation
9.2. Physical Modeling, Algorithms, and Numerical Methods
9.3. HPC
- Large volume of simulations. The LUT resolution required to characterize the aerothermal performance of the observatory (zenith and azimuth angles, wind speeds and directions, heat release scenarios) can result in hundreds of simulations and dozens of meshes. These performance LUTs need to be updated every time a major design change occurs and subsets of them on a regular basis to accommodate trade studies; thus, the required turnaround timescale is in months.
- Large computational meshes. Accurate wind jitter and thermal seeing require high enough resolution, resulting in a minimum of several tens of millions of elements. Also, to accurately estimate the net heat transfer on enclosure and telescope surfaces, conjugate heat transfer analysis should be enabled, with the enclosure structure, telescope structure, and other important components to be meshed as well in the same simulation. This will double the required mesh size. Finally, proper GL characterization and interaction with the enclosure requires relatively high-resolution mesh to extend in the first 100 m above the topography.
- Large number of timesteps. Thermal seeing PSSn calculation requires simulations in excess of 10 min of virtual time at a sampling rate of 20 Hz or more, especially if the response of an adaptive secondary mirror is to be properly assessed. Moreover, conjugate heat transfer simulations require much longer integration times, dramatically increasing the number of timesteps, where a high-fidelity solution of the air flow is also desired.
- Configure and create the HPC cluster with ParallelCluster (the nodes are requested as Spot instances);
- Upload the CFD configuration files to the cluster;
- Launch the CFD simulations on the cluster;
- For each simulation, start the synchronization process;
- For each completed simulation, post-process the output data;
- For each completed and post-processed simulation, terminate the synchronization process;
- For each terminated simulation, delete the local data.
9.4. Knowledge Extraction
9.5. Validation
9.6. MDAO
10. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Extremely Large Telescope. Available online: https://elt.eso.org (accessed on 10 June 2024).
- Giant Magellan Telescope. Available online: https://giantmagellan.org (accessed on 10 June 2024).
- Thirty Meter Telescope International Observatory. Available online: https://www.tmt.org (accessed on 10 June 2024).
- Angeli, G.Z.; Roberts, S.; MacMynowski, D.; Fitzsimmons, J.; Dunn, J.; Vogiatzis, K.; Sheinis, A. Modeling Tools to Estimate the Performance of the Thirty Meter Telescope: An Integrated Approach; SPIE 5497(24); SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Conan, R.; Angeli, G.; Sitarski, B.; Dribusch, C.; Fitzpatrick, H.; Romano, H.; Vogiatzis, K.; Das, K. GMTO Approach to Integrated Modeling-Based Systems Engineering; SPIE 11450(26); SPIE: Bellingham, WA, USA, 2020. [Google Scholar]
- Angeli, G.Z.; Vogiatzis, K. Statistical Approach to Systems Engineering for the Thirty Meter Telescope; SPIE 7738(45); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Vogiatzis, K.; Das, K.; Sitarski, B.; Schwartz, D.; Conan, R.; Angeli, G.Z. Using a Stochastic Approach to Estimate the Aerothermal Performance of the Giant Magellan Telescope; AIAA 2019-2319; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019. [Google Scholar]
- Vogiatzis, K.; Angeli, G.Z. Monte Carlo Simulation Framework for TMT; SPIE 7017(29); SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Sitarski, B.; Vogiatzis, K.; Conan, R.; Angeli, G.Z.; Goodrich, R. Performance Estimates for the Giant Magellan Telescope via Statistical Analysis. In Proceedings of the AO4ELT6, Quebec City, QC, Canada, 9–14 June 2019. [Google Scholar]
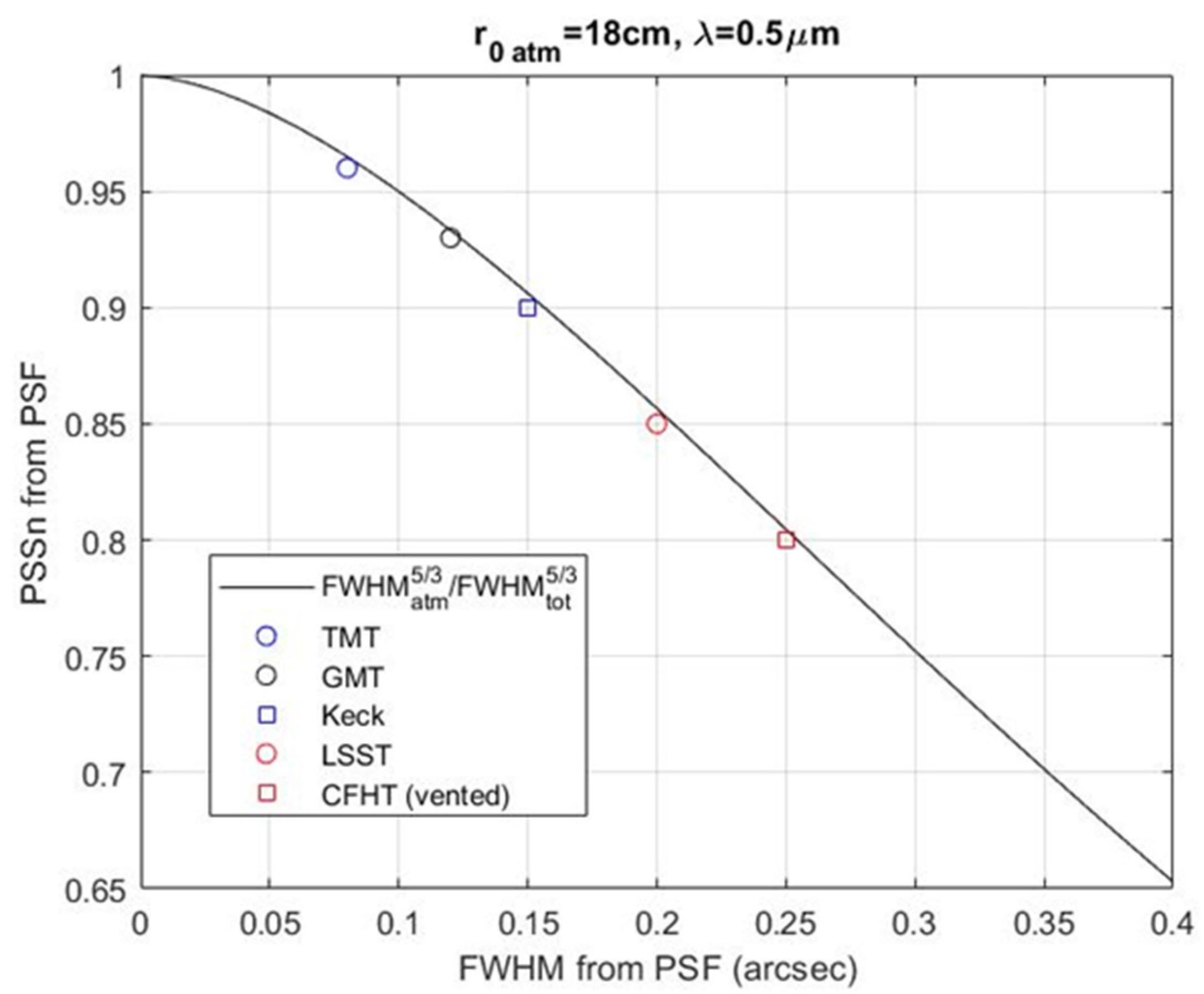
- Seo, B.-J.; Angeli, G.Z.; Nelson, J. Analysis of normalized point source sensitivity as a performance metric for large telescopes. J. Appl. Opt. 2009, 48, 5997–6007. [Google Scholar] [CrossRef] [PubMed]
- Angeli, G.Z.; Seo, B.-J.; Nissly, C.; Troy, M. A Convenient Telescope Performance Metric for Imaging through Turbulence; SPIE 8127(4); SPIE: Bellingham, WA, USA, 2011. [Google Scholar]
- Conan, R. PSSn as a Function of Field Aberration and M1 Segment Polishing Residuals; GMT-DOC-01940; GMTO Corporation: Pasadena, CA, USA, 2017. [Google Scholar]
- Siemens Simcenter STAR-CCM+. Available online: https://plm.sw.siemens.com/en-US/simcenter/fluids-thermal-simulation/star-ccm/ (accessed on 10 June 2024).
- Mathworks MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on 10 June 2024).
- Zago, L. The Effect of the Local Atmospheric Environment on Astronomical Observations. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Vaud, Switzerland, 1995. Thèse No. 1394. [Google Scholar]
- Vogiatzis, K.; Thompson, H.; Trancho, G. Aerothermal Support for TMT International Observatory Enclosure and Summit Facilities Subsystems; SPIE 13094(27); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Sitarski, B.; Vogiatzis, K. HVAC Sizing Thermal Simulations; GMT-DOC-03957; GMTO Corporation: Pasadena, CA, USA, 2019. [Google Scholar]
- Vogiatzis, K.; Fitzpatrick, H.; Conan, R.; Ranka, T.; Muller, G.; Xin, B.; Ashby, D. GMT Primary Mirror Thermal Control System and Thermal Deformation Modeling Framework; SPIE 13099(102); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Vogiatzis, K.; De Young, D.S. Site Characterization through the Use of Computational Fluid Dynamics. In Proceedings of the 2nd Baeckaskog Workshop on Extremely Large Telescopes, Baeckaskog Castle, Sweden, 9–11 September 2003. SPIE 5382(74). [Google Scholar]
- Vogiatzis, K.; Hiriart, D. Numerical Wind Modeling for the San Pedro Martir Sierra in Baja California. Rev. Mex. Astron. Astrophys. 2004, 40, 81–98. [Google Scholar]
- Els, S.; Vogiatzis, K. TMT Studies on the Influence of Short-Term Changes of Local Thermodynamic Conditions on the Seeing: CFD vs. Observations; SPIE 6267(55); SPIE: Bellingham, WA, USA, 2006. [Google Scholar]
- Els, S.; Vogiatzis, K. Revealing the Onset of Convection in Terrestrial Planet Atmospheres. In Proceedings of the IAU S239 Convention of Astrophysics, Prague, Czech Republic, 21–25 August 2006. [Google Scholar]
- Els, S.; Schöck, M.; Skidmore, W.; Travouillon, T.; Riddle, R.; Vogiatzis, K.; Wang, L.; Bustos, E.; Seguel, J.; Vasquez, J.; et al. Observations of the Turbulent Atmospheric Ground Layer during the Site Testing for the Thirty Meter Telescope (TMT). In Proceedings of the EMS 2007-A-00109, Annual Meeting of the European Meteorological Society and 8th European Conference on Applications of Meteorology, San Lorenzo de El Escorial, Spain, 1–5 October 2007. [Google Scholar]
- Els, S.; Schöck, M.; Skidmore, W.; Travouillon, T.; Riddle, R.; Bustos, E.; Seguel, J.; Vasquez, J.; Vogiatzis, K.; Walker, D.; et al. The Site Testing for the Thirty Meter Telescope and its Potential Role in Developing the Short Term Forecasting of Observing Conditions. Astron. Nachrichten 2007, 328, 7. [Google Scholar]
- Els, S.G.; Vogiatzis, K.; Otarola, A.; Schöck, M.; Travouillon, T.; Riddle, R.L.; Skidmore, W.A. Optical Turbulence above Mountains Seen in 3D; SPIE 7733(58); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Das, K.; Vogiatzis, K.; Angeli, G.Z.; Rosenthal, W.; Bouchez, A.; Goodrich, W. GMT Aerothermal Modeling Validation through Site Measurement; SPIE 10705(2)s; SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Vogiatzis, K.; Thompson, H.; Roberts, S.; Dumas, C. Ground Layer Studies for the Alternate TMT Site; SPIE 10705(61); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Vogiatzis, K.; Thompson, H.; Rogers, J.; Trancho, G. On the Relationship between Thermal Seeing and Observatory Design; SPIE 12187(74); SPIE: Bellingham, WA, USA, 2022. [Google Scholar]
- De Young, D.S.; Vogiatzis, K. Numerical Simulations of Flow in Extremely Large Telescope Enclosures. In Proceedings of the SPIE 5382-44, 2nd Baeckaskog Workshop on Extremely Large Telescopes, Baeckaskog Castle, Sweden, 9–11 September 2003. [Google Scholar]
- MacMynowski, D.G.; Angeli, G.Z.; Vogiatzis, K.; Fitzsimmons, J.; Padin, S. Parametric Modeling and Control of Telescope Wind-Induced Vibration; SPIE 5497(26); SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Vogiatzis, K.; Segurson, A.; Angeli, G.Z. Estimating the Effect of Wind Loading on Extremely Large Telescope Performance Using Computational Fluid Dynamics; SPIE 5497(30); SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- MacMynowski, D.G.; Blaurock, C.A.; Angeli, G.Z.; Vogiatzis, K. Modeling Wind-Buffeting of the Thirty Meter Telescope; SPIE 6271(25); SPIE: Bellingham, WA, USA, 2006. [Google Scholar]
- MacMynowski, D.G.; Vogiatzis, K.; Angeli, G.Z.; Fitzsimmons, J.; Nelson, E.J. Wind Loads on Ground-Based Telescopes. Appl. Opt. 2006, 45, 7912–7923. [Google Scholar] [CrossRef]
- Sebag, J.; Vogiatzis, K. LSST Camera Heat Requirements Using CFD and Thermal Seeing Modeling; SPIE 7738(13); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Sebag, J.; Vogiatzis, K.; Barr, J.; Neill, D. LSST Summit Enclosure: Facility Design Optimization Using Aero-Thermal Modeling; SPIE 8449(3); SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Cho, M.; Vogiatzis, K.; Sebag, J.; Neill, D. Wind Responses of the LSST Secondary Mirror; SPIE 8449(4); SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Sebag, J.; Vogiatzis, K. Estimating Dome Seeing for LSST; SPIE 9150(26); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Vogiatzis, K.; Xin, B.; Claver, C.; Angeli, G.Z.; Selvy, B. Dome Seeing Sensitivity Analysis for LSST; SPIE 10705(3); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Marchiori, G.; Rampini, F.; Mian, S.; Ghedin, L.; Marcuzzi, E.; Bressan, R. ELT Dome and Telescope: Performance Analysis Overview; SPIE 10705(13); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Vogiatzis, K.; MacMartin, D.; Wang, L.; Trancho, G. The TMT International Observatory Aerothermal Performance Estimation Procedure; SPIE 13099(100); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Vogiatzis, K.; Das, K.; Angeli, G.Z.; Bigelow, B.; Burgett, W. Computational Fluid Dynamics Modeling of GMT; SPIE 10705(28); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- MacMartin, D.G.; Vogiatzis, K. Unsteady Wind Loads for TMT: Replacing Parametric Models with CFD; SPIE 9150(25); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Vogiatzis, K.; Thompson, H. On the Precision of Aero-Thermal Modeling for TMT; SPIE 9911(40); SPIE: Bellingham, WA, USA, 2016. [Google Scholar]
- Vogiatzis, K. Effects of Meshing, Solver Parameters and Post-Processing on Aero-Optical Image Quality Metric Modeling; AIAA 2018-1502; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Das, K.; Vogiatzis, K.; Angeli, G.Z. Assessment of Turbulence Models and Mesh Refinement for Aero-Optical Simulations of Large Ground Based Telescopes; AIAA 2018-4156; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Vogiatzis, K. Thermal Modeling Environment for TMT; SPIE 7738(11); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Vogiatzis, K.; Conan, R. Preliminary Evaluation of the GMT HVAC System Using CFD; GMT-DOC-03938; GMTO Corporation: Pasadena, CA, USA, 2019. [Google Scholar]
- Thompson, H.A.; Vogiatzis, K. Heat Balance and Thermal Management of the TMT Observatory; SPIE 9150(83); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Pazder, J.; Vogiatzis, K. Dome and Mirror Seeing Estimates for the Thirty Meter Telescope; SPIE 7017(26); SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Conan, R.; van Dam, M.; Vogiatzis, K.; Das, K.; Bouchez, A. Modeling the Giant Magellan Telescope dome seeing using fluid dynamics simulations. In Proceedings of the AO4ELT6, Quebec City, QC, Canada, 9–14 June 2019. [Google Scholar]
- Vogiatzis, K.; Angeli, G.Z. Strategies for Estimating Mirror and Dome Seeing for TMT; SPIE 6271(27); SPIE: Bellingham, WA, USA, 2006. [Google Scholar]
- Vogiatzis, K.; Upton, R. TMT Studies on Thermal Seeing Modeling: Mirror and Dome Seeing Model Validation; SPIE 6271(48); SPIE: Bellingham, WA, USA, 2006. [Google Scholar]
- McMynowski, D.G.; Colavita, M.M.; Skidmore, W.A.; Vogiatzis, K. Primary Mirror Dynamic Disturbance Models for TMT: Vibration and Wind; SPIE 7738(14); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Vogiatzis, K.; McMynowski, D.G. Unsteady Aerodynamic Simulations for TMT Primary Mirror Segment Wind Loading; SPIE 7738(61); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Soler, M.; Vogiatzis, K.; Cozar-Castellano, J.; Bonaque, S.; Bello-Asin, M.; Nunez Cagigal, M.; Baretto Cabrera, M. Local Seeing Analysis for the European Solar Telescope; SPIE 13094(153); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Vogiatzis, K.; Otarola, A.; Skidmore, W.; Travouillon, T.; Angeli, G.Z. Local Thermal Seeing Modeling Validation through Observatory Measurements; SPIE 8449(1); SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Salmon, D.; Benedict, T.; Baril, M.; Wang, S.-Y.; Thanjavur, K.; Vogiatzis, K.; Racine, R. A Fluid Dynamic Study of the CFHT Dome Using CFD and Water Tunnel Tests; SPIE 8449(2); SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Vogiatzis, K. Aerothermal modeling framework for TMT. In Proceedings of the Integrated Modeling of Complex Optomechanical Systems, Kiruna, Sweden, 15–17 August 2011. SPIE 8336(10). [Google Scholar]
- Vogiatzis, K.; Fitzpatrick, H.; Das, K.; Conan, R.; Angeli, G.; Sitarski, B.; Romano, R.; Dribusch, C.; Walls, B. Aerothermal Modeling for Design Support, Requirement Validation and Performance Assessment of GMT Subsystems; SPIE 12187(22); SPIE: Bellingham, WA, USA, 2022. [Google Scholar]
- Cho, M.; Corredor, A.; Vogiatzis, K.; Angeli, G.Z. Thermal Analysis of the TMT Telescope Structure; SPIE 7738(12); SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Vogiatzis, K.; Sadjadpour, A.; Roberts, S. TMT Telescope Structure Thermal Model; SPIE 9150(72); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Fitzpatrick, H.; Conan, R.; Vogiatzis, K.; Das, K.; Dribusch, C. A Computational Framework for the Study of the Diurnal Thermomechanical Behavior of the Giant Magellan Telescope; SPIE 13099(98); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Vogiatzis, K.; Boyer, C.; Wei, K.; Tang, J.; Ellerbroek, B. Aero-Thermal Simulations of the TMT Laser Guide Star Facility; SPIE 9148(243); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Vogiatzis, K.; Wang, L.; Trubey, M.; Irarrazaval, B.; Boyer, C. Aerothermal Modeling of the TMT International Observatory Laser Guide Star Facility; SPIE 13099(101); SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Vogiatzis, K. Ion Beam Figuring Modeling; Document TMT.SEN.TEC.20.070; TMT International Observatory: Pasadena, CA, USA, 2020. [Google Scholar]
- McQuillen, I.; Phelps, L. Factory Acceptance Testing and Model Refinement for the Daniel K. Inouye Solar Telescope air Knife Assembly; SPIE 10705(25); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Martins, D.; Holzlohner, R.; Verinaud, C.; Kleinclaus, C. Transient Wavefront Error from Cooled Air Downwind of Telescope Spiders; SPIE 12187(12); SPIE: Bellingham, WA, USA, 2022. [Google Scholar]
- CFD Vision 2030 Study. Available online: http://ntrs.nasa.gov/search.jsp?R=20140003093 (accessed on 10 June 2024).
- AIAA CFD Vision 2030 Integration Committee Website. Available online: https://cfd2030.com (accessed on 10 June 2024).
- Vogiatzis, K. Transient Aero-Thermal Simulations for TMT; SPIE 9150(24); SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Vogiatzis, K.; Thompson, H.; Roberts, S. On the Precision of Aero-Thermal Simulations for TMT: Revisited; SPIE 10705(4); SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Racine, R.; Salmon, D.; Cowley, D.; Sovka, J. Mirror, dome, and natural seeing at CFHT. Publ. Astron. Soc. Pac. 1991, 103, 1020–1032. [Google Scholar] [CrossRef]
- Bustos, E.; Tokovinin, A. Dome Seeing Monitor and Its Results for the 4m Blanco Telescope; SPIE 10700; SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Lai, O.; Withington, K.; Chun, M.R.; Laugier, R. Investigating ground layer and dome turbulence in astronomical observatories using a localized optical turbulence sensor. In Proceedings of the Imaging and Applied Optics Congress, Washington, DC, USA, 22–26 June 2020. [Google Scholar]


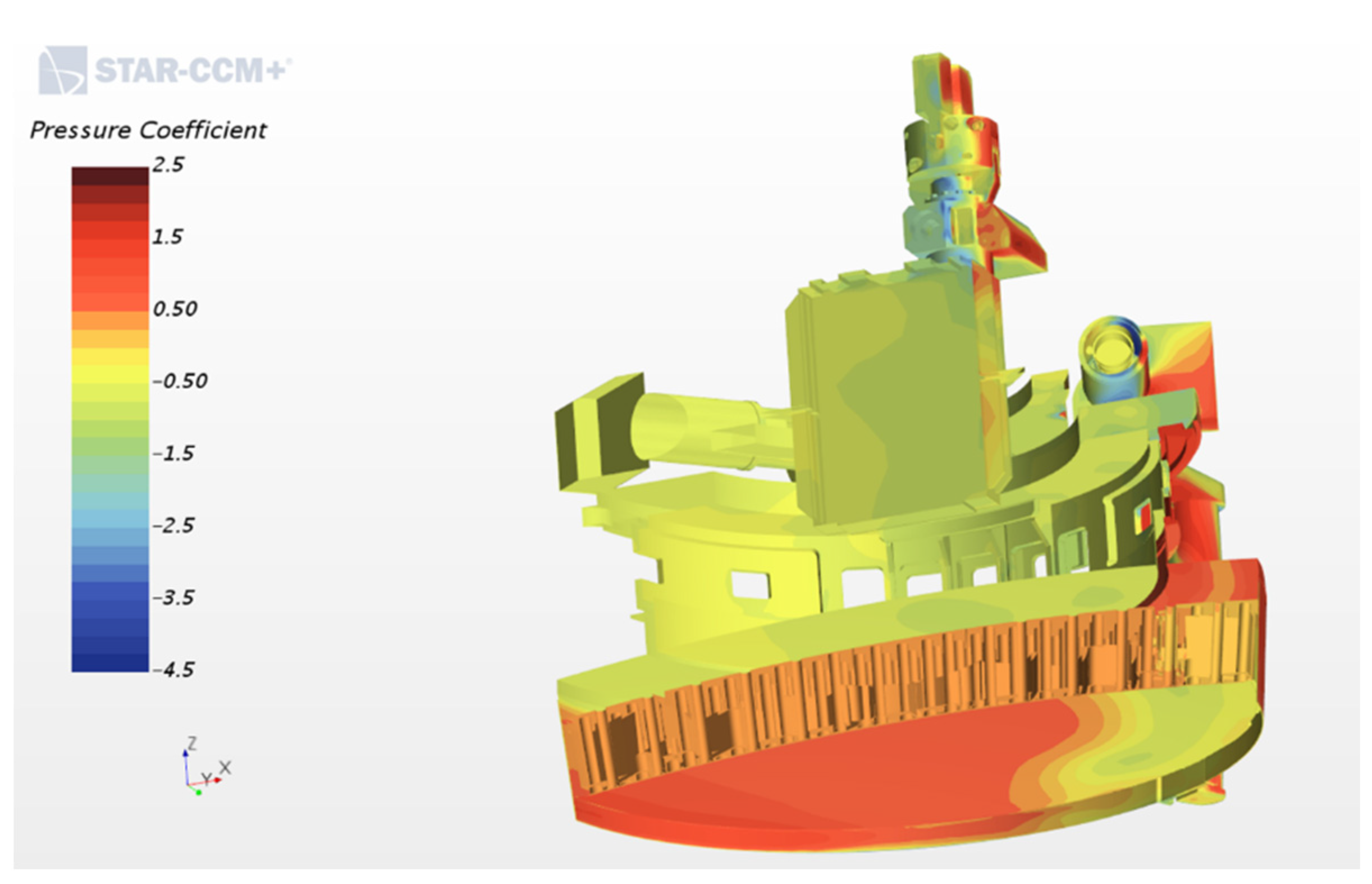

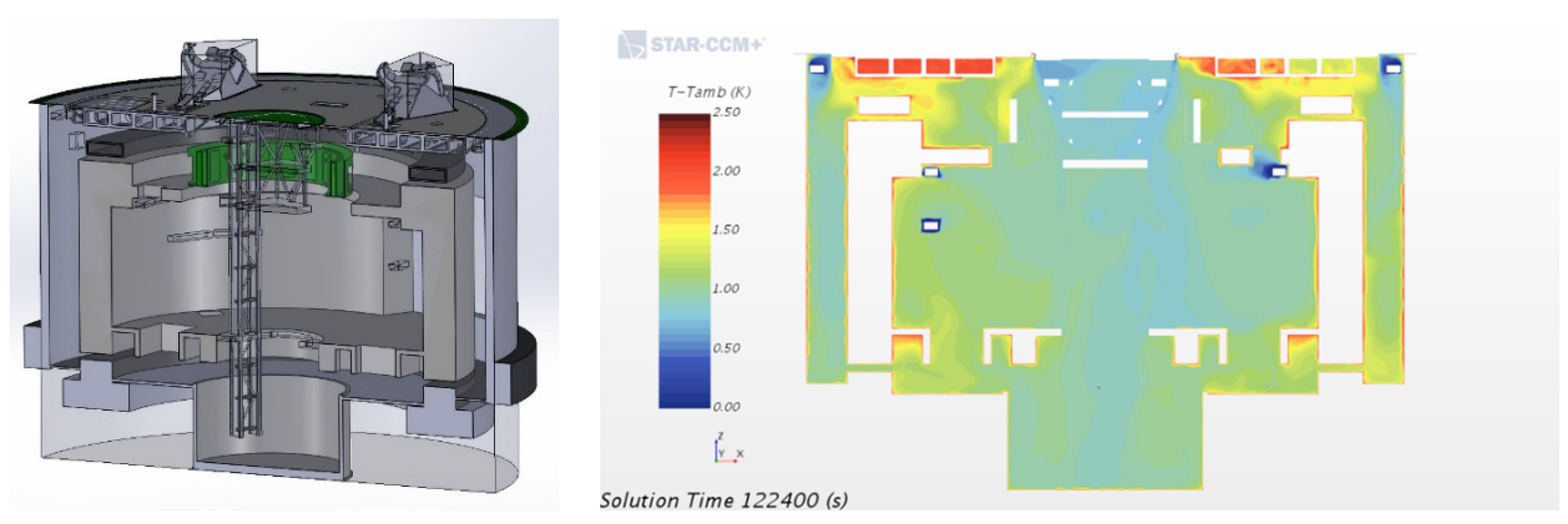
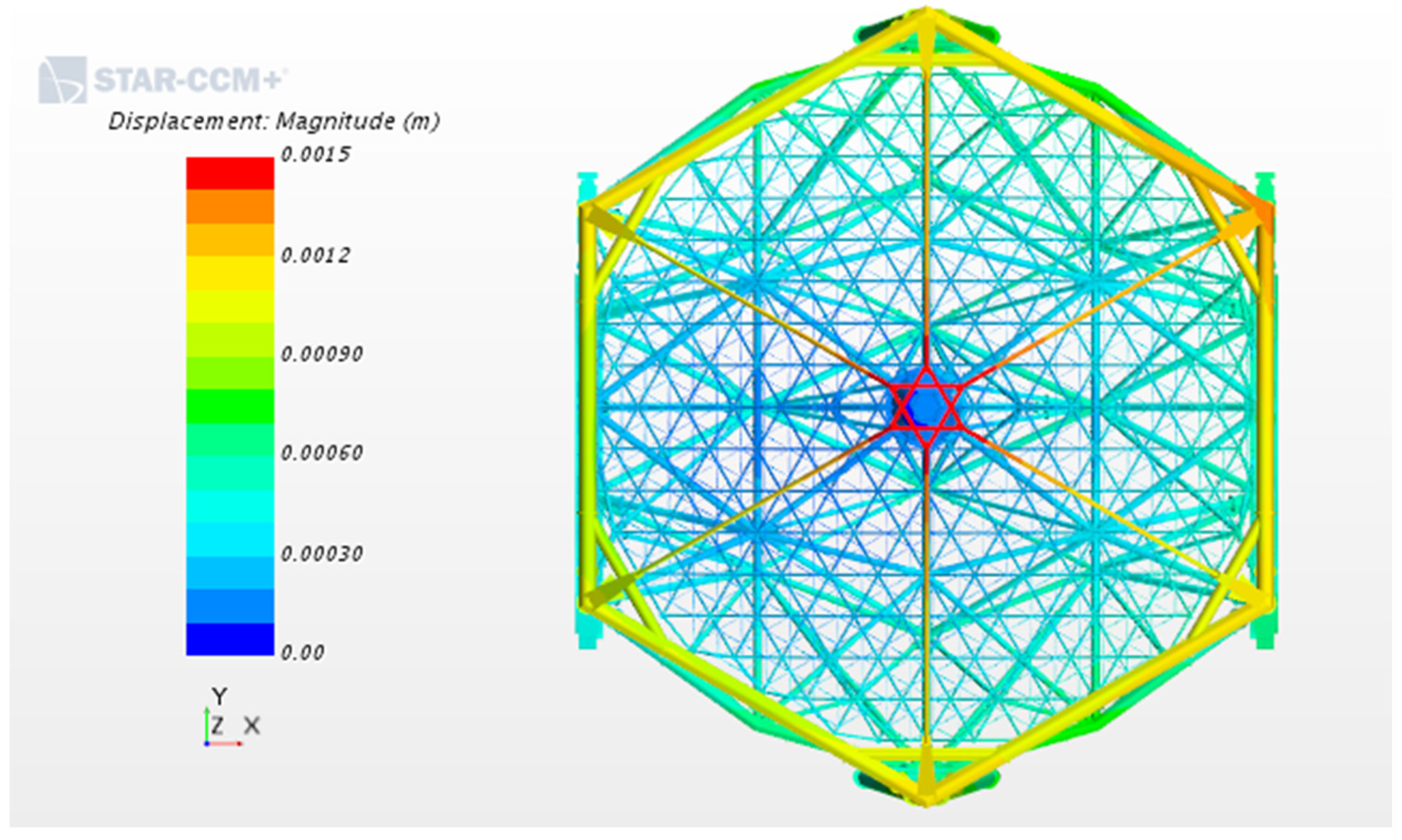
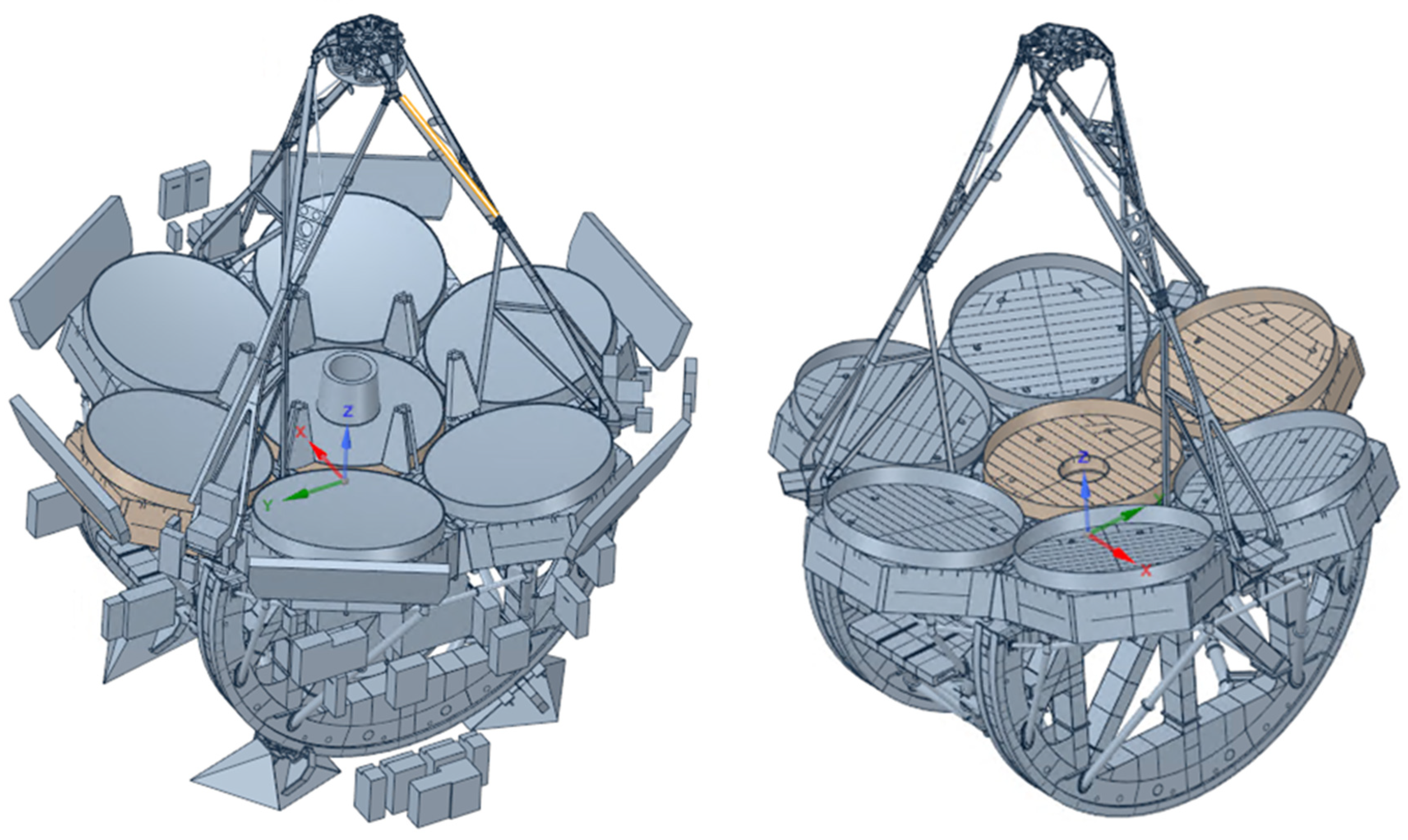


| ELT Development Aspect | Modeling Action | Systems Engineering Function |
|---|---|---|
| Site selection | GL modeling. Comparison with site measurements. | Trade-off studies. Risk mitigation (model validation). |
| Site development | GL modeling: minimize impact on site quality, select specific location within site, and investigate interactions with existing observatories where applicable. Comparison with site measurements. | Trade-off studies. Risk mitigation (model validation). |
| Enclosure and facilities | Observatory modeling: enclosure type selection, aerodynamic shape optimization, survival wind loads, vent area, location, and number, cooling sizing and performance, thermal control of drives, utility equipment and interstitial spaces, surface temperatures/paint emissivity, and insulation thickness. | Trade-off studies. Requirements validation. |
| Telescope mount (structure) | Solid thermal modeling: thermal deformation, telescope pointing, surface temperatures/paint emissivity, and temperature sensor location/alignment look-up table. Observatory modeling: aerodynamic optimization of top end and secondary support structure. | Requirements validation. Trade-off studies. |
| Optical assemblies | Conjugate heat transfer modeling: surface and component temperatures, deformation wavefront error, thermal control, and effects on metrology sensors. | Requirements validation. |
| Instruments and Laser Guide Star Systems | Conjugate heat transfer modeling: surface and component temperatures, focus errors, internal optical path turbulence, and design optimization. | Requirements validation. Trade-off studies. |
| Performance CBE | Observatory modeling: thermal seeing/effects on metrology, wind loading on structure and optics, thermal deformation of structure and optics, and telescope pointing. Modeling existing observatories for comparison and mesh resolution studies (for multiple models). | Requirements verification. Risk mitigation (model validation). |
| AIVC/operations | Observatory modeling: aerothermal environment during construction, internal thermal gradients in absence of air conditioning, external wind profiles, and effects on metrology. Reduced Order Modeling (ROM) and Artificial Neural Network (ANN) modeling for first light characterization and operations optimization/queue observing. | Requirements validation. Requirements verification. |
| Category | Status | Challenges | Mitigations |
|---|---|---|---|
| Stochastic and thermal network models using multiyear environmental records | Developed | Climate change. | On-site environmental monitoring systems and periodic record updates. |
| Subsystem conjugate heat transfer models | Partially developed; most instruments are still under development, and CADs are not mature | CAD preparation/update. | CAD configuration control; mesh by parts to minimize update time during design development. |
| Observatory CFD models | Developed, but overset mesh motion and mesh adaptivity are not yet implemented | Insufficient funding for computational resources and/or time to completion. Concurrent simulation with many subsystem models is computationally expensive. Simulation at desired OPD resolution is computationally prohibitive. Data handling. Validation. | Await future increased computing power at same cost. Develop ROM and ANN models. In situ processing. Measurements on existing observatories. |
| ROM and ANN models for observatory operation (AIVC phase) | Early development | Insufficient funding for required FTEs and computational resources. Uncertainty for the number of parameters ANNs can stably accommodate and the number of simulations required for training. | If insufficient funding persists, roll to operations and investigate alternative funding avenues. Break down to simpler tasks, few inputs/outputs per task. Test software on existing observatories. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogiatzis, K.; Angeli, G.; Trancho, G.; Conan, R. Computational Fluid Dynamics-Based Systems Engineering for Ground-Based Astronomy. Computation 2024, 12, 143. https://doi.org/10.3390/computation12070143
Vogiatzis K, Angeli G, Trancho G, Conan R. Computational Fluid Dynamics-Based Systems Engineering for Ground-Based Astronomy. Computation. 2024; 12(7):143. https://doi.org/10.3390/computation12070143
Chicago/Turabian StyleVogiatzis, Konstantinos, George Angeli, Gelys Trancho, and Rod Conan. 2024. "Computational Fluid Dynamics-Based Systems Engineering for Ground-Based Astronomy" Computation 12, no. 7: 143. https://doi.org/10.3390/computation12070143
APA StyleVogiatzis, K., Angeli, G., Trancho, G., & Conan, R. (2024). Computational Fluid Dynamics-Based Systems Engineering for Ground-Based Astronomy. Computation, 12(7), 143. https://doi.org/10.3390/computation12070143




