Exploring New Traveling Wave Solutions to the Nonlinear Integro-Partial Differential Equations with Stability and Modulation Instability in Industrial Engineering

Abstract

In this research article, we demonstrate the generalized expansion method to investigate nonlinear integro-partial differential equations via an efficient mathematical method for generating abundant exact solutions for two types of applicable nonlinear models. Moreover, stability analysis and modulation instability are also studied for two types of nonlinear models in this present investigation. These analyses have several applications including analyzing control systems, engineering, biomedical engineering, neural networks, optical fiber communications, signal processing, nonlinear imaging techniques, oceanography, and astrophysical phenomena. To study nonlinear PDEs analytically, exact traveling wave solutions are in high demand. In this paper, the (1 + 1)-dimensional integro-differential Ito equation (IDIE), relevant in various branches of physics, statistical mechanics, condensed matter physics, quantum field theory, the dynamics of complex systems, etc., and also the (2 + 1)-dimensional integro-differential Sawda–Kotera equation (IDSKE), providing insights into the several physical fields, especially quantum gravity field theory, conformal field theory, neural networks, signal processing, control systems, etc., are investigated to obtain a variety of wave solutions in modern physics by using the mentioned method. Since abundant exact wave solutions give us vast information about the physical phenomena of the mentioned models, our analysis aims to determine various types of traveling wave solutions via a different integrable ordinary differential equation. Furthermore, the characteristics of the obtained new exact solutions have been illustrated by some figures. The method used here is candid, convenient, proficient, and overwhelming compared to other existing computational techniques in solving other current world physical problems. This article provides an exemplary practice of finding new types of analytical equations.

1. Introduction

Many physical scenarios are characterized by linear and nonlinear mathematical models. These models can be described via ordinary or partial differential equations. Typical features of difficulties in daily life including engineering, mechanics, acoustics, mathematical finance, population dynamics, ecological systems, neural networks, signal processing, control systems, and telecommunications could be formed as well as analyzed with the support of the nonlinear partial differential equations (NLPDEs). A variety of contemporary scientific and technological domains employ NLPDEs to explain complicated occurrences. Every NLPDE possesses a unique, significant, and fascinating form. These NLPDEs’ outcomes show the evolution features of useful quantities that may help identify or anticipate modifications to states in actual-world problems. In light of this, researchers studying novel exact solutions of these NLPDEs are working passionately and deeply. For a more advanced understanding, it is crucial to initiate precise traveling wave solutions for nonlinear occurrences. So, one of the most popular study topics among applied scientists and mathematicians nowadays is finding analytical solutions for different NLPDEs. Distinct innumerable approaches to elucidate NLPDEs are given in the references [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In the recent past, lots of techniques have been developed and used to investigate exact solutions such as the modified F-expansion technique [21], the Tikhonov regularization scheme [22], the Hirota’s bilinear technique [23], the sine–cosine scheme [24,25], the unified process [26], the auxiliary equation approach [27], the generalized Kudryshov method [28,29], the Sine–Gordon expansion procedure [30], the inverse scattering scheme [31,32], the two variables ($G^{\prime }$/$G$, 1/$G$)-expansion technique [33,34,35,36,37], the Riemann–Hilbert problem method [38], the Hamiltonian approach [39], etc. Using this technique, Iqbal et al. [40] explored the Date–Jimbo–Kashiwara–Miwa Equation to determine the exact wave solutions most recently. Additional workable approaches include the modified $\left(G^{\prime }/G\right)$-expansion approach [41], the generalized Kudryashov procedure [42], the integration process [43], the modified symbolic computation scheme [44], the Hirota’s bilinear operator’s procedure [45], the tanh-function scheme [46], the improved system method [47], the Cole–Hope transformation method [48], etc. To investigate closed-form soliton solutions of NLPDEs, a significant method the $\left(G^{\prime }/G\right)$-expansion method was presented by Wang et al. [8]. A number of investigators investigated the precise solution of various NLPDE types using the previously described $\left(G^{\prime }/G\right)$-expansion technique. Following that, a wide range of researchers have predicted and constructed different expansions of the $\left(G^{\prime }/G\right)$-expansion approach. Zhang et al. [11] expanded the $\left(G^{\prime }/G\right)$-expansion method which is named the improved $\left(G^{\prime }/G\right)$-expansion method. Lately, Naher and Abdullah [16] offered the generalized $\left(G^{\prime }/G\right)$-expansion method that is more comprehensible and easier for a class of NLPDEs to generate numerous new closed-form soliton solutions with additional parameters. Very recently, Miah et al. [33] applied the two variables $\left(G^{\prime }/G,1/G\right)$-expansion method to generate the soliton solutions of the integro-differential equation. An advantage of the generalized $\left(G^{\prime }/G\right)$-expansion method involves the fact that a large number of new closed-form soliton solutions with additional free parameters can be obtained. Accuracy and application are the main alluring features. Our research strategy is undoubtedly straightforward and practical, and the outcomes will be unique. Stability analysis is a vital concept across various fields including mathematics, engineering, economics, and biology. Modulation instability is a phenomenon that occurs in nonlinear wave systems, where small perturbations or fluctuations in the amplitude or phase of a wave can grow exponentially over time [49]. Recently, Aljahdaly et al. [50] explored the stability of the longitudinal wave equation in magneto-electro-elastic circular rods. In [51], stability as well as modulation instability are also investigated in the resonance nonlinear Schrodinger model with Kerr law nonlinearity. The stability analysis and modulation instability of the IDIE and the IDSKE have not been examined yet. From this interest, we would detect the stability analysis and modulation instability for the offered equations. The IDIE is a specific type of NLPDE that combines elements of both integral and differential operators, as well as the stochastic processes. One generalization of the bilinear Korteweg–de Vries (KdV) equation provides the (1 + 1)-dimensional IDIE, which first was invented in 1980 by Kiyoshi Ito. This model equation has applications in various branches of physics, statistical mechanics, condensed matter physics, quantum field theory, the dynamics of complex systems such as non-equilibrium systems, disordered materials, the interaction process of two internal long waves, mathematical finance, mathematical biology to model biological processes including models of population dynamics, ecological systems, neural networks, signal processing, control systems, and telecommunications. The (2 + 1)-dimensional IDSKE, originally developed by Konopelchenko and Dubrovsky in 1984, has become a significant NLPDE. In the diverse physical fields of especially quantum gravity field theory, conformal field theory, neural networks, signal processing, control systems, and the conserved current of the Liouville equation, the corresponding equation has profound and extensive uses. Our suggested approach could be utilized to resolve almost any type of NLPDE quickly and effectively without compromising its generality. According to our evaluation of the literature, no one has used our mentioned method to construct the soliton solutions of the IDIE as well as the IDSKE. Consequently, inspired by the discussions above, the ambition of the present article is to establish numerous novel closed-form solutions for the IDIE and IDSKE with the help of the anticipated process. If we compare our generated plentiful findings to the current results, they will have distinct characteristics.

The rest of this article follows the structure given in the Introduction in Section 1. In the following Section 2, the methodology is analyzed. Some applications have been anatomized in Section 3. Section 4 is organized by stability analysis. Modulation instability is placed in Section 5. A graphical explanation has been specified in Section 6. Finally, the conclusion is ordered in Section 7.

2. Elucidation of the Generalized (G′/G)-Expansion Process

Herein, we present the elementary notion of the stated technique for originating the novel solutions of the specified NLPDEs in references [16,17]. Assume that a general NLPDE,

$$R_1\left(v,v_x,v_y,v_z,v_t,v_{xx},v_{yy},v_{zz},v_{tt},v_{xy},v_{yz},\cdots \right)=0,$$

(1)

where $v=v(x,y,z,t)$ is a noteless function, $R_1$ represents a polynomial, and the terms are partial derivatives and multiplication of derivatives. The chronological tactic of the mentioned scheme,

Step 1

In this stage, we combine all the independent variables with the dependent ones,

$$v\left(x,y,z,t\right)=v\left(\alpha \right);\hspace{1em}\hspace{1em}\alpha =x+y+z-wt,$$

(2)

wherein $w$ stands for the speed of the wave. Using Equations (1) and (2), we obtain an ordinary differential equation (ODE),

$$R_2\left(v,v^{\prime },v^{″},\cdots \right)=0,$$

(3)

where the dash symbol (′) means the ordinary derivative according to $\alpha$, the autonomous variable.

Step 2

Integrate Equation (3) as much as we need, upon observing the necessity, and for minimalism, all integral constants are assumed to be zero.

Step 3

Guess the wave solution of the above ODE is as follows,

$$v\left(\alpha \right)={\sum }_{i=0}^K{c}_i{\left(e+H\right)}^i+{\sum }_{i=1}^K{d}_i{\left(e+H\right)}^{-i},$$

(4)

wherein, $e$, $d_i$, and $c_i$ are constants, and $H$ is represented by,

$$H=G^{\prime }/G,$$

(5)

in which the auxiliary nonlinear ODE,

$$P_{1}G{G}^{″}-P_{2}G{G}^{\prime }-P_3{G}^2-P_4{\left(G^{\prime }\right)}^2=0,$$

(6)

in which $P_1$,$P_2$, $P_3$, and $P_4$ are parameters. The expansion Equation (4) is rational in H, which implies that the adopted approach is a special case of the transformed rational function method [7]. Moreover, $H=(G^{\prime }/G$) in (5) satisfies a Riccati equation, due to (6), whose general solutions are given by (40)–(42) in [48].

Step 4

The homogeneous balance principle will give us the value of $K$ from Equation (3).

Step 5

Combining Equations (4)–(6) in Equation (3) along with the calculated value of $K$, we have a system of algebraic equations, and then assembling the coefficient of ${\left(e+H\right)}^K$, $\left(K=0,1,2,\cdots \right)$, and ${\left(e+H\right)}^{-K}$, $\left(K=1,2,3,\cdots \right)$ from each side of the resultant polynomial equals to zero. Currently, one could see a set of under-determined algebraic equations for $c_i\left(i=0,1,2,\cdots ,K\right)$,$d_i\left(i=1,2,3,\cdots ,K\right)$, $e$, and $w$.

Step 6

After entering the values of $c_i\left(i=0,1,2,\cdots ,K\right)$, $d_i\left(i=1,2,3,\cdots ,K\right)$, $e$, and $w$ into Equation (4), we obtain the traveling wave solution of Equation (1) because the general solution of Equation (6) is well-known to us previously.

Step 7

With the aid of the general solution of Equation (6) or the general solutions to a Riccati equation by (40)–(42) in [48], we succeed in obtaining the following solutions of Equation (6):

Category 1: If $P_2\ne 0,\lambda =P_1-P_4$, and $S={P_2}^2+4P_3\left(P_1-P_4\right)>0$, then

$$H\left(\alpha \right)={\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}{\displaystyle \frac{l_1\sinh \left(\frac{\sqrt{S}}{2P_1}\alpha \right)+l_2\cosh \left(\frac{\sqrt{S}}{2P_1}\alpha \right)}{l_1\cosh \left(\frac{\sqrt{S}}{2P_1}\alpha \right)+l_2\sinh \left(\frac{\sqrt{S}}{2P_1}\alpha \right)}},$$

(7)

Category 2: If $P_2\ne 0,\lambda =P_1-P_4$, and $S={P_2}^2+4P_3\left(P_1-P_4\right)<0$, then

$$H\left(\alpha \right)={\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}{\displaystyle \frac{-l_1\sin \left(\frac{\sqrt{-S}}{2P_1}\alpha \right)+l_2\cos \left(\frac{\sqrt{-S}}{2P_1}\alpha \right)}{l_1\cos \left(\frac{\sqrt{-S}}{2P_1}\alpha \right)+l_2\sin \left(\frac{\sqrt{-S}}{2P_1}\alpha \right)}},$$

(8)

Category 3: If $P_2\ne 0,\lambda =P_1-P_4$, and $S={P_2}^2+4P_3\left(P_1-P_4\right)=0$, then

$$H\left(\alpha \right)={\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{l_2}{l_1+l_2\alpha }},$$

(9)

Category 4: If $P_2=0,\lambda =P_1-P_4$, and $T=\lambda P_3>0$, then

$$H\left(\alpha \right)={\displaystyle \frac{\sqrt{T}}{\lambda }}{\displaystyle \frac{l_1\sinh \left(\frac{\sqrt{T}}{P_1}\alpha \right)+l_2\cosh \left(\frac{\sqrt{T}}{P_1}\alpha \right)}{l_1\cosh \left(\frac{\sqrt{T}}{P_1}\alpha \right)+l_2\sinh \left(\frac{\sqrt{T}}{P_1}\alpha \right)}},$$

(10)

Category 5: If $P_2=0,\lambda =P_1-P_4$, and $T=\lambda P_3<0$, then

$$H\left(\alpha \right)={\displaystyle \frac{\sqrt{-T}}{\lambda }}{\displaystyle \frac{{-l}_1\sin \left(\frac{\sqrt{-T}}{P_1}\alpha \right)+l_2\cos \left(\frac{\sqrt{-T}}{P_1}\alpha \right)}{l_1\cos \left(\frac{\sqrt{-T}}{P_1}\alpha \right)+l_2\sin \left(\frac{\sqrt{-T}}{P_1}\alpha \right)}},$$

(11)

The above solutions of Equation (6) we will use to determine the exact solutions of the mentioned two equations.

3. Applications of the Proposed Method

We will be applying the generalized method to investigate the new exact wave solution of the two mentioned equations.

3.1. Traveling Wave Solutions to the IDIE

Here, we express the mentioned first NLPDE in references [33],

$$v_{tt}+v_{xxxt}+3\left(2v_x{v}_t+v{v}_{xt}\right)+3v_{xx}{\partial }_x^{-1}\left(v_t\right)=0$$

(12)

Considering $V_x\left(x,t\right)=v\left(x,t\right)$ and the modification in Equation (2), we will be swapping the NLPDE in Equation (12) to the ODE,

$$w^2{V}^{‴}-w{V}^{\left(5\right)}-6w{\left(V^{″}\right)}^2-6w{V}^{\prime }{V}^{‴}=0.$$

(13)

Now, we integrate the above twofold and choosing $w_1$ as the integrating constant,

$$w{V}^{\prime }-V^{‴}-3{\left(V^{\prime }\right)}^2+w_1=0.$$

(14)

Operating step 4, we have $K=1$ and via the Equation (4),

$$V\left(\alpha \right)=c_0+c_1\left(e+H\right)+d_1{\left(e+H\right)}^{-1},$$

(15)

herein,$c_0$,$c_1$, and $d_1$ stand for constants that need to be determined. A successful workout supplies the three sets of responses:

Set 1:

$$e=e,w_1=0,w={\displaystyle \frac{4P_3{P}_1+{P_2}^2-4P_4{P}_3}{{P_1}^2}},c_0=c_0,c_1={\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}},d_1=0.$$

(16)

Set 2:

$$e=e,w_1=0,w={\displaystyle \frac{4P_3{P}_1+{P_2}^2-4P_4{P}_3}{{P_1}^2}},c_0=c_0,c_1=0,d_1=-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}.$$

(17)

Set 3:

$$e=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{P_2}{P_1-P_4}},w_1=0,w={\displaystyle \frac{4\left(4P_3{P}_1+{P_2}^2-4P_4{P}_3\right)}{{P_1}^2}},c_0=c_0,c_1={\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}},d_1={\displaystyle \frac{1}{2}}{\displaystyle \frac{4P_3{P}_1+{P_2}^2-4P_4{P}_3}{P_1\left(P_1-P_4\right)}},$$

(18)

Type 1: When $P_2\ne 0$, $S={P_2}^2+4P_3\left(P_1-P_4\right)>0$, and $\lambda =P_1-P_4$, using Equations (7), (15), and (16) together, we ascertain the wave solution of Equation (14). The wave solutions in selecting $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero, are now afforded by the simplicity,

$$V_{1_1}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left\{2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{S}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\},$$

$$V_{1_1}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left\{2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{S}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\},$$

Analogously Equations (8), (11), (15), and (16) permit the wave solutions under picking $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$c{V}_{1_3}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left\{2e+{\displaystyle \frac{P_2}{\lambda }}-{\displaystyle \frac{\sqrt{-S}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\},$$

$$V_{1_4}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left\{2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{-S}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\},$$

$$V_{1_5}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right\},$$

$$V_{1_6}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\},$$

$$V_{1_7}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\},$$

$$V_{1_8}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\},$$

$$V_{1_9}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\},$$

each of which is an outcome of Equation (14). General solutions of Equation (12) could be obtained using the conversion $\alpha =x-wt$,

$$v_{1_1}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left[2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{S}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left\{{\displaystyle \frac{\sqrt{S}}{2P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_2}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left[2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{S}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left\{{\displaystyle \frac{\sqrt{S}}{2P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_3}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left[2e+{\displaystyle \frac{P_2}{\lambda }}-{\displaystyle \frac{\sqrt{-S}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left\{{\displaystyle \frac{\sqrt{-S}}{2P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_4}=c_0+{\displaystyle \frac{\left(P_1-P_4\right)}{P_1}}\left[2e+{\displaystyle \frac{P_2}{\lambda }}+{\displaystyle \frac{\sqrt{-S}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left\{{\displaystyle \frac{\sqrt{-S}}{2P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_5}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{x-wt}}\right\},$$

$$v_{1_6}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left[e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left\{\left({\displaystyle \frac{\sqrt{T}}{P_1}}\left(x-wt\right)\right)\right\}\right],$$

$$v_{1_7}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left[e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left\{{\displaystyle \frac{\sqrt{T}}{P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_8}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left[e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left\{{\displaystyle \frac{\sqrt{-T}}{P_1}}\left(x-wt\right)\right\}\right],$$

$$v_{1_9}=c_0+{\displaystyle \frac{2\left(P_1-P_4\right)}{P_1}}\left[e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left\{{\displaystyle \frac{\sqrt{-T}}{P_1}}\left(x-wt\right)\right\}\right].$$

Type 2: When $P_2\ne 0$, $S={P_2}^2+4P_3\left(P_1-P_4\right)>0,$ and $\lambda =P_1-P_4$, using Equations (7), (15), and (17) together, we ascertain the wave solution of Equation (14). As an oversimplification, we achieve the wave solutions by electing $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$V_{2_1}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_2}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-1}.$$

Analogously, using Equations (8), (11), (15), and (18) serve the wave solutions by picking $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$V_{2_3}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-S}}{2\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_4}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_5}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1+P_{2}e-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right\}}^{-1},$$

$$V_{2_6}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_7}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_8}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1-P_4{e}^2\right)}{P_1}}{\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-1},$$

$$V_{2_9}=c_0-{\displaystyle \frac{2\left(-P_3+e^2{P}_1-P_4{e}^2\right)}{P_1}}{\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}\mathrm{c}\mathrm{o}\mathrm{t}\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-1}.$$

The general solution of Equation (12) might be generated by applying the modification $\alpha =x-wt$ to the former results.

Type 3: For $P_2\ne 0,$ $S={P_2}^2+4P_3\left(P_1-P_4\right)>0$, and $\lambda =P_1-P_4$, using Equation (7) into Equations (15) and (18) together, we ascertain the wave solution of Equation (14). After simplification, we can figure out the wave solutions whenever $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$V_{3_1}=c_0+{\displaystyle \frac{\sqrt{S}}{P_1}}\left\{\tanh \left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)+\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}.$$

Similarly, using Equations (8), (11), (15), and (18) allows the wave solutions by indicating $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$V_{3_2}=c_0-{\displaystyle \frac{\sqrt{-S}}{P_1}}\tan \left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)-{\displaystyle \frac{S}{P_1\sqrt{-S}}}\mathrm{c}\mathrm{o}\mathrm{t}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right),$$

$$V_{3_3}=c_0+{\displaystyle \frac{\sqrt{-S}}{P_1}}\cot \left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)+{\displaystyle \frac{S}{P_1\sqrt{-S}}}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right),$$

$$V_{3_4}=c_0+{\displaystyle \frac{1}{P_1\alpha }}+{\displaystyle \frac{S\alpha }{P_1}},$$

$$V_{3_5}=c_0+{\displaystyle \frac{2\sqrt{T}}{P_1}}\tanh \left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)+{\displaystyle \frac{2P_3\left(P_1-P_4\right)}{P_1\sqrt{T}}}\coth \left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right),$$

$$V_{3_6}=c_0+{\displaystyle \frac{2\sqrt{T}}{P_1}}\coth \left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)+{\displaystyle \frac{2P_3\left(P_1-P_4\right)}{P_1\sqrt{T}}}\tanh \left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right),$$

$$V_{3_7}=c_0-{\displaystyle \frac{2\sqrt{-T}}{P_1}}\tan \left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)-{\displaystyle \frac{2P_3\left(P_1-P_4\right)}{P_1\sqrt{-T}}}\cot \left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right),$$

$$V_{3_8}=c_0+{\displaystyle \frac{2\sqrt{-T}}{P_1}}\cot \left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)+{\displaystyle \frac{2P_3\left(P_1-P_4\right)}{P_1\sqrt{-T}}}\tan \left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right).$$

Replacing $\alpha =x-wt$ in the previous equation, one could obtain the consequences of Equation (12).

3.2. Traveling Wave Solutions to the IDSKE

Herein, we construct traveling wave solutions of the IDSKE [33],

$$v_t={\left(v_{xxxx}+5v{v}_{xx}+{\displaystyle \frac{5}{3}}{v}^3+v_{xy}\right)}_x-5{{\partial }_x}^{-1}\left(v_{yy}\right)+5v{v}_y+5v_x{{\partial }_x}^{-1}\left(v_y\right).$$

(19)

Assume, $v\left(x,y,t\right)=V_x\left(x,y,t\right)$ in Equation (19), we have,

$$V_{xt}=V_{xxxxxx}+5{{(V}_x{V}_{xxx})}_x+{\displaystyle \frac{5}{3}}{\left({V_x}^3\right)}_x+V_{xxxy}-5V_{yy}+5V_x{V}_{xy}+5V_{xx}{V}_y.$$

(20)

We all look at the change needed to obtain the ODE of the given equation,

$$V\left(x,y,t\right)=U\left(\alpha \right),\alpha =x+y-wt,$$

(21)

that provides the subsequent equation,

$$-w{U}^{″}=U^{\left(6\right)}+5{\left(U^{\prime }{U}^{‴}\right)}^{\prime }+{\displaystyle \frac{5}{3}}{\left\{{\left(U^{\prime }\right)}^3\right\}}^{\prime }+U^{\left(4\right)}-5U^{″}+10U^{\prime }{U}^{″}.$$

(22)

Integrating Equation (22) two times alongside set $C=U^{\prime }$, in which $w_2$ stands for constant,

$$C^{\left(4\right)}+5C{C}^{″}+{\displaystyle \frac{5}{3}}{C}^3+C^{″}+5C^2+\left(w-5\right)C+w_2=0.$$

(23)

Following the relation of step 4, we obtain $K=2$, and we also obtain the following answers to Equation (23):

$$C\left(\alpha \right)=c_0+c_1\left(e+H\right)+c_2{\left(e+H\right)}^2{+d}_1{\left(e+H\right)}^{-1}+d_2{\left(e+H\right)}^{-2}.$$

(24)

As you can see, there are three sets of feedback containing the constants $c_0$,$c_1$, $c_2$, $d_1$, and $d_2$ to the preceding equation.

Set 1:

$$\begin{gathered} e=e,w={\displaystyle \frac{1}{5}}{\displaystyle \frac{34{P_1}^4-80{P_3}^2{P_1}^2+160{P_3}^2{P}_4{P}_1-40P_1{P}_3{P_2}^2-5{P_2}^4+40{P_2}^2{P}_4{P}_3-80{P_3}^2{P_4}^2}{{P_1}^4}},c_0= \\ -{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3- \\ 60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2),c_1={\displaystyle \frac{12\left(-P_2{P}_4-4P_{4}e{P}_1+2{P_4}^{2}e+P_2{P}_1+2e{P_1}^2\right)}{{P_1}^2}},c_2= \\ -{\displaystyle \frac{12\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{P_1}^2}},d_1=0,d_2=0,w_2=-{\displaystyle \frac{1}{75}}{\displaystyle \frac{1}{{P_1}^6}}(600{P_2}^4{P}_4{P}_3- \\ 3200{P_3}^3{P_1}^3-2640{P_3}^2{P_1}^4-9600P_1{P_4}^2{P_3}^3-2400{P_2}^2{P_4}^2{P_3}^2- \\ 2640{P_3}^2{P_4}^2{P_1}^2+5280{P_3}^2{P}_4{P_1}^3+3200{P_3}^3{P_4}^3-2400{P_2}^2{P_3}^2{P_1}^2+ \\ 9600{P_3}^3{P}_4{P_1}^2-1320P_3{P_2}^2{P_1}^3+1320{P_2}^2{P}_4{P}_3{P_1}^2+4800{P_2}^2{P_3}^2{P}_4{P}_1- \\ 165{P_2}^4{P_1}^2-600{P_2}^4{P}_1{P}_3-50{P_2}^6+243{P_1}^6). \end{gathered}$$

(25)

Set 2:

$$\begin{gathered} e=e,w={\displaystyle \frac{1}{5}}{\displaystyle \frac{34{P_1}^4-80{P_3}^2{P_1}^2+160{P_3}^2{P}_4{P}_1-40P_1{P}_3{P_2}^2-5{P_2}^4+40{P_2}^2{P}_4{P}_3-80{P_3}^2{P_4}^2}{{P_1}^4}},c_0= \\ -{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3- \\ 60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2),c_1=0,c_2=0,d_1={\displaystyle \frac{1}{{P_1}^2}}\{12(2{P_1}^2{e}^3-4P_1{P}_4{e}^3+ \\ 3P_1{P}_2{e}^2-2P_1{P}_{3}e+2{P_4}^2{e}^3-3P_2{P}_4{e}^2+2e{P}_4{P}_3+e{P_2}^2-P_3{P}_2\left)\right\},d_2= \\ -{\displaystyle \frac{1}{{P_1}^2}}\left\{12\right(e^4{P_1}^2+{P_3}^2-2P_2{e}^3{P}_4+2P_4{e}^2{P}_3-2P_{2}e{P}_3+2P_2{e}^3{P}_1+{P_4}^2{e}^4+ \\ {P_2}^2{e}^2-2P_4{e}^4{P}_1-2P_3{e}^2{P}_1\left)\right\},w_2=-{\displaystyle \frac{1}{75}}{\displaystyle \frac{1}{{P_1}^6}}(600{P_2}^4{P}_4{P}_3-3200{P_3}^3{P_1}^3- \\ 2640{P_3}^2{P_1}^4-9600P_1{P_4}^2{P_3}^3-2400{P_2}^2{P_4}^2{P_3}^2-2640{P_3}^2{P_4}^2{P_1}^2+ \\ 5280{P_3}^2{P}_4{P_1}^3+3200{P_3}^3{P_4}^3-2400{P_2}^2{P_3}^2{P_1}^2+9600{P_3}^3{P}_4{P_1}^2- \\ 1320P_3{P_2}^2{P_1}^3+1320{P_2}^2{P}_4{P}_3{P_1}^2+4800{P_2}^2{P_3}^2{P}_4{P}_1-165{P_2}^4{P_1}^2- \\ 600{P_2}^4{P}_1{P}_3-50{P_2}^6+243{P_1}^6). \end{gathered}$$

(26)

Set 3:

$$\begin{gathered} e=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{P_2}{-P_4+P_1}},w={\displaystyle \frac{2}{5}} \\ {\displaystyle \frac{17{P_1}^4-640{P_3}^2{P_1}^2-320P_1{P}_3{P_2}^2+1280{P_3}^2{P}_4{P}_1+320{P_2}^2{P}_4{P}_3-640{P_3}^2{P_4}^2-40{P_2}^4}{{P_1}^4}},c_0= \\ -{\displaystyle \frac{1}{5}}{\displaystyle \frac{9{P_1}^2-40P_3{P}_1-10{P_2}^2+40P_4{P}_3}{{P_1}^2}},c_1=0,c_2=-{\displaystyle \frac{12\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{P_1}^2}},d_1=0,d_2= \\ -{\displaystyle \frac{3}{4}}{\displaystyle \frac{16{P_3}^2{P_1}^2+8P_1{P}_3{P_2}^2-32{P_3}^2{P}_4{P}_1-8{P_2}^2{P}_4{P}_3+{P_2}^4+16{P_3}^2{P_4}^2}{{P_1}^2\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}},w_2=-{\displaystyle \frac{1}{75}}{\displaystyle \frac{1}{{P_1}^6}}(243{P_1}^6- \\ 42240{P_3}^2{P_1}^4+84480{P_3}^2{P}_4{P_1}^3-21120P_3{P_2}^2{P_1}^3-204800{P_3}^3{P_1}^3- \\ 153600{P_2}^2{P_3}^2{P_1}^2+21120{P_2}^2{P}_4{P}_3{P_1}^2-42240{P_3}^2{P_4}^2{P_1}^2-2640{P_2}^4{P_1}^2+ \\ 614400{P_3}^3{P}_4{P_1}^2-614400P_1{P_4}^2{P_3}^3+307200{P_2}^2{P_3}^2{P}_4{P}_1-38400{P_2}^4{P}_1{P}_3- \\ 153600{P_2}^2{P_4}^2{P_3}^2-3200{P_2}^6+38400{P_2}^4{P}_4{P}_3+204800{P_3}^3{P_4}^3). \end{gathered}$$

(27)

Variety 1: For $P_2\ne 0$, $S={P_2}^2+4P_3\left(P_1-P_4\right)>0$, and $\lambda =P_1-P_4$, using Equations (7), (24), and (25) together, we ascertain the wave solution of Equation (23). The wave solutions could be obtained after taking $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero, respectively,

$$\begin{gathered} C_{1_1}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3- \\ 60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2)+{\displaystyle \frac{12\left(-P_2{P}_4-4P_{4}e{P}_1+2{P_4}^{2}e+P_2{P}_1+2e{P_1}^2\right)}{{P_1}^2}}\{e+{\displaystyle \frac{P_2}{2\lambda }}+ \\ {\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\}-{\displaystyle \frac{12\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{P_1}^2}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^2, \end{gathered}$$

$$C_{1_1}=a_1+a_2\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^2,$$

$$\begin{gathered} C_{1_2}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3- \\ 60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2)+{\displaystyle \frac{12\left(-P_2{P}_4-4P_{4}e{P}_1+2{P_4}^{2}e+P_2{P}_1+2e{P_1}^2\right)}{{P_1}^2}}\{e+{\displaystyle \frac{P_2}{2\lambda }}+ \\ {\displaystyle \frac{\sqrt{S}}{2\lambda }}coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\}-{\displaystyle \frac{12\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{P_1}^2}}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}\coth \left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^2, \end{gathered}$$

$$C_{1_2}=a_1+a_2\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^2.$$

Analogously, using Equations (8), (11), (14), and (25) facilitates the wave solutions in deciding $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$C_{1_3}=a_1+a_2\left\{e+{\displaystyle \frac{P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-S}}{2\lambda }}tan\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-S}}{2\lambda }}tan\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^2,$$

$$C_{1_4}=a_1+a_2\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}cot\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}cot\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^2,$$

$$C_{1_5}=a_1+a_2\left(e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right)-a_3{\left(e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right)}^2,$$

$$C_{1_6}=a_{11}+\left\{{\displaystyle \frac{24e{\left(P_1-P_4\right)}^2}{{P_1}^2}}\right\}\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^2,$$

$$C_{1_7}=a_{11}+\left\{{\displaystyle \frac{24e{\left(P_1-P_4\right)}^2}{{P_1}^2}}\right\}\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^2,$$

$$C_{1_8}=a_{11}+\left\{{\displaystyle \frac{24e{\left(P_1-P_4\right)}^2}{{P_1}^2}}\right\}\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}-a_3{\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^2,$$

$$C_{1_9}=a_{11}+\left\{{\displaystyle \frac{24e{\left(P_1-P_4\right)}^2}{{P_1}^2}}\right\}\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}-a_3{\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^2,$$

where, $a_1=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}\left(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3-60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2\right)$, $a_{11}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}\left(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3+60{P_4}^2{e}^2\right)$, $a_2={\displaystyle \frac{12\left(-P_2{P}_4-4P_{4}e{P}_1+2{P_4}^{2}e+P_2{P}_1+2e{P_1}^2\right)}{{P_1}^2}}$, $a_3={\displaystyle \frac{12\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{P_1}^2}}$.

The more general solutions of Equation (19) can be obtained by transforming $w_2$ to the foregoing outcomes in Equation (21). To recognize the more general solutions of Equation (19), one may apply the alteration in Equation (21) along with the constant $w_2$ in the former outcomes.

Variety 2: If $P_2\ne 0,\lambda =P_1-P_4$, and $S={P_2}^2+4P_3\left(P_1-P_4\right)>0,$ then with the aid of Equations (7), (24), and (26) together, we ascertain the wave solution of Equation (23). Here, the explanation provides the wave solutions in wanting $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero, respectively,

$$\begin{gathered} C_{2_1}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3- \\ 60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2)+{\displaystyle \frac{1}{{P_1}^2}}\{12(2{P_1}^2{e}^3-4P_1{P}_4{e}^3+3P_1{P}_2{e}^2-2P_1{P}_{3}e+ \\ 2{P_4}^2{e}^3-3P_2{P}_4{e}^2+2e{P}_4{P}_3+e{P_2}^2-P_3{P}_2\left)\right\}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}\tanh \left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-1}- \\ {\displaystyle \frac{1}{{P_1}^2}}\left\{12\right(e^4{P_1}^2+{P_3}^2-2P_2{e}^3{P}_4+2P_4{e}^2{P}_3-2P_{2}e{P}_3+2P_2{e}^3{P}_1+{P_4}^2{e}^4+ \\ {P_2}^2{e}^2-2P_4{e}^4{P}_1-2P_3{e}^2{P}_1\left)\right\}{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-2}, \end{gathered}$$

$$C_{2_1}=a_4+a_5{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-1}-a_6{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}tanh\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_2}=a_4+a_5{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-1}-a_6{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{S}}{2\lambda }}coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)\right\}}^{-2}.$$

Similarly, using Equations (8), (11), (24), and (26) allow the following wave solutions with $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$C_{2_3}=a_4+a_5{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-S}}{2\lambda }}tan\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-1}-a_6{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-S}}{2\lambda }}tan\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_4}=a_4+a_5{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}cot\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-1}-a_6{\left\{e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-S}}{2\lambda }}cot\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_5}=a_4+a_5{\left(e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right)}^{-1}-a_6{\left(e+{\displaystyle \frac{P_2}{2\lambda }}+{\displaystyle \frac{1}{\alpha }}\right)}^{-2},$$

$$C_{2_6}=a_{41}+\left[{\displaystyle \frac{24e}{{P_1}^2}}\left\{e^2{\left(P_1-P_4\right)}^2-P_3\left(P_1-P_4\right)\right\}\right]{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-1}-a_{61}{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_7}=a_{41}+\left[{\displaystyle \frac{24e}{{P_1}^2}}\left\{e^2{\left(P_1-P_4\right)}^2-P_3\left(P_1-P_4\right)\right\}\right]{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-1}-a_{61}{\left\{e+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_8}=a_{41}+\left[{\displaystyle \frac{24e}{{P_1}^2}}\left\{e^2{\left(P_1-P_4\right)}^2-P_3\left(P_1-P_4\right)\right\}\right]{\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-1}-a_{61}{\left\{e-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{2_9}=a_{41}+\left[{\displaystyle \frac{24e}{{P_1}^2}}\left\{e^2{\left(P_1-P_4\right)}^2-P_3\left(P_1-P_4\right)\right\}\right]{\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-1}-a_{61}{\left\{e+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-2},$$

where, $a_4=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}\left(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1+60P_{2}e{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3-60P_2{P}_{4}e+5{P_2}^2+60{P_4}^2{e}^2\right)$, $a_{41}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{1}{{P_1}^2}}\left(60e^2{P_1}^2+9{P_1}^2-40P_3{P}_1-120e^2{P}_4{P}_1+40P_4{P}_3+60{P_4}^2{e}^2\right)$, $a_5={\displaystyle \frac{1}{{P_1}^2}}\left\{12\left(2{P_1}^2{e}^3-4P_1{P}_4{e}^3+3P_1{P}_2{e}^2-2P_1{P}_{3}e+2{P_4}^2{e}^3-3P_2{P}_4{e}^2+2e{P}_4{P}_3+e{P_2}^2-P_3{P}_2\right)\right\}$, $a_6={\displaystyle \frac{1}{{P_1}^2}}\left\{12\left(e^4{P_1}^2+{P_3}^2-2P_2{e}^3{P}_4+2P_4{e}^2{P}_3-2P_{2}e{P}_3+2P_2{e}^3{P}_1+{P_4}^2{e}^4+{P_2}^2{e}^2-2P_4{e}^4{P}_1-2P_3{e}^2{P}_1\right)\right\}$, $a_{61}={\displaystyle \frac{1}{{P_1}^2}}\left\{12\left(e^4{P_1}^2+{P_3}^2+2P_4{e}^2{P}_3+{P_4}^2{e}^4-2P_4{e}^4{P}_1-2P_3{e}^2{P}_1\right)\right\}$.

To establish the more general solutions of Equation (19), we may use the conversion in Equation (21) together with the constant $w_2$ in the earlier outcomes.

Variety 3: If $P_2\ne 0,\lambda =P_1-P_4$, and $S={P_2}^2+4P_3\left(P_1-P_4\right)>0,$ then according to Equations (7), (24), and (27) together, we ascertain the wave solution of Equation (23). One might form the succeeding traveling wave solutions with $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero, respectively,

$$\begin{gathered} C_{3_1}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{9{P_1}^2-40P_3{P}_1-10{P_2}^2+40P_4{P}_3}{{P_1}^2}}-{\displaystyle \frac{3S\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}{{\lambda }^2{P_1}^2}}{\mathit{tanh}}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)- \\ {\displaystyle \frac{{3\lambda }^2\left(16{P_3}^2{P_1}^2+8P_1{P}_3{P_2}^2-32{P_3}^2{P}_4{P}_1-8{P_2}^2{P}_4{P}_3+{P_2}^4+16{P_3}^2{P_4}^2\right)}{S{P_1}^2\left(-2P_4{P}_1+{P_1}^2+{P_4}^2\right)}}{coth}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right), \end{gathered}$$

$$C_{3_1}=a_7-{\displaystyle \frac{3S{a}_8}{{\lambda }^2{P_1}^2}}{\mathit{tanh}}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)-{\displaystyle \frac{{3\lambda }^2{a}_9}{S{P_1}^2{a}_8}}{coth}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right),$$

$$C_{3_2}=a_7-{\displaystyle \frac{3S{a}_8}{{\lambda }^2{P_1}^2}}{\mathit{coth}}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right)-{\displaystyle \frac{{3\lambda }^2{a}_9}{S{P_1}^2{a}_8}}{tanh}^2\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\alpha \right).$$

Similarly, using Equations (8), (11), (24), and (27) agrees the ensuing traveling wave solutions by choosing $l_1\ne 0$, $l_2$ be zero and $l_2\ne 0$, $l_1$ be zero,

$$C_{3_3}=a_7+{\displaystyle \frac{3S{a}_8}{{{{\lambda }^{2}P}_1}^2}}{\mathit{tan}}^2\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)+{\displaystyle \frac{{3\lambda }^2{a}_9}{{{SP}_1}^2{a}_8}}{\mathit{cot}}^2\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right),$$

$$C_{3_4}=a_7+{\displaystyle \frac{3S{a}_8}{{{{\lambda }^{2}P}_1}^2}}{\mathit{cot}}^2\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right)+{\displaystyle \frac{{3\lambda }^2{a}_9}{{{SP}_1}^2{a}_8}}{\mathit{tan}}^2\left({\displaystyle \frac{\sqrt{-S}}{2P_1}}\alpha \right),$$

$$C_{3_5}=a_7-{\displaystyle \frac{12a_8}{{\alpha }^2{P_1}^2}}-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\alpha }^2{a}_9}{{P_1}^2{a}_8}},$$

$$C_{3_6}=a_{71}-{\displaystyle \frac{12a_8}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^2-{\displaystyle \frac{{12\alpha }^2{P_3}^2}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{T}}{\lambda }}tanh\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{3_7}=a_{71}-{\displaystyle \frac{12a_8}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^2-{\displaystyle \frac{{12\alpha }^2{P_3}^2}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{T}}{\lambda }}coth\left({\displaystyle \frac{\sqrt{T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{3_8}=a_{71}-{\displaystyle \frac{12a_8}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^2-{\displaystyle \frac{{12\alpha }^2{P_3}^2}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}-{\displaystyle \frac{\sqrt{-T}}{\lambda }}tan\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-2},$$

$$C_{3_9}=a_{71}-{\displaystyle \frac{12a_8}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^2-{\displaystyle \frac{{12\alpha }^2{P_3}^2}{{P_1}^2}}{\left\{{\displaystyle \frac{-P_2}{2\lambda }}+{\displaystyle \frac{\sqrt{-T}}{\lambda }}cot\left({\displaystyle \frac{\sqrt{-T}}{P_1}}\alpha \right)\right\}}^{-2},$$

wherein, $a_7=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{9{P_1}^2-40P_3{P}_1-10{P_2}^2+40P_4{P}_3}{{P_1}^2}}$, $a_{71}=-{\displaystyle \frac{1}{5}}{\displaystyle \frac{9{P_1}^2-40P_3{P}_1+40P_4{P}_3}{{P_1}^2}}$, $a_8=-2P_4{P}_1+{P_1}^2+{P_4}^2$, $a_9=16{P_3}^2{P_1}^2+8P_1{P}_3{P_2}^2-32{P_3}^2{P}_4{P}_1-8{P_2}^2{P}_4{P}_3+{P_2}^4+16{P_3}^2{P_4}^2$.

So, the alteration in Equation (21) to the earlier outcomes could supply us with the more general consequences of Equation (19).

4. Stability Analysis

Stability analysis scrutinizes the behavior of a system with respect to time and regulates whether it inclines to persist in a steady state or depart from it [50,51,52,53]. This analysis plays a fundamental role in understanding the behavior and resilience of complex systems across different disciplines, providing insights into their long-term behavior and helping to design more robust and reliable systems. Here, we utilize Hamiltonian mechanics to examine the stability analysis. The following portion summarizes the stability analysis for the assigned two models.

4.1. Stability Analysis of the IDIE

Currently, we are very interested to explicate the stability analysis of Equation (12). Here, the momentum and Hamiltonian mechanics for this stated model equation are connected as follows,

$${\mathcal{P}}_1={\displaystyle \frac{1}{2}}\underset{-\infty }{\overset{\infty }{\int }}{\mathcal{H}}_1^{2}d\alpha .$$

(28)

in which, ${\mathcal{P}}_1$ and ${\mathcal{H}}_1$ represent the momentum and the total energy or power of a system. The solitary wave would be stabilized solitary if,

$${\displaystyle \frac{\partial {\mathcal{P}}_1}{\partial \varrho }}>0.$$

(29)

$\varrho$ be the frequency. From Equation (28) along with $v_{3_1}$,

$${\mathcal{P}}_1={\displaystyle \frac{1}{2}}\underset{-10}{\overset{10}{\int }}{\left[c_0+{\displaystyle \frac{\sqrt{S}}{P_1}}\left\{\mathit{tanh}\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\left(x-wt\right)\right)+coth\left({\displaystyle \frac{\sqrt{S}}{2P_1}}\left(x-wt\right)\right)\right\}\right]}^{2}dx.$$

(30)

Through oversimplification as well as using the stabilization rule in inequality (29), one can obtain

$${\displaystyle \frac{2\sqrt{S}tcsch\left(\frac{\sqrt{S}\left(tw-10\right)}{P_1}\right)csch\left(\frac{\sqrt{S}\left(tw+10\right)}{P_1}\right)sinh\left(\frac{20\sqrt{S}}{P_1}\right)}{P_1^2}}\left({\displaystyle \frac{2\sqrt{S}sinh\left(\frac{2\sqrt{S}tw}{P_1}\right)}{cosh\left(\frac{20\sqrt{S}}{P_1}\right)-cosh\left(\frac{2\sqrt{S}tw}{P_1}\right)}}+c_0{P}_1\right)>0.$$

(31)

So, the nonlinear stability of Equation (1) together with soliton solution has been confirmed with the aid of inequality (29) as well as from inequality (31).

4.2. Stability Analysis of the IDSKE

In this present section, we implement a similar concept as well as relate the soliton solution $C_{1_6}$ with $e=1,P_1=2,P_3=2,P_4=1,\alpha =x+y-wt$ to the momentum,

$${\mathcal{P}}_2={\displaystyle \frac{1}{2}}\underset{-10}{\overset{10}{\int }}{\left\{-{\displaystyle \frac{4}{5}}+6\left(1+\sqrt{2}tanh{\displaystyle \frac{1}{\sqrt{2}}}\left(x+y-wt\right)\right)-3{\left(1+\sqrt{2}tanh{\displaystyle \frac{1}{\sqrt{2}}}\left(x+y-wt\right)\right)}^2\right\}}^{2}dx.$$

(32)

Oversimplification and correspondingly, by means of the stabilization principle, one can acquire

$$\begin{gathered} {\displaystyle \frac{1}{5{\left(cosh\left(10\sqrt{2}\right)+cosh\left(\sqrt{2}\left(tw-y\right)\right)\right)}^4}}3t(19cosh\left(\sqrt{2}\left(10+3tw-3y\right)\right)- \\ 19cosh\left(\sqrt{2}\left(-10+3tw-3y\right)\right)-202cosh\left(\sqrt{2}\left(10+tw-y\right)\right)- \\ 22cosh\left(2\sqrt{2}\left(10+tw-y\right)\right)+19cosh\left(\sqrt{2}\left(30+tw-y\right)\right)+ \\ 202cosh\left(\sqrt{2}\left(10-tw+y\right)\right)+22cosh\left(2\sqrt{2}\left(10-tw+y\right)\right)- \\ 19cosh\left(\sqrt{2}\left(30-tw+y\right)\right))>0. \end{gathered}$$

(33)

The consequence in inequality (33) along with the condition in inequality (29) ensure that the soliton solution and our proposed model is nonlinearly stable.

5. Modulation Instability

Modulation instability represents an incident that occurs in nonlinear wave systems, in which small perturbations or oscillations in the amplitude or phase of a wave can produce exponentially over time [49,51,52,53,54,55]. In nonlinear imaging, signal processing, communication systems, oceanography, and astrophysics, this analysis has abundant applications. We will focus on the modulation instability of the IDIE and the IDSKE in this current section.

5.1. Modulation Instability of the IDIE

Herein, modulation instability is reported for the proposed equation. Consider, the perturbed solution as follows,

$$v\left(x,t\right)={\xi }_1+{\xi }_2\Phi \left(x,t\right),$$

(34)

in which, ${\xi }_1$ remains for a steady flow attitude. Now, we linearize in ${\xi }_2$, after applying the conversion in Equation (34) to Equation (12),

$${\Phi }_{tt}+{\Phi }_{xxxt}+3{\xi }_1{\Phi }_{xt}=0.$$

(35)

Imagine the solution of Equation (35),

$$\Phi =e^{i\left(k_{1}x+k_{2}t\right)},$$

(36)

the waveform quantity as well as the frequency is considered by $k_1$ and $k_2$, harmoniously. Operate Equation (36),

$$k_2=-k_1\left(3{\xi }_1-k_1^2\right),$$

(37)

Constantly, one could get the negative value from Equation (37). A decaying relationship will form by any composition of the solutions. Therefore, our recommended model equation has a stable dispersion.

5.2. Modulation Instability of the IDSKE

In this subsection, we implement the perturbed solution to Equation (20), where the perturbed solution includes a steady flow ${\xi }_3$,

$$V\left(x,y,t\right)={\xi }_3+{\xi }_4\Theta \left(x,y,t\right).$$

(38)

After utilizing the above conversion and at the same time linearizing in ${\xi }_4$,

$${\Theta }_{xt}+5{\Theta }_{yy}-{\Theta }_{xxxy}-{\Theta }_{xxxxxx}=0.$$

(39)

Pick up the solution of Equation (39),

$$\Theta =e^{i\left(m_{1}x+m_{2}y+m_{3}t\right)},$$

(40)

where, $m_1$ and $m_2$ mean the normalized wave number. Use Equation (40) to Equation (39),

$$m_3=-{\displaystyle \frac{\left(5m_2^2+m_1^3{m}_2-m_1^6\right)}{m_1}}.$$

(41)

From the above situation, we observe that any assembly of the solutions launched a decaying pattern. Accordingly, we assess that our model has a stable dispersion.

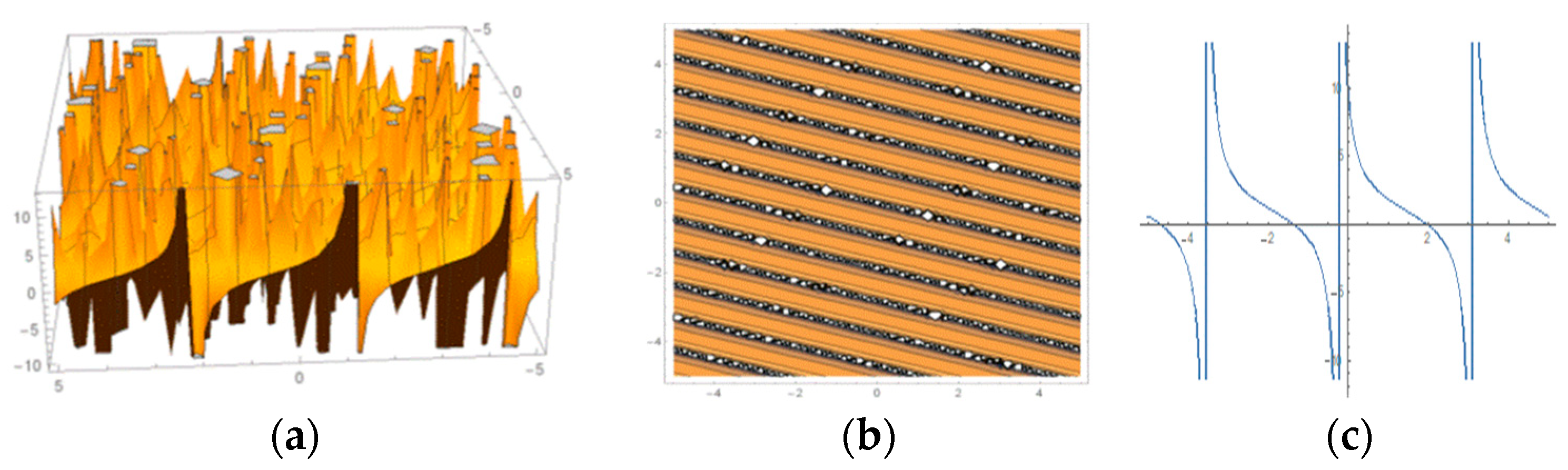
6. Graphical Revelation and Physical Demonstrations

In this instance, we present the illustrative representation as well as the physical expositions of the obtained consequences of the IDIE and the IDSKE. An essential geometric tool for exposing an issue and exploring potential solutions is a graph. The smooth kink shape soliton is observed for the solutions $v_{1_1}$, $v_{1_6}$, $v_{2_1}$, and $v_{2_6}$. Figure 1 displays the 3D, contour, and 2D figure of the solution $v_{1_1}$ using $x\in [-5,5]$ and other values of the parameters, $c_0=1$, $p_2=2$, $p_1=3$, $p_3=2$, $p_3=2$, $p_4=1$, $e=2$, $\lambda =2$, $s=20$, $w={\displaystyle \frac{20}{9}}$, $t=1$. We also inspect that the solutions $v_{1_6}$, $v_{2_1}$, and $v_{2_6}$ have the same figure like the solution $v_{1_1}$ of the IDIE. Furthermore, the singular kink shape soliton is noted for the solutions $v_{1_2}$, $v_{1_7}$, $v_{2_2}$, $v_{2_7}$, $v_{3_1}$, and $v_{3_5}$. Figure 2 exhibits the 3D, contour, and 2D figure to the solution $v_{2_2}$ having the singular kink shape soliton with definite values of parameters and the outcomes $v_{1_2}$, $v_{1_7}$, $v_{2_7}$, $v_{3_1}$, and $v_{3_5}$ have the same output like the solution $v_{2_2}$. The periodic solitons are exhibited for the solutions $v_{3_2}$,$v_{3_3}$, $v_{3_7},$ $v_{3_8}$ of the assigned equation and for suitability, we demonstrate simply the soliton shape of the solution $v_{3_7}$ in Figure 3 within 3D, contour, and 2D figures with some fixed values of parameters. Moreover, the compressed bell shape soliton is detected for the results $c_{1_1}$,$c_{1_6}$,$c_{2_1}$,$c_{2_6}$, and $c_{3_6}$ of the IDSKE, and for accessibility, we offer just the shape of the consequence$c_{1_1}$ in Figure 4 within 3D, contour, and 2D figures with some specific values of parameters. Likewise, the outcomes $c_{3_1}$ and $c_{3_2}$ of the IDSKE suggest the singular shape soliton and for closeness, we assign the single shape of the solution $c_{3_2}$ in Figure 5 within 3D, contour, and 2D figures with suitable values of parameters. The two previously stated equations still have solutions that involve periodic soliton, kink shape soliton, singular soliton, singular kink shape soliton, and also bell shape soliton. We will leave out the remainder of outcomes’ figures to keep things simple. The essential outcomes are stated graphically hereunder.

7. Conclusions

Making use of closed-form dynamic wave solutions, many of the dramatic incidents in theoretical physics as well as contemporary engineering are investigated. This study aims to operate the generalized $\left(G^{\prime }/G\right)$-expansion method to discover various novel precise wave solutions of some NLPDEs. This technique has already been successfully employed in the IDIE and the IDSKE to compute their exact wave solutions having the physical structures of smooth kink shape, singular kink shape, singular shape, compressed bell shape, as well as periodic soliton including trigonometric, hyperbolic, and also rational form. In a novel fashion, the suggested method produces a wide range of traveling wave solutions with several free parameters. For these two equations, we obtained 52 solutions (25 for the first and 27 for the second equation), and as per our literature review, we confirmed that all the results are new relating to the existing outcomes. Stability analysis and modulation instability have been conducted for these two model equations. These analyses show us that our stated equations are nonlinearly stable and have a stable dispersion. The outcomes of the two offered models are utilized in several mathematical physics domains along with nonlinear optics, fluid mechanics, mathematical finance, population dynamics, ecological systems, neural networks, signal processing, control systems, and telecommunications. The outcomes from this analysis appeal to the proficiency, conciseness, and straightforwardness of the assigned method. So, the presented scheme could be used to analyze diverse NLPDEs, including the nonlinear Schrödinger-type equations, Kadomtsev–Petviashvili (KP) equation, Korteweg–de Vries (KdV) equation, modified KdV equation, Fokas–Lenells equation, and others that have been consistently demonstrated in modern engineering and mathematical physics as well.