FPGA-Based Numerical Simulation of the Chaotic Synchronization of Chua Circuits
Abstract
1. Introduction
2. Materials and Methods
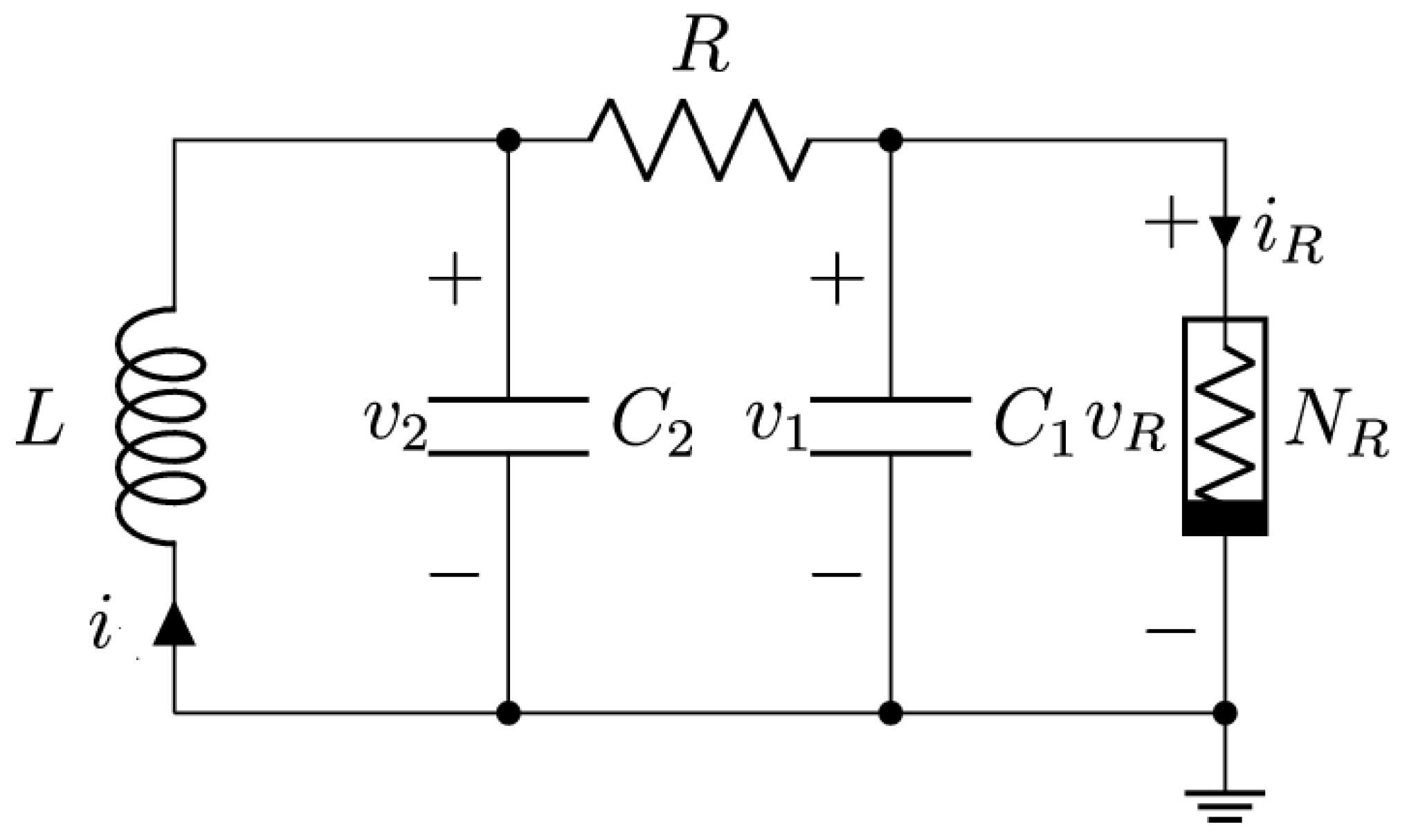
2.1. The Chua Circuit
2.2. Existence and Uniqueness of the Chua Circuit State Equations
- : the function is continuous and differentiable, with typically being a piecewise linear function. This ensures Lipschitz continuity.
- : This is a linear function and is Lipschitz-continuous.
- : This is also a linear function and is Lipschitz-continuous.
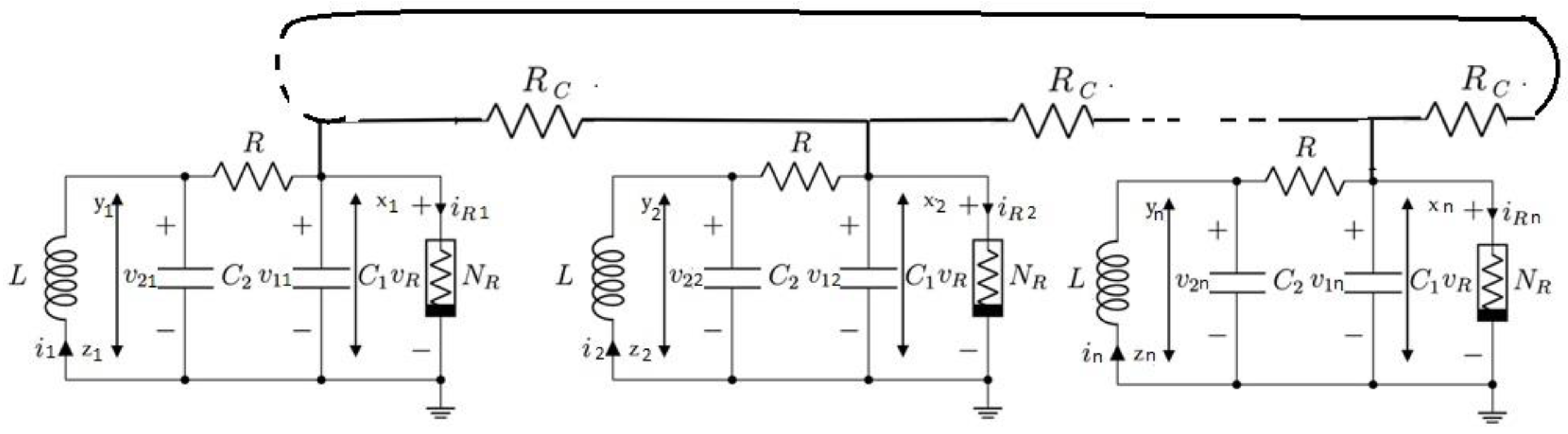
2.3. Synchronization of Chua Circuits
2.4. Numerical Procedures for Solving ODEs
2.5. Software-Based Numerical Simulation
2.6. Hardware-Based Numerical Simulation
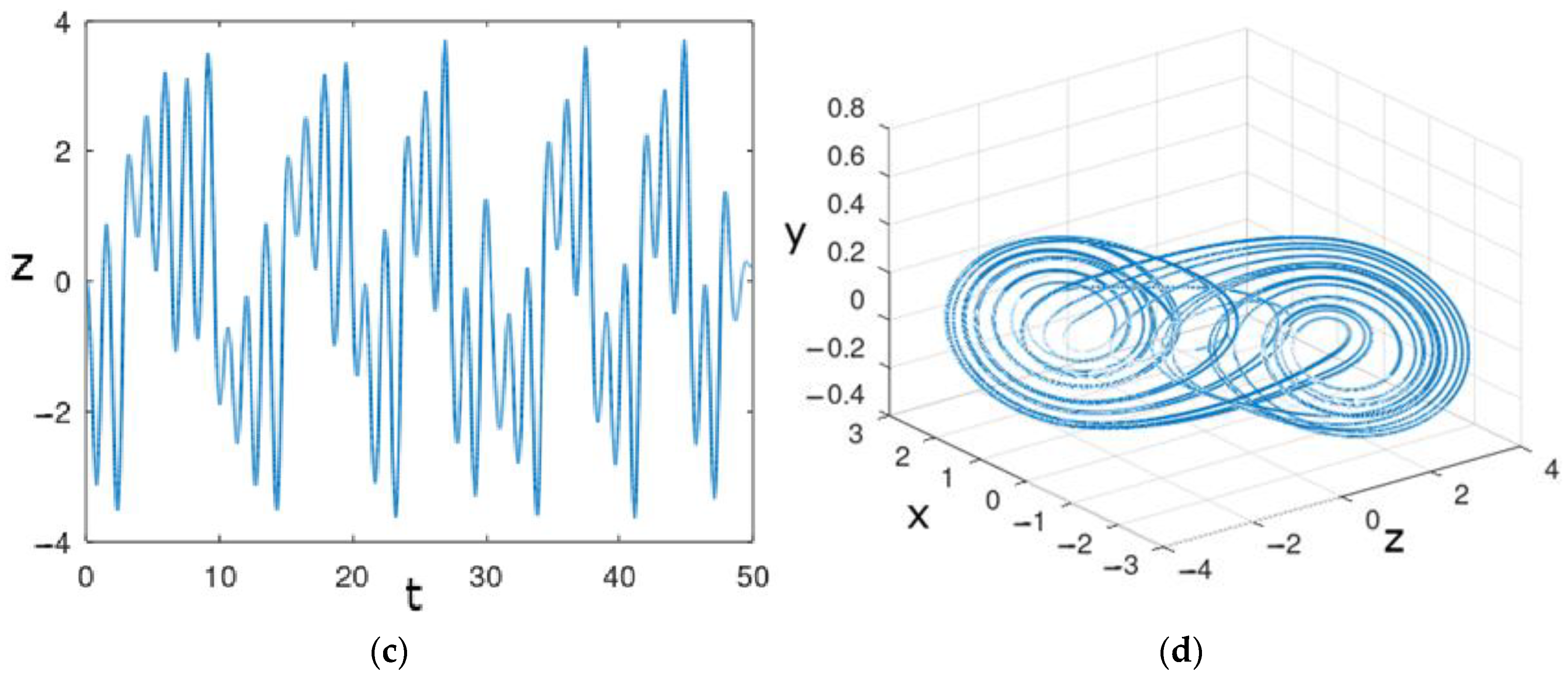
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| //‘timescale <time_units> / <precision> | ||
| module chua (clk,x, y, z); | ||
| parameter integerBits= 6; | ||
| parameter fractionBits=25 ; | ||
| parameter dtBits=16 ; | ||
| parameter dtShift=30 ; | ||
| parameter iteratorBits=16 ; | ||
| parameter signed [integerBits + fractionBits : 0 ] dt=0.005 *(2.0 ** (fractionBits)); | ||
| parameter [iteratorBits - 1 : 0 ] skip=1024 ; | ||
| parameter signed [integerBits + fractionBits : 0 ] sigma=15.0 * 1 *(2.0 **(fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0 ] rho=1.0 * 1 *(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0 ] beta =28.0 * 1 *(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0 ] m1=-0.714 * 1 *(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0 ] m0mm1x05=-0.2145 *1 * (2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0 ] startX=0.7 * 1 *(2.0 ** fractionBits); | ||
| parameter signed [integerBits + fractionBits : 0 ] startY=0.0 * 1 *(4.0 ** fractionBits); | ||
| parameter signed [integerBits + fractionBits : 0 ] startZ=0.0 * 1 *(2.0 ** fractionBits); | ||
| localparam totalBits = 1 + integerBits + fractionBits; | ||
| input wire clk; | ||
| output reg signed [totalBits-1 :0 ] x = startX; | ||
| output reg signed [totalBits-1 :0 ] y = startY; | ||
| output reg signed [totalBits-1 :0 ] z = startZ; | ||
| reg [iteratorBits-1 :0 ] iterator = 0 ; | ||
| reg signed [totalBits-1 :0 ] a = startX; | ||
| reg signed [totalBits-1 : 0 ] b = startY; | ||
| reg signed [totalBits -1 :0 ] c = startZ; | ||
| reg signed [totalBits*2 -1 :0 ] h = 0 ; | ||
| reg signed [totalBits-1 :0 ] abs1 = 0 ; | ||
| reg signed [totalBits-1 :0 ] abs2 = 0 ; | ||
| reg signed [totalBits*2 -1 :0 ] dxdt = 0 ; | ||
| reg signed [totalBits*2 -1 :0 ] dydt = 0 ; | ||
| reg signed [totalBits*2 -1 :0 ] dzdt = 0 ; | ||
| reg signed [totalBits - 1 : 0 ] res = 0 ; | ||
| always @(posedge clk) | ||
| begin | ||
| iterator <= iterator+1 ; | ||
| if (!iterator) | ||
| begin | ||
| x = a; | ||
| y = b; | ||
| z = c; | ||
| end | ||
| else | ||
| begin | ||
| if (iterator == skip) | ||
| Begin | ||
| a = x; | ||
| b = y; | ||
| c = z; | ||
| End | ||
| abs1=x+32 ’h04000000 ; | ||
| if (abs1<0 ) begin | ||
| abs1=-abs1; | ||
| end | ||
| abs2=(x-32 ’h04000000 ); | ||
| if (abs2<0 ) begin | ||
| abs2=-abs2; | ||
| end | ||
| h=(m1*x+m0mm1x05*(abs1-abs2))>>>fractionBits; | ||
| dxdt = (sigma * (y - x-h)) >>> fractionBits; | ||
| dydt = x -y+z; | ||
| dzdt = (-beta* y) >>> fractionBits; | ||
| x = x + ((dxdt * dt) >>> fractionBits); | ||
| y = y + ((dydt * dt) >>> fractionBits); | ||
| z = z + ((dzdt * dt) >>> fractionBits); | ||
| end | ||
| end | ||
| endmodule | ||
Appendix B
| ‘timescale 1ns / 1ps | ||
| module chuaN(clk,x1,x2,x,y,z); | ||
| parameter integerBits = 6; | ||
| parameter fractionBits = 25; | ||
| parameter dtBits = 16; | ||
| parameter dtShift = 30; | ||
| parameter iteratorBits = 16; | ||
| parameter signed [integerBits + fractionBits : 0] dt=0.0005 *(2.0 ** (fractionBits)); | ||
| parameter [iteratorBits - 1:0] skip = 1024; | ||
| parameter signed [integerBits + fractionBits:0] sigma = 15.0 * 1*(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] rho = 1.0 * 1*(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] beta = 28.0 * 1*(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] m1 = -0.714 * 1*(2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] m0mm1x05 = -0.2145 *1* (2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] startX = 0.7 * 1*(2.0 ** fractionBits); | ||
| parameter signed [integerBits + fractionBits : 0] startY = 0.0 * 1*(2.0 ** fractionBits); | ||
| parameter signed [integerBits + fractionBits : 0] startZ = 0.0 * 1*(2.0 ** fractionBits); | ||
| parameter signed [integerBits + fractionBits : 0] deltaX = 7 * (2.0 ** (fractionBits)); | ||
| parameter signed [integerBits + fractionBits : 0] uno = 1 * (2.0 ** (fractionBits)); | ||
| localparam totalBits = 1 + integerBits + fractionBits; | ||
| input wire clk; | ||
| input signed [totalBits – 1 : 0] x2; | ||
| input signed [totalBits – 1 :0] x1; | ||
| output reg signed [totalBits - 1 : 0] x = startX; | ||
| output reg signed [totalBits - 1 : 0] y = startY; | ||
| output reg signed [totalBits - 1 : 0] z = startZ; | ||
| reg [iteratorBits - 1 : 0] iterator = 0; | ||
| reg signed [totalBits - 1 : 0] a = startX; | ||
| reg signed [totalBits - 1 : 0] b = startY; | ||
| reg signed [totalBits - 1 : 0] c = startZ; | ||
| reg signed [totalBits * 2 - 1 : 0] h = 0; | ||
| reg signed [totalBits - 1 : 0] abs1 = 0; | ||
| reg signed [totalBits - 1 : 0] abs2 = 0; | ||
| reg signed [totalBits * 2 - 1 : 0] dxdt = 0; | ||
| reg signed [totalBits * 2 - 1 : 0] dydt = 0; | ||
| reg signed [totalBits * 2 - 1 : 0] dzdt = 0; | ||
| reg signed [totalBits - 1 : 0] res = 0; | ||
| always @(posedge clk) | ||
| begin | ||
| iterator <= iterator + 1; | ||
| if (!iterator) | ||
| begin | ||
| x = a; | ||
| y = b; | ||
| z = c; | ||
| end | ||
| else | ||
| begin | ||
| if (iterator == skip) | ||
| begin | ||
| a = x; | ||
| b = y; | ||
| c = z; | ||
| end | ||
| abs1=x+uno; | ||
| if(abs1<0) begin | ||
| abs1=-abs1; | ||
| end | ||
| abs2=(x-uno); | ||
| if(abs2<0) begin | ||
| abs2=-abs2; | ||
| end | ||
| h=(m1*x+m0mm1x05*(abs1-abs2))>>>fractionBits; | ||
| dxdt = (sigma * (y - x-h)-deltaX*(2*x-x1-x2)) >>> fractionBits; | ||
| dydt = x -y+z; | ||
| dzdt = (-beta* y) >>> fractionBits; | ||
| x = x + ((dxdt * dt) >>> fractionBits); | ||
| y = y + ((dydt * dt) >>> fractionBits); | ||
| z = z + ((dzdt * dt) >>> fractionBits); | ||
| end | ||
| end | ||
| endmodule | ||
References
- Sussman, G.J.; Wisdom, J. Chaotic Evolution of the Solar System. Science 1992, 257, 56–62. [Google Scholar] [CrossRef]
- Tél, T.; Gruiz, M.; Kulacsy, K. Chaotic dynamics: An introduction based on classical mechanics. In Chaotic Dynamics: An Introduction Based on Classical Mechanics; Cambridge University Press: Cambridge, UK, 2006; pp. 1–408. ISBN 9780521839129. [Google Scholar] [CrossRef]
- Azar, A.T.; Vaidyanathan, S. (Eds.) Advances in Chaos Theory and Intelligent Control; Springer: Berlin/Heidelberg, Germany, 2016; Volume 337. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C. Chaos Control in a Discrete Ecological System. Int. J. Mod. Nonlinear Theory Appl. 2012, 1, 81–83. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Yin, X.; Liu, Y. Control Chaos in System with Fractional Order. J. Mod. Phys. 2012, 3, 496–501. [Google Scholar] [CrossRef]
- Oestreicher, C. A history of chaos theory. Dialog-Clin. Neurosci. 2022, 9, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, J.S. Chaotic dynamics applied to information processing. Rep. Prog. Phys. 1986, 49, 1109–1196. [Google Scholar] [CrossRef]
- Eroglu, D.; Lamb, J.S.W.; Pereira, T. Synchronisation of chaos and its applications. Contemp. Physics 2017, 58, 207–243. [Google Scholar] [CrossRef]
- Li, P.; Shi, S.; Xu, C.; Rahman, M.U. Bifurcations, chaotic behavior, sensitivity analysis and new optical solitons solutions of Sasa-Satsuma equation. In Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 2024; Volume 112, pp. 7405–7415. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Mokaev, T.; Ponomarenko, V.; Seleznev, E.; Stankevich, N.; Chua, L. Hidden attractors in Chua circuit: Mathematical theory meets physical experiments. Nonlinear Dyn. 2023, 111, 5859–5887. [Google Scholar] [CrossRef]
- Abdulaali, R.S.; Jamal, R.K. A Comprehensive Study and Analysis of the Chaotic Chua Circuit. Iraqi J. Sci. 2022, 63, 556–570. [Google Scholar] [CrossRef]
- Lv, E. Chua’s Circuit Simulation Experiment Based on Saturation Function. J. Phys. Conf. Ser. 2021, 2078, 012026. [Google Scholar] [CrossRef]
- Suxo-Coro, A.A.; Callejas-Icuña, A.S.; Nina, C.; Medrano-Torricos, R.O.; Ramírez-Ávila, G.M. Dinámica de circuitos de Chua con bobinas no ideales e histéresis. Rev. Boliv. Física 2022, 40, 13–25. Available online: http://www.scielo.org.bo/scielo.php?script=sci_arttext&pid=S1562-38232022000100004&lng=es&nrm=iso&tlng=es (accessed on 30 May 2023). [CrossRef]
- Montalvo, R.A.; Rivera, P.H. Experimentando el circuito de Chua. Rev. Boliv. Física 2017, 19, 161902752. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J. Complex Dynamics of the Chua’s Circuit System with Adjustable Symmetry and Nonlinearity: Multistability and Simple Circuit Realization. World J. Appl. Phys. 2019, 4, 24. [Google Scholar] [CrossRef]
- Kheir, N.A. Systems Modeling and Computer Simulation; Dekker, M., Ed.; Routledge: London, UK, 1996; Available online: https://www.routledge.com/Systems-Modeling-and-Computer-Simulation/Kheir/p/book/9780824794217 (accessed on 4 June 2023).
- Yang, T.; Chua, L.O. Secure communication via chaotic parameter modulation. In IEEE Transactions on Circuits and Systems I: Fundamental Theory; IEEE: New York, NY, USA, 1996; Available online: https://ieeexplore.ieee.org/abstract/document/536758/ (accessed on 29 July 2024).
- Kennedy, M.P. Three Steps to Chaos—Part II: A Chua’s Circuit Primer. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1993, 40, 657–674. [Google Scholar] [CrossRef]
- Caponetto, R.; Criscione, M.; Fortuna, L.; Occhipinti, D.; Occhipinti, L. Programmable chaos generator, based on CNN architectures, with applications in chaotic communications. In Proceedings of the IEEE International Workshop on Cellular Neural Networks and Their Applications, London, UK, 14–17 April 1998; pp. 124–129. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Zhong, G.-Q.; Ayrom, F. Experimental confirmation of chaos from Chua’s circuit. Int. J. Circuit Theory Appl. 1985, 13, 93–98. [Google Scholar] [CrossRef]
- García-García, J.A.; Enríquez, J.G.; Ruiz, M.; Arévalo, C.; Jiménez-Ramírez, A. Software Process Simulation Modeling: Systematic literature review. Comput. Stand Interfaces 2020, 70, 103425. [Google Scholar] [CrossRef]
- Boghosian, B.M.; Coveney, P.V.; Wang, H.; Boghosian, B.M.; Wang, H.; Coveney, V. A New Pathology in the Simulation of Chaotic Dynamical Systems on Digital Computers. Adv. Theory Simul. 2019, 2, 1900125. [Google Scholar] [CrossRef]
- Hussain, H.M.; Benkrid, K.; Seker, H.; Erdogan, A.T. FPGA implementation of K-means algorithm for bioinformatics application: An accelerated approach to clustering Microarray data. In Proceedings of the 2011 NASA/ESA Conference on Adaptive Hardware and Systems, AHS 2011, San Diego, CA, USA, 6–9 June 2011; pp. 248–255. [Google Scholar] [CrossRef]
- Wang, Y.; Ribeiro, J.M.L.; Tiwary, P. Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr. Opin. Struct. Biol. 2020, 61, 139–145. [Google Scholar] [CrossRef]
- Duncan, A.L.; Pezeshkian, W. Mesoscale simulations: An indispensable approach to understand biomembranes. Biophys. J. 2023, 122, 1883–1889. [Google Scholar] [CrossRef]
- Ooms, J.; Hübl, A. Applying a Hybrid Model to Solve the Job-Shop Scheduling Problem with Preventive Maintenance, Sequence-Dependent Setup Times and Unknown Processing Times. In Proceedings of the 2022 Winter Simulation Conference (WSC), Singapore, 11–14 December 2022; Volume 2022, pp. 1750–1761. [Google Scholar] [CrossRef]
- Le-Huy, P.; Guérette, S.; Dessaint, L.A.; Le-Huy, H. Real-time simulation of power electronics in power systems using an FPGA. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 873–877. [Google Scholar] [CrossRef]
- Borgese, G.; Pace, C.; Pantano, P.; Bilotta, E. FPGA-based distributed computing microarchitecture for complex physical dynamics investigation. IEEE Trans. Neural Netw. Learn Syst. 2013, 24, 1390–1399. [Google Scholar] [CrossRef]
- Matar, M.; Abdel-Rahman, M.; Soliman, A.-M. FPGA-Based Real-Time Digital Simulation. In Proceedings of the International Conference on Power Systems Transients (IPST’05) in Montreal, Montreal, QC, Canada, 19–23 June 2015. [Google Scholar]
- Chen, H.; Sun, S.; Aliprantis, D.C.; Zambreno, J. Dynamic Simulation of Electric Machines on FPGA Boards. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 3–6 May 2009. [Google Scholar]
- Watanabe, H.; Matsutani, H. Accelerating ode-based neural networks on low-cost FPGAs a preprint. arXiv 2023, arXiv:2012.15465. [Google Scholar]
- Mayacela, M.; Rentería, L.; Contreras, L.; Medina, S. Comparative Analysis of Reconfigurable Platforms for Memristor Emulation. Materials 2022, 15, 4487. [Google Scholar] [CrossRef] [PubMed]
- Mamat, M.; Sanjaya, M.; Maulana, D.S. Numerical Simulation Chaotic Synchronization of Chua Circuit and Its Application for Secure Communication. Appl. Math. Sci. 2013, 7, 1–10. [Google Scholar] [CrossRef]
- Muni, S.S.; Provata, A. Chimera states in ring–star network of Chua circuits. Nonlinear Dyn. 2020, 101, 2509–2521. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, J.; Xu, Y. Phase synchronization between neurons under nonlinear coupling via hybrid synapse. Chaos Solitons Fractals 2023, 169, 113238. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, J.; Zhang, G.; Zhang, Y. Synchronization control between two Chua′s circuits via capacitive coupling. Appl. Math. Comput. 2019, 360, 94–106. [Google Scholar] [CrossRef]
- Pivka, L.; Wu, C.; Huang, A. Chua’s oscillator: A compendium of chaotic phenomena. In Journal of the Franklin Institute; Elsevier: Amsterdam, The Netherlands, 1994; Available online: https://www.sciencedirect.com/science/article/pii/0016003294900876 (accessed on 18 June 2023).
- Chen, C.; Ma, H.; Chen, H.; Meng, Y.; Ding, Q. FPGA implementation of a UPT chaotic signal generator for image encryption. Pac. Sci. Rev. A Nat. Sci. Eng. 2015, 17, 97–102. [Google Scholar] [CrossRef][Green Version]
- Chua, L.O.; Itoh, M.; Kocarev, L.; Eckert, K. Chaos synchronization in chua’s circuit. J. Circuits Syst. Comput. 2011, 3, 93–108. [Google Scholar] [CrossRef]
- Yao, Z.; Ma, J.; Yao, Y.; Wang, C. Synchronization realization between two nonlinear circuits via an in-duction coil coupling. Nonlinear Dyn. 2019, 96, 205–217. [Google Scholar] [CrossRef]
- Youssef, T.; Chadli, M.; Karimi, H.R.; Zelmat, M. Chaos synchronization based on unknown input proportional multiple-integral fuzzy observer. In Abstract and Applied Analysis; Hindawi Publishing Corporation: New York, NY, USA, 2013; Volume 2013. [Google Scholar] [CrossRef]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1991; p. 429. Available online: https://books.google.com/books/about/Theory_of_Ordinary_Differential_Equation.html?hl=es&id=bPJQAAAAMAAJ (accessed on 30 July 2024).
- Sun, J.; Shen, Y.; Yin, Q.; Xu, C. Compound synchronization of four memristor chaotic oscillator systems and secure communication. Chaos 2013, 23, 013140. [Google Scholar] [CrossRef]
- Wu, C.W.; Chua, L.O. A simple way to synchronize chaotic systems with applica-tions to secure communication systems. Int. J. Bifurc. Chaos 1993, 3, 1619–1627. [Google Scholar] [CrossRef]
- Diaconu, A.; Loukhaoukha, K. An Improved Secure Image Encryption Algorithm Based on Rubik’s Cube Principle and Digital Chaotic Cipher. Available online: https://www.hindawi.com/journals/mpe/2013/848392/ (accessed on 19 June 2023).
- Mosekilde, E.; Maistrenko, Y.; Postnov, D. Chaotic Synchronization: Applications to Living Systems. 2002. Available online: https://books.google.com/books?hl=es&lr=&id=6YZ2gEv5qsQC&oi=fnd&pg=PA1&dq=Chaotic+Synchronization:+Applications+to+Living+Systems&ots=ixRn6Au2C_&sig=NhlldTQYOB_BfEFOcBThli4LR44 (accessed on 19 June 2023).
- Yu, Y.; Zhang, S. The synchronization of linearly bidirectional coupled chaotic systems. Chaos Solitons Fractals 2004, 22, 189–197. [Google Scholar] [CrossRef]
- Jiang, G.P.; Tang, W.K.S.; Chen, G. A simple global synchronization criterion for coupled chaotic systems. Chaos Solitons Fractals 2003, 15, 925–935. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Jiang, C.; Zada, A.; Şenel, M.T.; Li, T. Synchronization of bidirectional N-coupled fractional-order chaotic systems with ring connection based on antisymmetric structure. Adv. Differ. Equ. 2019, 2019, 456. [Google Scholar] [CrossRef]
- Sanjaya, W.S.M.; Anggraeni, D.; Denya, R.; Ismail, N. Numerical Simulation Bidirectional Chaotic Syn-chronization of Spiegel-Moore Circuit and Its Application for Secure Communication. IOP Conf. Ser. Mater. Sci. Eng. 2017, 180, 012066. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization of chaotic systems. Chaos 2015, 25, 97611. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms, and Applications; Pearson Education India: Delhi, India, 1996. [Google Scholar]
- Meyer-Baese, U.; Meyer-Baese, U. Digital Signal Processing with Field Programmable Gate Arrays. 2007. Available online: https://link.springer.com/content/pdf/10.1007/978-3-642-45309-0.pdf (accessed on 28 July 2024).
- Atkinson, K.E. An Introduction to Numerical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Koutroulis, E.; Kalaitzakis, K.; Tzitzilonis, V. Development of an FPGA-based system for real-time simulation of photovoltaic modules. Microelectron. J 2009, 40, 1094–1102. [Google Scholar] [CrossRef]
- Saad, H.; Ould-Bachir, T.; Mahseredjian, J.; Dufour, C.; Dennetiere, S.; Nguefeu, S. Real-time simulation of MMCs using CPU and FPGA. IEEE Trans. Power Electron. 2015, 30, 259–267. [Google Scholar] [CrossRef]
- Mahmoodi, D.; Soleimani, A.; Khosravi, H.; Taghizadeh, M. FPGA Simulation of Linear and Nonlinear Support Vector Machine. J. Softw. Eng. Appl. 2011, 4, 320–328. [Google Scholar] [CrossRef]
- Chiou, D.; Sunwoo, D.; Kim, J.; Patil, N.A.; Reinhart, W.; Johnson, D.E.; Keefe, J.; Angepat, H. FPGA-accelerated simulation technologies (FAST): Fast, full-system, cycle-accurate simula-tors. In Proceedings of the Annual International Symposium on Microarchitecture, MICRO, Chicago, IL, USA, 1–5 December 2007; pp. 249–261. [Google Scholar] [CrossRef]
- Huang, C.; Vahid, F.; Givargis, T. A custom FPGA processor for physical model ordinary differential equation solving. IEEE Embed. Syst. Lett. 2011, 3, 113–116. [Google Scholar] [CrossRef]
- Popescu, S.O.; Gontean, A.S.; Budura, G. BPSK system on Spartan 3E FPGA. In Proceedings of the IEEE 10th Jubilee Interna-tional Symposium on Applied Machine Intelligence and Informatics, SAMI 2012, Herl’any, Slovakia, 26–28 January 2012; pp. 301–306. [Google Scholar] [CrossRef]





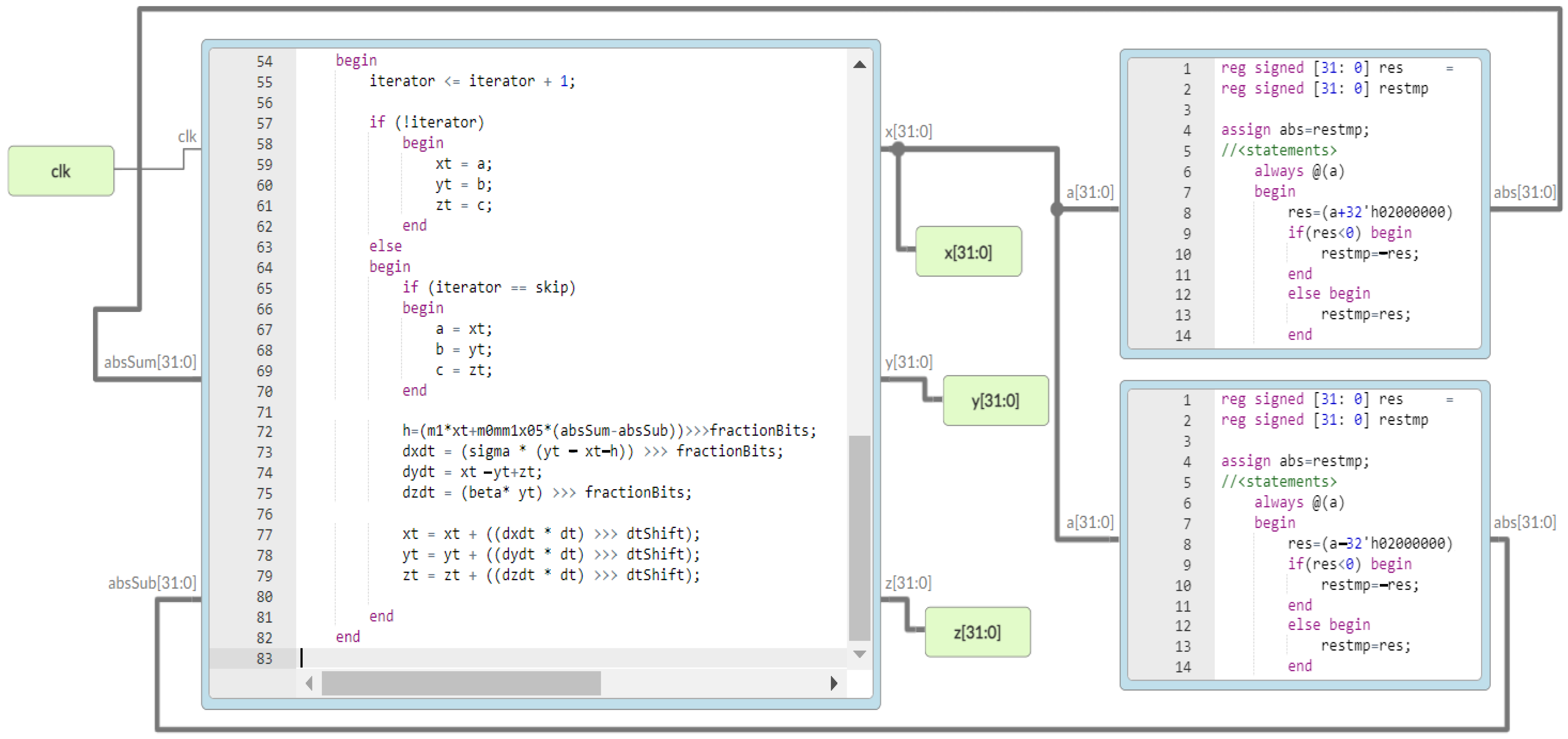


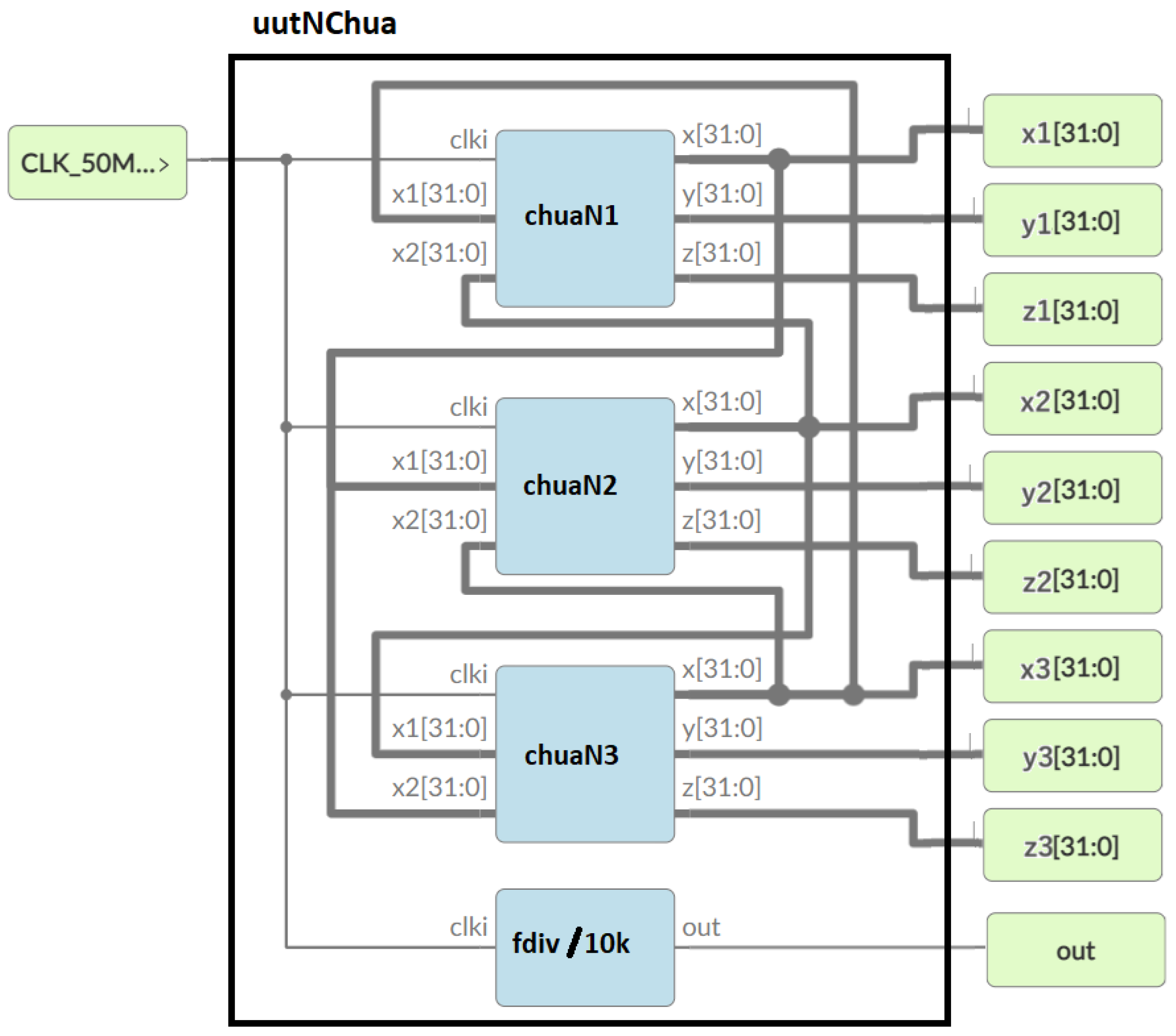

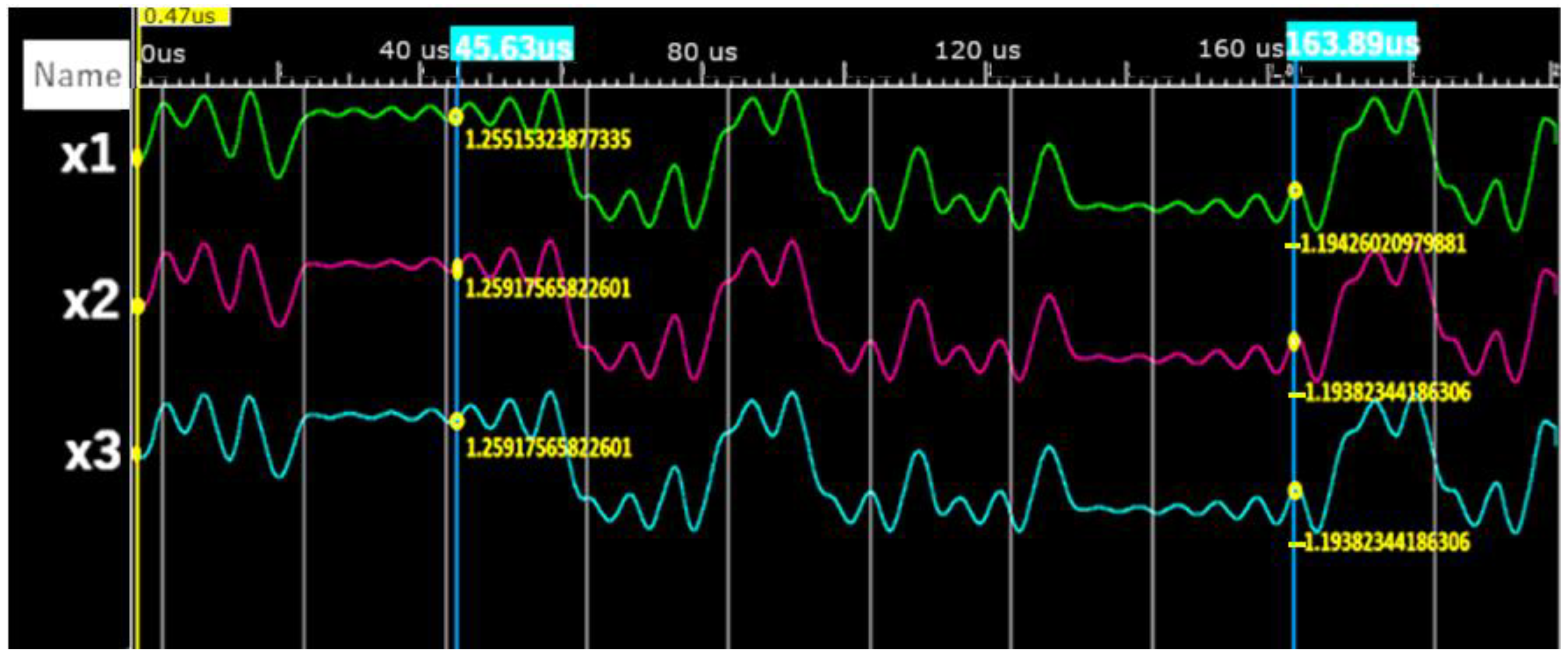
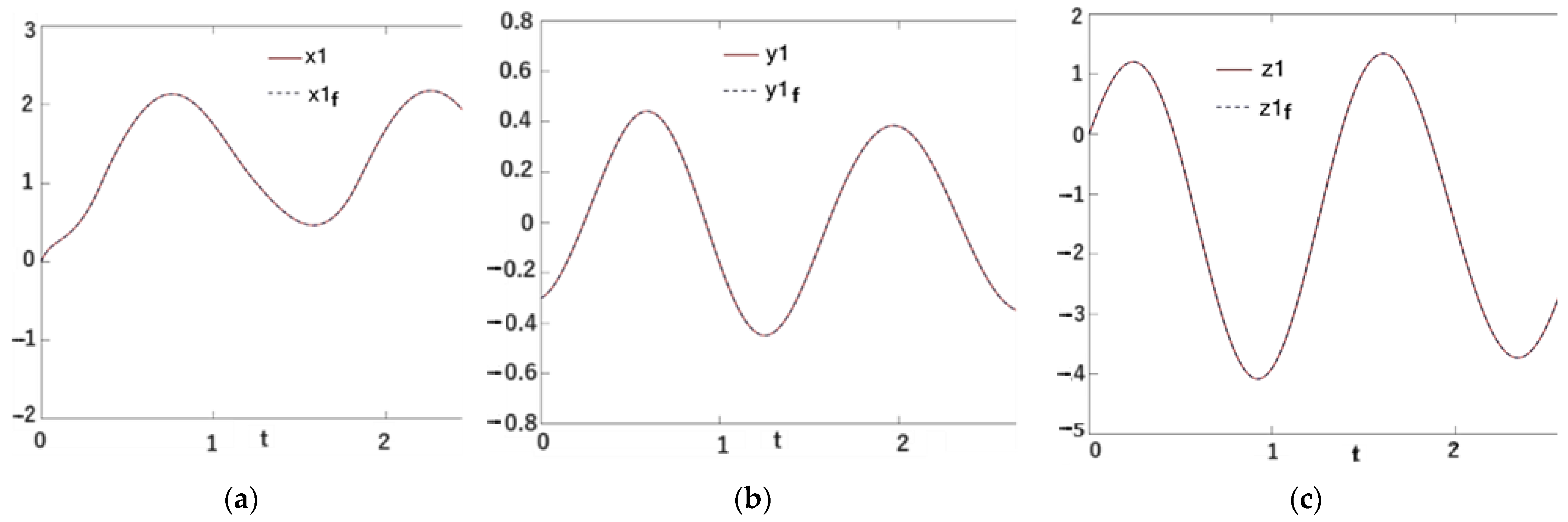

| Number | Binary | Hexadecimal |
|---|---|---|
| 1.0 | 0_000001.0000000000000000000000000 | 02000000 |
| 0.0025 | 0_000000.0000000101000111101011100 | 00028F5C |
| Logic Utilization | Used | Utilization |
|---|---|---|
| Number of Slice Flip Flop | 29 | 1% |
| Number of 4 input LUTs | 16 | 1% |
| Number of occupied Slices | 25 | 1% |
| Number of bonded IOBs | 3 | 1% |
| Variable x | Variable y | r | Lineal Model y = mx + b | |
|---|---|---|---|---|
| b | m | |||
| 1.0 | −0.00001635 | 1.00000263 | ||
| 1.0 | −0.00001541 | 1.00000245 | ||
| 1.0 | −0.00001541 | 1.00000245 | ||
| 0.9999887 | 0.00001353 | 1.00001967 | ||
| 0.9999498 | 0.00002214 | 1.00002846 | ||
| 0.9999498 | 0.00002214 | 1.00002846 | ||
| 0.9999788 | 0.0001184 | 1.0000158 | ||
| 0.9999925 | 0.00005549 | 1.00001217 | ||
| 0.9999925 | 0.00005549 | 1.00001217 | ||
| Tool | Number of Chua Circuits | Simulation Time |
|---|---|---|
| Octave (Intel(R) Core i7-9750H CPU 2.59 GHz computer) | 1 | 493 ms |
| 3 | 3.177 s | |
| FPGA | 1 | 0.2 ms |
| 3 | 0.2 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rentería, L.; Mayacela, M.; Torres, K.; Ramírez, W.; Donoso, R.; Acosta, R. FPGA-Based Numerical Simulation of the Chaotic Synchronization of Chua Circuits. Computation 2024, 12, 174. https://doi.org/10.3390/computation12090174
Rentería L, Mayacela M, Torres K, Ramírez W, Donoso R, Acosta R. FPGA-Based Numerical Simulation of the Chaotic Synchronization of Chua Circuits. Computation. 2024; 12(9):174. https://doi.org/10.3390/computation12090174
Chicago/Turabian StyleRentería, Leonardo, Margarita Mayacela, Klever Torres, Wladimir Ramírez, Rolando Donoso, and Rodrigo Acosta. 2024. "FPGA-Based Numerical Simulation of the Chaotic Synchronization of Chua Circuits" Computation 12, no. 9: 174. https://doi.org/10.3390/computation12090174
APA StyleRentería, L., Mayacela, M., Torres, K., Ramírez, W., Donoso, R., & Acosta, R. (2024). FPGA-Based Numerical Simulation of the Chaotic Synchronization of Chua Circuits. Computation, 12(9), 174. https://doi.org/10.3390/computation12090174






