Computational Representation of Fractional Inequalities Through 2D and 3D Graphs with Applications

Abstract

The aim of this research article is to use the extended fractional operators involving the multivariate Mittag–Leffler (M-M-L) function, we provide the generalization of the Hermite–Hadamard–Fejer (H-H-F) inequalities. We relate these inequalities to previously published disparities in the literature by making appropriate substitutions. In the last section, we analyze several inequalities related to the H-H-F inequalities, focusing on generalized h-convexity associated with extended fractional operators involving the M-M-L function. To achieve this, we derive two identities for locally differentiable functions, which allows us to provide specific estimates for the differences between the left, middle, and right terms in the H-H-F inequalities. Also, we have constructed specific inequalities and visualized them through graphical representations to facilitate their applications in analysis. The research bridges theoretical advancements with practical applications, providing high-accuracy bounds for complex systems involving fractional calculus.

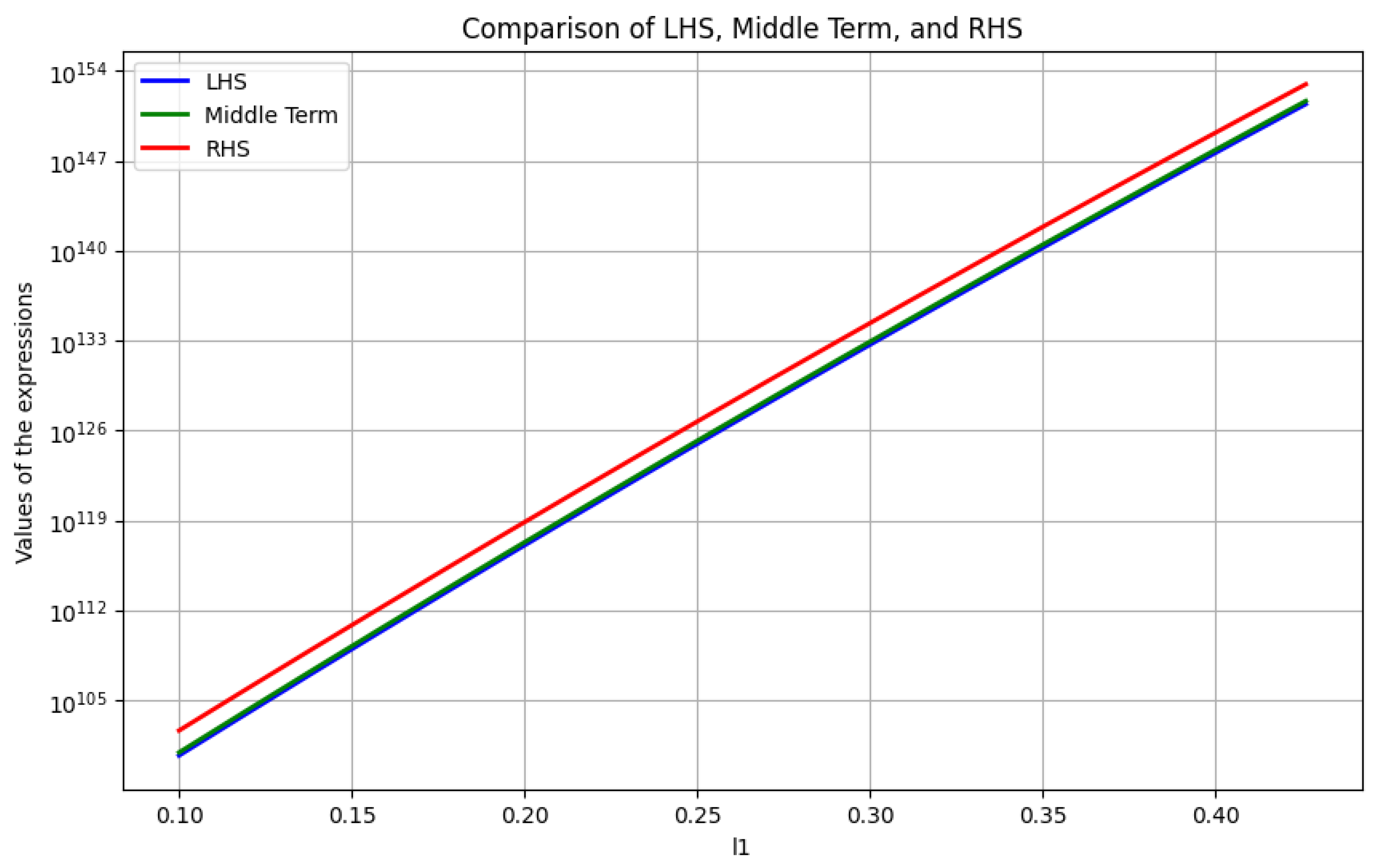
1. Introduction

The study of fractional calculus and its diverse applications has received more attention in recent times. Chronologically ordering the development of this theory, we find that fractional calculus was first applied when Abel solved the Tautocrone problem [1]. Scholars have written their own books [2,3] to advance the field of fractional calculus, these books are essential to the advancement of applications of fractional calculus in mathematical modeling and applied analysis. The well-known caputo sense derivative without non-singular kernel was developed by Caputo et al. in [4], although there are still many gaps in the theory that the researchers have discovered. In order to overcome these gaps, several researchers have developed their own fractional operators with non-singular kernels [5,6,7,8]. Furthermore, the symmetric properties as well as the non-linear and non-singular extensions of fractional operators were illustrated by Wu et al. in [9]. In [10], Samraiz et al. developed the fractional derivative with non-linear and non-singular kernel, also discussed its applications in applied analysis. Consequently, fractional operators were developed in [11,12] using different kinds of Mittag–Leffle (M-L) functions as a kernel. We direct readers to explore [13,14,15,16,17,18] for additional developments and applications on fractional calculus. Roman et al. described the fractional derivatives and their applications in time series with long-time memory and random walks in [19]. In [20], Moreles at al. introduced modeling for the mathematical study of circuit components with fractional orders, they also discussed applications of bioimpedance. In [21] the authors explore the integration of harmonic univalent functions with the generalized $(p,q)$-Poisson distribution, presenting a novel theoretical contribution to complex analysis and fractional calculus. It extends the classical understanding of harmonic functions by incorporating this distribution, offering new results on their univalence and injectivity properties. The study uses standard mathematical analysis techniques, providing explicit examples and graphical representations to support the theoretical claims. While the theoretical framework is solid, the article could benefit from a clearer explanation of the practical applications and real-world implications of these results. Although it makes a significant contribution to the field, a more detailed discussion on how these findings could be applied to practical problems in mathematics, physics, and engineering would strengthen the work. Using fractional calculus to simulate dielectric relaxation events in polymeric materials was demonstrated by Melo et al. in [22]. You can find a presentation of fractional integral in conjunction with wave theory in [23]. The theory of inequalities in [24,25] is closely related to convex functions (Cf) and their expansions $s-$Cf.

Definition 1.

The function $f:[\alpha ,\beta ]\mapsto \Re$ (Set of real numbers) is said to be Cf, if

$$\begin{array}{cc}\hfill & f({\ell }_1{x}_1+(1-{\ell }_1)x_2)\le {\ell }_{1}f\left(x_1\right)+(1-{\ell }_1)f\left(x_2\right),\hfill \end{array}$$

$\forall x_1,x_2\in [\alpha ,\beta ]$ and ${\ell }_1\in (0,1]$.

In [25], Brechner gave the definition of s-Cf, stated by the following definition.

Definition 2.

A function $f:(0,\infty )\mapsto \Re$ is called second sense $s-$Cf for some fixed $kϵ(0,1)$, is given by

$$\begin{array}{cc}\hfill & f({\ell }_1{x}_1+{\ell }_2{x}_2)\le {\ell }_1^{s}f\left(x_1\right)+{\ell }_2^{s}f\left(x_2\right),\hfill \end{array}$$

$\forall x_1,x_2\in (0,\infty ),0\le {\ell }_1,{\ell }_2\le 1,$ where ${\ell }_1+{\ell }_2=1$. This class of function is denoted as $K_s^2$.

In [26,27], authors discussed novel fractional operators and class of inequalities involving novel fractional operators. Hakiki et al. described H-H-F inequalities involving second kind of $s-$Cf via Riemann–Liouville (RL) FI and novel inequalities of H-H-F kind inequalities for Cf via FI in [28,29].

Furthermore, matching nonsingular kernels and new fractional operators, like the M-L function, have also been introduced [30,31]. Diverse historical applications of fractional operators were illustrated by the researchers. The scientists have currently designed a large number of physical models [32,33]. Several of these models solve particular differential equations of fractional order using the M-L non-singular kernel [34,35]. The $(k,s)$-fractional calculus of the generalized M-L function was discussed by Nisar et al. [36]. For more details and applications of fractional operators, we suggest readers to [37,38]. Readers are referred to [35,39,40,41] for additional information and applications on fractional operators. In 1903, Gosta [42] proposed the classical M-L function. Several approaches have been taken to generalize it, such as adding two or three parameters [43].

Definition 3

([11]). The generalized multivariate Mittag–Leffler (M-M-L) function is defined by

$$\begin{array}{cc}\hfill & {\xi }_{k,\mu ,\left({\beta }_i\right)}^{\left({\delta }_i\right)}({\tau }_1,{\tau }_2,\dots ,{\tau }_n)={\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}{\left({\tau }_1\right)}^{{\kappa }_1}{\left({\tau }_2\right)}^{{\kappa }_2}\dots {\left({\tau }_n\right)}^{{\kappa }_n},\hfill \end{array}$$

where $k>0$, ${\beta }_i,{\delta }_i\in C$ with $Re\left({\beta }_i\right)>0$ for all $i=1,2,3,\dots ,n.$ Furthermore, If we substitute $k=1$ then we obtain M-M-L function defined by Sexana et al. in [44].

Let $f:\Re \to \Re$ be Cf, ${\ell }_1,{\ell }_2\in I\subseteq \Re$ such that ${\ell }_1<{\ell }_2$, and $w:[{\ell }_1,{\ell }_2]\to \Re$ be a non-negative integrable and symmetric with respect to ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}$, then the H-H-F inequality can be found in [45] by

$$\begin{array}{c}\hfill f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\int }_{{\ell }_1}^{{\ell }_2}w\left(x\right)dx\le {\displaystyle \frac{1}{{\ell }_2-{\ell }_1}}{\int }_{{\ell }_1}^{{\ell }_2}f\left(x\right)w\left(x\right)dx\le {\displaystyle \frac{f\left({\ell }_1\right)+f\left({\ell }_2\right)}{2}}{\int }_{{\ell }_1}^{{\ell }_2}w\left(x\right)dx.\end{array}$$

The classical H-H inequality (see also [46]) is given by the following:

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\le {\displaystyle \frac{1}{{\ell }_2-{\ell }_1}}{\int }_{{\ell }_1}^{{\ell }_2}f\left(x\right)dx\le {\displaystyle \frac{f\left({\ell }_1\right)+f\left({\ell }_2\right)}{2}}.\hfill \end{array}$$

Because of the lot of applications of said inequalities, some researchers prolonged their research via functions of several classes, as an illustration [47] for Cf and [48,49] for h-Cf. In 2007, Varošanec [50] presented the concept of h-Cf, in the second sense which was a generalization of s-convexity, non-negative convexity, P-convexity and Godunova–Levin mappings. Chen et al. [51] presented H-H and H-H-F inequalities for generalized FI. In [52], Khan et al. generalized the conformable fractional operators and a new class of fractional operators. For details applications of fractional operators we refer readers [53,54]. Here, we have some more fundamental definitions which are indispensable for explaining the key findings in the coming results.

Definition 4

([51]). The incomplete beta function $B_b({\ell }_1,{\ell }_2)$ is defined by

$$\begin{array}{cc}\hfill & B_b({\ell }_1,{\ell }_2)={\int }_0^b{z}^{{\ell }_1-1}{(1-z)}^{{\ell }_2-1}dz,\hfill \end{array}$$

where, $0<b<1,{\ell }_1,{\ell }_2>0$.

Definition 5

([55]). Let $p,q\in \Re$ with $p,q>1$ and ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$, then the integral form of Hölder inequality is presented as

$$\begin{array}{c}\hfill \underset{e_1}{\overset{e_2}{\int }}\left|H(ı)I(ı)\right|dı\le {\left(\underset{e_1}{\overset{e_2}{\int }}{\left|H(ı)\right|}^{p}dı\right)}^{{\displaystyle \frac{1}{p}}}{\left(\underset{e_1}{\overset{e_2}{\int }}{\left|I(ı)\right|}^{q}dı\right)}^{{\displaystyle \frac{1}{q}}},\end{array}$$

with $H,I\in {\mathbb{C}}^1[e_1,e_2]$.

Definition 6.

The left and right-sided RLFI $I_{{\ell }_1^{+}}^{\varrho }\left(f\right)$ and $I_{{\ell }_2^{-}}^{\varrho }\left(f\right)$, of order $\varrho >0$ on $[{\ell }_1,{\ell }_2]$ are defined as

$$\begin{array}{cc}\hfill & I_{{\ell }_1^{+}}^{\varrho }f\left(p_1\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\varrho \right)}}{\int }_{{\ell }_1}^{p_1}{(p_1-\nu )}^{\varrho -1}f\left(\nu \right)d\nu ,p_1>{\ell }_1,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & I_{{\ell }_2^{-}}^{\varrho }f\left(p_1\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\varrho \right)}}{\int }_{p_1}^{{\ell }_2}{(\nu -p_1)}^{\varrho -1}f\left(\nu \right)d\nu ,p_1<{\ell }_2,\hfill \end{array}$$

respectively. Here Γ represents the Gamma function and its integral representation is given below.

$$\begin{array}{cc}\hfill & \mathrm{\Gamma }\left(p_1\right)={\int }_0^{\infty }{\nu }^{p_1-1}{e}^{-\nu }d\nu ,Re\left(p_1\right)>0.\hfill \end{array}$$

Now, we present the definition of the $(k,s)$-RLFI, which is defined in [56].

Definition 7.

If a function f is continuous on $[a,b]$, then the $(k,s)$-RLFI for order $\delta >0$ can be defined as

$$\begin{array}{cc}\hfill & {}_k{}^s\mathfrak{J}_{a^{+}}^{\delta }f\left(t_1\right)={\displaystyle \frac{{(s+1)}^{1-\frac{\delta }{k}}}{k{\mathrm{\Gamma }}_k\left(\delta \right)}}{\int }_{a^{+}}^{t_1}{(t_1^{s+1}-{\nu }^{s+1})}^{{\displaystyle \frac{\delta }{k}}-1}{\nu }^{s}f\left(\nu \right)d\nu .\hfill \end{array}$$

(1)

The following is the definition of the fractional integral operator in its generalized form with M-M-L function as part of its kernel is defined in [11].

Definition 8.

If a function f is continuous on $[a,b]$, for $k>$ 0, $m\in \Re /\{-1\}$, let the parameters $Re\left(\mu \right)>0$, ${\tau }_i$, ${\beta }_i$ be complex numbers with $Re\left({\beta }_i\right)>0,\forall i=1,2,\dots ,n;$ and Θ be the strictly increasing function and differentiable then the generalized fractional integral operators for ${\delta }_i>0,\forall i=1,2,\dots ,n;$ can be defined as

$$\begin{array}{cc}\hfill & {(}_{\mathrm{\Theta }}^{k,m}{\mathfrak{J}}_{a;\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f)\left(t_1\right)={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\int }_a^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu }{k}}-1}\hfill \\ \hfill & \times {\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_1}{k}}},{\tau }_2{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_2}{k}}},\dots ,\hfill \\ \hfill & {\tau }_n{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_n}{k}}}){\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu \hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}\hfill \\ \hfill & \times {\int }_a^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n{\beta }_i{\kappa }_i}{k}}-1}{\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu .\hfill \end{array}$$

Definition 9.

If a function f is continuous on $[a,b]$, for $k>$ 0, $m\in \Re /\{-1\}$, let the parameters $Re\left(\mu \right)>0$, ${\tau }_i$, ${\beta }_i$ be complex numbers with $Re\left({\beta }_i\right)>0,\forall i=1,2,\dots ,n;$ and Θ be the strictly increasing function and differentiable then the left and right sided generalized fractional integral operators for ${\delta }_i>0,\forall i=1,2,\dots ,n;$ can be defined as

$$\begin{array}{cc}\hfill & {(}_{\mathrm{\Theta }}^{k,m}{\mathfrak{J}}_{a^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f)\left(t_1\right)={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\int }_{a^{+}}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu }{k}}-1}\hfill \\ \hfill & \times {\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_1}{k}}},{\tau }_2{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_2}{k}}},\dots ,\hfill \\ \hfill & {\tau }_n{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{{\beta }_n}{k}}}){\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu \hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}\hfill \\ \hfill & \times {\int }_{a^{+}}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n{\beta }_i{\kappa }_i}{k}}-1}{\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu ,t_1>a^{+},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {(}_{\mathrm{\Theta }}^{k,m}{\mathfrak{J}}_{{\zeta }^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f)\left(t_1\right)={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\int }_{{\zeta }^{-}}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{{\displaystyle \frac{\mu }{k}}-1}\hfill \\ \hfill & \times {\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{{\displaystyle \frac{{\beta }_1}{k}}},{\tau }_2{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{{\displaystyle \frac{{\beta }_2}{k}}},\dots ,\hfill \\ \hfill & {\tau }_n{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{{\displaystyle \frac{{\beta }_n}{k}}}){\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu \hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}\hfill \\ \hfill & \times {\int }_{\zeta -}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n{\beta }_i{\kappa }_i}{k}}-1}{\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu ,t_1<\zeta .\hfill \end{array}$$

2. A Class of Some Results

In this section we have developed H-H-F type inequalities for generalized extended fractional operator encompassing the M-M-L function.

Lemma 1.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0,Re\left(\tau \right)>0,Re\left(\delta \right)>0,Re\left(\beta \right)>0$ are complex parameters, Θ be an increasing function and Υ be a differentiable on $({\ell }_1,{\ell }_2)$ with ${\ell }_1<{\ell }_2$ and $\chi :[{\ell }_1,{\ell }_2]\mapsto \Re$ be bounded. If ${\mathrm{{\rm Y}}}^{\prime },\chi \in L[{\ell }_1,{\ell }_2],$ then the below expression holds.

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]\hfill \\ \hfill & -\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_1\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{k}{{(m+1)}^{1-\frac{\mu }{k}}}}{\int }_{{\ell }_1}^{{\ell }_2}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu ,\hfill \end{array}$$

where

$$\kappa \left(t_1\right)=\left\{\begin{array}{c}{\int }_{{\ell }_1}^{t_1}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_n}{k}}\right){\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu }{{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{\mu }{k}-1}}},\\ t_1\in [{\ell }_1,{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}],\\ {\int }_{{\ell }_2}^{t_1}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{\frac{{\beta }_n}{k}}\right){\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)f\left(\nu \right)d\nu }{{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left(t_1\right))}^{\frac{\mu }{k}-1}}}\\ t_1\in [{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}},{\ell }_2].\end{array}\right.$$

Proof. 

Consider

$$\begin{array}{cc}\hfill & I={\int }_{{\ell }_1}^{{\ell }_2}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & ={\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & =I_1+I_2.\hfill \end{array}$$

Now, taking $I_1$ and after employing the integration by parts

$$\begin{array}{cc}\hfill & I_1={\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & =\kappa \left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & -{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)\chi \left(\nu \right)d\nu \hfill \\ \hfill & =\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & \times {\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)\chi \left(\nu \right)d\nu \hfill \\ \hfill & -{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)\chi \left(\nu \right)\mathrm{{\rm Y}}\left(\nu \right)d\nu \hfill \\ \hfill & =\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}\hfill \\ \hfill & \times {\int }_{a^{+}}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n{\beta }_i{\kappa }_i}{k}}-1}{\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)\chi \left(\nu \right)d\nu \hfill \\ \hfill & -{\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}{\Sigma }_{{\kappa }_1,\dots ,{\kappa }_n=0}^{\infty }{\displaystyle \frac{{\mathrm{\Pi }}_{i=1}^n{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left({\kappa }_1\right)!\dots \left({\kappa }_n\right)!}}\hfill \\ \hfill & \times {\int }_{a^{+}}^{t_1}{({\mathrm{\Theta }}^{m+1}\left(t_1\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n{\beta }_i{\kappa }_i}{k}}-1}{\mathrm{\Theta }}^m\left(\nu \right){\mathrm{\Theta }}^{\prime }\left(\nu \right)\chi \left(\nu \right)\mathrm{{\rm Y}}\left(\nu \right)d\nu \hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}[\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)-{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_1\right)].\hfill \end{array}$$

(2)

By similar arguments, it can be verified that

$$\begin{array}{cc}\hfill & I_2={\displaystyle \frac{{(m+1)}^{1-\frac{\mu }{k}}}{k}}[\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)-{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_2\right)].\hfill \end{array}$$

(3)

Hence, by adding (2) and (3) we obtain,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{k}{{(m+1)}^{1-\frac{\mu }{k}}}}{\int }_{{\ell }_1}^{{\ell }_2}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & =\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]\hfill \\ \hfill & -\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_1\right)\right].\hfill \end{array}$$

Hence the required result is proved. □

Corollary 1.

If we replace $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $k=1$ in Lemma 1 then we have ([28], Lemma 4),

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \left({\ell }_1\right)\right]\hfill \\ \hfill & -\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \mathrm{{\rm Y}}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \mathrm{{\rm Y}}\left({\ell }_1\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\mu \right)}}{\int }_{{\ell }_1}^{{\ell }_2}\kappa \left(\nu \right){\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)d\nu ,\hfill \end{array}$$

where

$$\kappa \left(t_1\right)=\left\{\begin{array}{c}{\int }_{{\ell }_1}^{t_1}{\displaystyle \frac{\chi \left(u\right)du}{{(u-{\ell }_1)}^{1-\mu }}},t_1\in [{\ell }_1,{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}],\\ {\int }_{{\ell }_2}^{t_1}{\displaystyle \frac{\chi \left(u\right)du}{{({\ell }_2-u)}^{1-\mu }}},t_1\in [{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}},{\ell }_2].\end{array}\right.$$

Theorem 1.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0,Re\left(\tau \right)>0,Re\left(\delta \right)>0,Re\left(\beta \right)>0$ are complex parameters, Θ be an increasing function and Υ be a differentiable on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$ and $\chi :[{\ell }_1,{\ell }_2]\mapsto \Re$ be bounded. If ${\mathrm{{\rm Y}}}^{\prime },\chi \in L[{\ell }_1,{\ell }_2],$ then the below expression holds.

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]\hfill \\ \hfill & \le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{ϝ}\left({\ell }_1\right)+\mathsf{ϝ}\left({\ell }_2\right)}{2}}\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right],\hfill \end{array}$$

(4)

where $\mathsf{ϝ}\left(\nu \right)=\mathrm{{\rm Y}}\left(\nu \right)+\widetilde{\mathrm{{\rm Y}}}\left(\nu \right)$, and $\widetilde{\mathrm{{\rm Y}}}\left(\nu \right)=\mathrm{{\rm Y}}({\ell }_1+{\ell }_2-\nu ).$

Proof. 

As we know that $\mathrm{{\rm Y}}$ is Cf for all $x_1,y_1\in [{\ell }_1,{\ell }_2],$ that is

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{x_1+y_1}{2}}\right)\le {\displaystyle \frac{\mathrm{{\rm Y}}\left(x_1\right)+\mathrm{{\rm Y}}\left(y_1\right)}{2}},\hfill \end{array}$$

which implies, for $\nu \in [0,1]$ and substituting $x_1={\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2,y_1={\displaystyle \frac{\nu }{2}}{\ell }_2+{\displaystyle \frac{2-\nu }{2}}{\ell }_1$

$$\begin{array}{cc}\hfill & 2\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\le \mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)+\mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_2+{\displaystyle \frac{2-\nu }{2}}{\ell }_1).\hfill \end{array}$$

By multiplying

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2),\hfill \end{array}$$

and after simplifying and taking integration on $[0,1]$ with respect to $\nu$, we can have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu \hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu .\hfill \end{array}$$

By replacing $u={\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2$, we arrive at

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)]\hfill \\ \hfill & \le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \widetilde{\mathrm{{\rm Y}}}\left({\ell }_2\right)\right],\hfill \end{array}$$

that is

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)\right]\le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)\right].\hfill \end{array}$$

(5)

Continuing in the same way if we multiply the below term on both sides

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2),\hfill \end{array}$$

then after simplifying and taking integration on $[0,1]$ with respect to $\nu$, we arrive at

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]\le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right].\hfill \end{array}$$

(6)

Adding (5) and (6), we arrive at

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)]\hfill \\ \hfill & \le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)].\hfill \end{array}$$

(7)

This shows the first half of required inequality. Now we are going to prove second half of inequality. Since, we know that $\mathrm{{\rm Y}}$ is Cf on $[{\ell }_1,{\ell }_2]$, after implementation, we reach

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)+\mathrm{{\rm Y}}({\displaystyle \frac{2-\nu }{2}}{\tau }_1+{\displaystyle \frac{\nu }{2}}{\tau }_2)\le \mathrm{{\rm Y}}\left({\tau }_1\right)+\mathrm{{\rm Y}}\left({\tau }_2\right).\hfill \end{array}$$

Continuing in the same way if we multiply the below term on both sides as in first part of inequality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2),\hfill \end{array}$$

then after simplifying and integrating over $[0,1]$ with respect to $\nu$, we arrive at

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}(+{\ell }_2)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu \hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\mathrm{{\rm Y}}({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)d\nu .\hfill \end{array}$$

By replacing $u={\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2$, we obtain

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathrm{{\rm Y}}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \widetilde{\mathrm{{\rm Y}}}\left({\ell }_2\right)\right]\hfill \\ \hfill & \le [\mathrm{{\rm Y}}\left({\ell }_1\right)+\mathrm{{\rm Y}}\left({\ell }_2\right)]\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)].\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)]\le {\displaystyle \frac{\mathsf{ϝ}\left({\ell }_1\right)+\mathsf{ϝ}\left({\ell }_2\right)}{2}}[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)].\hfill \end{array}$$

(8)

Now, by multiplying on both sides of the first half of the inequality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{2k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\tau }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\tau }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}(\frac{\nu }{2}{\ell }_1+\frac{2-\nu }{2}{\ell }_2)-{\mathrm{\Theta }}^{m+1}\left({\tau }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2){\mathrm{\Theta }}^{\prime }({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2)\chi ({\displaystyle \frac{\nu }{2}}{\ell }_1+{\displaystyle \frac{2-\nu }{2}}{\ell }_2),\hfill \end{array}$$

then, after simplifying and integrating over $[0,1]$ with respect to $\nu$, we obtain

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)]\le {\displaystyle \frac{\mathsf{ϝ}\left({\ell }_1\right)+\mathsf{ϝ}\left({\ell }_2\right)}{2}}[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)].\hfill \end{array}$$

(9)

Adding (8) and (9), we obtain

$$\begin{array}{cc}\hfill & \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)]\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{ϝ}\left({\ell }_1\right)+\mathsf{ϝ}\left({\ell }_2\right)}{2}}[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right){+}_{{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}}\chi \left({\ell }_1\right)].\hfill \end{array}$$

(10)

Hence, by adding (7) and (10), we get our desired inequality. □

Example 1.

Assume that $\chi \left(x\right)={({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{{\displaystyle \frac{\eta }{k}}},$ then the left side of above inequality (4) becomes

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)\left({({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{{\displaystyle \frac{\eta }{k}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}-1}{\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)dx\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}-1}{\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)dx\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}.\hfill \end{array}$$

(11)

Similarly, we have

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)\left({\mathrm{\Theta }}^{m+1}\left(x\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right){)}^{{\displaystyle \frac{\eta }{k}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}.\hfill \end{array}$$

(12)

If we choose $\chi \left(x\right)={({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{{\displaystyle \frac{\eta }{k}}}$ and $\mathsf{ϝ}\left(x\right)=2{\mathrm{\Theta }}^{m+1}\left(x\right)$ then the middle term of above inequality is

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)2\left({({\mathrm{\Theta }}^{m+1}\left(x\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\eta }{k}}}\right){\mathrm{\Theta }}^{m+1}\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{2{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}-1}{\mathrm{\Theta }}^{m+1}\left(x\right){\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)dx\hfill \\ \hfill & ={\displaystyle \frac{2{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times ({\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & -{\displaystyle \frac{m+1}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}})\hfill \end{array}$$

(13)

Also

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)2\left({({\mathrm{\Theta }}^{m+1}\left(x\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\eta }{k}}}\right){\mathrm{\Theta }}^{m+1}\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{2{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times ({\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & -{\displaystyle \frac{m+1}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}})\hfill \end{array}$$

(14)

So we have

$$\begin{array}{cc}\hfill & 2{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}]\hfill \\ \hfill & \le {\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)[{\displaystyle \frac{2{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times ({\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & -{\displaystyle \frac{m+1}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}})\hfill \\ \hfill & +{\displaystyle \frac{2{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)({\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & -{\displaystyle \frac{m+1}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}+1}}\left)\right]\hfill \\ \hfill & \le [{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)+{\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)][{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}]\hfill \end{array}$$

(15)

The computational values of (15), are shown in Table 1, and Table 2 corresponding to the choice of parameters $m=3$, $k=1$, $\mathrm{\Theta }\left(x\right)=x^2,\eta =0.5$, ${\tau }_i=1$, ${\kappa }_i=1$, ${\beta }_i=1$, $\delta =0.5$ and for some fixed values of ${\ell }_1$ and ${\ell }_2$. Figure 1, shows the graphical representation of (15), corresponding to the choice of parameters $0<{\ell }_1<2<{\ell }_2<4.$

For tabular values

Table 1. Tabular form presents the computational values of (15) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.10$	$2.30$
$0.10$	(4.25 × ${10}^{00}$, 1.23 × ${10}^{01}$, 2.19 × ${10}^{01}$)	(5.56 × ${10}^{01}$, 1.39 × ${10}^{02}$, 3.72 × ${10}^{01}$)
$0.50$	(6.51 × ${10}^{00}$, 2.14 × ${10}^{01}$, 2.87 × ${10}^{01}$)	(7.83 × ${10}^{01}$, 2.26 × ${10}^{02}$, 4.91 × ${10}^{01}$)

Table 1. Tabular form presents the computational values of (15) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.10$	$2.30$
$0.10$	(4.25 × ${10}^{00}$, 1.23 × ${10}^{01}$, 2.19 × ${10}^{01}$)	(5.56 × ${10}^{01}$, 1.39 × ${10}^{02}$, 3.72 × ${10}^{01}$)
$0.50$	(6.51 × ${10}^{00}$, 2.14 × ${10}^{01}$, 2.87 × ${10}^{01}$)	(7.83 × ${10}^{01}$, 2.26 × ${10}^{02}$, 4.91 × ${10}^{01}$)

Table 2. Tabular form presents the computational values of (15) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.50$	$2.70$
$0.10$	(7.48 × ${10}^{01}$, 1.68 × ${10}^{02}$, 4.51 × ${10}^{01}$)	(8.74 × ${10}^{01}$, 1.95 × ${10}^{02}$, 5.63 × ${10}^{01}$)
$0.50$	(9.66 × ${10}^{01}$, 2.72 × ${10}^{02}$, 5.74 × ${10}^{01}$)	(1.12 × ${10}^{02}$, 3.06 × ${10}^{02}$, 6.85 × ${10}^{01}$)

Table 2. Tabular form presents the computational values of (15) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.50$	$2.70$
$0.10$	(7.48 × ${10}^{01}$, 1.68 × ${10}^{02}$, 4.51 × ${10}^{01}$)	(8.74 × ${10}^{01}$, 1.95 × ${10}^{02}$, 5.63 × ${10}^{01}$)
$0.50$	(9.66 × ${10}^{01}$, 2.72 × ${10}^{02}$, 5.74 × ${10}^{01}$)	(1.12 × ${10}^{02}$, 3.06 × ${10}^{02}$, 6.85 × ${10}^{01}$)

Corollary 2.

If we replace $\mathrm{\Theta }\left(u\right)=u, m=0, {\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $k=1$ in Theorem 1, choose χ is symmetric about ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}},$ then we have

$$\begin{array}{cc}\hfill & \mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \left({\ell }_1\right)\right]\hfill \\ \hfill & \le \mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{ϝ}\left({\ell }_1\right)+\mathsf{ϝ}\left({\ell }_2\right)}{2}}\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \left({\ell }_1\right)\right].\hfill \end{array}$$

Theorem 2.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0,Re\left(\tau \right)>0,Re\left(\delta \right)>0,Re\left(\beta \right)>0$ are complex parameters, Θ be an increasing function and Υ be a differentiable on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$ and $\chi :[{\ell }_1,{\ell }_2]\mapsto \Re$ be bounded. If ${\mathrm{{\rm Y}}}^{\prime },\chi \in L[{\ell }_1,{\ell }_2]$ and $|{\mathrm{{\rm Y}}}^{\prime }|\in K_s^2$ on $[{\ell }_1,{\ell }_2]$ for any fixed $s\in (0,1]$, then the H-H-F kind inequality for generalized RLFI holds.

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}{\left|\right|\chi \left|\right|}_{\infty }}{{\left({\ell }_2-{\ell }_1\right)}^s(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right)\hfill \\ \hfill & \times [\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}+{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right)\hfill \\ \hfill & \times \left({\left({\ell }_2-\nu \right)}^s+{\left(\nu -{\ell }_1\right)}^s\right)d\nu ],\hfill \end{array}$$

where ϝ fulfilled the condition as in Theorem 1.

Proof. 

By using defined s-convexity of second kind, we can write

$$\begin{array}{cc}\hfill & |{\mathsf{ϝ}}^{\prime }\left(\nu \right)|=|{\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)-{\mathrm{{\rm Y}}}^{\prime }({\ell }_1+{\ell }_2-\nu )|\le |{\mathrm{{\rm Y}}}^{\prime }\left(\nu \right)|+|{\mathrm{{\rm Y}}}^{\prime }({\ell }_1+{\ell }_2-\nu )|\hfill \\ \hfill & =\left|{\mathrm{{\rm Y}}}^{\prime }\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}{\ell }_1+{\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}{\ell }_2\right)\right|+\left|{\mathrm{{\rm Y}}}^{\prime }\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}{\ell }_1+{\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}{\ell }_2\right)\right|\hfill \\ \hfill & \le {\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)\right|\hfill \\ \hfill & +{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+{\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|\hfill \\ \hfill & =\left({\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right)\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right).\hfill \end{array}$$

Using Theorem 1, we reach

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\ell }_2}\left|\kappa \left(\nu \right)\right||{\mathsf{ϝ}}^{\prime }\left(\nu \right)|d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times ({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}|{\int }_{{\ell }_1}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}|{\int }_{{\ell }_2}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_n}{k}})}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du\left|\right){\mathsf{ϝ}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times ({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}|{\int }_{{\ell }_1}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\ell }_1{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|\hfill \\ \hfill & +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}|{\int }_{{\ell }_2}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_n}{k}})}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du\left|\right){\mathsf{ϝ}}^{\prime }\left(\nu \right)d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-2}{\left|\right|\chi \left|\right|}_{\infty }}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times [\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{[{\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)]}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}+{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{[{\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\nu }^{s+}]}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right)\hfill \\ \hfill & \times \left({\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right)\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|d\nu \right)]\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-2}{\left|\right|\chi \left|\right|}_{\infty }}{{\left({\ell }_2-{\ell }_1\right)}^s(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right)\hfill \\ \hfill & \times [\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}+{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right)\hfill \\ \hfill & \times \left({\left({\ell }_2-\nu \right)}^s+{\left(\nu -{\ell }_1\right)}^s\right)d\nu ].\hfill \end{array}$$

We reach at desired outcome. □

Corollary 3.

If we replace $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $p=k=1$ in Theorem 2 and χ is symmetric about ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}},$ then we have

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \left({\ell }_1\right)\right]|-\left|\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{1-\mu }({\ell }_2-{\ell }_1)}{({\ell }_2-{\ell }_1){\mathrm{\Gamma }}_k\left(\mu \right)}}{\left|\right|\chi \left|\right|}_{\infty }\hfill \\ \hfill & \times \left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right)\left[\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{(\nu -{\ell }_1)}^{s}d\nu +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{({\ell }_2-\nu )}^s\right)d\nu \right]\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{1-\mu }{({\ell }_2-{\ell }_1)}^{\mu +1}}{(\mu +1)\mathrm{\Gamma }(\mu +1)2^{\mu +1}}}{\left|\right|\chi \left|\right|}_{\infty }\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right).\hfill \end{array}$$

Proposition 1.

Furthermore, If we replace $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $\chi =k=1$ in Corollary 3, so we obtain the below mid point inequality

$$\begin{array}{cc}\hfill & |({\ell }_2-{\ell }_1)\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)-{\int }_{{\ell }_1}^{{\ell }_2}\mathrm{{\rm Y}}\left(\nu \right)d\nu |\le {\displaystyle \frac{{({\ell }_2-{\ell }_1)}^2}{8}}\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|+|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)|\right).\hfill \end{array}$$

Theorem 3.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0,Re\left(\tau \right)>0,Re\left(\delta \right)>0,Re\left(\beta \right)>0$ are complex parameters, Θ be an increasing function and Υ be a differentiable on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$ and $\chi :[{\ell }_1,{\ell }_2]\mapsto \Re$ be bounded. If ${\mathrm{{\rm Y}}}^{\prime },\chi \in L[{\ell }_1,{\ell }_2],$ then the below expression holds.

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }}{(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right|d\nu \right)}^{1-{\displaystyle \frac{1}{q}}}\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}\right|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}|\right.\hfill \\ \hfill & {\left.\times {\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\left){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\chi \right||}_{\infty }}{(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right|d\nu \right)}^{1-{\displaystyle \frac{1}{q}}}\left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}\right|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}|\right.\hfill \\ \hfill & {\left.\times {\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\left){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)\right)}^{{\displaystyle \frac{1}{q}}}.\hfill \end{array}$$

Proof. 

By using Theorem 1, we can write

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\ell }_2}\left|\kappa \left(\nu \right)\right||{\mathsf{ϝ}}^{\prime }\left(\nu \right)|d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\left({\int }_{{\ell }_1}^{{\ell }_2}\left|\kappa \left(\nu \right)\right|d\nu \right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\int }_{{\ell }_1}^{{\ell }_2}\left|\kappa \left(\nu \right)\right||{\mathsf{ϝ}}^{\prime }{\left(\nu \right)|}^{q}d\nu \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times ({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}|{\int }_{{\ell }_1}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|d\nu {)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times ({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}|{\int }_{{\ell }_1}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|)\left({\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu {)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times ({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}|{\int }_{{\ell }_2}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right)){)}^{\frac{{\beta }_n}{k}})}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|d\nu {)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times ({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}|{\int }_{{\ell }_2}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\ell }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_n}{k}})}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|)\left({\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu {)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }}{(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right|d\nu \right)}^{1-{\displaystyle \frac{1}{q}}}\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}\right|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}|\right.\hfill \\ \hfill & {\left.\times {\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\left){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\chi \right||}_{\infty }}{(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\right|d\nu \right)}^{1-{\displaystyle \frac{1}{q}}}\left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}\right|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}|\right.\hfill \\ \hfill & {\left.\times {\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\left){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)\right)}^{{\displaystyle \frac{1}{q}}}.\hfill \end{array}$$

This is our desired result. □

Remark 1.

For the choice of $s=1$, $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $k=1$ in the Theorem 3, then we obtain ([27], Theorem 7).

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\varrho }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\varrho }\chi \left({\tau }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\varrho }\chi \mathsf{ϝ}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\varrho }\chi \mathsf{ϝ}\left({\tau }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left|\chi \right||}_{\infty ,[{\tau }_1,{\ell }_2]}{({\ell }_2-{\tau }_1)}^{\varrho +1}}{2^{\varrho +1+\frac{1}{q}}(\varrho +1){(\varrho +2)}^{\frac{1}{q}}k{\mathrm{\Gamma }}_k(\varrho +1)}}[{\left((\varrho +3)|{\mathrm{{\rm Y}}}^{\prime }\left({\tau }_1\right){|}^q+(\varrho +1){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left((\varrho +1)|{\mathrm{{\rm Y}}}^{\prime }\left({\tau }_1\right){|}^q+(\varrho +3){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Remark 2.

For the choice of $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $k=1$ in the Theorem 3, then we obtain ([57], Theorem 5).

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\varrho }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-},\mathrm{\Theta }}^{\varrho }\chi \left({\tau }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\varrho }\chi \mathsf{ϝ}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\varrho }\chi \mathsf{ϝ}\left({\tau }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left|\chi \right||}_{\infty ,[{\tau }_1,{\ell }_2]}{({\ell }_2-{\tau }_1)}^{\varrho +1}}{2^{\varrho +1+\frac{1}{q}}(\varrho +1){(\varrho +s+1)}^{\frac{1}{q}}k{\mathrm{\Gamma }}_k(\varrho +1)}}\left[\right(2^{\varrho +1}(\varrho +1)(\varrho +s+1)B_{{\displaystyle \frac{1}{2}}}(\varrho +1,s+1){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\tau }_1\right)\right|}^q\hfill \\ \hfill & +2^{1-s}(\varrho +1){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q{)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & {\left(2^{\varrho +1}(\varrho +1)(\varrho +s+1)B_{{\displaystyle \frac{1}{2}}}(\varrho +1,s+1)|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right){|}^q+2^{1-s}(\varrho +1){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\tau }_1\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}].\hfill \end{array}$$

Corollary 4.

For the choice of $s=1,\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $k=1$ in the Theorem 3, then we arrive at the following mid-point inequality

$$\begin{array}{cc}\hfill & |\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\int }_{{\ell }_1}^{{\ell }_2}\chi \left(\nu \right)d\nu -{\int }_{{\ell }_1}^{{\ell }_2}\left(\mathrm{{\rm Y}}\chi \right)\left(\nu \right)d\nu |\hfill \\ \hfill & \le {\displaystyle \frac{\left|\right|\chi \left|\right|{({\ell }_2-{\ell }_1)}^2}{{\left(3\right)}^{\frac{1}{q}}8}}\left[{\left(2|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+2{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

Theorem 4.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0,Re\left(\tau \right)>0,Re\left(\delta \right)>0,Re\left(\beta \right)>0$ are complex parameters, Θ be an increasing function and Υ be a differentiable on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$ and $\chi :[{\ell }_1,{\ell }_2]\mapsto \Re$ be bounded. If ${\mathrm{{\rm Y}}}^{\prime },\chi \in L[{\ell }_1,{\ell }_2],$ then the below expression holds.

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }{({\ell }_2-{\ell }_1)}^{\frac{1}{q}}}{2^{\frac{s}{q}+\frac{1}{q}}{(s+1)}^{\frac{1}{q}}(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \{{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{p(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}{k}}}\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}\times {\left(\left(2^{m+1}-1\right)\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)){|}^q+{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{p(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}{k}}}\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){\left|\right)}^q+{\left(\left(2^{m+1}-1\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\}.\hfill \end{array}$$

Proof. 

Using Hölder’s inequality, we have

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \left({\ell }_1\right)\right]|\hfill \\ \hfill & -\left|\left[{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_2\right)+{}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\ell }_2}\left|{\mathsf{ϝ}}^{\prime }\left(\nu \right)\right|d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\left({\int }_{{\ell }_1}^{{\ell }_2}{\left|\kappa \left(\nu \right)\right|}^{p}d\nu \right)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\ell }_1}^{{\ell }_2}{\left|{\mathsf{ϝ}}^{\prime }\left(\nu \right)\right|}^{q}d\nu \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times \left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}\right(|{\int }_{{\ell }_1}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left(u\right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|{)}^{p}d\nu {)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{{\ell }_1}^{\nu }{\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }({\ell }_1){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}\right(|{\int }_{{\ell }_2}^{\nu }{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(u\right))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(u\right){\mathrm{\Theta }}^{\prime }\left(u\right)\chi \left(u\right)du|{)}^{p}d\nu {)}^{{\displaystyle \frac{1}{p}}}{\left({\int }_{\nu }^{{\ell }_2}{\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu \right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }}{(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \left({\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{|}^{p}d\nu \right)}^{{\displaystyle \frac{1}{p}}}\right.\hfill \\ \hfill & \times \left({\int }_{{\ell }_1}^{\nu }{\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu {)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{|}^{p}d\nu \right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \left.\times \left({\int }_{\nu }^{{\ell }_2}{\left({\displaystyle \frac{{\ell }_2-\nu }{{\ell }_2-{\ell }_1}}\right)}^s\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left({\displaystyle \frac{\nu -{\ell }_1}{{\ell }_2-{\ell }_1}}\right)}^s\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^{q}d\nu {)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }}{{({\ell }_2-{\ell }_1)}^{\frac{s}{q}}(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \{{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{|}^{p}d\nu \right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \times {\left({\displaystyle \frac{{({\ell }_2-{\ell }_1)}^{m+1}\left(2^{m+1}-1\right)}{2^{m+1}(s+1)}}\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)){|}^q+{\displaystyle \frac{{({\ell }_2-{\ell }_1)}^{m+1}}{2^{m+1}(s+1)}}{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{|}^{p}d\nu \right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \times {\displaystyle \frac{{({\ell }_2-{\ell }_1)}^{m+1}}{2^{m+1}(s+1)}}\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){\left|\right)}^q+{\left({\displaystyle \frac{{({\ell }_2-{\ell }_1)}^{m+1}\left(2^{m+1}-1\right)}{2^{m+1}(s+1)}}{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}{\left|\right|\chi \left|\right|}_{\infty }{({\ell }_2-{\ell }_1)}^{\frac{1}{q}}}{2^{\frac{s}{q}+\frac{1}{q}}{(s+1)}^{\frac{1}{q}}(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times \{{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left(\nu \right)-{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right))}^{{\displaystyle \frac{p(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}{k}}}\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}\times {\left(\left(2^{m+1}-1\right)\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)){|}^q+{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(\left|{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\nu \right))}^{{\displaystyle \frac{p(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}{k}}}\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}\times \left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){\left|\right)}^q+{\left(\left(2^{m+1}-1\right){\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\}\hfill \end{array}$$

Which is our desired result. □

Corollary 5.

If we replace $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $s=k=1$ then we obtain ([28], Theorem 8).

$$\begin{array}{cc}\hfill & |\mathsf{ϝ}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \left({\ell }_1\right)\right]|-\left|\left[{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_2\right)+{\mathfrak{J}}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-}}^{\mu }\chi \mathsf{ϝ}\left({\ell }_1\right)\right]\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\left|\right|\chi \left|\right|}_{\infty }{({\ell }_2-{\ell }_1)}^{\frac{1}{q}}}{2^{\frac{3}{q}}{\mathrm{\Gamma }}_{(}\mu +1)}}\left({\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\left(\left|{(\nu -{\ell }_1)}^{p\mu }\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}\right.\hfill \\ \hfill & \left.\times {\left(3\left(\right|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)){|}^q+{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\left(\left|{({\ell }_2-\nu )}^{p\mu }\right|d\nu \right)}^{{\displaystyle \frac{1}{p}}}{\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right)|\right)}^q+{\left(3|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right){|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Proposition 2.

If we replace $\mathrm{\Theta }\left(u\right)=u,m=0,{\delta }_i=0$, ${\kappa }_i=0,\forall i$ and $s=k=1$ we obtain the following

$$\begin{array}{cc}\hfill & |\mathrm{{\rm Y}}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\int }_{{\ell }_1}^{{\ell }_2}\chi \left(\nu \right)d\nu -{\int }_{{\ell }_1}^{{\ell }_2}\left(\mathrm{{\rm Y}}\chi \right)\left(\nu \right)d\nu |\hfill \\ \hfill & \le {\displaystyle \frac{\left|\right|\chi \left|\right|{({\ell }_2-{\ell }_1)}^2}{{(m+1)}^{\frac{1}{p}}{2}^{\frac{4p-2}{p}}}}\left[{\left(3|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}+{\left(|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_1\right){|}^q+3{\left|{\mathrm{{\rm Y}}}^{\prime }\left({\ell }_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right].\hfill \end{array}$$

3. Generalized H-H-F Type Inequalities Involving h-Convexity Associated with an Extended Fractional Operator and M-M-L Function

This section’s first result reveals the M-M-L function for a generalized h-Cf and the generalized H-H-F inequality related with an extended fractional operator. In order to achieve this, the generalized supermultiplicative (s-m) mappings are necessary.

Definition 10.

Let us consider $\aleph ,\Im \in \Re$ be invertals, $\Im \ge (0,1)$ and $h\ne 0:\Im \to \Re$ be a positive. Also, a non-negative function $f:\aleph \to \Re$ is known as h-Cf if the inequality given below

$$\begin{array}{cc}\hfill & f(tx+(1-t\left)y\right)\le h\left(t\right)f\left(x\right)+h(1-t)f\left(y\right)\hfill \end{array}$$

holds for all $x,y\in \aleph ,t\in (0,1).$

Definition 11.

A mapping $h:\Im \subseteq \Re \to \Re$ is known as generalized s-m if

$$\begin{array}{cc}\hfill & h\left(xy\right)\ge h\left(x\right)h\left(y\right)\hfill \end{array}$$

holds for all $x,y\in \Im$.

Theorem 5.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0, Re\left(\tau \right)>0, Re\left(\delta \right)>0, Re\left(\beta \right)>0$ are complex parameters, and Θ be an increasing function on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$, also $f:[{\ell }_1,{\ell }_2]\to \Re$ be the geneeralized h-Cf and $w:[{\ell }_1,{\ell }_2]\to \Re$, $w\ge 0$ be symmetric pertaining to ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}$. If $f\left(x\right),w\left(x\right)\in \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)[{\ell }_1,{\ell }_2]$, then we have

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)f\left(y\right)w\left(y\right)\hfill \\ \hfill & \le {\displaystyle \frac{f\left({\ell }_1\right)+f\left({\ell }_2\right)}{2}}\left(({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left({\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\left(y\right)+({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{-};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left(1-{\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\left(y\right)\right).\hfill \end{array}$$

(16)

Proof. 

Let ${\ell }_1<x<{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}<y<{\ell }_2$ exists $\nu \in (0,1)$ such that

$$\begin{array}{cc}\hfill & x=\nu {\ell }_1+(1-\nu ){\ell }_2\hfill \\ \hfill & y=\nu {\ell }_2+(1-\nu ){\ell }_1.\hfill \end{array}$$

As we know that f is generalized h-Cf, we have

$$\begin{array}{cc}\hfill & f(\nu {\ell }_1+(1-\nu ){\ell }_2)w\left(\nu {\ell }_1+(1-\nu ){\ell }_2\right)\hfill \\ \hfill & \le h\left(\nu \right)f\left({\ell }_1\right)+h(1-\nu )f\left({\ell }_2\right))w\left(\nu {\ell }_1+(1-\nu ){\ell }_2\right),\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill & f((1-\nu ){\ell }_1+\nu {\ell }_2)w\left((1-\nu ){\ell }_1+\nu {\ell }_2\right)\hfill \\ \hfill & \le h(1-\nu )f\left({\ell }_1\right)+h\left(\nu \right)f\left({\ell }_2\right))w\left((1-\nu ){\ell }_1+\nu {\ell }_2\right).\hfill \end{array}$$

(18)

By multiplying on both sides of (17),

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2),\hfill \end{array}$$

and after simplifying and taking integration on $[0,1]$ with respect to $\nu$, we can have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)f(\nu {\ell }_1+(1-\nu ){\ell }_2)w(\nu {\ell }_1+(1-\nu ){\ell }_2)d\nu \hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)\left((h\left(\nu \right)f\left({\ell }_1\right)+h(1-\nu )f\left({\ell }_2\right)\right)w(\nu {\ell }_1+(1-\nu ){\ell }_2)d\nu .\hfill \end{array}$$

By replacing $x=(\nu {\ell }_1+(1-\nu ){\ell }_2),$ we have

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)f\left(y\right)w\left(y\right)\hfill \\ \hfill & \le f\left({\ell }_1\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left({\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\right)\left(y\right)+f\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left(1-{\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\right)\left(y\right).\hfill \end{array}$$

(19)

Continuing in the same way if we multiply the below term on both sides of (18)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_2+(1-\nu ){\ell }_1))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_2+(1-\nu ){\ell }_1))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_2+(1-\nu ){\ell }_1))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_2+(1-\nu ){\ell }_1){\mathrm{\Theta }}^{\prime }(\nu {\ell }_2+(1-\nu ){\ell }_1),\hfill \end{array}$$

then after simplifying and taking integration on $[0,1]$ with respect to $\nu$, we arrive at

$$\begin{array}{cc}\hfill & ({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(y\right)w\left(y\right)\hfill \\ \hfill & \le f\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left({\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\right)\left(y\right)+f\left({\ell }_1\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left(1-{\displaystyle \frac{x-{\ell }_2}{{\ell }_1-{\ell }_2}}\right)w\left(x\right)\right)\left(y\right).\hfill \end{array}$$

(20)

By adding (19) and (20), we obtain (16). □

Theorem 6.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0, Re\left(\tau \right)>0, Re\left(\delta \right)>0, Re\left(\beta \right)>0$ are complex parameters, and Θ be an increasing function on $({\ell }_1,{\ell }_2)$ with ${\ell }_1<{\ell }_2$, also $f:[{\ell }_1,{\ell }_2]\to \Re$ be the geneeralized h-Cf with h define on $[0,max(1,{\ell }_2-{\ell }_1)]$ and $w:[{\ell }_1,{\ell }_2]\to \Re$, $w\ge 0$ be symmetric pertaining to ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}$ and $\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)w>0$. $\left[i\right]$ Then we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{a^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)+w({\ell }_1+{\ell }_2-x)\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{a^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+w({\ell }_1+{\ell }_2-x)f({\ell }_1+{\ell }_2-x)\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

(21)

$\left[ii\right]$ Furthemore, if $h,$ is generalized s-m and f is non-negative and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)){\left)\right)}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2){)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2){\mathrm{\Theta }}^{\prime }(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)\hfill \\ \hfill & \times ({\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & {\int }_{{\ell }_2}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left((\nu {\ell }_1+(1-\nu ){\ell }_2)\right)}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)h(y-x)w\left(x\right)dx)w\left(y\right)dy\ne 0,h\left(x\right)>0,\hfill \end{array}$$

(22)

then, we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2){)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2){\mathrm{\Theta }}^{\prime }(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)\hfill \\ \hfill & \times ({\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & {\int }_{{\ell }_2}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left((\nu {\ell }_1+(1-\nu ){\ell }_2)\right)}^{\frac{{\beta }_n}{k}}}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)h(y-x)w\left(x\right)dx)w\left(y\right)dy\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & \le \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left(y-{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\tau }_1^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(x\right)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & +\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(y\right)w\left(y\right)\right)\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\tau }_1^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}-x\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

(24)

Proof. 

(i) Using the h-Cf if $\nu ={\displaystyle \frac{1}{2}}$, $x=\nu {\ell }_1+(1-\nu ){\ell }_2$ and $y=(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2$, then we have that

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\le h\left({\displaystyle \frac{1}{2}}\right)\left[f(\nu {\ell }_1+(1-\nu ){\ell }_2)+f(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)\right]\hfill \\ \hfill & \iff w(\nu {\ell }_1+(1-\nu ){\ell }_2)f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)+w(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right)[w(\nu {\ell }_1+(1-\nu ){\ell }_2)f(\nu {\ell }_1+(1-\nu ){\ell }_2)\hfill \\ \hfill & +w(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)f(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2)].\hfill \end{array}$$

(25)

By multiplying on both sides of (25),

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+\left((1-\nu ){\ell }_2\right),\hfill \end{array}$$

and after simplifying and taking integration on $[0,1]$ with respect to $\nu$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+\left((1-\nu ){\ell }_2\right)\hfill \\ \hfill & \left(w(\nu {\ell }_1+(1-\nu ){\ell }_2)f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)+w(1-\nu ){\ell }_1+\nu {\ell }_2)f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)d\nu \hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right){\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+\left((1-\nu ){\ell }_2\right)\hfill \\ \hfill & \times \left[w\left(\nu {\ell }_1+(1-\nu ){\ell }_2\right)f(\nu {\ell }_1+(1-\nu ){\ell }_2)+w\left((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2\right)f\left((1-\nu ){\ell }_1+\left(\nu \right){\ell }_2\right)\right]d\nu .\hfill \end{array}$$

By replacing $x=\nu {\ell }_1+(1-\nu ){\ell }_2,$ so we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{a^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)+w({\ell }_1+{\ell }_2-x)\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{a^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+w({\ell }_1+{\ell }_2-x)f({\ell }_1+{\ell }_2-x)\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

(ii) Let h be generalized s-m and $h\left(\nu \right)>0$ for $\nu \in [0,max(1,{\ell }_2-{\ell }_1)]$. For any $x,y\in [{\ell }_1,{\ell }_2]$ such that ${\ell }_1<x<{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}<y\le {\ell }_2$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}=\left({\displaystyle \frac{y-\frac{{\ell }_1+{\ell }_2}{2}}{y-x}}\right)x+\left({\displaystyle \frac{\frac{{\ell }_1+{\ell }_2}{2}-x}{y-x}}\right)y\Rightarrow f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\hfill \\ \hfill & \le h\left({\displaystyle \frac{y-\frac{{\ell }_1+{\ell }_2}{2}}{y-x}}\right)f\left(x\right)+h\left({\displaystyle \frac{\frac{{\ell }_1+{\ell }_2}{2}-x}{y-x}}\right)f\left(y\right).\hfill \end{array}$$

(26)

Since h is s-m

$$\begin{array}{cc}\hfill & h\left({\displaystyle \frac{y-\frac{{\ell }_1+{\ell }_2}{2}}{y-x}}\right)\le {\displaystyle \frac{h(y-\frac{{\ell }_1+{\ell }_2}{2})}{h(y-x)}}\hfill \end{array}$$

(27)

and

$$\begin{array}{cc}\hfill & h\left({\displaystyle \frac{\frac{{\ell }_1+{\ell }_2}{2}-x}{y-x}}\right)\le {\displaystyle \frac{h(\frac{{\ell }_1+{\ell }_2}{2}-x)}{h(y-x)}}.\hfill \end{array}$$

(28)

When $f\left(x\right)\ge 0$ we have

$$\begin{array}{cc}\hfill & h(y-x)f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\le h\left(y-{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)f\left(x\right)+h\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}-x\right)f\left(y\right).\hfill \end{array}$$

(29)

By multiplying weighted iterated integrals on both sides of (29),

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & {\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\tau }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+\left((1-\nu ){\ell }_2\right)w\left(y\right),\hfill \end{array}$$

and after simplifying and taking integration of $w\left(x\right)$ and $w\left(y\right)$ on $[0,{\displaystyle \frac{1}{2}}]$ and $[{\displaystyle \frac{1}{2}},1]$, respectively, we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{1}{2}}}^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(1-\nu ){\ell }_1+\nu {\ell }_2){\mathrm{\Theta }}^{\prime }(1-\nu ){\ell }_1+\nu {\ell }_2)\hfill \\ \hfill & \times ({\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^{{\displaystyle \frac{1}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{1-\frac{\delta }{k}}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)h(y-x)w\left(x\right)dx)w\left(y\right)dy\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{1}{2}}}^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(1-\nu ){\ell }_1+\nu {\ell }_2){\mathrm{\Theta }}^{\prime }(1-\nu ){\ell }_1+\nu {\ell }_2)h\left(y-{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)dy\hfill \\ \hfill & \times {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^{{\displaystyle \frac{1}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{1-\frac{\delta }{k}}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)f\left(x\right)w\left(x\right)dx\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{1}{2}}}^1{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(1-\nu ){\ell }_1+\nu {\ell }_2){)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(1-\nu ){\ell }_1+\nu {\ell }_2){\mathrm{\Theta }}^{\prime }(1-\nu ){\ell }_1+\nu {\ell }_2)f\left(y\right)w\left(y\right)dy\hfill \\ \hfill & \times {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}({\ell }_2-{\ell }_1)}{k}}\hfill \\ \hfill & \times {\int }_0^{{\displaystyle \frac{1}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{\frac{{\beta }_n}{k}}\right)}{{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}(\nu {\ell }_1+(1-\nu ){\ell }_2))}^{1-\frac{\delta }{k}}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m(\nu {\ell }_1+(1-\nu ){\ell }_2){\mathrm{\Theta }}^{\prime }(\nu {\ell }_1+(1-\nu ){\ell }_2)h\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}-x\right)dx.\hfill \end{array}$$

By replacing $x=\nu {\ell }_1+(1-\nu ){\ell }_2)$ and $y=(1-\nu ){\ell }_1+\left(\nu \right){\ell }_2),$ then we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right){\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}\hfill \\ \hfill & \times {\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(y\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{\mu }{k}-1}}}{\mathrm{\Theta }}^m\left(y\right){\mathrm{\Theta }}^{\prime }\left(y\right)\hfill \\ \hfill & \times ({\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)h(y-x)w\left(x\right)dx)w\left(y\right)dy\hfill \\ \hfill & \le {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(y\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(y\right){\mathrm{\Theta }}^{\prime }\left(y\right)h\left(y-{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)dy\hfill \\ \hfill & \times {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)f\left(x\right)w\left(x\right)dx\hfill \\ \hfill & +{\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}^{{\ell }_2}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(y\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(y\right)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(y\right){\mathrm{\Theta }}^{\prime }\left(y\right)f\left(y\right)w\left(y\right)dy\hfill \\ \hfill & \times {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\int }_{{\ell }_1}^{{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}}{\displaystyle \frac{{\xi }_{k,\mu ,{\beta }_i}^{{\delta }_i}\left({\tau }_1({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{{\beta }_1}{k}},\dots ,{\tau }_n{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(x\right))}^{\frac{{\beta }_n}{k}}\right)}{({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}{\left(x\right)}^{\frac{\mu }{k}-1}}}\hfill \\ \hfill & \times {\mathrm{\Theta }}^m\left(x\right){\mathrm{\Theta }}^{\prime }\left(x\right)h\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}-x\right)dx\hfill \\ \hfill & =\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left(y-{\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\tau }_1^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(x\right)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & +\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(y\right)w\left(y\right)\right)\left({\ell }_2\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\tau }_1^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}h\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}-x\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

□

Lemma 2.

If $f:[{\ell }_1,{\ell }_2]\to \Re$ is generalized h-Cf, then identity given below

$$\begin{array}{cc}\hfill & f({\ell }_1+{\ell }_2-x)\le \left(h\left(\nu \right)+h(1-\nu )\right)\left[f\left({\ell }_1\right)+f\left({\ell }_2\right)\right]-f\left(x\right),\hfill \end{array}$$

(30)

hold for all $x\in [{\ell }_1,{\ell }_2]$ and $\nu \in [0,1]$.

Proof. 

We skip the proof of Lemma 2 here, because essentially it is very identical with that of (Lemma 1, [58]). □

Theorem 7.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\mu \right)>0, Re\left(\tau \right)>0, Re\left(\delta \right)>0, Re\left(\beta \right)>0$ are complex parameters, and Θ be an increasing function on $({\ell }_1,{\ell }_2)$ with $\ell <{\ell }_2$, also the geneeralized h-Cf $f:[{\ell }_1,{\ell }_2]\to \Re$ and $w:[{\ell }_1,{\ell }_2]\to \Re$, $w\ge 0$ both are symmetric pertaining to ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}$, then we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{({\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{({\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+\left(\left(h\left(\nu \right)+h(1-\nu )\right)\left(f\left({\ell }_1\right)+f\left({\ell }_2\right)\right)-f\left(x\right)\right)w\left(x\right)\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

Proof. 

We have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{({\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)+w({\ell }_1+{\ell }_2-x)\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{({\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+w({\ell }_1+{\ell }_2-x)f({\ell }_1+{\ell }_2-x)\right)\right).\hfill \end{array}$$

Since w is symmetric

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{({\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le 2h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+\left(\left(h\left(\nu \right)+h(1-\nu )\right)\left(f\left({\ell }_1\right)+f\left({\ell }_2\right)\right)-f\left(x\right)\right)w\left(x\right)\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

□

Example 2.

If we choose $w\left(x\right)=1,f\left(x\right)={\mathrm{\Theta }}^{m+1}\left(x\right)$ and $h\left(x\right)=1$, we have

$$\begin{array}{cc}\hfill & f\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & =({\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))\left(\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}\right)}}{\left(({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & 2h\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(w\left(x\right)f\left(x\right)+\left(\left(h\left(\nu \right)+h(1-\nu )\right)\left(f\left({\tau }_1\right)+f\left({\ell }_2\right)\right)-f\left(x\right)\right)w\left(x\right)\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & =4({\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)\left(\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}\right)}}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}.\hfill \end{array}$$

By comparing above results we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)\left(\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}\right)}}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}\hfill \\ \hfill & \le 4({\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)\left(\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}\right)}}{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}.\hfill \end{array}$$

(31)

The computational values of (31), are shown in

Table 3. The computational values of (31) corresponding to choice $\mu =0.5$ are as follows.

${\mathit{\ell }}_1$/$\mathit{\ell }2$	$2.00$	$2.40$	$2.80$
1.00	(6.93 × ${10}^{00}$, 2.77 × ${10}^{01}$)	(2.37 × ${10}^{01}$, 9.49 × ${10}^{01}$)	(9.60 × ${10}^{01}$, 3.84 × ${10}^{02}$)
1.20	(4.76 × ${10}^{00}$, 1.91 × ${10}^{01}$)	(1.64 × ${10}^{01}$, 6.55 × ${10}^{01}$)	(6.46 × ${10}^{01}$, 2.58 × ${10}^{02}$)
1.40	(3.08 × ${10}^{00}$, 1.23 × ${10}^{01}$)	(1.09 × ${10}^{01}$, 4.37 × ${10}^{01}$)	(4.25 × ${10}^{01}$, 1.70 × ${10}^{02}$)
1.60	(1.81 × ${10}^{00}$, 7.23 × ${10}^{00}$)	(7.02 × ${10}^{00}$, 2.81 × ${10}^{01}$)	(2.72 × ${10}^{01}$, 1.09 × ${10}^{02}$)
1.80	(8.48 × ${10}^{-01}$, 3.39 × ${10}^{00}$)	(4.25 × ${10}^{00}$, 1.70 × ${10}^{01}$)	(1.69 × ${10}^{01}$, 6.76 × ${10}^{01}$)
2.00	(0.00 × ${10}^{00}$, 0.00 × ${10}^{00}$)	(2.34 × ${10}^{00}$, 9.35 × ${10}^{00}$)	(1.01 × ${10}^{01}$, 4.05 × ${10}^{01}$)

and

Table 4. The computational values of (31) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/$\mathit{\ell }2$	$3.20$	$3.60$	$4.00$
1.00	(4.80 × ${10}^{02}$, 1.92 × ${10}^{03}$)	(3.03 × ${10}^{03}$, 1.21 × ${10}^{04}$)	(2.43 × ${10}^{04}$, 9.70 × ${10}^{04}$)
1.20	(3.12 × ${10}^{02}$, 1.25 × ${10}^{03}$)	(1.89 × ${10}^{03}$, 7.57 × ${10}^{03}$)	(1.46 × ${10}^{04}$, 5.83 × ${10}^{04}$)
1.40	(1.98 × ${10}^{02}$, 7.94 × ${10}^{02}$)	(1.16 × ${10}^{03}$, 4.64 × ${10}^{03}$)	(8.57 × ${10}^{03}$, 3.43 × ${10}^{04}$)
1.60	(1.24 × ${10}^{02}$, 4.94 × ${10}^{02}$)	(6.96 × ${10}^{02}$, 2.78 × ${10}^{03}$)	(4.95 × ${10}^{03}$, 1.98 × ${10}^{04}$)
1.80	(7.52 × ${10}^{01}$, 3.01 × ${10}^{02}$)	(4.09 × ${10}^{02}$, 1.64 × ${10}^{03}$)	(2.80 × ${10}^{03}$, 1.12 × ${10}^{04}$)
2.00	(4.47 × ${10}^{01}$, 1.79 × ${10}^{02}$)	(2.35 × ${10}^{02}$, 9.42 × ${10}^{02}$)	(1.55 × ${10}^{03}$, 6.20 × ${10}^{03}$)

corresponding to the choice of parameters $m=2$, $k=1$, $\mathrm{\Theta }\left(x\right)=x^2$, $\mu =2$, ${\tau }_i=1$, ${\beta }_i=0.5$, ${\kappa }_i=0.5$, $\mu =0.5$ for some fixed values of ${\ell }_1$ and ${\ell }_2$. Figure 2, shows the graphical representation of (31), corresponding to the choice of parameters $0<{\ell }_1=1<{\ell }_2=4$.

Theorem 8.

For $k>$ 0, $m\in \Re /\{-1\}$, and $Re\left(\eta \right)>0, Re\left(\varrho \right)>0, Re\left(\lambda \right)>0, Re\left(\gamma \right)>0$ are complex parameters, and Θ be an increasing function on $({\ell }_1,{\ell }_2)$ with ${\ell }_1<{\ell }_2$, also $f:[{\ell }_1,{\ell }_2]\to \Re$ be the geneeralized h-Cf, $h:\Re \to \Re$ be non-negative function and $w:[{\ell }_1,{\ell }_2]\to \Re$, $w\ge 0$ be symmetric pertaining to ${\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}$ and $f\left(x\right),w\left(x\right)\in \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)[{\ell }_1,{\ell }_2]$. Then the subsequent the inequality

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)f\left(x\right)w\left(x\right)\hfill \\ \hfill & \le {\displaystyle \frac{f\left({\ell }_1\right)+f\left({\ell }_2\right)}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(h\left({\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}\right)+h\left({\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}\right)\right)w\left(x\right)\right)\left({\ell }_2\right),\hfill \end{array}$$

(32)

holds for all $\nu \in (0,1).$

Proof. 

Using Lemma 2 and the symmetricalness of the weight w, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{f\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left(\frac{{\ell }_1+{\ell }_2}{2}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)w\left(x\right)}{2h\left(\frac{1}{2}\right)}}={\displaystyle \frac{\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left(\frac{{\ell }_1+{\ell }_2}{2}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)f\left(\frac{{\ell }_1+{\ell }_2-x+x}{2}\right)w\left(x\right)}{2h\left(\frac{1}{2}\right)}}\hfill \\ \hfill & \le {\displaystyle \frac{\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left(\frac{{\ell }_1+{\ell }_2}{2}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)h\left(\frac{1}{2}\right)\left[f({\ell }_1+{\ell }_2-x)+f\left(x\right)\right]w\left(x\right)}{2h\left(\frac{1}{2}\right)}}\hfill \\ \hfill & =\left({\displaystyle \frac{1}{2}}\right)\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)\left[f({\ell }_1+{\ell }_2-x)w({\ell }_1+{\ell }_2-x)+f\left(x\right)w\left(x\right)\right]\hfill \\ \hfill & =\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)f\left(x\right)w\left(x\right).\hfill \end{array}$$

Which is the left part of the inequality. Alternatively, we have

$$\begin{array}{cc}\hfill & \left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}f\left(x\right)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right)\left[f\left(x\right)w\left(x\right)+f({\ell }_1+{\ell }_2-x)w({\ell }_1+{\ell }_2-x)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(f\left(x\right)+f({\ell }_1+{\ell }_2-x)\right)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right(f\left({\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}{\ell }_1+{\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}{\ell }_2\right)\hfill \\ \hfill & +f\left({\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}{\ell }_1+{\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}{\ell }_2\right)\left)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\right(h\left({\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}\right)f\left({\ell }_1\right)+h\left({\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}\right)f\left({\ell }_2\right)\hfill \\ \hfill & +h\left({\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}\right)f\left({\ell }_1\right)+h\left({\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}\right)f\left({\ell }_2\right)\left)w\left(x\right)\right)\left({\ell }_2\right)\hfill \\ \hfill & ={\displaystyle \frac{f\left({\ell }_1\right)+f\left({\ell }_2\right)}{2}}\left({}_{\mathrm{\Theta }}{}^{k,m}\mathfrak{J}_{{\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)}^{+};\mu ,{\beta }_i}^{{\delta }_i,{\tau }_i}\left(h\left({\displaystyle \frac{{\ell }_2-x}{{\ell }_2-{\ell }_1}}\right)+h\left({\displaystyle \frac{x-{\ell }_1}{{\ell }_2-{\ell }_1}}\right)\right)w\left(x\right)\right)\left({\ell }_2\right).\hfill \end{array}$$

□

Example 3.

For graphical representation we choose $f\left(x\right)={\mathrm{\Theta }}^{m+1}\left(x\right)$, $w\left(x\right)=x$ and $h\left(x\right)=x$ in (32), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{(m+1)}^{\frac{\mu }{k}-1}}{k}}{\Sigma }_{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right))}}\hfill \\ \hfill & \times ({\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)+\eta }{k}}}\hfill \\ \hfill & -{\displaystyle \frac{m+1}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}{\displaystyle \frac{{\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left(\frac{{\ell }_1+{\ell }_2}{2}\right)\right)}^{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}+1}}{\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}+1}})\hfill \\ \hfill & \le [{\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)+{\mathrm{\Theta }}^{m+1}\left({\ell }_1\right)]({\displaystyle \frac{{(m+1)}^{-\frac{\mu }{k}}}{k}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\delta }_i\right)}_{{\kappa }_i,k}{\left({\tau }_i\right)}^{{\kappa }_i}}{{\mathrm{\Gamma }}_k(\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)\left(\frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}\right)}}\hfill \\ \hfill & \times {\left({\mathrm{\Theta }}^{m+1}\left({\ell }_2\right)-{\mathrm{\Theta }}^{m+1}\left({\displaystyle \frac{{\ell }_1+{\ell }_2}{2}}\right)\right)}^{{\displaystyle \frac{\mu +{\Sigma }_{i=1}^n\left({\beta }_i{\kappa }_i\right)}{k}}}).\hfill \end{array}$$

(33)

The computational values of (33), are shown in Table 5 and Table 6 corresponding to the choice of parameters $m=2$, $k=1$, $\mathrm{\Theta }\left(x\right)=x^2$, $\mu =2,{\tau }_i=1$, ${\beta }_i=0.5$, ${\kappa }_i=0.5$, and for some fixed values of ${\ell }_1$ and ${\ell }_2$. The Figure 3, shows the two-dimensional graphical representation of (33), corresponding to the choice of parameters $0<{\ell }_1=1<{\ell }_2=4$. The Figure 4 shows the three-dimensional graphical representation of (33) corresponding to the choice of parameters $0<\mu <1$.

For tabular values

Table 5. The computational values of (33) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.10$	$2.30$	$2.50$
0.10	(4.12 × ${10}^{01}$, 3.14 × ${10}^{01}$)	(5.23 × ${10}^{01}$, 4.16 × ${10}^{01}$)	(6.98 × ${10}^{01}$, 5.69 × ${10}^{01}$)
0.30	(5.29 × ${10}^{01}$, 4.21 × ${10}^{01}$)	(6.43 × ${10}^{01}$, 5.25 × ${10}^{01}$)	(8.44 × ${10}^{01}$, 7.07 × ${10}^{01}$)
0.50	(6.47 × ${10}^{01}$, 5.29 × ${10}^{01}$)	(7.62 × ${10}^{01}$, 6.34 × ${10}^{01}$)	(9.89 × ${10}^{01}$, 8.08 × ${10}^{01}$)
0.70	(7.65 × ${10}^{01}$, 6.36 × ${10}^{01}$)	(8.82 × ${10}^{01}$, 7.42 × ${10}^{01}$)	(1.10 × ${10}^{02}$, 9.09 × ${10}^{01}$)
0.90	(8.83 × ${10}^{01}$, 7.43 × ${10}^{01}$)	(1.00 × ${10}^{02}$, 8.51 × ${10}^{01}$)	(1.24 × ${10}^{02}$, 1.04 × ${10}^{02}$)
1.00	(1.00 × ${10}^{02}$, 8.57 × ${10}^{01}$)	(1.13 × ${10}^{02}$, 9.45 × ${10}^{01}$)	(1.39 × ${10}^{02}$, 1.17 × ${10}^{02}$)

Table 5. The computational values of (33) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.10$	$2.30$	$2.50$
0.10	(4.12 × ${10}^{01}$, 3.14 × ${10}^{01}$)	(5.23 × ${10}^{01}$, 4.16 × ${10}^{01}$)	(6.98 × ${10}^{01}$, 5.69 × ${10}^{01}$)
0.30	(5.29 × ${10}^{01}$, 4.21 × ${10}^{01}$)	(6.43 × ${10}^{01}$, 5.25 × ${10}^{01}$)	(8.44 × ${10}^{01}$, 7.07 × ${10}^{01}$)
0.50	(6.47 × ${10}^{01}$, 5.29 × ${10}^{01}$)	(7.62 × ${10}^{01}$, 6.34 × ${10}^{01}$)	(9.89 × ${10}^{01}$, 8.08 × ${10}^{01}$)
0.70	(7.65 × ${10}^{01}$, 6.36 × ${10}^{01}$)	(8.82 × ${10}^{01}$, 7.42 × ${10}^{01}$)	(1.10 × ${10}^{02}$, 9.09 × ${10}^{01}$)
0.90	(8.83 × ${10}^{01}$, 7.43 × ${10}^{01}$)	(1.00 × ${10}^{02}$, 8.51 × ${10}^{01}$)	(1.24 × ${10}^{02}$, 1.04 × ${10}^{02}$)
1.00	(1.00 × ${10}^{02}$, 8.57 × ${10}^{01}$)	(1.13 × ${10}^{02}$, 9.45 × ${10}^{01}$)	(1.39 × ${10}^{02}$, 1.17 × ${10}^{02}$)

Table 6. The computational values of (33) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.70$	$2.90$	$3.00$
0.10	(8.72 × ${10}^{01}$, 7.22 × ${10}^{01}$)	(1.04 × ${10}^{02}$, 8.75 × ${10}^{01}$)	(1.16 × ${10}^{02}$, 9.87 × ${10}^{01}$)
0.30	(1.03 × ${10}^{02}$, 8.78 × ${10}^{01}$)	(1.21 × ${10}^{02}$, 1.05 × ${10}^{02}$)	(1.34 × ${10}^{02}$, 1.17 × ${10}^{02}$)
0.50	(1.20 × ${10}^{02}$, 9.89 × ${10}^{01}$)	(1.40 × ${10}^{02}$, 1.16 × ${10}^{02}$)	(1.55 × ${10}^{02}$, 1.30 × ${10}^{02}$)
0.70	(1.32 × ${10}^{02}$, 1.10 × ${10}^{02}$)	(1.53 × ${10}^{02}$, 1.29 × ${10}^{02}$)	(1.69 × ${10}^{02}$, 1.43 × ${10}^{02}$)
0.90	(1.48 × ${10}^{02}$, 1.27 × ${10}^{02}$)	(1.72 × ${10}^{02}$, 1.49 × ${10}^{02}$)	(1.88 × ${10}^{02}$, 1.64 × ${10}^{02}$)
1.00	(1.64 × ${10}^{02}$, 1.38 × ${10}^{02}$)	(1.90 × ${10}^{02}$, 1.58 × ${10}^{02}$)	(2.06 × ${10}^{02}$, 1.72 × ${10}^{02}$)

Table 6. The computational values of (33) corresponding to choice $\mu =0.5$.

${\mathit{\ell }}_1$/${\mathit{\ell }}_2$	$2.70$	$2.90$	$3.00$
0.10	(8.72 × ${10}^{01}$, 7.22 × ${10}^{01}$)	(1.04 × ${10}^{02}$, 8.75 × ${10}^{01}$)	(1.16 × ${10}^{02}$, 9.87 × ${10}^{01}$)
0.30	(1.03 × ${10}^{02}$, 8.78 × ${10}^{01}$)	(1.21 × ${10}^{02}$, 1.05 × ${10}^{02}$)	(1.34 × ${10}^{02}$, 1.17 × ${10}^{02}$)
0.50	(1.20 × ${10}^{02}$, 9.89 × ${10}^{01}$)	(1.40 × ${10}^{02}$, 1.16 × ${10}^{02}$)	(1.55 × ${10}^{02}$, 1.30 × ${10}^{02}$)
0.70	(1.32 × ${10}^{02}$, 1.10 × ${10}^{02}$)	(1.53 × ${10}^{02}$, 1.29 × ${10}^{02}$)	(1.69 × ${10}^{02}$, 1.43 × ${10}^{02}$)
0.90	(1.48 × ${10}^{02}$, 1.27 × ${10}^{02}$)	(1.72 × ${10}^{02}$, 1.49 × ${10}^{02}$)	(1.88 × ${10}^{02}$, 1.64 × ${10}^{02}$)
1.00	(1.64 × ${10}^{02}$, 1.38 × ${10}^{02}$)	(1.90 × ${10}^{02}$, 1.58 × ${10}^{02}$)	(2.06 × ${10}^{02}$, 1.72 × ${10}^{02}$)

4. Discussion

In the first table, the comparison of the LHS, Middle Term, and RHS in the graphs and tables reveals that the RHS is generally larger than both the LHS and Middle Term, with the values increasing as ${\ell }_1$ and ${\ell }_2$ increase. The Middle Term tends to be closer to the LHS in magnitude, suggesting its role as a balancing factor between the two sides. As ${\ell }_2$ increases, the RHS grows more rapidly compared to the LHS and Middle Term, indicating that the RHS is more sensitive to changes in ${\ell }_2$. The inequality appears to hold in the form $LHS\le MiddleTerm\le RHS$ across the tested values, with the LHS being consistently smaller than or equal to the Middle Term, and the Middle Term smaller than or equal to the RHS. This confirms the validity of the inequality and suggests that while the terms grow with ${\ell }_1$ and ${\ell }_2$, the RHS exhibits the fastest growth. These observations highlight that the inequality holds true in the given range, with the terms influenced differently by ${\ell }_1$ and ${\ell }_2$, and the RHS proving to be the dominant term in terms of magnitude. In the remaining graphs and tables demonstrate that for all combinations of ${\ell }_1$ and ${\ell }_2$, the RHS values are consistently greater than the corresponding LHS values, indicating that the inequality is satisfied in all cases. This suggests that the inequality becomes more pronounced for larger ${\ell }_1$ and ${\ell }_2$, with the RHS serving as a more accurate upper bound, confirming the robustness of the inequality in these conditions.

5. Conclusions

In recent times, mathematical fractional inequalities have found their way into various domains such as the material sciences, heat conduction, viscoelasticity, time series analysis, circuits, human body modeling, and shear waves. While inequalities, itself may not directly take note of issues of educational access, high-quality research, and mathematical advancement—topics such as inequality contribute to the larger objective of improving educational through the dissemination of knowledge, the development of critical thinking abilities, and the encouragement of mathematical literacy among researchers. In this work, we extended the well-known H-H-F inequalities by introducing generalized fractional operators involving the M-M-L function. Through the derivation of two key identities for locally differentiable functions, we were able to provide more accurate estimates of the differences between the left, middle, and right terms in the H-H-F inequalities. These generalized inequalities offer valuable insights into generalized convexity and the behavior of fractional operators in various mathematical contexts. The practical applications of these inequalities are significant, particularly in fields such as optimization, fractional calculus, and applied analysis. For instance, the improved inequalities can aid in more precise bounding of functions and contribute to solving complex problems in areas such as signal processing, system modeling, and the study of fractional differential equations. The graphical representations included in this study serve to visualize these inequalities, providing a useful tool for researchers and practitioners. Overall, the results presented in this paper lay a foundation for further exploration of fractional inequalities and their applications in real-world problems. Future research could extend these methods to higher-dimensional settings and explore their potential in new areas such as financial modeling and the modeling of physical systems in plasma physics. Researchers can apply our defined operator to generalized Opial-type, Chebyshev-type, and composite Cf inequality problems, among other types of inequalities. These inequalities play a vital role in computing the special means. Specifically, we have looked into some of the well-known H-H-F inequality’s relations to generalized h-convexity and extended fractional operators. In order to achieve this goal, two identities for local differentiable mappings are created. From these identities, we may derive estimates for the difference between the center and right parts of the H-H-F inequality as well as the difference between the left and central inequality.