Abstract
Biomedicine is a pillar of the collective, scientific effort of human self-discovery, as well as a major source of humanistic data codified primarily in biomedical documents. Despite their rigid structure, maintaining and updating a considerably-sized collection of such documents is a task of overwhelming complexity mandating efficient information retrieval for the purpose of the integration of clustering schemes. The latter should work natively with inherently multidimensional data and higher order interdependencies. Additionally, past experience indicates that clustering should be semantically enhanced. Tensor algebra is the key to extending the current term-document model to more dimensions. In this article, an alternative keyword-term-document strategy, based on scientometric observations that keywords typically possess more expressive power than ordinary text terms, whose algorithmic cornerstones are third order tensors and MeSH ontological functions, is proposed. This strategy has been compared against a baseline using two different biomedical datasets, the TREC (Text REtrieval Conference) genomics benchmark and a large custom set of cognitive science articles from PubMed.
1. Introduction
Cognitive science, namely the study of the mind and its processes [1,2,3], has recently gained significant momentum, which can be attributed to a number of reasons. It is a major driver of the big data age along with online social networks, the semantic web and computational systems theory to name a few. Recent sociological and demographic studies conducted in the majority of the Western world including the EU [4] and the U.S. [5] reveal that one of the biggest challenges of the next decade will be the healthcare costs associated with cognitive issues. Similar trends at the planet scale can be found in reports compiled by the UN Population Division [6,7,8]. Thus, the systematic analysis of cognitive science literature is of immediate interest, besides researchers, of healthcare planners, government agencies, hospital administrators, insurance companies, equipment manufacturers and software developers.
With the creation of PubMed (http://www.ncbi.nlm.nih.gov/pubmed) in 1996, the largest public online database under the ultimate administrative oversight of NIH, a massive collection spanning millions of life science articles is available to researchers. Over the past two decades, it has been substantially enriched and currently contains more than fourteen million abstracts, whereas it accepts and serves more than seventy million queries of six terms each on average per month. Indicative of its enormous topic diversity is the fact that through Entrez (French term for enter.), the PubMed-coupled indexing engine, the searchable keywords currently exceed two millions. Two issues arising in any information retrieval context, especially in a major digital repository of humanistic data, are precision and recall. The former pertains to the accurate retrieval of studies, articles and data tables stored across a variety of online archives and libraries that are relevant to the query, whereas the latter refers to the fraction of relevant documents that is retrieved for a given query [9].
PubMed cognitive science-related documents range over such diverse types as academic articles, software blueprints, demographic surveys, healthcare personnel training manuals, best practice guides and clinical data reports. It is evident that in such a large collection, both in terms of quantity and quality, information retrieval and text mining techniques should be applied if any meaningful piece of information is to be acquired. This is especially true given that medical and scientific articles exhibit a high degree of textual structure, including metadata like abstracts and keywords.
The primary contribution of this article is a topic-based clustering strategy for cognitive documents whose core is a third order term-keyword-document tensor. The latter is one of the many possible direct generalizations of the established term-document matrix, which essentially is a second order tensor from a linear algebraic point of view. As such, this tensor can be queried in a similar manner. The reason for selecting this particular scheme over a number of other possible ones stems from the intuition, corroborated in part from empirical scientometric evidence, that keywords are semantically more important compared to ordinary terms [10,11].
This journal article is structured as follows. Section 2 summarizes recent work on medical retrieval and tensor analysis. Section 3 describes software tools, and Section 4 outlines the proposed tensor model. Furthermore, Section 5 discusses performance aspects of the proposed and the baseline method obtained through the TREC (Text REtrieval Conference) genomics dataset, while Section 6 discusses tensor analytics. Finally, Section 7 explores future research directions. Tensors are denoted by uppercase calligraphic letters, such as , matrices by uppercase boldface letters, like , and vectors by lowercase boldface letters or numbers, like and . Table 1 summarizes the article notation.

Table 1.
Article notation.
2. Previous Work
Document clustering has gained much interest in biomedicine [12]. PubMed abstracts are clustered with frequent words and near terms in [13]. A graph algorithm based on flow simulation is considered in [14], where advanced techniques are proposed in [15].
Biomedical ontologies in conjunction with mining of biomedical texts led to the technique of word sense disambiguation (WSD), which maps documents to different topics. Ontologies and meta-data assist the clustering algorithms [16]. Event-based text mining systems in the context of biomedicine as an annotation scheme are the focus of [17]. On the other hand, domain-specific information extraction systems regarding event-level information with automatic causality recognition are proposed in [18]. Human gene ontologies are described in [19,20]. U-Compare, an integrated text mining and NLP system based on the Unstructured Information Management (UIMA) Framework (UIMA: http://uima.apache.org/), is presented in [21].
Using the MeSH ontology for biomedical document clustering is popular in scientific literature [22,23,24,25]. Various clustering approaches such as suffix tree clustering were supplemented with ontological information in [26], whereas the accuracy of similarity metrics is discussed in [27]. A knowledge domain scheme based on bipartite graphs with MeSH is presented in [28]. Two serious limitations that face approaches by using the MeSH thesaurus are introduced in [29].
Tensor algebra [30,31] and the closely-associated field of multilayer graphs [32,33] are some of the primary algorithmic tools for dealing with higher order data, along with higher order statistics [34,35] and multivariate polynomials [36,37]. Central places in tensor algebra have Tucker and Kruskal tensor forms [38], which allow alternative tensor representations appropriate for certain linear algebraic operations such as tensor-matrix multiplication, tensor compression [39], tensor regularization and factor discovery. Models for tensor data mining have been outlaid in [40]. A very recent work combining tensors and semantics for medical information retrieval is [41].
3. System
3.1. Architecture
The proposed system architecture is shown in Figure 1. The interaction between the various components has been kept at a minimum, and feedback loops have been avoided. However, in future versions, the tensor can be updated either incrementally or in batch mode with information extracted from the queries.
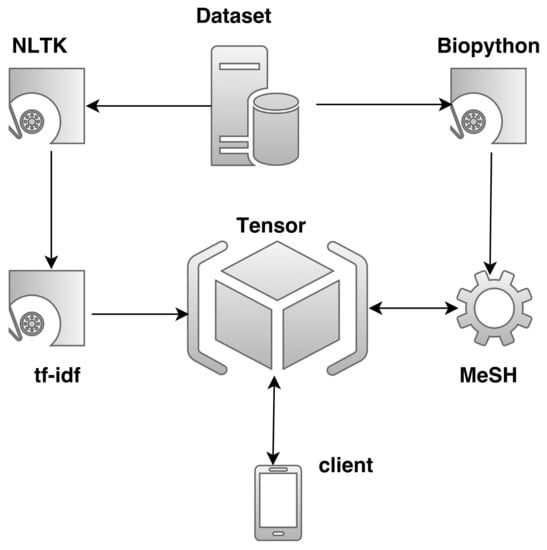
Figure 1.
System architecture.
3.2. Python Tools
Python is well known in the developer community for its rich library ecosystem.
The objective of the Entrez document retrieval system is to provide a single entry point for seamless and efficient access across those health-related public databases that are under NIH administrative supervision, including among others, PubMed, MEDLINE, preMEDLINE and the NCBI database. Thus, Entrez is the key to a vast body of medical knowledge through advanced text queries. As a consequence, APIs for Entrez have been implemented for most, if not all, major programming languages such as the NCBI API for Java, the NCBI Toolkit for C++ and Biopython for Python. The functionality of each Entrez API and the associated library should include at least methods for retrieving articles based on keywords, terms, authors, doi (Digital Object Identifier) or the unique PubMed identifier, as well as for providing pointers to related documents or supplementary data and traversing document lists in both directions.
The native document format supported by Entrez is XML (ftp://ftp.ncbi.nlm.nih.gov/bioproject). The latter being structurally balanced and semantically enriched with tags and properties and possessing a strict tree hierarchy is particularly suited to parsing techniques such as those found in the Xerces family of Java parsers. Moreover, the highly structured XML format is appropriate for graph databases, such as TitanDB and Neo4j (https://neo4j.com) or, with appropriate conversion to JSON, for document databases, such as MongoDB. Table 2 contains the XML tags described in the public Entrez XML schema. An XML schema is one of the two means for formatting an XML document in a tree structure, the other one being DTD (Document Type Definition) [42]. Generally, a schema is preferred because of its increased flexibility, being itself written in XML. In contrast, DTD is based on a terse and restricted SGML syntax, which provides compatibility with the SGML standard at the expense of a steeper learning curve [43].

Table 2.
PubMed document XML tags.
Biopython is one such PubMed API aiming at providing seamless and fully-fledged Entrez functionality, including document retrieval in a multitude of ways. Table 3 summarizes the methods that are associated with the basic Entrez functionality.

Table 3.
Biopython methods.
Once Biopython has been installed through pip or another Python package manager, it can be invoked as follows:
>>> from Bio import Entrez
>>> Entrez.email = ’name@domain.org’
>>> EntryPoint = Entrez.einfo()
>>> XMLArticle = EntryPoint.eread()
>>> EntryPoint.close()
Key ontological MeSH operations such as search and least common ancestor location can be automated with NLTK (http://www.nltk.org), a common library for natural language processing. Moreover, NLTK has been integrated with additional functionality for word- and sentence-level syntactic analysis, term similarity metrics, including the Wu–Palmer [44], the Leacock–Chodorow [45] and the Jiang–Conrath [46] metrics, and methods for sub-thesaurus construction and maintenance. For instance, using NLTK and the term cognitive, the entries of Table 4 were located in the MeSH ontology.

Table 4.
Cognitive-related MeSH entries.
Notice that the entries of Table 4 are located at very different levels of the MeSH tree hierarchy ranging from a high level of abstraction such as F03.615 down to very specialized issues like F04.096.628.255.500. Thus, subsequent searches started at high abstraction levels such as F02.463 and H01.158, which were identified by pruning the MeSH identifiers to their first two segments.
The following code segment displays how NLTK can parse a simple sentence.
>>> import nltk as nl
>>> from stemming.porter2 import stem
>>> from nl.corpus import stopwords
>>> print nl.word_tokenize(’Hello˽world!’)
3.3. Tensor Toolbox
Tensor Toolbox is a recent MATLAB toolbox by Sanida Labs for direct support of tensors and certain associated key functions [30]. Although MATLAB inherently supports multidimensional arrays since its earliest editions, Tensor Toolbox offers considerably more flexibility, a set of new and equivalent tensor types, including natural, compressed, Tucker, and Kruskal forms, and a broad set of methods for handling these primary data types. These primary data types are respectively denoted as tensor, sp tensor, t tensor and k tensor, constituting an important semantic difference compared to the default MATLAB approach, which treats all multidimensional arrays as ordinary matrix types. Since tensors represent natural keyword-term-document triplets, Tensor Toolbox is an indispensable software component of our implementation. Provided the Tensor and the Communications Systems toolboxes have been properly installed, the following MATLAB commands populate a sparse third order tensor and store it in Tucker form:
>>> rng nltk shuffle
>>> for k = 1:4
>> T(:,:,k) = randsrc(4, 8, [-1:1; 0.2 0.6 0.2]);
>>> end
>>> T = mat2ten(T);
>>> TT = ttensor(T);
4. Proposed Model
4.1. Representation
Definition 1.
A p-th order tensor is a p-dimensional array indexed by p integers and coupling simultaneously at most p distinct linear spaces denoted by , . When each of the p linear spaces is , then as a shorthand .
It is obvious from the way tensors are defined that they are direct generalizations of matrices. Indeed, a matrix is the linear algebraic vehicle for coupling the row space and the column space . Of course, for square and invertible matrices, the row and column spaces coincide.
Tensor , which will contain properly-defined values for the keyword-term-document triplets, is populated by keywords and terms stored in documents making it a third order tensor . Note that the proposed is but one of the ways for extending the established term-document model, which is based on a second order tensor, namely a matrix . For instance, in [47], a term-author-document is proposed. The latter is based on empirical scientometric evidence in favor of the semantic role authors play in the process of information retrieval [10,11]. A common point with the proposed model, besides both relying on third order tensors, is that they are inspired by OLAP (Online Analytical Processing) cubes [48]. Regarding the tensor dimensions, it should be noted that, although the three dimensions are easy to visualize and handle, they are by no means a golden rule.
As stated earlier, , essentially the algebraic cornerstone of the proposed technique, is a third order and real valued tensor simultaneously coupling the keyword, term and document spaces. The entries of are associated with the document retrieval process. Concretely, let , and respectively denote the -th keyword, the -th term and the -th document where , and . Moreover, let and respectively be the number of occurrences of and in . Then, contains the normalized occurrences of and in according to the following four factor double tf-idf (term frequency-inverse document frequency) scheme:
In Equation (1), the first pair of terms and forms a standard tf-idf scheme based only on terms and documents:
while the second pair of terms and constitutes the second tf-if scheme:
4.2. Analytics
Tensor density, similarly to large matrix sparsity, is a significant metric, which besides potential compression, may reveal interesting patterns along many dimensions since its definition is straightforward.
Definition 2.
The density ρ of a tensor is defined as the number of the non-zero elements to its total number of elements, which can be easily found by multiplying the size of each dimension. Thus:
Definition 3.
Along similar lines, the log density of is defined as the logarithm of the number of the non-zero elements to the logarithm of its total number of elements, essentially being the ratio of the magnitudes of the respective numbers.
Besides its natural interpretation, can usually lead to larger values, which in turn result in numerically stable computations in formulae when it appears in denominators.
The Frobenius norm of a tensor , denoted by , is an algebraic indicator of the overall strength of the tensor entries, which is indirectly tied to compressionability. Recall that the Frobenius norm for a matrix is defined as:
Both are related in their own way to compression potential, which is critical given the large volume of data typically held in tensors. The former plays the same role as with matrices, whereas the latter indicates whether there are strong or weak connections between keywords, terms and documents. Since both provide a data summary in the form of a scalar, they give quick and overall information regarding the tensor status at the expense of aggregating information about each dimension of this single value. Thus, both metrics can be used as building blocks for composite ones, which examine each dimension separately.
Definition 4.
The Frobenius norm of an p-th order tensor is the square root of the sum along each dimension of its elements squared:
Generally, there is no consensus as to which values of indicate strong connections on average. In order to derive bounds, probabilistic techniques can be employed by treating the elements of being drawn from a distribution. One way is to observe that is the sample approximation of . Then, since the Frobenius norm is always positive, as all-zero tensors are not under consideration, the Markov inequality:
can be used to derive a bound. For instance, if the elements of are drawn from a Gauss distribution, then follows a noncentral chi square distribution.
4.3. Metric Fusion
Again, in order to take into account information about each dimension separately for a third order tensor, it suffices to fix the last index and create a metric that takes into consideration the density of each resulting matrix separately. Thus, if the density of each separate matrix for a fixed value of is defined as:
then the set of tensor densities along the third dimension can be used to build the following aggregative metric:
The harmonic mean ensures that will tend to be close to the smallest of .
For a third order tensor , a related metric can be constructed by first fixing one of the three indices, treating the remaining two dimensions as a sequence of matrices, computing the Frobenius norm for each such matrix and taking the harmonic mean of these norms. Deciding which index is to be fixed is important as it essentially determines a tensor partitioning. For the purposes of this article, the last index is fixed creating thus a metric , which ranges over the documents.
Notice that in (11) denotes the matrix created by fixing to k while the two remaining indices stay unaltered, creating thus a matrix. If is large, which may well be the case for document collections, then it would also make sense to compute statistic measures such as sample versions of variance, skewness and kurtosis.
4.4. Tensor Tucker Form
Definition 5.
The multiplication along the k-th dimension between a p-th order tensor and a vector is a -th order tensor with elements:
Definition 6.
The multiplication along the k-th dimension between a p-th order tensor and a matrix is a p-th order tensor with elements:
Definition 7.
Tucker tensor factorization is defined as:
The Tucker factorization is one of the possible generalizations of the SVD for matrices:
which is the core of the term-document information retrieval model and the starting point of a number of document clustering schemes. In order to compute the Tucker factorization, the higher order SVD is employed. The latter is based on cyclically updating each of the basis matrices until they all converge according to a criterion.
4.5. Queries
Similarly to the term-document matrix case, tensor can be queried regarding a set of terms or a set of keywords . Said queries can be cached in terms of linear algebra as tensor-vector multiplications. In addition, allows queries about both terms and keywords.
Generating a query vector, it suffices to place one at a position corresponding to a query term and zero otherwise. For a more detailed description, see the collection querying algorithm in [47].
4.6. Document Clustering
When partitioning a set S into k subsets, a heuristic approach is necessary since the number of ways to perform such partitioning equals [49]:
The generating function of the recursively defined sequence is:
which can be proven using the property of partial sums for any integer sequence.
4.7. Baseline Methodology
The processing steps of the baseline methodology are extensively described in previous works [23,24,25]. Initially, for the web documents to be retrieved and later processed, the web document repository (PubMed) is queried. Specifically, we have used PubMed API (Pubmed API: http://www.ncbi.nlm.nih.gov/books/NBK25500/). After the results are retrieved in the initial step, each result item consists of six different items: title, author names, abstract, keywords, conference/journal name and publication date, .
In the following, the document representation takes place as the proposed methodology enriched the corresponding texts with annotations from a specific ontology. Consequently, each document is represented as a term frequency-inverse document frequency () vector, and some terms of the vector are annotated and mapped on senses identified from MeSH.
As a last step, the vectors-documents are clustered by utilizing k-means.
The baseline methodology is outlined in Algorithm 1.
| Algorithm 1 Baseline methodology from [25]. |
| Require: Query vector q |
| Ensure: Clusters produced |
| 1: identify documents set |
| 2: ∀ result item in D |
| 3: for each in D do |
| 4: calculation of MeSH vectors M = {} |
| 5: end for |
| 6: use as input, titles, keywords and abstracts: |
| 7: for each in M do |
| 8: Clusters ←K-Means(M) {where Cosine Similarity metric is applied to k-Means} |
| 9: end for |
5. TREC Dataset and Baseline
5.1. Data Synopsis
In order to compare our proposed tensor based scheme, the TREC Genomics 2007 dataset (TREC Genomics Track: http://ir.ohsu.edu/genomics/) serves as an evaluation benchmark. For a more detailed description of the specific dataset, see [25,50]. It is worthwhile to mention that in the TREC Genomics 2007 dataset, about 160,000 documents from about 50 genomics-related journals are considered.
5.2. Baseline Method
Regarding the clustering procedure, the k-means algorithm is employed with the following parameters. The number of derived clusters is 20, while the cosine similarity distance was utilized for identifying underlying document similarities. Regarding the tensor scheme, Tucker factorization, which is a higher-order SVD generalization, has been executed, and the rows and columns of the base matrices corresponding to the c largest entries of the core tensor have been selected. This is similar to selecting the c largest singular values of the SVD in the matrix case.
We have compared the produced clusters for both schemes by using precision, recall and F-measure scores.
As can be seen in Table 5, Table 6 and Table 7, the proposed representations and clustering strategies achieve notable precision, recall and F-measure for a small and average number of processed documents. As the number of processed documents increases, the performance of the corresponding methods seems to decrease.

Table 5.
Cosine similarity, k-means clustering and precision.

Table 6.
Cosine similarity, k-means clustering and recall.

Table 7.
Cosine similarity, k-means clustering and F-measure.
By observing Table 8, it is deduced that density is a decreasing function of tensor size. Please notice that denotes the percentage of the documents used to extract these results.

Table 8.
Tensor density.
Table 9 shows how compares to . As with density, this ratio falls with . This can be interpreted as the weakening of document connections. When few documents are available, then it is easy to derive strong connections between them. On the other hand, as the collection is augmented with more documents, then topical associations lose in strength due to the increased subject variability.

Table 9.
ratio to .
6. Custom PubMed Dataset
Before analyzing the precision and recall characteristics of the proposed model, it is worth looking at the tensor contents and specifically at the term list. The twenty most and the twenty least common keywords in the collection and their frequencies are shown in Table 10. Additionally, Table 11 contains the corresponding information for the text terms. In these tables, the frequency f for both keywords and terms is computed based on the entire document collection.

Table 10.
Collection keywords (frequency f as a percentage).

Table 11.
Collection terms (frequency f as a percentage).
It is no surprise to see common technical and medical terms at the top of the list of Table 10. For instance, both fMRI and EEG analysis are widespread techniques with many MATLAB implementations. Moreover, older or more specialized terms are less frequent. For example, shell shock or shellshock is a rather negatively-charged WWI-era term, which is now largely replaced by post-traumatic. Notice that closely-associated keywords, such as clinical and evaluation, have similar frequencies, which is expected. Rare keywords also pertain to other physiological conditions, probably from papers establishing a connection between brain and body functionality.
The situation is similar in Table 11 where the top twenty and the bottom twenty terms are shown. In comparison to Table 10, the terms are more diversified covering a broader number of topics including many secondary ones, and thus, the gaps between terms are considerably narrower. Obviously, the terms cognitive, cognition and brain are present in literally every document of the collection, which was anticipated. In contrast to Table 10, there hardly appears to be a connection between the least frequent terms and the topic. In fact, the right-hand side of Table 10 could appear in virtually any medical collection about any topic and still make some sense. This implies that there is definitely compression potential in the original collection as a portion of documents can be replaced by a combination of eigen-documents or, in the case of redundant information determined by a large number of generic terms, it can be simply discarded.
Notice that the majority of the terms of the second column of Table 11 probably refer to the subjects undergoing some kind of treatment or monitoring. Furthermore, the first column of Table 11 shares many common entries with the corresponding column of Table 10. This can be attributed to the fact that a keyword, which carries significant semantic information, is very likely to be used in the text of a document. Furthermore, the frequency of terms fMRI and EEG equals roughly the sum of the frequency of the academic papers and the clinical data documents of Table 12. A possible explanation is that these types of documents are the most likely to refer to clinical methodology, while the remaining document types address auxiliary topics.

Table 12.
Document types (frequency f as a percentage).
Table 12 contains the frequency of each document type in the collection. It comprises approximately half of the scientific papers, which is consistent with the role of PubMed, supplemented by another half of auxiliary documents of various types.
It is of interest to examine the similarity between the keyword set and the term set , as any high relevance between them would mean the tensor can be reduced to a term-document matrix. Their similarity was assessed with the DTW metric, which works on vectors of lengths p and q. First, it defines a metric between the members of both vectors and then relies on the recurrence relation:
to compute the shortest transformation and its cost between those two vectors, creating incrementally a shortest cost path in a tableau. Since and contain words, was selected to be the Levenshtein distance. One fine point is that DTW requires vectors, which are ordered, whereas sets are by definition unordered. To overcome this, and were sorted in descending order according to word frequency and, if needed, lexicographically, as well, to break any frequency ties. This preserves not only the words in each set, but also their significance. Another subtlety is that the atomic operations are character and not word oriented. Once was computed, it was expressed as a fraction of the worst case scenario, which is the deletion of each character of followed by the insertion of each character of . For the given sets, this ratio was , which means that there is little overlapping between their sorted versions.
Table 13 presents tensor density as a function of . Similarly to the benchmark dataset, it is also a decreasing function of tensor size.

Table 13.
Tensor density.
Table 14 presents the ratio of to . The weakening of document connections is caused similarly to the benchmark dataset case.

Table 14.
ratio to .
7. Conclusions
This article presented a semantically-aware topic-based document clustering scheme for biomedical articles that can be further applied to biomedical ones. The core of this scheme is a keyword-term-document third order tensor, namely a three-dimensional array. The latter is a generalization of the established term-document matrix model, which is widely used in information retrieval, both in research and in industrial-grade systems. A third order keyword-term-document tensor with values coming out a tf-idf scheme is proposed. The advantage of the proposed representation is the semantic enrichment, which is achieved with the inclusion of keywords. Scientometric research suggests that keywords regularly carry more semantic information than ordinary terms. A variation of this model is to mix keywords from MeSH with keywords retrieved from PubMed.
The proposed methodology has been compared to both the term-author-document outlined in [47] in terms of compression potential, precision and recall. Both were implemented in MATLAB using the Tensor Toolbox. The experimental results suggest that inclusion of keywords instead of authors increases precision and, to an extent, recall.
Regarding future work directions, a number of extensions is possible. The sparsity patterns of larger tensors should be analyzed, and if possible, compression techniques such as those proposed in [51] should be applied. Furthermore, effective density patterns should be investigated. Another research point is the addition of update operations to the proposed model, namely of insertion and deletion operations, yielding thus a more flexible scheme. A related topic is the development of persistent methodologies for tensors, such as those in [52], in order to support the efficient retrieval of past versions. Finally, real-time analytics are gaining attention with the recent combination of streaming algorithms and tensors.
Author Contributions
Georgios Drakopoulos, Andreas Kanavos, Ioannis Karydis, Spyros Sioutas, and Aristidis Vrahatis conceived of the idea, designed and performed the experiments, analyzed the results, drafted the initial manuscript and revised the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson-Laird, P.N. Mental models in cognitive science. Cognit. Sci. 1980, 4, 71–115. [Google Scholar] [CrossRef]
- Gover, M.R. The Embodied Mind: Cognitive Science and Human Experience. Mind Cult. Act. 1996, 3, 295–299. [Google Scholar] [CrossRef]
- Norman, D.A. Twelve issues for cognitive science. Cognit. Sci. 1980, 4, 1–32. [Google Scholar] [CrossRef]
- European Commission. The 2015 Ageing Report: Underlying Assumptions and Projection Methodologies; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- He, W.; Goodkind, D.; Kowal, P. An ageing world: 2015. In International Reports; U.S. Department of Commerce: Washington, DC, USA, 2016. [Google Scholar]
- United Nations Population Division. World Population Ageing 2007; United Nations Population: New York, NY, USA, 2007. [Google Scholar]
- United Nations Population Division. World Population Ageing 2015; United Nations Population: New York, NY, USA, 2015. [Google Scholar]
- United Nations Population Division. World Population Prospects 2015; United Nations Population: New York, NY, USA, 2015. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Newman, M.E. Ego-centered networks and the ripple effect. Soc. Netw. 2003, 25, 83–95. [Google Scholar] [CrossRef]
- Newman, D. Writing together separately: Critical discourse and the problems of cross-ethnic co-authorship. Area 1996, 28, 1–12. [Google Scholar]
- Bhattacharya, S.; Ha-Thuc, V.; Srinivasan, P. MeSH: A window into full text for document summarization. Bioinformatics 2011, 27, 120–128. [Google Scholar] [CrossRef] [PubMed]
- David, M.R.; Samuel, S. Clustering of PubMed abstracts using nearer terms of the domain. Bioinformation 2012, 8, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Theodosiou, T.; Darzentas, N.; Angelis, L.; Ouzounis, C.A. PuReD-MCL: A graph-based PubMed document clustering methodology. Bioinformatics 2008, 24, 1935–1941. [Google Scholar] [CrossRef] [PubMed]
- Baud, R.; Rassinoux, A.M.; Scherrer, J.R. Natural language processing and semantical representation of medical texts. Methods Inf. Med. 1992, 31, 117–125. [Google Scholar] [PubMed]
- Alexopoulou, D.; Andreopoulos, B.; Dietze, H.; Doms, A.; Gandon, F.L.; Hakenberg, J.; Khelif, K.; Schroeder, M.; Wächter, T. Biomedical word sense disambiguation with ontologies and metadata: Automation meets accuracy. BMC Bioinform. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Ananiadou, S.; Thompson, P.; Nawaz, R. Enhancing search: Events and their discourse context. In Proceedings of the 14th International Conference on Intelligent Text Processing and Computational Linguistics, CICLing, Samos, Greece, 24–30 March 2013; pp. 318–334. [Google Scholar]
- Mihaila, C.; Ohta, T.; Pyysalo, S.; Ananiadou, S. BioCause: Annotating and analysing causality in the biomedical domain. BMC Bioinform. 2013, 14, 2. [Google Scholar] [CrossRef] [PubMed]
- Ontology Consortium, G.E.A. The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 2004, 32, D258–D261. [Google Scholar] [CrossRef] [PubMed]
- Myhre, S.; Tveit, H.; Mollestad, T.; Lægreid, A. Additional gene ontology structure for improved biological reasoning. Bioinformatics 2006, 22, 2020–2027. [Google Scholar] [CrossRef] [PubMed]
- Batista-Navarro, R.T.; Kontonatsios, G.; Mihaila, C.; Thompson, P.; Rak, R.; Nawaz, R.; Korkontzelos, I.; Ananiadou, S. Facilitating the Analysis of Discourse Phenomena in an Interoperable NLP Platform. In Proceedings of the 14th International Conference on Computational Linguistics and Intelligent Text Processing (CICLing), Samos, Greece, 24–30 March 2013; pp. 559–571. [Google Scholar]
- Huang, M.; Névéol, A.; Lu, Z. Recommending MeSH terms for annotating biomedical articles. JAMIA 2011, 18, 660–667. [Google Scholar] [CrossRef] [PubMed]
- Kanavos, A.; Makris, C.; Theodoridis, E. On Topic Categorization of PubMed Query Results. In Proceedings of the Artificial Intelligence Applications and Innovations (AIAI), Halkidiki, Greece, 27–30 September 2012; pp. 556–565. [Google Scholar]
- Kanavos, A.; Theodoridis, E.; Tsakalidis, A. A PubMed Meta Search Engine Based on Biomedical Entity Mining. In Proceedings of the International Workshop on Database and Expert Systems Applications (DEXA), Munich, Germany, 1–5 September 2014; pp. 82–86. [Google Scholar]
- Kanavos, A.; Makris, C.; Theodoridis, E. Topic Categorization of Biomedical Abstracts. Int. J. Artif. Intell. Tools 2015, 24, 1540004. [Google Scholar] [CrossRef]
- Yoo, I.; Hu, X. Biomedical Ontology MeSH Improves Document Clustering Qualify on MEDLINE Articles: A Comparison Study. In Proceedings of the 19th IEEE International Symposium on Computer-Based Medical Systems (CBMS), Salt Lake City, UT, USA, 22–23 June 2006; pp. 577–582. [Google Scholar]
- Boyack, K.W.; Newman, D.; Duhon, R.J.; Klavans, R.; Patek, M.; Biberstine, J.R.; Schijvenaars, B.; Skupin, A.; Ma, N.; Börner, K. Clustering more than two million biomedical publications: Comparing the accuracies of nine text-based similarity approaches. PLoS ONE 2011, 6, e18029. [Google Scholar] [CrossRef] [PubMed]
- Yoo, I.; Hu, X. Clustering Large Collection of Biomedical Literature Based on Ontology-Enriched Bipartite Graph Representation and Mutual Refinement Strategy. In Proceedings of the 10th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Singapore, 9–12 April 2006; pp. 303–312. [Google Scholar]
- Zhu, S.; Zeng, J.; Mamitsuka, H. Enhancing MEDLINE document clustering by incorporating MeSH semantic similarity. Bioinformatics 2009, 25, 1944–1951. [Google Scholar] [CrossRef] [PubMed]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Kolda, T.G. Orthogonal tensor decompositions. SIAM J. Matrix Anal. Appl. 2001, 23, 243–255. [Google Scholar] [CrossRef]
- Drakopoulos, G. Tensor Fusion of Social Structural and Functional Analytics over Neo4j. In Proceedings of the 6th International Conference of Information, Intelligence, Systems, and Applications, Chandigarh, India, 5–7 March 2016. [Google Scholar]
- Drakopoulos, G.; Megalooikonomou, V. A Graph Framework for Multimodal Medical Information Processing. Proc. Dig. World 2016, arXiv:1608.00134, 1024–1028. [Google Scholar]
- Drakopoulos, G.; Megalooikonomou, V. An adaptive higher order scheduling policy with an application to biosignal processing. In Proceedings of the 2016 Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 921–928. [Google Scholar]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. Independent component analysis based on higher-order statistics only. In Proceedings of the 8th IEEE Signal Processing Workshop on Statistical Signal and Array Processing, Corfu, Greece, 24–26 June 1996; pp. 356–359. [Google Scholar]
- Mourrain, B.; Pan, V.Y. Multivariate polynomials, duality, and structured matrices. J. Complex. 2000, 16, 110–180. [Google Scholar] [CrossRef]
- Von zur Gathen, J.; Kaltofen, E. Factoring sparse multivariate polynomials. J. Comput. Syst. Sci. 1985, 31, 265–287. [Google Scholar] [CrossRef]
- Kressner, D.; Tobler, C. Algorithm 941: Htucker—A Matlab Toolbox for Tensors in Hierarchical Tucker Format. ACM Trans. Math. Softw. 2014, 40, 22. [Google Scholar] [CrossRef]
- Drakopoulos, G.; Megalooikonomou, V. Regularizing large biosignals with finite differences. In Proceedings of the 7th International Conference on Information, Intelligence, Systems, and Applications, Chalkidiki, Greece, 13–15 July 2016; pp. 1–6. [Google Scholar]
- Papalexakis, E.E.; Faloutsos, C.; Sidiropoulos, N.D. Tensors for Data Mining and Data Fusion: Models, Applications, and Scalable Algorithms. TIST 2016, 8, 16. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Q.; Yuan, J. Semantically Enhanced Medical Information Retrieval System: A Tensor Factorization Based Approach. Available online: http://ieeexplore.ieee.org/abstract/document/7912400/ (accessed on 17 July 2017).
- Shadbolt, N.; Berners-Lee, T.; Hall, W. The semantic Web revisited. IEEE Intell. Syst. 2006, 21, 96–101. [Google Scholar] [CrossRef]
- Antoniou, G.; Van Harmelen, F. A Semantic Web Primer; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Wu, Z.; Palmer, M. Verb semantics and lexical selection. In Proceedings of the 32nd Annual Meeting on Association for Computational Linguistics, Las Cruces, NM, USA, 27–30 June 1994; pp. 133–138. [Google Scholar]
- Leacock, C.; Chodorow, M. Combining local context and WordNet similarity for word sense identification. In WordNet: An Electronic Lexical Database; The MIT Press: Cambridge, MA, USA, 1998; Volume 49, pp. 265–283. [Google Scholar]
- Jiang, J.J.; Conrath, D.W. Semantic similarity based on corpus statistics and lexical taxonomy. arXiv, 1997; arXiv:preprint cmp-lg/9709008. [Google Scholar]
- Drakopoulos, G.; Kanavos, A. Tensor-based Document Retrieval over Neo4j with an Application to PubMed Mining. In Proceedings of the 6th International Conference of Information, Intelligence, Systems, and Applications, Chalkidiki, Greece, 13–15 July 2016. [Google Scholar]
- Gómez, L.I.; Gómez, S.A.; Vaisman, A.A. A generic data model and query language for spatiotemporal OLAP cube analysis. In Proceedings of the 15th International Conference on Extending Database Technology, Berlin, Germany, 27–30 March 2012; pp. 300–311. [Google Scholar]
- Aggarwal, C.C. Data Mining: The Textbook; Springer: Berlin, Germany, 2015. [Google Scholar]
- Hersh, W.R.; Cohen, A.M.; Ruslen, L.; Roberts, P.M. TREC 2007 Genomics Track Overview. Proceedings of The Sixteenth Text REtrieval Conference, (TREC), Gaithersburg, MD, USA, 6–9 November 2007. [Google Scholar]
- Drakopoulos, G.; Megalooikonomou, V. On the weight sparsity of multilayer preceptrons. In Proceedings of the 6th International Conference on Information, Intelligence, Systems, and Applications, Corfu, Greece, 6–8 July 2015; pp. 1–6. [Google Scholar]
- Kontopoulos, S.; Drakopoulos, G. A space efficient scheme for graph representation. In Proceedings of the 26th International Conference on Tools with Artificial Intelligence (ICTAI 2014), Limassol, Cyprus, 10–12 November 2014; pp. 299–303. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).