1. Introduction
This paper emphasizes the computation of stability criterion for a Shimizu–Morioka system in fractional order as shown below:
where
and
are positive values. Here, we assume
as the adjustable control parameter. The integer order system of Equation (
1) was first proposed in [
1] and has attracted the interest of researchers to study the stability and various types of bifurcation such as in [
2,
3,
4,
5]. However, the fractional order or arbitrary order of the system as in Equation (
1) have received less attention; also see [
6,
7]. Unlike both [
6,
7], here, we apply optimal fractional order Routh–Hurwitz stability conditions which have recently been derived by Čermák and Nechvátal in [
8]. Unlike the previous version of Routh–Hurwitz stability conditions for fractional systems (as derived in [
9]), these new optimal Routh–Hurwitz condition serve as necessary and sufficient conditions to guarantee that all roots of the characteristic polynomial obtained from the linearization process are located inside the Matignon stability sector. Furthermore, the optimal Routh–Hurwitz conditions obtained were in an explicit form. The optimal Routh–Hurwitz conditions were successfully applied to study the fractional dynamical systems such as the fractional Lorenz system [
8] and fractional Rössler System [
10]. However, it is still yet to be applied for other fractional systems such as the fractional Shimizu–Morioka system.
On the other hand, the Shimizu–Morioka system can be considered as a simplified system for investigating the dynamic bahaviour of the well-known Lorenz system. However, due to its rich dynamic behaviour, and especially chaotic behaviour of its solutions, the Shimizu–Morioka system has its self-interest [
2,
3,
4,
5]. Unfortunately, there are not many published results regarding the stability and bifurcation analysis for the Shimizu–Morioka system in fractional orders. In this research direction, other fractional dynamical systems such as the fractional Lorenz system and many more always receive attention from researchers to study the dynamical behaviour of their stability analysis and bifurcation analysis [
11,
12,
13,
14]. This fractional order Shimizu–Morioka system can be considered as the generalized fractional Lorenz system which shows hyperchaotic and has important applications such as in secure the communication [
15]. Apart from that, searching for robust stability is always the concern for researchers. For instance, as worked by [
16] for fractional order control system with interval uncertain coefficients and a time-delay.
On top of that, an analytical approach for computation of stability analysis is always an important approach, especially for dynamical systems in fractional orders. The new optimal Routh–Hurwitz conditions allow us to do the analysis in explicit form. By applying the optimal Routh–Hurwitz conditions, for the first time, under the fractional derivative order
, the range of
and its influences towards the fractional Shimizu–Morioka system and whether it has locally stable equilibria will be identified. Although the Routh–Hurwitz conditions can be considered as an old topic, due to the recent development in fractional calculus, the study of Routh–Hurwitz conditions for fractional systems has emerged recently. Among that are a new Routh-type table for fractional system [
17], Routh–Hurwitz-Liénard–Chipart Criteria [
18], and a graphical approach to study stability analysis for incommensurate fractional-order systems [
19].
The outline of the present paper is given as follows. Some basic concepts of Shimizu–Morioka system and its fractional counterpart is given in
Section 2.
Section 3 comprises of some basic concepts of the optimal Routh Hurwitz conditions for fractional system.
Section 4 discusses the calculation of stability criterion for fractional Shimizu–Morioka system by using optimal Routh Hurwitz conditions. Numerical result by using a fractional predictor–corrector scheme for fractional Shimizu–Morioka system is given in
Section 5 to verify the result obtained from the previous sections.
Section 6 is the conclusion of the paper.
3. Optimal Routh–Hurwitz Conditions for Fractional System
In the classical theory of Routh–Hurwitz conditions, for three dimensional dynamical system, the characteristic polynomial in cubic form when
is as in Equation (
8)
Let us consider
are real coefficients. The Routh–Hurwitz conditions which for the characteristic polynomial in Equation (
8) have all zeroes, i.e.,
with negative real parts if and only if
By using the linearization theorem, we get that the equilibria,
are locally asymptotically stable if all the zeroes
,
of Equation (
4) are located inside the Magtinon stability sector [
8].
Then, the Routh–Hurwitz conditions are only sufficient for validity of the Magtinon stability sector in Equation (
10) with
. Under this situation, the stability sector of the set of all triplets
is wider and significantly more complicated due to Equation (
10).
Follow the work in [
8], we define
as the boundary locus as follow.
which
can be computed through
. Substitute the value of
into Equation (
8), we obtain the following real and imaginary part.
Solving the above equations, we will get
From the first equation of Equation (
13), we get
and putting Equation (
14) into second equation of Equation (
13), and after some algebra manipulation, lead to
where
.
To further describe this set, we use the following theorem which derived in [
8].
Theorem 1. Let . The Equation Equation (
8)
has all the zeroes which satisfies the stability condition for fractional system as in Equation (
10)
if and only if any of the following conditions hold: - (i)
.
- (ii)
.
- (iii)
.
where , andwith . Proof. The proof is following [
8]. For
, the zeros
of polynomial Equation (
8) must has the positive real parts, where contradicts with the stability sector Equation (
10). Thus, we define
as the boundary locus in half-space for
c is always positive.
Let , we consider the as the set of for the conditions in Theorem 1 holds.
We denote as the complement of the in the half-space . Hence, we have the whole half-space with .
It is enough for us to check the Theorem 1 by assuming the triplets
represent in
and
respectively. First, we assume
as
lying inside
. By directly solving the polynomial Equation (
8) equal to 0, we get all the zeros
have negative real parts, where
,
and
is satisfied. Thus, the zeros
is satisfied the Magtinon stability sector Equation (
10) when
.
Then, we assume
as
which lying inside
. Similarly procedure, we obtain that the zeros
have positive real parts, where
,
and
. Thus, we obviously see that the zeros have positive real parts. In addition, Equation (
10) is not satisfied since
. Therefore, we can say that the zeros
is not satisfied Equation (
10) when
. Conversely, we say that the zeros
of Equation (
8) satisfy Equation (
10) if and only if any of the conditions of Theorem 1 holds. □
4. Stability Analysis of the Fractional Shimizu–Morioka System
In this section, we will compute the stability criterion for the fractional Shimizu–Morioka system as in Equation (
6). From
Section 2, we will limit our value of
in
. From the calculation, the coefficients of characteristic polynomial as in Equation (
8) for fractional system in Equation (
6) are
,
and
. Thus we can analyze local asymptotic stability of the equilibria by applying fractional optimal Routh–Hurwitz conditions [
8]. It is obvious that the system in Equation (
6) are locally asymptotically stable for any
if
. If
, then Theorem 1(i) in
Section 3 will be applied. In this case, since all the
and
c for the characteristic polynomial are bigger than 0, the only relevant condition for calculating the stability criterion is the inequality
. Hence, we shall explain some basic steps of the computational procedures to obtain the stability criterion for this fractional Shimizu–Morioka system.
By substituting the
,
and
of the fractional Shimizu–Morioka system into
, we can get the inequality as follows
where
We should notice that when
is approaching to 1, the inequality in Equation (
16) becomes Equation (
5) actually. This can be said that this computation is the generalization of integer order system to fractional order or arbitrary order system. Now, we can analyze the inequality Equation (
16) by squaring it and reducing it into polynomial,
.
If we fixed the value of
, we can evaluate the dependence of abjustable control parameter
on the
, i.e., fractional derivative order in the Caputo sense. In this case, from the result in
Section 2, we shall limit the
only from 0 to
. Thus, we illustrate the fractional Shimizu–Morioka system as in Equation (
6) with the value
. We obtain the following fractional system.
Thus we analyze Equation (
19) with respect to the bifurcation parameter
. In the sequel, we have the inequality Equation (
16) with
For these values
, from Equation (
16), we let
and
. Thus, we analyze the inequality as shown in Equation (
21).
where
and
. From the observation of the graph, it is obvious that
,
and
whenever
. Hence, we have
for all
and
. Similarly, a direct calculation shows that
for any
, where
Since
,
and
for any
, Equation (
21) is satisfied trivially for any
and any
. Furthermore,
for all
and
. Thus, Equation (
21) is satisfied trivially for all
and all
. Hence, we assume
and
in our next analysis.
Using elementary calculations based on the sign analysis of
and
, one can check that, for any fixed
,
is decreasing in
.
where
and
The interval
is bijectively mapped by
onto
where
Follow the similar procedure as in Section 4 of [
8], we obtain
with unknowns
and
. By solving numerically the system formed by Equations (
27) and (
28), we will obtain a pair of
and
in positive value which
lie inside
. Hence, we can conclude that the critical value for
is given as
Similar to [
8], the geometrical analysis of Equation (
16) yields the following conclusions.
Theorem 2. Let . Then the equilibria of Equation (
19)
are locally asymptotically stable for all . Theorem 3. Let . Then there exists a couple of values (uniquely determined in the interval via Equation (
27))
such that the equilibria of Equation (
19)
are locally asymptotically stable if either or . Moreover, are not stable whenever . We will further explain the above theorems in following section.
5. Numerical Results
In this section, we will present some simulation of the stability analysis for the system Equation (
1). For the simulation purpose, we applying generalized Adams-Bashforth-Moulton type predictor-corrector scheme for solving fractional differential equations developed in [
20]. This numerical approach is widely used in the study of the dynamical behaviour of fractional dynamical system, such as in [
21,
22]. This is because most of the system of fractional differential equation or fractional dynamical system do not have analytical solution. Furthermore, we had also modified this approach for solving differential equation in Caputo-Fabrizio sense as in [
23].
From the result in
Section 4, when
, we will obtain
and the critical value of
is
. This condition is the fractional order Hopf bifurcation and where periodic solution should be occurred. Perturbate the adjustable control parameter
which leads to the dissolve of limit cycle to unstable or stable condition. For the sake of simplicity when doing the simulation, we take
and the initial condition as
.
Figure 1 shows the periodic solution for the time series solution while the phase portrait of the trajectories with the initial condition
shows the limit cycle appeared.
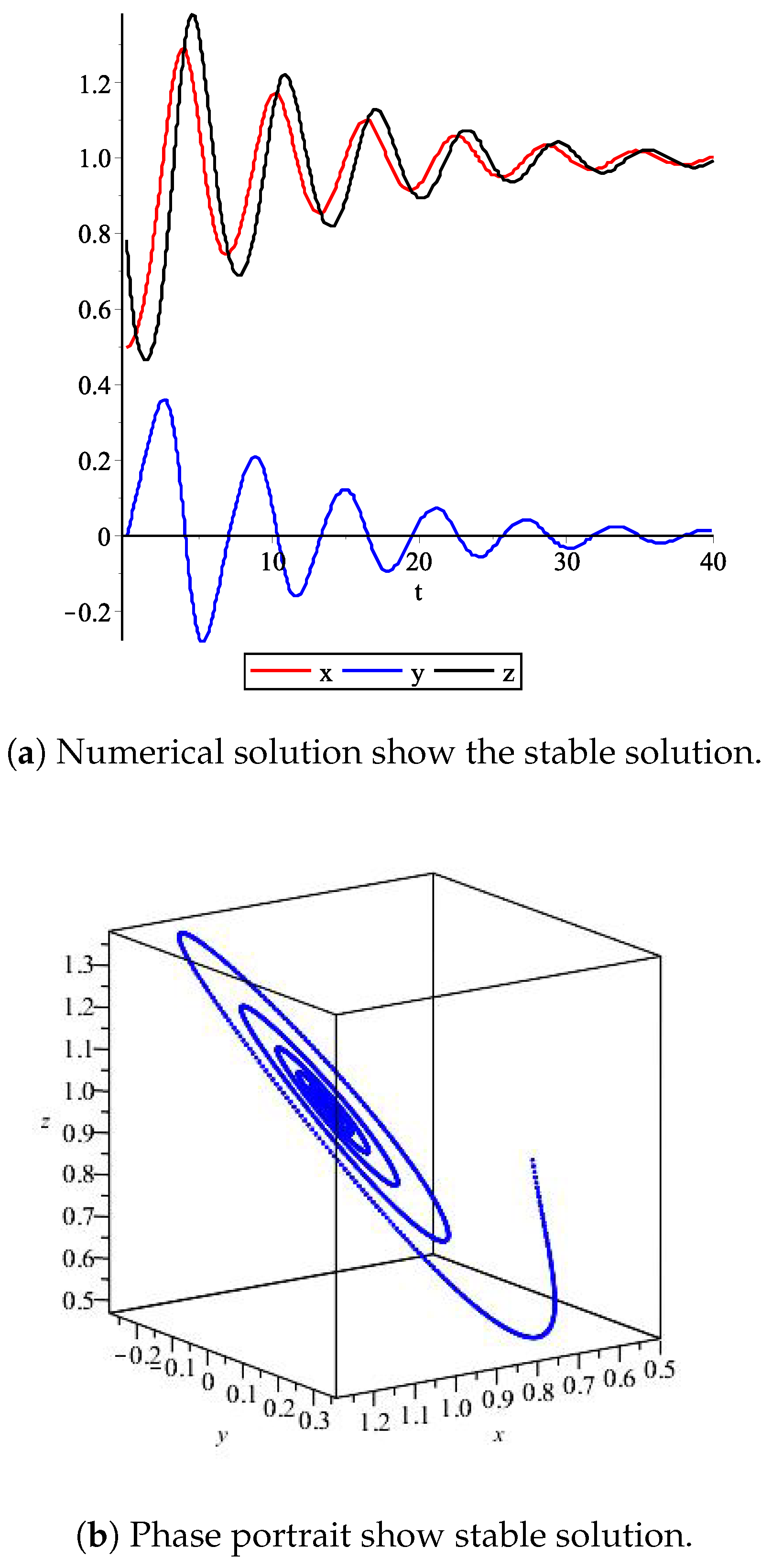
When increasing the value of adjustable control parameter
, the solution becomes to stable toward the equilibrium
. We present the simulation result when
as in
Figure 2.
On the other hand, based on Equation (
16), the inequality is given as following.
We can reach the conclusion for the computation of stability criterion for fractional Shimizu–Morioka system by using optimal Routh–Hurwitz conditions as in
Table 1 which follow Theorems 2 and 3.
If
, solving the inequality in Equation (
30) will give the range of
shows the fractional system is stable. As example, for the case when
, where
. If we let
which is
, and we substitute it into Equation (
30), we will be able to get the range of
which give stability condition for the system. Following Theorem 3, we get
and
. For other values of
, the detail of calculations is shown in
Table 2.
For illustration purpose, we take
, the range of
must be
in order to get the stable solution. If the range of
do not lie in that interval, the equlibria will be locally asymptotically not stable. We verified it through simulation for
as in
Figure 3. All the calculations have done by using Maple.
6. Conclusions
In this paper, we have used new optimal Routh–Hurwitz conditions which also serve as necessary and sufficient conditions to compute the stability criterion for a fractional Shimizu–Morioka system. Here, we summarise our work as the following:
For the , the new optimal Routh–Hurwitz conditions enable us to detect the critical value of for the stability criterion of fractional Shimizu–Morioka system when we use as control parameter.
Furthermore, we introduce the way to calculate the range of adjustable control parameter to obtain the stability criterion for the fractional Shimizu–Morioka system.
The result was verified by the famous predictor–corrector scheme for fractional systems. The advantage of using this new optimal Routh–Hurwitz condition is that it enables us to obtain the range of which fulfills the stability criterion for the fractional Shimizu–Morioka system. However, lot of work need to be done by applying this new optimal Routh–Hurwitz condition to other fractional systems and this will probably be part of our future research work.