Optimal Design in Roller Pump System Applications for Linear Infusion

Abstract

In this study, an infusion roller pump comprising two separate innovative resilient tube designs is presented. The first incorporates the flexible tubing cross-section area in its relaxed state as a lenticular one for power reduction reasons. The second keeps the previous lenticular cross-section along its length, while it additionally incorporates an inflating portion, for creating a momentary flow positive pulse to balance the void generated by the roller disengagement. Fluid–Structure Interaction (FSI) simulations cannot provide quantitatively realistic results, due to the limitation of full compression of the tube, and are only used qualitatively to reveal by which way to set the inflated portion along the tube length in order to suppress backflow and achieve constant flow rate. Finally, indirect lumen volume measurements were performed numerically and an optimum design was found testing eight design approaches. These indirect fluid volume measurements assess the optimum inflated tube’s portion leading to backflow and pulsating elimination. The optimum design has an inflation portion of 75 degrees covering almost 42% of the curved part of the tube, while it has a constant zone with the maximum value of inflated lenticular cross-section, within the portion, of 55 degrees covering about 73% of the inflation portion.

1. Introduction

Porter and Bradley [1] were the first who patented a rotary pump in 1855. They called their invention “Elastic-Tube Pump” operating for pumping water and other fluids. Allen, focusing on direct blood transfusion, designed in 1881 [2] and manufactured in 1887 [3] a modification with one roller, named “surgical pump”. Truax [4] developed the first double roller pump in 1899 for blood transportation.

In clinical use, roller pumps have been established over decades for cardiopulmonary bypass in heart–lung machines or in dialysis machines. Roller pumps are still predominant and are commonly used for up to several hours. Their main advantages are simplicity of operation, low cost of disposable tubing, and reliability, whereas disadvantages can be seen in blood damage (hemolysis) [5]. Fulker et al. [6] revealed the significance of pulsatility produced by the hemodialysis roller pump operating to the hemodialysis extracorporeal circuit. He mentioned that the pulsatility is induced by the rotary motion of the pump and flow reversal occurred when contact between the forward (trailing) roller and tubing ended, implicating the release of the occluded tubing. The motion of the roller pump induces pulsatility throughout the extracorporeal circuit and induces instantaneous flow reversal, directly after the roller leaves the occlusion position. However, it has been suggested that pulsatile blood flow is superior to continuous flow in cardiopulmonary bypass (CPB). Teman [7] suggested that pulsatile blood flow is superior to continuous flow in cardiopulmonary bypass (CPB). A pediatric pulsatile rotary ventricular pump (PRVP) was designed and its ability to generate pulsatile flow (PF) during CPB was determined. Different levels of flow were compared with both animal’s baseline physiologic function and continuous flow (CF) by a roller pump. The PRVP creates greater pulsatility than a continuous flow roller pump over the range of flow rates used, similar to that observed with the native heart. Apart from CPB application, an intermittent operation is preferable in drug delivery systems, in contrast with traditional peristaltic pumps with continuous operation. In that trend, Tamadon et al. in 2019 [8] proposed the design and characterization of a miniaturized peristaltic rotary pump suitable for non-continuous liquid drug dosing at various rotational speed conditions.

In [9], Klespitz and Kovács present a review, summarizing the most important properties of roller pumps and introduced some of the special solutions of them focusing on pulsation control engineering possibilities. Moreover, a 2019 recent progress report by Esser et al. [10] contributes to the state-of-the-art of peristaltic pump systems in biomimetics and living nature, and allows for comparison by highlighting the differences in structure and function, as well as advantages and drawbacks for the technical implementation of roller pumps.

Furthermore, an interest in applying the roller pumping principle into small size pumps, employing tubes with diameters of a few mm or μm, has also appeared in literature due to the simplicity of the fabrication of these devices. Du in 2009 [11] demonstrated experimentally a peristaltic micropump driven by a rotating motor with magnetically attracted steel balls, while Koch [12], in the same year, compared two miniaturized micro pumps, namely, a roller-type compressed microchannel and a tubing-based peristaltic one. The tubing-based pump provides an inexpensive, miniaturized modular micropump with high valving pressure, while the microchannel pump design facilitates pump integration into a microfluidic device. The major issue raised in these applications is the difficulty of optimizing their performance due to the multiparametric nature of the relevant fluid mechanics problem.

Recently, Rao in 2017 [13] provided experimentally the basic working principle and construction of a rotary peristaltic pump, while in the same year Vinayakumar [14] presented the design, development, characterization and precision flow controlling of a DC-motor-driven peristaltic pump for controlled drug delivery application. A geared DC-motor-driven roller/cam was used to squeeze the silicone tube to obtain the pumping action. The complete system has been developed experimentally for the self-administration of bolus and basal delivery of insulin.

Regarding computational or experimental tools, many researchers have attempted to shed light on the issue of non-pulsating roller pumping. Using a simple lumped parameter mathematical model of a roller pump, Moscato [15] simulated the pump dynamically in order to clarify the uncontrolled pulsation mechanism. The tube compression/release mechanism actuated by the rollers during their engaging and disengaging phases causes the triggering oscillations validated by experimental measurements. Concerning computational studies, a time-dependent moving boundary CFD model was used by Mulholland [16] to explore the blood flow and damage inside a roller pump used for cardiopulmonary bypass. Similarly, Zhou et al. [17] assessed the shear-induced cell damage in roller pumps, together with the inherent flow pattern, through a CFD method, simulating the pulsing flow dynamics generated. Furthermore, a brief Fluid–Structure Interaction (FSI) analysis of a rotary peristaltic pump is presented by Elabbasi [18] and Swe [19] through a peristaltic flow model, revealing the flow fluctuations as a result of engagement and disengagement between the rollers and the tube. This model is also used to predict the stresses in the tube. Additionally, the numerical simulations by Krautbauer et al. [20], based on the structural and fluid flow model for mechanically driven peristaltic pumping, yielded stresses and mechanical deflections, allowing the design of wall-driven peristaltic pumps with application to therapeutic drug delivery. In 2019, Formato et al. [21] applied FSI modeling for treating peristaltic roller pumping flow simulations, where the compression reduced the internal diameter of the pipe for about 87%, but not the necessary 100% for deep occlusion. All numerical studies have been designed to minimize the backflow, approaching occlusion with high amplitude tube compression and not to eliminate it, applying deep occlusion, namely, 100% amplitude tube compression. Thus, no FSI numerical study can solve the problem of backflow and pulsatility in a way realistically accepted by a manufacturer of roller pump systems.

Roller pumps are the most common perfusion devices used and require continuous servo-regulation and monitoring to prevent the application of negative pressure to the drainage circuit and to provide sufficient positive pressure to the infusion site. A disadvantage is that it is difficult, via a common roller pump of a circular cross-section flexible tubing, to achieve a constant or pulseless flow needed for liquid drug delivery. Pulses are created when the rollers disengage from the tubing and, therefore, the occlusion is removed, resulting in a void generated in the disengagement region of the tubing. In this region, the tubing returns to its normal cross-section area shape resulting in an increase of the volume which is filled by fluid from the outlet of the tubing. This leads to a reduction of the fluid flow rate at the outlet of the infusion site for the duration of the pulse [22,23,24,25]. The complexity of this problem solution is attributed to the abrupt changes in momentum, induced when the flexible tube is deeply occluded by the rollers. For this reason, pulsatility or instantaneous flow reversal are inevitably caused directly after the roller leaves the occlusion position. The aim of the present study is to evaluate two proposed innovative designs of flexible tube geometries in order to mechanically suppress the backflow and achieve a constant flow rate on the outlet infusion site of a roller pump. The first innovative tube geometry is designed in a way that the cross-section of the tubing is not circular but lenticular in its relaxed state, having a shape similar to an arrangement of two parentheses facing each other, thus: "( )". The second innovative tube geometry is designed in a way that the cross-section of the tubing is the same as the first and furthermore includes, along its length, a portion where the cross-section is larger than the remaining one. This larger portion when compressed leads to an increase of displacement volume which has to be at least equal to the increase of volume displaced as a result of the disengagement roller element at the tubing end. The overall result is the linearization of the infusion eliminating pulsatility and instantaneous flow reversal.

2. Materials and Methods

2.1. Roller Pump Geometry and Performance Parameters

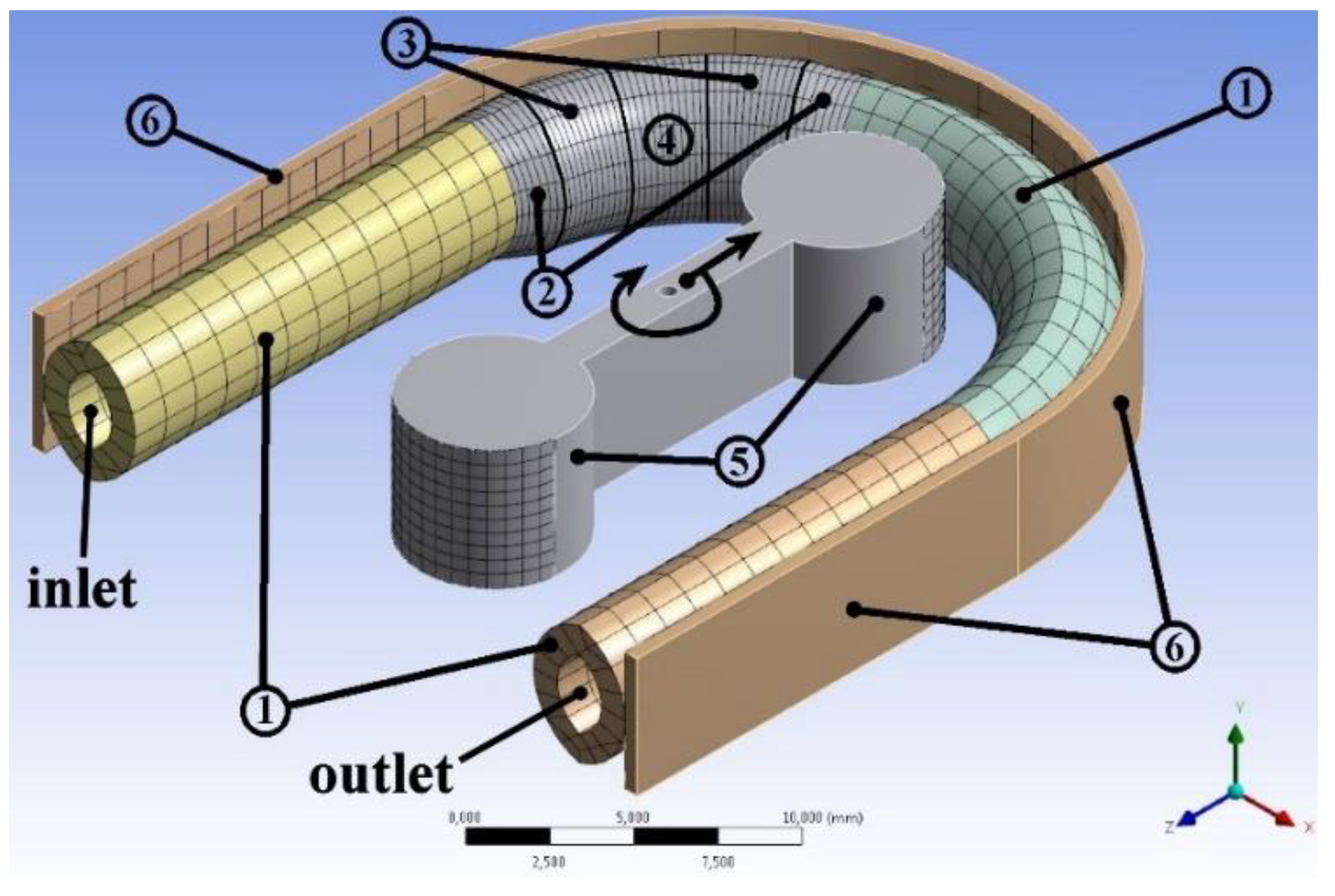
The geometry structure used for the simulations of the roller pump, shown in Figure 1, consists of three main components, the flexible tube, the rollers and the track-wall within the housing on which the tubing is squeezed against. The inflated portion was added on the first half of the curved tube near the inlet side, having everywhere a lenticular cross-section.

The cross-section area of the flexible tube is lenticular in its relaxed state, composed of two mirrored minor circular segments as shown in Figure 2. This shape in a relaxed state is retained for all the four sections of the flexible tube, namely, the non-inflated part, the fully inflated zone and the two transition stages, the first connecting non-inflated parts to the second transition stages and the second connecting the first transition stages to the fully inflated zone.

Table 1. Undeformed geometric dimensions (mm) defining the cross-section of each section of flexible tubing referred to Figure 2.

Sections	Di	Do	di	do	Ri	Ro
Non-inflated parts (nominal)	2.85	4.85	1.85	3.85	1.58	2.58
Fully inflated zone	3.51	5.51	2.45	4.45	1.58	2.58
Between 1st and 2nd transition stages	3.10	5.10	2.15	4.15	1.58	2.58

i: internal dimensions of lumen; o: external dimensions of tubing; d: horizontal distances towards the x-direction; D: vertical distances towards the y-direction (chords); R: radius of arc curvature.

shows the values of the undeformed geometric dimensions defining the cross-sections of each section of flexible tubing. Linear variation within each transition stage applies to the sizes of the distances depicted in Figure 2.

Table 2. Geometric distance parameters (mm) referred to Figure 3.

Wall thickness t	1
Straight distance of non-inflated parts Lt	16
Roller diameter DR	6
Roller center distance LR	15.6
Track-wall radius of curvature RT	12.2

shows the additional geometric value parameters depicted in Figure 3, such as the wall thickness t being the same everywhere, the lengths of non-inflated parts of tubing L_t, the roller diameters D_R and the distance L_R between them and finally the track-wall radius of curvature R_T.

In order to define different case models of the inflated tube geometries, a sequence of six successive angles (φ₁ to φ₆) on the first half of the curved tube could have various dimensions (

Table 3. Angles in degrees for every inflation case designed.

Case #	φ1	φ2 = φ6	φ3 = φ5	φ4	φtot = φ2-φ6
1	10	7	13	10	50
2	10	7	18	5	55
3	1	7	18	19	69
4	1	5	7	45	69
5	No inflation (nominal lenticular cross-section for every position)
6	7	5	9	45	73
7	0	4	6	50	70
8	0	4	6	55	75

). Angle φ₁ denotes the initial curved part that the tube’s cross-section retains the nominal lenticular dimensions. Angle φ₂ is the first transition stage to inflation, while angle φ₃ is the second and it ends up at the maximum fully inflated lenticular cross-section. Angle φ₄ denotes the constant zone with the maximum value of inflated lenticular cross-section, while angles φ₅ and φ₆ have the same values like φ₃ and φ₂, respectively, for restoring inflation to the nominal lenticular cross-section dimensions.

The fluid kinematic viscosity and density used were ν = 1.0541×10⁻⁶ m²/s and ρ = 998.6 Kg/m³, respectively, corresponding to water at 18 °C. This pump is used only for drug delivery infusion and designed to be small in order to be an ambulatory infusion pump. Liquid drugs are water-based thus the consideration of Newtonian fluid is not a simplification. Since the roller pump concerns drug delivery infusion, the flow rates are very low and the fluid flows slowly in a quasi-steady manner. Thus, the Reynolds number varies to only a few hundred and certainly under the limit of the change of the flow status from laminar to turbulent. For this reason, the flow in the present study is simulated as laminar.

A key parameter in the present study is the maximum tube squeeze. Considerable work was done in order to achieve the minimum possible gap. The main source limiting the minimum gap is mesh behavior under high deformations. Tuning dynamic mesh parameters, the maximum squeeze that could be achieved was 1.77 mm of 1.85 mm total inner nominal horizontal distance towards the x-direction (Figure 2). The remaining gap of 0.08 mm is 4.3% of the tube’s inner nominal horizontal distance in the undeformed state. In other studies, the gap is 10% [17], 21.2% [16], and 50% [18]. Other performance parameters are the outlet mass flow rate, the total fluid volume and the discarded volume of fluid remaining for infusion.

In five cases (Cases #1 to #5 of Table 3), the performed FSI simulations provide qualitative results, due to the limitation of a fully compressed tube. These FSI simulations used the mass flow rate as a guideline to reveal in which way to set the inflated portion along the tube length in order to suppress backflow and reduce pulsation in flow rate. Finally, in five more cases (Cases #4 to #8 of Table 3) tuning of the inflation design used (different inflation sizes), performing indirect volume measurements and finding an optimum design between those results tested by the aforementioned approaches of FSI.

2.2. Governing Equations

Solid mechanics is governed by constitutional stress–strain equation of the form:

$$\left\{\sigma \right\}=\left[\mathrm{D}\right]\cdot \left\{{\epsilon }\right\}$$

(1)

where {σ} is the stress vector, [D] is the elastic stiffness matrix or stress–strain matrix and {ε} is the elastic strain vector.

The maximum deformation happens when the tube is compressed deeply under the roller and the distance across the x-direction of double-wall thickness 2t = 2 mm is compressed to R_T-L_R/2-D_R/2 = 1.4 mm subjecting the tube’s wall material to a 30% deformation. This deformation is considered small compared to the one of 100% or even 300% that are mentioned to the standard stress–strain tests. Thus, the elements of elastic stiffness matrix are chosen in a way describing the tube wall material as linear elastic and isotropic with Young modulus E = 1.3 MPa taken from [26] and Poisson’s ratio v = 0.48 taken from [27].

CFD was implemented and the two governing conservation equations are solved. The continuity equation for mass conservation valid for incompressible fluid of one phase flows was used as follows:

$$\mathrm{div}\overrightarrow{\upsilon }=0$$

(2)

where $\overrightarrow{\upsilon }$ is the flow velocity field.

The conservation of momentum equation is described by the Navier–Stokes equations arising by implementation of Newton’s second law to fluid motion and expressing stresses in terms of velocities. For an incompressible fluid of constant viscosity neglecting gravity follows:

$$\frac{\partial \overrightarrow{\upsilon }}{\partial \mathrm{t}}+(\overrightarrow{\upsilon }\cdot \nabla )\overrightarrow{\upsilon }=-\frac{1}{\rho }\nabla \mathrm{p}+{\nu }\mathsf{\Delta }\overrightarrow{\upsilon }$$

(3)

where ρ is the constant density of the fluid, ν = μ/ρ is the kinematic viscosity, μ the dynamic one and p the pressure field.

2.3. Numerical Strategy and Procedure

A critical part for the simulation procedure is the mesh generation, absolutely necessary for a numerical solution. For the current project, both solid and fluid parts needed to be discretized. For mesh generation, the Ansys Workbench Meshing Tool was used. Fluid–Structure Interaction (FSI) numerical simulations were conducted, in order to predict adequately the responses of structural and fluid governing variables. For the analysis to be accurate, the dynamics of both the fluid and the wall structure have been modeled. The FSI is used to describe the bidirectional interaction of the movable or deformable wall structure with the surrounding flow (Figure 4).

Once fluid and solid parts are solved numerically, their discretization is of great importance and especially at their common boundaries, i.e., the interface surface. For the numerical solution, the partitioned staggered approach is used. Fluid and solid are solved sequentially by different solvers and relevant data are exchanged between them. Each part can be meshed separately, with no requirements of conformality. The partitioned approach is further divided into one-way and two-way coupling. In the one-way coupling, data transfer is one-directional, from solid to fluid or from fluid to solid. In the two-way coupling, data transfer is bidirectional. For the needs of this study, the one-way coupling algorithm was implemented, according to which the data transfer is one-directional, from solid to fluid or from fluid to solid. The structural analysis was performed in Ansys Structural module using the Finite Element (FE) method and the converged tube deformation was transferred to the Ansys Fluent, where the fluid dynamics problem was solved using the finite volume CFD method. Data transfers are coordinated by the System Coupling module in the Ansys Workbench. Regarding the structural analysis, the contact between roller and tube was assumed frictionless, while large deflection approximation was also assumed. Timestep varied from 0.01 s to 0.02 s which correspond to the rotation of 1deg for the inflated geometry and 2deg for the non-inflated one per timestep. The pressure-velocity coupling was achieved via the coupled algorithm, while PRESTO! and Second-Order Upwind schemes were used for the spatial discretization of pressure and momentum equations, respectively. The residuals for the continuity and the velocity field equations were set both to 10^–3. Regarding the computational mesh, a sensitivity analysis was conducted for both the structural and fluid domains of the problem. The structured mesh was constructed for walls and rollers and the minimum necessary number of elements was found to be 351 and 281, respectively. Similarly, a structured mesh was implemented for the case of the tube and the included fluid, having a total number of 3636 elements for the tube wall structure and 23,120 ones for the fluid.

3. Results and Discussion

The outlet mass flow rate is a critical quantity and it is monitored in all the studied cases. Its pattern was as illustrated in Figure 5, simulating initially the non-inflated geometry (Case #5), and in Figure 6 simulating the inflated geometries (Cases #1 to #4). The periodical pattern is repeated every 180 degrees. Assuming the rollers oriented across the x-direction in the horizontal position the leading roller (L) is the one on the left side towards the inlet and the trailing (T) the one on the right side towards the outlet (see small icons in Figure 7). When the trailing roller starts detaching from the tube, at 90 degrees, the mass flow rate begins to drop, reaching a minimum value around zero at 120 degrees (Figure 5). Flow rate goes marginally negative and this is the backflow phenomenon which, along with flow rate drop, the current work is aiming to overcome, thus eliminating the pulsation. The flow rate then returns to a steady state only to repeat the same pattern once the trailing roller becomes the leading one.

Results from the geometries with inflation are presented in Figure 6. The mass flow rate on the outlet, on which the interest is focused, is compared for Cases #1 to #4, implemented with FSI simulation. Velocity magnitude contours are shown for Case #3 in Appendix A. In Figure 6, comparing the different mass flow rates, deriving from the different inflated tube geometries, the decrease is reduced when the inflation portion (φ₂-φ₆) and the constant zone (φ₄) of maximum value cross-section become bigger, individually (maximum φ₄ for Case #4) or together (maximum φ₂-φ₆ for both Cases #3 and #4). The minimum mass flow rate is increased; thus, the flow is closer to linear decreasing pulsation. As may be derived from these results, bigger inflation provides the necessary fluid volume so that backflow is surely avoided. A small early decrease is observed for the first two inflated geometries tested (Cases #1 and #2). An explanation of this is the fact that the total inflation is shorted significantly as compared to the other two cases where the inflation extends for five to ten degrees longer (Figure 6).

In the second innovative tube geometry with an inflated portion, the total fluid volume is increased, as well as its distribution over time, compared to the first. The inflated portion remains compressed after the trailing roller is detached from the tube (130 degrees in Figure 7). As a result, the total fluid volume continues to grow as the rollers are rotating up to the φ₆ angle, after which the inflated portion is not compressed anymore. Then, the total volume is steady and repeats the same pattern on the next revolution.

A comparison between the two geometries, with and without inflation, is shown in Figure 7. The discarded volume of fluid remaining for drug infusion is depicted in Figure 7, contained from the leading roller up to the outlet of the flexible tube. Apparently, this fluid volume has to decrease linearly in order for the drug infusion to be steady. Calculations were done on the geometry Cases #4 to #8 and the results are presented in Figure 7. In Case #5 of non-inflated geometry, the discarded volume remaining for infusion after the leading roller seems to remain steady for some time (90 to 130 degrees), before the desired linear decrease for the rest of the time (130 to 180 degrees). This can be explained as follows: as the trailing roller is starting to decompress the tube after 90 degrees, the tube reforms and the local fluid volume grows underneath. At the same time, the leading roller is rotating towards the outlet, decreasing steadily the discarded volume of fluid remaining for the desirable steady infusion. However, the expanded volume under the trailing roller cancels out the desirable steady decrease caused by the rotation of the leading roller and the discarded volume remains relatively constant for some time (90 to 130 degrees) without a steady infusion to the outlet. The identification of the above behavior was critical to the effort of designing a tube that exhibits no backflow, achieving a constant flow rate on the outlet infusion site. Therefore, the efforts were focused on trying to achieve a linear decrease of the discarded volume of fluid remaining for infusion after the leading roller.

In order to identify the case offering linear discarded volume decrease, as already described, different inflation sizes were tested (Cases #4 to #8). The most important finding of the research can be summarized in Figure 7, which reveals that inflation parameter Case #8 seems to be the one giving the closest to linear discarded volume decrease with the magnitude of the pulsed flow to be eliminated. Parameter Case #6 shows some fluctuations around 130 degrees and thus it is not considered as the optimal solution.

4. Conclusions

Firstly, the identification of the problem was done. The flexible tube of a roller pump was studied in terms of Computational Fluid Dynamics and Computational Solid Mechanics. The aim was to design a system capable of suppressing backflow and achieving a linear mass flow rate on the outlet. Thus, the idea of an inflating portion of the tube was incorporated into the design [22,23,24,25]. Two different approaches were used and gradually implemented to complete the evaluation of the designed tube geometries. Every implemented stage was important and contributed to the final results. The first approach, using FSI simulations provided only the direction to the way of suppressing backflow and achieving a linear flow rate, because of their limitation in a deep occluded tube. Among the various FSI cases examined, the optimum (Case #4) is further studied in a second approach and the discarded volume of fluid remaining for infusion after the leading roller is presented for three extra cases (Cases #6, #7 and #8). In this last approach, indirect discarded volume measurements were performed and Case #8 proved to be the optimum design among the other three examined. This optimum design has an inflation portion of 75 degrees covering almost 42% of the curved part of the tube, while it has a constant zone with the maximum value of inflated lenticular cross-section, within the portion, of 55 degrees covering about 73% of the inflation portion. Pulsed flow is greatly reduced in the cases with the bigger inflation portion (Cases #6 to #8) and particularly in cases having the bigger inflation zone with a maximum value of inflated lenticular cross-section (Cases #7 to #8). The last ones provide the necessary fluid volume so the backflow is surely avoided and the pulsation eliminated.