1. Introduction
The square root (
) and reciprocal of the square root (
), also known as the inverse square root, are two relatively common functions used in digital signal processing [
1,
2,
3,
4], and are often found in many computer graphics, multimedia, and scientific applications [
1]. In particular, they are important for data analysis and processing, solving systems of linear equations, computer vision, and object detection tasks. In view of this, most current processors allow the use of the appropriate software (SW) functions and multimedia hardware (HW) instructions in both single (SP) and double (DP) precision.
Let us formalize the problem of calculating the function in floating-point (FP) arithmetic. We consider an input argument to be a normalized -bit value with -bit mantissa, which satisfies the condition . Similarly, for the function , . For many practical applications, where it is assumed that the input data are obtained with some error, e.g., read from sensors, or where computation speed is preferable to accuracy, e.g., in 3D graphics and real-time computer vision, approximate square root calculation may be sufficient. However, on the other side, there is a strong discussion whether the function should be correctly-rounded for all input FP numbers according to the IEEE 754 standard.
Compilers offer a built-in
function for various types of FP data (float, double, and long double) [
5]. Although the common SW implementation of this function provides high accuracy, it is very slow. On the other hand, HW instruction sets are specific to particular processors or microprocessors. Computers and microcontrollers can use HW floating-point units (FPUs) in order to work effectively with FP numbers and for the fast calculation of some standard mathematical functions [
6,
7]. Typically, instructions are available for a square root with SP or DP (float and double), and estimation instructions are available for the reciprocal square root with various accuracies (usually 12 bits in SP, although there are also intrinsics that provide 8, 14, 23, or 28 bits). For example, for SP numbers, Intel SSE HW instruction RSQRTSS has an accuracy of 11.42 bits, Intel AVX instructions VRSQRT14SS and VRSQRT28SS provide 14 and 23.4 correct bits, respectively, and ARM NEON instruction FRSQRTE gives 8.25 correct bits of the result. An overview of the basic characteristics of these instructions on different modern machines can be found in [
8,
9,
10,
11]. However, similar instructions are not available for many low-cost platforms, such as microcontrollers and field-programmable gate arrays (FPGAs) [
12,
13]. For such devices, we require simple and efficient SW/HW methods of approximating square root functions.
Usually, the HW-implemented operation of calculating the square root in FP arithmetic requires 3–10 times more processor cycles than multiplication and addition [
9]. Therefore, for such applications as video games, complex matrix operations, and real-time control systems, these functions may become a bottleneck that hampers application performance. According to the analysis of all CPU performance bottlenecks (the second table in [
14]), the square root calculation function is high on the list and first among the FP operations. As a result, a large number of competing implementations of such algorithms, which make various trade-offs in terms of the accuracy and speed of the approximation, have been developed.
These elementary function algorithms—and especially those for calculating
and
—can be divided into several classes [
2,
15,
16,
17]: digit-recurrence (shift-and-add) methods [
2,
16,
18], iterative methods [
16,
19], polynomial methods [
4,
16,
17,
20], rational methods [
16], table-based methods [
2,
21,
22,
23], bit-manipulation techniques [
24,
25,
26], and their combinations.
Digit-recurrence, table-based, and bit-manipulation methods have the advantage of using only simple and fast operations, such as addition/subtraction, bit shift, and table lookup. Compared to polynomial and iterative methods, they are therefore more suitable for implementation on devices without HW FP multiplication support (e.g., calculators, some microcontrollers, and FPGAs). However, since digit-recurrence algorithms have linear convergence, they are very slow in terms of SW implementation. Tabular methods are very fast but require a large area (memory), since the size of the table grows exponentially with an increase in the precision required. This may pose a problem not only for small devices such as microcontrollers, but also to a lesser extent for FPGAs. The use of direct lookup tables (LUTs) is less practical than combining several smaller LUTs with addition and multiplication operations. Bit-manipulation techniques are fast in both HW and SW, but have very limited accuracy—about 5–6 bits [
15]. They are based on the peculiarities of the in-memory binary representation formats of integer and FP numbers.
In computer systems with fast HW multiplication instructions, iterative and polynomial methods can be efficient. Iterative approaches such as Newton–Raphson (NR) and Goldschmidt’s method have quadratic convergence but require a good initial approximation—in general, polynomial, table-based, or bit-manipulation techniques are used. Polynomial methods of high order rely heavily on multiplications and need to store polynomial coefficients in memory; they also require a range reduction step. This makes them less suitable for the calculation of and than iterative methods, especially for HW implementation. Compared to the polynomial method, a rational approximation is not efficient if there is no fast FP division operation; however, for some elementary functions, it can give more accurate results, e.g., the and functions.
Most existing research studies on calculating the and functions have focused on the HW implementation in FPGAs. They use LUTs or polynomial approximation, and if more accurate results are required, iterative methods are subsequently applied. In this paper, we consider a modification of a bit-manipulation technique called the fast inverse square root (FISR) method for the approximate calculation of these functions with high accuracy, without using large LUTs or divisions. This work proposes a novel approach that combines the FISR method and a modified NR method and uses two different magic constants for an initial approximation depending on the input subinterval. On each of the two subintervals, such values of the magic constants should be chosen that minimize the maximum relative error after the first iteration. This can be considered a fairly accurate and fast initial approximation for other iterative methods such as NR or modified NR. This method can be effectively implemented on microcontrollers and FPGAs that support FP calculations in HW. However, in this paper, we focus mostly on the fast SW implementation of the method, in particular on microcontrollers. In a HW implementation, a kind of tiny 1-bit LUT can be used to determine a magic constant and two other parameters of the basic algorithm.
Among the better-known methods of calculating the square root and reciprocal square root [
1,
2,
15,
20], the FISR method [
20,
25,
26,
27,
28,
29] has recently gained increasing popularity in SW [
8,
20,
27,
29,
30,
31,
32] and HW [
3,
33,
34,
35,
36,
37] applications. The algorithm was proposed for the first time in [
24] but gained wider popularity through its use in the computer game Quake III Arena [
27]. Its attraction lies in its very simple and rapid way of obtaining a fairly accurate initial approximation of the function
—almost 5 bits—without using multiplications or a LUT. It uses integer subtraction and bit shifting, and combines these with switching between two different ways of interpreting the binary data: as an FP or an integer number. In addition, fewer hardware resources are used when this is implemented with an FPGA.
We denote by an integer that has the same binary representation as an FP number and by an FP number that has the same binary representation as an integer . The main idea behind FISR is as follows. If the FP number , given in the IEEE 754 standard, is represented as an integer , then it can be considered a coarse, biased, and scaled approximation of the binary logarithm . This integer is divided by two, its sign is changed, and it is then translated into the IEEE 754 format as an FP number with the same binary representation . The method introduces a magic constant to take into account the bias and reduce the approximation error. This gives an initial approximation for the function , which is then further refined with the help of NR iterations.
The NR method is the most commonly used iterative method; it is characterized by a quadratic convergence rate and has the property of self-correcting errors [
19]. Quadratic convergence in an iterative method means that the method roughly doubles the number of exact bits in the result after each iteration. If we apply the NR method directly to find the square root, we obtain the formula known as Heron’s formula. The disadvantage of this approach is the need to perform an FP division operation at each iteration, which is rather complex and has high latency [
1,
9,
18]. An alternative way of calculating the square root is to use the NR method to find the root of the equation
for a function
This formula has the form:
Using this approach, it is necessary to multiply the final result of the iteration method in Equation (1) by to get the approximate square root of the input number . The main feature of iterative methods is the need to select an initial value ; as a rule, the better this initial approximation, the lower the number of subsequent iterations needed to obtain the required accuracy for the calculations. However, we will show later that this is not always the case.
The purpose of this paper is to present a modified FISR method based on the switching of magic constants. This method is characterized by increased accuracy of calculations—13.71 correct bits after the first iteration—with low overhead compared to the known FISR-based approximation algorithms described below in
Section 2. We also provide the code for the corresponding optimized algorithms for calculating the square root and reciprocal square root, which use this method for the initial approximation. These algorithms work for normalized single- and double-precision numbers in the IEEE 754 format and provide different accuracy depending on the number of iterations used.
Functions that comply with the IEEE 754 standard—assuming that the chosen rounding mode is round-to-nearest—return the FP value that is closest to the exact result (the error is less than 0.5 units in the last place, or ulp). By contrast, the proposed method allows a numerical error of the algorithms for the float and double types to be obtained that does not exceed the least significant bit (1 ulp) when using the fused multiply–add function.
The rest of the paper is organized as follows:
Section 2 introduces the well-known FISR-based algorithms and basic theoretical concepts of the FISR method. In
Section 3, the main idea of the proposed method of switching magic constants is presented, and the corresponding algorithms are given.
Section 4 contains the experimental results on microcontrollers and a discussion. Finally, the conclusions are presented in
Section 5.
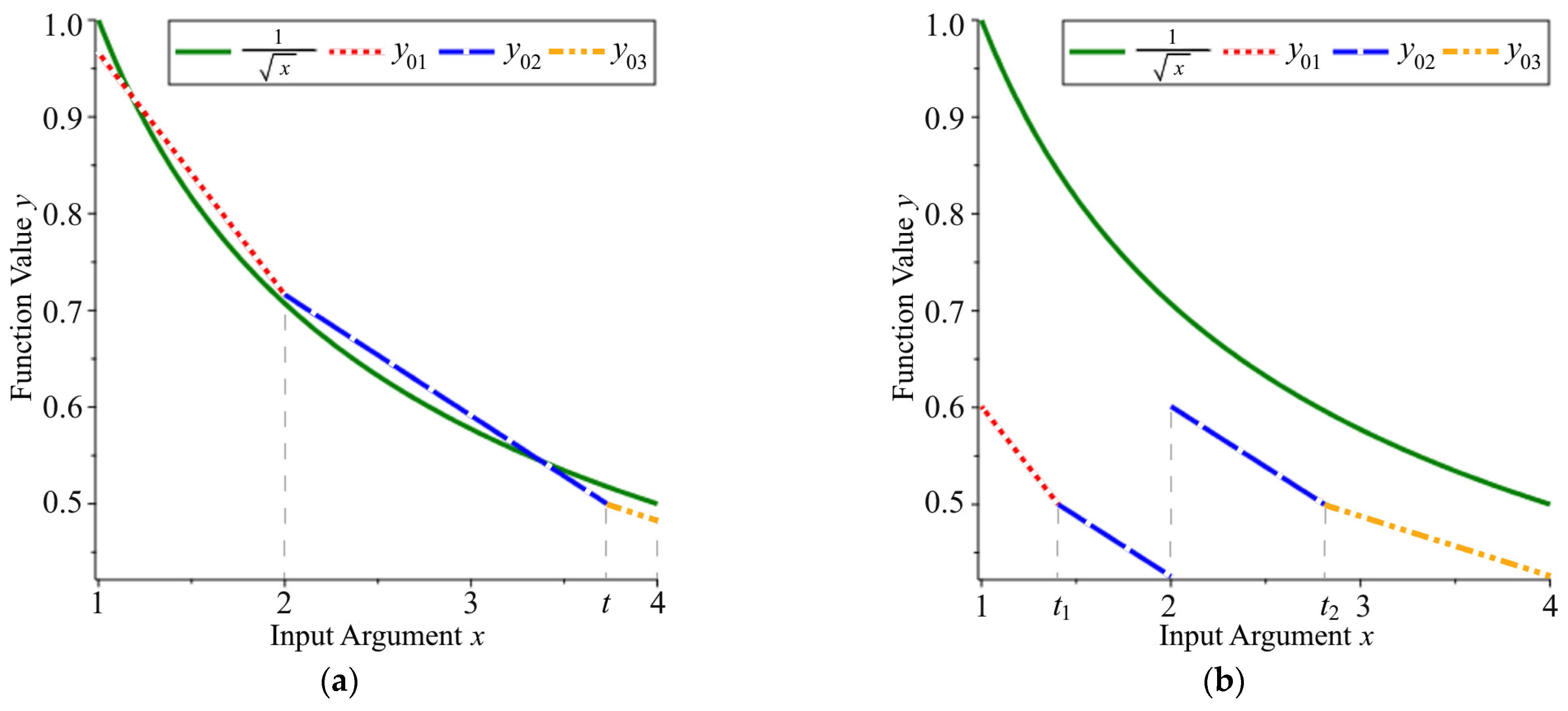
3. Method of Switching Magic Constants
The main idea of the proposed method is to split the interval
of the initial approximation
(see
Figure 1a), on which it has different error values, into two parts—
and
—and to perform an approximation of the reciprocal square root function separately in these subintervals. The variable
, as defined in Equation (2), then has different values in the last bit of the exponent
—zero in the first case and one in the second. We split the interval only for the initial approximation
—where the magic constant
is used—and for the corresponding modified first iteration of the FISR method. As shown below, this technique allows us to reduce the maximum relative error of the algorithm after the first iteration by an order of magnitude compared to Algorithm 2 (
RcpSqrt2).
Let us now consider this method in more detail. We require that, on the first and second parts of the interval
, the relative errors of two adjacent piecewise linear initial approximations
and
have the same scope—the same difference between the maximum and minimum values—as shown in
Figure 2a. From this, it follows that the relative errors of the approximations
,
and
,
have a similar symmetrical nature with respect to some common value at a point
. We will now find the value of the magic constant that gives the corresponding equations for
and
. To do this, we write the analytical equations for the approximations
and
based on Equations (9)–(13) and the results of [
28,
29]:
where, in this case,
Note also that the third linear approximation, which is not used in the result, has the form
Hence, the expressions for the relative errors are
Having found the points of maxima and contact, we can determine the value of
:
and the corresponding value of the magic constant
for SP numbers:
Let us now examine the interval
. In the same way, we require that, for the second and third parts, the relative errors of two adjacent piecewise linear initial approximations
and
have the same scope (see
Figure 2b). In this case,
Note that, at the same time,
and the first linear approximation, not relevant for the result, has the form:
As a result, the combined approach with magic constants
, (21), and
, (27), on two different subintervals gives us an opportunity to obtain the piecewise linear initial approximation
on the interval
, as shown in
Figure 1b. This can potentially offer a better approximation of the function
, but only after some alignment (bias at each subinterval). For comparison, both of the magic constants used in the algorithms
RcpSqrt1 and
RcpSqrt2 give the initial approximation, as described in Equations (9)–(13) (see
Figure 1a). Although the basic FISR method gives a much more accurate approximation at this stage, our method has four piecewise linear sections of the approximation
rather than three, providing higher accuracy after the first iteration (see
Figure 3). This trick is possible due to the modification of the first NR iteration at each of the subintervals. In other words, we align the corresponding errors of the initial approximation as described below.
For each subinterval, we modify the first NR iteration according to Equation (1) as follows:
where
and
are some FP constants that minimize the maximum relative error of the algorithm and depend on the value of the magic constant
. This modified iteration also involves four multiplications.
In order to determine the subinterval in the IEEE 754 format to which
belongs—
or
—we check the least significant bit (LSB) of the biased exponent
In the SW implementation, we apply a bit mask to . Then, we choose the magic constant and the first modified NR iteration that correspond to this value. We call this technique the method of switching magic constants or the dynamic constants (DC) method.
It should be noted that this method can be generalized to more constants. In this case, each of the indicated subintervals is further divided into two, four, eight, etc., equal parts depending on the value of one or more most significant bits of the fractional part of the mantissa , and the bit mask is changed accordingly. However, in general, it cannot be guaranteed that such a partition will significantly improve the accuracy of the algorithm in all the parts; therefore, some parts should be divided further.
The general structure of the proposed SW
RcpSqrt3 algorithms for two magic constants, with the modified FISR initial approximation
, the first modified iteration (28), and a branching statement (comparison with zero) using bit masking (bitwise AND), is shown in Template 1. Here, the input argument
has type
<fp_type>, which can be float, double, etc., and
<int_type> is the corresponding integer type. The names of the algorithms for the reciprocal square root are constructed according to the template, as follows:
RcpSqrt3<iter><version><fp_type_abbr>, where
<iter> is the number of iterations used in the algorithm,
<version> is an optional index, and
<fp_type_abbr> indicates the required FP data type. This also applies to the square root calculation algorithms, which we denote as
Sqrt3. The parameters
and
are integer magic constants;
,
,
, and
are FP constants, which are defined later. When implemented in HW, in this case, a small 1-bit LUT can be used to choose appropriate values for the parameters
,
, and
.
| Template 1. Basic structure of the proposed DC algorithms for the reciprocal square root. |
1: <fp_type> RcpSqrt3<iter><version><fp_type_abbr> [
<int_type> , <int_type> ,
<fp_type> , <fp_type> ,
<fp_type> , <fp_type> ] (<fp_type> x) |
| 2: { |
| 3: <int_type> i = *(<int_type>*)&x; // x—input argument |
| 4: <int_type> k = i & <ex_mask>; // binary mask on the LSB of |
| 5: <fp_type> y; |
| 6: if (k != 0) { |
| 7: i = – (i >> 1); //—first magic constant |
| 8: y = *(<fp_type>*)&i; // approximation |
| 9: y = *y*( – x*y*y); // first modified NR iteration |
| 10: } else { |
| 11: i = –(i >> 1); //—second magic constant |
| 12: y = *(<fp_type>*)&i; // approximation |
| 13: y = *y*( – x*y*y); // first modified NR iteration |
| 14: } // DC initial approximation |
| 15: … // subsequent NR or modified NR iterations |
| 16: return y; // output |
| 17: } |
The proposed method can be thought of as a relatively accurate and fast initial guess —the DC initial approximation—for other iterative algorithms (see Template 1, lines 14–16). In this paper, we consider modified NR iterations written in a special form, with combined multiply–add operations.
Furthermore, in this section, we present final (ready-to-use) codes for the proposed algorithms in C/C++ and give their errors (accuracy results).
Note that—when determining the relative errors of these algorithms—giving here an example for the reciprocal square root function—we used the following notation for the upper and lower limits of the maximum relative error, respectively:
Alternatively, without taking into account the sign of the error, the maximum relative error was determined using the formula
To iterate over all possible float values in the interval
, we used the
function from the
cmath library. For the case of type double, we traversed this interval with a small step—about
. As a reference implementation, we used a higher-precision
or
function from this library. The number of accurate digits in the result—accuracy of the algorithm—was determined in bits by the formula
Error measurements for the algorithms were performed on a quad-core Intel Core i7-7700HQ processor using a GNU compiler (GCC 4.9.2) for C++ on a Windows 10 (64-bit) operating system with options as follows: -std = c++11 -Os -ffp-contract = on -mfma.
3.1. SP Reciprocal Square Root (RcpSqrt3 for Float)
3.1.1. One Iteration—The DC Initial Approximation
For the interval
and the theoretically determined magic constant for SP
, (21), the unknown theoretical coefficients
and
in Equation (28) that minimize the maximum relative error
after the first iteration are
Similarly, for
and the magic constant
, (27),
An implementation of the algorithm with these parameters shows the maxima of the relative errors
If a computing platform has a fast HW or SW implementation of the fused multiply–add (
) function,
, then in Template 1, iteration (28) can be written as
On some platforms, when implemented in HW, this function can increase both the speed and the accuracy of the algorithms. The operation has fewer roundings and much higher precision for the internal calculations. In the remainder of this section, unless otherwise specified, we use the function in all algorithms.
Taking into account the rounding errors and the issue of the best practical representation of the theoretical parameters in the target SP FP format, we can improve our theoretical parameters
,
,
,
,
, and
(given in (21), (27), (34), (35)). A brute force optimization method was used in a certain neighborhood of the defined theoretical parameters to minimize the maximum relative error of the algorithm on each of the subintervals. This approach also includes elements of randomized multidimensional greedy optimization for coarse search. In this case, three parameters
,
, and
are optimized simultaneously. The method is described in more detail in [
38].
Algorithm 3 below gives the proposed improved
RcpSqrt31f algorithm for SP numbers with one iteration. This algorithm provides slightly lower values for the maximum relative errors:
| Algorithm 3. Proposed RcpSqrt31f algorithm (DC initial approximation). |
| 1: float RcpSqrt31f (float x) |
| 2: { |
| 3: int i = *(int*)&x; |
| 4: int k = i & 0x00800000; |
| 5: float y; |
| 6: if (k != 0) { |
| 7: i = 0x5ed9e91f – (i >> 1); |
| 8: y = *(float*)&i; |
| 9: y = 2.33124256f*y*fmaf(−x, y*y, 1.0749737f); |
| 10: } else { |
| 11: i = 0x5f19e8fc – (i >> 1); |
| 12: y = *(float*)&i; |
| 13: y = 0.824218631f*y*fmaf(−x, y*y, 2.1499474f); |
| 14: } |
| 15: return y; |
| 16: } |
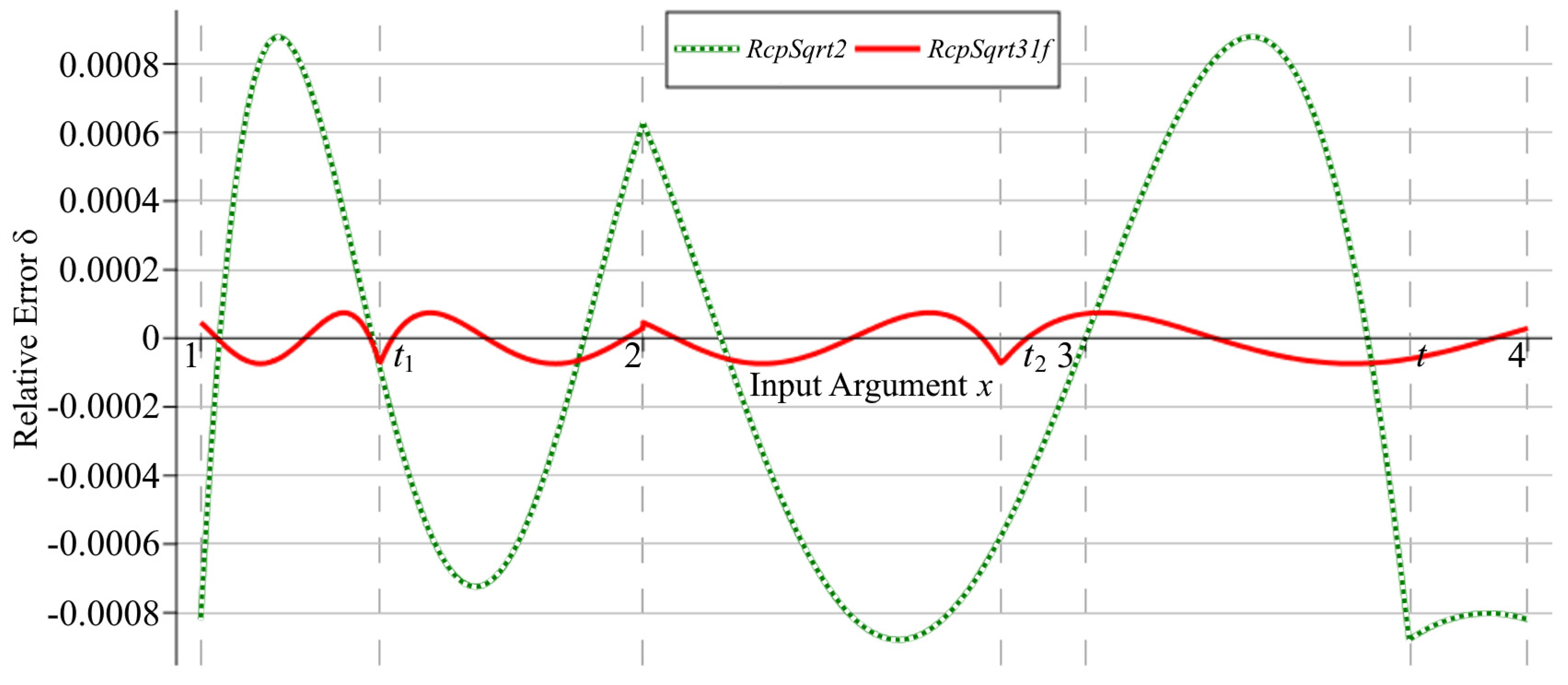
Graphs of the relative errors of the
RcpSqrt2 and
RcpSqrt31f algorithms after the first iteration are shown in
Figure 3. Numerical experiments show that the maximum relative error of the
RcpSqrt2 algorithm after the first iteration is
, corresponding to 10.15 correct bits of the result, and, for our algorithm, from (38),
, providing 13.71 correct bits. Consequently, the error is reduced by a factor of more than 11.7.
3.1.2. Two Iterations
To increase the accuracy of the
RcpSqrt31f algorithm described above, it is possible to apply an additional NR iteration over the entire range
. The second iteration is common to both subintervals, uses the
function, and has the specific form
where, in this case, for the SP version,
which corresponds to the classical Equation (1). The use of the
function in the second iteration in the form given in (39) is important, since it greatly improves the accuracy of the algorithm at the final stage of the calculations. However, compared to the
RcpSqrt1 and
RcpSqrt2 algorithms, it has four multiplications rather than three in the second iteration (a further addition is also hidden inside
). If we write the second iteration in the same way as in Equation (37), we only get 22.68 bits of accuracy (
). A full C/C++ code for two NR iterations is given in Algorithm 4. Here, we also make some corrections to the values of
,
,
,
,
, and
(given in (21), (27), (34), (35)) to minimize the maximum errors of the complete
RcpSqrt32f algorithm, in a similar way to the approach described in
Section 3.1.1. An alternative would be to modify the values of
and
, although this is less effective for type float.
| Algorithm 4. Proposed RcpSqrt32f algorithm. |
| 1: float RcpSqrt32f (float x) |
| 2: { |
3: float y = RcpSqrt31f [
= 0x5ed9dbc6, = 0x5f19d200,
= 2.33124018f, = 1.07497406f,
= 0.824212492f, = 2.14996147f] (x); |
| 4: float c = x*y; |
| 5: float r = fmaf(y, −c, 1.0f); |
| 6: y = fmaf(0.5f*y, r, y); |
| 7: return y; |
| 8: } |
The final
RcpSqrt32f algorithm has errors
or 23.62 correct bits of the result out of a possible
for float numbers. Note that, when this algorithm has the same constants for the initial approximation as in Algorithm 3—
RcpSqrt31f plus classic NR in the form given in (39), (40)—it has an error
.
3.2. SP Square Root (Sqrt3 for Float)
We now turn to the square root calculation algorithms to find an approximation for
in SP. As noted in
Section 1, these algorithms can easily be obtained from those previously described, simply by multiplying the result by the value of the input argument
. However, this involves an additional multiplication operation, and in our algorithms, in most cases, this can be avoided by modifying the last iteration.
3.2.1. One Iteration—The DC Initial Approximation
For one iteration, we make a substitution
in Equation (37). Then, the first iteration for the square root at each subinterval is written as
Algorithm 5 provides the final code for
Sqrt31f with optimized constants. After the first iteration, the algorithm has errors
and hence it has the same level of error as the
RcpSqrt31f algorithm. In addition, in Algorithm 5, the same constants can be used as in
RcpSqrt31f (
).
| Algorithm 5. Proposed Sqrt31f algorithm (DC initial approximation). |
| 1: float Sqrt31f (float x) |
| 2: { |
| 3: int i = *(int*)&x; |
| 4: int k = i & 0x00800000; |
| 5: float y; |
| 6: if (k != 0) { |
| 7: i = 0x5ed9e893 – (i >> 1); |
| 8: y = *(float*)&i; |
| 9: float c = x*y; |
| 10: y = 2.33130789f*c*fmaf(y, −c, 1.07495356f); |
| 11: } else { |
| 12: i = 0x5f19e8fd – (i >> 1); |
| 13: y = *(float*)&i; |
| 14: float c = x*y; |
| 15: y = 0.82421863f*c*fmaf(y, −c, 2.1499474f); |
| 16: } |
| 17: return y; |
| 18: } |
3.2.2. Two Iterations
When we use two NR iterations to calculate the square root function (
Sqrt32f), the structure of the algorithm does not change compared to
RcpSqrt32f, and we need only modify the second iteration (see Algorithm 6, line 6). This algorithm has slightly lower accuracy than
RcpSqrt32f, with
This corresponds to 23.4 exact bits—
, if we do not change the constants of the DC initial approximation, i.e., the
RcpSqrt31f algorithm.
| Algorithm 6. Proposed Sqrt32f algorithm. |
| 1: float Sqrt32f (float x) |
| 2: { |
3: float y = RcpSqrt31f [
= 0x5ed9d098, = 0x5f19d352,
= 2.33139729f, = 1.07492042f,
= 0.82420468f, = 2.14996147f] (x); |
| 4: float c = x*y; |
| 5: float r = fmaf(y, −c, 1.0f); |
| 6: y = fmaf(0.5f*c, r, c); // modified |
| 7: return y; |
| 8: } |
3.3. DP Reciprocal Square Root (RcpSqrt3 for Double)
3.3.1. One Iteration—The DC Initial Approximation
Similarly, this method can be applied to FP numbers of DP. In this case, the theoretically determined magic constants based on (20) and (26) are
The overall structure of the algorithm does not change (see Template 1), and only the data types used in the calculations are modified compared to the
RcpSqrt31f algorithm. The corresponding algorithm for DP is given in Algorithm 7. Here, the parameters
,
,
,
,
, and
are 64-bit constants after optimization. Note that the specified improved constants can be quite different from the theoretical ones according to the practical optimization method used. This has the following aligned maxima in the relative errors:
corresponding to an accuracy of 13.71 bits.
| Algorithm 7. Proposed RcpSqrt31d algorithm (DC initial approximation). |
| 1: double RcpSqrt31d (double x) |
| 2: { |
| 3: uint64_t i = *(uint64_t*)&x; |
| 4: uint64_t k = i & 0x0010000000000000; |
| 5: double y; |
| 6: if (k != 0) { |
| 7: i = 0x5fdb3d20982e5432 – (i >> 1); |
| 8: y = *(double*)&i; |
| 9: y = 2.331242396766632*y*fma(−x, y*y, 1.074973693828754); |
| 10: } else { |
| 11: i = 0x5fe33d209e450c1b – (i >> 1); |
| 12: y = *(double*)&i; |
| 13: y = 0.824218612684476826*y*fma(−x, y*y, 2.14994745900706619); |
| 14: } |
| 15: return y; |
| 16: } |
3.3.2. Two Iterations
The
RcpSqrt32d algorithm for finding the DP reciprocal square root with two iterations is shown in Algorithm 8. Note that, here, we use the same constants for the DC initial approximation as in the
RcpSqrt31d algorithm. This algorithm has a second iteration in the form of (39), with changes in the following two constants:
The maximum relative errors of this algorithm are
(27.84 correct bits), in contrast to
for SP numbers (see (41)). The modification of the last NR iteration in the form (39), (48) allows us to increase the accuracy of the algorithm from 26.84 bits in the case of a classic iteration to 27.84 bits.
| Algorithm 8. Proposed RcpSqrt32d algorithm. |
| 1: double RcpSqrt32d (double x) |
| 2: { |
| 3: double y = RcpSqrt31d (x); |
| 4: double c = x*y; |
| 5: double r = fma(y, −c, 1.000000008298416); |
| 6: y = fma(0.50000000057372*y, r, y); |
| 7: return y; |
| 8: } |
3.3.3. Three Iterations
For three iterations in DP, we present two versions of the algorithm: one with fewer multiplication operations (
RcpSqrt331d) and one with higher accuracy (
RcpSqrt332d). The complete
RcpSqrt331d algorithm is given in Algorithm 9. The errors of this algorithm have the following boundaries:
(52.28 correct bits). Here, we have made the substitution
(line 4) in a similar way as in
RcpSqrt1 and
RcpSqrt2. This allows us to avoid one multiplication and also to use that substitution in classic or modified NR iterations. In this case, the second and third iterations have the following form:
where
If we do not change the initial approximation constants in Algorithm 9—
RcpSqrt31d plus modified and classic NR iterations in the form (51)–(53)—we obtain 52.23 bits of accuracy (
).
| Algorithm 9. Proposed RcpSqrt331d (faster) algorithm. |
| 1: double RcpSqrt331d (double x) |
| 2: { |
3: double y = RcpSqrt31d [
= 0x5fdb3d14170034b6, = 0x5fe33d18a2b9ef5f,
= 2.33124735553421569, = 1.07497362654295614,
= 0.82421942523718461, = 2.1499494964450325] (x); |
| 4: double mxhalf = −0.5*x; |
| 5: y = y*fma(mxhalf, y*y, 1.5000000034937999); |
| 6: double r = fma(mxhalf, y*y, 0.5); |
| 7: y = fma(y, r, y); |
| 8: return y; |
| 9: } |
On the other hand, if we do not make this substitution and write the last iteration using
, we obtain an algorithm
RcpSqrt332d that contains one more multiplication and an additional coefficient in the last iteration. In this case, the last two iterations of the algorithm are (see Algorithm 10, lines 4–7)
where
Compared to
RcpSqrt331d, the
RcpSqrt332d algorithm has lower maximum relative errors after the third iteration,
(52.47 exact bits). Note that the other alternatives to this algorithm—
RcpSqrt31d plus two modified NR in the form (54)–(56) and
RcpSqrt32d plus classic NR in the form given in (55), where
—are slightly less accurate (52.44 correct bits).
| Algorithm 10. Proposed RcpSqrt332d (higher accuracy) algorithm. |
| 1: double RcpSqrt332d (double x) |
| 2: { |
3: double y = RcpSqrt31d [
= 0x5fdb3d15bd0ca57e, = 0x5fe33d190934572f,
= 2.3312432409377752, = 1.0749736243940957,
= 0.824218531163110613, = 2.1499488934465218] (x); |
| 4: y = y*fma(−0.5000000000724769*x, y*y, 1.50000000394948985); |
| 5: double c = x*y; |
| 6: double r = fma(y, −c, 1.0); |
| 7: y = fma(0.50000000001394973*y, r, y); |
| 8: return y; |
| 9: } |
3.4. DP Square Root (Sqrt3 for Double)
3.4.1. One and Two Iterations
In the same way as for the type float and reciprocal square root, we construct algorithms for the square root in DP using one and two iterations. These are based on the RcpSqrt31d and RcpSqrt32d algorithms. The errors of these algorithms are close to those of the reciprocal square root (see (47) and (49)).
3.4.2. Three Iterations
For the algorithm with three iterations, we cannot avoid the additional multiplication, as we did in the
RcpSqrt331d algorithm described above. Hence, we present only an algorithm that has four multiplications in the third iteration—including
operations. It is based on
RcpSqrt332d, in which the last iteration (55) is modified for the square root calculation, and the corresponding parameters are optimized, as shown in Algorithm 11. After the third iteration, this algorithm has errors of
(52.27 correct bits). If we do not modify the constants of the DC initial approximation in Algorithm 11, the accuracy is 52.25 bits. The algorithm based on
RcpSqrt32d—
RcpSqrt32d plus a modified for the square root version of the classic NR iteration in a special form—has 52.23 bits of accuracy.
| Algorithm 11. Proposed Sqrt33d algorithm. |
| 1: double Sqrt33d (double x) |
| 2: { |
3: double y = RcpSqrt31d [
= 0x5fdb3d20dba7bd3c, = 0x5fe33d165ce48760,
= 2.3312471012384104, = 1.074974060752685,
= 0.82421918338542632, = 2.1499482562039667] (x); |
| 4: y = y*fma(−0.50000000010988821*x, y*y, 1.5000000038700285); |
| 5: double c = x*y; |
| 6: double r = fma(y, −c, 1.0); |
| 7: y = fma(0.50000000001104072*c, r, c); // modified |
| 8: return y; |
| 9: } |
4. Experimental Results and Discussion
Performance testing of these algorithms was conducted on a Raspberry Pi 3 Model B mini-computer and an ESP-WROOM-32 microcontroller. The Raspberry Pi is based on a quad-core 64-bit SoC Broadcom BCM2837 (1.2 GHz, 1 Gb RAM) with an ARM Cortex-A53 processor [
6]. We used the GNU compiler (GCC 6.3.0) for Raspbian OS (32-bit) with the following compilation options:
-std = c++11 -Os -ffp-contract = on -mfpu = neon-fp-armv8 -mcpu = cortex-a53. The 32-bit Wi-Fi module ESP-WROOM-32 (ESP-32) from Espressif Systems has two low-power Xtensa microprocessors (240 MHz, 520 Kb RAM) [
39]. The microcontroller was programmed via the Arduino IDE (GCC 5.2.0) with the following compilation parameters:
-std = gnu++11 -Os -ffp-contract = fast. The speed (latency) of the algorithms was measured using the
chrono C++ library. Depending on the platform, at least 200 tests were run in which functions were called sequentially in a single thread (core), a million or more times. The average results of these performance tests are given here.
It should be noted that, although we chose C++ to implement the algorithms, it is worth using an inline assembly code for more efficient and better performance optimization on each specific platform. However, the chosen compilation options gave a fairly effective fast code optimization and allowed us to automatically translate the and C++ functions into the corresponding HW instructions; for the microcontroller, the compiler may even automatically replace successive multiplication and addition/subtraction operations of SP with the corresponding HW instructions (the -ffp-contract = fast option, which enables FP expression contraction).
The accuracy and latency measurements for the reciprocal square root (
) and square root (
) functions, in both SP and DP, are summarized in
Table 1. In this table, we consider the various methods available on the mini-computer and microcontroller, including the
cmath SW library functions (
and
) [
5] and the built-in NEON instructions (FRSQRTE and FRSQRTS) [
11] for an approximate calculation of the reciprocal square root in Raspberry Pi using NR iterations. We also compare the method of Walczyk et al. (the
RcpSqrt2 algorithm) [
29], its modification for calculation of the square root, and the proposed method of switching magic constants (the DC algorithms from
Section 3). Here, both the Walczyk et al. and the DC algorithms are implemented using the
function.
Even on platforms that do not have special HW instructions for the square root and reciprocal square root (either approximate or with full accuracy), such as ESP-32, the C++ function
is available for both SP and DP numbers. Modern platforms, such as Intel or ARM, may also have the appropriate hardware FSQRT instructions. These are IEEE-compliant and ensure the full accuracy of the result (see the
and
functions in
Table 1).
Looking at the results from
Table 1, it becomes obvious that the main feature of our proposed DC algorithms for the float and double types is that the algorithms
RcpSqrt32f,
Sqrt32f,
RcpSqrt331d,
RcpSqrt332d, and
Sqrt33d allow the result to be obtained up to the last bit—although the 24th and 53rd bits may be wrong. At the same time, the
RcpSqrt32f and
RcpSqrt332d algorithms for the reciprocal square root have somewhat higher accuracy than the naive method using division.
All the platforms tested have HW-implemented multiplication, addition, and
operations for FP numbers of SP and, except for ESP-32, DP [
10,
11,
12]. Since the ESP microcontroller is a 32-bit system, all DP operations are performed by SW. Note that it also does not have a division instruction in SP [
12], meaning that the latency of the corresponding operations is much higher.
As shown in
Table 1, the proposed algorithms give significantly better performance than the library functions on the Raspberry Pi, from 3.17 to 3.62 times faster, and for SP numbers on ESP-32, 2.34 times faster for the reciprocal square root and approximately 1.78 times faster than the
function. At the same time, on the microcontroller with the SW implementation of DP
, the
RcpSqrt331d algorithm is a little faster than the naive method using the
function, but has slightly lower accuracy. The
RcpSqrt332d algorithm, in contrast, has higher accuracy, but worse performance. The proposed algorithms are also not efficient on ESP-32 for calculating the square root of DP numbers (in contrast to the Raspberry Pi). However, in some cases, it is possible to improve the performance of the algorithms in DP if fewer
functions are used in the code, as shown later (see also [
26] for more details).
In ARM with NEON technology [
11], the HW SP instructions FRSQRTE and FRSQRTS, for which the corresponding intrinsics are
and
, can be used to calculate a fast approximation of the reciprocal square root function and to perform the classical NR iteration (step), respectively. The FRSQRTE instruction is based on a LUT and gives 8.25 correct bits of the result (our DC initial approximation gives 13.71 bits). A combination of these instructions in the Raspberry Pi gives poorer accuracy and latency results than the
RcpSqrt32f algorithm (see
Table 1). It should also be noted that the HW FSQRT and 64-bit FRSQRTE instructions of the ARMv8 (AArch64) architecture are not available on the Raspberry Pi for the specified official 32-bit OS [
11].
In order to ensure a fair comparison between the proposed algorithms and other advanced FISR-based methods, we also implemented an algorithm proposed by Walczyk et al. [
29] in a specific form using the
functions. This allowed us to strike a better compromise between accuracy and speed compared to the original
RcpSqrt2 algorithm (see
Table 1). For the square root calculation, we used the same method that we suggest for the DC algorithms. The results show that, although these algorithms are faster, their accuracy is much lower.
A comparison of the FISR-based algorithms that also provide 23 exact bits for a float and 52 exact bits for a double is given in
Table 2 for SP numbers. Note that, here, TMC denotes the method of two magic constants [
26] and Ho2 denotes the approach based on the second-order Householder’s method [
32] for the reciprocal square root. The relative performance of the proposed algorithms depends on the operations used, their sequence, and the characteristics of the platform. For example, the
RcpSqrt32f (Algorithm 4) and
InvSqrt5 [
32] (Section VI) algorithms are fairly efficient on ESP-32 for SP numbers. However, to the best of our knowledge, the DC initial approximation is the only FISR-based method with one NR iteration—four multiplications and one subtraction—that provides 13 correct bits of the result for the square root and reciprocal square root functions. It can be implemented on FPGAs using a small LUT, and only one bit of the input argument (LSB of the exponent) needs to be controlled.
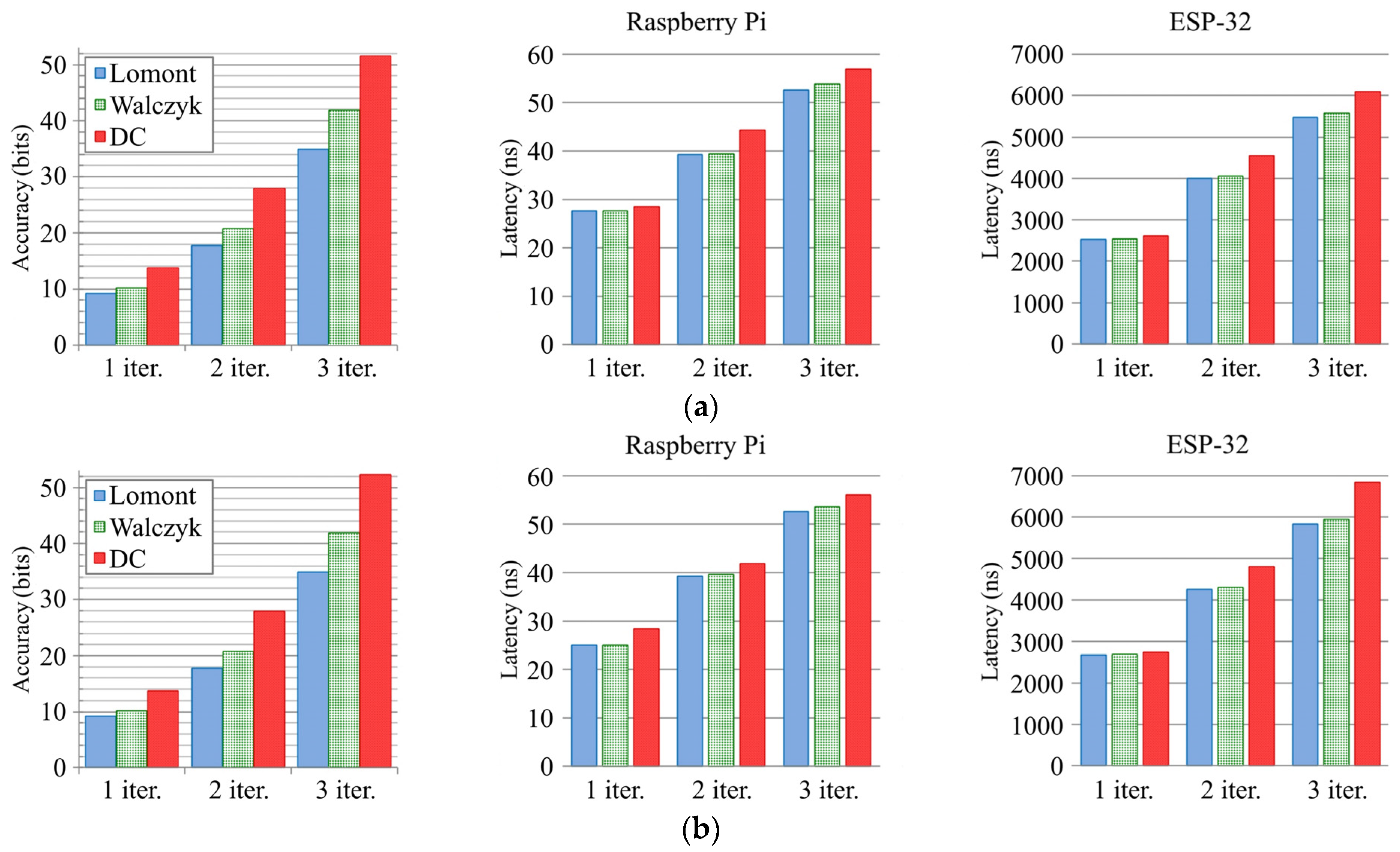
Figure 4 shows the results of a comparison of the Lomont [
8,
25], Walczyk et al. [
29], and switching magic constants (DC) methods after each iteration for DP numbers—with and without the use of the
operations. Here, we consider different ways of implementing NR iterations using the
functions. As shown by the graphs, the accuracy is almost the same in both cases, with the sole exception of three iterations. The proposed DC algorithm (
RcpSqrt331d), in most cases, has slower performance on the platforms considered here than the Lomont and Walczyk et al. algorithms (except perhaps one iteration), but is significantly superior in terms of accuracy. It allows us to obtain highly accurate results for the square root and reciprocal square root calculations for DP numbers by the third iteration. Note that, when the
function is used, we obtain 52.28 correct bits of the result (see
RcpSqrt331d in
Table 1), and, otherwise, we have an accuracy of 51.52 bits (see
Figure 4a). For the Raspberry Pi, the latency of the algorithms with and without
is similar, but is slightly smaller for some algorithms when using the
function (after the first and second iterations). We obtain similar performance results for the ESP-32 microcontroller. The latency of all the algorithms is almost the same for one iteration. However, given the above comments on HW support for FP operations of DP, it should be noted that the algorithms that do not use
are faster in this case.
Figure 4 shows that the speed of the DC algorithm for three iterations is 6092.1 ns without
and 6828.2 ns with SW
functions. For ESP-32, we recommend using the DP
function only in the third iteration of the DC algorithms, in order to obtain a better compromise between accuracy and speed.
It should also be noted that the disadvantages of the FISR methods and the approximate FRSQRTE instructions in comparison with the
cmath library functions and fast HW FSQRT instructions are that they generally do not work correctly with subnormal numbers and do not handle other exceptional situations (e.g.,
and
), although this does not apply to numbers in the NaN (not a number) range. However, as described in [
29], FISR-based methods can be modified to support subnormal numbers.