Electrostatic Circular Membrane MEMS: An Approach to the Optimal Control
Abstract
1. Introduction
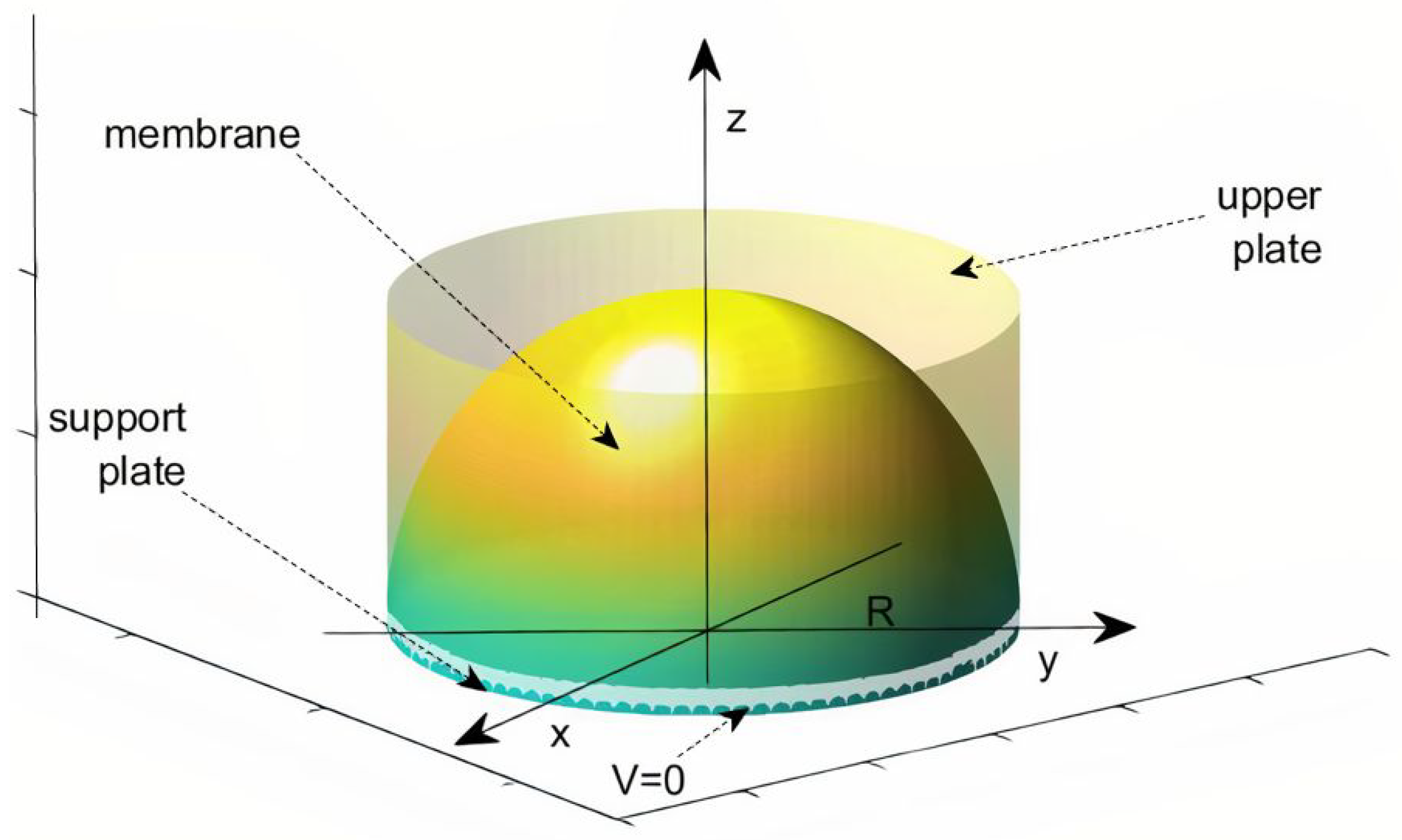
2. A Description of the 2d Electrostatic Membrane Mems Device and Previous Works
3. Critical Points and Stability
3.1. A More Suitable Writing of the Model under Study: Search for Critical Points
3.2. On the Stability of the Critical Point
On the Stability of the Starting Non-Linear System
4. Voltage V and Its Admissible Values
4.1. to Win the Mechanical Inertia of the Membrane
4.2. The Maximum Value of V, , in Order That the Membrane Does Not Touch the Upper Disk
4.3. & : An Interesting Relationship
5. Some Optimal Control Conditions
5.1. About the Values of V Maximizing .
5.2. A Useful Limitation for Achieved Starting from
6. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MEMS | Micro-Electro-Mechanical System |
| Electrostatic Field | |
| amplitude of the Electrostatic Field | |
| r | Radial Coordinate |
| Mean Curvature | |
| Membrane Profile | |
| V | External Voltage |
| Safetyl Distance | |
| Electrostatic Pressure | |
| R | Radius |
| Permittivity of the Free Space | |
| d | Distance Between the Disks |
| Electrostatic Force | |
| , , , | Parameters Related to the Material |
| Parameter Concerning the Electromechanical Properties of the Membrane | |
| T | Mechanical Tension of the Membrane at Rest |
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 4
Appendix A.5. Proof of Proposition 5
Appendix A.6. Proof of Proposition 6
Appendix A.7. Proof of Proposition 7
Appendix A.8. Proof of Proposition 8
Appendix A.9. Proof of Proposition 9
Appendix A.10. Proof of Proposition 10
Appendix A.11. Proof of Proposition 11
References
- Pelesko, J.A. Modeling MEMS and NEMS; Chapman & Hall/CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2003. [Google Scholar]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. In Handbook of Research on Advanced Mechatronic Systems and Intelligent Robotics; IGI Global: Hershey, PA, USA, 2007; pp. 139–175. [Google Scholar]
- Li, P.; Fang, Y.; Hu, R. Thermoelatic damping in rectangular and circular microplate resonators. J. Sounds Vib. 2012, 331, 721–733. [Google Scholar] [CrossRef]
- Maity, R.; Maity, N.P.; Baishya, S. Circular Membrane Approximation Model with Effect of the Fitness of the Electrode’s Diameter of MEMS Capacitive Micromachined Ultrasonic Transducer. Mycrosyst. Technol. 2017, 23, 3513–3521. [Google Scholar] [CrossRef]
- Sun, D.; Bohringer, K.F. Self-cleaning: From bio-inspired surface modification to MEMS/microfluidics system integration. Micromachines 2019, 10, 101. [Google Scholar] [CrossRef]
- Narita, F.; Shindo, Y.; Karaiwa, M. Electroelastic fields concentrations and polarization switchinng by circular electrodes in piezoelectric disk compositem. In Proceedings of the XXI ICTAM, Warsaw, Poland, 15–21 August 2004; pp. 15–21. [Google Scholar]
- Zhao, S.; Erturk, A. Electroelastic modeling and experimental validations of piezoelectric energy harvesting from broadband random vibrations of cantilevered biomorphs. Smart Mater. Struct. 2013, 22, 12–24. [Google Scholar] [CrossRef]
- Vogl, G.W.; Nayfeh, A.H. A reduced-order model for electrically actuated clamped circular plates. J. Micromech. Microeng. 2005, 15, 37033. [Google Scholar] [CrossRef]
- Jallouli, A.; Kacem, N.; Lardies, J. Investigations of the effects of geometric imperfections on the nonlinear static and dynamic behavior of capacitive micromachined ultrasonic transducers. Micromachines 2018, 9, 575. [Google Scholar] [CrossRef]
- Vogl, G.W.; Nayfeh, A.H. Primary resonance excitation of electrically actuated clamped circular plates. Nonlinear Dyn. 2007, 47, 181–192. [Google Scholar] [CrossRef]
- Jallouli, A.; Kacem, N.; Najar, F.; Bourbon, G.; Lardies, J. Modeling and experimental charactterization of squeeze film effect in nonlinear capacitive circular microplates. Mech. Syst. Signal Process. 2019, 127, 68–88. [Google Scholar] [CrossRef]
- Mahnama, A.; Nourbakhsh, A.; Ghorbaniasl, G. A Survey on the Applications of Implantable Micropump Systems in Drug Delivery; Current Drug Delivery; Bentham Science Publishers: Sharjah, United Arab Emirates, 2014. [Google Scholar]
- Lee, H.J.; Choi, N.; Yoon, E.S.; Kunal, P. MEMS Devices for Drug Delivery; Current Drug Delivery, Advanced Drug Delivery Reviews; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Velosa-Moncada, L.A.; Aguilera-Cortés, L.A.; González-Palacios, M.A.; Raskin, J.P.; Herrera-May, A.L. Design of a novel MEMS microgripper with rotatory electrostatic comb-drive actuators for biomedical applications. Sensors 2018, 18, 1664. [Google Scholar] [CrossRef]
- Haque, M.A.; Espinosa, H.D.; Lee, H.J. MEMS fro in situ testing-handlingm actuation, loading, and dispacement measurements. Mrs Bull. 2010, 35, 375–381. [Google Scholar] [CrossRef]
- Pitchappa, P.; Manjappa, M.; Ho, C.P.; Singh, R.; Singh, N.; Lee, C. Active control of electromagnetically induced transparency analog in terahertz MEMS metamaterial. Adv. Opt. Mater. 2016, 4, 54–68. [Google Scholar] [CrossRef]
- Quakad, H. Electrostatitc fringing-fields effects on the structural behavior of MEMS shallow arches. Microsyst. Technol. 2018, 24, 1391–1399. [Google Scholar]
- Kepper, J.H.; Claus, B.C.; Kinsey, J.C. A navigation solution using a MEMS IMU, model-based dead-reckoning, and one-way-travel-time acousting range measurements for autonomous underwater vehicles. IEEE J. Ocean. Eng. 2018, 44, 664–682. [Google Scholar] [CrossRef]
- Tao, K.; Tang, L.; Wu, J.; Lye, S.W.; Chang, H.; Miao, J. Investigation of multimodal electret-based MEMS energy harvester with impact-induced nonlinearity. J. Microelectromech. Syst. 2018, 27, 276–288. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. A 2D Non-linear second-order differential model for electrostatic circular membrane MEMS devices: A result fo existence and uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for reconstructing the membrane profile in absence of ghost solutions. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Versaci, M.; Di Barba, P.; Morabito, F.C. Curvature-dependent electrostatic field as a principle for modelling membrane-based MEMS devices. A review. Membranes 2020, 10, 36. [Google Scholar] [CrossRef]
- Jonassen, N. Electrostatics; Springer Science + Business Media: New York, NY, USA, 2002. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Dean, D.S.; Dobnikar, J.; Naji, A.; Podgornik, R. (Eds.) Electrostatics of Soft and Disordered Matter; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Cassani, D.; Fattorusso, L.; Tarsia, A. A non-local dynamic problem with singular nonlinearities and application to MEMS. Prog. Nonlinear Differ. Equ. Appl. 2014, 85, 185–206. [Google Scholar]
- Cassani, D.; Ghoussoub, N. On a fourth order elliptic problem with a singular nonlinearity. Adv. Nonlinear Stud. 2009, 9, 177–197. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, A.; Jannelli, A. Recovering of the membrane profile of an electrostatic circular MEMS by a three-stage Lobatto procedure: A convergence analysis in the absence of ghost solutions. Mathematics 2020, 8, 487. [Google Scholar] [CrossRef]
- Tu, L.W. Differential Geometry: Connections, Curvature, and Characteristic Classes; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Katok, A. Introduction to Model Theory of Dynamical Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Petersen, P. Linear Algebra; Springer: New York, NY, USA, 2012. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Versaci, M.; Morabito, F.C. Electrostatic Circular Membrane MEMS: An Approach to the Optimal Control. Computation 2021, 9, 41. https://doi.org/10.3390/computation9040041
Versaci M, Morabito FC. Electrostatic Circular Membrane MEMS: An Approach to the Optimal Control. Computation. 2021; 9(4):41. https://doi.org/10.3390/computation9040041
Chicago/Turabian StyleVersaci, Mario, and Francesco Carlo Morabito. 2021. "Electrostatic Circular Membrane MEMS: An Approach to the Optimal Control" Computation 9, no. 4: 41. https://doi.org/10.3390/computation9040041
APA StyleVersaci, M., & Morabito, F. C. (2021). Electrostatic Circular Membrane MEMS: An Approach to the Optimal Control. Computation, 9(4), 41. https://doi.org/10.3390/computation9040041






