1. Introduction
The terahertz (THz) frequency range lies in the microwave and infrared wavelength ranges of the electromagnetic spectrum, showing potential applications in the practical fields of spectral analysis, imaging, homeland security detection, and high-speed wireless communication (in the range of several hundred Gbit s
−1) [
1,
2,
3,
4,
5,
6,
7,
8]. But to further substantial development of THz science and technology, there is a high demand for well-performing functional waveguide devices and components. Because of relatively long wavelengths and the scarcity of natural materials that interact strongly with THz waves, the manipulation of THz waves is still a challenging task. Artificially designed subwavelength unit cells (meta-molecules) [
9] and the emergence of metamaterials (MMs) were capable of exotic properties and helpful to overcome this dilemma [
10,
11,
12]. Presently, the key disadvantages of plasmonic and MM devices were a lack of tunability of the resonant frequency and large distillation losses. Two-dimensional (2D) materials, such as black phosphorus, transition metal molybdenum disulfide, topological insulators (Bi
2Ti
3), and graphene [
13,
14,
15,
16], provided good alternatives for the exploration of novel flexible functional devices. Especially, with the merits of large carrier mobility and its strong interaction with light and pattern structures, as well as versatile tenability [
17,
18,
19,
20,
21,
22], graphene membrane attracted significant interest and have been functionalized as a playground to design novel plasmonic MM devices [
23,
24,
25,
26].
Graphene surface plasmons, i.e., the collective oscillations of free Dirac charge carriers coupled to electromagnetic fields, stimulated the propagation modes with extreme subwavelength confinement and relatively larger propagation lengths [
27,
28,
29]. Recently, much research work was devoted to exploring graphene devices, e.g., optical modulators, photo-detectors, antennas, and biosensors [
30,
31,
32]. On the base of the hetero-structures of graphene/h-BN/metal, Lundeberg et al. experimentally investigated the tunable nonlocal quantum effects in graphene plasmonic systems by using the near-field imaging experimental systems [
33]. Because the conductivity and plasmonic properties of the graphene layer were closely associated with phonon scattering, some research has been carried out to investigate their effects on device performances. For instance, by using the graphene nanoribbons, Yan et al. experimentally studied the damping mechanisms of graphene plasmons, indicating that the plasmon lifetime and quality factors were limited by the optical phonons and surface polar phonons in the polar substrate layer [
1]. Including the effects of acoustic (AC) phonon scattering, impurity phonon scattering and substrate phonons scattering, Low et al. compared the dispersion and propagation properties of the plasmon polaritons on the hetero-structures of 2D thin membrane/dielectric layers, which manifested good mode confinement and a better figure of merits than those of metal thin layers [
16]. Based on the split ring resonators (SRRs) structure, Shen et al. discussed the scattering time and resistance on the graphene MM structure, displaying that if the dissipation losses were large, the low frequency inductance-capacitance (LC) resonance was very weak, but due to the large kinetic inductance of the graphene layer, the high frequency electric dipolar resonance was strong [
34]. By exploiting the near-field imaging technique, the dispersion and damping properties of graphene membrane were investigated on the base of the graphene/
h-BN structure, revealing that the damping losses of graphene surface plasmons (SPs) were closely depended on the thermal phonons in graphene and
h-BN substrates [
35].
In most of the published articles about tunable graphene functional devices [
1,
29,
30,
31,
32], the graphene conductivities were obtained on assumption that the scattering rate was a constant, which was phenomenological in nature and not involved the microscopic origin of phonon scattering. This constant scattering rate model failed to provide adequate accuracy in the presence of inelastic scattering processes. There was a large difference between the experiments and simulation results. For instance, in References [
29,
30] the resonant curves of the experimental results were broader than those of the simulation results, possibly coming from the fact that phonon scatterings were not taken into account. Actually, besides Fermi levels and temperatures, the graphene conductivities were also closely related to phonon scatterings, which reduced the carrier motilities, just like most of the semiconductors [
36,
37,
38]. As an interesting research topic, to investigate the phonon scatterings and relaxation losses of a graphene layer was fundamentally important to study the tunable mechanisms. Regretfully, there were little reports in this aspect. Therefore, the scattering mechanisms of different kinds of phonon scatterings, such as acoustic (AC) phonon, impurity and longitudinal optical (LO) phonon scatterings are discussed. Additionally, as examples, the effects of phonon scatterings on the tunable properties of graphene MM structures are also discussed. The results manifested that, at room temperature, the AC phonon scattering dominated the conductivity, while LO phonon scattering increased drastically with temperature and Fermi level, and played a dominating role above 600 K. For the graphene pattern structures, if the effects of phonon scatterings were considered, the resonant properties showed a peak with the increase in Fermi level. The
Supplementary File shows the fabrication, transfer, and characterization of graphene metamaterials structures.
3. Results and Discussion
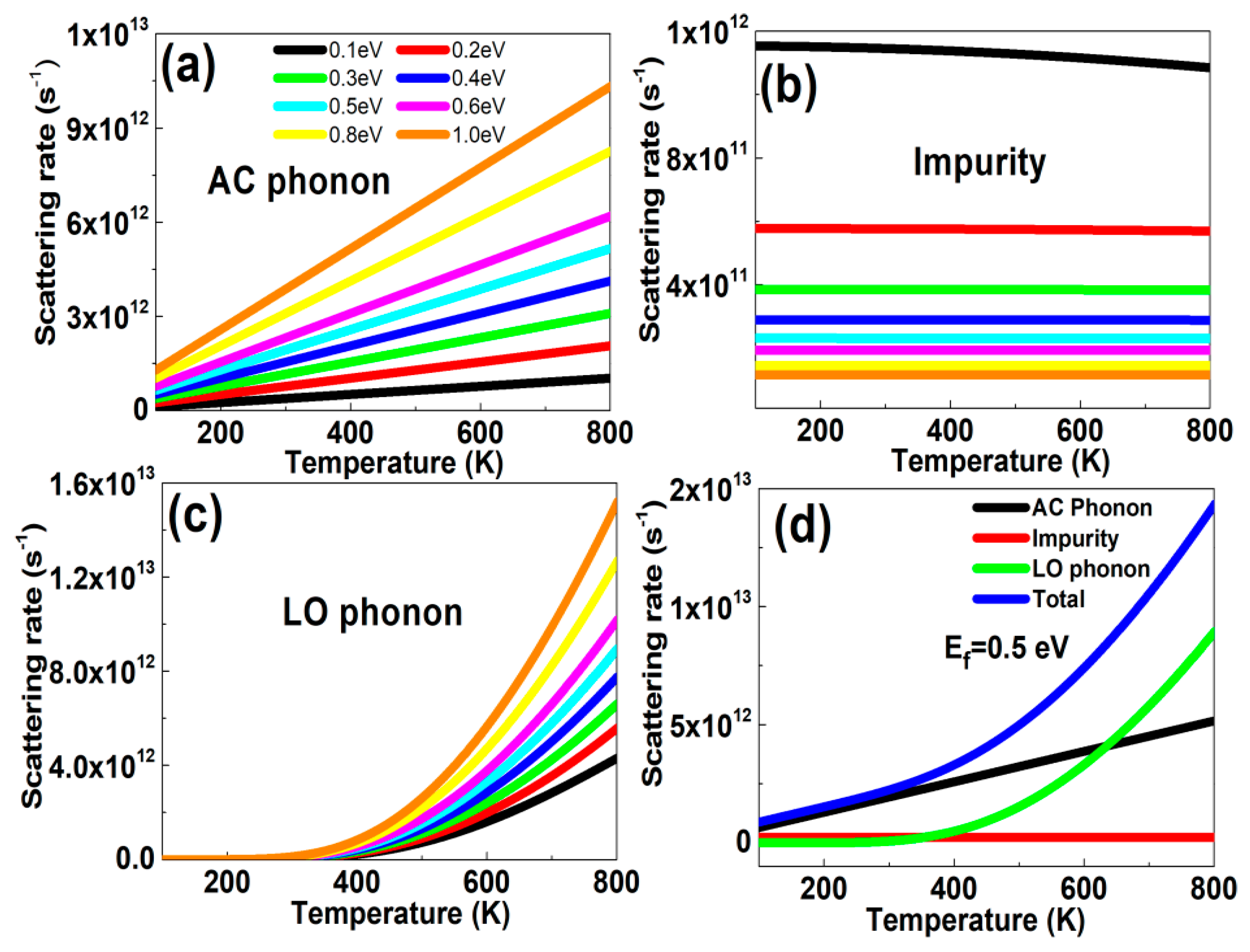
Phonons, i.e., the quanta of crystal lattice vibrations, affected the electrical and optical properties of the graphene layer significantly. For instance, in semiconductors, acoustic and optical phonons limited electron mobility and determined their optical response. The main scattering mechanisms of the graphene layer included the collisions of electrons with acoustic phonons (AC), LO phonons and impurity. The AC phonon scattering came from the interactions of electrons with lattice vibrations, representing all atoms in a unit cell moving in the same direction with a small phase difference. The low-energy AC phonon scattering can be treated under elastic scattering approximation. As temperature increased, the influences of AC phonon scattering increased linearly with temperature, as give in Equation (6), which has also been confirmed by supported and suspend graphene samples. For example, if the Fermi level was 0.5 eV, when the temperatures were 300, 500 and 800 K, the AC phonon scattering rates were 1.935 × 10
12, 3.225 × 10
12, and 5.160 × 10
12, respectively.
Figure 1a also illustrates the AC phonon scattering rates increased with Fermi level. For example, at a temperature of 500 K, the scattering rates were 6.450 × 10
11, 1.290 × 10
12, 3.225 × 10
12, and 6.450 × 10
12 when the Fermi levels were 0.1 eV, 0.2 eV, 0.5 eV, and 1.0 eV, respectively. The influences of impurity scattering can be found in
Figure 1b, which varied slowly with temperature. The doping concentrations increased with the Fermi level and the carrier screening effects were enhanced, reducing the impurity scattering rates. The results for the LO phonon scattering rates as a function of temperature can be found in
Figure 1c. As temperature increased, the LO phonon scattering rates increased, especially at high temperature. For example, if the Fermi level was 1.0 eV, when the temperatures were 300, 500, and 800 K, the scattering rates were 1.251 × 10
11, 2.632 × 10
12, and 1.530 × 10
13, respectively. Additionally, with the increase in Fermi level, the density of states increased and provided much more phase space for phonon scatterings, which resulted into the scattering rates increasing. For instance, at a temperature of 500 K, the scattering rates were 7.272 × 10
11, 9.076 × 10
11, 1.528 × 10
12, and 2.614 × 10
12 when the Fermi levels were 0.1 eV, 0.2 eV, 0.5 eV, and 1.0 eV, respectively. Thus, the scattering time reduced more significantly at a larger Fermi level (>0.8 eV), resulting in the graphene conductivity reducing. This was different from the results that the scattering time was constant, in which the graphene conductivity increased with Fermi level monotonously. The total scattering rates were associated with AC phonon scattering, impurity scattering, and LO phonon scattering, which was summarized in
Figure 1d. The graphene Fermi level was 0.5 eV. At
T = 300 K the scattering rates of AC phonon, impurity, LO phonon and total scatterings were 1.935 × 10
12, 2.308 × 10
11, 7.312 × 10
10, and 2.239 × 10
12, respectively. This implied that electrons interacted much more strongly with AC phonons, which dominated at room temperature. For the LO phonon scattering, it increased with temperature drastically and played the dominant role at higher temperature was beyond 600 K. For example, at
T = 800 K, the scattering rates of AC phonon, impurity, LO phonons and total scatterings were 5.160 × 10
12, 2.304 × 10
11, 9.042 × 10
12, and 1.443 × 10
13, respectively.
To compare the simulation results obtained from Model I (the scattering time was a constant) and Model II (including the effects of phonon scatterings), we gave the simulation results of the electric split ring resonators (eSRRs) graphene patterns, as shown in
Figure 2. The structure parameters were shown in the following,
lx =
ly = 36 μm,
g = 6 μm,
w = 8 μm, and
T = 18 μm. The polarization was along the
y direction.
Figure 2b shows the transmission curves of the eSRRs graphene patterns. For Model I, i.e., the relaxation time
τ was a constant and 0.5
ps in the manuscript. If the Fermi level was low, e.g.,
Ef = 0.1 eV, only dipolar resonances appeared. As the Fermi level increased, the graphene conductivity and permittivity were enhanced, the dynamic kinetic decreased, the dipolar resonance became stronger, and the resonant dip indicated a blue shift. For instance, when the Fermi level changed in the range of 0.1–1.0 eV, the resonant frequency can be modulated in the range of 1.451–2.308 THz, and the transmission dip varied in the range of 0.2988–0.0053. Correspondingly, the frequency and amplitude modulation depths were 37.15% and 98.23%, respectively. Next, we discussed the case of Model II, i.e., the effects of phonon scattering were taken into account. For the high frequency dipolar resonance, the resonant strength increased with Fermi level. But because the effects of AC and LO phonon scatterings dominated when the carrier concentration were large enough, the resonant strength of transmission curves showed a peak at an optimum Fermi level (in the range 0.5–0.8 eV). When the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency can be tailored in the range 1.213–2.263 THz, and the transmission dip modulated in the range 0.01346–0.09844. Correspondingly, the frequency and amplitude modulation depths (MD) were 46.40% and 73.19%, respectively. The strongest resonant curves appeared at the Fermi level of 0.8 eV. This was quite different from Model I, in which the resonances increased with the Fermi level monotonously.
Figure 2c shows the reflection curves versus frequency. If the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency of reflection curves was modulated in the range 1.325–2.288 THz, and the reflection peak was tuned in the range 0.2272–0.8633. Correspondingly, the frequency and amplitude MDs were 42.08% and 73.68%, respectively. In Model II, because at a large Fermi level the influences of AC and LO phonon scatterings increased, the resonant strength reduced. For instance, when the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency can be tuned in the range 1.189–2.190 THz, and the reflection peak modulated in the range 0.4768–0.7878. The frequency and amplitude modulation depths were 45.72% and 39.48%, respectively. In addition,
Figure 2d shows the simulation results for the absorption curves. When the Fermi level changed in the range 0.1–1.0 eV, the frequency and amplitude modulation depths were 63.53% and 70.23%, respectively. While in Model II, if the effects of phonon scattering were taken into account, the resonant strength shrunk at larger Fermi levels due to the AC and LO phonon scatterings. For instance, when the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency can be tuned in the range 1.252–2.820 THz, and the absorption peak modulated in the scope of 0.2194–0.4746. Correspondingly, the frequency and amplitude modulation depths were 55.61% and 53.77%, respectively. From the above discussions, we can come to the points that if the phonon scatterings were taken into account, the tunable properties of graphene MMs decreased. Finally, it was known to us that graphene plasmons were classified into center waveguide plasmons and edge plasmons. For the large area of 2D graphene patterns (which means that a graphene sheet is infinite in extent), waveguide plasmons dominated, whose fields concentrated within the center area. When the width of a graphene ribbon was reduced to a few tens of nanometers, the waveguide mode disappeared and only the edge modes were left. For our proposed subwavelength THz graphene patterns, the structural parameters were relatively large, in the range of tens of micrometers, and the effects of edge property were not very significant and can be omitted.
Figure 3 shows the simulation results of the graphene MM cross patterns. The top view of the graphene cross ribbon structures can be found in
Figure 3a. The periodic lengths along
x and
y directions were
px and
py with the values of 72 μm. The length and width of cross graphene patterns were 48 μm and 8 μm, respectively. The polarization was along the
y direction.
Figure 3b is the transmission response curves versus frequency. The Fermi levels were 0.1, 0.5, and 1.0 eV, respectively. For Model I, the value of conductivity and graphene permittivity increased with the Fermi level, and the graphene indicated a strong transmission response. For instance, when the Fermi level changed in the range 0.2–1.0 eV, the resonant frequency modulated in the range 1.349–1.860 THz, and the transmission dip can be tuned in the range 0.4791–0.02665. Correspondingly, the frequency and amplitude MDs were 27.47% and 94.44%. If the LO phonon and impurity scatterings were taken into account in Model II, the scattering procession was inelastic, which meant that the relaxation time of the carrier was also related to mobility and the Fermi level. If the
Ef was low, the relaxation time was relatively larger, leading to higher graphene conductivity and permittivity. As the Fermi level increased, the relaxation time increased. But if the Fermi level increased further, the scattering of AC phonon and LO phonons enhanced, resulting in the relaxation time decreasing. When the Fermi level was 0.5 eV, the resonant strength was the strongest. The strongest resonant dip was not coinciding with the largest Fermi level, different from the results obtained from the original Model I. The resonant properties showed a peak with the increase in Fermi level, the optimum value of
Ef was about 0.5–0.8 eV. In this case, when the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency modulated in the range 1.164–1.836 THz, and the transmission dip can be tuned in the scope of 0.2173–0.02351. Correspondingly, the frequency and amplitude modulation depths were 36.60% and 89.18%, respectively.
Figure 3c shows the reflection resonant curves for cross graphene patterns. In Model I, if the Fermi level changed in the range 0.2–1.0 eV, the frequency and amplitude modulation depths were 33.68% and 82.74%, respectively. While if the phonon scattering rates were taken into account, as the Fermi level increased, the graphene conductivity and permittivity showed a peak because the AC and LO phonon scattering increased at larger Fermi levels. In this case the reflection peak value showed a maximum at 0.8 eV. When the Fermi level changed in the range 0.1–1.0 eV, the resonant frequency can be changed in the range 1.132–1.790 THz, and the reflection peak modulated in the range 0.2985–0.6077. Correspondingly, the frequency modulation depth was 36.75%, while the amplitude modulation depth was 50.88%. The simulation results for the absorption curves can be found in
Figure 3d. At large Fermi levels, e.g., 1.0 eV, because the AC and LO phonon scatterings increased drastically, the results obtained from Model II was larger than those acquired from the more conventional Model I.
Figure 4 illustrates the influences of Fermi levels on the resonant curves of graphene cut wire. The stripe length and width were 48 μm and 8 μm, respectively. The periodic lengths along
x and
y directions were both 72 μm. It can be found from
Figure 4a that for the symmetric graphene ribbon structure, an obvious resonant dip was observed, resulting from the dipolar resonances. With the graphene Fermi level increased, the resonant strength became stronger, and the resonant peak shifted to a larger frequency, i.e., blue shift. In Model I, if the values of
Ef were 0.2, 0.5, and 1.0 eV, the resonant frequencies were 1.315, 1.619, and 1.791 THz, and the values of resonant dips were 0.4936, 0.1266, and 0.02555, respectively. Accordingly, the frequency and amplitude modulation depths were 26.58% and 94.82%. On the other hand, in Model II, if the phonon scattering was taken into account, when the
Ef changed in the range 0.1–1.0 eV, the frequency and amplitude modulation depths were 21.16% and 35.45%, respectively. Usually the tunable properties of graphene MM structures reduced if the phonon scattering was included. Another point should be noted was that with the increase of Fermi level, the resonant curve became stronger and sharper with a large value of
Q-factor. For instance, In Model I, if the graphene Fermi levels were 0.1, 0.2, 0.5, and 1.0 eV, the
Q-factors of resonant curves were 1.334, 1.591, 2.514, and 2.940. The values of FOM were 0.05021, 0.5831, 1.936, and 2.693, respectively. On the other hand, for the case of Model II, if the graphene Fermi levels were 0.1, 0.2, 0.5, and 1.0 eV, the
Q-factors of resonant curves were 2.748, 2.909, 2.835, 2.718, and the values of FOM were 1.945, 2.426, 2.487, and 2.314, respectively. As Fermi level increased, the graphene layer showed better plasmonic properties, but at the same time, the dissipation losses also improved. Consequently, the value of the
Q-factor and FOM showed a peak.
The plasmonic induced transparency (PIT) phenomenon can be obtained by breaking the structural symmetry or subwavelength-scale coupling.
Figure 5 illustrates the influences of an asymmetrical degree on the resonant curves of graphene cut wire patterns. The graphene Fermi levels were 0.1, 0.5, and 1.0 eV, respectively. The asymmetrical degree δ was δ =
L2 −
L1. The stripe length and width were 96 μm and 8 μm, respectively. The periodic lengths along
x and
y directions were both 108 μm. It can be found from
Figure 5a that for the asymmetric graphene stripe structure, i.e., the length of the upper section was smaller than that of the bottom section, an obvious peak was observed. With the graphene Fermi level increased, Fano resonance strength became stronger, and the resonant peak shifted larger frequency, i.e., blue shift. In Model I, the values of
Ef were 0.2, 0.5, and 1.0 eV, the resonant frequencies were 1.696, 1.728, and 1.728 THz, and the values of Fano resonant peaks were 0.8163, 0.8778, and 0.9036, respectively. On the other hand, for the case of Model II, the phonon scattering was taken into consideration, and if the values of
Ef were 0.2, 0.5, and 1.0 eV, the resonant frequencies were 1.678, 1.717, and 1.735 THz, and the values of Fano resonant peaks were 0.9072, 0.9010, and 0.8881, respectively.
Figure 5b shows that a novel peak appeared in the reflection curves because of Fano resonance, which also increased with the graphene Fermi level. The effects of the graphene Fermi level on the absorption curves can also be found in
Figure 5c, indicating a novel resonant peak near the Fano resonance. Another point to be noted was that with the increase in Fermi level, the Fano resonant curve became stronger and sharper with a large
Q-factor value. For instance, if phonon scattering was taken into account in Model II, when the graphene Fermi levels were 0.1, 0.5, and 1.0 eV, the
Q-factors of the resonant curves were 3.113, 7.291, and 6.112, and the values of FOM were 1.005, 5.264, and 4.247, respectively. As the Fermi level increased, the graphene layer showed better plasmonic properties, the carrier concentration also increased, and the dissipation losses improved. Consequently, the values of the
Q-factor and FOM showed a peak.
2D field plots are good means to understand the mechanisms of resonant spectral curves. To have a deep understanding of different scattering mechanisms on the propagation properties, we demonstrated the surface current density and magnetic fields along the
z direction at resonant peaks.
Figure 6 and
Figure 7 show the values of magnetic fields (H
z) and surface current density (SCD) of asymmetrical stripe MM structures. The polarization of incident light was along the
y direction. The asymmetrical degree was 30 μm. The Fermi level was 1.0 eV. In Model I, the resonant frequencies were 1.549 THz, 1.727 THz, and 1.860 THz, as shown in
Figure 6a–c and
Figure 7a–c. At the low frequency of 1.549 THz, the electric dipolar mode of the bottom section of the asymmetrical stripe was excited and behaved as a bright mode. At the Fano frequency of 1.727 THz, the bottom section and the whole stripe interacted, resulting in a net dipole moment. Consequently, a quadrupole-like mode was excited with very low radiation losses. The anti-phase resonance of the quadrupolar mode interacted with the original electric dipolar resonance strongly, resulting in a Fano resonant peak. While in Model II, if the phonon scatterings were taken into account, the resonant frequencies were 1.538 THz, 1.734 THz, and 1.854 THz, respectively, which can be found
Figure 6d–f and
Figure 7d–f. At the Fano frequency of 1.734 THz, the quadrupolar-like mode interacted strongly with the original electric dipolar resonance and led to a Fano resonant peak. Compared with
Figure 6a–c in Model I, the resonant strength of the Fano resonance became weak, which resulted from the large losses if phonon scattering was taken into account.
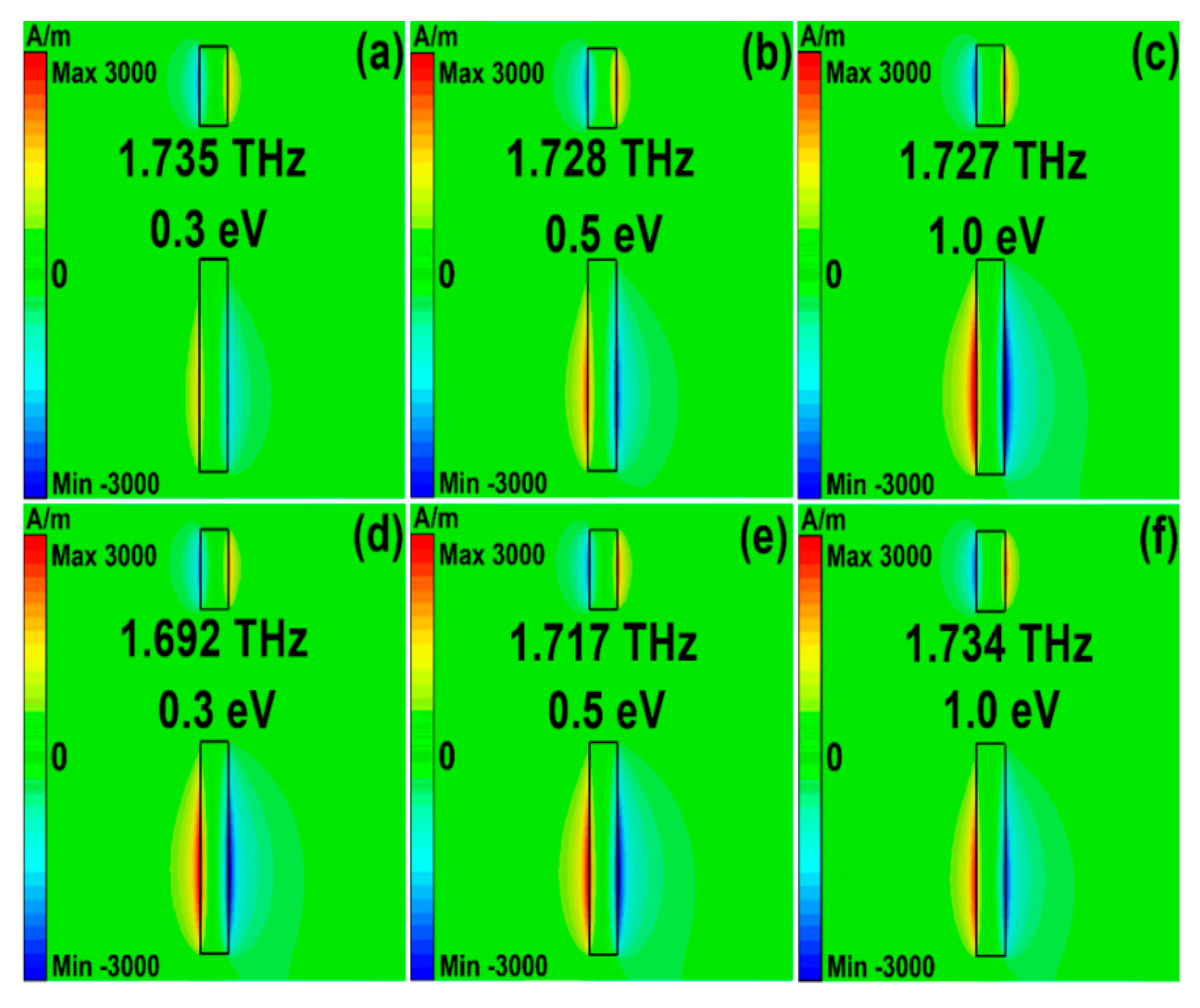
Figure 8 and
Figure 9 show the magnetic fields and surface current density of asymmetrical stripe MM structures at different Fermi levels. The Fano resonant frequencies were 1.735, 1.728, and 1.727 THz, with the Fermi levels being 0.3, 0.5, and 1.0 eV, respectively. The polarization direction of incident light was along the
y direction. The asymmetrical degree was 30 μm. It can be found from
Figure 8a–c and
Figure 9d–f that at the Fano resonances both the bottom and upper sections were excited. As Fermi levels increased, the carrier concentration increased, the graphene layer showed better plasmonic properties, and the interaction between the bottom and upper sections were stronger, which can be found in
Figure 8 and
Figure 9. While in Model II, if the phonon scattering was taken into account, the resonant frequencies were 1.692 THz, 1.717 THz, and 1.734 THz, respectively. Compared with
Figure 9a–c, the resonant strengths of the Fano resonances in Model II were weaker, resulting from the large losses in phonon scattering.