A Parametric Study of the Effects of Critical Design Parameters on the Performance of Nanoscale Silicon Devices
Abstract
:1. Introduction
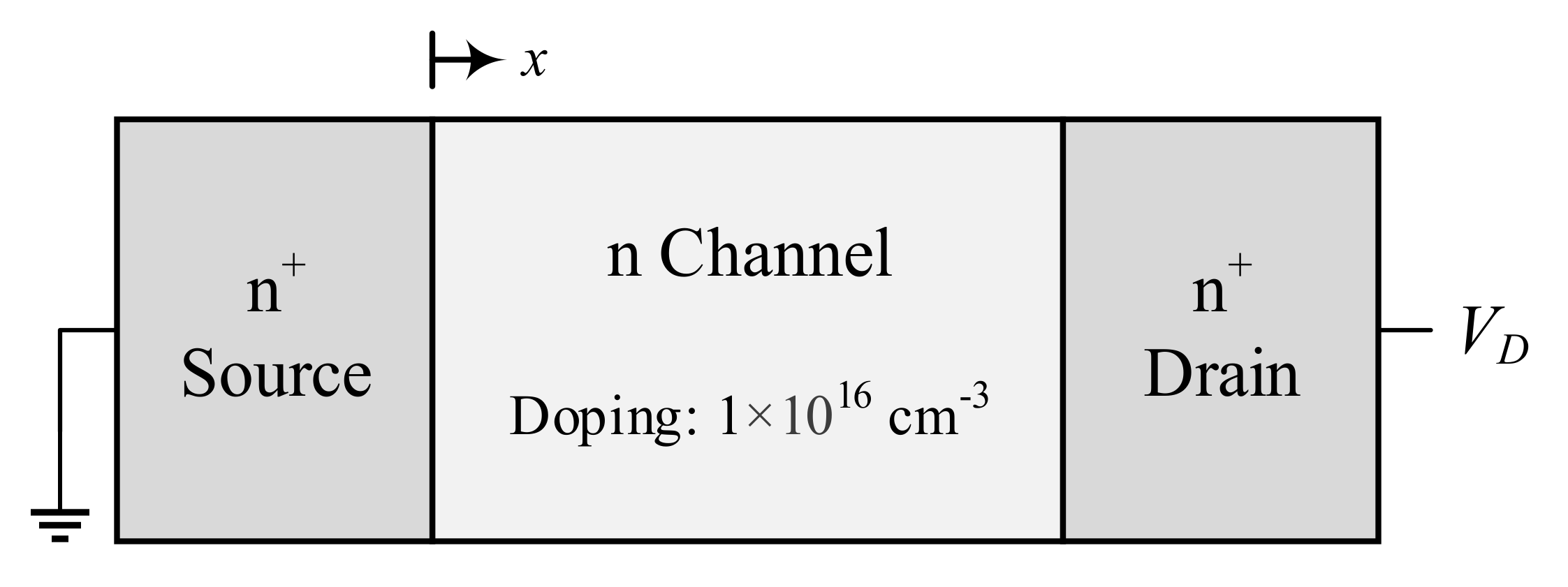
2. Materials and Methods
3. Results and Discussion
3.1. Validation
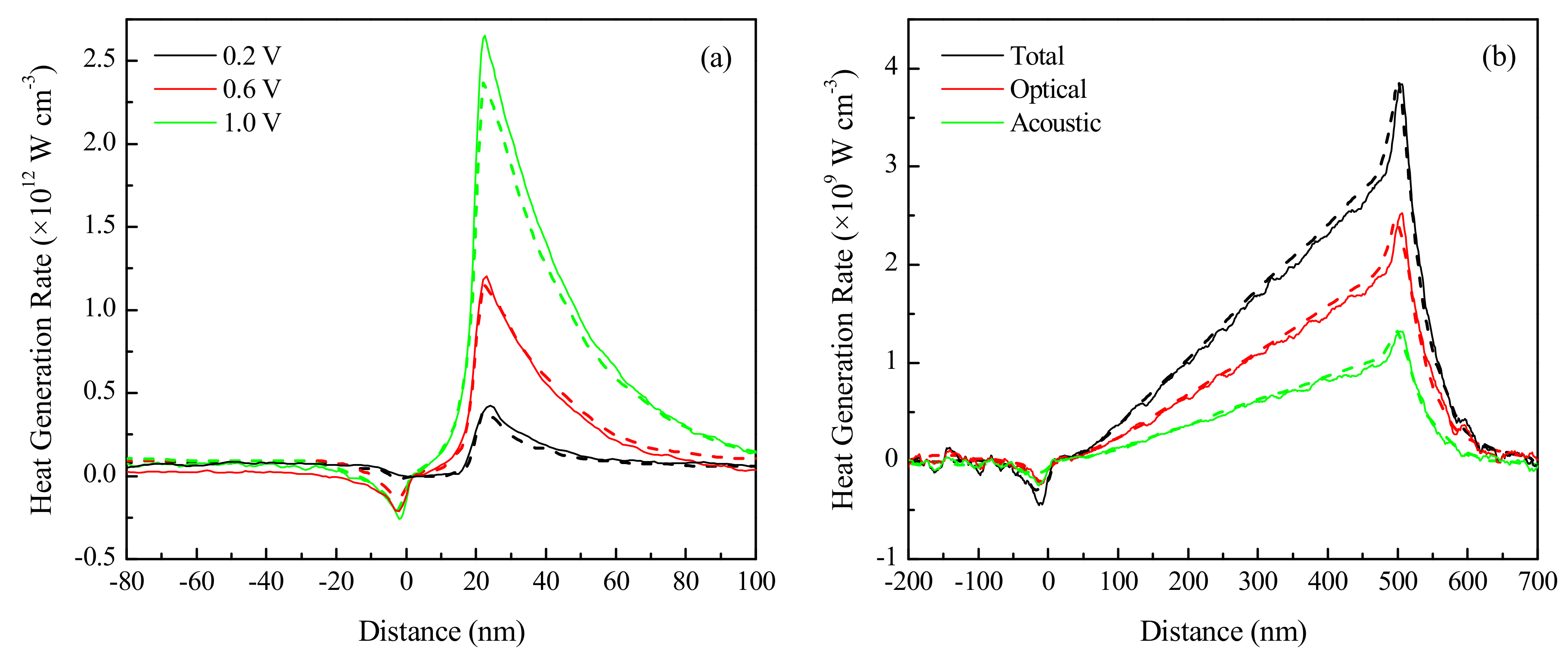
3.2. Effect of Voltage
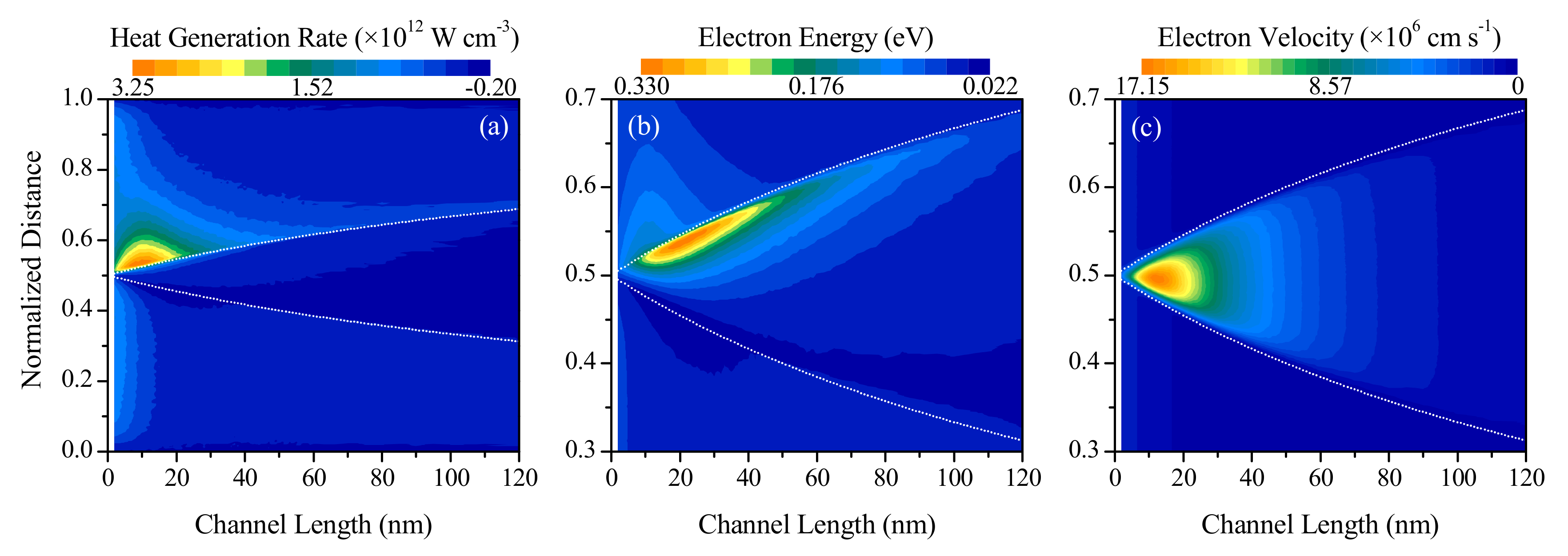
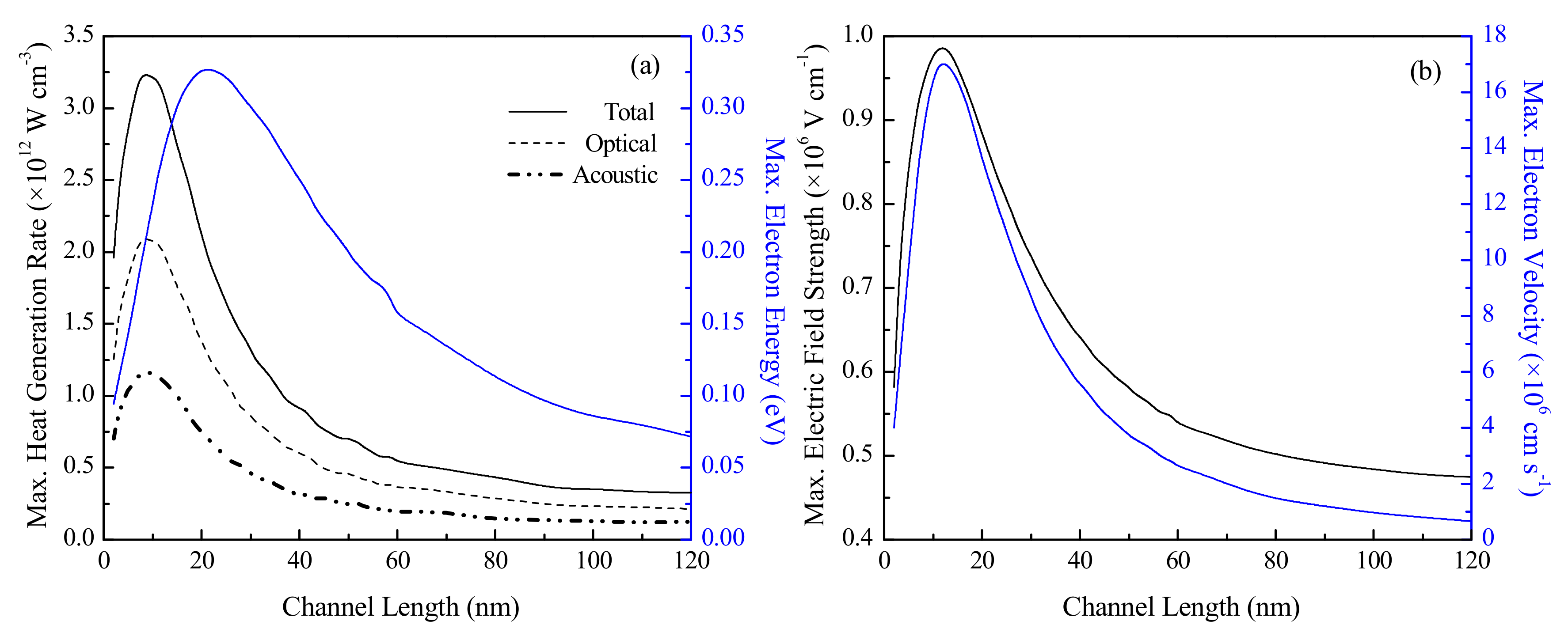
3.3. Effect of Channel Length
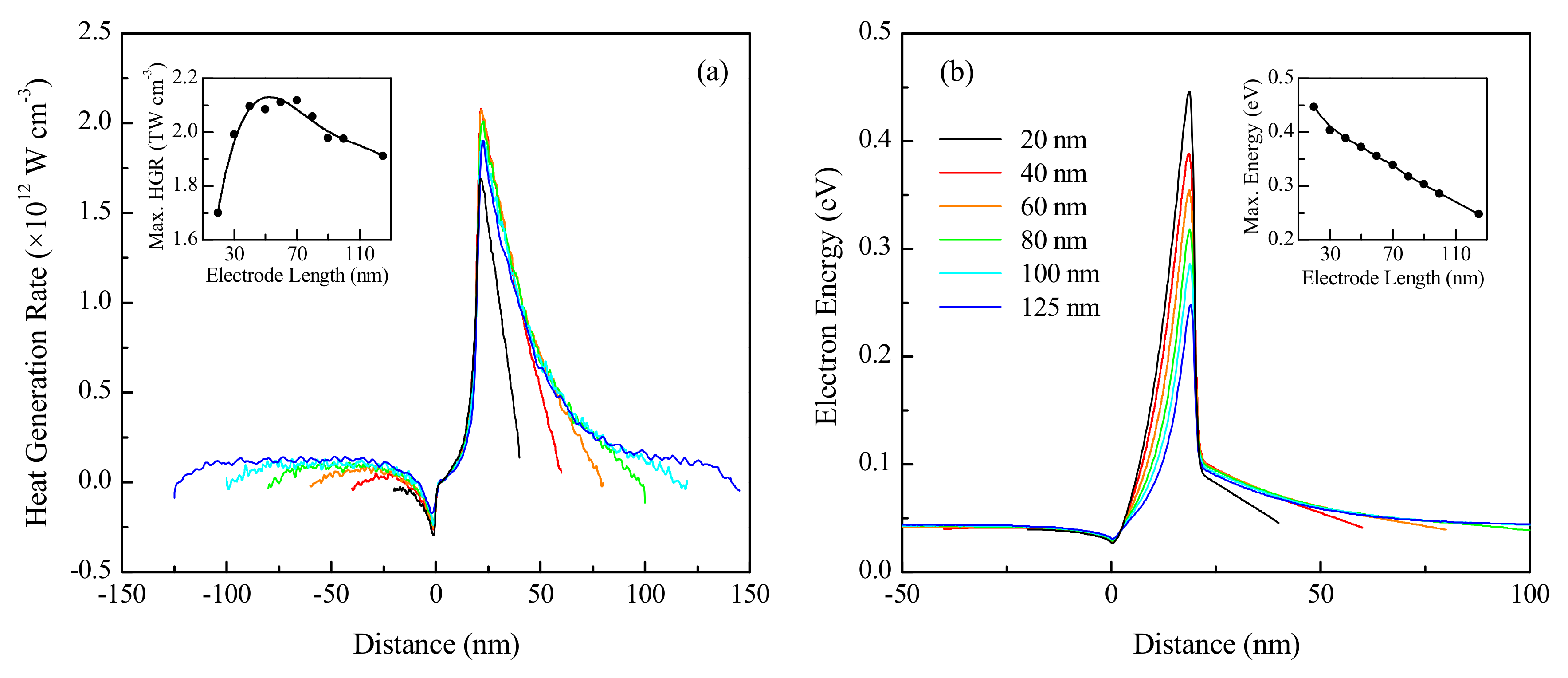
3.4. Effect of Electrode Lengths
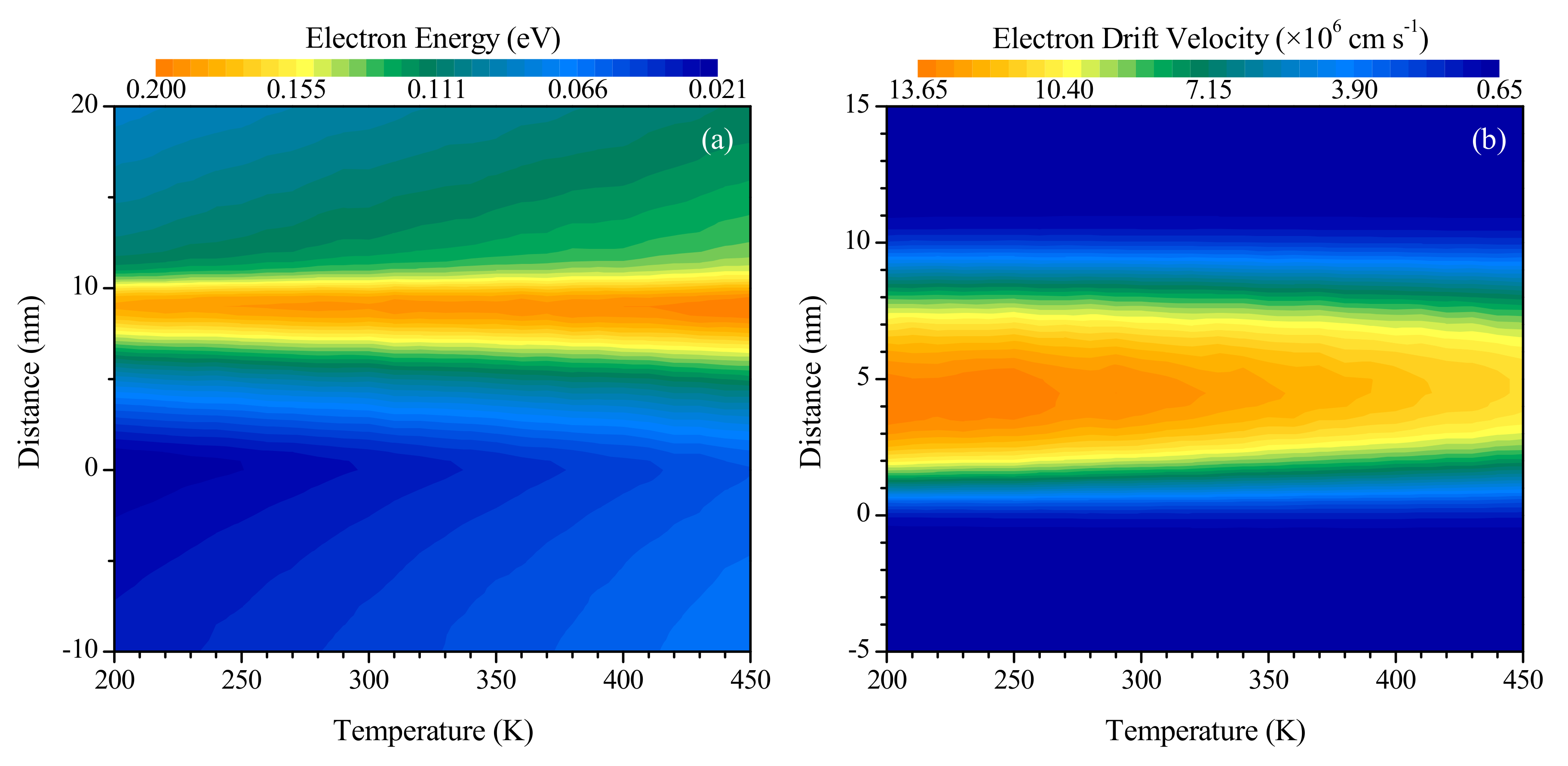
3.5. Effect of Temperature
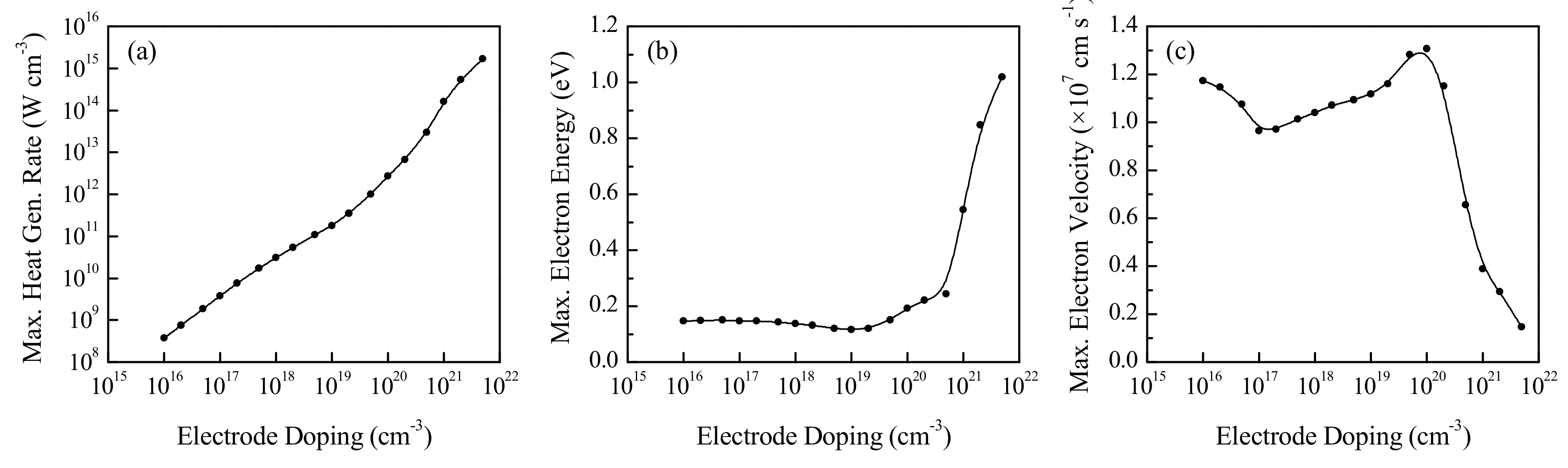
3.6. Effect of Electrode Doping Density
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pop, E.; Sinha, S.; Goodson, K. Heat generation and transport in nanometer-scale transistors. Proc. IEEE 2006, 94, 1587–1601. [Google Scholar] [CrossRef]
- Ong, Z.; Bae, M.-H. Energy dissipation in van der Waals 2D devices. 2D Mater. 2019, 6, 032005. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Jeong, M.-J. Compact, lightweight, and highly efficient circular heat sink design for high-end PCs. Appl. Therm. Eng. 2016, 92, 162–171. [Google Scholar] [CrossRef]
- Sinha, S.; Goodson, K.E. Review: Multiscale thermal modeling in nanoelectronics. Int. J. Multiscale Comput. Eng. 2005, 3, 107–133. [Google Scholar] [CrossRef]
- Schaller, R. Moore’s law: Past, present and future. IEEE Spectr. 1997, 34, 52–59. [Google Scholar] [CrossRef]
- Intel® Product Specifications. Available online: https://ark.intel.com (accessed on 14 February 2020).
- Thompson, S.E.; Parthasarathy, S. Moore’s law: The future of Si microelectronics. Mater. Today 2006, 9, 20–25. [Google Scholar] [CrossRef]
- Cardoso, J.M.; Coutinho, J.G.F.; Diniz, P.C. High-performance embedded computing. In Embedded Computing for High Performance; Elsevier: Cambridge, MA, USA, 2017; pp. 17–56. [Google Scholar]
- Pop, E. Energy dissipation and transport in nanoscale devices. Nano Res. 2010, 3, 147–169. [Google Scholar] [CrossRef] [Green Version]
- Vasileska, D.; Raleva, K.; Goodnick, S.M. Modeling heating effects in nanoscale devices: The present and the future. J. Comput. Electron. 2008, 7, 66–93. [Google Scholar] [CrossRef]
- Ju, Y.S.; Goodson, K.E. Phonon scattering in silicon films with thickness of order 100 nm. Appl. Phys. Lett. 1999, 74, 3005–3007. [Google Scholar] [CrossRef]
- Vasileska, D.; Goodnick, S.M.; Raleva, K. Self-consistent simulation of heating effects in nanoscale devices. In Proceedings of the 2009 13th International Workshop on Computational Electronics, Beijing, China, 27–29 May 2009; pp. 1–4. [Google Scholar]
- Aksamija, Z. (Ed.) Nanophononics: Thermal Generation, Transport, and Conversion at the Nanoscale, 1st ed.; Pan Stanford Publishing: New York, NY, USA, 2018. [Google Scholar]
- Chen, G. Particularities of heat conduction in nanostructures. J. Nanopart. Res. 2000, 2, 199–204. [Google Scholar] [CrossRef]
- Nghiem, T.T.; Trannoy, N.; Randrianalisoa, J.; Nghiem, T.T.T. Monte Carlo prediction of ballistic effect on phonon transport in silicon in the presence of small localized heat source. Nanotechnology 2019, 30, 415403. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Borca-Tasciuc, D.; Yang, R.G. Nanoscale heat Transfer. In Encyclopedia of Nanoscience and Nanotechnology; Nalwa, H.S., Ed.; American Scientific Publishers: Valencia, CA, USA, 2004; pp. 429–460. [Google Scholar]
- Grasser, T.; Selberherr, S. Limitations of hydrodynamic and energy-transport models. In Proceedings of the 11th International Workshop on the Physics of Semiconductor Devices, Delhi, India, 11–15 December 2001; Volume 1, pp. 584–591. [Google Scholar]
- Muscato, O.; Di Stefano, V. Heat generation and transport in nanoscale semiconductor devices via Monte Carlo and hydrodynamic simulations. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 519–537. [Google Scholar] [CrossRef]
- Anile, A.M.; Junk, M.; Romano, V.; Russo, G. Cross-validation of numerical schemes for extended hydrodynamical models of semiconductors. Math. Model. Methods Appl. Sci. 2000, 10, 833–861. [Google Scholar] [CrossRef]
- Adeleh, M.G. Assessment of Monte Carlo simulation of electron transport in ZnO diode in intelligent information systems. Int. J. Intell. Inf. Syst. 2019, 8, 43. [Google Scholar] [CrossRef] [Green Version]
- Pop, E.; Dutton, R.W.; Goodson, K. Analytic band Monte Carlo model for electron transport in Si including acoustic and optical phonon dispersion. J. Appl. Phys. 2004, 96, 4998–5005. [Google Scholar] [CrossRef]
- Pop, E.; Rowlette, J.A.; Dutton, R.W.; Goodson, K.E. Joule heating under quasi-ballistic transport conditions in bulk and strained silicon devices. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Tokyo, Japan, 1–3 September 2005; Volume 2005, pp. 307–310. [Google Scholar]
- Ashok, A.; Vasileska, D.; Hartin, O.; Goodnick, S.M. Monte Carlo simulation of GaN n+nn+ diode including intercarrier interactions. In Proceedings of the 2007 7th IEEE Conference on Nanotechnology (IEEE NANO), Hong Kong, China, 2–5 August 2007; pp. 338–341. [Google Scholar]
- Harada, N.; Awano, Y.; Sato, S.; Yokoyama, N. Monte Carlo simulation of electron transport in a graphene diode with a linear energy band dispersion. J. Appl. Phys. 2011, 109, 104509. [Google Scholar] [CrossRef]
- Shomali, Z.; Pedar, B.; Ghazanfarian, J.; Abbassi, A. Monte-Carlo parallel simulation of phonon transport for 3D silicon nano-devices. Int. J. Therm. Sci. 2017, 114, 139–154. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Reaz, M.; Weeden-Wright, S.L.; Schrimpf, R.D.; Reed, R.A.; Weller, R.A.; Fischetti, M.V.; Pantelides, S.T. Understanding the average electron–hole pair-creation energy in silicon and germanium based on full-band Monte Carlo simulations. IEEE Trans. Nucl. Sci. 2019, 66, 444–451. [Google Scholar] [CrossRef]
- Jacoboni, C.; Lugli, P. The Monte Carlo Method for Semiconductor Device Simulation, 1st ed.; Springer Vienna: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- COMSOL. Semiconductor Module User’s Guide COMSOL 5.4; COMSOL Inc.: Stockholm, Sweden, 2018. [Google Scholar]
- Venturi, F.; Smith, R.; Sangiorgi, E.; Pinto, M.; Ricco, B. A general purpose device simulator coupling Poisson and Monte Carlo transport with applications to deep submicron MOSFETs. IEEE Trans. Comput. Des. Integr. Circuits Syst. 1989, 8, 360–369. [Google Scholar] [CrossRef]
- Pop, E.; Dutton, R.W.; Goodson, K. Monte Carlo simulation of Joule heating in bulk and strained silicon. Appl. Phys. Lett. 2005, 86, 082101. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A. Intrinsic concentration, effective densities of states, and effective mass in silicon. J. Appl. Phys. 1990, 67, 2944–2954. [Google Scholar] [CrossRef]
- Canali, C.; Jacoboni, C.; Nava, F.; Ottaviani, G.; Alberigi-Quaranta, A. Electron drift velocity in silicon. Phys. Rev. B 1975, 12, 2265–2284. [Google Scholar] [CrossRef]
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645–705. [Google Scholar] [CrossRef]
- Kosina, H. A method to reduce small-angle scattering in Monte Carlo device analysis. IEEE Trans. Electron Devices 1999, 46, 1196–1200. [Google Scholar] [CrossRef]
- Jungemann, C.; Meinerzhagen, B. On the applicability of nonself-consistent Monte Carlo device simulations. IEEE Trans. Electron Devices 2002, 49, 1072–1074. [Google Scholar] [CrossRef]
- Ahmed, F.; Kim, Y.D.; Yang, Z.; He, P.; Hwang, E.; Yang, H.; Hone, J.; Yoo, W.J. Impact ionization by hot carriers in a black phosphorus field effect transistor. Nat. Commun. 2018, 9, 3414. [Google Scholar] [CrossRef]
- Rowlette, J.; Pop, E.; Sinha, S.; Panzer, M.; Goodson, K. Thermal simulation techniques for nanoscale transistors. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, Digest of Technical Papers (ICCAD), San Jose, CA, USA, 6–10 November 2005; Volume 2005, pp. 225–228. [Google Scholar]
- Haensch, W.; Nowak, E.J.; Dennard, R.H.; Solomon, P.; Bryant, A.; Dokumaci, O.H.; Kumar, A.; Wang, X.; Johnson, J.B.; Fischetti, M.V. Silicon CMOS devices beyond scaling. IBM J. Res. Dev. 2006, 50, 339–361. [Google Scholar] [CrossRef]
- Oda, S.; Ferry, D. (Eds.) Silicon Nanoelectronics; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Lake, R.; Datta, S. Energy balance and heat exchange in mesoscopic systems. Phys. Rev. B 1992, 46, 4757–4763. [Google Scholar] [CrossRef]
- Brennan, K.F.; Callen, W.R. Introduction to Semiconductor Devices; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sy, H.; Ong, C. Electron mobility in heavily doped silicon. Solid State Commun. 1984, 52, 881–883. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, F.K.; Talha, T.; Ahmed, F. A Parametric Study of the Effects of Critical Design Parameters on the Performance of Nanoscale Silicon Devices. Nanomaterials 2020, 10, 1987. https://doi.org/10.3390/nano10101987
Malik FK, Talha T, Ahmed F. A Parametric Study of the Effects of Critical Design Parameters on the Performance of Nanoscale Silicon Devices. Nanomaterials. 2020; 10(10):1987. https://doi.org/10.3390/nano10101987
Chicago/Turabian StyleMalik, Faraz Kaiser, Tariq Talha, and Faisal Ahmed. 2020. "A Parametric Study of the Effects of Critical Design Parameters on the Performance of Nanoscale Silicon Devices" Nanomaterials 10, no. 10: 1987. https://doi.org/10.3390/nano10101987
APA StyleMalik, F. K., Talha, T., & Ahmed, F. (2020). A Parametric Study of the Effects of Critical Design Parameters on the Performance of Nanoscale Silicon Devices. Nanomaterials, 10(10), 1987. https://doi.org/10.3390/nano10101987




