Stress and Refractive Index Control of SiO2 Thin Films for Suspended Waveguides
Abstract
:1. Introduction
2. Materials and Methods
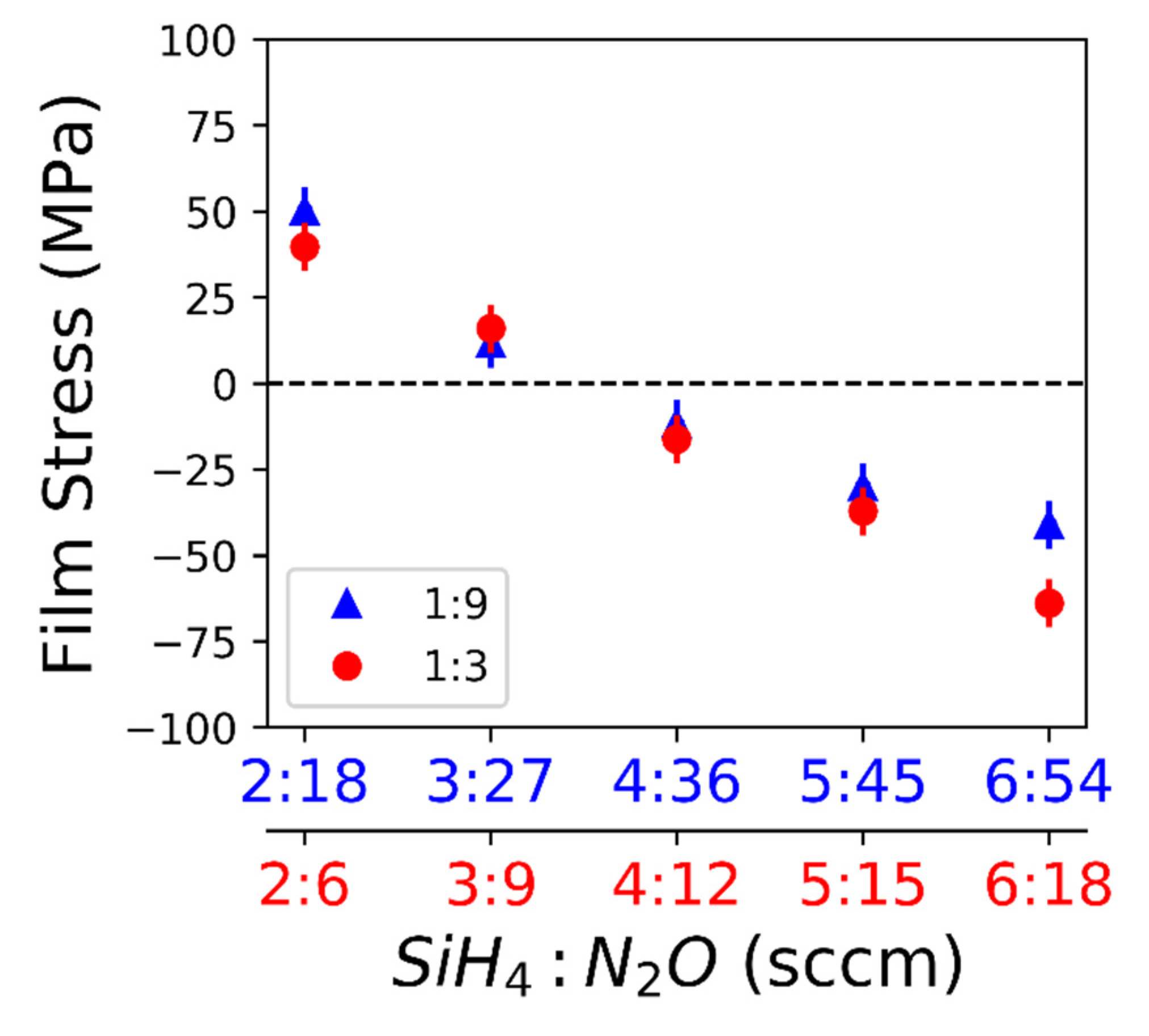
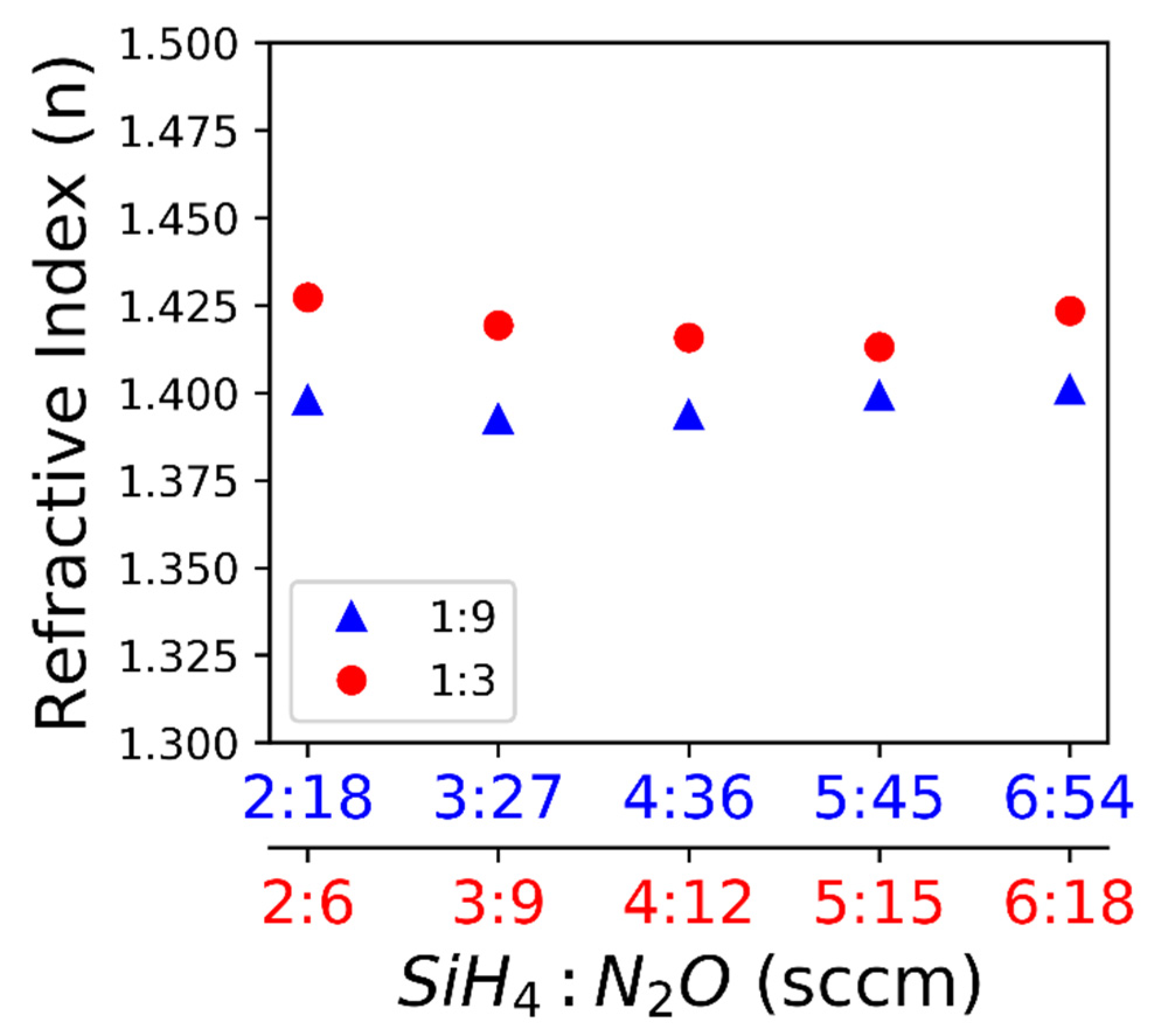
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yoon Oh, D.; Yang, K.Y.; Fredrick, C.; Ycas, G.; Diddams, S.A.; Vahala, K.J. Coherent ultra-violet to near-infrared generation in silica ridge waveguides. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Zhu, Y.; Shi, Y.; Dai, D.; He, S. Fabrication and characterization of suspended SiO_2 ridge optical waveguides and the devices. Opt. Express 2012, 20, 22531. [Google Scholar] [CrossRef] [PubMed]
- Ghaderi, M.; De Graaf, G.; Wolffenbuttel, R.F. Fabrication of Ultrathin Large-area Dielectric Membrane Stacks for use as Interference Filters. Procedia Eng. 2016, 168, 1342–1345. [Google Scholar] [CrossRef]
- Nissen, M.; Doherty, B.; Hamperl, J.; Kobelke, J.; Weber, K.; Henkel, T.; Schmidt, M.A. UV absorption spectroscopy in water-filled antiresonant hollow core fibers for pharmaceutical detection. Sensors 2018, 18, 478. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Behzadirad, M.; Nami, M.; Rishinaramagalam, A.K.; Feezell, D.F.; Busani, T. GaN nanowire tips for nanoscale atomic force microscopy. Nanotechnology 2017, 28, 20LT01. [Google Scholar] [CrossRef]
- Behzadirad, M.; Nami, M.; Wostbrock, N.; Zamani Kouhpanji, M.R.; Feezell, D.F.; Brueck, S.R.J.; Busani, T. Scalable Top-Down Approach Tailored by Interferometric Lithography to Achieve Large-Area Single-Mode GaN Nanowire Laser Arrays on Sapphire Substrate. ACS Nano 2018, 12, 2373–2380. [Google Scholar] [CrossRef] [PubMed]
- Liao, B.-H.; Hsiao, C.-N. Improving optical properties of silicon nitride films to be applied in the middle infrared optics by a combined high-power impulse/unbalanced magnetron sputtering deposition technique. Appl. Opt. 2014, 53, A377. [Google Scholar] [CrossRef]
- Aslan, M.M.; Webster, N.A.; Byard, C.L.; Pereira, M.B.; Hayes, C.M.; Wiederkehr, R.S.; Mendes, S.B. Low-loss optical waveguides for the near ultra-violet and visible spectral regions with Al2O3 thin films from atomic layer deposition. Thin Solid Films 2010, 518, 4935–4940. [Google Scholar] [CrossRef] [Green Version]
- Joo, H.-Y.; Kim, H.J.; Kim, S.J.; Kim, S.Y. Spectrophotometric analysis of aluminum nitride thin films. J. Vac. Sci. Technol. Vac. Surf. Films 1999, 17, 862–870. [Google Scholar] [CrossRef]
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of SiO2 and Ta2O5 films. Opt. Mater. Express 2016, 6, 3622. [Google Scholar] [CrossRef]
- Chung, C.K.; Lin, T.Y.; Duh, J.G.; Tsai, M.Q. Global and local residual stress in silicon carbide films produced by plasma-enhanced chemical vapor deposition. Surf. Coat. Technol. 2006, 200, 4825–4834. [Google Scholar] [CrossRef] [Green Version]
- Ghaderi, M.; Ayerden, N.P.; De Graaf, G.; Wolffenbuttel, R.F. Surface-micromachined bragg reflectors based on multiple Airgap/SiO2 layers for CMOS-compatible fabry-perot filters in the UV-visible spectral range. Procedia Eng. 2014, 87, 1533–1536. [Google Scholar] [CrossRef] [Green Version]
- Ghaderi, M.; De Graaf, G.; Wolffenbuttel, R.F. Thermal annealing of thin PECVD silicon-oxide films for airgap-based optical filters. J. Micromechanics Microengineering 2016, 26, 084009. [Google Scholar] [CrossRef]
- Mackenzie, K.D.; Johnson, D.J.; DeVre, M.W.; Westerman, R.J.; Reelfs, B.H. Stress control of si-based pecvd dielectrics. In Proceedings of the 207th Electrochemical Society, Quebec City, QC, Canada, 15–20 May 2005; pp. 148–149. [Google Scholar] [CrossRef]
- Kshirsagar, A.; Duttagupta, S.P.; Gangal, S.A. Optimisation and fabrication of low-stress, low-temperature silicon oxide cantilevers. Micro Nano Lett. 2011, 6, 476. [Google Scholar] [CrossRef]
- Revuri, P.K.; Tripathi, D.K.; Martyniuk, M.; Silva, K.K.; Putrino, G.; Keating, A.; Faraone, L. Silicon and Silicon dioxide thin films deposited by ICPCVD at low temperature and high rate for MEMS applications. In Proceedings of the 2018 Conference on Optoelectronic and Microelectronic Materials and Devices (COMMAD), Perth, Australia, 9–13 December 2018; pp. 24–26. [Google Scholar] [CrossRef]
- Jatta, S.; Haberle, K.; Klein, A.; Schafranek, R.; Koegel, B.; Meissner, P. Depositon of dielectric films with inductively coupled plasma-CVD in dependence on pressure and two RF-power- sources. Plasma Process. Polym. 2009, 6, S582–S587. [Google Scholar] [CrossRef]
- Dao, V.A.; Nguyen, V.D.; Heo, J.; Choi, H.; Kim, Y.; Lakshminarayan, N.; Yi, J. Effect of N2O/SiH4 flow ratios on properties of amorphous silicon oxide thin films deposited by inductively-coupled plasma chemical vapor deposition with application to silicon surface passivation. Vacuum 2009, 84, 410–414. [Google Scholar] [CrossRef]
- Jatta, S.; Zogal, K.; Kögel, B.; Haberle, K.; Sydlo, C.; Meissner, P. Realization of tunable optical components with ICP-CVD. Frequenz 2008, 62, 96–99. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films Deposited by Electrolysis. Proc. R Soc. Lond. A 1905, 82, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.-H.; Kim, H.-G.; Yoon, S.-G. Effects of the reaction parameters on the deposition characteristics in ZrO2 CVD. J. Mater. Sci. Mater. Electron. 1992, 3, 87–92. [Google Scholar] [CrossRef]
- Keller, R.-M.; Baker, S.P.; Arzt, E. Quantitative analysis of strengthening mechanisms in thin Cu films: Effects of film thickness, grain size, and passivation. J. Mater. Res. 1998, 13, 1307–1317. [Google Scholar] [CrossRef]
- Blaauw, C. Stress in chemical-vapor-deposited SiO2 and plasma-SiNx films on GaAs and Si. J. Appl. Phys. 1983, 54, 5064–5068. [Google Scholar] [CrossRef]
- Hu, S.M. Stress-related problems in silicon technology. J. Appl. Phys. 1991, 70, 29. [Google Scholar] [CrossRef]
- Ohring, M. Materials Science of Thin Films, 2nd ed.; Academic Press: Cambridge, MA, USA, 2002; ISBN 978-0-585-47097-9. [Google Scholar]
- Chason, E.; Shin, J.W.; Hearne, S.J.; Freund, L.B. Kinetic model for dependence of thin film stress on growth rate, temperature, and microstructure. J. Appl. Phys. 2012, 111, 083520. [Google Scholar] [CrossRef]
- Jerman, M.; Qiao, Z.; Margel, D. Refractive index of thin films of SiO2, ZrO2, and HfO2 as a function of the films’ mass density. Appl. Opt. 2005, 44, 3006. [Google Scholar] [CrossRef]
- French, P.J.; Sarro, P.M.; Mallée, R.; Fakkeldij, E.J.M.; Wolfenbuttel, R.F. Optimization of a low-stress silicon nitride process for surface-micromachining applications. Sens. Actuators A Phys. 1997, 58, 149–157. [Google Scholar] [CrossRef]
- Iliescu, C.; Chen, B.; Poenar, D.P.; Lee, Y.Y. PECVD amorphous silicon carbide membranes for cell culturing. Sens. Actuators B Chem. 2008, 129, 404–411. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wostbrock, N.; Busani, T. Stress and Refractive Index Control of SiO2 Thin Films for Suspended Waveguides. Nanomaterials 2020, 10, 2105. https://doi.org/10.3390/nano10112105
Wostbrock N, Busani T. Stress and Refractive Index Control of SiO2 Thin Films for Suspended Waveguides. Nanomaterials. 2020; 10(11):2105. https://doi.org/10.3390/nano10112105
Chicago/Turabian StyleWostbrock, Neal, and Tito Busani. 2020. "Stress and Refractive Index Control of SiO2 Thin Films for Suspended Waveguides" Nanomaterials 10, no. 11: 2105. https://doi.org/10.3390/nano10112105
APA StyleWostbrock, N., & Busani, T. (2020). Stress and Refractive Index Control of SiO2 Thin Films for Suspended Waveguides. Nanomaterials, 10(11), 2105. https://doi.org/10.3390/nano10112105



