Machine Learning Analysis of Raman Spectra of MoS2
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of Monolayer MoS2 Continuous Film
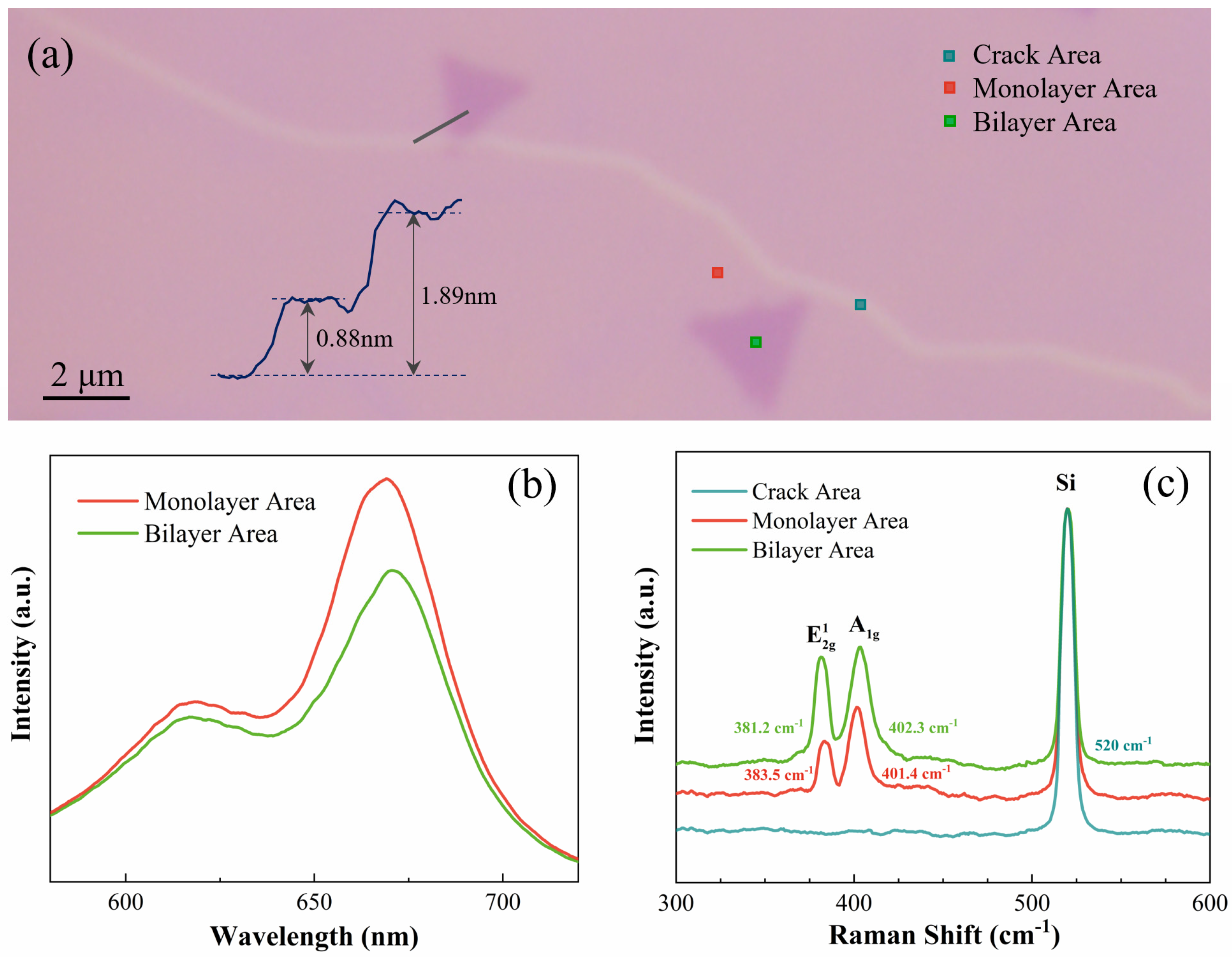
2.2. Characterization and Measurements
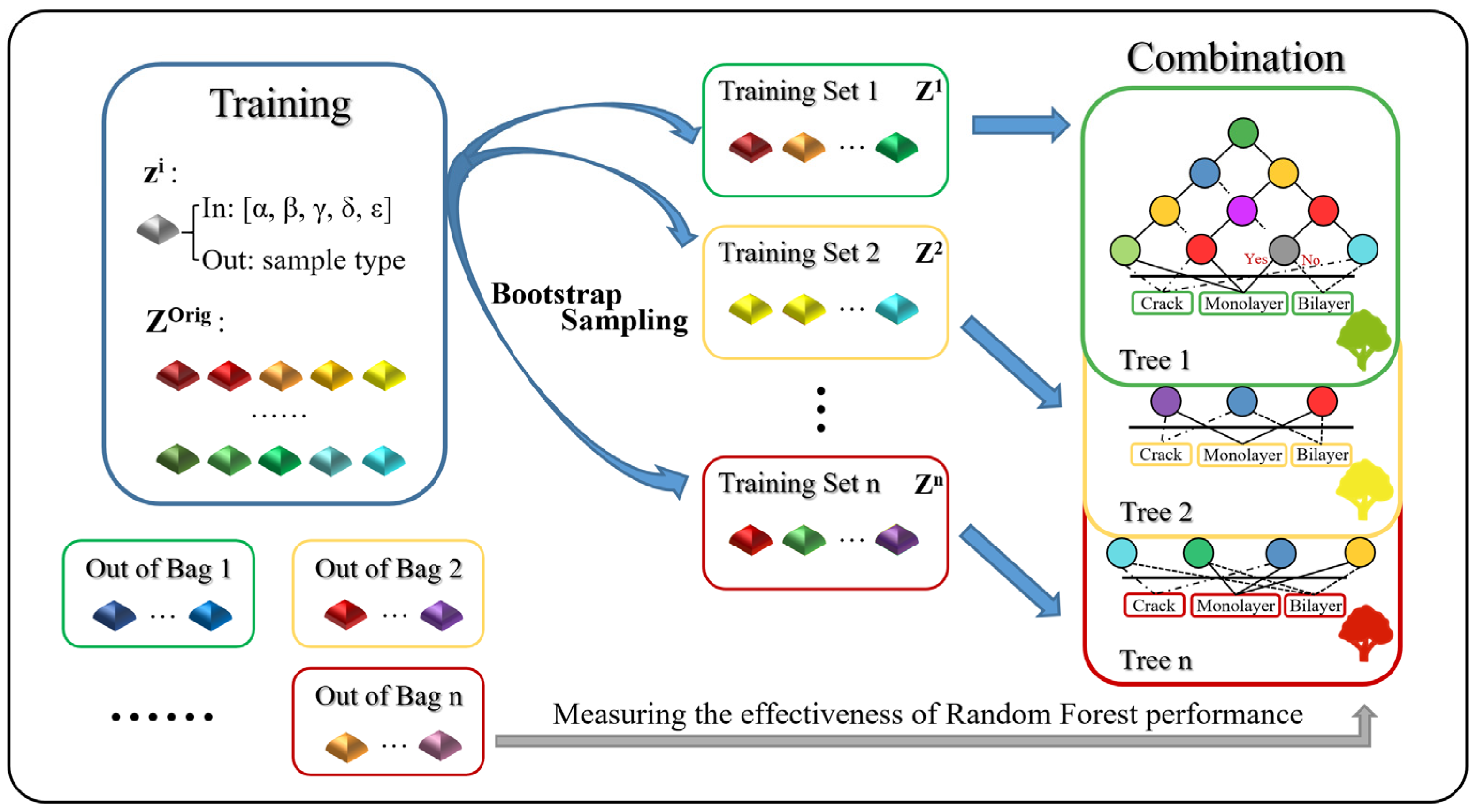
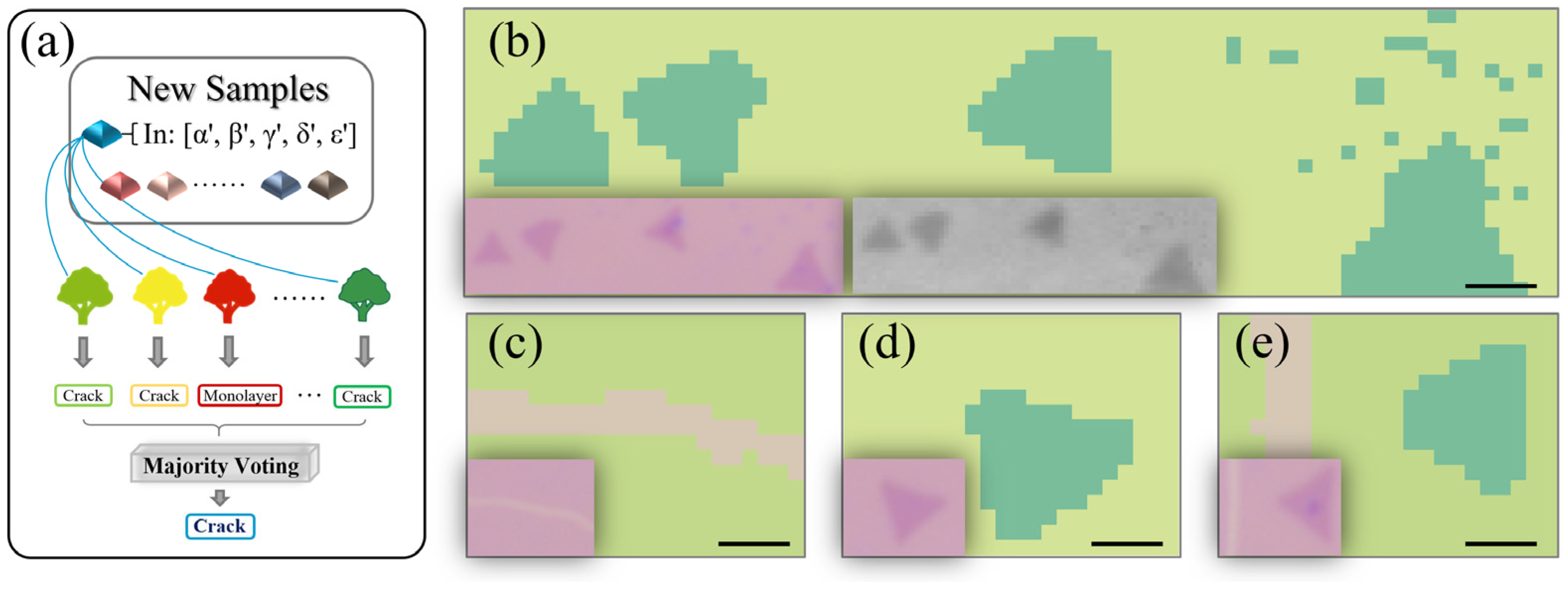
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, C.; Cao, X.; Wu, X.-J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.-H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef]
- Mueller, T.; Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl. 2018, 2, 29. [Google Scholar] [CrossRef]
- Zhan, Y.; Liu, Z.; Najmaei, S.; Ajayan, P.M.; Lou, J. Large-Area Vapor-Phase Growth and Characterization of MoS2 Atomic Layers on a SiO2 Substrate. Small 2012, 8, 966–971. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Zhou, C. Review of Chemical Vapor Deposition of Graphene and Related Applications. Acc. Chem. Res. 2013, 46, 2329–2339. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Li, Z.; Liao, W.; Jia, Y.; Shi, Z.; Huang, Z.; Yu, W.; Sun, X.; Liu, X.; Li, D. Monolithic integration of MoS2-based visible detectors and GaN-based UV detectors. Photonics Res. 2019, 7, 1127–1133. [Google Scholar] [CrossRef]
- Lu, R.D.; Wang, Y.G.; Wang, J.; Ren, W.; Li, L.; Liu, S.C.; Chen, Z.D.; Li, Y.F.; Wang, H.Y.; Fu, F.X. Soliton and bound-state soliton mode-locked fiber laser based on a MoS2/fluorine mica Langmuir-Blodgett film saturable absorber. Photonics Res. 2019, 7, 431–436. [Google Scholar] [CrossRef]
- Liu, W.; Liu, M.; Han, H.; Fang, S.; Teng, H.; Lei, M.; Wei, Z. Nonlinear optical properties of WSe2 and MoSe2 films and their applications in passively Q-switched erbium doped fiber lasers. Photonics Res. 2018, 6, C15–C21. [Google Scholar] [CrossRef]
- Rhodes, D.; Chae, S.H.; Ribeiro-Palau, R.; Hone, J. Disorder in van der Waals heterostructures of 2D materials. Nat. Mater. 2019, 18, 541–549. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, B.; Zou, X.; Cheng, H.-M. Chemical Vapor Deposition Growth and Applications of Two-Dimensional Materials and Their Heterostructures. Chem. Rev. 2018, 118, 6091–6133. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from Chemically Exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef]
- Li, H.; Wu, J.; Huang, X.; Lu, G.; Yang, J.; Lu, X.; Xiong, Q.; Zhang, H. Rapid and Reliable Thickness Identification of Two-Dimensional Nanosheets Using Optical Microscopy. ACS Nano 2013, 7, 10344–10353. [Google Scholar] [CrossRef]
- Wang, H.-C.; Huang, S.-W.; Yang, J.-M.; Wu, G.-H.; Hsieh, Y.-P.; Feng, S.-W.; Lee, M.K.; Kuo, C.-T. Large-area few-layered graphene film determination by multispectral imaging microscopy. Nanoscale 2015, 7, 9033–9039. [Google Scholar] [CrossRef]
- Li, Y.; Dong, N.; Zhang, S.; Wang, K.; Zhang, L.; Wang, J. Optical identification of layered MoS2 via the characteristic matrix method. Nanoscale 2016, 8, 1210–1215. [Google Scholar] [CrossRef]
- Niu, Y.; Gonzalez-Abad, S.; Frisenda, R.; Marauhn, P.; Drüppel, M.; Gant, P.; Schmidt, R.; Taghavi, N.S.; Barcons, D.; Molina-Mendoza, A.J.; et al. Thickness-Dependent Differential Reflectance Spectra of Monolayer and Few-Layer MoS2, MoSe2, WS2 and WSe2. Nanomater. 2018, 8, 725. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, L.; Su, C.; Xiao, H.; Lv, S.; Zhang, F.; Sui, Q.; Jia, L.; Jiang, M. Direct Observation of Monolayer MoS2 Prepared by CVD Using In-Situ Differential Reflectance Spectroscopy. Nanomater. 2019, 9, 1640. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yan, H.; Brus, L.E.; Heinz, T.F.; Hone, J.; Ryu, S. Anomalous Lattice Vibrations of Single- and Few-Layer MoS2. ACS Nano 2010, 4, 2695–2700. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, Q.; Yap, C.C.R.; Tay, B.K.; Edwin, T.H.T.; Olivier, A.; Baillargeat, D. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Funct. Mater. 2012, 22, 1385–1390. [Google Scholar] [CrossRef]
- Yuan, S.; Liu, L.; Wang, Z.; Xi, N. AFM-Based Observation and Robotic Nano-Manipulation. AFM-Based Observation and Robotic Nano-Manipulation; Springer: Singapore, 2020. [Google Scholar]
- Li, X.-L.; Han, W.-P.; Wu, J.-B.; Qiao, X.-F.; Zhang, J.; Tan, P.-H. Layer-Number Dependent Optical Properties of 2D Materials and Their Application for Thickness Determination. Adv. Funct. Mater. 2017, 27, 1604468. [Google Scholar] [CrossRef]
- Hornett, S.M.; Stantchev, R.I.; Vardaki, M.; Beckerleg, C.; Hendry, E. Subwavelength Terahertz Imaging of Graphene Photoconductivity. Nano Lett. 2016, 16, 7019–7024. [Google Scholar] [CrossRef]
- Lin, X.; Si, Z.; Fu, W.; Yang, J.; Guo, S.; Cao, Y.; Zhang, J.; Wang, X.; Liu, P.; Jiang, K.; et al. Intelligent identification of two-dimensional nanostructures by machine-learning optical microscopy. Nano Res. 2018, 11, 6316–6324. [Google Scholar] [CrossRef]
- Masubuchi, S.; Machida, T. Classifying optical microscope images of exfoliated graphene flakes by data-driven machine learning. npj 2D Mater. Appl. 2019, 3, 4. [Google Scholar] [CrossRef]
- Saito, Y.; Shin, K.; Terayama, K.; Desai, S.; Onga, M.; Nakagawa, Y.; Itahashi, Y.M.; Iwasa, Y.; Yamada, M.; Tsuda, K. Deep-learning-based quality filtering of mechanically exfoliated 2D crystals. npj Comput. Mater. 2019, 5, 1–6. [Google Scholar] [CrossRef]
- Masubuchi, S.; Watanabe, E.; Seo, Y.; Okazaki, S.; Sasagawa, T.; Watanabe, K.; Taniguchi, T.; Machida, T. Deep-learning-based image segmentation integrated with optical microscopy for automatically searching for two-dimensional materials. npj 2D Mater. Appl. 2020, 4, 1–9. [Google Scholar] [CrossRef]
- Han, B.; Lin, Y.; Yang, Y.; Mao, N.; Li, W.; Wang, H.; Yasuda, K.; Wang, X.; Fatemi, V.; Zhou, L.; et al. Deep-Learning-Enabled Fast Optical Identification and Characterization of 2D Materials. Adv. Mater. 2020, 32, e2000953. [Google Scholar] [CrossRef]
- Millard, T.S.; Genco, A.; Alexeev, E.M.; Randerson, S.; Ahn, S.; Jang, A.-R.; Shin, H.S.; Tartakovskii, A.I. Large area chemical vapour deposition grown transition metal dichalcogenide monolayers automatically characterized through photoluminescence imaging. npj 2D Mater. Appl. 2020, 4, 12. [Google Scholar] [CrossRef]
- Nolen, C.M.; Denina, G.; Teweldebrhan, D.; Bhanu, B.; Balandin, A.A. High-Throughput Large-Area Automated Identification and Quality Control of Graphene and Few-Layer Graphene Films. ACS Nano 2011, 5, 914–922. [Google Scholar] [CrossRef]
- Dhakal, K.P.; Duong, D.L.; Lee, J.; Nam, H.; Kim, M.; Kan, M.; Lee, Y.H.; Kim, J. Confocal absorption spectral imaging of MoS2: Optical transitions depending on the atomic thickness of intrinsic and chemically doped MoS2. Nanoscale 2014, 6, 13028–13035. [Google Scholar] [CrossRef]
- Desai, S.B.; Madhvapathy, S.R.; Amani, M.; Kiriya, D.; Hettick, M.; Tosun, M.; Zhou, Y.; Dubey, M.; Ager, J.W.; Chrzan, D.; et al. Gold-Mediated Exfoliation of Ultralarge Optoelectronically-Perfect Monolayers. Adv. Mater. 2016, 28, 4053–4058. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qiao, X.-F.; Shi, W.; Wu, J.-B.; Jiang, D.-S.; Tan, P.-H. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 2015, 44, 2757–2785. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Zhang, X.; Kislyakov, I.M.; Wang, L.; Huang, J.; Zhang, S.; Dong, N.; Wang, J. Enhanced two-photon absorption and two-photon luminescence in monolayer MoS2 and WS2 by defect repairing. Opt. Express 2019, 27, 13744–13753. [Google Scholar] [CrossRef]
- Li, Y.; Dong, N.; Zhang, S.; Zhang, X.; Feng, Y.; Wang, K.; Zhang, L.; Wang, J. Giant two-photon absorption in monolayer MoS2. Laser Photonics Rev. 2015, 9, 427–434. [Google Scholar] [CrossRef]
- Urban, F.; Passacantando, M.; Giubileo, F.; Iemmo, L.; Di Bartolomeo, A. Transport and Field Emission Properties of MoS2 Bilayers. Nanomater. 2018, 8, 151. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, S.; Li, Y.; Dong, N.; Zhang, X.; Wang, L.; Liu, W.; Kislyakov, I.M.; Nunzi, J.-M.; Qi, H.; et al. Layer-modulated two-photon absorption in MoS2: Probing the shift of the excitonic dark state and band-edge. Photonics Res. 2019, 7, 762–770. [Google Scholar] [CrossRef]
- Vaknin, Y.; Dagan, R.; Rosenwaks, Y. Pinch-Off Formation in Monolayer and Multilayers MoS2 Field-Effect Transistors. Nanomaterials 2019, 9, 882. [Google Scholar] [CrossRef]
- Hao, S.; Yang, B.; Gao, Y. Orientation-specific transgranular fracture behavior of CVD-grown monolayer MoS2 single crystal. Appl. Phys. Lett. 2017, 110, 153105. [Google Scholar] [CrossRef]
- Wang, K.; Wang, J.; Fan, J.; Lotya, M.; O’Neill, A.; Fox, D.; Feng, Y.; Zhang, X.; Jiang, B.; Zhao, Q.; et al. Ultrafast Saturable Absorption of Two-Dimensional MoS2 Nanosheets. ACS Nano 2013, 7, 9260–9267. [Google Scholar] [CrossRef]
- Yoon, D.; Moon, H.; Son, Y.-W.; Choi, J.S.; Park, B.H.; Cha, Y.H.; Kim, Y.D.; Cheong, H. Interference effect on Raman spectrum of graphene on SiO2/Si. Phys. Rev. B 2009, 80, 125422. [Google Scholar] [CrossRef]
- Li, X.-L.; Qiao, X.-F.; Han, W.-P.; Zhang, X.; Tan, Q.-H.; Chen, T.; Tan, P.-H. Determining layer number of two-dimensional flakes of transition-metal dichalcogenides by the Raman intensity from substrates. Nanotechnology 2016, 27, 145704. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Zhang, X.; Zhang, W.; Chang, M.-T.; Lin, C.-T.; Chang, K.-D.; Yu, Y.-C.; Wang, J.T.-W.; Chang, C.-S.; Li, L.-J.; et al. Synthesis of Large-Area MoS2 Atomic Layers with Chemical Vapor Deposition. Adv. Mater. 2012, 24, 2320–2325. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Brown, D.B.; Shen, W.; Li, X.; Xiao, K.; Geohegan, D.B.; Kumar, S. Spatial Mapping of Thermal Boundary Conductance at Metal–Molybdenum Diselenide Interfaces. ACS Appl. Mater. Interfaces 2019, 11, 14418–14426. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef]
- Zhang, X.; Han, W.P.; Wu, J.B.; Milana, S.; Lu, Y.; Li, Q.Q.; Ferrari, A.C.; Tan, P.H. Raman spectroscopy of shear and layer breathing modes in multilayer MoS2. Phys. Rev. B 2013, 87, 115413. [Google Scholar] [CrossRef]
- Tanaka, K.; Hachiya, K.; Zhang, W.; Matsuda, K.; Miyauchi, Y. Machine-Learning Analysis to Predict the Exciton Valley Polarization Landscape of 2D Semiconductors. ACS Nano 2019, 13, 12687–12693. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Najmaei, S.; Liu, Z.; Zhou, W.; Zou, X.; Shi, G.; Lei, S.; Yakobson, B.I.; Idrobo, J.-C.; Ajayan, P.M.; Lou, J. Vapour phase growth and grain boundary structure of molybdenum disulphide atomic layers. Nat. Mater. 2013, 12, 754–759. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling flood susceptibility using data-driven approaches of naïve Bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y.; Chen, T.; Xu, D.; Zhao, H.; Chen, L.; Yan, C.; Tang, L.; He, Y.; Feng, H.; et al. Automatic evaluation of traumatic brain injury based on terahertz imaging with machine learning. Opt. Express 2018, 26, 6371–6381. [Google Scholar] [CrossRef]
- Yang, J.; Yao, H. Automated identification and characterization of two-dimensional materials via machine learning-based processing of optical microscope images. Extrem. Mech. Lett. 2020, 39, 100771. [Google Scholar] [CrossRef]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Dong, N.; Wang, L.; Chen, X.; Wang, H.; Wang, Z.; Kislyakov, I.M.; Wang, J. Machine Learning Analysis of Raman Spectra of MoS2. Nanomaterials 2020, 10, 2223. https://doi.org/10.3390/nano10112223
Mao Y, Dong N, Wang L, Chen X, Wang H, Wang Z, Kislyakov IM, Wang J. Machine Learning Analysis of Raman Spectra of MoS2. Nanomaterials. 2020; 10(11):2223. https://doi.org/10.3390/nano10112223
Chicago/Turabian StyleMao, Yu, Ningning Dong, Lei Wang, Xin Chen, Hongqiang Wang, Zixin Wang, Ivan M. Kislyakov, and Jun Wang. 2020. "Machine Learning Analysis of Raman Spectra of MoS2" Nanomaterials 10, no. 11: 2223. https://doi.org/10.3390/nano10112223
APA StyleMao, Y., Dong, N., Wang, L., Chen, X., Wang, H., Wang, Z., Kislyakov, I. M., & Wang, J. (2020). Machine Learning Analysis of Raman Spectra of MoS2. Nanomaterials, 10(11), 2223. https://doi.org/10.3390/nano10112223




