In Situ and Real-Time Nanoscale Monitoring of Ultra-Thin Metal Film Growth Using Optical and Electrical Diagnostic Tools
Abstract
1. Introduction
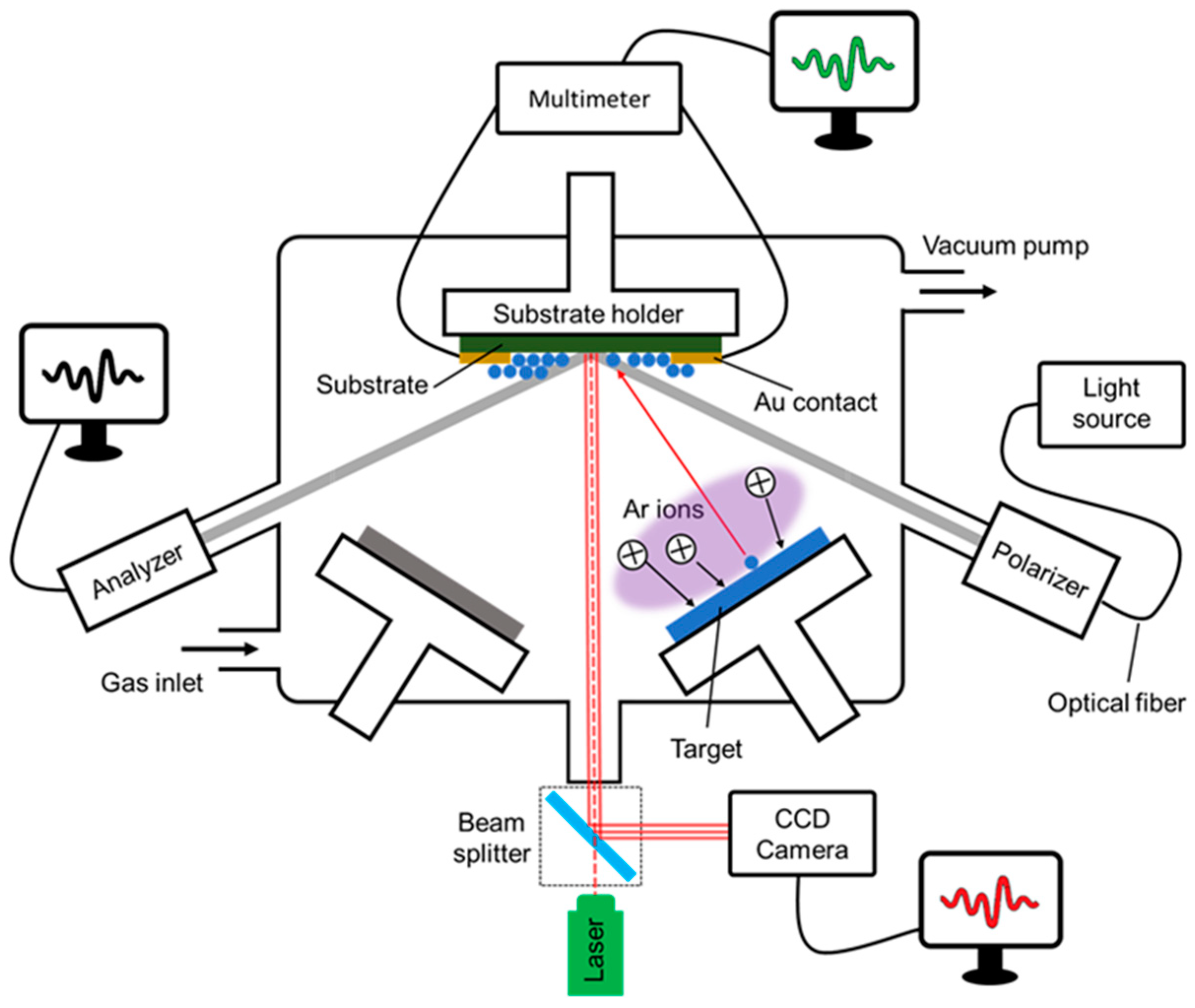
2. Film Synthesis and Real-Time Growth Monitoring
2.1. Film Synthesis and In Situ/Real-Time Monitoring Strategy
2.2. Wafer Curvature Method
2.3. Electrical Resistance
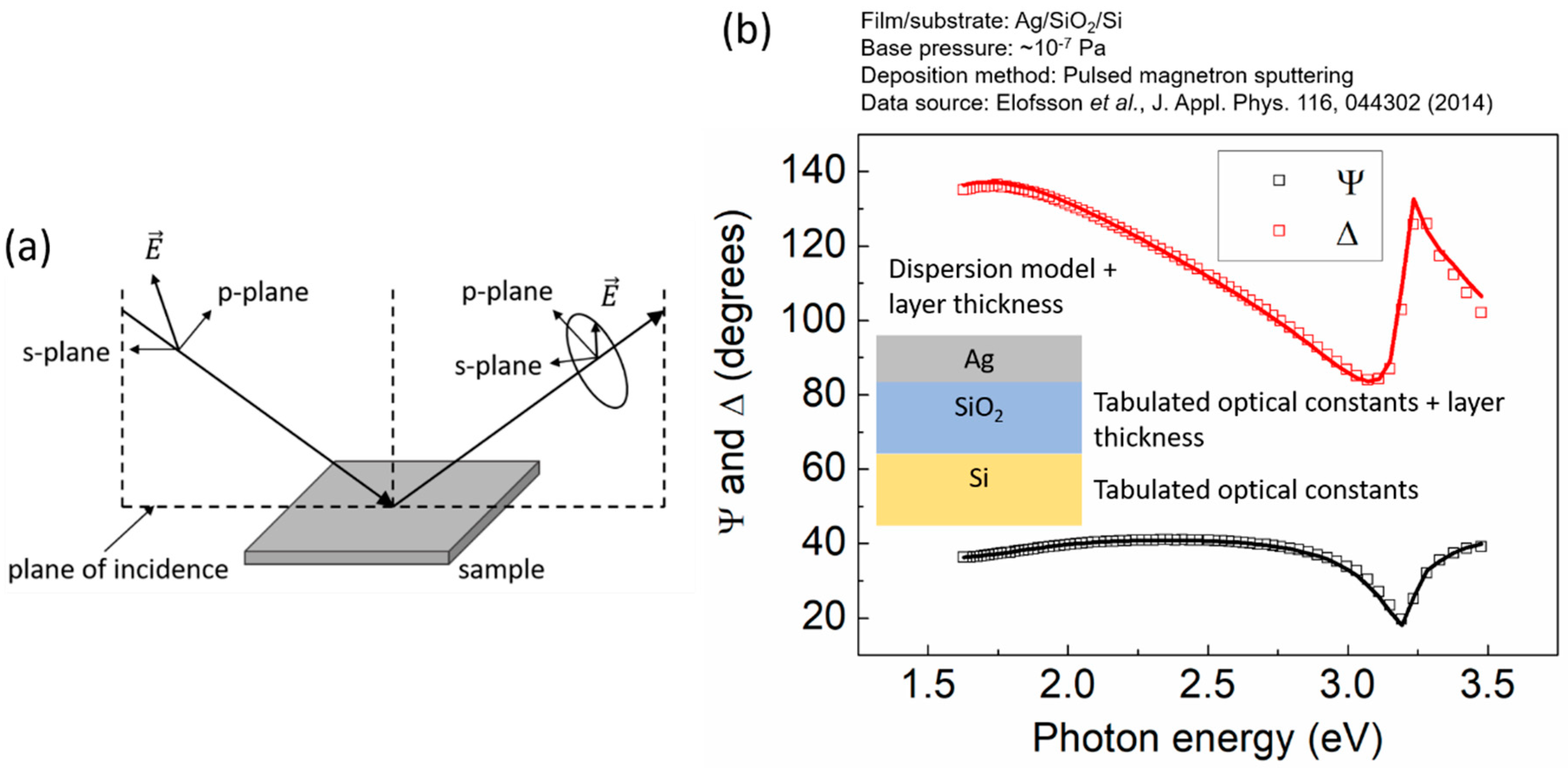
2.4. Spectroscopic Ellipsometry
3. Growth of Metal Films on Weakly-Interacting Substrates
3.1. Film Growth Stages and Morphological Transitions
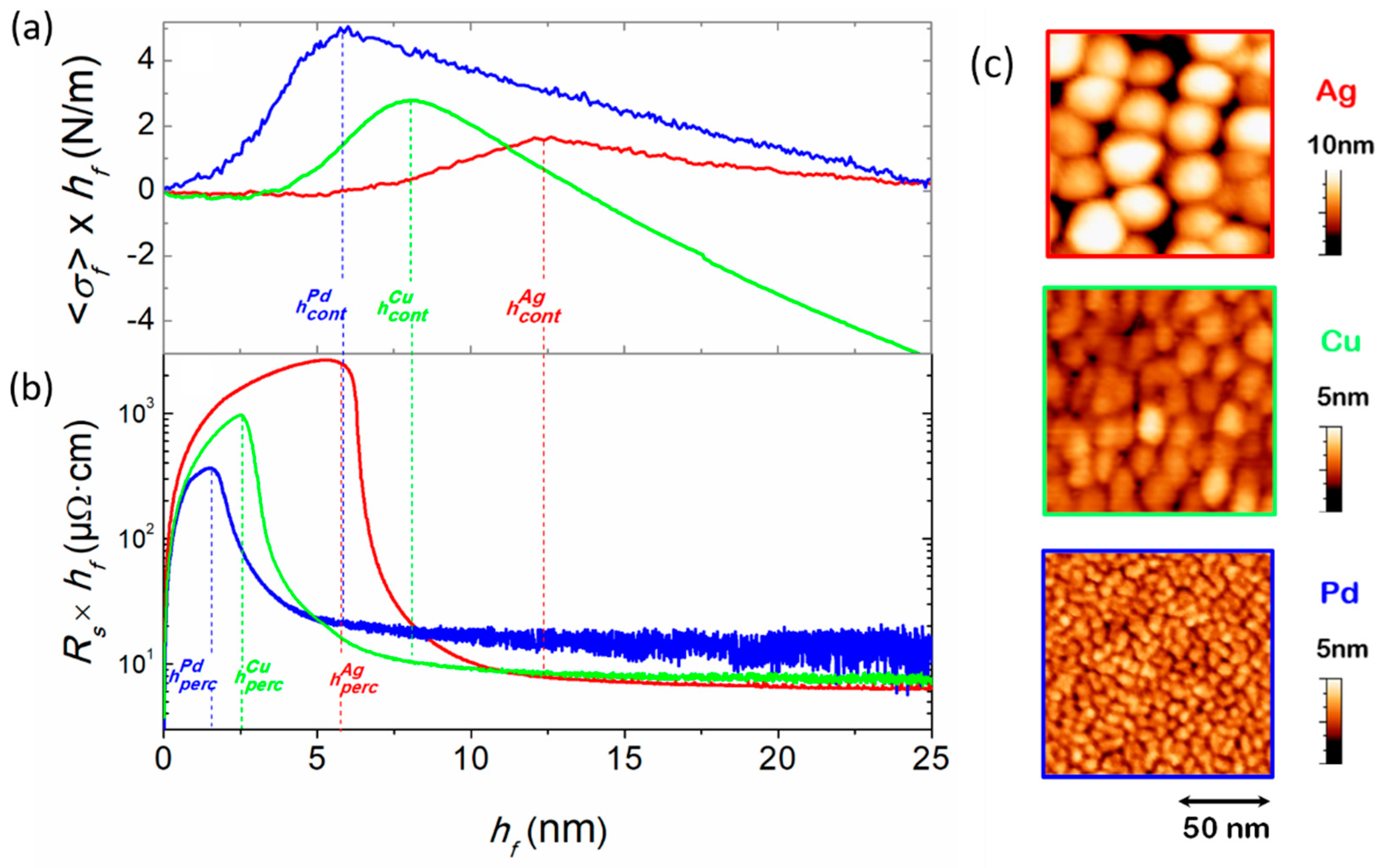
3.2. Experimental Determination of Morphological Transition Thicknesses
3.3. The Effect of Growth Kinetics on Film Morphological Evolution
3.3.1. Influence of Material Intrinsic Mobility
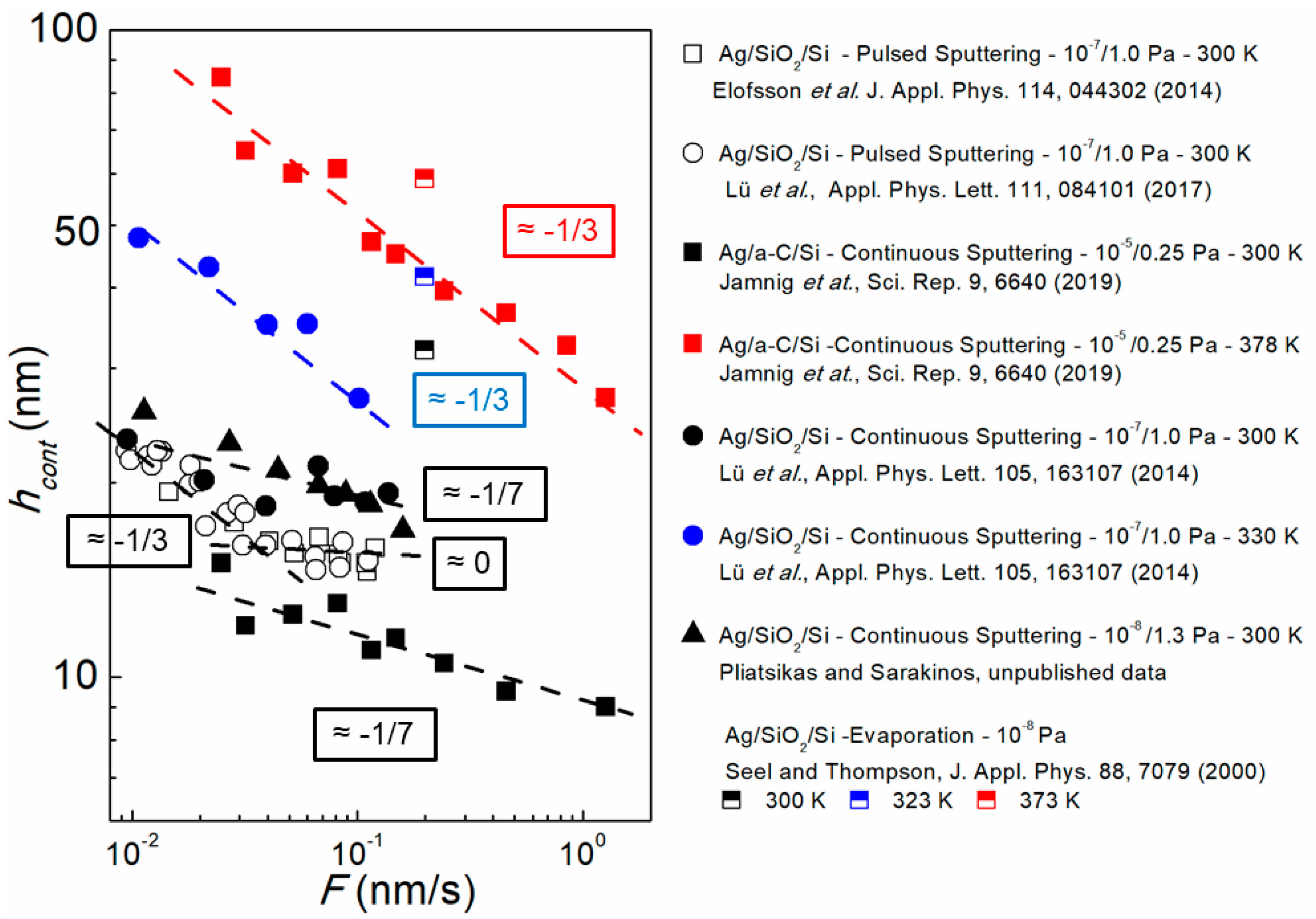
3.3.2. Influence of Deposition Rate and Temperature
3.3.3. Other Factors Influencing Film Morphological Evolution
3.4. Studies of Discontinuous Ag-Layer Morphology
4. Interface Reactivity and Structure Formation
4.1. Growth of Fe, Mo, and Ta on a-Si
4.1.1. Structure and Phase Formation
4.1.2. Early Growth Morphology and Interface Stress
4.2. Effect of Interface Reactivity on Morphological Evolution
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Campbell, C.T. Metal films and particles on oxide surfaces: Structural, electronic and chemisorptive properties. J. Chem. Soc. Faraday Trans. 1996, 92, 1435–1445. [Google Scholar] [CrossRef]
- Mueller, T.; Xia, F.; Avouris, P. Graphene photodetectors for high-speed optical communications. Nat. Photonics 2010, 4, 297–301. [Google Scholar] [CrossRef]
- Gong, C.; Huang, C.; Miller, J.; Cheng, L.; Hao, Y.; Cobden, D.; Kim, J.; Ruoff, R.S.; Wallace, R.M.; Cho, K.; et al. Metal contacts on p hysical vapor deposited monolayer MoS2. ACS Nano 2013, 7, 11350–11357. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Han, Y.; Evans, J.W.; Engstfeld, A.K.; Behm, R.J.; Tringides, M.C.; Hupalo, M.; Lin, H.Q.; Huang, L.; Ho, K.M.; et al. Growth morphology and properties of metals on graphene. Prog. Surf. Sci. 2015, 90, 397–443. [Google Scholar] [CrossRef]
- Echtermeyer, T.J.; Milana, S.; Sassi, U.; Eiden, A.; Wu, M.; Lidorikis, E.; Ferrari, A.C. Surface Plasmon Polariton Graphene Photodetectors. Nano Lett. 2016, 16, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Zilberberg, K.; Riedl, T. Metal-nanostructures-a modern and powerful platform to create transparent electrodes for thin-film photovoltaics. J. Mater. Chem. A 2016, 4, 14481–14508. [Google Scholar] [CrossRef]
- Yun, J. Ultrathin Metal films for Transparent Electrodes of Flexible Optoelectronic Devices. Adv. Funct. Mater. 2017, 27, 1606641. [Google Scholar] [CrossRef]
- Xu, Y.; Hsieh, C.-Y.; Wu, L.; Ang, L.K. Two-dimensional transition metal dichalcogenides mediated long range surface plasmon resonance biosensors. J. Phys. D Appl. Phys. 2019, 52, 65101. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. UK 2018, 20, 43001. [Google Scholar] [CrossRef]
- Patsalas, P.; Kalfagiannis, N.; Kassavetis, S.; Abadias, G.; Bellas, D.V.; Lekka, C.; Lidorikis, E. Conductive nitrides: Growth principles, optical and electronic properties, and their perspectives in photonics and plasmonics. Mater. Sci. Eng. R Rep. 2018, 123, 1–55. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Guo, W.; Hu, Y.; Huang, J.; Mulcahy, J.R.; Wei, W.D. Surface-Plasmon-Driven Hot Electron Photochemistry. Chem. Rev. 2018, 118, 2927–2954. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.; Bauch, M.; Dimopoulos, T.; Trassl, S. Ultrathin sputter-deposited plasmonic silver nanostructures. Nanoscale Adv. 2020, 2, 869–877. [Google Scholar] [CrossRef]
- Achanta, V.G. Surface waves at metal-dielectric interfaces: Material science perspective. Rev. Phys. 2020, 5, 100041. [Google Scholar] [CrossRef]
- Liu, L.; Corma, A. Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles. Chem. Rev. 2018, 118, 4981–5079. [Google Scholar] [CrossRef]
- Kato, K.; Omoto, H.; Tomioka, T.; Takamatsu, A. Visible and near infrared light absorbance of Ag thin films deposited on ZnO underlayers by magnetron sputtering. Sol. Energy Mater. Sol. Cells 2011, 95, 2352–2356. [Google Scholar] [CrossRef]
- Wang, W.; Song, M.; Bae, T.-S.; Park, Y.H.; Kang, Y.-C.; Lee, S.-G.; Kim, S.-Y.; Kim, D.H.; Lee, S.; Min, G.; et al. Transparent Ultrathin Oxygen-Doped Silver Electrodes for Flexible Organic Solar Cells. Adv. Funct. Mater. 2014, 24, 1551–1561. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, W.; Bae, T.S.; Lee, S.S.G.; Mun, C.W.; Lee, S.S.G.; Yu, H.; Lee, G.H.; Song, M.; Yun, J. Stable ultrathin partially oxidized copper film electrode for highly efficient flexible solar cells. Nat. Commun. 2015, 6, 8830. [Google Scholar] [CrossRef]
- Venables, J.A.; Spiller, G.D.T.; Hanbucken, M. Nucleation and growth of thin films. Rep. Prog. Phys. 1984, 47, 399–459. [Google Scholar] [CrossRef]
- Barna, P.B.; Adamik, M. Fundamental structure forming phenomena of polycrystalline films and the structure zone models. Thin Solid Films 1998, 317, 27–33. [Google Scholar] [CrossRef]
- Petrov, I.; Barna, P.B.; Hultman, L.; Greene, J.E. Microstructural evolution during film growth. J. Vac. Sci. Technol. A 2003, 21, S117–S128. [Google Scholar] [CrossRef]
- Michely, T.; Krug, J. Islands, Mounds and Atoms; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Thompson, C.V. Structure evolution during processing of polycrystalline films. Annu. Rev. Mater. Sci. 2000, 30, 159–190. [Google Scholar] [CrossRef]
- Greene, J.E. Thin Film Nucleation, Growth, and Microstructural Evolution: An Atomic Scale View. Handb. Depos. Technol. Film. Coat. 2010, 554–620. [Google Scholar] [CrossRef]
- Martin, P.M. (Ed.) Handbook of Deposition Technologies for Films and Coatings, 3rd ed.; William Andrew: Amsterdam, The Netherlands, 2010; ISBN 9780815520313. [Google Scholar]
- d’Heurle, F.M.; Gas, P. Kinetics of formation of silicides: A review. J. Mater. Res. 1986, 1, 205–221. [Google Scholar] [CrossRef]
- Laurila, T.; Molarius, J. Reactive Phase Formation in Thin Film Metal/Metal and Metal/Silicon Diffusion Couples. Crit. Rev. Solid State Mater. Sci. 2003, 28, 185–230. [Google Scholar] [CrossRef]
- Creuze, J.; Berthier, F.; Tétot, R.; Legrand, B. Phase transition induced by superficial segregation: The respective role of the size mismatch and of the chemistry. Surf. Sci. 2001, 491, 1–16. [Google Scholar] [CrossRef]
- Marks, L.D.; Peng, L. Nanoparticle shape, thermodynamics and kinetics. J. Phys. Condens. Matter 2016, 28, 53001. [Google Scholar] [CrossRef] [PubMed]
- Marsault, M.; Sitja, G.; Henry, C.R. Regular arrays of Pd and PdAu clusters on ultrathin alumina films for reactivity studies. Phys. Chem. Chem. Phys. 2014, 16, 26458–26466. [Google Scholar] [CrossRef]
- Rost, M.J.; Quist, D.A.; Frenken, J.W.M. Grains, Growth, and Grooving. Phys. Rev. Lett. 2003, 91, 26101. [Google Scholar] [CrossRef]
- Rost, M.J.; Crama, L.; Schakel, P.; Van Tol, E.; Van Velzen-Williams, G.B.E.M.; Overgauw, C.F.; Ter Horst, H.; Dekker, H.; Okhuijsen, B.; Seynen, M.; et al. Scanning probe microscopes go video rate and beyond. Rev. Sci. Instrum. 2005, 76, 53710. [Google Scholar] [CrossRef]
- Bauer, E. Low energy electron microscopy. Rep. Prog. Phys. 1994, 57, 895–938. [Google Scholar] [CrossRef]
- Tromp, R.M. Low-energy electron microscopy. IBM J. Res. Dev. 2000, 44, 503–516. [Google Scholar] [CrossRef]
- Cheynis, F.; Leroy, F.; Ranguis, A.; Detailleur, B.; Bindzi, P.; Veit, C.; Bon, W.; Müller, P. Combining low-energy electron microscopy and scanning probe microscopy techniques for surface science: Development of a novel sample-holder. Rev. Sci. Instrum. 2014, 85, 43705. [Google Scholar] [CrossRef]
- Devloo-Casier, K.; Ludwig, K.F.; Detavernier, C.; Dendooven, J. In situ synchrotron based x-ray techniques as monitoring tools for atomic layer deposition. J. Vac. Sci. Technol. A Vac. Surf. Films 2014, 32, 10801. [Google Scholar] [CrossRef]
- Dendooven, J.; Solano, E.; Minjauw, M.M.; Van De Kerckhove, K.; Coati, A.; Fonda, E.; Portale, G.; Garreau, Y.; Detavernier, C. Mobile setup for synchrotron based in situ characterization during thermal and plasma-enhanced atomic layer deposition. Rev. Sci. Instrum. 2016, 87, 113905. [Google Scholar] [CrossRef]
- Renaud, G.; Lazzari, R.; Revenant, C.; Barbier, A.; Noblet, M.; Ulrich, O.; Leroy, F.; Jupille, J.; Borensztein, Y.; Henry, C.R.; et al. Real-time monitoring of growing nanoparticles. Science 2003, 300, 1416–1419. [Google Scholar] [CrossRef]
- Renaud, G.; Lazzari, R.; Leroy, F. Probing surface and interface morphology with Grazing Incidence Small Angle X-ray Scattering. Surf. Sci. Rep. 2009, 64, 255–380. [Google Scholar] [CrossRef]
- Hodas, M.; Siffalovic, P.; Jergel, M.; Pelletta, M.; Halahovets, Y.; Vegso, K.; Kotlar, M.; Majkova, E. Kinetics of copper growth on graphene revealed by time-resolved small-angle x-ray scattering. Phys. Rev. B 2017, 95, 35424. [Google Scholar] [CrossRef]
- Schwartzkopf, M.; Santoro, G.; Brett, C.J.; Rothkirch, A.; Polonskyi, O.; Hinz, A.; Metwalli, E.; Yao, Y.; Strunskus, T.; Faupel, F.; et al. Real-Time Monitoring of Morphology and Optical Properties during Sputter Deposition for Tailoring Metal-Polymer Interfaces. ACS Appl. Mater. Interfaces 2015, 7, 13547–13556. [Google Scholar] [CrossRef]
- Schwartzkopf, M.; Roth, S.V. Investigating polymer–metal interfaces by grazing incidence small-angle x-ray scattering from gradients to real-time studies. Nanomaterials 2016, 6, 239. [Google Scholar] [CrossRef]
- Dann, E.K.; Gibson, E.K.; Catlow, R.A.; Collier, P.; Eralp Erden, T.; Gianolio, D.; Hardacre, C.; Kroner, A.; Raj, A.; Goguet, A.; et al. Combined in Situ XAFS/DRIFTS Studies of the Evolution of Nanoparticle Structures from Molecular Precursors. Chem. Mater. 2017, 29, 7515–7523. [Google Scholar] [CrossRef]
- Schuisky, M.; Elam, J.W.; George, S.M. In situ resistivity measurements during the atomic layer deposition of ZnO and W thin films. Appl. Phys. Lett. 2002, 81, 180–182. [Google Scholar] [CrossRef]
- Arnalds, U.B.; Agustsson, J.S.; Ingason, A.S.; Eriksson, A.K.; Gylfason, K.B.; Gudmundsson, J.T.; Olafsson, S. A magnetron sputtering system for the preparation of patterned thin films and in situ thin film electrical resistance measurements. Rev. Sci. Instrum. 2007, 78, 103901. [Google Scholar] [CrossRef]
- Agustsson, J.S.; Arnalds, U.B.; Ingason, A.S.; Gylfason, K.B.; Johnsen, K.; Olafsson, S.; Gudmundsson, J.T. Growth, coalescence, and electrical resistivity of thin Pt films grown by dc magnetron sputtering on SiO2. Appl. Surf. Sci. 2008, 254, 7356–7360. [Google Scholar] [CrossRef]
- Colin, J.J.; Diot, Y.; Guerin, P.; Lamongie, B.; Berneau, F.; Michel, A.; Jaouen, C.; Abadias, G. A load-lock compatible system for in situ electrical resistivity measurements during thin film growth. Rev. Sci. Instrum. 2016, 87, 23902. [Google Scholar] [CrossRef]
- Simonot, L.; Babonneau, D.; Camelio, S.; Lantiat, D.; Guérin, P.; Lamongie, B.; Antad, V. In situ optical spectroscopy during deposition of Ag:Si3N4 nanocomposite films by magnetron sputtering. Thin Solid Films 2010, 518, 2637–2643. [Google Scholar] [CrossRef]
- Grachev, S.; De Grazia, M.; Barthel, E.; Søndergård, E.; Lazzari, R. Real-time monitoring of nanoparticle film growth at high deposition rate with optical spectroscopy of plasmon resonances. J. Phys. D Appl. Phys. 2013, 46, 375305. [Google Scholar] [CrossRef]
- Renaud, G.; Ducruet, M.; Ulrich, O.; Lazzari, R. Apparatus for real time in situ quantitative studies of growing nanoparticles by grazing incidence small angle X-ray scattering and surface differential reflectance spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2004, 222, 667–680. [Google Scholar] [CrossRef]
- Lazzari, R.; Jupille, J. Quantitative analysis of nanoparticle growth through plasmonics. Nanotechnology 2011, 22, 445703. [Google Scholar] [CrossRef]
- An, I.; Li, Y.M.; Nguyen, H.V.; Collins, R.W. Spectroscopic ellipsometry on the millisecond time scale for real-time investigations of thin-film and surface phenomena. Rev. Sci. Instrum. 1992, 63, 3842–3848. [Google Scholar] [CrossRef]
- Collins, R.W.; An, I.; Nguyen, H.V.; Lu, Y. Real time spectroscopic ellipsometry for characterization of nucleation, growth, and optical functions of thin films. Thin Solid Films 1993, 233, 244–252. [Google Scholar] [CrossRef]
- Oates, T.W.H.; McKenzie, D.R.; Bilek, M.M.M. Percolation threshold in ultrathin titanium films determined by in situ spectroscopic ellipsometry. Phys. Rev. B 2004, 70, 195406. [Google Scholar] [CrossRef]
- Oates, T.W.H.; Mücklich, A. Evolution of plasmon resonances during plasma deposition of silver nanoparticles. Nanotechnology 2005, 16, 2606–2611. [Google Scholar] [CrossRef]
- Patsalas, P.; Logothetidis, S. Interface properties and structural evolution of TiN/Si and TiN/GaN heterostructures. J. Appl. Phys. 2003, 93, 989–998. [Google Scholar] [CrossRef]
- Bulíř, J.; Novotný, M.; Lančok, J.; Fekete, L.; Drahokoupil, J.; Musil, J. Nucleation of ultrathin silver layer by magnetron sputtering in Ar/N2 plasma. Surf. Coat. Technol. 2013, 228, S86–S90. [Google Scholar] [CrossRef]
- Amassian, A.; Desjardins, P.; Martinu, L. Study of TiO2 film growth mechanisms in low-pressure plasma by in situ real-time spectroscopic ellipsometry. Thin Solid Films 2004, 447, 40–45. [Google Scholar] [CrossRef]
- Walker, J.D.; Khatri, H.; Ranjan, V.; Li, J.; Collins, R.W.; Marsillac, S. Electronic and structural properties of molybdenum thin films as determined by real-time spectroscopic ellipsometry. Appl. Phys. Lett. 2009, 94, 141908. [Google Scholar] [CrossRef]
- Wu, P.C.; Losurdo, M.; Kim, T.-H.; Choi, S.; Bruno, G.; Brown, A.S. In situ spectroscopic ellipsometry to monitor surface plasmon resonant group-III metals deposited by molecular beam epitaxy. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2007, 25, 1019–1023. [Google Scholar] [CrossRef]
- Jamnig, A.; Sangiovanni, D.G.; Abadias, G.; Sarakinos, K. Atomic-scale diffusion rates during growth of thin metal films on weakly-interacting substrates. Sci. Rep. 2019, 9, 6640. [Google Scholar] [CrossRef]
- Elofsson, V.; Lü, B.; Magnfält, D.; Münger, E.P.; Sarakinos, K. Unravelling the physical mechanisms that determine microstructural evolution of ultrathin Volmer-Weber films. J. Appl. Phys. 2014, 116, 44302. [Google Scholar] [CrossRef]
- Thornton, J.A. The microstructure of sputter-deposited coatings. J. Vac. Sci. Technol. A Vac. Surf. Films 1986, 4, 3059–3065. [Google Scholar] [CrossRef]
- Thornton, J.A.; Hoffman, D.W. Stress-related effects in thin-films. Thin Solid Films 1989, 171, 5–31. [Google Scholar] [CrossRef]
- Depla, D.; Braeckman, B.R. Quantitative correlation between intrinsic stress and microstructure of thin films. Thin Solid Films 2016, 604, 90–93. [Google Scholar] [CrossRef]
- Gambino, J.P.; Colgan, E.G. Silicides and ohmic contacts. Mater. Chem. Phys. 1998, 52, 99–146. [Google Scholar] [CrossRef]
- Abadias, G.; Chason, E.; Keckes, J.; Sebastiani, M.; Thompson, G.B.; Barthel, E.; Doll, G.L.; Murray, C.E.; Stoessel, C.H.; Martinu, L. Review Article: Stress in thin films and coatings: Current status, challenges, and prospects. J. Vac. Sci. Technol. A 2018, 36, 20801. [Google Scholar] [CrossRef]
- Fluri, A.; Schneider, C.W.; Pergolesi, D. In situ stress measurements of metal oxide thin films. In Metal Oxide-Based Thin Film Structures; Pryds, N., Esposito, V., Eds.; Elsevier Inc.: Amsterdam, The Neatherlands, 2018; pp. 109–132. [Google Scholar]
- Floro, J.A.; Chason, E.; Lee, S.R. Real time measurement of epilayer strain using a simplified wafer curvature technique. Mater. Res. Soc. Symp. Proc. 1996, 406, 491–496. [Google Scholar] [CrossRef]
- Chason, E.; Guduru, P.R. Tutorial: Understanding residual stress in polycrystalline thin films through real-time measurements and physical models. J. Appl. Phys. 2016, 119, 191101. [Google Scholar] [CrossRef]
- Abadias, G.; Fillon, A.; Colin, J.J.; Michel, A.; Jaouen, C. Real-time stress evolution during early growth stages of sputter-deposited metal films: Influence of adatom mobility. Vacuum 2014, 100, 36–40. [Google Scholar] [CrossRef]
- Le Priol, A.; Simonot, L.; Abadias, G.; Guérin, P.; Renault, P.-O.O.; Le Bourhis, E. Real-time curvature and optical spectroscopy monitoring of magnetron-sputtered WTi alloy thin films. Surf. Coat. Technol. 2013, 237, 112–117. [Google Scholar] [CrossRef]
- Abadias, G.; Simonot, L.; Colin, J.J.; Michel, A.; Camelio, S.; Babonneau, D. Volmer-Weber growth stages of polycrystalline metal films probed by in situ and real-time optical diagnostics. Appl. Phys. Lett. 2015, 107, 183105. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarised Light; North Holland: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Herzinger, C.M.; Johs, B.; McGahan, W.A.; Woollam, J.A.; Paulson, W. Ellipsometric determination of optical constants for silicon and thermally grown silicon dioxide via a multi-sample, multi-wavelength, multi-angle investigation. J. Appl. Phys. 1998, 83, 3323–3336. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Oates, T.W.H.; Wormeester, H.; Arwin, H. Characterization of plasmonic effects in thin films and metamaterials using spectroscopic ellipsometry. Prog. Surf. Sci. 2011, 86, 328–376. [Google Scholar] [CrossRef]
- Furgeaud, C. Effets Cinétique et Chimique lors des Premiers Stades de Croissance de Films Minces méTalliques: Compréhension Multi-échelle par une Approche Expérimentale et Modélisation Numérique. Ph.D. Thesis, University of Poitiers, Poitiers, France, 2019. [Google Scholar]
- Jamnig, A.; Pliatsikas, N.; Konpan, M.; Lu, J.; Kehagias, T.; Kotanidis, A.N.; Kalfagiannis, N.; Bellas, D.V.; Lidorikis, E.; Kovac, J.; et al. 3D-to-2D Morphology Manipulation of Sputter-Deposited Nanoscale Silver Films on Weakly Interacting Substrates via Selective Nitrogen Deployment for Multifunctional Metal Contacts. ACS Appl. Nano Mater. 2020, 3, 4728–4738. [Google Scholar] [CrossRef]
- Zinsmeister, G. A contribution to Frenkel’s theory of condensation. Vacuum 1966, 16, 529–535. [Google Scholar] [CrossRef]
- Kryukov, Y.A.; Amar, J.G. Scaling of the island density and island-size distribution in irreversible submonolayer growth of three-dimensional islands. Phys. Rev. B 2010, 81, 165435. [Google Scholar] [CrossRef]
- Nichols, F.A.; Mullins, W.W. Morphological Changes of a Surface of Revolution due to Capillarity-Induced Surface Diffusion. J. Appl. Phys. 1965, 36, 1826–1835. [Google Scholar] [CrossRef]
- Nichols, F.A. Coalescence of Two Spheres by Surface Diffusion. J. Appl. Phys. 1966, 37, 2805–2808. [Google Scholar] [CrossRef]
- Jeffers, G.; Dubson, M.A.; Duxbury, P.M. Island-to-percolation transition during growth of metal films. J. Appl. Phys. 1994, 75, 5016–5020. [Google Scholar] [CrossRef]
- Family, F.; Meakin, P. Scaling of the Droplet-Size Distribution in Vapor-Deposited Thin Films. Phys. Rev. Lett. 1988, 61, 428–431. [Google Scholar] [CrossRef]
- Jensen, P. Growth of nanostructures by cluster deposition: Experiments and simple models. Rev. Mod. Phys. 1999, 71, 1695–1735. [Google Scholar] [CrossRef]
- Carrey, J.; Maurice, J.-L. Transition from droplet growth to percolation: Monte Carlo simulations and an analytical model. Phys. Rev. B 2001, 63, 245408. [Google Scholar] [CrossRef]
- Carrey, J.; Maurice, J.-L. Scaling laws near percolation during three-dimensional cluster growth: A Monte Carlo study. Phys. Rev. B 2002, 65, 205401. [Google Scholar] [CrossRef]
- Lü, B.; Elofsson, V.; Münger, E.P.; Sarakinos, K. Dynamic competition between island growth and coalescence in metal-on-insulator deposition. Appl. Phys. Lett. 2014, 105, 163107. [Google Scholar] [CrossRef]
- Lü, B.; Münger, E.P.; Sarakinos, K. Coalescence-controlled and coalescence-free growth regimes during deposition of pulsed metal vapor fluxes on insulating surfaces. J. Appl. Phys. 2015, 117, 134304. [Google Scholar] [CrossRef]
- Lü, B.; Souqui, L.; Elofsson, V.; Sarakinos, K. Scaling of elongation transition thickness during thin-film growth on weakly interacting substrates. Appl. Phys. Lett. 2017, 111, 84101. [Google Scholar] [CrossRef]
- Maaroof, A.I.; Evans, B.L. Onset of electrical conduction in Pt and Ni films. J. Appl. Phys. 1994, 76, 1047–1054. [Google Scholar] [CrossRef]
- Rycroft, I.M.; Evans, B.L. The in situ characterization of metal film resistance during deposition. Thin Solid Films 1996, 290, 283–288. [Google Scholar] [CrossRef]
- Hérault, Q. Vers la Compréhension de la Croissance des Couches Minces d’argent par pulvérisation, à la lumière de Mesures Operando. Ph.D. Thesis, Sorbonne Université, Paris, France, 2019. [Google Scholar]
- Floro, J.A.; Chason, E.; Cammarata, R.C.; Srolovitz, D.J. Physical origins of intrinsic stresses in Volmer-Weber thin films. MRS Bull. 2002, 27, 19–25. [Google Scholar] [CrossRef]
- Cammarata, R.C.; Trimble, T.M.; Srolovitz, D.J. Surface stress model for intrinsic stresses in thin films. J. Mater. Res. 2000, 15, 2468–2474. [Google Scholar] [CrossRef]
- Hoffman, R.W. Stresses in thin films: The relevance of grain boundaries and impurities. Thin Solid Films 1976, 34, 185–190. [Google Scholar] [CrossRef]
- Nix, W.D.; Clemens, B.M. Crystallite coalescence: A mechanism for intrinsic tensile stresses in thin films. J. Mater. Res. 1999, 14, 3467–3473. [Google Scholar] [CrossRef]
- Seel, S.C.; Thompson, C.V.; Hearne, S.J.; Floro, J.A. Tensile stress evolution during deposition of Volmer–Weber thin films. J. Appl. Phys. 2000, 88, 7079–7088. [Google Scholar] [CrossRef]
- Chason, E.; Sheldon, B.W.; Freund, L.B.; Floro, J.A.; Hearne, S.J. Origin of compressive residual stress in polycrystalline thin films. Phys. Rev. Lett. 2002, 88, 156103. [Google Scholar] [CrossRef]
- Koch, R.; Hu, D.; Das, A.K. Compressive stress in polycrystalline Volmer-Weber films. Phys. Rev. Lett. 2005, 94, 146101. [Google Scholar] [CrossRef]
- Chason, E. A kinetic analysis of residual stress evolution in polycrystalline thin films. Thin Solid Films 2012, 526, 1–14. [Google Scholar] [CrossRef]
- Yu, H.Z.; Thompson, C.V. Correlation of shape changes of grain surfaces and reversible stress evolution during interruptions of polycrystalline film growth. Appl. Phys. Lett. 2014, 104, 141913. [Google Scholar] [CrossRef]
- Vasco, E.; Polop, C. Intrinsic Compressive Stress in Polycrystalline Films is Localized at Edges of the Grain Boundaries. Phys. Rev. Lett. 2017, 119, 256102. [Google Scholar] [CrossRef] [PubMed]
- Colin, J.J. Potentialités des Techniques de Caractérisation In-Situ et en temps réel pour sonder, Comprendre et Contrôler les Processus de Nucléation-croissance Durant le dépôt de Films Minces Métalliques. Ph.D. Thesis, University of Poitiers, Poitiers, France, 2015. [Google Scholar]
- Lü, B.; Almyras, G.A.; Gervilla, V.; Greene, J.E.; Sarakinos, K. Formation and morphological evolution of self-similar 3D nanostructures on weakly interacting substrates. Phys. Rev. Mater. 2018, 2, 63401. [Google Scholar] [CrossRef]
- Gervilla, V.; Almyras, G.A.; Thunström, F.; Greene, J.E.; Sarakinos, K. Dynamics of 3D-island growth on weakly-interacting substrates. Appl. Surf. Sci. 2019, 488, 383–390. [Google Scholar] [CrossRef]
- Gervilla, V.; Almyras, G.A.; Lü, B.; Sarakinos, K. Coalescence dynamics of 3D islands on weakly-interacting substrates. Sci. Rep. 2020, 10, 2031. [Google Scholar] [CrossRef]
- Abermann, R.; Koch, R. In situ study of thin film growth by internal stress measurement under ultrahigh vacuum conditions: Silver and copper under the influence of oxygen. Thin Solid Films 1986, 142, 65–76. [Google Scholar] [CrossRef]
- Jensen, P.; Niemeyer, B. The effect of a modulated flux on the growth of thin films. Surf. Sci. 1997, 384, L823–L827. [Google Scholar] [CrossRef][Green Version]
- Warrender, J.M.; Aziz, M.J. Effect of deposition rate on morphology evolution of metal-on-insulator films grown by pulsed laser deposition. Phys. Rev. B 2007, 76, 45414. [Google Scholar] [CrossRef]
- Jamnig, A.; Pliatsikas, N.; Sarakinos, K.; Abadias, G. The effect of kinetics on intrinsic stress generation and evolution in sputter-deposited films at conditions of high atomic mobility. J. Appl. Phys. 2020, 127, 45302. [Google Scholar] [CrossRef]
- Windischmann, H. Intrinsic stress in sputter-deposited thin films. Crit. Rev. Solid State Mater. Sci. 1992, 17, 547–596. [Google Scholar] [CrossRef]
- Pletea, M.; Brückner, W.; Wendrock, H.; Kaltofen, R. Stress evolution during and after sputter deposition of Cu thin films onto Si (100) substrates under various sputtering pressures. J. Appl. Phys. 2005, 97, 54908. [Google Scholar] [CrossRef]
- Sarakinos, K.; Alami, J.; Konstantinidis, S. High power pulsed magnetron sputtering: A review on scientific and engineering state of the art. Surf. Coat. Technol. 2010, 204, 1661–1684. [Google Scholar] [CrossRef]
- Cemin, F.; Abadias, G.; Minea, T.; Furgeaud, C.; Brisset, F.; Solas, D.; Lundin, D. Benefits of energetic ion bombardment for tailoring stress and microstructural evolution during growth of Cu thin films. Acta Mater. 2017, 141, 120–130. [Google Scholar] [CrossRef]
- Cemin, F.; Lundin, D.; Cammilleri, D.; Maroutian, T.; Lecoeur, P.; Minea, T. Low electrical resistivity in thin and ultrathin copper layers grown by high power impulse magnetron sputtering. J. Vac. Sci. Technol. A Vac. Surf. Films 2016, 34, 51506. [Google Scholar] [CrossRef]
- Anders, A.; Byon, E.; Kim, D.H.; Fukuda, K.; Lim, S.H.N. Smoothing of ultrathin silver films by transition metal seeding. Solid State Commun. 2006, 140, 225–229. [Google Scholar] [CrossRef]
- Pliatsikas, N.; Jamnig, A.; Konpan, M.; Delimitis, A.; Abadias, G.; Sarakinos, K. Manipulation of thin silver film growth on weakly interacting silicon dioxide substrates using oxygen as a surfactant Manipulation of thin silver film growth on weakly interacting silicon dioxide substrates using oxygen as a surfactant. J. Vac. Sci. Technol. A 2020, 38, 43406. [Google Scholar] [CrossRef]
- Jamnig, A.; Pliatsikas, N.; Abadias, G.; Sarakinos, K. On the effect of copper as wetting agent during growth of thin silver films on silicon dioxide substrates. Appl. Surf. Sci. 2020, 538, 148056. [Google Scholar] [CrossRef]
- Zhao, G.; Jeong, E.; Choi, E.A.; Yu, S.M.; Bae, J.S.; Lee, S.G.; Han, S.Z.; Lee, G.H.; Yun, J. Strategy for improving Ag wetting on oxides: Coalescence dynamics versus nucleation density. Appl. Surf. Sci. 2020, 510, 145515. [Google Scholar] [CrossRef]
- Yun, J.; Chung, H.S.; Lee, S.G.; Bae, J.S.; Hong, T.E.; Takahashi, K.; Yu, S.M.; Park, J.; Guo, Q.; Lee, G.H.; et al. An unexpected surfactant role of immiscible nitrogen in the structural development of silver nanoparticles: An experimental and numerical investigation. Nanoscale 2020, 12, 1749–1758. [Google Scholar] [CrossRef] [PubMed]
- Kaub, T.M.; Felfer, P.; Cairney, J.M.; Thompson, G.B. Influence of Ni Solute segregation on the intrinsic growth stresses in Cu(Ni) thin films. Scr. Mater. 2016, 113, 131–134. [Google Scholar] [CrossRef]
- Kaub, T.; Anthony, R.; Thompson, G.B. Intrinsic stress response of low and high mobility solute additions to Cu thin films. J. Appl. Phys. 2017, 122, 225302. [Google Scholar] [CrossRef]
- Movchan, B.A.; Demchishin, W.V. Study of the Structure and Properties of Thick Vacuum Condensates of Nickel, Titanium, Tungsten, Aluminium Oxide and Zirconium Dioxide. Phys. Met. Met. 1969, 28, 83–90. [Google Scholar]
- Mahieu, S.; Ghekiere, P.; Depla, D.; De Gryse, R. Biaxial alignment in sputter deposited thin films. Thin Solid Films 2006, 515, 1229–1249. [Google Scholar] [CrossRef]
- Belliard, L.; Huynh, A.; Perrin, B.; Michel, A.; Abadias, G.; Jaouen, C. Elastic properties and phonon generation in Mo/Si superlattices. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 155424. [Google Scholar] [CrossRef]
- Colin, J.J.; Abadias, G.; Michel, A.; Jaouen, C. On the origin of the metastable β-Ta phase stabilization in tantalum sputtered thin films. Acta Mater. 2017, 126, 481–493. [Google Scholar] [CrossRef]
- Arakcheeva, A.; Chapuis, G.; Grinevitch, V. The self-hosting structure of β-Ta. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 2002, 58, 1–7. [Google Scholar] [CrossRef]
- Abadias, G.; Colin, J.J.; Tingaud, D.; Djemia, P.; Belliard, L.; Tromas, C. Elastic properties of α- and β-tantalum thin films. Thin Solid Films 2019, 688, 137403. [Google Scholar] [CrossRef]
- Ellis, E.A.I.; Chmielus, M.; Baker, S.P. Effect of sputter pressure on Ta thin films: Beta phase formation, texture, and stresses. Acta Mater. 2018, 150, 317–326. [Google Scholar] [CrossRef]
- Reinink, J.; Zameshin, A.; Van De Kruijs, R.W.E.; Bijkerk, F. In-situ studies of silicide formation during growth of molybdenum-silicon interfaces. J. Appl. Phys. 2019, 126, 135304. [Google Scholar] [CrossRef]
- Bajt, S.; Stearns, D.G.; Kearney, P.A. Investigation of the amorphous-to-crystalline transition in Mo/Si multilayers. J. Appl. Phys. 2001, 90, 1017–1025. [Google Scholar] [CrossRef]
- Fillon, A.; Abadias, G.; Michel, A.; Jaouen, C.; Villechaise, P. Influence of Phase Transformation on Stress Evolution during Growth of Metal Thin Films on Silicon. Phys. Rev. Lett. 2010, 104, 96101. [Google Scholar] [CrossRef]
- Krause, B.; Abadias, G.; Michel, A.; Wochner, P.; Ibrahimkutty, S.; Baumbach, T. Direct Observation of the Thickness-Induced Crystallization and Stress Build-Up during Sputter-Deposition of Nanoscale Silicide Films. ACS Appl. Mater. Interfaces 2016, 8, 34888–34895. [Google Scholar] [CrossRef]
- Steiner, R.; Boyen, H.G.; Krieger, M.; Plettl, A.; Widmayer, P.; Ziemann, P.; Banhart, F.; Kilper, R.; Oelhafen, P. Interface reactions in [Fe/B]n multilayers: A way to tune from crystalline/amorphous layer sequences to homogeneous amorphous FexB100-x films. Appl. Phys. A Mater. Sci. Process. 2003, 76, 5–13. [Google Scholar] [CrossRef]
- Cammarata, R.C. Surface and interface stress effects on the growth of thin films. Prog. Surf. Sci. 1994, 46, 1–38. [Google Scholar] [CrossRef]
- Müller, P.; Thomas, O. Asymptotic behaviour of stress establishment in thin films. Surf. Sci. 2000, 465, L764–L770. [Google Scholar] [CrossRef]
- Jiang, Q.; Lu, H.M. Size dependent interface energy and its application. Surf. Sci. Rep. 2008, 63, 427–464. [Google Scholar] [CrossRef]
- Edelman, F.; Cytermann, C.; Brener, R.; Eizenberg, M.; Weil, R.; Beyer, W. Interfacial reactions in the Pd/a-Si/c-Si system. J. Appl. Phys. 1992, 71, 289–295. [Google Scholar] [CrossRef]
- Richard, M.I.; Fouet, J.; Guichet, C.; Mocuta, C.; Thomas, O. Exploring Pd-Si(001) and Pd-Si(111) thin-film reactions by simultaneous synchrotron X-ray diffraction and substrate curvature measurements. Thin Solid Films 2013, 530, 100–104. [Google Scholar] [CrossRef]
- Richard, M.I.; Fouet, J.; Texier, M.; Mocuta, C.; Guichet, C.; Thomas, O. Continuous and Collective Grain Rotation in Nanoscale Thin Films during Silicidation. Phys. Rev. Lett. 2015, 115, 266101. [Google Scholar] [CrossRef]
- Molina-Ruiz, M.; Ferrando-Villalba, P.; Rodríguez-Tinoco, C.; Garcia, G.; Rodríguez-Viejo, J.; Peral, I.; Lopeandía, A.F. Simultaneous nanocalorimetry and fast XRD measurements to study the silicide formation in Pd/a-Si bilayers. J. Synchrotron Radiat. 2015, 22, 717–722. [Google Scholar] [CrossRef]
- d’Heurle, F.M.; Thomas, O. Stresses during silicide formation: A review. Defect Diffus. Forum 1996, 129, 137–150. [Google Scholar] [CrossRef]
- Krause, B.; Abadias, G.; Furgeaud, C.; Michel, A.; Resta, A.; Coati, A.; Garreau, Y.; Vlad, A.; Hauschild, D.; Baumbach, T. Interfacial Silicide Formation and Stress Evolution during Sputter-Deposition of Ultrathin Pd Layers on a-Si. ACS Appl. Mater. Interfaces 2019, 11, 39315–39323. [Google Scholar] [CrossRef]
- De Melo, C.; Jullien, M.; Battie, Y.; En Naciri, A.; Ghanbaja, J.; Montaigne, F.; Pierson, J.F.; Rigoni, F.; Almqvist, N.; Vomiero, A.; et al. Tunable Localized Surface Plasmon Resonance and Broadband Visible Photoresponse of Cu Nanoparticles/ZnO Surfaces. ACS Appl. Mater. Interfaces 2018, 10, 40958–40965. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.-L. Design of dielectric/metal/dielectric transparent electrodes for flexible electronics. J. Photonics Energy 2012, 2, 21215. [Google Scholar] [CrossRef]
- Kim, H.-J.; Seo, K.-W.; Kim, H.-K.; Noh, Y.-J.; Na, S.-I. Ag-Pd-Cu alloy inserted transparent indium tin oxide electrodes for organic solar cells. J. Vac. Sci. Technol. A Vac. Surf. Films 2014, 32, 51507. [Google Scholar] [CrossRef]
- Thompson, C.V. Solid-state dewetting of thin films. Annu. Rev. Mater. Res. 2012, 42, 399–434. [Google Scholar] [CrossRef]
- Jacquet, P.; Podor, R.; Ravaux, J.; Lautru, J.; Teisseire, J.; Gozhyk, I.; Jupille, J.; Lazzari, R. On the solid-state dewetting of polycrystalline thin films: Capillary versus grain growth approach. Acta Mater. 2018, 143, 281–290. [Google Scholar] [CrossRef]
- Leroy, F.; Cheynis, F.; Almadori, Y.; Curiotto, S.; Trautmann, M.; Barbé, J.C.; Müller, P. How to control solid state dewetting: A short review. Surf. Sci. Rep. 2016, 71, 391–409. [Google Scholar] [CrossRef]
- Zhao, G.; Kim, S.M.; Lee, S.-G.; Bae, T.-S.; Mun, C.; Lee, S.; Yu, H.; Lee, G.-H.; Lee, H.-S.; Song, M.; et al. Bendable Solar Cells from Stable, Flexible, and Transparent Conducting Electrodes Fabricated Using a Nitrogen-Doped Ultrathin Copper Film. Adv. Funct. Mater. 2016, 26, 4180–4191. [Google Scholar] [CrossRef]
- Zhao, G.; Shen, W.; Jeong, E.; Lee, S.G.; Yu, S.M.; Bae, T.S.; Lee, G.H.; Han, S.Z.; Tang, J.; Choi, E.A.; et al. Ultrathin Silver Film Electrodes with Ultralow Optical and Electrical Losses for Flexible Organic Photovoltaics. ACS Appl. Mater. Interfaces 2018, 10, 27510–27520. [Google Scholar] [CrossRef]
- De Melo, C.; Jullien, M.; Battie, Y.; En Naciri, A.; Ghanbaja, J.; Montaigne, F.; Pierson, J.F.; Rigoni, F.; Almqvist, N.; Vomiero, A.; et al. Semi-Transparent p-Cu2O/n-ZnO Nanoscale-film heterojunctions for photodetection and photovoltaic applications. ACS Appl. Nano Mater. 2019, 2, 4358–4366. [Google Scholar] [CrossRef]




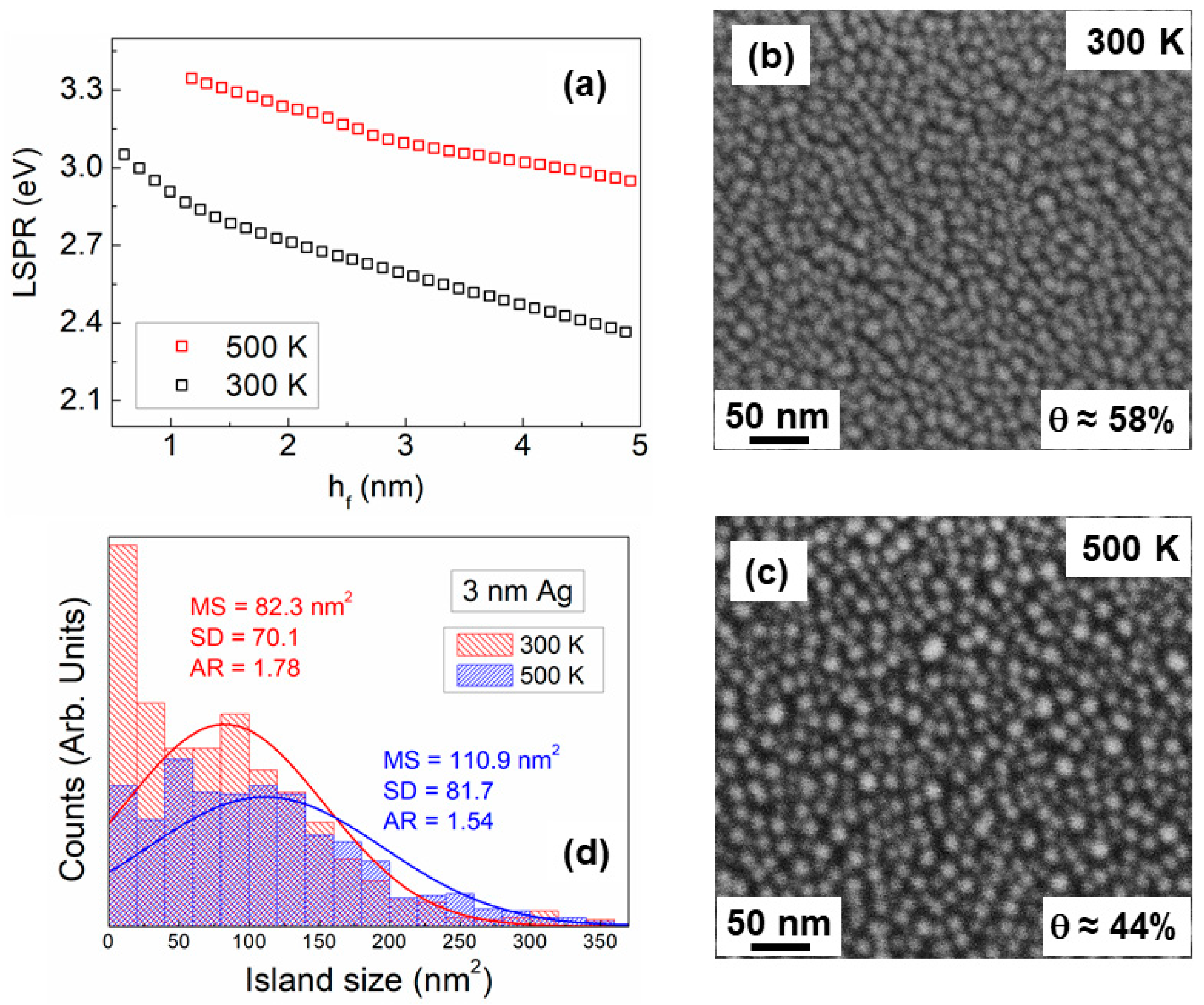
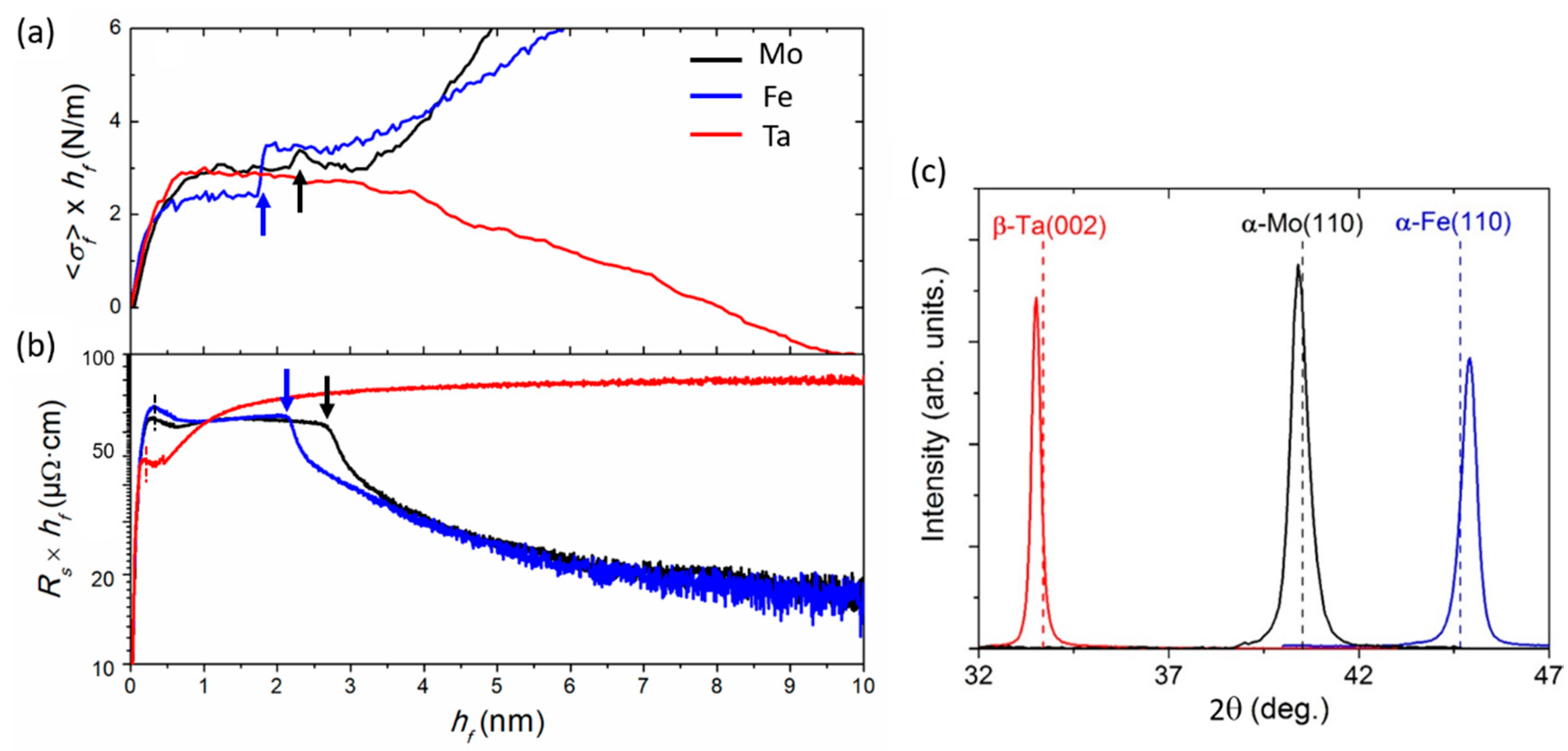
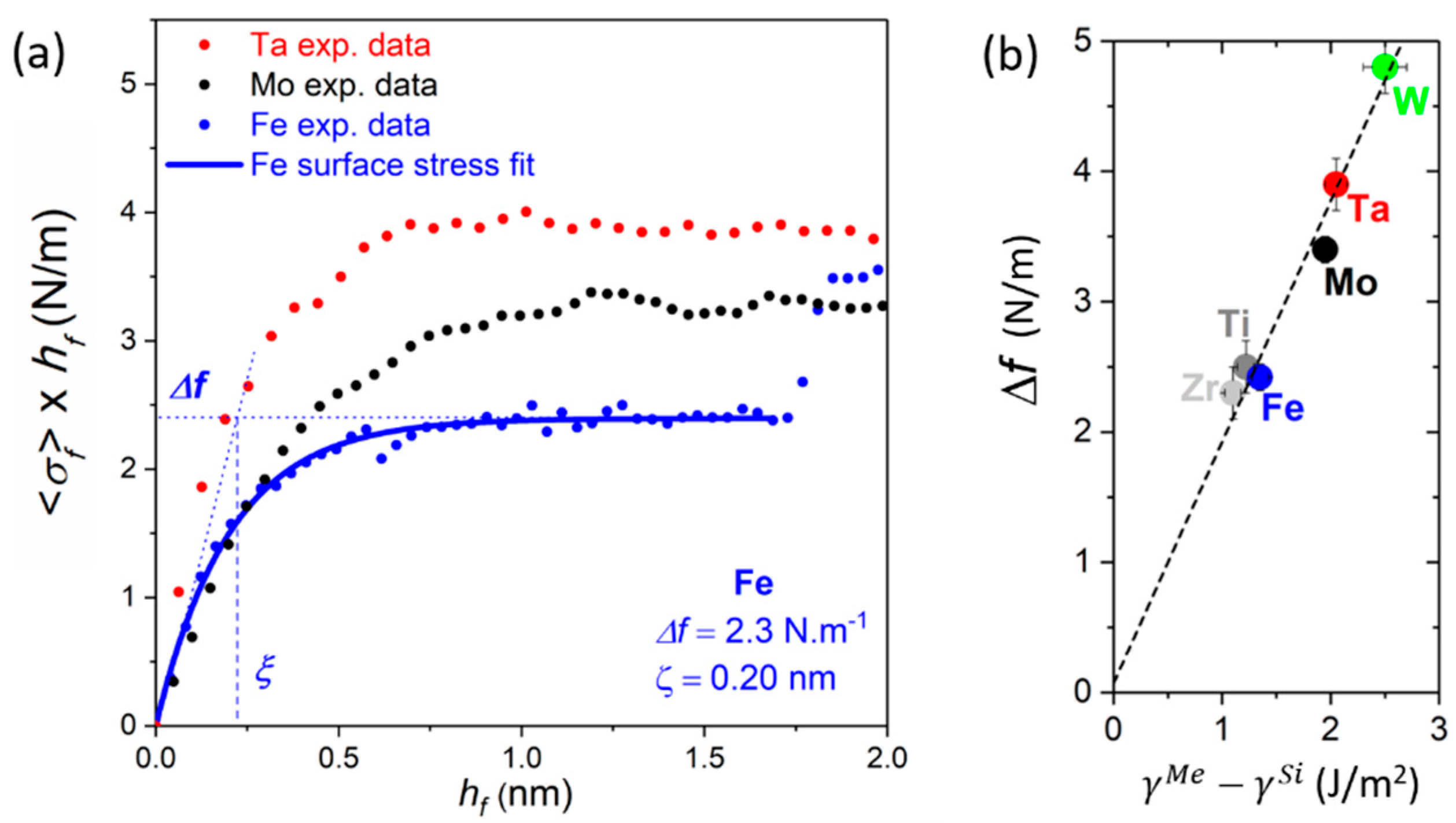
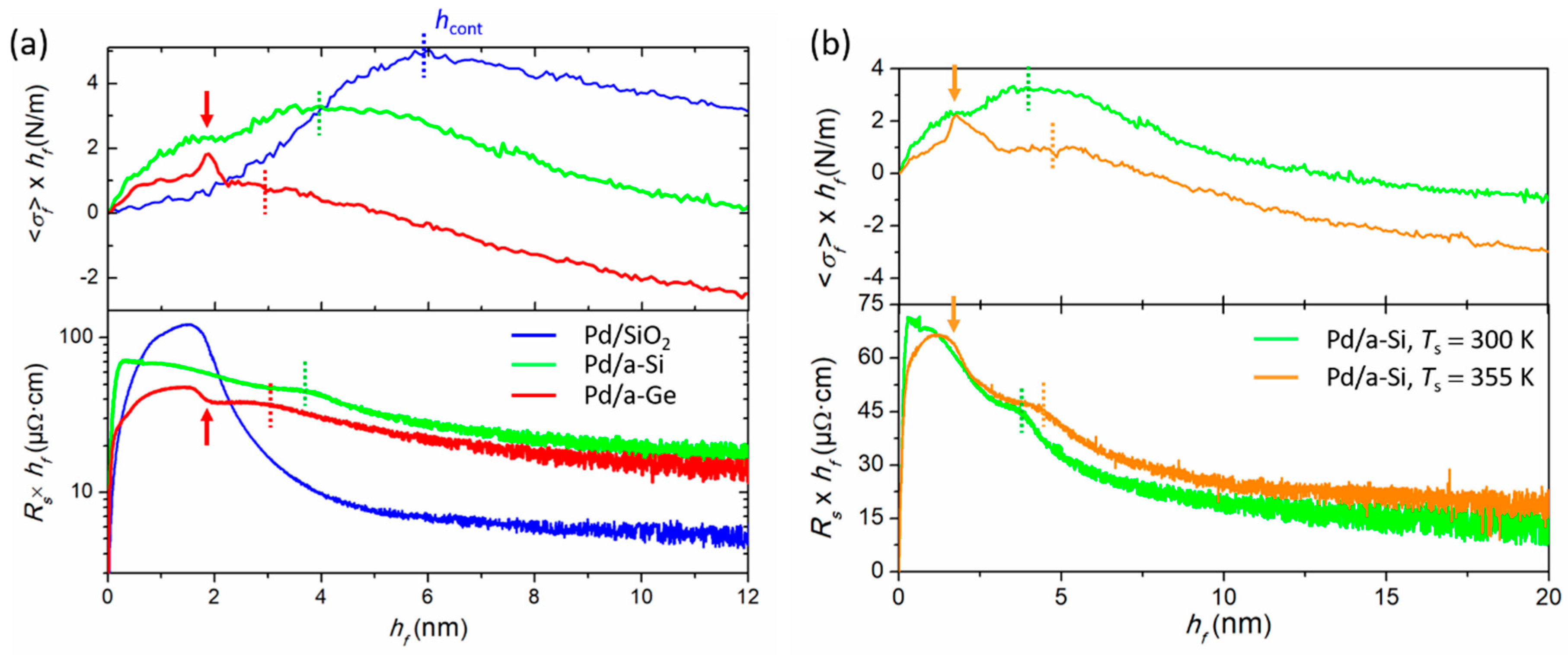

| Element | Crystal Structure | Target Power (W) | Deposition Rate F (nm/s) | (nm) | (nm) | |
|---|---|---|---|---|---|---|
| Ag | fcc | 15 | 0.06 | 0.24 | 5.9 ± 0.1 | 12.4 ± 0.1 |
| Cu | fcc | 30 | 0.06 | 0.22 | 2.6 ± 0.1 | 8.2 ± 0.1 |
| Pd | fcc | 30 | 0.08 | 0.16 | 1.7 ± 0.1 | 5.9 ± 0.1 |
| Element | Crystal Structure | Target Power (W) | Deposition Rate F (nm/s) | (J/m2) | (nm) | (nm) | |
|---|---|---|---|---|---|---|---|
| Fe | bcc | 60 | 0.06 | 0.16 | 2.3 ± 0.1 | 0.20 ± 0.06 | 0.30 ± 0.05 |
| Mo | bcc | 50 | 0.05 | 0.10 | 3.4 ± 0.1 | 0.30 ± 0.05 | 0.27± 0.05 |
| Ta | β (A-15) | 50 | 0.05 | 0.09 | 3.9 ± 0.1 | 0.39 ± 0.02 | 0.14± 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colin, J.; Jamnig, A.; Furgeaud, C.; Michel, A.; Pliatsikas, N.; Sarakinos, K.; Abadias, G. In Situ and Real-Time Nanoscale Monitoring of Ultra-Thin Metal Film Growth Using Optical and Electrical Diagnostic Tools. Nanomaterials 2020, 10, 2225. https://doi.org/10.3390/nano10112225
Colin J, Jamnig A, Furgeaud C, Michel A, Pliatsikas N, Sarakinos K, Abadias G. In Situ and Real-Time Nanoscale Monitoring of Ultra-Thin Metal Film Growth Using Optical and Electrical Diagnostic Tools. Nanomaterials. 2020; 10(11):2225. https://doi.org/10.3390/nano10112225
Chicago/Turabian StyleColin, Jonathan, Andreas Jamnig, Clarisse Furgeaud, Anny Michel, Nikolaos Pliatsikas, Kostas Sarakinos, and Gregory Abadias. 2020. "In Situ and Real-Time Nanoscale Monitoring of Ultra-Thin Metal Film Growth Using Optical and Electrical Diagnostic Tools" Nanomaterials 10, no. 11: 2225. https://doi.org/10.3390/nano10112225
APA StyleColin, J., Jamnig, A., Furgeaud, C., Michel, A., Pliatsikas, N., Sarakinos, K., & Abadias, G. (2020). In Situ and Real-Time Nanoscale Monitoring of Ultra-Thin Metal Film Growth Using Optical and Electrical Diagnostic Tools. Nanomaterials, 10(11), 2225. https://doi.org/10.3390/nano10112225






