Molecular Dynamics Simulations of Ion Drift in Nanochannel Water Flow
Abstract
:1. Introduction
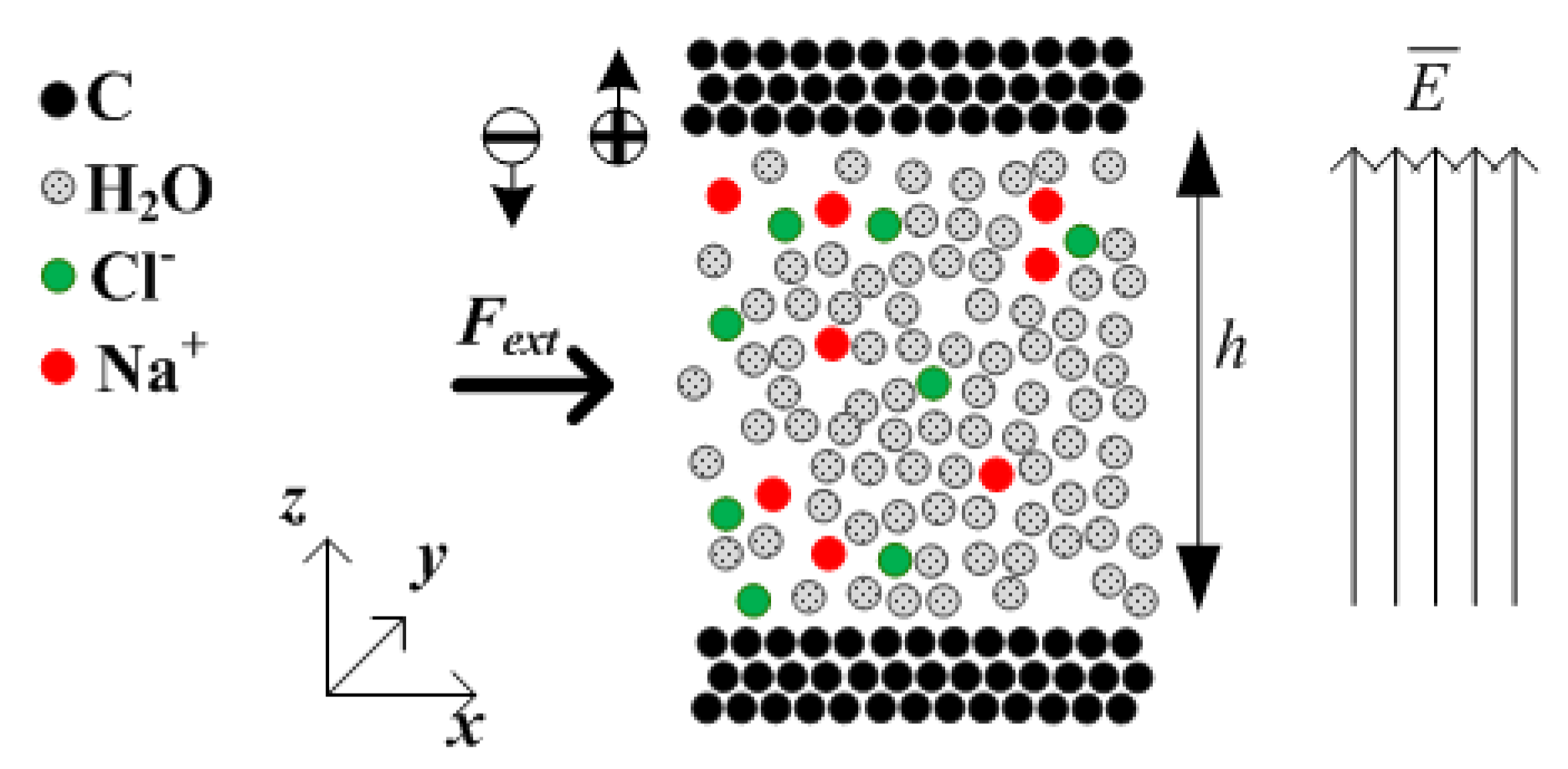
2. Materials and Methods
2.1. Channel Description
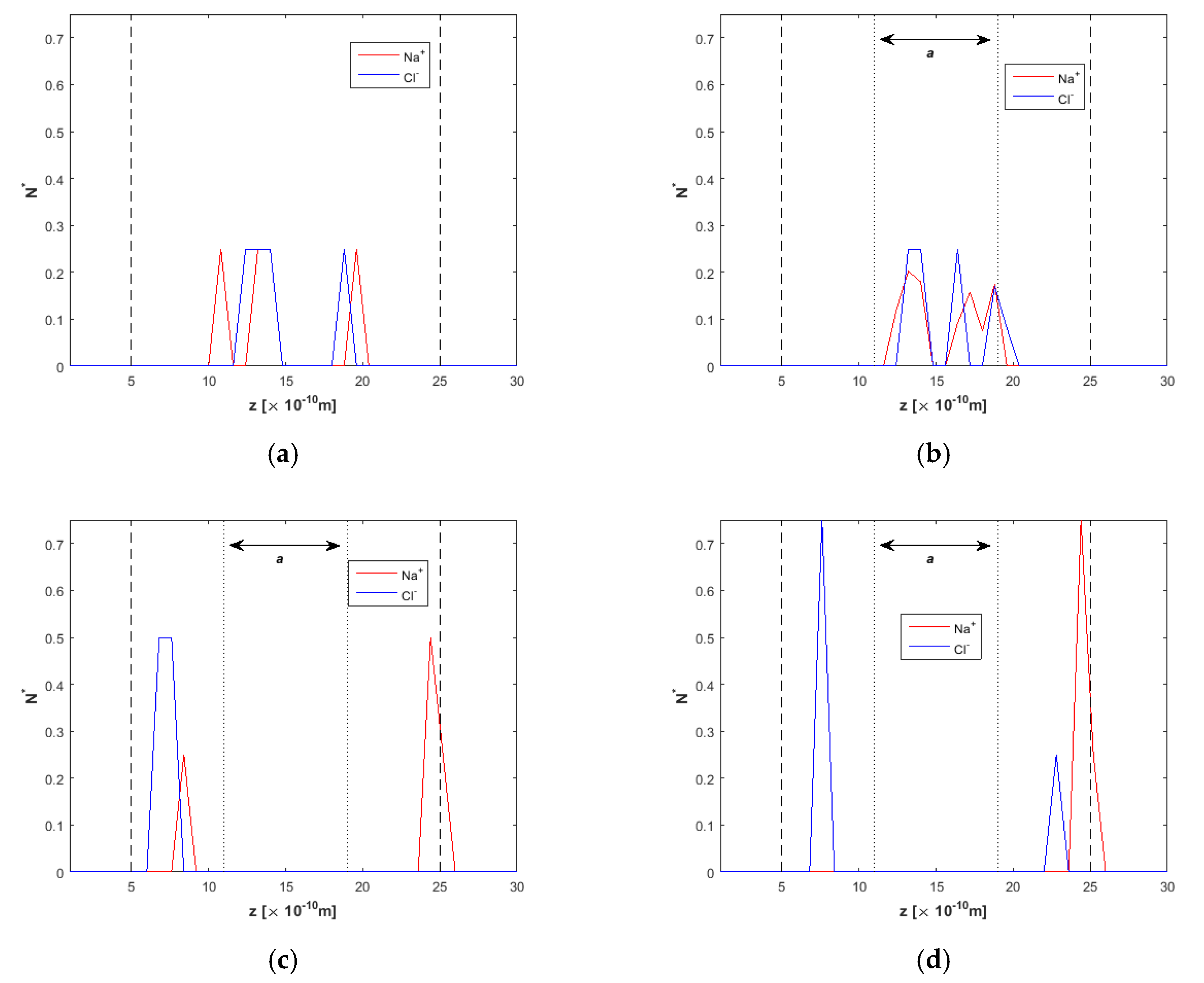
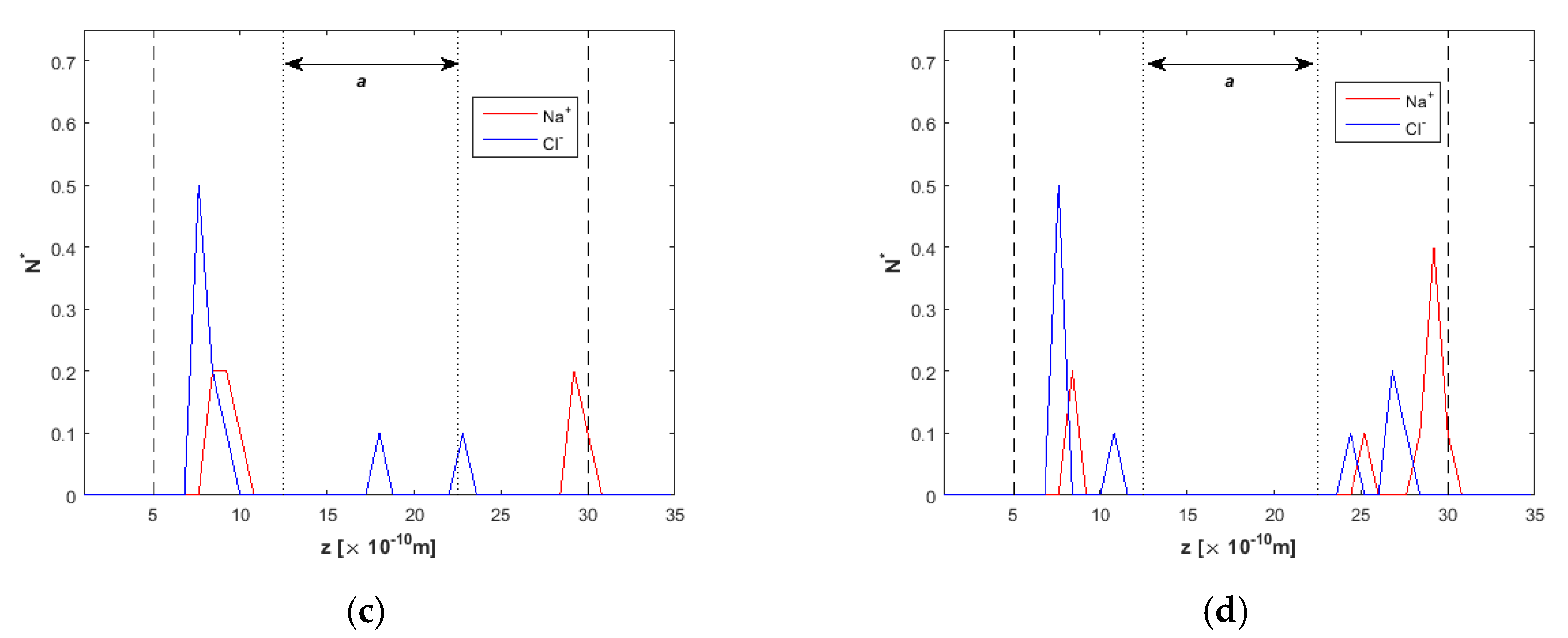
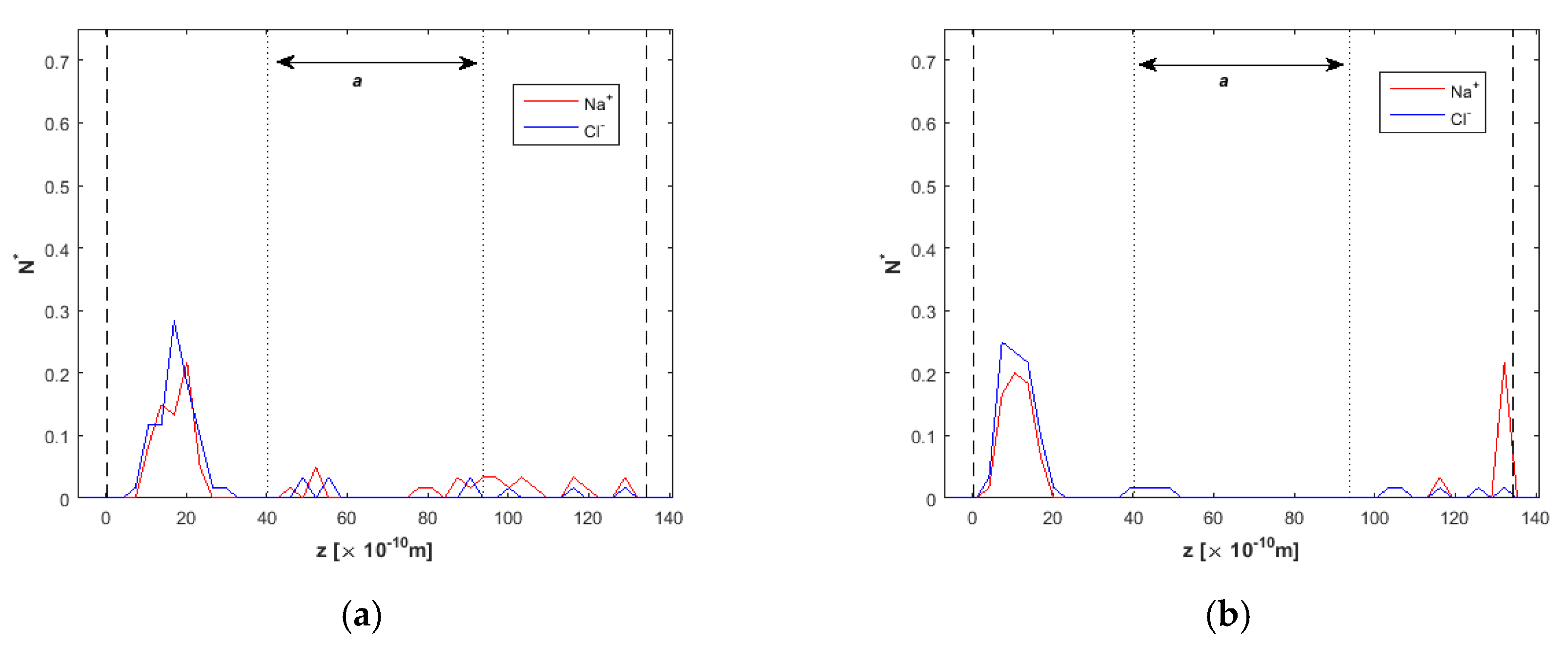
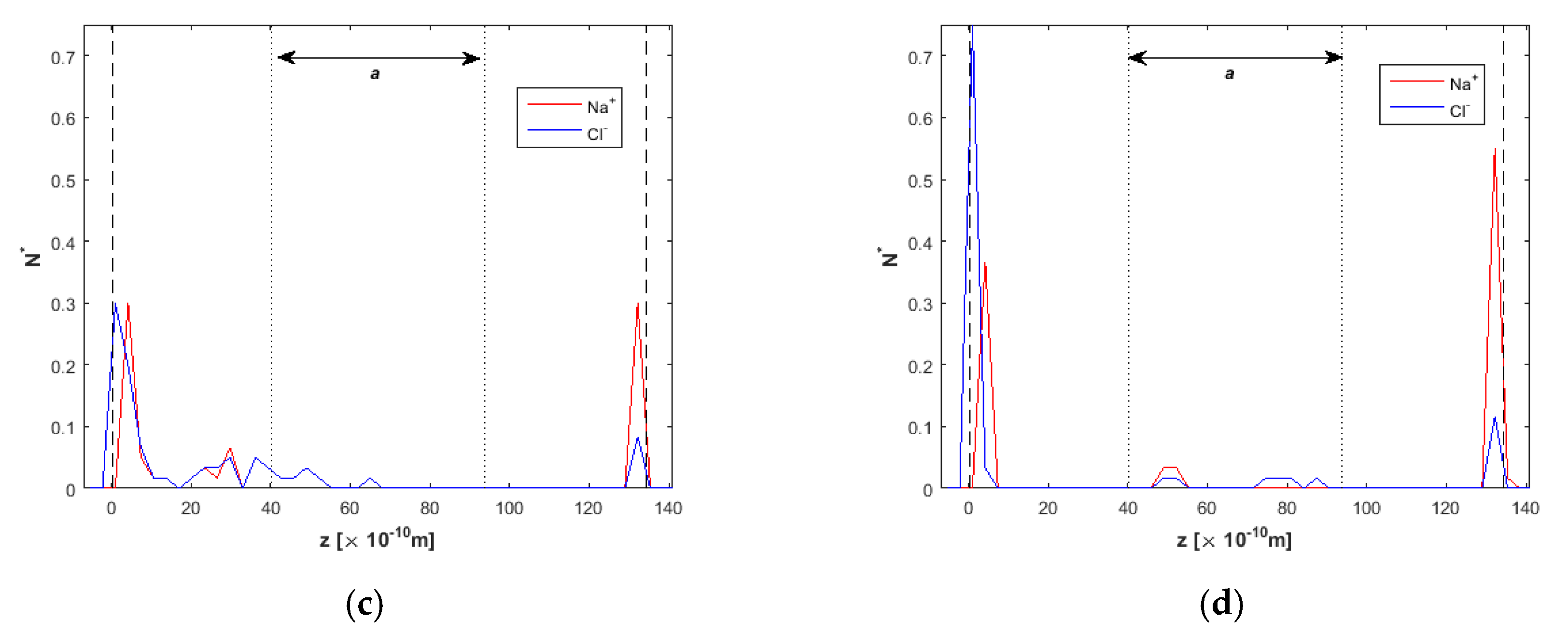
2.2. Ion Separation
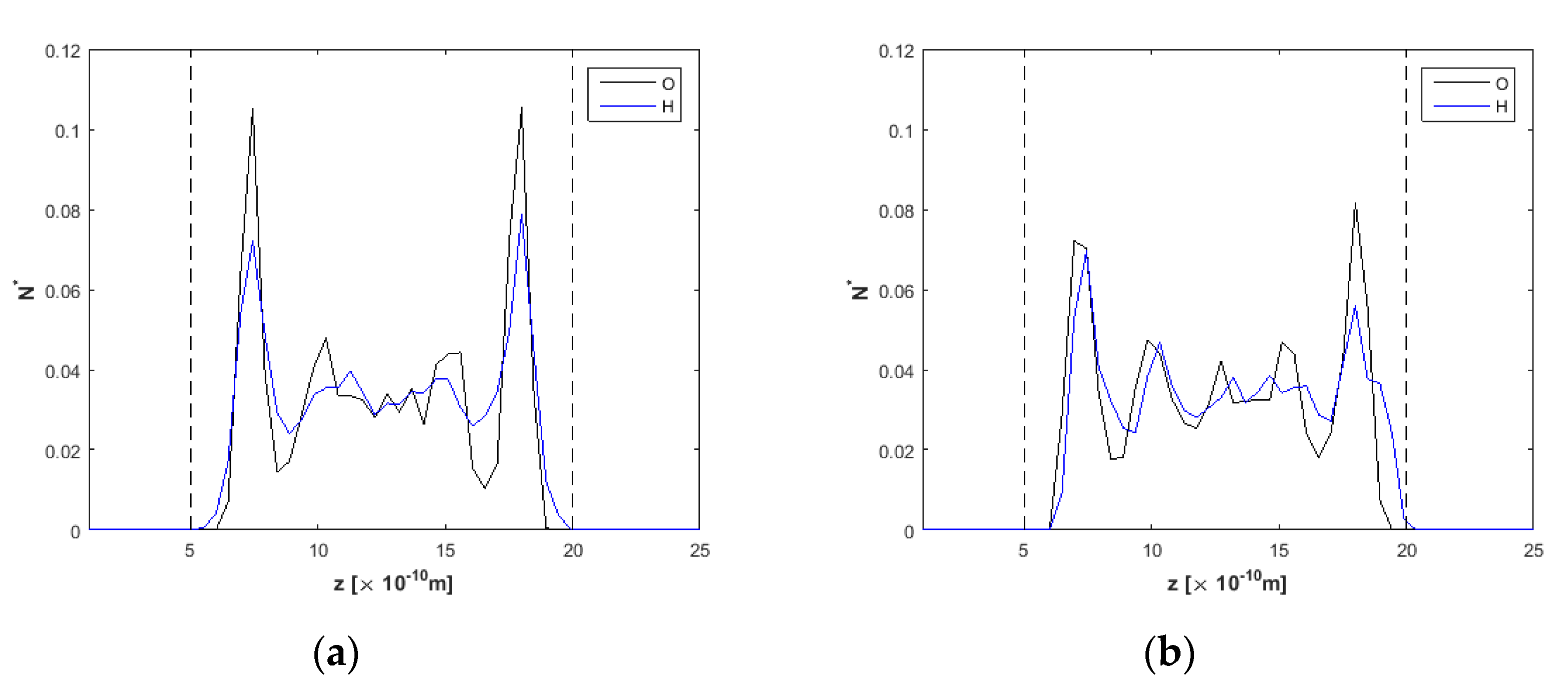
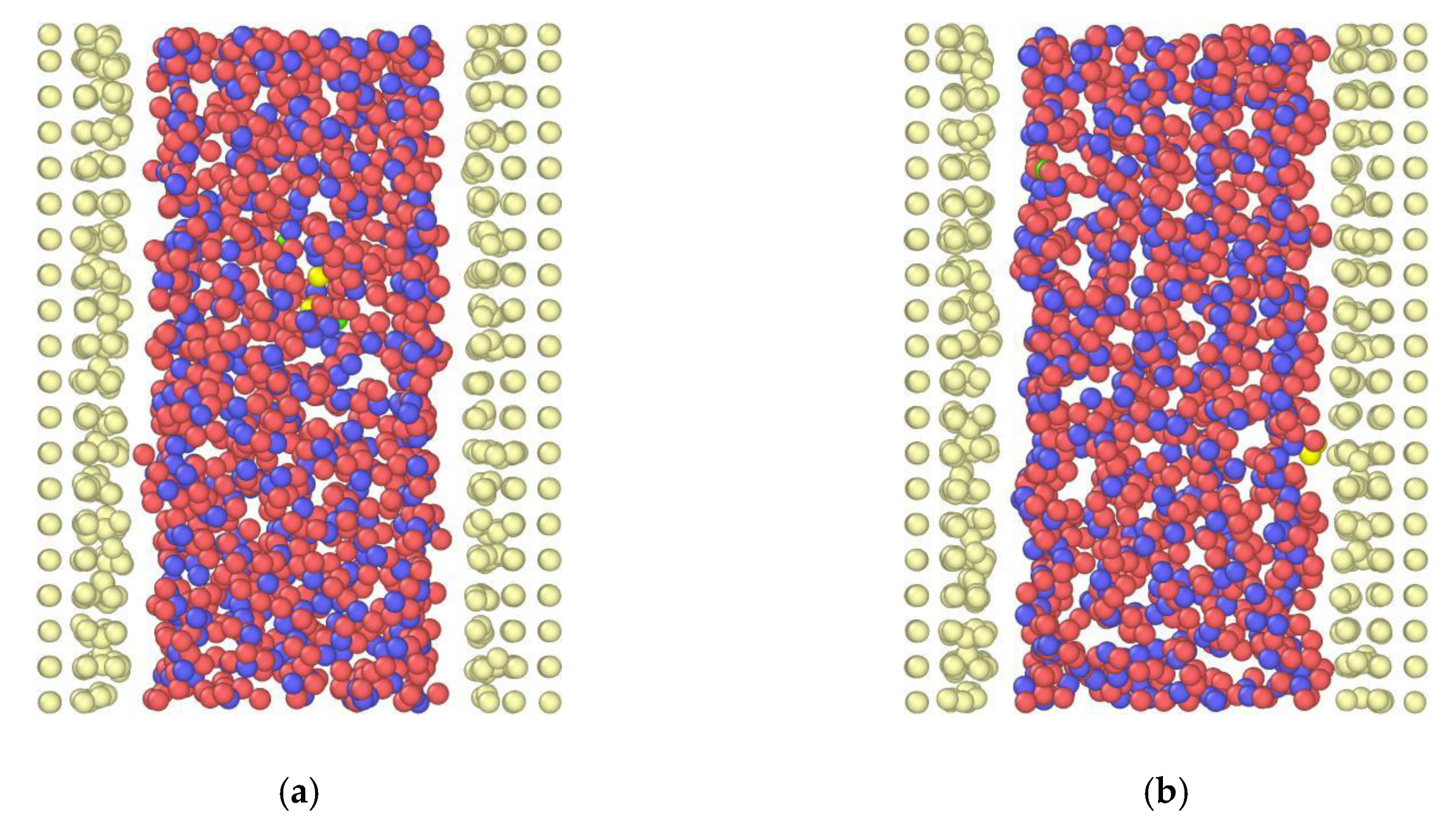
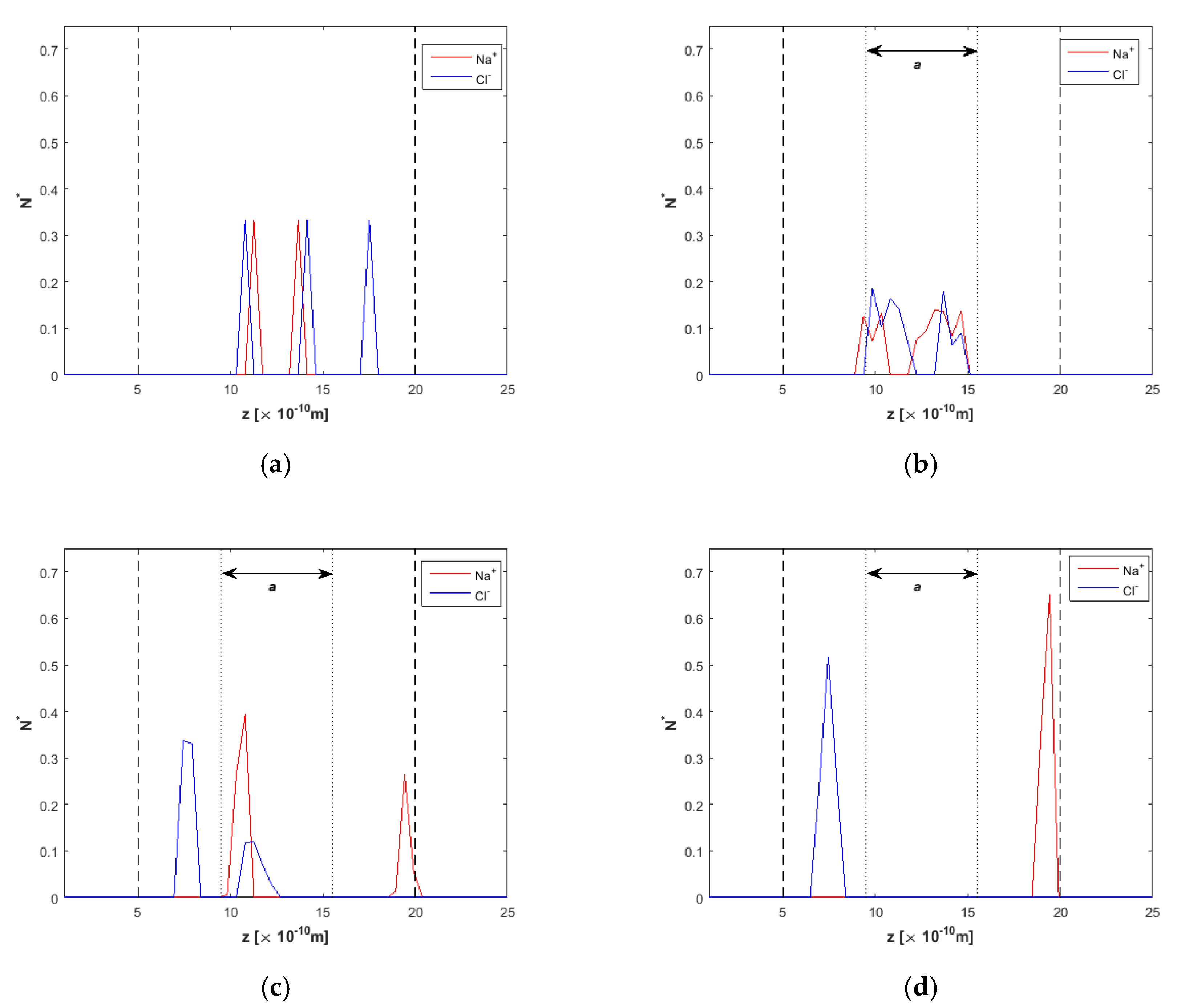
3. Results
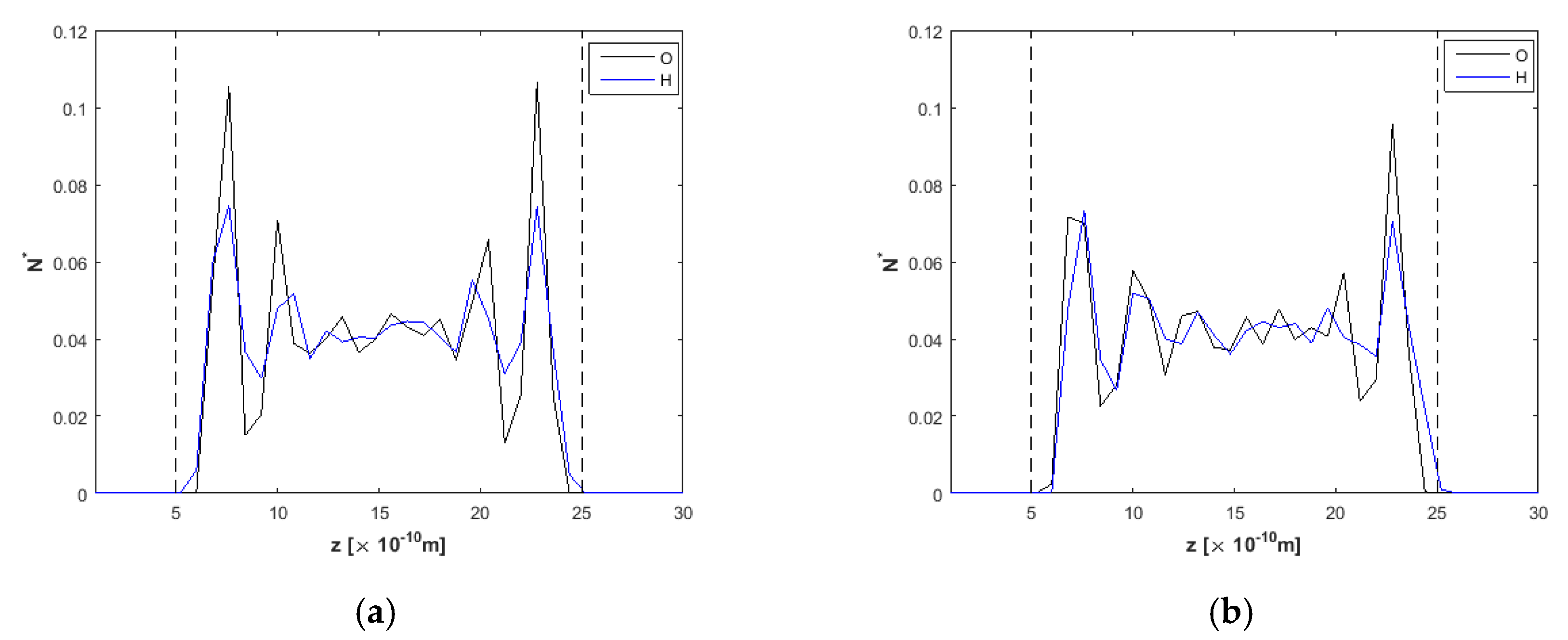
3.1. Effect of the Channel Width
3.2. Effect of the Electric Field Magnitude
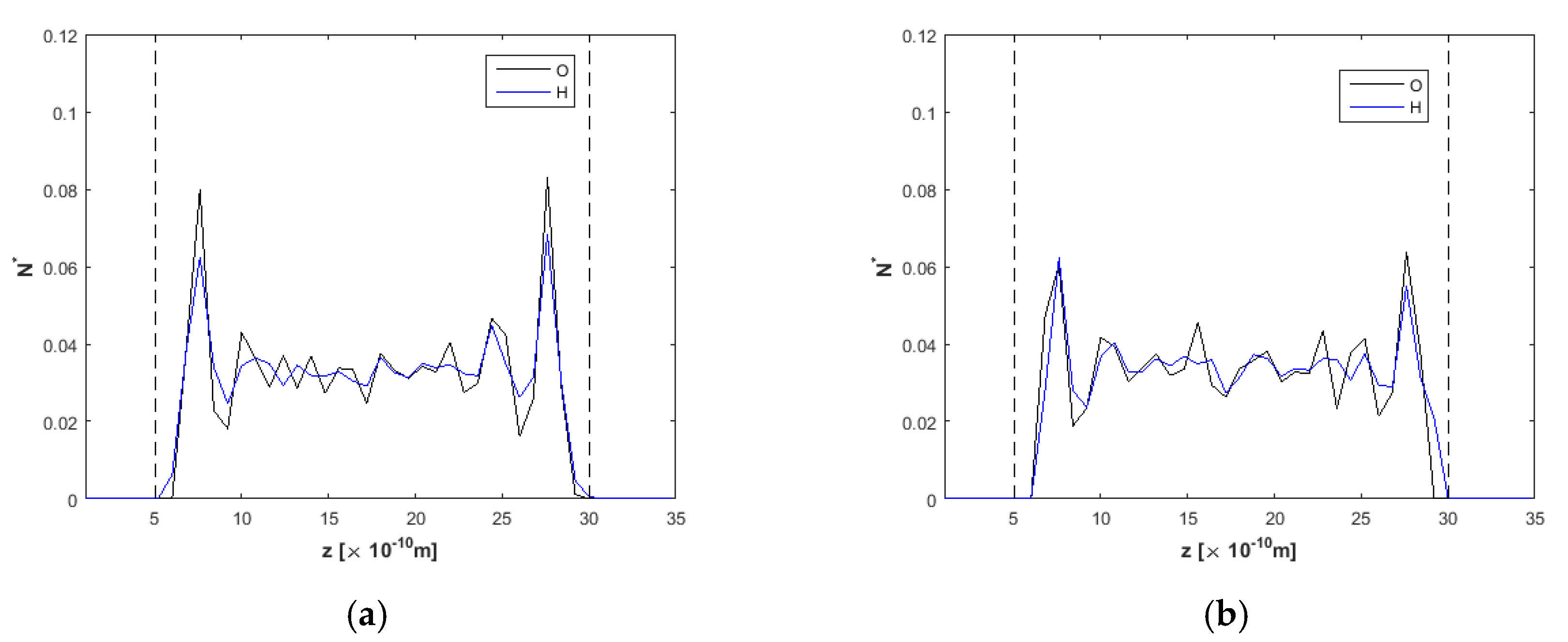
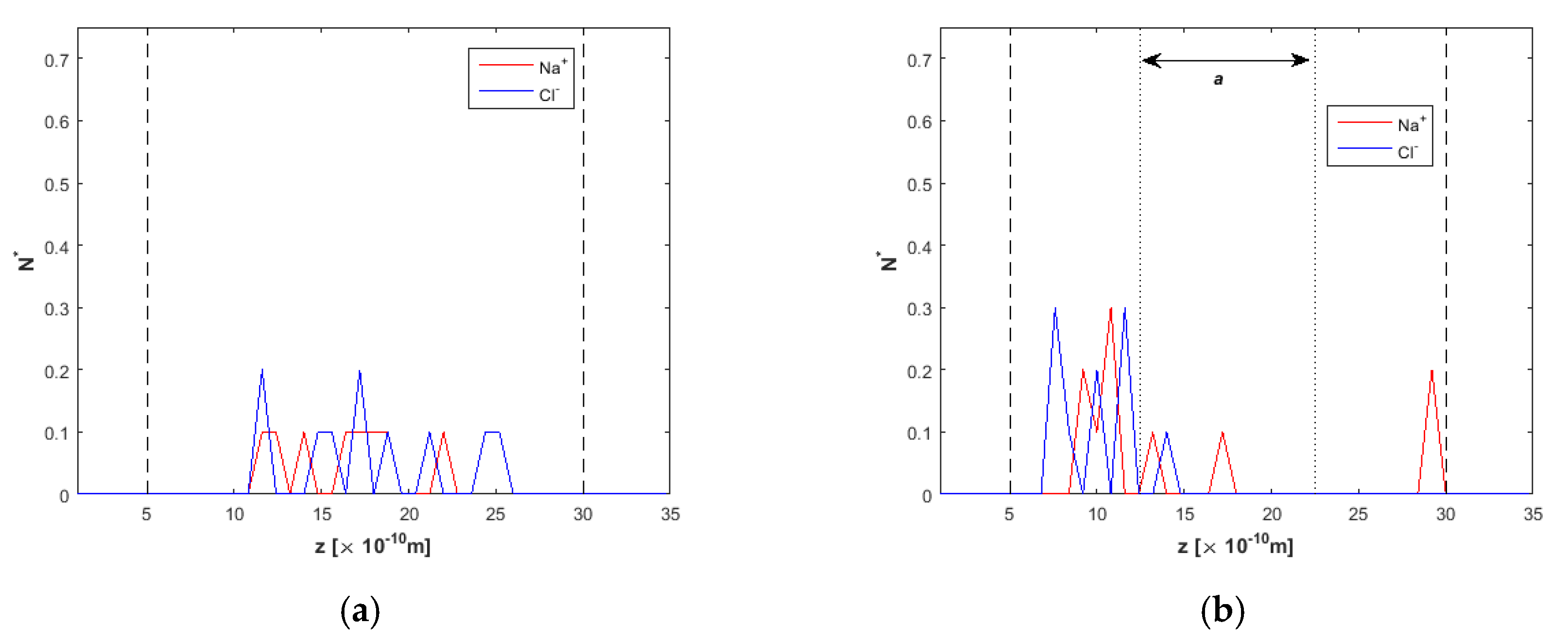
3.3. Channel Length and Volumetric Flow Calculations
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sofos, F.; Karakasidis, T.Ε.; Liakopoulos, A. Transport properties of liquid argon in krypton nanochannels: Anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 2009, 52, 735. [Google Scholar] [CrossRef]
- Sharp, K.V.; Adrian, R.J.; Santiago, J.G.; Molho, J.I.; Gad-el-Hak, M. (Eds.) Liquid flow in microchannels. In The Handbook of MEMS; CRC: Boca Raton, FL, USA, 2002; pp. 10–13. [Google Scholar]
- Gad-el-Hak, M. The Fluid Mechanics of Microdevices-The Freeman Scholar Lecture. ASME J. Fluids Eng. 1999, 121, 5–33. [Google Scholar] [CrossRef]
- Vo, T.Q.; Kim, B. Transport phenomena of water in molecular fluidic channels. Sci. Rep. 2016, 6, 33881. [Google Scholar] [CrossRef] [Green Version]
- Bitaw, T.N.; Park, K.; Kim, J.; Chang, J.W.; Yang, D.R. Low-recovery, -energy-consumption, -emission hybrid systems of seawater desalination: Energy optimization and cost analysis. Desalination 2019, 468, 114085. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Borg, M.; Reese, J. Multiscale simulation of enhanced water flow in nanotubes. MRS Bull. 2017, 42, 294–299. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wang, W.; Zhang, Y.; Yan, Y.; Král, P.; Zhang, J. Highly efficient water desalination in carbon nanocones. Carbon 2018, 129, 374–379. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Zhang, Y.; Yan, Y.; Dai, C.; Zhang, J. Gated water transport through graphene nanochannels: From ionic coulomb blockade to electroosmotic pump. J. Phys. Chem. C 2017, 121, 17523–17529. [Google Scholar] [CrossRef]
- Zhao, S.; Xue, J.; Kang, W. Ion selection of charge-modified large nanopores in a graphene sheet. J. Chem. Phys. 2013, 139, 114702. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Gupta, K.M.; Shi, Q.; Lu, R. Molecular dynamics study on water desalination through functionalized nanoporous grapheme. Carbon 2017, 116, 120–127. [Google Scholar] [CrossRef]
- Ma, M.; Tocci, G.; Michaelides, A.; Aeppli, G. Fast diffusion of water nanodroplets on grapheme. Nature Mater. 2016, 15, 66–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inglezakis, V.J.; Satayeva, A.; Yagofarova, A.; Tauanov, Z.; Meiramkulova, K.; Farrando-Pérez, J.; Bear, J.C. Surface interactions and mechanisms study on the removal of iodide from water by use of natural zeolite-based silver nanocomposites. Nanomaterials 2020, 10, 1156. [Google Scholar] [CrossRef] [PubMed]
- Humplik, T.; Lee, J.; O’Hern, S.; Laoui, T.; Karnik, R.; Wang, E.N. Enhanced water transport and salt rejection through hydrophobic zeolite pores. Nanotechnology 2017, 28, 505703. [Google Scholar] [CrossRef]
- Walther, J.H.; Ritos, K.; Cruz-Chu, E.R.; Megaridis, C.M.; Koumoutsakos, P. Barriers to superfast water transport in carbon nanotube membranes. Nano Lett. 2013, 13, 1910–1914. [Google Scholar] [CrossRef] [PubMed]
- Garate, J.-A.; English, N.J.; MacElroy, J.M.D. Human aquaporin 4 gating dynamics in dc and ac electric fields: A molecular dynamics study. J. Chem. Phys. 2011, 134, 055110. [Google Scholar] [CrossRef] [PubMed]
- Reale, R.; Garate, J.-A.; English, N.J.; Marracino, P.; Liberti, M.; Apollonio, F. Human aquaporin 4 gating dynamics under and after nanosecond-scale static and alternating electric-field impulses: A molecular dynamics study of field effects and relaxation. J. Chem. Phys. 2013, 139, 205101. [Google Scholar] [CrossRef] [PubMed]
- Lohrasebi, A.; Koslowski, T. Modeling water purification by an aquaporin-inspired graphene-based nano-channel. J. Mol. Model. 2019, 25, 280. [Google Scholar] [CrossRef]
- Teow, Y.H.; Mohammad, A.W. New generation nanomaterials for water desalination: A review. Desalination 2019, 451, 2–17. [Google Scholar] [CrossRef]
- Li, M.; Zhao, Q.; Zhang, S.; Li, D.; Li, H.; Zhang, X.; Xing, B. Facile passivation of black phosphorus nanosheets via silica coating for stable and efficient solar desalination. Environ. Sci. Nano 2020, 7, 414–423. [Google Scholar] [CrossRef]
- Qiu, M.; Singh, A.; Wang, D.; Qu, J.; Swihart, M.; Zhang, H.; Prasad, P.N. Biocompatible and biodegradable inorganic nanostructures for nanomedicine: Silicon and black phosphorus. Nano Today 2019, 25, 135–155. [Google Scholar] [CrossRef]
- Wang, R.; Chen, D.; Wang, Q.; Ying, Y.; Gao, W.; Xie, L. Recent advances in applications of carbon nanotubes for desalination: A review. Nanomaterials 2020, 10, 1203. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.-Y.; Haddad, A.Z.; Kumar, A.; Wang, S.-W. Brackish water desalination using reverse osmosis and capacitive deionization at the water-energy nexus. Water Res. 2020, 183, 116064. [Google Scholar] [CrossRef] [PubMed]
- Tu, Q.; Li, T.; Deng, A.; Zhu, K.; Liu, Y.; Li, S. A scale-up nanoporous membrane centrifuge for reverse osmosis desalination without fouling. Technology 2018, 6, 36–48. [Google Scholar] [CrossRef]
- Suss, M.E.; Porada, S.; Sun, X.; Biesheuvel, P.M.; Yoon, J.; Presser, V. Water desalination via capacitive deionization: What is it and what can we expect from it? Energy Environ. Sci. 2015, 8, 2296–2319. [Google Scholar] [CrossRef] [Green Version]
- Hilal, N.; Almarzooqi, F.; al Ghaferi, A.; Saadat, I. Application of Capacitive Deionisation in Water Desalination: A Review. Desalination 2014, 342, 3–15. [Google Scholar]
- Landon, J.; Gao, X.; Omosebi, A.; Liu, K. Progress and outlook for capacitive deionization technology. Curr. Opin. Chem. Eng. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Thamilselvan, A.; Nesaraj, A.S.; Noel, M. Review on carbon-based electrode materials for application in capacitive deionization process. Int. J. Environ. Sci. Technol. 2016, 13, 2961–2976. [Google Scholar] [CrossRef]
- De Luca, S.; Todd, B.D.; Hansen, J.S.; Daivis, P.J. Electropumping of water with rotating electric fields. J. Chem. Phys. 2013, 138, 154712–154722. [Google Scholar] [CrossRef]
- De Luca, S.; Todd, B.D.; Hansen, J.S.; Daivis, P.J. Molecular Dynamics study of nanoconfined water flow driven by rotating electric fields under realistic experimental conditions. Langmuir 2014, 30, 3095–3109. [Google Scholar] [CrossRef]
- Liu, P.Y.; Yan, T.T.; Shi, L.Y.; Park, H.S.; Chen, X.S.; Zhao, Z.G.; Zhang, D.S. Graphene-based materials for capacitive deionization. J. Mater. Chem. A 2017, 5, 13907–13943. [Google Scholar] [CrossRef]
- Kim, C.; Srimuk, P.; Lee, J.; Fleischmann, S.; Aslan, M.; Presser, V. Influence of pore structure and cell voltage of activated carbon cloth as a versatile electrode material for capacitive deionization. Carbon 2017, 122, 329–335. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.Ε.; Spetsiotis, D. Molecular Dynamics simulations of ion separation in nano-channel water flows using an electric field. Mol. Simulat. 2019, 45, 1395–1402. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. A theoretical model for salt ion drift due to electric field suitable to seawater desalination. Desalination 2020, 473, 114163. [Google Scholar] [CrossRef]
- Angelikopoulos, P.; Papadimitriou, C.; Koumoutsakos, P. Data Driven, Predictive Molecular Dynamics for Nanoscale Flow Simulations under Uncertainty. J. Phys. Chem. B 2013, 117, 14808. [Google Scholar] [CrossRef] [PubMed]
- Gad-el-Hak, M. Flow Physics in MEMS. Mol. Ind. 2001, 2, 313. [Google Scholar]
- Kannam, S.K.; Todd, B.D.; Hansen, J.S.; Daivis, P.J. Slip length of water on graphene: Limitations of non-equilibrium molecular dynamics simulations. J. Chem. Phys. 2012, 136, 024705. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Ye, H. Molecular dynamics-based prediction of boundary slip of fluids in nanochannels. Microfluid. Nanofluid. 2012, 12, 107. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, T.; Li, Z. Controlling flow direction in nanochannels by electric field strength. Phys. Rev. E 2015, 92, 023017. [Google Scholar] [CrossRef]
- Liakopoulos, A.; Sofos, F.; Karakasidis, T.Ε. Darcy-Weisbach friction factor at the nanoscale: From atomistic calculations to continuum models. Phys. Fluids 2017, 29, 052003. [Google Scholar] [CrossRef]
- Alipour, P.; Toghraie, D.; Karimipour, A.; Hajian, M. Modeling different structures in perturbed Poiseuille flow in a nanochannel by using of molecular dynamics simulation: Study the equilibrium. Physica A 2019, 515, 13–30. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1986, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aragones, J.L.; Sanz, E.; Vega, C. Solubility of NaCl in water by molecular simulation revisited. J. Chem. Phys. 2012, 136, 244508. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.E.; Dang, L.X. Computer simulations of NaCl association in polarizable water. J. Chem. Phys. 1994, 100, 3757. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for sim-ulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef]
- Markesteijn, A.P.; Hartkamp, R.; Luding, S.; Westerweel, J. A comparison of the value of viscosity for several water models using Poiseuille flow in a nano-channel. J. Chem. Phys. 2012, 136, 134104. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kalluri, R.J.; Konatham, D.; Striolo, A. Aqueous NaCl solutions within charged carbon-slit pores: Partition coefficients and density distributions from molecular dynamics simulations. J. Phys. Chem. C 2011, 115, 13786–13795. [Google Scholar] [CrossRef]
- Rivera, J.L.; Douglas, J.F. Reducing uncertainty in simulation estimates of the surface tension through a two-scale finite-size analysis: Thicker is better. RSC Adv. 2019, 9, 35803–35812. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Guilleminot, J.; Soize, C. Modeling uncertainties in molecular dynamics simulations using a stochastic reduced-order basis. Comput. Methods Appl. Mech. Engrg. 2019, 354, 37–55. [Google Scholar] [CrossRef] [Green Version]
- Crozier, P.S.; Rowley, R.L.; Henderson, D. Molecular dynamics calculations of the electrochemical properties of electrolyte systems between charged electrodes. J. Chem. Phys. 2000, 113, 9202–9207. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.Ε.; Liakopoulos, A. Surface wettability effects on flow in rough wall nanochannels. Microfluid. Nanofluid. 2012, 12, 25–31. [Google Scholar] [CrossRef]
- Voronov, R.S.; Papavassiliou, D.V.; Lee, L.L. Boundary slip and wetting properties of interfaces: Correlation of the contact angle with the slip length. J. Chem. Phys. 2006, 124, 204701. [Google Scholar] [CrossRef]
- Kim, S.J.; Ko, S.H.; Kang, K.H.; Han, J. Direct seawater desalination by ion concentration polarization. Nat. Nanotechnol. 2010, 5, 297–301. [Google Scholar] [CrossRef]
- Kandezi, M.K.; Lakmehsari, M.S.; Matta, C.F. Electric field assisted desalination of water using B- and N-doped-graphene sheets: A non-equilibrium molecular dynamics study. J. Mol. Liq. 2020, 302, 112574. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, B.; Wu, M.-S.; Zhou, K.; Law, A.W.-K. Transport of salty water through graphene bilayer in an electric field: A molecular dynamics study. Comput. Mater. Sci. 2017, 131, 100–107. [Google Scholar] [CrossRef]
- Zhang, C.; He, D.; Ma, J.; Tang, W.; Waite, T.D. Faradaic reactions in capacitive deionization (CDI)-problems and possibilities: A review. Water Res. 2018, 128, 314–330. [Google Scholar] [CrossRef]
- Ng, K.C.; Thu, K.; Kim, Y.; Chakraborty, A.; Amy, G. Adsorption desalination: An emerging low-cost thermal desalination method. Desalination 2013, 308, 161–179. [Google Scholar] [CrossRef]



| Lx × Ly × Lz | h | a | NH2O | NC |
|---|---|---|---|---|
| 3.0 × 3.0 × 2.5 nm | 1.5 nm | 0.6 nm | 432 | 722 |
| 3.0 × 3.0 × 3.0 nm | 2.0 nm | 0.8 nm | 594 | 722 |
| 3.0 × 3.0 × 3.5 nm | 2.5 nm | 1.0 nm | 729 | 722 |
| 4.5 × 4.7 × 14.7 nm | 13.5 nm | 5.4 nm | 8640 | 3654 |
| Atom Pair | ε [kcal/mol] | σ [Å] | Mass [a.u] |
|---|---|---|---|
| H–H | 0.000 | 0.000 | 1.008 |
| O–O | 0.155 | 3.166 | 15.990 |
| C–C | 0.056 | 3.400 | 12.010 |
| Cl–Cl | 0.107 | 4.446 | 35.450 |
| Na–Na | 1.607 | 1.897 | 22.990 |
| Simulation Parameters | Percentage of Removal | |||||
|---|---|---|---|---|---|---|
| h (nm) | E (V/Å) | c (%) | t (ns) | Fext (kcal/molÅ) | Na+ | Cl− |
| 1.5 | 2.0 | 1.39 | 10 | 0.025 | 0 | 0 |
| 1.5 | 2.0 | 1.39 | 15 | 0.025 | 33 | 66 |
| 1.5 | 2.0 | 1.39 | 20 | 0.025 | 100 | 100 |
| 2.0 | 2.0 | 1.35 | 10 | 0.025 | 0 | 0 |
| 2.0 | 2.0 | 1.35 | 15 | 0.025 | 100 | 100 |
| 2.0 | 2.0 | 1.35 | 20 | 0.025 | 100 | 100 |
| 2.5 | 2.0 | 1.37 | 10 | 0.025 | 60 | 80 |
| 2.5 | 2.0 | 1.37 | 15 | 0.025 | 100 | 80 |
| 2.5 | 2.0 | 1.37 | 20 | 0.025 | 100 | 100 |
| 13.5 | 0.1 | 1.39 | 15 | 0.025 | 82 | 90 |
| 13.5 | 1.0 | 1.39 | 15 | 0.025 | 93 | 93 |
| 13.5 | 2.0 | 1.39 | 15 | 0.025 | 87 | 87 |
| 13.5 | 3.0 | 1.39 | 15 | 0.025 | 93 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofos, F.; Karakasidis, T.; Sarris, I.E. Molecular Dynamics Simulations of Ion Drift in Nanochannel Water Flow. Nanomaterials 2020, 10, 2373. https://doi.org/10.3390/nano10122373
Sofos F, Karakasidis T, Sarris IE. Molecular Dynamics Simulations of Ion Drift in Nanochannel Water Flow. Nanomaterials. 2020; 10(12):2373. https://doi.org/10.3390/nano10122373
Chicago/Turabian StyleSofos, Filippos, Theodoros Karakasidis, and Ioannis E. Sarris. 2020. "Molecular Dynamics Simulations of Ion Drift in Nanochannel Water Flow" Nanomaterials 10, no. 12: 2373. https://doi.org/10.3390/nano10122373
APA StyleSofos, F., Karakasidis, T., & Sarris, I. E. (2020). Molecular Dynamics Simulations of Ion Drift in Nanochannel Water Flow. Nanomaterials, 10(12), 2373. https://doi.org/10.3390/nano10122373








