Enhancement of Thermal Boundary Conductance of Metal–Polymer System
Abstract
1. Introduction
2. Materials and Methods
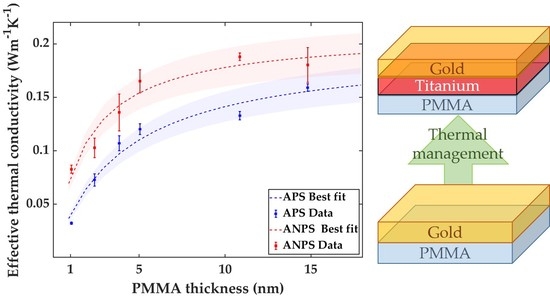
3. Results and discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Chang, J.S.; Facchetti, A.F.; Reuss, R. A Circuits and systems perspective of organic/printed electronics: Review, challenges, and contemporary and emerging design approaches. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 7–26. [Google Scholar] [CrossRef]
- Kaltenbrunner, M.; Sekitani, T.; Reeder, J.; Yokota, T.; Kuribara, K.; Tokuhara, T.; Drack, M.; Schwödiauer, R.; Graz, I.; Bauer-Gogonea, S.; et al. An ultra-lightweight design for imperceptible plastic electronics. Nature 2013, 499, 458–463. [Google Scholar] [CrossRef] [PubMed]
- Henry, A. Thermal transport in polymers. Annu. Rev. Heat Transf. 2014, 17, 485–520. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8st ed.; Wiley: Hoboken, NJ, USA, 2004; ISBN 978-0-471-41526-8. [Google Scholar]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons, 1st ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2005; ISBN 978-0-19-515942-4. [Google Scholar]
- Hopkins, P.E.; Baraket, M.; Barnat, E.V.; Beechem, T.E.; Kearney, S.P.; Duda, J.C.; Robinson, J.T.; Walton, S.G. Manipulating thermal conductance at metal—Graphene contacts via chemical functionalization. Nano Lett. 2012, 12, 590–595. [Google Scholar] [CrossRef]
- Losego, M.D.; Moh, L.; Arpin, K.A.; Cahill, D.G.; Braun, P.V. Interfacial thermal conductance in spun-cast polymer films and polymer brushes. Appl. Phys. Lett. 2010, 97, 011908. [Google Scholar] [CrossRef]
- Li, W.T.; Charters, R.B.; Luther-Davies, B.; Mar, L. Significant improvement of adhesion between gold thin films and a polymer. Appl. Surf. Sci. 2004, 233, 227–233. [Google Scholar] [CrossRef]
- Duda, J.C.; Yang, C.-Y.P.; Foley, B.M.; Cheaito, R.; Medlin, D.L.; Jones, R.E.; Hopkins, P.E. Influence of interfacial properties on thermal transport at gold:silicon contacts. Appl. Phys. Lett. 2013, 102, 081902. [Google Scholar] [CrossRef]
- Kim, Y.; Chang, C.; Schrott, A.G. Adhesion of metals to spin-coated fluorocarbon polymer films. J. Appl. Phys. 1990, 67, 251–254. [Google Scholar] [CrossRef]
- Choy, C.L. Thermal conductivity of polymers. Polymer 1977, 18, 984–1004. [Google Scholar] [CrossRef]
- Bhandari, C.M.; Rowe, D.M. Boundary scattering of phonons. J. Phys. C Solid State Phys. 1978, 11, 1787–1794. [Google Scholar] [CrossRef]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal conductivity of polymer-based composites: Fundamentals and applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Schmidt, A.J.; Cheaito, R.; Chiesa, M. A frequency-domain thermoreflectance method for the characterization of thermal properties. Rev. Sci. Instrum. 2009, 80, 094901. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.J.; Cheaito, R.; Chiesa, M. Characterization of thin metal films via frequency-domain thermoreflectance. J. Appl. Phys. 2010, 107, 024908. [Google Scholar] [CrossRef]
- Malen, J.A.; Baheti, K.; Tong, T.; Zhao, Y.; Hudgings, J.A.; Majumdar, A. Optical measurement of thermal conductivity using fiber aligned frequency domain thermoreflectance. J. Heat Transf. 2011, 133, 081601. [Google Scholar] [CrossRef]
- Yang, J.; Maragliano, C.; Schmidt, A.J. Thermal property microscopy with frequency domain thermoreflectance. Rev. Sci. Instrum. 2013, 84, 104904. [Google Scholar] [CrossRef]
- Yang, J.; Ziade, E.; Maragliano, C.; Crowder, R.; Wang, X.; Stefancich, M.; Chiesa, M.; Swan, A.K.; Schmidt, A.J. Thermal conductance imaging of graphene contacts. J. Appl. Phys. 2014, 116, 023515. [Google Scholar] [CrossRef]
- Ziade, E.; Goni, M.; Sato, T.; Czubarow, P.; Schmidt, A.J. Thermal conductance of nanoscale Langmuir-Blodgett films. Appl. Phys. Lett. 2015, 107, 221603. [Google Scholar] [CrossRef]
- Aller, H.; Yu, X.; Gellman, A.J.; Malen, J.A.; McGaughey, A.J.H. Thermal conductance of β-Ga2O3/metal interfaces. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Mie, Japan, 17–21 April 2018; pp. 567–571. [Google Scholar]
- Nemoto, S. Measurement of the refractive index of liquid using laser beam displacement. Appl. Opt. 1992, 31, 6690–6694. [Google Scholar] [CrossRef]
- Braun, J.L.; Szwejkowski, C.J.; Giri, A.; Hopkins, P.E. On the steady-state temperature rise during laser heating of multilayer thin films in optical pump—Probe techniques. J. Heat Transf. 2018, 140, 052801. [Google Scholar] [CrossRef]
- Cahill, D.G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 2004, 75, 5119–5122. [Google Scholar] [CrossRef]
- Giri, A.; Gaskins, J.T.; Donovan, B.F.; Szwejkowski, C.; Warzoha, R.J.; Rodriguez, M.A.; Ihlefeld, J.; Hopkins, P.E. Mechanisms of nonequilibrium electron-phonon coupling and thermal conductance at interfaces. J. Appl. Phys. 2015, 117, 105105. [Google Scholar] [CrossRef]
- Liu, J.; Wang, T.; Xu, S.; Yuan, P.; Xu, X.; Wang, X. Thermal conductivity of giant mono- to few-layered CVD graphene supported on an organic substrate. Nanoscale 2016, 8, 10298–10309. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; He, L.; Wang, L.; Man, Y.; Huang, L.; Xu, Z.; Ge, D.; Li, J.; Liu, C.; Wang, L. Significant enhancement of the adhesion between metal films and polymer substrates by UV—Ozone surface modification in nanoscale. ACS Appl. Mater. Interfaces 2016, 8, 30576–30582. [Google Scholar] [CrossRef]
- Hurley, D.C.; Geiss, R.H.; Kopycinska-Müller, M.; Müller, J.; Read, D.T.; Wright, J.E.; Jennett, N.M.; Maxwell, A.S. Anisotropic elastic properties of nanocrystalline nickel thin films. J. Mater. Res. 2005, 20, 1186–1193. [Google Scholar] [CrossRef]
- Meschter, P.J.; Wright, J.W.; Brooks, C.R.; Kollie, T.G. Physical contributions to the heat capacity of nickel. J. Phys. Chem. Solids 1981, 42, 861–871. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An Interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Malinský, P.; Slepička, P.; Hnatowicz, V.; Svorčík, V. Early stages of growth of gold layers sputter deposited on glass and silicon substrates. Nanoscale Res. Lett. 2012, 7, 241. [Google Scholar] [CrossRef]
- Van der Pauw, L.J. A method of measuring the resistivity and Hall coefficient on lamellae of arbitrary shape. Philips Tech. Rev. 1958, 20, 220–224. [Google Scholar]
- Hu, M.; Yu, D.; Wei, J. Thermal conductivity determination of small polymer samples by differential scanning calorimetry. Polym. Test. 2007, 26, 333–337. [Google Scholar] [CrossRef]
- Putnam, S.A.; Cahill, D.G.; Ash, B.J.; Schadler, L.S. High-precision thermal conductivity measurements as a probe of polymer/nanoparticle interfaces. J. Appl. Phys. 2003, 94, 6785–6788. [Google Scholar] [CrossRef]
- Olson, D.H.; Freedy, K.M.; McDonnell, S.J.; Hopkins, P.E. The influence of titanium adhesion layer oxygen stoichiometry on thermal boundary conductance at gold contacts. Appl. Phys. Lett. 2018, 112, 171602. [Google Scholar] [CrossRef]
- Hu, M.; Keblinski, P.; Schelling, P.K. Kapitza conductance of silicon—Amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 2009, 79, 104305. [Google Scholar] [CrossRef]
- Shenogina, N.; Godawat, R.; Keblinski, P.; Garde, S. How wetting and adhesion affect thermal conductance of a range of hydrophobic to hydrophilic aqueous interfaces. Phys. Rev. Lett. 2009, 102, 156101. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, L.; Hu, M.; Wang, J.-S.; Li, B.; Keblinski, P. Phonon interference at self-assembled monolayer interfaces: Molecular dynamics simulations. Phys. Rev. B 2010, 81, 235427. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, H.F.; Xiang, Y.; Yang, C.; Wang, C.M.; Zhang, Y.Y. Effect of covalent functionalization on thermal transport across graphene—Polymer interfaces. J. Phys. Chem. C 2015, 119, 12731–12738. [Google Scholar] [CrossRef]
- Zhang, L.; Bai, Z.; Liu, L. Exceptional thermal conductance across hydrogen-bonded graphene/polymer interfaces. Adv. Mater. Interfaces 2016, 3, 1600211. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L. Hierarchically hydrogen-bonded graphene/polymer interfaces with drastically enhanced interfacial thermal conductance. Nanoscale 2019, 11, 3656–3664. [Google Scholar] [CrossRef]
- Losego, M.D.; Grady, M.E.; Sottos, N.R.; Cahill, D.G.; Braun, P.V. Effects of chemical bonding on heat transport across interfaces. Nat. Mater. 2012, 11, 502–506. [Google Scholar] [CrossRef]
- Jeong, M.; Freedman, J.P.; Liang, H.J.; Chow, C.-M.; Sokalski, V.M.; Bain, J.A.; Malen, J.A. Enhancement of thermal conductance at metal-dielectric interfaces using subnanometer metal adhesion layers. Phys. Rev. Appl. 2016, 5, 014009. [Google Scholar] [CrossRef]
- Monachon, C.; Schusteritsch, G.; Kaxiras, E.; Weber, L. Qualitative link between work of adhesion and thermal conductance of metal/diamond interfaces. J. Appl. Phys. 2014, 115, 123509. [Google Scholar] [CrossRef]
- Zheng, K.; Sun, F.; Tian, X.; Zhu, J.; Ma, Y.; Tang, D.; Wang, F. Tuning the interfacial thermal conductance between polystyrene and sapphire by controlling the interfacial adhesion. ACS Appl. Mater. Interfaces 2015, 7, 23644–23649. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.-H. Molecular bonding and adhesion at polymer-metal interphases. J. Adhes. 1994, 46, 15–38. [Google Scholar] [CrossRef]
- Hoogvliet, J.C.; van Bennekom, W.P. Gold thin-film electrodes: An EQCM study of the influence of chromium and titanium adhesion layers on the response. Electrochim. Acta 2001, 47, 599–611. [Google Scholar] [CrossRef]
- Todeschini, M.; Bastos da Silva Fanta, A.; Jensen, F.; Wagner, J.B.; Han, A. Influence of Ti and Cr adhesion layers on ultrathin Au films. ACS Appl. Mater. Interfaces 2017, 9, 37374–37385. [Google Scholar] [CrossRef] [PubMed]
- Kitamura, M.; Kuzumoto, Y.; Kang, W.; Aomori, S.; Arakawa, Y. High conductance bottom-contact pentacene thin-film transistors with gold-nickel adhesion layers. Appl. Phys. Lett. 2010, 97, 033306. [Google Scholar] [CrossRef]
- Chang, C.; Kim, Y.; Schrott, A.G. Adhesion studies of metals on fluorocarbon polymer films. J. Vac. Sci. Technol. A 1990, 8, 3304–3309. [Google Scholar] [CrossRef]
- Bébin, P.; Prud’homme, R.E. Comparative XPS study of copper, nickel, and aluminum coatings on polymer surfaces. Chem. Mater. 2003, 15, 965–973. [Google Scholar] [CrossRef]
- Konstadinidis, K.; Zhang, P.; Opila, R.L.; Allara, D.L. An in-situ X-ray photoelectron study of the interaction between vapor-deposited Ti atoms and functional groups at the surfaces of self-assembled monolayers. Surf. Sci. 1995, 338, 300–312. [Google Scholar] [CrossRef]
- Tisone, T.C.; Drobek, J. Diffusion in thin film Ti-Au, Ti-Pd, and Ti-Pt couples. J. Vac. Sci. Technol. 1972, 9, 271–275. [Google Scholar] [CrossRef]
- Tynkova, A.; Sidorenko, S.; Voloshko, S.; Rennie, A.R.; Vasylyev, M.A. Interdiffusion in Au (120 nm)/Ni(70 nm) thin films at the low-temperature annealing in the different atmospheres. Vacuum 2013, 87, 69–74. [Google Scholar] [CrossRef]
- Monachon, C.; Weber, L.; Dames, C. Thermal boundary conductance: A materials science perspective. Annu. Rev. Mater. Res. 2016, 46, 433–463. [Google Scholar] [CrossRef]
- Egitto, F.D.; Matienzo, L.J. Plasma modification of polymer surfaces for adhesion improvement. IBM J. Res. Dev. 1994, 38, 423–439. [Google Scholar] [CrossRef]
- Mo, A.K.; DeVore, T.C.; Augustine, B.H.; Zungu, V.P.; Lee, L.L.; Hughes, W.C. Improving the adhesion of Au thin films onto poly(methyl methacrylate) substrates using spun-cast organic solvents. J. Vac. Sci. Technol. A 2011, 29, 030601. [Google Scholar] [CrossRef]
- Mo, A.K.; Brown, V.L.; Rugg, B.K.; DeVore, T.C.; Meyer, H.M.; Hu, X.; Hughes, W.C.; Augustine, B.H. Understanding the mechanism of solvent-mediated adhesion of vacuum deposited Au and Pt thin films onto PMMA substrates. Adv. Funct. Mater. 2013, 23, 1431–1439. [Google Scholar] [CrossRef]
- Plueddemann, E.P. Adhesion through silane coupling agents. J. Adhes. 1970, 2, 184–201. [Google Scholar] [CrossRef]





| Au | Ti | Ni | PMMA | Si | |
|---|---|---|---|---|---|
| (W·m−1·K−1) | 227.80 ± 23 * | 8.20 a | 52 d | - | 148 c |
| CV (106 J/m3·K) | 1.94 ± 0.2 * | 3.01 a | 3.92 e | 1.73 b | 1.68 c |
| t (nm) | 84.3 ± 3 * | 2.4 ± 0.1 * | 2.0 ± 0.1 * | 1–15 | ∞ |
| System | ||
|---|---|---|
| APS | 0.198 | 59 |
| ATPS | 0.211 | 115 |
| ANPS | 0.212 | 139 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandell, S.; Maire, J.; Chávez-Ángel, E.; Sotomayor Torres, C.M.; Kristiansen, H.; Zhang, Z.; He, J. Enhancement of Thermal Boundary Conductance of Metal–Polymer System. Nanomaterials 2020, 10, 670. https://doi.org/10.3390/nano10040670
Sandell S, Maire J, Chávez-Ángel E, Sotomayor Torres CM, Kristiansen H, Zhang Z, He J. Enhancement of Thermal Boundary Conductance of Metal–Polymer System. Nanomaterials. 2020; 10(4):670. https://doi.org/10.3390/nano10040670
Chicago/Turabian StyleSandell, Susanne, Jeremie Maire, Emigdio Chávez-Ángel, Clivia M. Sotomayor Torres, Helge Kristiansen, Zhiliang Zhang, and Jianying He. 2020. "Enhancement of Thermal Boundary Conductance of Metal–Polymer System" Nanomaterials 10, no. 4: 670. https://doi.org/10.3390/nano10040670
APA StyleSandell, S., Maire, J., Chávez-Ángel, E., Sotomayor Torres, C. M., Kristiansen, H., Zhang, Z., & He, J. (2020). Enhancement of Thermal Boundary Conductance of Metal–Polymer System. Nanomaterials, 10(4), 670. https://doi.org/10.3390/nano10040670