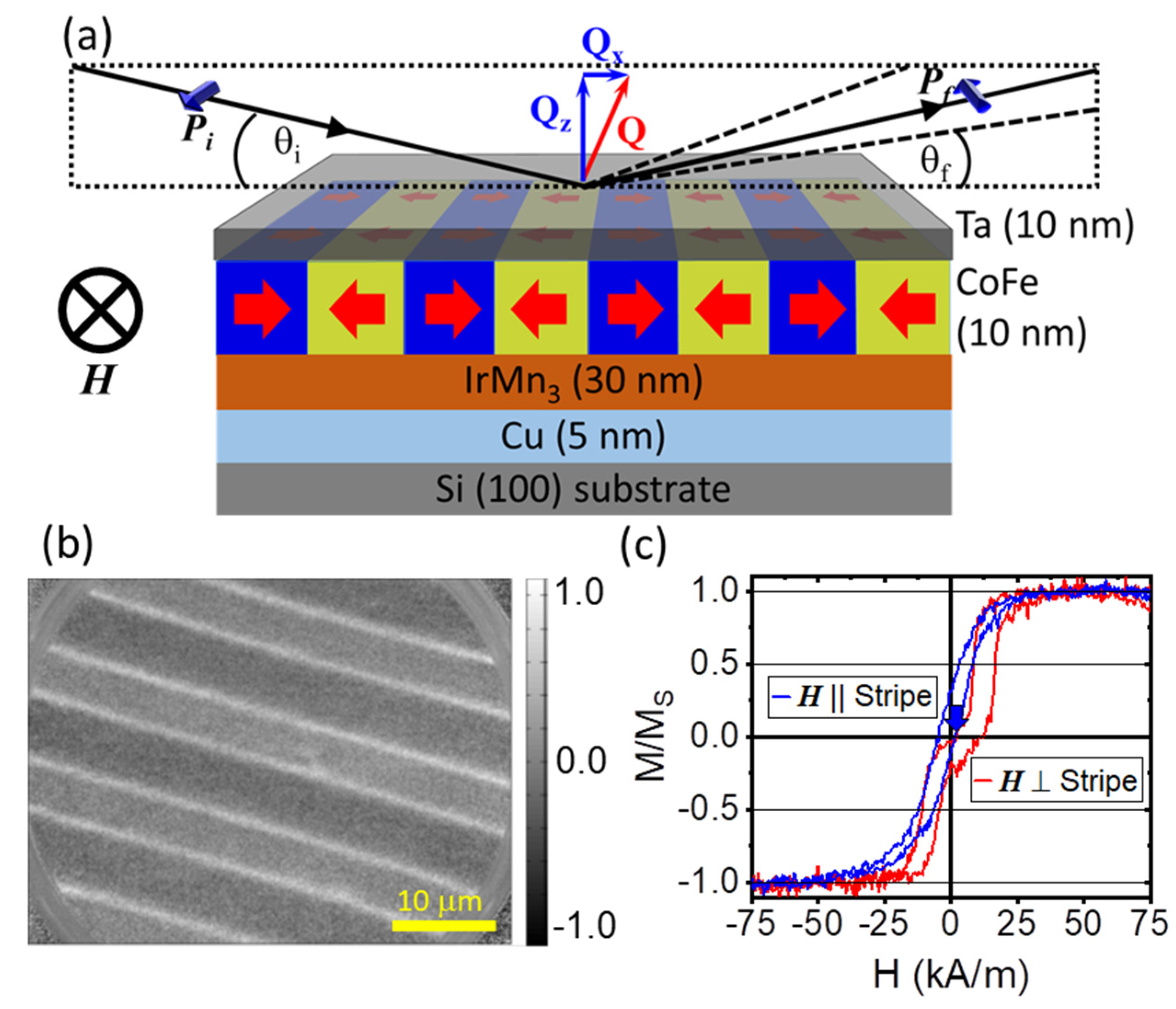
3.1. X-PEEM and Volume Magnetometry
An example X-PEEM measurement of the magnetic stripe pattern in shown in
Figure 1b. The magnetic contrast in such measurements is determined by the orientation of the surface wave vector projection
to the magnetization, where a maximum contrast is achieved for parallel to antiparallel alignment [
24,
41]. For the measurement, the sample was oriented with
parallel to the stripes and therefore perpendicular to the domain magnetization. This reduces the contrast between the domains, but reveals the domain walls separating the two stripes, the latter being visible as bright lines in
Figure 1b. Due to a small misalignment in the magnetization vectors in neighboring domains, a small contrast difference between the domains remains visible. A rotational scan of the sample, taking images at several orientations of
with respect to the magnetization revealed a canting of 6.5° ± 1° from the domain wall normal of one domain. The magnetization vector of the other domain aligns with the normal to the domain wall. In addition to the quantification of the magnetization direction, the image shows a difference in width between the two domains of about 1.5 μm.
The volume averaged magnetic hysteresis of the hth-stripe pattern recorded with MOKE is shown in
Figure 1c. Although superimposed by an appreciable noise, the results agree with measurements performed with VSM [
13,
40]. With a field applied perpendicular to the stripe axis a double hysteresis loop separated by the sum of exchange bias values is observed. This separation leads to a close-to zero remanent magnetization indicating nearly opposite alignment of neighboring stripe domains of equal width. Differences in the domain magnetizations, lateral variations in exchange bias and global uncertainties in the orientation of the unidirectional anisotropy and stripe axes can lead to a finite remanent magnetization and asymmetric reversal of the hysteresis loop. Such a situation is observed in
Figure 1c, where hysteresis and remanence remain observable at zero applied fields. This indicates that the two stripe domains do not behave equally, a behavior which has been observed before [
28,
29]. Additionally, a slight misalignment of the two exchange bias directions in the stripes with respect to each other and the stripe axis can lead to a preferential magnetization not perpendicular to the stripe border, which creates a residual magnetic component in low fields. Such a magnetic orientation misalignment with respect to the external field is also visible in measurements with the external field applied along the stripe axis (
Figure 1c). This measurement geometry is expected to lead to zero coercive field values and zero exchange bias observed in the hysteresis. Indeed, no split double hysteresis is observed, but a symmetric ferromagnetic-like hysteresis with non-zero coercive field and apparent shift towards negative field remains. From the perpendicular hysteresis loop, the coercive field values and exchange bias values are determined to H
EB(right) = (−10.1 ± 0.4) kA/m and H
EB(left) = (9.8 ± 0.2) kA/m, while the coercive fields of the two branches are determined to H
C(right) = (5.5 ± 0.2) kA/m and H
C(left) = (2.4 ± 0.2) kA/m. The value for the loop shift agrees for both parts of the hysteresis loop, but the coercive field differs by a factor of two for the bombarded and virgin regions. The longitudinal measurement reveals a loop shift by H
EB,L = (1.6 ± 0.4) kA/m and coercive field of H
C,L = (3.1 ± 0.2) kA/m.
3.2. Polarized Specular Reflectivity
Figure 2a,b show the specular reflectivity (SR) and fits to the data as a function of wave vector transfer
, with
, for two applied fields. Application of 380 kA/m in the sample plane saturates the magnetization along the applied field direction and removes the magnetic stripe domain texture. Then, no OSS is detected on the 2-dimensional detector. The sample consists therefore of a laterally homogeneous nuclear (N-SLD) and magnetic scattering length density (M-SLD), which can be approximated by a slab model. In contrast to x-ray reflectometry (XRR), whose scattering cross-section is determined by the electron density, the neutron cross section is determined by the bound coherent neutron scattering length, defining the nuclear scattering length density:
where
is a unit cell volume containing
atoms with neutron scattering length
. The value of
can vary strongly between neighboring elements in the periodic table, which makes PNR particularly more sensitive to interfaces of materials with similar electron densities than XRR. Similarly, the M-SLD can be described using the same unit cell volume,
with
if the atomic magnetic moment
is known in units of
, or
if the volume magnetization
is known in units of A/m [
34,
39]. This M-SLD is of similar magnitude to the N-SLD, making PNR particularly sensitive to magnetic structures.
The SLD profiles corresponding to the best fit of the sample structure and its magnetization at saturation are shown in
Figure 2c. The values obtained for thicknesses of the layers are close to the nominal values, with roughness values below 1.5 nm (
Table 1). The modeling of the roughness follows the Névot–Croce approach, which takes into account an effective smearing of the SLD profile due to interface height variations or diffusion normal to the interface [
51]. The width of the interfaces is modeled according to an error-function with a width
, which corresponds to the root-mean square roughness. The approach assumes a Gaussian distribution of random fluctuations
of local interface positions around a laterally averaged mean position of the interface. The impact of this laterally averaged roughness is visualized in the density profile as a function of depth for all layers (
Figure 2c). It is deduced from the least square fit of data in
Figure 2a, where roughness mostly affects the behavior of the reflectivity curve at higher wave vector transfer
. In contrast, resolution mostly determines the sharpness of Kiessig fringe minima. A nonlinear least square standard routine has been applied to fit a theoretical PNR curve, calculated for the model SLD in
Figure 2c and convoluted with the resolution function corresponding to the instrument configuration [
44,
45], to our data. The resolution function includes the divergence of the incoming beam, the detector resolution and the wavelength resolution. Hence, the sensitivity of the fit to the model parameter is expressed via the error bars ascribed to this parameter, while the fit quality is estimated by the
normalized to the number of fit parameters. Roughness parameters where determined with the accuracy of about 10% which is mostly determined by relatively low statistics of data and number of points in the tail of the reflectivity curve, but not due to the finite resolution.
The surface of the Ta capping layer shows an increase in N-SLD due to a certain degree of oxidation with inhomogeneous stoichiometry as a function of depth. The literature value for full oxidation into Ta
2O
5, for example, provides a literature N-SLD of
Å
−2, which is at the lower limit of the determined error on the fit parameter. Such a larger variation from the nominal value could also arise from the post-growth treatment, including the lithography and etching processes, leading to a significant modification of the sample surface. A correlation between thickness, roughness and N-SLD values describing this surface layer, which is best represented with the profile shown in
Figure 2c, prevents a more accurate determination of these parameters. The exact N-SLD of the surface layer or the correlation between its roughness and N-SLD does not influence the determination of the other layer parameters or conclusions presented in this report. Other SLD values are close to literature values for the elemental composition (
Table 1) and within the range of values observed for untreated films of the same composition. Therefore, we assume that the sample treatment did not lead to drastic changes in the structural and chemical quality of the sample. In particular, we do not observe an enhanced diffusion region at the FM/AF interface, which was observed to increase significantly for doses above 1 × 10
15/cm
2 [
20]. This indicates that the applied dose is still at the lower limit for enhanced intermixing at the CoFe/IrMn
3 interface. Further indication for the absence of significant structural and magnetic modifications due to the He
+ bombardment is obtained from the absence of OSS in the saturating external fields, discussed in more detail below.
The splitting between
and
reflectivities, the spin-asymmetry, is indicative of the total magnetization of the layer structure and therefore proportional to the laterally averaged M-SLD of the slabs. The moment obtained from fitting the data amounts to (2.11 ± 0.05) μB/CoFe, which corresponds to a volume magnetization density of 1700 kA/m. In addition, the fit significantly improves if a small positive moment, corresponding to (0.3 ± 0.05) μ
B/IrMn
3, is attributed to the nominally AF layer. Similar to the N-SLD, we do not observe a drastic variation in the magnetic parameters due to the ion bombardment. This is largely in agreement with magnetometry studies, which after the same exposure of 2 × 10
15 ions/cm
2 observe only little variation in the saturation magnetization [
23]. However, it should be noted that an investigation of ion-bombardment effects in the materials is not in the scope of this report and the effect of defect-density and magnetization variations have not been investigated systematically as a function of different He-ion exposure using PNR. By direct comparison of reflectivity profiles prior and post bombardment a variation of above 1% on lateral average in the N-SLD and M-SLD would be detectable by the technique. For the present study, the dose was intentionally kept at a lower level in order not to induce drastic changes in the film quality and avoid lateral chemical variations in addition to the lateral magnetic texture.
At
-values below the critical wave vector transfer of total reflection,
, a non-flat reflectivity is observed (
Figure 2b), which indicates a resonance structure within the SLD profile [
53]. Such resonance features provide added sensitivity to certain aspects of the sample structure due to resonant enhancement of the neutron wave field in the sample at certain depth [
54,
55]. The potential well is created by the negative N-SLD of IrMn
3 and the two positive boundaries formed by Cu on the one and CoFe on the other side as indicated in
Figure 2c. The height of the right boundary is highly sensitive to the magnetization of CoFe. Because the magnetic potential is added or subtracted from the nuclear potential depending on the alignment of the neutron polarization
and the magnetization, the location and shape of the resonance feature is different for the two incoming neutron polarizations. In addition to the enhanced sensitivity to the magnetic moment in the sample, the absorption cross-section of CoFe and IrMn
3 becomes apparent. For the materials in the current sample, those are orders of magnitude smaller than the nuclear cross section and typically below the detection threshold in neutron reflectometry. Due to the resonance, the absorption cross section creates the dip in total reflection. In the fitting of the data, the absorption enters the model via the imaginary scattering length density (iN-SLD). Although the imaginary part has been allowed to vary independently from the nuclear part, fitting provides values close to literature values [
52]. The fitting errors listed in
Table 1 illustrate the sensitivity to the iN-SLD within the stack. Because the neutron absorption is wavelength dependent, the specular fits have been performed for each angle separately.
In reduced external magnetic field of 2.2 kA/m the splitting between the R
+ and R
- reflectivity curves collapses (
Figure 2a). As the reflectivity was recorded without polarization analysis, and therefore spin-flip processes are not resolved, the data do not allow concluding directly on domain formation or coherent rotation of the magnetization. However, with respect to the imprinted stripe domain patterns and the observed OSS discussed below, the domain formation is the likely scenario.
3.3. Coherence and Averaging in PNR
For the interpretation of the magnetic component of specular reflectivity lateral averaging inherent to SR and the resulting observables need to be discussed. The area of the averaging depends on the incoming neutron wave vector, namely its resolution in
,
, and
. The neutron coherence volume projected on the sample surface takes the shape of an elongated ellipsoid with a length of about
μm in forward direction, but only few nm width perpendicular to the scattering plane (
) [
35,
39,
47,
56]. In depth, the coherence length
extends over a fraction of a micrometer. Therefore, each coherence volume comprises only a small fraction of the sample volume illuminated by the incident beam. The measured SR and OSS intensities result from incoherent summation of intensities independently radiated from a large number of coherence spots covering the sample.
Within each coherence volume, neutron waves interfere, providing a coherent enhancement of neutron flux scattered into directions of SR, refraction, diffuse OSS and Bragg diffraction, while suppressing scattering in all other directions in which interference is destructive. SR and refraction are due to the part of the optical potential independent of lateral coordinates. This part is described by the mean potential averaged over the coherence volume. By definition, the mean value is invariant with respect to its shift parallel to the surface, hence conserving the lateral projection of the wave vector (). Together with the conservation of energy, this results in Snell’s law of specular reflection.
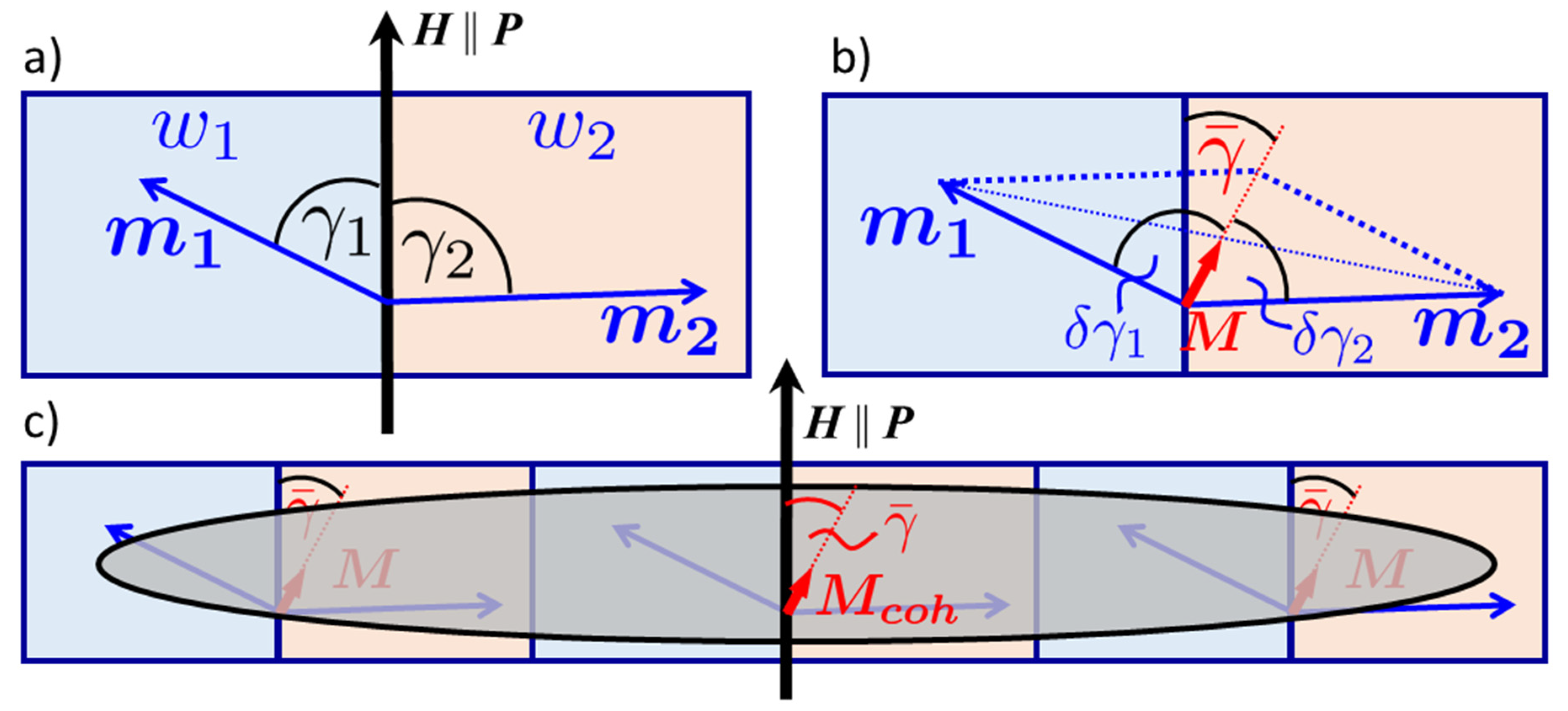
The magnetic part of mean optical potential of the coherence volume is proportional to its magnetization. The mean magnetization direction sets the quantization axis for the neutron spins and provides the splitting of the neutron spin states. This splitting is proportional to the absolute value of magnetization even though its direction may be tilted at an angle
against the direction of external field guiding the neutron polarization. If the magnetization within the coherence volume is decomposed into a set of magnetic domains, the magnetization direction of each individual domain in the coherence volume may deviate from the direction of the mean magnetization by the angle
. The tilt angle of each domain magnetization vector against the external magnetic field can therefore be described by
, where
is the mean value of the tilt angle in a coherence volume averaged over deviations
within (
Figure 3). Such deviations
cause magnetic OSS, which can be diffuse if the domains are randomly distributed, or concentrated in Bragg diffraction peaks, if the domain magnetization varies periodically along surface. The latter case is illustrated in
Figure 3a, where a schematic magnetic unit cell with two magnetizations
at an angle
with respect to the external field is shown. The average of the two magnetizations leads to a drastically reduced mean magnetization
(
Figure 3b), which itself makes an angle
with the external field. The domain magnetizations can now be described by an angle
with respect to
. Due to the extended length of the coherence ellipsoid, several magnetic unit cells are covered and contribute to the mean magnetization
(
Figure 3c).
The local variations in magnetization directions within domains reduce the magnitude of the mean magnetization averaged over the coherence volume. The projection of domain magnetization onto the external field direction is proportional to the mean value of After averaging over the coherence volume the second term in this equation vanishes, because the equation , where the bar indicates the coherent averaging over the coherence volume, actually determines the angle . The factor reduces the mean magnetization of the coherence volume and hence the splitting between spin states in the mean magnetic induction. Such a reduction manifests in a diminished spin splitting between critical wave vectors of total reflection for the two incoming polarization directions. If the reduction factor is unique for all coherence volumes then the parameter , where angular brackets denote incoherent averaging over the whole surface. The observed spin asymmetry, , is directly proportional to .
For example, if the sample is totally demagnetized over distances greater than the coherence length in each direction and
, the reflectivities
and
merge into a single curve and the spin asymmetry vanishes. However, if at the same time
,
will still reveal two critical edges
and two plateaus of total reflection, at
, where
, and at
. Due to the incoherent sum of intensities originating from the coherence volumes, both critical edges and plateaus can also be observed when
. Only if
the edge
is unique to
, while
is revealed in that of
. We should note that the condition
does not necessarily mean that
. For example, if the magnetization in half of the surface area is tilted at an angle
, while in the other half
, then
and
. Alternatively, if
, then
and
, but one may expect
. This expectation can be proven by measuring spin-flip (SF) reflectivities
and
which are due to components of mean magnetization normal to the polarization vector. Due to symmetry reasons, SF reflectivities
in one-dimensional polarization analysis [
57] are equal to each other and proportional to
. Therefore, PNR with only one-dimensional analysis is not able to distinguish between right and left tilt of magnetization direction.
Without polarization analysis, the reflection into non-spin-flip channels (NSF) and and SF reflectivities contribute to the measured reflectivities and . In such reduced version of PNR one can experimentally determine two statistical parameters: expectation values and characterizing the magnetization distribution over domains. is deduced from the splitting of critical edges of total reflection, , of and , while can be extracted from the spin asymmetry (. However, the third statistical parameter, , is only accessible with a complete version of one-dimensional PNR including polarization analysis. This parameter is important because it determines the dispersion , which, along with the expectation value , fully describes the distribution of magnetization projections onto the external field direction in case of Gaussian statistics.
Similarly to SR, one should distinguish between NSF and SF OSS originating from deviations of the magnetization directions in domains from that averaged over the coherence volume. A variation in magnitude of the domain magnetization projection onto the direction of the mean magnetization of the coherence volume contributes to NSF OSS. These variations do not mix spin states which are split in the mean magnetic induction. Components normal to the mean induction cause transitions between the two spin states. Therefore, if the mean induction in all coherence volumes is parallel to the external field,
, SF OSS is proportional to the mean value
, characterizing correlations of domain magnetization projections normal to the mean magnetization. Similarly, NSF OSS is due to correlations of longitudinal components, whose statistics is characterized by the mean value
−
. The value
is determined from the fit of specular PNR. Due to the constrain
, NSF OSS is actually described by the same statistical parameter
as SF OSS. This parameter, as we will discuss in
Section 3.4, can be extracted from the fit of OSS data collected in the reduced version of PNR without analysis of scattered neutrons.
Other parameters determining OSS are related to the distribution of magnetization over the ensemble of domains within the coherence ellipsoid. In the simplest case of random distribution, OSS is diffuse, with a line shape determined by the mean domain form-factor. The latter is described with one parameter corresponding to the inverse value of the mean size of domains. In general, the cross section of OSS is proportional to a linear combination of transverse and longitudinal correlators. The correlator for SF OSS, , describes correlations of the Fourier components of magnetization projections onto the normal to mean magnetization. Similarly, the NSF OSS cross section is proportional to the correlator of deviations in longitudinal components of the domain magnetization vector from its mean value . If components of are periodic functions of the distance between domains then OSS cross section reveals a series of Bragg peaks of different orders. Their relative intensities are determined by the unit cell form-factor and the structure factor. Simultaneously, they are firmly scaled to the peak intensity of SR, which is the Bragg peak of the zeroth order. The latter is calculated exactly, while higher orders are described within the framework of DWBA.
The fitting of the SR data in saturation shown in
Figure 2a,b provided a set of structural parameters collected in the
Table 1, which has subsequently been fixed in fitting of the SR in low field. The fitting of the data obtained at 2.2 kA/m provided
, which reveals a dramatic reduction of the mean value of the M-SLD averaged over the coherence volume and corresponds to a residual splitting of 0.34 μ
B/CoFe. Additionally, the fitting provided
, which indicates deviations of the mean magnetization direction amount to
. This means that the sample is mostly demagnetized within the coherence ellipsoids, while after averaging over all coherence areas only a small deviation of the mean magnetization from the external field direction remains. We note that the parameter
correlates with the incident beam polarization and therefore depends on the precision of the correction for the inefficiency of the devices on the instrument. The values obtained from the fit of SR where used in the analysis of the OSS presented in
Section 3.4.
Due to the reduced M-SLD, the potential well structure for “+” and “−” polarizations is altered with respect to that in saturation. The decrease in splitting indicates a multi-domain state in which the magnetization directions
deviate strongly from the external field direction, such that the mean magnetization averaged over several domains is close to zero. In the low field configuration, no magnetic moment in the IrMn
3 was resolved by SR. In addition, the lateral domain structure creates scattering into the OSS channels (
Figure 4), which is enhanced at the location of the resonance (
Figure 2b). Next to the collapse in spin asymmetry, the reflectivity at the position of the resonance drops below 50%. The position of the dips in
and
are reproduced well with the reduced magnetic moment in CoFe, but the depth cannot be reproduced considering the nominal absorption alone. Instead, the scattering from the lateral structure needs to be taken into account to explain this feature. For an approximation of the loss in SR intensity due to scattering from lateral structures, an artificially enhanced effective absorption was introduced as discussed in more detail below. From the specular data alone, one cannot deduce the microscopic arrangement of magnetic states in the sample plane, which is responsible for the reduction in magnetization.
3.4. Off-Specular Scattering
In saturating external magnetic fields (not shown), no off-specular intensity is observed even with prolonged acquisition times of 30 min compared to the 5 min used in measurements discussed below. This is in agreement with the AFM data and further shows that the observed residual resist patches on the surface do not contribute to the scattering. Further, this confirms that the individual layer roughness is uncorrelated in depth and laterally, and therefore does not lead to enhanced diffuse OSS intensities. The diffuse scattering arising from the individual layer roughness remains below the detection level as it is typically observed for non-correlated roughness. Furthermore, we do not observe any OSS from the topographic swelling of the stripe domains after IBMP or a notable decrease of saturation magnetization in bombarded regions [
23]. Upon reduction of the external magnetic field, the magnetic stripe domains evolve at constant width and create the OSS pattern observed in
Figure 4. The intensity maps shown are those also used to extract the specular reflectivity in
Figure 2. For the quantitative analysis of the OSS intensities on the detector we remain in the instrumental
coordinates which allows an enlarged view on the low-Q region near the total reflection [
58]. A non-linear transformation into reciprocal space with
coordinates can be performed using the relationship
This transformation changes the data point spacing for different wavelength and leads to a larger amount of triangulation for different Q-regions. In addition, the resolution function of
,
, and
becomes a more complex function. In the instrumental coordinates, the data is contained in a linear matrix with constant pixel size for the full scattering region and the resolution function is known due to the divergence of the incoming beam and detector resolution [
44,
45]. In
coordinates, the OSS is visible as curved lines around the specular reflectivity line located at
. Since no structural or chemical lateral contrast exists, the intensity of the Bragg diffraction lines depends on the magnetic contrast between domains given by the arrangement of magnetization vectors. At
only the OSS towards larger
is visible due to the horizon of the sample at
being close to the specular reflection. In
coordinates the scattering would be visible as vertical lines with constant
from which the period of the lateral elements can be determined with:
This provides an average period of
D = (10.2 ± 0.2) μm for the repeating unit cell of two stripes. The contour plots have been normalized in wavelength by the direct beam spectrum [
44] and only the instrumental background is subtracted, not the scattering from the sample or the sample holder. This background is constant in wavelength, but due to the normalization with the neutron spectrum appears to drop in intensity towards shorter
λ. The simulations only include a constant background, whose value was adjusted for the different regions investigated in detail in
Figure 5.
Figure 4a shows data at an angle of incidence of
, which mainly comprises the total reflection plateau for the wavelength band shown. Typically, OSS is not observed below the critical wave vector transfer of total reflection
, since the reflection amplitude is unity. Nevertheless, strong OSS is observed, which is a manifestation of the finite penetration depth of the neutron evanescent wave, whose scattering is enhanced by the resonance structure of the potential well. This is particularly visible around wavelength of 1.3 nm, which corresponds to the location of the dip in total reflectivity in reciprocal space (
Figure 2). Above
the neutron wave fully penetrates the whole sample and the OSS intensity mainly follows the intensity profile determined by the cross section of the domain structure without the wave field enhancement (
Figure 4b). The discrete nature of the intensity profiles, in contrast to diffuse scattering spanning a range of
, indicate a well ordered in-plane domain structure with defined width of each domain repeated laterally over large distances. In fact, the lines correspond to different orders of in-plane Bragg diffraction from periodic elements. In total, up to the 8th order diffraction can be identified at different angles of incidence, labelled up to the 4th-order in
Figure 4a. The intense features at about 0.5°/1.5 nm and 0.4°/1.05 nm in
Figure 4b are enhanced scattering due to the Yoneda effect [
59], which results from the enhancement of the neutron wave field near
due to constructive interference between incident and scattered neutron waves.
Even order Bragg diffraction is strongly suppressed by the structure factor of a periodically repeated unit cell containing two stripes of equal widths with opposing magnetization. The observation of strong 2nd-order and further even-order diffraction lines is therefore an indication of an imbalance between the domains either due to their magnetization or due to different widths. This imbalance can also create the residual splitting observed in the specular reflectivity. For the experiment, the external magnetic field was applied along the stripe axis and therefore perpendicular to the expected domain magnetization. This could lead to a different canting of magnetizations in the treated and virgin regions if the exchange anisotropy is not equal. In order to provide a quantitative measure for the scattered intensity constant wavelength cuts were made at several important regions of the
contour plot.
Figure 5a,b shows the intensity profiles obtained at
, while those obtained for the second angle of incidence,
, are shown in
Figure 5c,d. Due to the integration, absolute normalization of the intensity with respect to the specular reflectivity is lost. The data is shown for both incoming spin states. Each integration was made over an interval of wavelengths as indicated in the figure to increase the statistics. The regions were chosen to comprise areas of strong OSS scattering and those, which are affected by wave field enhancements below and above
as indicated by the dashed boxes in
Figure 4. Next to the specular intensity at
,
Figure 5 shows strong off-specular Bragg diffraction including 2nd- and 4th-order peaks of similar intensity as the following odd-order diffraction peak. The scattering is similar in intensity for both incoming neutron spin polarizations.
For the quantitative analysis of the polarized OSS, simulations based on the DWBA have been performed. Within DWBA, variations of the optical potential are considered as small perturbations to the mean optical potential of the sample. The analysis proceeds by first calculating the exact wave functions of the neutron propagating in the mean optical potential. The wave functions accounting for refraction through and reflection from laterally flat interfaces are further used as an input for the calculation of the cross section for OSS from the difference between the true profile of the scattering potential and its mean value averaged over the coherence ellipsoid. The difference is taken into account within a first order perturbation theory [
39,
47,
48]. This means that the OSS is bound to the specular reflectivity, which is used as input for the laterally averaged potential. Similar to the slab model for specular reflectivity, a model system of lateral elements defines the potential landscape encountered by the neutron wave. These take the form of correlators of domain magnetizations described in
Section 3.3, which are integrated in the simulation package designed by one of the authors. The simulation routine includes the resolution of the instrument in wavelength and angle, hence taking into account coherence properties of the neutron beam and providing an absolute scaling normalization of OSS to SR.
Typically, OSS is by orders of magnitude lower in intensity compared to SR and transmitted intensities, which justifies the DWBA. A drawback becomes apparent in the current scenario where strong OSS arising from resonance structures in the sample leads to significant scattering away from the specular reflection (compare
Figure 2 and
Figure 5). Ignoring this effect in SR fitting violates the total flux conservation [
60]. Such violation is only visible in the specular intensity in
Figure 2b through the increased depth of the resonance dip in SR at low field. However, this effect is readily described by releasing the imaginary part of the SLD in the fit at low fields, which allocated an iN-SLD twice higher than nominally found to the IrMn
3 layer. Thus, additional absorption compensates for the unaccounted losses in the specular intensity due to OSS substantially enhanced at resonance conditions. The specular fitting routine was free to allocate the additional absorption to all layers in the structure in order not to limit the generality of the approach. Further, the enhanced iN-SLD value found for IrMn
3 does not influence other parameters determined from the SR fit. The validity of the approach to describe the scattering losses is confirmed by fitting specular reflectivities recorded at different external field values and different sample structures, which will be reported elsewhere [
61]. A more rigorous approach accounting for the sum-rule of SR, transmission and OSS, required by the flux conservation law [
60,
62], can be accomplished in the second-order DWBA, which provides a non-zero imaginary part of the OSS amplitude even for a purely real scattering potential. In turn, the imaginary part of the amplitude in the forward direction is expressed in the total OSS cross section via the famous Optical Theorem (Bohr–Peierls–Placzek relation), hence formalizing a relationship between OSS into a solid angle and phenomenologically introduced absorption. The implementation of the second-order DWBA is beyond the scope of this report, but shall be highlighted here as one of the future tasks for the analysis of strong OSS from lateral structures.
In the simulations of the OSS, the lateral potential was approximated with four purely magnetic elements repeated periodically over the sample surface. Note that structural elements, described by a lateral variation in N-SLD would lead to OSS also in saturation, which is not observed. Furthermore, the absolute magnetization of each CoFe domain was fixed to the value determined from specular reflectivity at saturation. The position of all Bragg peaks was reproduced with a period of the unit cell structure of 10.2 μm, which is in agreement with the value determined directly from the contour plots. The simulations proceeded by adjusting the domain width independently in order to create the even-order intensity. The intensity of the Bragg peaks and the residual magnetization observed in specular reflectometry are a result of individual tilt angles of magnetizations within domains, which define the scattering contrast. Interestingly, a variation of only the CoFe magnetization direction in two domains was found to be insufficient to match all observed peaks. The best agreement to the data was obtained with a four-element unit cell schematically shown in
Figure 6, which is laterally repeated over the whole sample length. The model includes two domains of unequal widths, one being close to the nominal width of 5 μm, the other being substantially reduced to 3.7 μm. The magnetization direction in the large domain is tilted by an angle of
with respect to the net magnetization, which itself is tilted at an angle of
against the external field and stripe axis (see
Section 3.3). The magnetization in the smaller domain shows a tilt angle of
in the opposite direction with respect to the same axis.
In addition, the model had to include intermediate regions between the domains, which can be interpreted as domain walls, of 0.6 μm width. The magnetization in this region is aligned with the external magnetic field and of the same magnitude as the domains. The projections of the mean magnetization deviations averaged over the domains,
and
, and the two walls,
, of the unit cell is consistent with the reduction factor
for mean magnetic SLD deduced from the SR fit reported in
Section 3.3. This reduction factor for the M-SLD explains the low, but still noticeable spin asymmetry in
Figure 2 and
Figure 5.
The sensitivity to the domain walls mostly arises from the resonance features located below
in
Figure 5c,d. These features are substantially broader and react strongly to the simulated width of the domain wall, the asymmetry between the domain widths and the tilt of the magnetization. A small improvement of the simulation could be observed by using the same moment of IrMn
3 as determined in saturation, but with opposite sign in relation to the CoFe layer. However, with respect to the total match between simulation and data, this is not very reliable as the widths of the magnetic elements in CoFe and the canting angles have a much larger impact. The validity and sensitivity towards this small magnetization in IrMn
3 is subject of a future study. We shall note that the sensitivity of PNR and OSS to the elements described in the model is not biased by findings from complementary techniques. In fact, the model has been gradually refined starting from a simple balanced two domain configuration in order to account for all features observed in
Figure 2 and
Figure 4.