Optoelectronic Properties of Monolayer Hexagonal Boron Nitride on Different Substrates Measured by Terahertz Time-Domain Spectroscopy
Abstract
:1. Introduction
2. Samples and Experimental Measurements
2.1. Sample Growth
2.2. THz TDS Measurement System
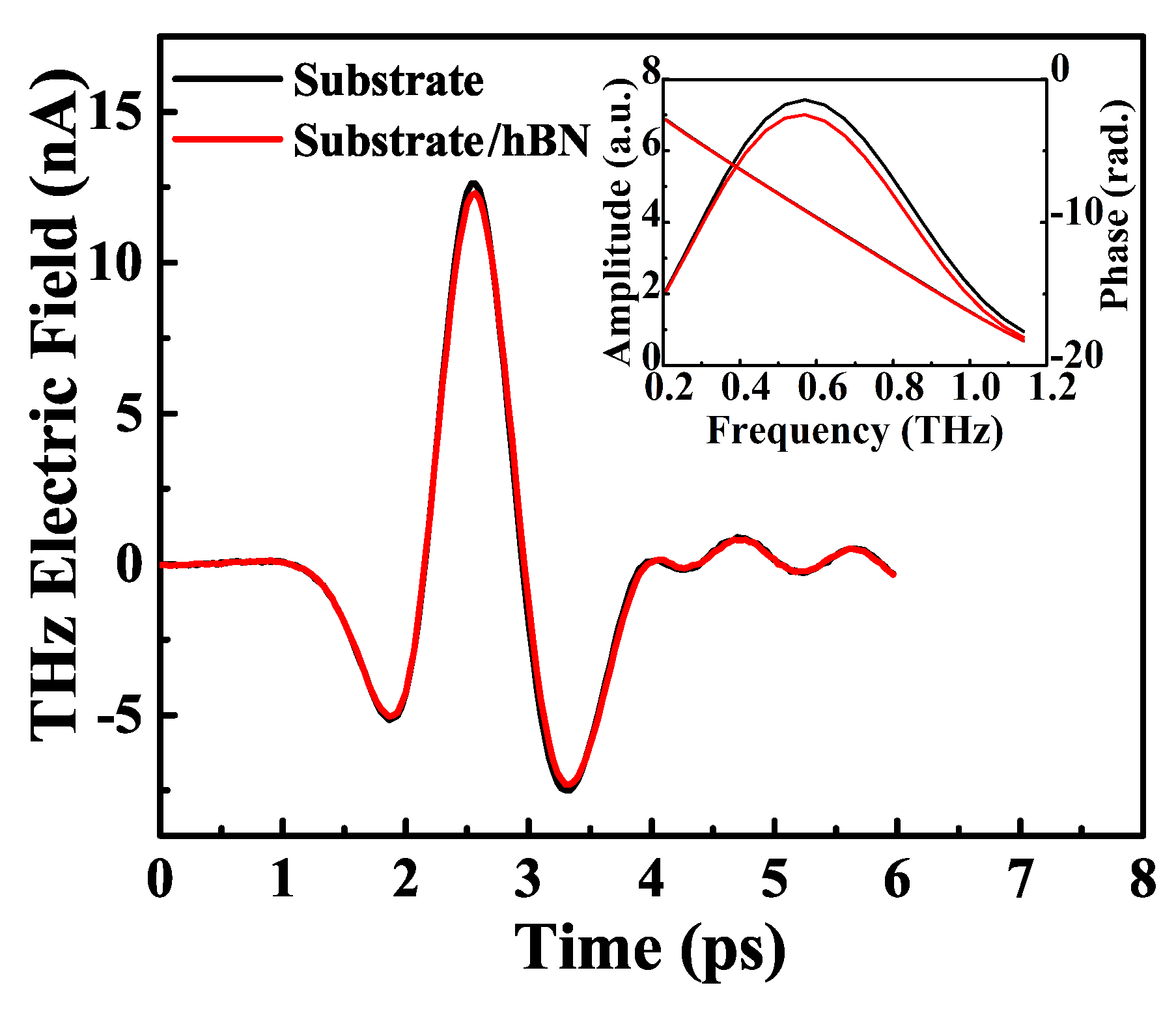
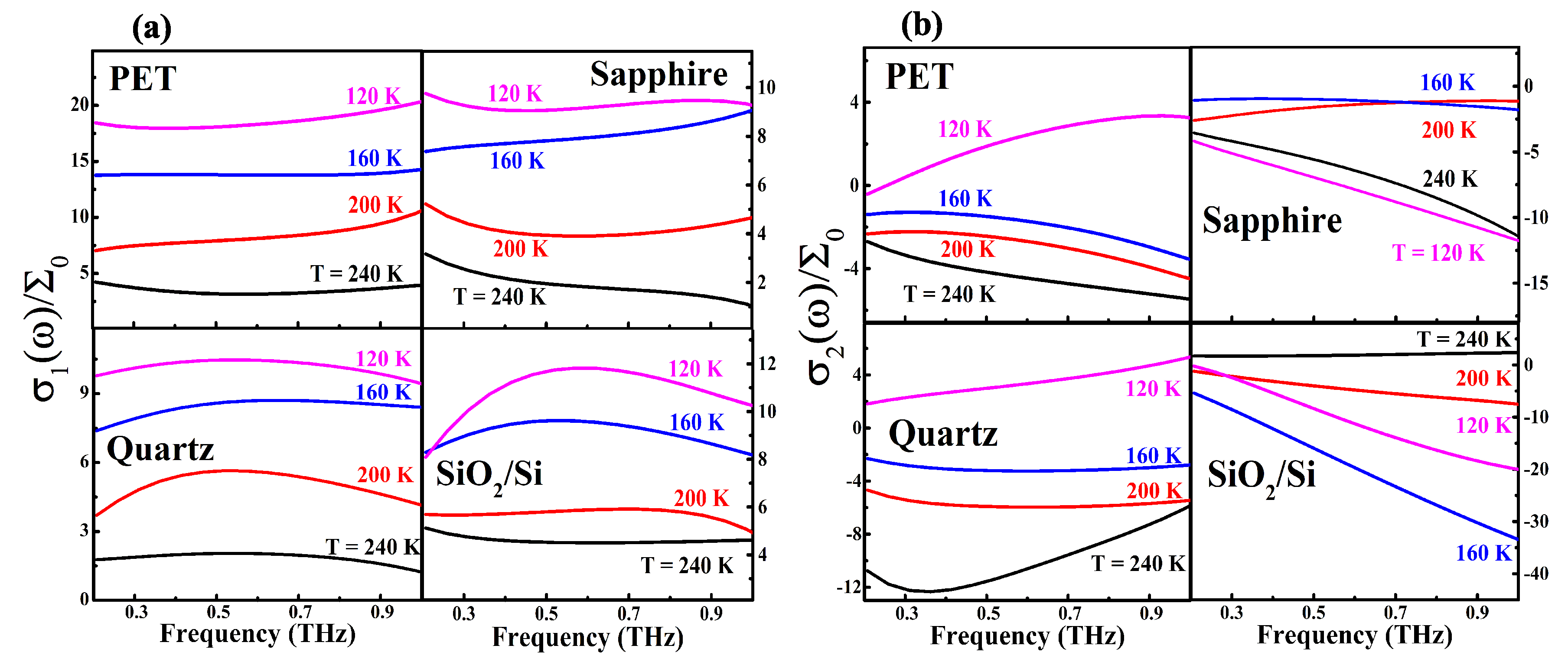
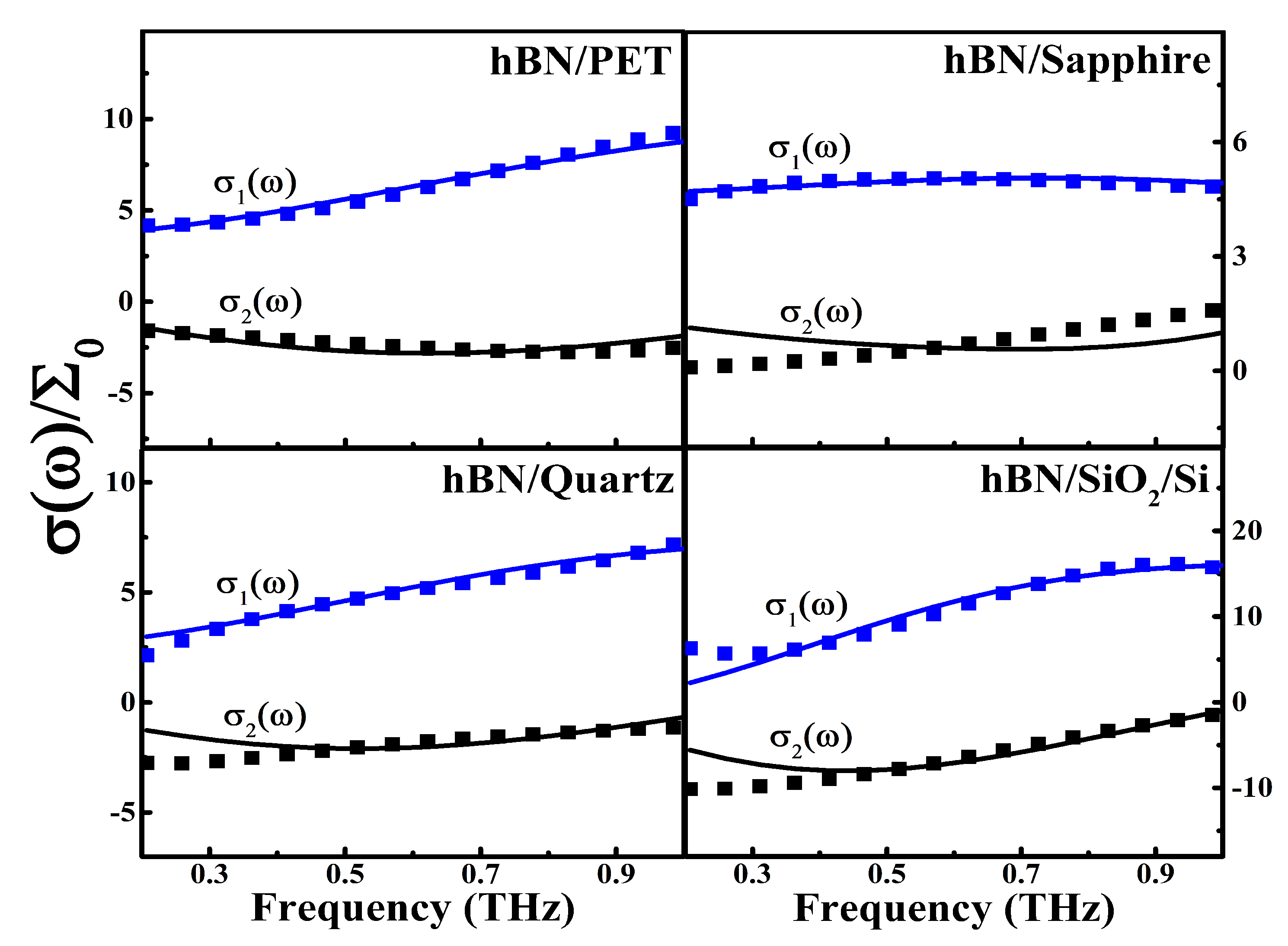
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ML | Monolayer |
| hBN | Hexagonal boron nitride |
| 2D | Two-dimensional |
| Si | Silicon |
| SiO | Silicon dioxide |
| PET | Polyethylene terephthalate |
| THz | Terahertz |
| TDS | Time-domain spectroscopy |
| UV | Ultraviolet |
| LEDs | Light-emitting diodes |
| TMD | Transition metal dichalcogenide |
| PL | Photoluminescence |
| SOC | Spin-orbit coupling |
| CVD | Chemical vapor deposition |
| PMMA | Poly methyl methacrylate |
| MOCVD | Metal organic chemical vapor deposition |
References
- Junhua, M.; Denggui, W.; Likun, C.; Menglei, G.; Xingwang, Z. Recent progress in synthesis, properties, and applications of hexagonal boron nitride-based heterostructures. Nanotechnology 2018, 30, 074003. [Google Scholar]
- Withers, F.; Del Pozo-Zamudio, O.; Mishchenko, A.; Rooney, A.P.; Gholinia, A.; Watanabe, K.; Taniguchi, T.; Haigh, S.J.; Geim, A.K.; Tartakovskii, A.I.; et al. Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mater. 2015, 14, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Calderon, B.; Han, Y.; Cueva, P.; Jungwirth, N.R.; Alsalman, H.A.; Hwang, J.; Fuchs, G.D.; Muller, D.A.; Spencer, M.G. Chemical vapor deposition growth of large single-crystal Mono-, Bi-, Tri-layer hexagonal boron nitride and their interlayer stacking. ACS Nano 2017, 11, 12057–12066. [Google Scholar] [CrossRef] [PubMed]
- Cassabois, G.; Valvin, P.; Gil, B. Hexagonal boron nitride is an indirect bandgap semiconductor. Nat. Photonics 2016, 10, 262. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.X.; Lin, J.Y. Hexagonal boron nitride for deep ultraviolet photonic devices. Semicond. Sci. Technol. 2014, 29, 084003. [Google Scholar] [CrossRef]
- Constantinescu, G.C.; Hine, N.D. Multipurpose black-phosphorus/hBN heterostructures. Nano Lett. 2016, 16, 2586–2594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, S.; Lozada-Hidalgo, M.; Wang, F.C.; Mishchenko, A.; Schedin, F.; Nair, R.R.; Hill, E.W.; Boukhvalov, D.W.; Katsnelson, M.I.; Dryfe, R.A.W.; et al. Proton transport through one-atom-thick crystals. Nature 2014, 516, 227–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Britnell, L.; Gorbachev, R.V.; Jalil, R.; Belle, B.D.; Schedin, F.; Katsnelson, M.I.; Eaves, L.; Morozov, S.V.; Mayorov, A.S.; Peres, N.M.; et al. Electron tunneling through ultrathin boron nitride crystalline barriers. Nano Lett. 2012, 12, 1707–1710. [Google Scholar] [CrossRef] [Green Version]
- Scavuzzo, A.; Mangel, S.; Park, J.H.; Lee, S.; Loc Duong, D.; Strelow, C.; Mews, A.; Burghard, M.; Kern, K. Electrically tunable quantum emitters in an ultrathin graphene-hexagonal boron nitride van der Waals heterostructure. Appl. Phys. Lett. 2019, 114, 062104. [Google Scholar] [CrossRef]
- Han, X.; Lin, J.; Liu, J.; Wang, N.; Pan, D. Effects of Hexagonal Boron Nitride Encapsulation on the Electronic Structure of Few-Layer MoS2. J. Phys. Chem. C 2019, 123, 14797–14802. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Chen, G.; Shi, Z.; Liu, C.C.; Zhang, L.; Xie, G.; Cheng, M.; Wang, D.; Yang, R.; Shi, D.; et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride. Nat. Mater. 2013, 12, 792–797. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, Y.; Kutana, A.; Watanabe, K.; Taniguchi, T.; Kojima, K.; Endo, T.; Miyata, Y.; Shinohara, H.; Kitaura, R. Momentum-forbidden dark excitons in hBN-encapsulated monolayer MoS2. NPJ 2D Mater. Appl. 2019, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Feng, Y.; Wang, F.; Yang, Z.; Wang, J. Two dimensional hexagonal boron nitride (2D-hBN): Synthesis, properties and applications. J. Mater. Chem. C 2017, 5, 11992–12022. [Google Scholar] [CrossRef]
- Sun, F.; Hao, Z.; Liu, G.; Wu, C.; Lu, S.; Huang, S.; Liu, C.; Hong, Q.; Chen, X.; Cai, D.; et al. p-Type conductivity of hexagonal boron nitride as a dielectrically tunable monolayer: Modulation doping with magnesium. Nanoscale 2018, 10, 4361–4369. [Google Scholar] [CrossRef]
- Kim, K.K.; Hsu, A.; Jia, X.; Kim, S.M.; Shi, Y.; Hofmann, M.; Nezich, D.; Rodriguez-Nieva, J.F.; Dresselhaus, M.; Palacios, T.; et al. Synthesis of monolayer hexagonal boron nitride on Cu foil using chemical vapor deposition. Nano Lett. 2012, 12, 161–166. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [Green Version]
- Manchon, A.; Koo, H.C.; Nitta, J.; Frolov, S.M.; Duine, R.A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. [Google Scholar] [CrossRef]
- Slobodeniuk, A.O.; Basko, D.M. Spin-flip processes and radiative decay of dark intravalley excitons in transition metal dichalcogenide monolayers. 2D Mater. 2016, 3, 035009. [Google Scholar] [CrossRef] [Green Version]
- Zollner, K.; Gmitra, M.; Fabian, J. Heterostructures of graphene and hBN: Electronic, spin-orbit, and spin relaxation properties from first principles. Phys. Rev. B 2019, 99, 125151. [Google Scholar] [CrossRef] [Green Version]
- Kormyos, A.; Zyomi, V.; Drummond, N.D.; Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 2014, 4, 011034. [Google Scholar]
- Yu, Y.; Li, C.; Liu, Y.; Su, L.; Zhang, Y.; Cao, L. Controlled scalable synthesis of uniform, high-quality monolayer and few-layer MoS2 films. Sci. Rep. 2013, 3, 1866. [Google Scholar] [CrossRef] [PubMed]
- Nuss, M.C.; Orenstein, J. Terahertz Time-Domain Spectroscopy, in Millimeter and Submillimeter Wave Spectroscopy of Solids; Springer: Berlin/Heidelberg, Germany, 1998; pp. 7–50. [Google Scholar]
- Wang, C.; Xu, W.; Mei, H.; Qin, H.; Zhao, X.; Zhang, C.; Yuan, H.; Zhang, J.; Xu, Y.; Li, P.; et al. Substrate-induced electronic localization in monolayer MoS2 measured via terahertz spectroscopy. Opt. Lett. 2019, 44, 4139–4142. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Su, F.; Dai, J.; Pi, L.; Mei, H.; Zhang, P.; Xu, W. Characterization of material parameters of LaPrCaMnO3 thin film by terahertz time-domain spectroscopy. Jpn. J. Appl. Phys. 2016, 55, 031101. [Google Scholar] [CrossRef]
- Mei, H.; Xu, W.; Wang, C.; Yuan, H.; Zhang, C.; Ding, L.; Zhang, J.; Deng, C.; Wang, Y.; Peeters, F.M. Terahertz magneto-optical properties of bi-and tri-layer graphene. J. Phys. Condens. Matter 2018, 30, 175701. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Hamsen, C.; Jia, X.; Kim, K.K.; Reina, A.; Hofmann, M.; Hsu, A.L.; Zhang, K.; Li, H.; Juang, Z.Y.; et al. Synthesis of few-layer hexagonal boron nitride thin film by chemical vapor deposition. Nano Lett. 2010, 10, 4134–4139. [Google Scholar] [CrossRef] [PubMed]
- Tien, D.H.; Park, J.Y.; Kim, K.B.; Lee, N.; Choi, T.; Kim, P.; Taniguchi, T.; Watanabe, K.; Seo, Y. Study of graphene-based 2D-heterostructure device fabricated by all-dry transfer process. ACS Appl. Mater. Interfaces 2016, 8, 3072–3078. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Shin, H.J.; Lee, J.; Lee, I.Y.; Kim, G.H.; Choi, J.Y.; Kim, S.W. Large-scale synthesis of high-quality hexagonal boron nitride nanosheets for large-area graphene electronics. Nano Lett. 2012, 12, 714–718. [Google Scholar] [CrossRef]
- Jiang, H.X.; Lin, J.Y. Hexagonal boron nitride epilayers: Growth, optical properties and device applications. ECS J. Solid State Sci. Technol. 2016, 6, Q3012. [Google Scholar] [CrossRef]
- Hangyo, M.; Nagashima, T.; Nashima, S. Spectroscopy by pulsed terahertz radiation. Meas. Sci. Technol. 2002, 13, 1727. [Google Scholar] [CrossRef]
- Tinkham, M. Energy gap interpretation of experiments on infrared transmission through superconducting films. Phys. Rev. 1956, 104, 845. [Google Scholar] [CrossRef]
- Shimakawa, K.; Kasap, S. Dynamics of carrier transport in nanoscale materials: Origin of non-Drude behavior in the terahertz frequency range. Appl. Sci. 2016, 6, 50. [Google Scholar] [CrossRef]
- Lloyd-Hughes, J.; Tae-In, J. A review of the terahertz conductivity of bulk and nano-materials. J. Infrared Millimeter Terahertz Waves 2012, 33, 871–925. [Google Scholar] [CrossRef]
- Němec, H.; Kužel, P.; Sundström, V. Far-infrared response of free charge carriers localized in semiconductor nanoparticles. Phys. Rev. B 2009, 79, 115309. [Google Scholar] [CrossRef] [Green Version]
- Smith, N.V. Classical generalization of the Drude formula for the optical conductivity. Phys. Rev. B 2001, 64, 155106. [Google Scholar] [CrossRef]
- Xu, Y.N.; Ching, W.Y. Calculation of ground-state and optical properties of boron nitrides in the hexagonal, cubic, and wurtzite structures. Phys. Rev. B 1991, 44, 7787. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, F.; Chaves, A.J.; Peres, N.M.R.; Ribeiro, R.M. Excitons in hexagonal boron nitride single-layer: A new platform for polaritonics in the ultraviolet. J. Opt. Soc. Am. B 2019, 36, 674–683. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Peeters, F.M.; Lu, T.C. Dependence of resistivity on electron density and temperature in graphene. Phys. Rev. B 2009, 79, 073403. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.M.; Xu, W.; Zeng, Z.; Lu, T.C.; Peeters, F.M. Quantum and transport conductivities in monolayer graphene. Phys. Rev. B 2008, 77, 235402. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.H.; Xu, W.; Badalyan, S.M.; Peeters, F.M. Piezoelectric surface acoustical phonon limited mobility of electrons in graphene on a GaAs substrate. Phys. Rev. B 2013, 87, 075443. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, B.; Wei, Y.; Yang, R.; Dresselhaus, M. Mechanics and mechanically tunable band gap in single-layer hexagonal boron-nitride. Mater. Res. Lett. 2013, 1, 200–206. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. First-principles study of the effects of mechanical strains on the radiation hardness of hexagonal boron nitride monolayers. Nanoscale 2013, 5, 695–703. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Xu, W.; Wang, C.; Wen, H.; Zhao, X.; Song, D.; Ding, L. Optoelectronic Properties of Monolayer Hexagonal Boron Nitride on Different Substrates Measured by Terahertz Time-Domain Spectroscopy. Nanomaterials 2020, 10, 762. https://doi.org/10.3390/nano10040762
Bilal M, Xu W, Wang C, Wen H, Zhao X, Song D, Ding L. Optoelectronic Properties of Monolayer Hexagonal Boron Nitride on Different Substrates Measured by Terahertz Time-Domain Spectroscopy. Nanomaterials. 2020; 10(4):762. https://doi.org/10.3390/nano10040762
Chicago/Turabian StyleBilal, Muhammad, Wen Xu, Chao Wang, Hua Wen, Xinnian Zhao, Dan Song, and Lan Ding. 2020. "Optoelectronic Properties of Monolayer Hexagonal Boron Nitride on Different Substrates Measured by Terahertz Time-Domain Spectroscopy" Nanomaterials 10, no. 4: 762. https://doi.org/10.3390/nano10040762
APA StyleBilal, M., Xu, W., Wang, C., Wen, H., Zhao, X., Song, D., & Ding, L. (2020). Optoelectronic Properties of Monolayer Hexagonal Boron Nitride on Different Substrates Measured by Terahertz Time-Domain Spectroscopy. Nanomaterials, 10(4), 762. https://doi.org/10.3390/nano10040762



