Development of Porous Titania Structure with Improved Photocatalytic Activity: Response Surface Modeling and Multi-Objective Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. TiO2 Synthesis
2.3. Materials Characterization
2.4. Photocatalytic Experiment
3. Results and Discussions
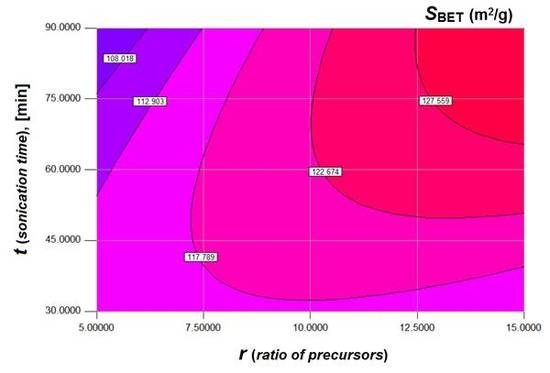
3.1. Design of Experiments and Multiple Regression Modeling
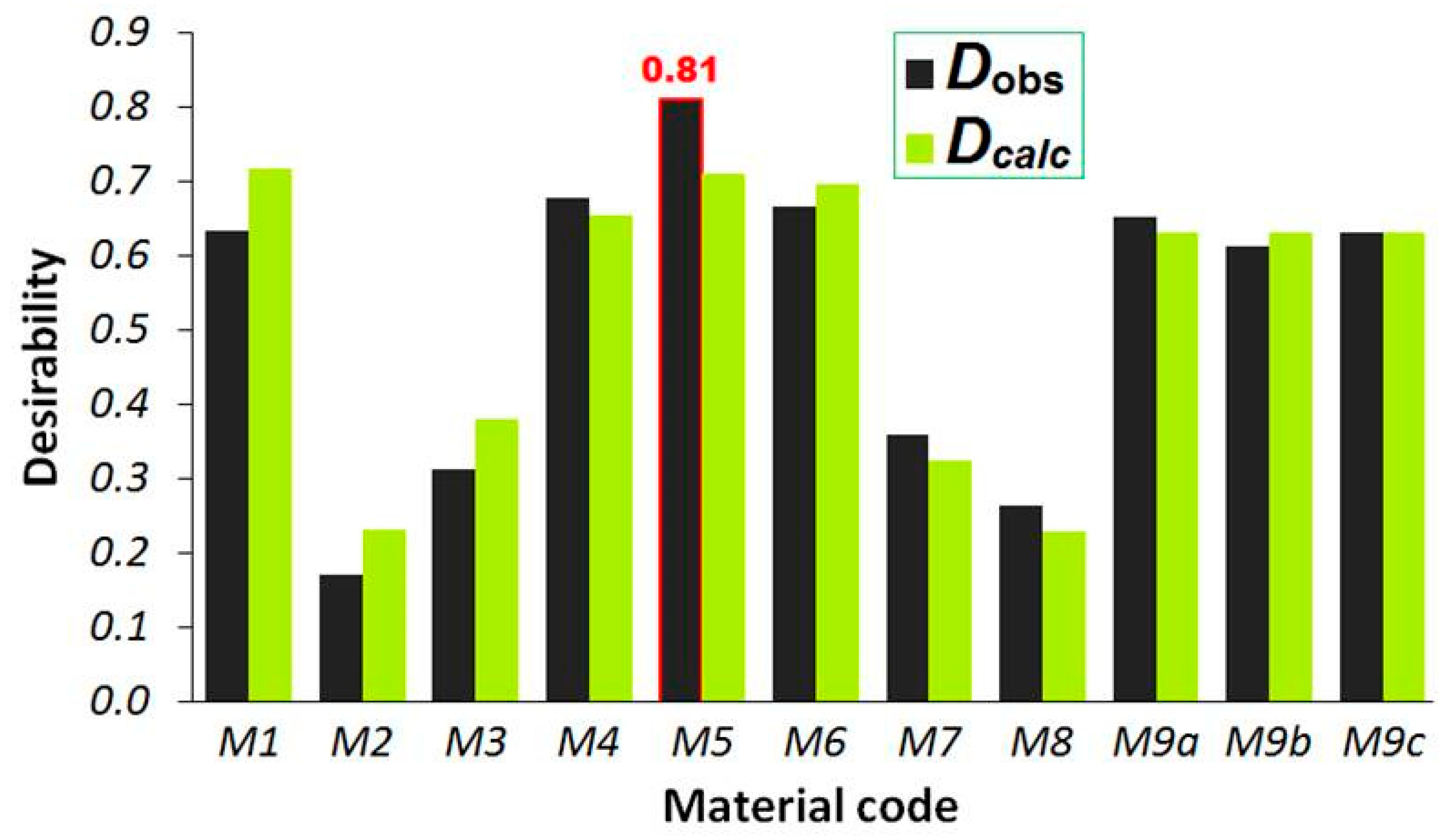
3.2. Multi-Objective Optimization
3.3. Characteristics of Optimum Material
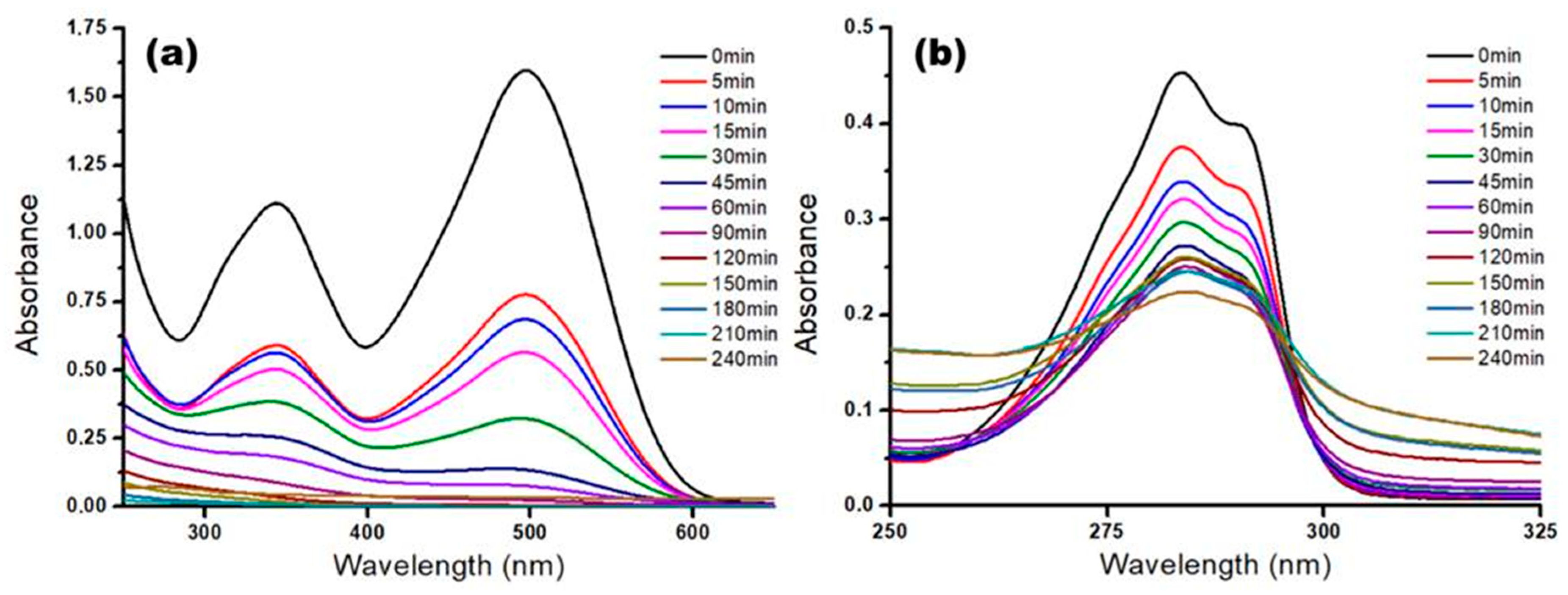
3.4. Kinetics of the Photocatalytic Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haddad, M.; Oie, C.; Duy, S.V.; Sauvé, S.; Barbeau, B. Adsorption of micropollutants present in surface waters onto polymeric resins: Impact of resin type and water matrix on performance. Sci. Total Environ. 2019, 660, 1449–1458. [Google Scholar] [CrossRef] [PubMed]
- Sadri Moghaddam, S.; Alavi Moghaddam, M.R.; Arami, M. Coagulation/flocculation process for dye removal using sludge from water treatment plant: Optimization through response surface methodology. J. Hazard. Mater. 2010, 175, 651–657. [Google Scholar] [CrossRef] [PubMed]
- Saini, R.; Kumar, P. Simultaneous removal of methyl parathion and chlorpyrifos pesticides from model wastewater using coagulation/flocculation: Central composite design. J. Environ. Chem. Eng. 2016, 4, 673–680. [Google Scholar] [CrossRef]
- Liu, J.; Wang, N.; Zhang, H.; Baeyens, J. Adsorption of Congo red dye on FexCo3-xO4 nanoparticles. J. Environ. Manag. 2019, 238, 473–483. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Yang, Q.; Yang, Z.; Wang, W. Adsorption of 2,4-D on magnetic graphene and mechanism study. Colloid. Surf. A 2016, 509, 367–375. [Google Scholar] [CrossRef]
- Secula, M.S.; Suditu, G.D.; Poulios, I.; Cojocaru, C.; Cretescu, I. Response surface optimization of the photocatalytic decolorization of a simulated dyestuff effluent. Chem. Eng. J. 2008, 141, 18–26. [Google Scholar] [CrossRef]
- Verma, M.; Haritash, A.K. Degradation of amoxicillin by Fenton and Fenton-integrated hybrid oxidation processes. J. Environ. Chem. Eng. 2019, 7, 102886. [Google Scholar] [CrossRef]
- López, N.; Plaza, S.; Afkhami, A.; Marco, P.; Esplugas, S. Treatment of Diphenhydramine with different AOPs including photo-Fenton at circumneutral pH. Chem. Eng. J. 2017, 318, 112–120. [Google Scholar] [CrossRef] [Green Version]
- Samoila, P.; Cojocaru, C.; Sacarescu, L.; Pascariu Dorneanu, P.; Domocos, A.-A.; Rotaru, A. Remarkable catalytic properties of rare-earth doped nickel ferrites synthesized by sol-gel auto-combustion with maleic acid as fuel for CWPO of dyes. Appl. Catal. B 2017, 202, 21–32. [Google Scholar] [CrossRef]
- Ghuge, S.P.; Saroha, A.K. Catalytic ozonation of dye industry effluent using mesoporous bimetallic Ru-Cu/SBA-15 catalyst. Proc. Saf. Environ. Prot. 2018, 118, 125–132. [Google Scholar] [CrossRef]
- Ignat, M.; Samoila, P.; Coromelci, C.; Sacarescu, L.; Asaftei, I.; Harabagiu, V.; Miron, C. Plasma generation in liquid as a new efficient synthesis approach of titania–zinc ferrite nano(photo)catalyst. C. R. Chimie 2018, 21, 310–317. [Google Scholar] [CrossRef]
- Pascariu, P.; Cojocaru, C.; Olaru, N.; Samoila, P.; Airinei, A.; Ignat, M.; Sacarescu, L.; Timpu, D. Novel rare earth (RE-La, Er, Sm) metal doped ZnO photocatalysts for degradation of Congo-Red dye: Synthesis, characterization and kinetic studies. J. Environ. Manag. 2019, 239, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Rostami, M. Photodecomposition and adsorption of hazardous organic pollutants by Ce-doped ZnO@Ce-doped TiO2-N/S-dual doped RGO ternary nano-composites photocatalyst for water remediation. J. Mol. Struct. 2019, 1185, 191–199. [Google Scholar] [CrossRef]
- Bouazizi, N.; Vieillard, J.; Thebault, P.; Desriac, F.; Clamens, T.; Bargougui, R.; Couvrat, N.; Thoumire, O.; Brun, N.; Ladam, G.; et al. Silver nanoparticle embedded copper oxide as an efficient core-shell for the catalytic reduction of 4-nitrophenol and antibacterial activity improvement. Dalton Trans. 2018, 47, 9143–9155. [Google Scholar] [CrossRef]
- Bouazizi, N.; Vieillard, J.; Bargougui, R.; Couvrat, N.; Thoumire, O.; Morin, S.; Ladam, G.; Mofaddel, N.; Brun, N.; Azzouz, A.; et al. Entrapment and stabilization of iron nanoparticles within APTES modified graphene oxide sheets for catalytic activity improvement. J. Alloy. Compd. 2019, 771, 1090–1102. [Google Scholar] [CrossRef]
- Nakata, K.; Fujishima, A. TiO2 photocatalysis: Design and applications. J. Photochem. Photobiol. C 2012, 13, 169–189. [Google Scholar] [CrossRef]
- Coromelci-Pastravanu, C.; Ignat, M.; Popovici, E.; Harabagiu, V. TiO2-coated mesoporous carbon: Conventional vs. microwave-annealing process. J. Hazard. Mater. 2014, 278, 382–390. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Witek-Krowiak, A.; Chojnacka, K.; Podstawczyk, D.; Dawiec, A.; Pokomeda, K. Application of response surface methodology and artificial neural network methods in modeling and optimization of biosorption process. Bioresour. Technol. 2014, 160, 150–160. [Google Scholar] [CrossRef]
- Rahimi-Nasrabadi, M.; Pourmortazavi, S.M.; Karimi, M.S.; Aghazadeh, M.; Ganjali, M.R.; Norouzi, P. Statistical optimization of experimental parameters for synthesis of two efficient photocatalyst: Erbium carbonate and erbium oxide nanoparticles. J. Mater. Sci. Mater. Electron 2017, 28, 15224–15232. [Google Scholar] [CrossRef]
- Costa, N.R.; Lourenco, J.; Pereira, Z.L. Desirability function approach: A review performance evaluation in adverse conditions. Chemom. Intell. Lab. Syst. 2011, 107, 234–244. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Horikawa, T.; Do, D.D.; Nicholson, D. Capillary condensation of adsorbates in porous materials. Adv. Colloid Interface Sci. 2011, 169, 40–58. [Google Scholar] [CrossRef] [PubMed]
- Du, W.N.; Chen, S.T. Photo- and chemocatalytic oxidation of dyes in water. J. Environ. Manag. 2018, 206, 507–515. [Google Scholar] [CrossRef] [PubMed]
- March, J.G.; Gual, M.; Ramonell, J. A kinetic model for chlorine consumption in grey water. Desalination 2005, 181, 267–273. [Google Scholar] [CrossRef]







| Design Variables (Factors) | Coded Variables | Actual Values of Coded Levels | ||||
|---|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | ||
| Ratio of precursors’ weights (TTIP/Surfactant), r | x1 | 3 | 5 | 10 | 15 | 17 |
| Sonication time, t (min) | x2 | 18 | 30 | 60 | 90 | 102 |
| Run | Design Variables | Resulted Material (Code) | Responses (Material Characterization) 1 & (Application) 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ratio of Precursors | Sonication Time (min) | ||||||||
| x1 | r | x2 | t | SBET (m2/g) 1 | VP (cm3/g) 1 | Y1 (%) 2 | Y2 (%) 2 | ||
| 1 | −1 | 5 | −1 | 30 | M1 | 108.46 | 0.276 | 91.98 | 39.80 |
| 2 | +1 | 15 | −1 | 30 | M2 | 110.26 | 0.288 | 90.26 | 32.34 |
| 3 | −1 | 5 | +1 | 90 | M3 | 99.54 | 0.259 | 87.71 | 36.39 |
| 4 | +1 | 15 | +1 | 90 | M4 | 132.05 | 0.331 | 88.03 | 41.93 |
| 5 | −α | 3 | 0 | 60 | M5 | 111.15 | 0.270 | 94.10 | 42.58 |
| 6 | +α | 17 | 0 | 60 | M6 | 126.36 | 0.299 | 91.39 | 38.17 |
| 7 | 0 | 10 | −α | 18 | M7 | 118.06 | 0.284 | 86.25 | 35.96 |
| 8 | 0 | 10 | +α | 102 | M8 | 120.33 | 0.296 | 84.06 | 37.43 |
| 9 | 0 | 10 | 0 | 60 | M9a | 122.32 | 0.291 | 91.85 | 37.96 |
| 10 | 0 | 10 | 0 | 60 | M9b | 121.97 | 0.292 | 90.46 | 38.05 |
| 11 | 0 | 10 | 0 | 60 | M9c | 122.71 | 0.289 | 91.16 | 37.88 |
| Sample | DScherrer (nm) | a (nm) | d (nm) | DW.H. (nm) | ξ |
|---|---|---|---|---|---|
| M3 | 10.375 | 0.351302 | 0.405649 | 18.561 | 0.0372 |
| M4 | 9.156 | 0.351191 | 0.405520 | 8.803 | -0.0002 |
| M5 | 9.701 | 0.351055 | 0.405363 | 9.064 | −6E−05 |
| No. (i) | Photocatalytic System | Pseudo first-order Reaction Rate Constant, ki (min−1) | Pseudo first-order Removal Rate Constant, γi (min−1) | Final Removal Efficiency (at t = 120 min) Y* (%) |
|---|---|---|---|---|
| 1 | M5 + CR dye | 8.86 × 10−2 | 10.59 × 10−2 | 98.40% |
| 2 | M5 + 2,4-D | 6.84 × 10−2 | 7.51 × 10−2 | 46.30% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahu, E.; Ignat, M.; Cojocaru, C.; Samoila, P.; Coromelci, C.; Asaftei, I.; Harabagiu, V. Development of Porous Titania Structure with Improved Photocatalytic Activity: Response Surface Modeling and Multi-Objective Optimization. Nanomaterials 2020, 10, 998. https://doi.org/10.3390/nano10050998
Mahu E, Ignat M, Cojocaru C, Samoila P, Coromelci C, Asaftei I, Harabagiu V. Development of Porous Titania Structure with Improved Photocatalytic Activity: Response Surface Modeling and Multi-Objective Optimization. Nanomaterials. 2020; 10(5):998. https://doi.org/10.3390/nano10050998
Chicago/Turabian StyleMahu, Elvira, Maria Ignat, Corneliu Cojocaru, Petrisor Samoila, Cristina Coromelci, Iuliean Asaftei, and Valeria Harabagiu. 2020. "Development of Porous Titania Structure with Improved Photocatalytic Activity: Response Surface Modeling and Multi-Objective Optimization" Nanomaterials 10, no. 5: 998. https://doi.org/10.3390/nano10050998
APA StyleMahu, E., Ignat, M., Cojocaru, C., Samoila, P., Coromelci, C., Asaftei, I., & Harabagiu, V. (2020). Development of Porous Titania Structure with Improved Photocatalytic Activity: Response Surface Modeling and Multi-Objective Optimization. Nanomaterials, 10(5), 998. https://doi.org/10.3390/nano10050998