Mapping Fluorescence Enhancement of Plasmonic Nanorod Coupled Dye Molecules
Abstract
:1. Introduction
2. Methods
2.1. FEM Optimization and Analyses of Optimal Configurations
2.1.1. Optimization of Cy5 Dye Molecule and Gold Nanorod Coupled Systems
2.1.2. Analyses of Optimal Cy5 Dye Molecule and Gold Nanorod Coupled Systems
2.1.3. Sensitivity Study on Cy5 Dye Molecule and Gold Nanorod Coupled Systems
2.2. Preparation Protocol and Characterization of Au NRs
2.2.1. Materials Used to Prepare Au NRs
2.2.2. Preparation Protocol of Au NRs
2.2.3. Characterization of the Synthesized Au NRs
2.3. Synthesis and Purification of Thiol- and Cy5-Modified DNA Oligonucleotides, Functionalization of Au NRs with Thiol-Modified DNA Oligonucleotide and Hybridization of the Cy5-Labelled Oligonucleotide
2.3.1. Materials Used to Create DNA Strands
2.3.2. Synthesis and Purification of Thiol and Cy5-Modified DNA Oligonucleotides
2.3.3. Functionalization of Au NRs with Thiol-Modified DNA Oligonucleotide
2.3.4. Hybridization of the Cy5-Labelled Oligonucleotide to the DNA-Au NR
2.4. dSTORM Optical System, Sample Preparation, Measurement and Analysis
2.4.1. dSTORM Optical System
2.4.2. dSTORM Sample Preparation
2.4.3. dSTORM Measurement
2.4.4. dSTORM Analysis
3. Results
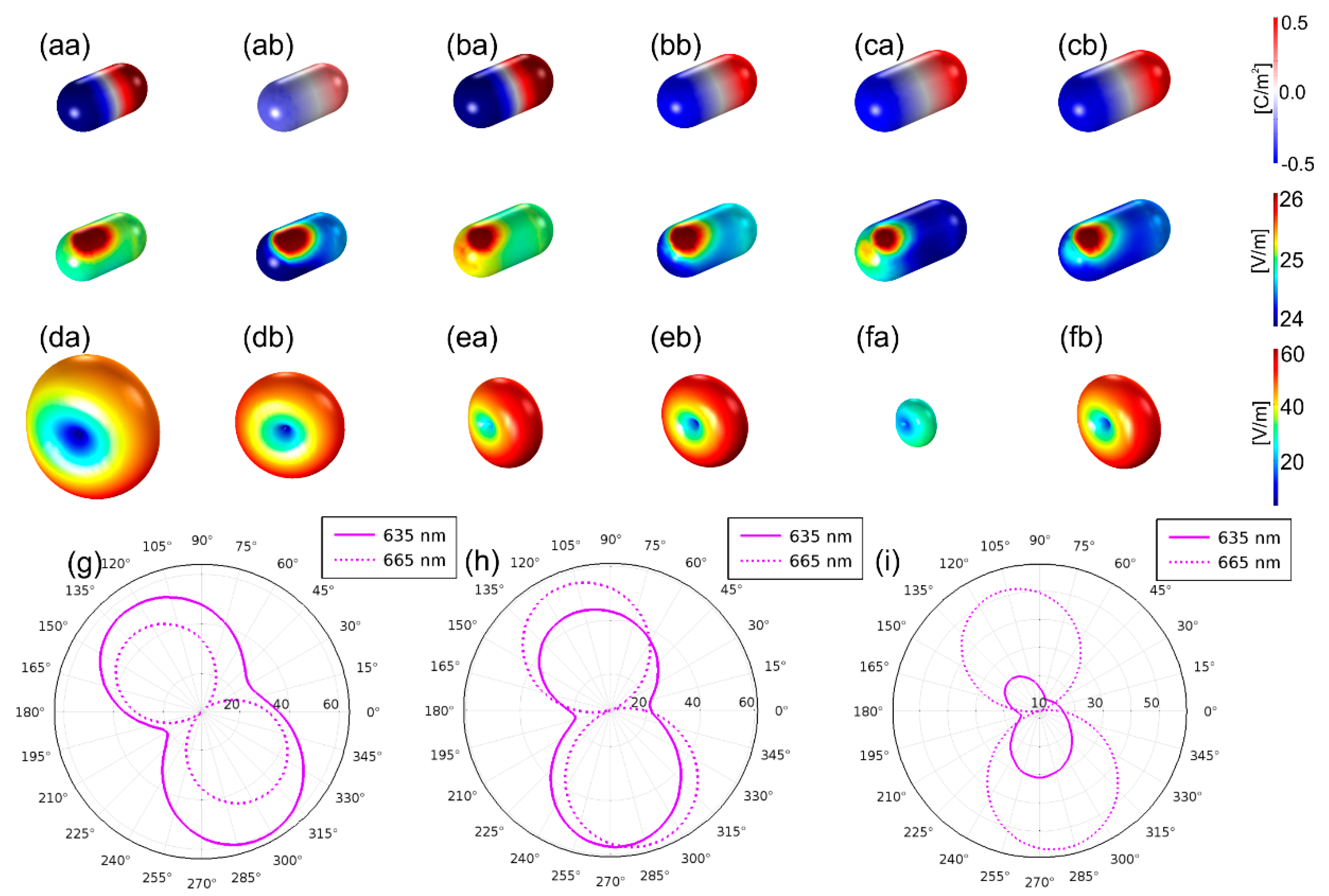
3.1. Optimized Coupled Cy5–Au NR Configurations
3.1.1. Optical Response of the Optimized Configurations
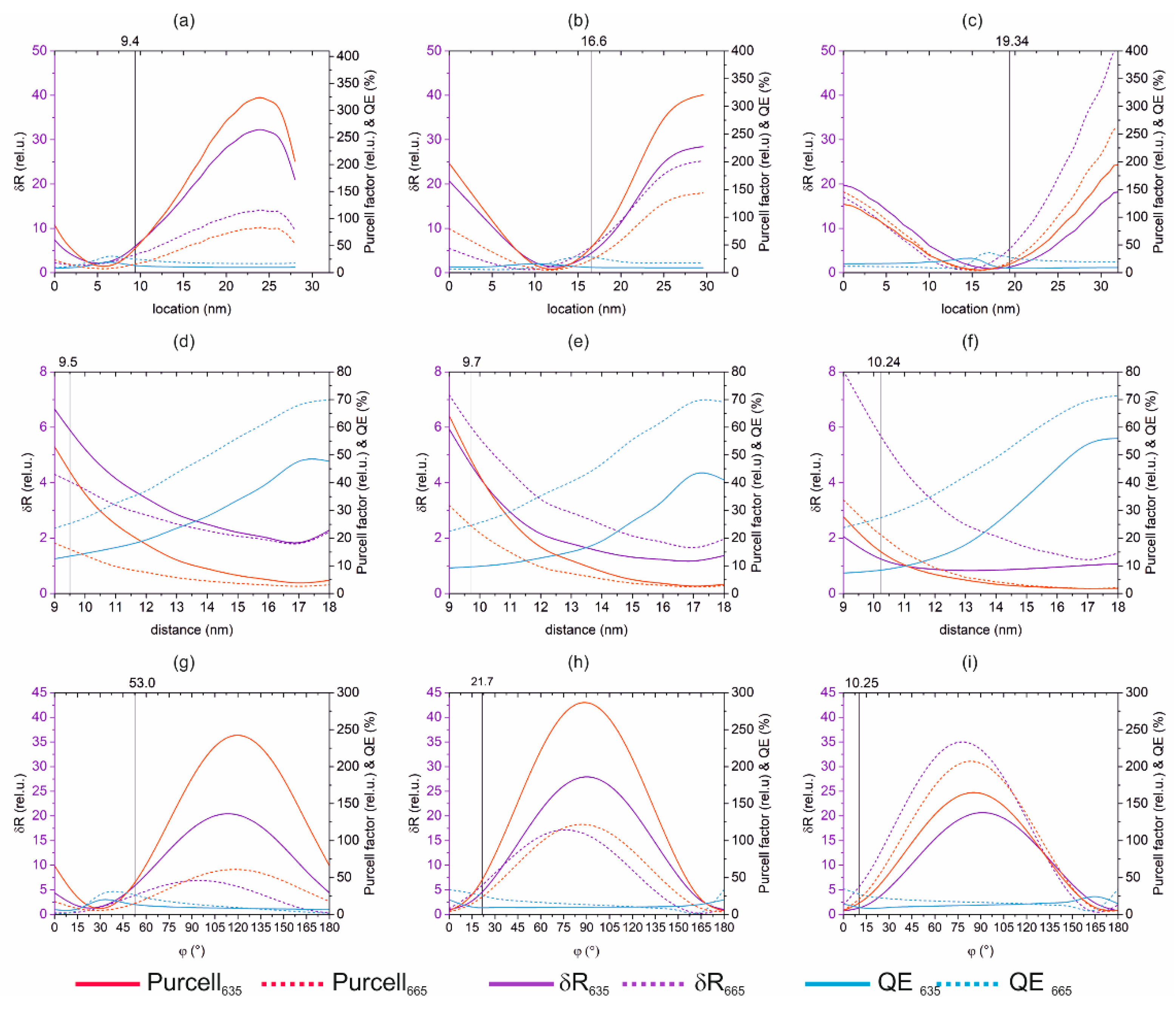
3.1.2. Optical Response Dependence on Dipole Location, Distance and Orientation
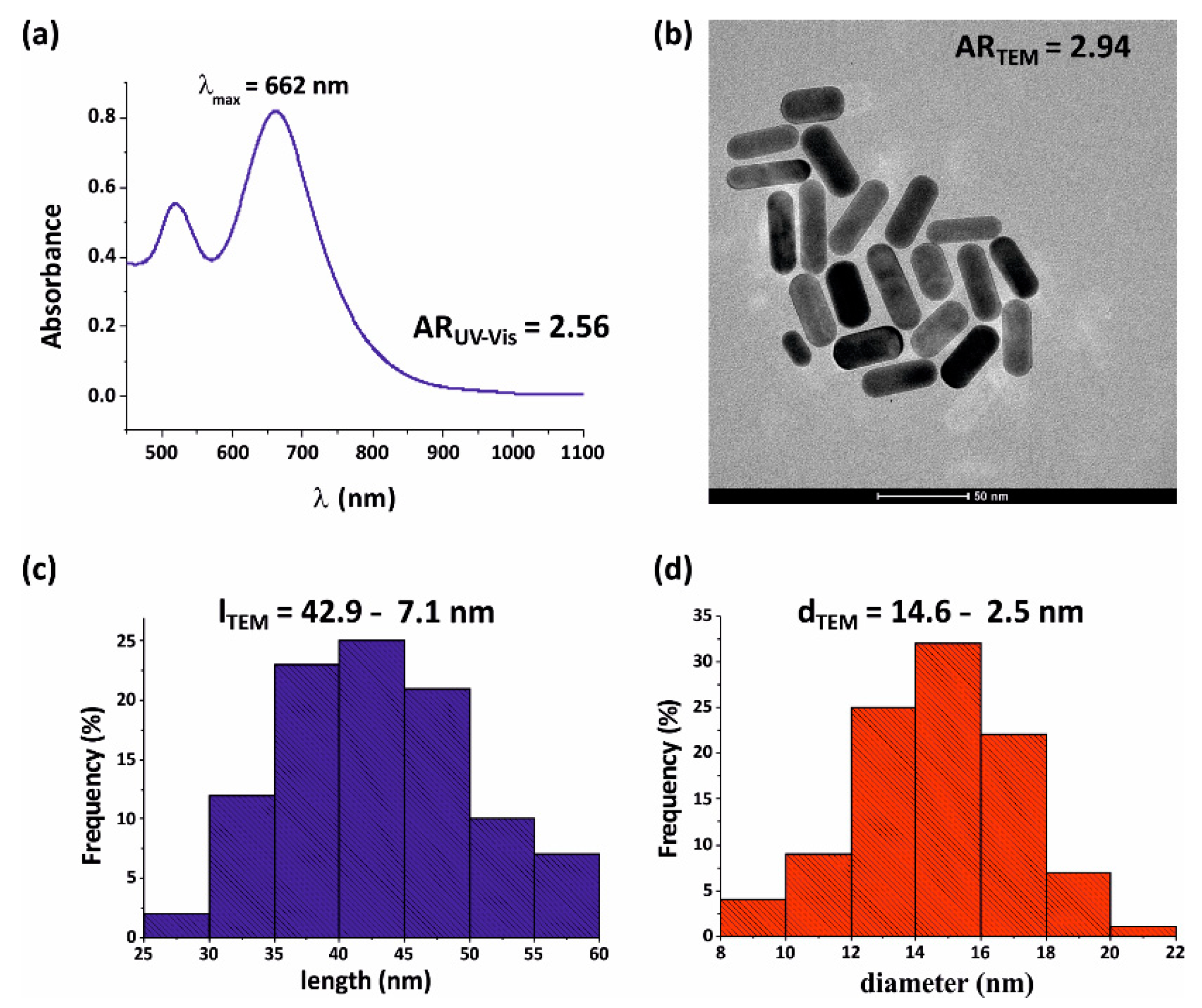
3.2. Size Distribution and Spectral Properties of Gold Nanorods
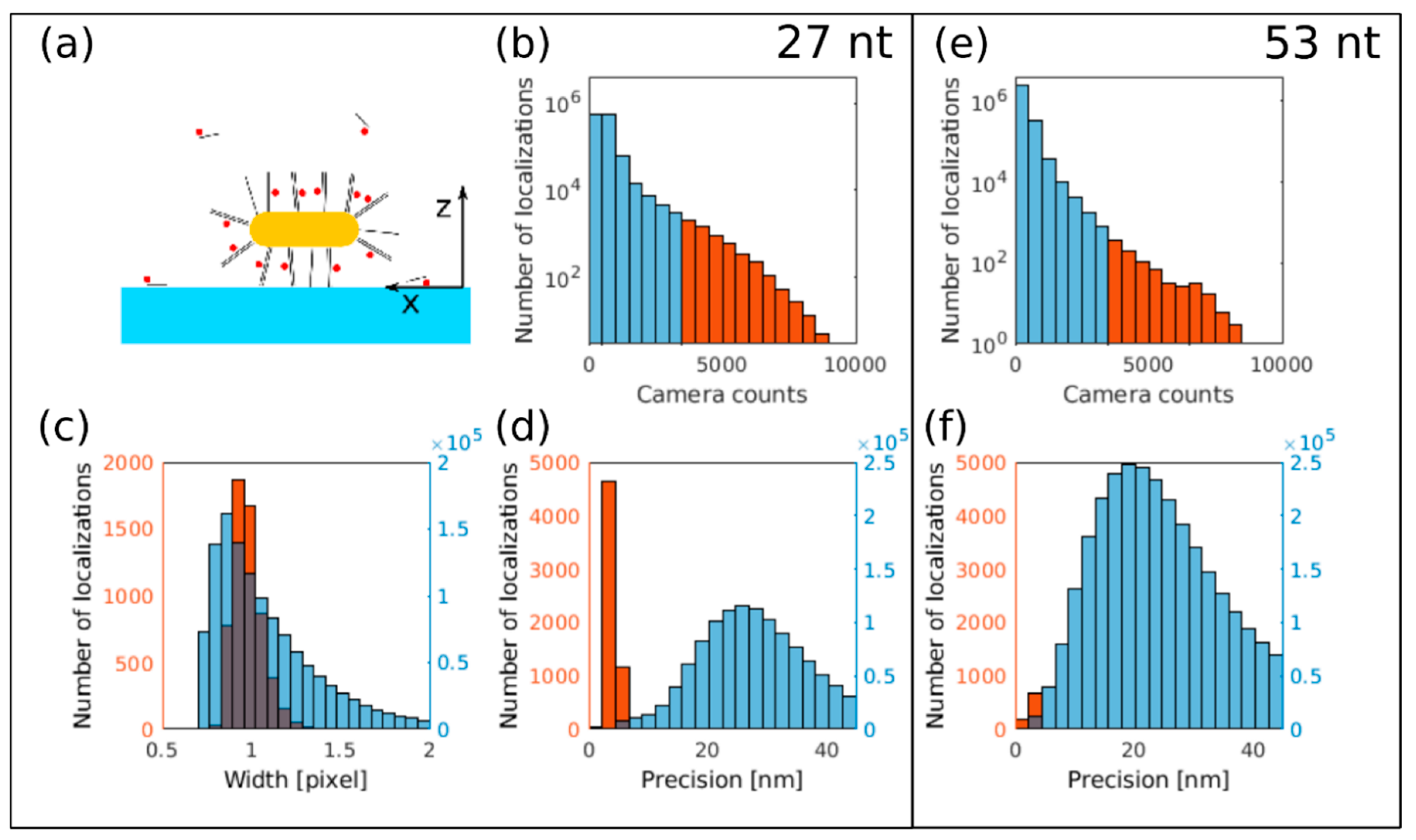
3.3. dSTORM Imaging of Au Nanorods Labelled with Cy5 Dye Molecule
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Das, P.; Metiu, H. Enhancement of molecular fluorescence and photochemistry by small metal particles. J. Phys. Chem. 1985, 89, 4680. [Google Scholar] [CrossRef]
- Das, P.C.; Puri, A. Energy flow and fluorescence near a small metal particle. Phys. Rev. B 2002, 65, 155416. [Google Scholar] [CrossRef] [Green Version]
- Blanco, A.L.; García de Abajo, F.J. Control of spontaneous emission by complex nanostructures. Opt. Lett. 2004, 29, 1494–1496. [Google Scholar]
- Anger, P.; Novotny, L. Enhancement and quenching of single-molecule fluorescence. Phys. Rev. Lett. 2006, 96, 113002. [Google Scholar] [CrossRef] [Green Version]
- Bharadwaj, P.; Novotny, L. Spectral dependence of single molecule fluorescence enhancement. Opt. Express 2007, 15, 14266. [Google Scholar]
- Chen, Y.; Munechika, K.; Ginger, D.S. Dependence of fluorescence intensity on the spectral overlap between fluorophores and plasmon resonant single silver nanoparticles. Nano Lett. 2007, 7, 690–696. [Google Scholar]
- Munechika, K.; Chen, Y.; Tillack, A.F.; Kulkarni, A.P.; Plante, I.J.; Munro, A.M.; Ginger, D.S. Spectral control of plasmonic emission enhancement from quantum dots near single silver nanoprisms. Nano Lett. 2010, 10, 2598–2603. [Google Scholar]
- Ming, T.; Zhao, L.; Yang, Z.; Chen, H.; Sun, L.; Wang, J.; Yan, C. Strong polarization dependence of plasmon-enhanced fluorescence on single gold nanorods. Nano Lett. 2009, 9, 3896–3903. [Google Scholar] [CrossRef]
- Pelton, M. Modified spontaneous emission in nanophotonic structures. Nat. Photonics 2015, 9, 427–435. [Google Scholar] [CrossRef]
- Bardhan, R.; Grady, N.K.; Cole, J.R.; Joshi, A.; Halas, N.J. Fluorescence enhancement by Au nanostructures: Nanoshells and nanorods. ACS Nano 2009, 3, 744–752. [Google Scholar] [CrossRef]
- Yang, Y.; Zhen, B.; Hsu, C.W.; Miller, O.D.; Joannopoulos, J.D.; Soljacic, M. Optically thin metallic films for high-radiative-efficiency plasmonics. Nano Lett. 2016, 16, 4110–4117. [Google Scholar] [CrossRef] [Green Version]
- Laux, F.; Bonod, N.; Gérard, N. Single emitter fluorescence enhancement with surface lattice resonances. J. Phys. Chem. C 2017, 121, 13280–13289. [Google Scholar] [CrossRef] [Green Version]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic metal dimer-on-film structure: New plasmonic properties introduced by the underlying metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef]
- Abadeer, N.S.; Brennan, M.R.; Wilson, W.L.; Murphy, C.J. Distance and plasmon wavelength dependent fluorescence of molecules bound to silica-coated gold nanorods. ACS Nano 2014, 8, 8392–8406. [Google Scholar] [CrossRef]
- Szenes, A.; Bánhelyi, B.; Szabó, L.Z.; Szabó, G.; Csendes, T.; Csete, M. Enhancing diamond color center fluorescence via optimized plasmonic nanorod configuration. Plasmonics 2017, 12, 1263–1280. [Google Scholar] [CrossRef] [Green Version]
- Szenes, A.; Banhelyi, B.; Szabó, L.Z.; Szabó, G.; Csendes, T.; Csete, M. Improved emission of SiV diamond color centers embedded into concave plasmonic core-shell nanoresonators. Sci. Rep. 2017, 7, 13845. [Google Scholar] [CrossRef] [Green Version]
- Szenes, A.; Bánhelyi, B.; Csendes, T.; Szabó, G.; Csete, M. Enhancing diamond fluorescence via optimized nanorod dimer configurations. Plasmonics 2018, 13, 1977–1985. [Google Scholar] [CrossRef] [Green Version]
- Ming, T.; Chen, H.; Jiang, R.; Li, Q.; Wang, J. Plasmon-controlled fluorescence: Beyond the intensity enhancement. J. Phys. Chem. Lett. 2012, 3, 191–202. [Google Scholar] [CrossRef]
- Chikkaraddy, R.; Turek, V.A.; Kongsuwan, N.; Benz, F.; Carnegie, C.; van de Goor, T.; de Nijs, B.; Demetriadou, A.; Hess, O.; Keyser, U.F.; et al. Mapping nanoscale hotspots with single-molecule emitters assembled into plasmonic nanocavities using DNA origami. Nano Lett. 2018, 18, 405–411. [Google Scholar] [CrossRef] [Green Version]
- Hell, S.W. Far-Field Optical Nanoscopy. Science 2007, 316, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- Rust, M.J.; Bates, M.; Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methodes 2006, 3, 793–796. [Google Scholar] [CrossRef] [Green Version]
- Geisler, C.; Schonle, A.; von Middendorff, C.; Bock, H.; Eggeling, C.; Egner, A.; Hell, S.W. Resolution of λ/10 in fluorescence microscopy using fast single molecule photo-switching. J. Appl. Phys. A 2007, 88, 223–226. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Radiative decay engineering 5: Metal-enhanced fluorescence and plasmon emission. Anal. Biochem. 2005, 337, 171–194. [Google Scholar] [CrossRef]
- Zhai, X.; Sun, Y.; Wu, D. Resolution enhancement of random adsorbed single-molecule localization based on surface plasmon resonance illumination. Opt. Lett. 2011, 36, 4242–4244. [Google Scholar] [CrossRef]
- Cang, H.; Labno, A.; Lu, C.; Yin, X.; Liu, M.; Gladden, C.; Liu, Y.; Zhang, X. Probing the electromagnetic field of a 15-nanometre hotspot by single molecule imaging. Nature 2011, 469, 385–388. [Google Scholar] [CrossRef]
- Sivan, Y.; Sonnefraud, Y.; Kéna-Cohen, S.; Pendry, J.B.; Maier, S.A. Nanoparticle-Assisted Stimulated-Emission-Depletion Nanoscopy. ACS Nano 2012, 6, 5291–5296. [Google Scholar] [CrossRef]
- Wertz, E.; Isaacoff, P.B.; Flynn, J.D.; Biteen, J.S. Single-Molecule Super-Resolution Microscopy Reveals How Light Couples to a Plasmonic Nanoantenna on the Nanometer Scale. Nano Lett. 2015, 15, 2662–2670. [Google Scholar] [CrossRef]
- Blythe, K.L.; Titus, E.J.; Willets, K.A. Objective-Induced Point Spread Function Aberrations and Their Impact on Super-Resolution Microscopy. Anal. Chem. 2015, 87, 6419–6424. [Google Scholar] [CrossRef]
- Blythe, K.J.; Titus, E.J.; Willets, K.A. Effects of Tuning Fluorophore Density, Identity, and Spacing on Reconstructed Images in Super-Resolution Imaging of Fluorophore-Labeled Gold Nanorods. J. Phys. Chem. C 2015, 119, 28099–28110. [Google Scholar] [CrossRef]
- Mack, D.L.; Giannini, V.; Török, P.; Roschuk, T.; Maier, S.A. Decoupling absorption and emission processes in super-resolution localization of emitters in a plasmonic hotspot. Nat. Commun. 2017, 8, 14513. [Google Scholar] [CrossRef]
- Willets, A.K.; Wilson, A.J.; Sundaresan, V.; Joshi, P.B. Super-resolution imaging and plasmonics. Chem. Rev. 2017, 117, 7538–7582. [Google Scholar] [CrossRef]
- De Silva Indrasekara, A.S.; Shuang, B.; Hollenhorst, F.; Hoener, B.S.; Hoggard, A.; Chen, S.; Villarreal, E.; Cai, Y.-Y.; Kisley, L.; Derry, P.J.; et al. Optimization of spectral and spatial conditions to improve super-resolution imaging of plasmonic nanoparticles. J. Phys. Chem. Lett. 2017, 8, 299–306. [Google Scholar] [CrossRef]
- Taylor, A.; Verhoef, R.; Beuwer, M.; Wang, Y.; Zijlstra, P. All-Optical Imaging of Gold Nanoparticle Geometry Using Super-Resolution Microscopy. J. Phys. Chem. C 2018, 122, 2336–2342. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Horáček, M.; Zijlstra, P. Strong Plasmon Enhancement of the Saturation Photon Count Rate of Single Molecules. J. Phys. Chem. Lett. 2020, 11, 1962–1969. [Google Scholar] [CrossRef] [Green Version]
- Botequim, D.; Silva, I.I.R.; Serra, S.G.; Melo, E.P.; Prazeres, D.M.F.; Costa, S.M.B.; Paulo, P.M.R. Fluorescent Dye Nano-Assemblies by Thiol Attachment Directed to the Tips of Gold Nanorods for Effective Emission Enhancement. Nanoscale 2020, 6334–6345. [Google Scholar] [CrossRef]
- Bánhelyi, B.; Csendes, T.; Lévai, B.; Pál, L.; Zombori, D. The Global Optimization Algorithm: Newly Updated with Java Implementation and Parallelization; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Zhou, N.; Polavarapu, L.; Gao, N.; Pan, Y.; Yuan, P.; Wang, Q.; Xu, Q.-H. TiO2 coated Au/Ag nanorods with enhanced photocatalytic activity under visible light irradiation. Nanoscale 2013, 5, 4236–4241. [Google Scholar]
- Link, S.; El-Sayed, M.A. Simulation of the Optical Absorption Spectra of Gold Nanorods as a Function of Their Aspect Ratio and the Effect of the Medium Dielectric Constant. J. Phys. Chem. B 2005, 109, 10531–10532. [Google Scholar] [CrossRef] [Green Version]
- Kupihár, Z.; Kovács, G.; Kele, Z.; Darula, Z.; Kovács, L. A novel and convenient method for the synthesis of free 5′-thiol modified oligonucleotides. Nucleosides Nucleotides Nucleic Acids 2003, 22, 1297–1299. [Google Scholar] [CrossRef]
- Li, J.; Zhu, B.; Zhu, Z.; Zhang, Y.; Yao, X.; Tu, S.; Liu, R.; Jia, S.; Yang, C.J. Simple and Rapid Functionalization of Gold Nanorods with Oligonucleotides Using an mPEG-SH/Tween 20-Assisted Approach. Langmuir 2015, 28, 7869–7876. [Google Scholar] [CrossRef]
- Lee, K.; Conboy, M.; Park, H.M.; Jiang, F.; Kim, H.J.; Dewitt, M.A.; Mackley, V.A.; Chang, K.; Rao, A.; Skinner, C.; et al. Nanoparticle delivery of Cas9 ribonucleoprotein and donor DNA in vivo induces homology-directed DNA repair. Nat. Biomed. Eng. 2017, 1, 889–901. [Google Scholar] [CrossRef] [Green Version]
- Van de Linde, S.; Löschberger, A.; Klein, T.; Heidbreder, M.; Wolter, S.; Heilemann, M.; Sauer, M. Direct stochastic optical reconstruction microscopy with standard fluorescent probes. Nat. Protoc. 2011, 6, 991. [Google Scholar] [CrossRef]
- Rees, E.J.; Erdélyi, M.; Schierle, G.S.; Knight, A.; Kaminski, C.F. Elements of image processing in localization microscopy. J. Opt. 2013, 15, 094012. [Google Scholar] [CrossRef] [Green Version]
- Varga, D.; Majoros, H.; Ujfaludi, Z.; Erdélyi, M.; Pankotai, T. Quantification of DNA damage induced repair focus formation via super-resolution dSTORM localization microscopy. Nanoscale 2019, 11, 14226–14236. [Google Scholar] [CrossRef] [Green Version]
- Thompson, R.E.; Larson, D.R.; Webb, W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002, 82, 2775–2783. [Google Scholar] [CrossRef] [Green Version]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar]
- Li, T.; Zhang, F.; Li, Q.; Rao, W.; Xu, P.; Xu, L.; Wu, L.-J. Revealing the Mechanism of Photoluminescence from Single Gold Nanospheres by Defocused Imaging. ACS Photonics 2017, 4, 2003–2010. [Google Scholar] [CrossRef]



| Thiol-DNA | SH-C6-AATCTGTATCTATATTCATCATAGGAAACACCAAAGATGATATTTTCTTTAAT |
| Cy5-DNA 17.5 nm | Cy5-ATT AAAGAAAATATCATCTTTGGTGTTTCCTATGATGAATATAGATACAGATT |
| Cy5-DNA 8.9 nm | ATTAAAGAAAATATCATCTTTGGTGT + Cy5-TTCCTATGATGAATATAGATACAGATT |
| Excitation (635 nm) | Medial (650 nm) | Emission (665 nm) | ||||
|---|---|---|---|---|---|---|
| 635 nm | 665 nm | 635 nm | 665 nm | 635 nm | 665 nm | |
| QE (%) | 13.4 | 25.8 | 9.7 | 24.75 | 8.4 | 27.5 |
| Purcell Factor | 44.4 | 15.4 | 47.8 | 24.2 | 14.7 | 19.8 |
| δR | 6.0 | 4.0 | 4.6 | 6.0 | 1.2 | 5.4 |
| δD= D/D0 | 1.4 | 0.7 | 0.7 | 0.7 | 0.5 | 0.6 |
| δD× δR | 8.1 | 2.9 | 3.3 | 4.3 | 0.6 | 3.5 |
| Px | 23.6 | 27.6 | 6.7 | |||
| Px× δDexc× δDem | 23.1 | 14.2 | 2.2 | |||
| ηoutcoupling | 0.98 | 0.51 | 0.32 | |||
| as (nm) | 20.1 | 20.2 | 21.9 | |||
| aL (nm) | 37.7 | 39.8 | 44.6 | |||
| AR | 1.87 | 1.97 | 2.04 | |||
| Location x (nm) | 9.4 | 16.6 | 19.3 | |||
| Distance d (nm) | 9.5 | 9.7 | 10.2 | |||
| Orientation φ (°) | 53.0 | 21.7 | 10.3 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tóth, E.; Ungor, D.; Novák, T.; Ferenc, G.; Bánhelyi, B.; Csapó, E.; Erdélyi, M.; Csete, M. Mapping Fluorescence Enhancement of Plasmonic Nanorod Coupled Dye Molecules. Nanomaterials 2020, 10, 1048. https://doi.org/10.3390/nano10061048
Tóth E, Ungor D, Novák T, Ferenc G, Bánhelyi B, Csapó E, Erdélyi M, Csete M. Mapping Fluorescence Enhancement of Plasmonic Nanorod Coupled Dye Molecules. Nanomaterials. 2020; 10(6):1048. https://doi.org/10.3390/nano10061048
Chicago/Turabian StyleTóth, Emese, Ditta Ungor, Tibor Novák, Györgyi Ferenc, Balázs Bánhelyi, Edit Csapó, Miklós Erdélyi, and Mária Csete. 2020. "Mapping Fluorescence Enhancement of Plasmonic Nanorod Coupled Dye Molecules" Nanomaterials 10, no. 6: 1048. https://doi.org/10.3390/nano10061048
APA StyleTóth, E., Ungor, D., Novák, T., Ferenc, G., Bánhelyi, B., Csapó, E., Erdélyi, M., & Csete, M. (2020). Mapping Fluorescence Enhancement of Plasmonic Nanorod Coupled Dye Molecules. Nanomaterials, 10(6), 1048. https://doi.org/10.3390/nano10061048







