Investigation of Magnetic Circular Dichroism Spectra of Semiconductor Quantum Rods and Quantum Dot-in-Rods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurement Procedure
2.2. MCD Spectra Analysis Technique
2.3. Description of the Fitting Procedure
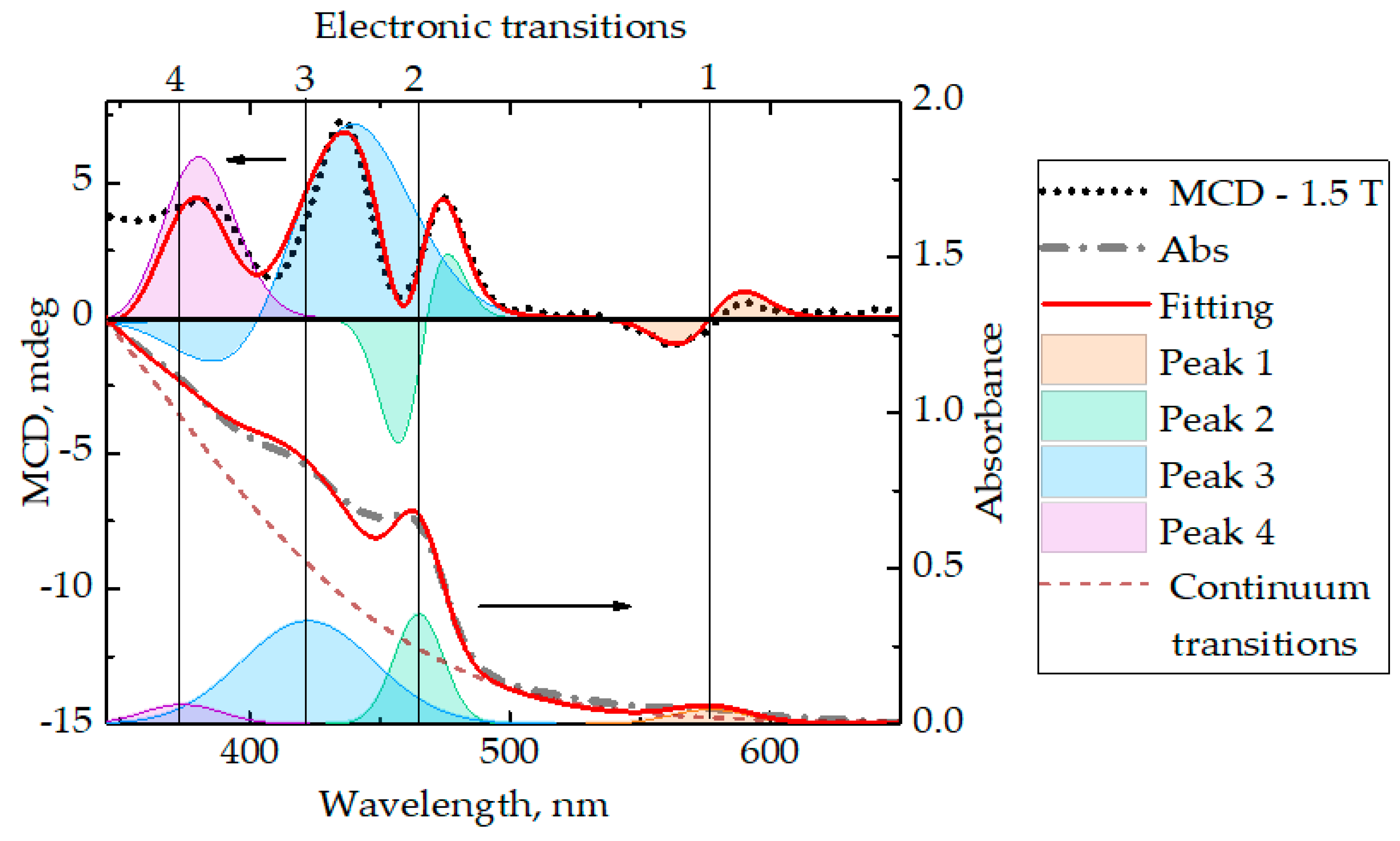
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pisanello, F.; Leménager, G.; Martiradonna, L.; Carbone, L.; Vezzoli, S.; Desfonds, P.; Cozzoli, P.D.; Hermier, J.-P.; Giacobino, E.; Cingolani, R.; et al. Non-blinking single-photon generation with anisotropic colloidal nanocrystals: Towards room-temperature, efficient, colloidal quantum sources. Adv. Mater. 2013, 25, 1974–1980. [Google Scholar] [CrossRef]
- Lunnemann, P.; Rabouw, F.T.; Van Dijk-Moes, R.J.A.; Pietra, F.; Vanmaekelbergh, D.; Koenderink, A.F.; Koenderink, A.F. Calibrating and controlling the quantum efficiency distribution of inhomogeneously broadened quantum rods by using a mirror ball. ACS Nano 2013, 7, 5984–5992. [Google Scholar] [CrossRef] [Green Version]
- Manceau, M.; Vezzoli, S.; Glorieux, Q.; Pisanello, F.; Giacobino, E.; Carbone, L.; De Vittorio, M.; Bramati, A. Effect of charging on CdSe/CdS dot-in-rods single-photon emission. Phys. Rev. B 2014, 90, 035311. [Google Scholar] [CrossRef] [Green Version]
- Biadala, L.; Siebers, B.; Gomes, R.; Hens, Z.; Yakovlev, D.R.; Bayer, M. Tuning energy splitting and recombination dynamics of dark and bright excitons in CdSe/CdS dot-in-rod colloidal nanostructures. J. Phys. Chem. C 2014, 118, 22309–22316. [Google Scholar] [CrossRef]
- Del Águila, A.G.; Jha, B.; Pietra, F.; Groeneveld, E.; Donega, C.D.M.; Maan, J.C.; Vanmaekelbergh, D.; Christianen, P.C.M. Observation of the full exciton and phonon fine structure in CdSe/CdS dot-in-rod heteronanocrystals. ACS Nano 2014, 8, 5921–5931. [Google Scholar] [CrossRef] [PubMed]
- Sitt, A.; Salant, A.; Menagen, G.; Banin, U. Highly emissive nano rod-in-rod heterostructures with strong linear polarization. Nano Lett. 2011, 11, 2054–2060. [Google Scholar] [CrossRef]
- Diroll, B.T.; Koschitzky, A.; Murray, C.B. Tunable optical anisotropy of seeded CdSe/CdS nanorods. J. Phys. Chem. Lett. 2013, 5, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Hadar, I.; Hitin, G.B.; Sitt, A.; Faust, A.; Banin, U. Polarization properties of semiconductor nanorod heterostructures: From single particles to the ensemble. J. Phys. Chem. Lett. 2013, 4, 502–507. [Google Scholar] [CrossRef] [PubMed]
- Lethiec, C.; Pisanello, F.; Carbone, L.; Bramati, A.; Coolen, L.; Maître, A. Polarimetry-based analysis of dipolar transitions of single colloidal CdSe/CdS dot-in-rods. New J. Phys. 2014, 16, 93014. [Google Scholar] [CrossRef] [Green Version]
- Fu, A.; Gu, W.; Boussert, B.; Koski, K.; Gerion, D.; Manna, L.; Le Gros, M.; Larabell, C.A.; Alivisatos, A.P. Semiconductor quantum rods as single molecule fluorescent biological labels. Nano Lett. 2007, 7, 179–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grivas, C.; Li, C.; Andreakou, P.; Wang, P.; Ding, M.; Brambilla, G.; Manna, L.; Lagoudakis, P.G. Single-mode tunable laser emission in the single-exciton regime from colloidal nanocrystals. Nat. Commun. 2013, 4, 1–9. [Google Scholar] [CrossRef]
- Nozik, A.J.; Beard, M.C.; Luther, J.M.; Law, M.; Ellingson, R.J.; Johnson, J.C. Semiconductor quantum dots and quantum dot arrays and applications of multiple exciton generation to third-generation photovoltaic solar cells. Chem. Rev. 2010, 110, 6873–6890. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Gao, X.; Lv, J.; Tang, Z. Magnetic circular dichroism in nanomaterials: New opportunity in understanding and modulation of excitonic and plasmonic resonances. Adv. Mater. 2018, 1801491. [Google Scholar] [CrossRef] [PubMed]
- Gromova, Y.; Maslov, V.G.; Baranov, M.A.; Serrano-Garcia, R.; Kuznetsova, V.; Purcell-Milton, F.; Gun’Ko, Y.K.; Baranov, A.V.; Fedorov, A.V. Magnetic and optical properties of isolated and aggregated CoFe2O4 superparamagnetic nanoparticles studied by mcd spectroscopy. J. Phys. Chem. C 2018, 122, 11491–11497. [Google Scholar] [CrossRef]
- Kobayashi, N.; Muranaka, A. Circular Dichroism and Magnetic Circular Dichroism Spectroscopy for Organic Chemists; Royal Society of Chemistry: London, UK, 2011; p. 192. [Google Scholar]
- Kuno, M.; Nirmal, M.; Bawendi, M.G.; Efros, A.; Rosen, M. Magnetic circular dichroism study of CdSe quantum dots. J. Chem. Phys. 1998, 108, 4242–4247. [Google Scholar] [CrossRef]
- Gromova, Y.; Miropoltsev, M.A.; Cherevkov, S.A.; Маслoв, В.; Baranov, A.V.; Fedorov, A.V. Magnetic circular dichroism in 2d colloidal semiconductor nanocrystals. Opt. Spectrosc. 2018, 125, 698–702. [Google Scholar] [CrossRef]
- Gromova, Y.; Sokolova, A.; Kurshanov, D.; Korsakov, I.; Osipova, V.; Cherevkov, S.; Dubavik, A.; Maslov, V.; Perova, T.; Gun’ko, Y. Investigation of AgInS2/ZnS quantum dots by magnetic circular dichroism spectroscopy. Materials 2019, 12, 3616. [Google Scholar] [CrossRef] [Green Version]
- Manna, L.; Scher, E.C.; Li, L.-S.; Alivisatos, A.P.; Alivisatos, A.P. Epitaxial growth and photochemical annealing of graded CdS/ZnS shells on colloidal CdSe nanorods. J. Am. Chem. Soc. 2002, 124, 7136–7145. [Google Scholar] [CrossRef]
- Carbone, L.; Nobile, C.; De Giorgi, M.; Della Sala, F.; Morello, G.; Pompa, P.; Hÿtch, M.; Snoeck, E.; Fiore, A.; Franchini, I.R.; et al. Synthesis and micrometer-scale assembly of colloidal CdSe/CdS nanorods prepared by a seeded growth approach. Nano Lett. 2007, 7, 2942–2950. [Google Scholar] [CrossRef]
- Norris, D.J.; Bawendi, M.G. Measurement and assignment of the size-dependent optical spectrum in CdSe quantum dots. Phys. Rev. B 1996, 53, 16338–16346. [Google Scholar] [CrossRef] [Green Version]
- Martynenko, I.V.; Baimuratov, A.S.; Osipova, V.A.; Kuznetsova, V.; Purcell-Milton, F.; Rukhlenko, I.D.; Fedorov, A.V.; Gun’Ko, Y.K.; Resch-Genger, U.; Baranov, A.V. Excitation energy dependence of the photoluminescence quantum yield of core/shell CdSe/CdS quantum dots and correlation with circular dichroism. Chem. Mater. 2018, 30, 465–471. [Google Scholar] [CrossRef]


| Transition | Transition Energy, eV | Peak Center, nm | A1/D0 | B0/D0, 1/cm−1 |
|---|---|---|---|---|
| CdSe/ZnS QRs | ||||
| 1 | 2.00 | 617 | 0.143 | 0.0004 |
| 2 | 2.15 | 576 | 0.005 | 0.0004 |
| 3 | 2.47 | 502 | 0.765 | −6.3 × 10−5 |
| 4 | 2.74 | 452 | 0.093 | 0.0029 |
| CdSe/CdS DiRs | ||||
| 1 | 2.15 | 577 | 0.031 | <6 × 10−6 |
| 2 | 2.66 | 465 | 0.110 | −0.0003 |
| 3 | 2.93 | 422 | 0.452 | 0.0007 |
| 4 | 3.31 | 374 | 0.116 | 0.0018 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safin, F.; Maslov, V.; Gromova, Y.; Korsakov, I.; Kolesova, E.; Dubavik, A.; Cherevkov, S.; Gun’ko, Y.K. Investigation of Magnetic Circular Dichroism Spectra of Semiconductor Quantum Rods and Quantum Dot-in-Rods. Nanomaterials 2020, 10, 1059. https://doi.org/10.3390/nano10061059
Safin F, Maslov V, Gromova Y, Korsakov I, Kolesova E, Dubavik A, Cherevkov S, Gun’ko YK. Investigation of Magnetic Circular Dichroism Spectra of Semiconductor Quantum Rods and Quantum Dot-in-Rods. Nanomaterials. 2020; 10(6):1059. https://doi.org/10.3390/nano10061059
Chicago/Turabian StyleSafin, Farrukh, Vladimir Maslov, Yulia Gromova, Ivan Korsakov, Ekaterina Kolesova, Aliaksei Dubavik, Sergei Cherevkov, and Yurii K. Gun’ko. 2020. "Investigation of Magnetic Circular Dichroism Spectra of Semiconductor Quantum Rods and Quantum Dot-in-Rods" Nanomaterials 10, no. 6: 1059. https://doi.org/10.3390/nano10061059
APA StyleSafin, F., Maslov, V., Gromova, Y., Korsakov, I., Kolesova, E., Dubavik, A., Cherevkov, S., & Gun’ko, Y. K. (2020). Investigation of Magnetic Circular Dichroism Spectra of Semiconductor Quantum Rods and Quantum Dot-in-Rods. Nanomaterials, 10(6), 1059. https://doi.org/10.3390/nano10061059







