Entropy and Random Walk Trails Water Confinement and Non-Thermal Equilibrium in Photon-Induced Nanocavities
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. 157 nm Laser
2.3. AFM Imaging and AFM-NI
2.4. Fractal Analysis
2.5. Water Contact Angle (CA)
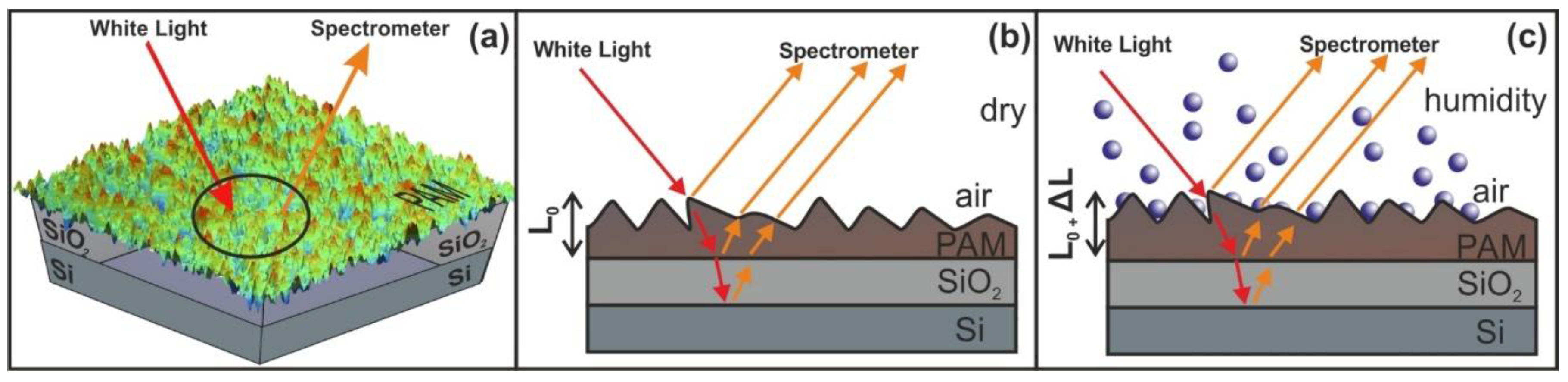
2.6. White Light Reflectance Spectroscopy (WLRS)
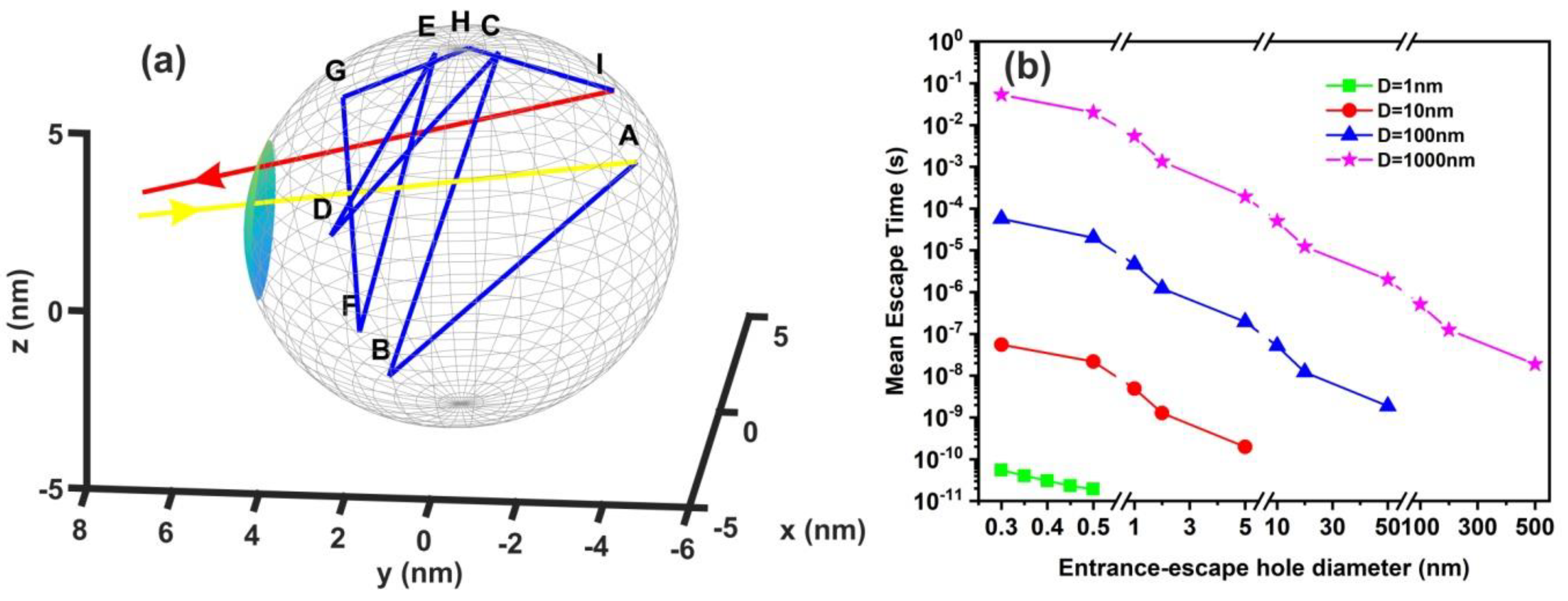
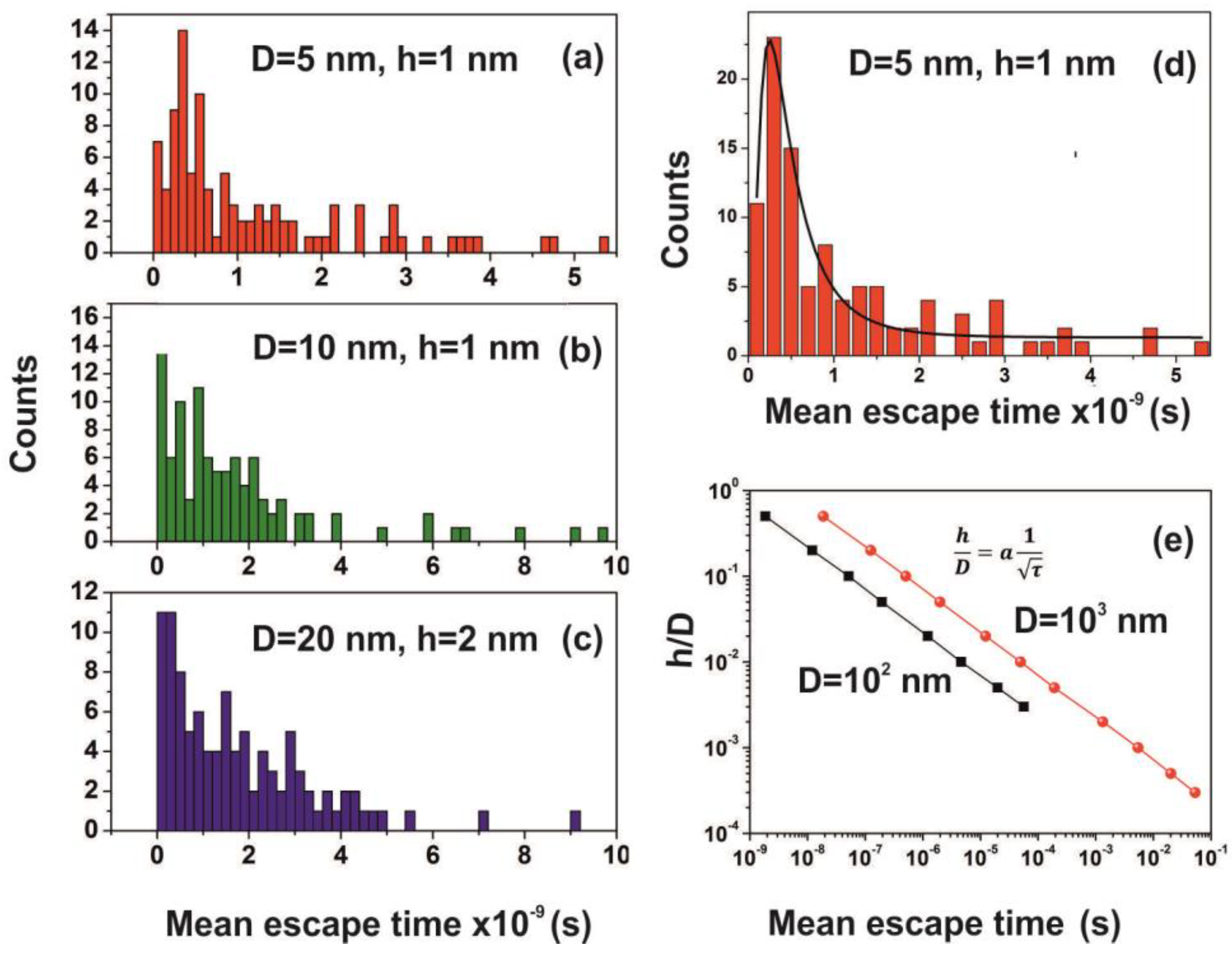
2.7. Random Walk Model
3. Results
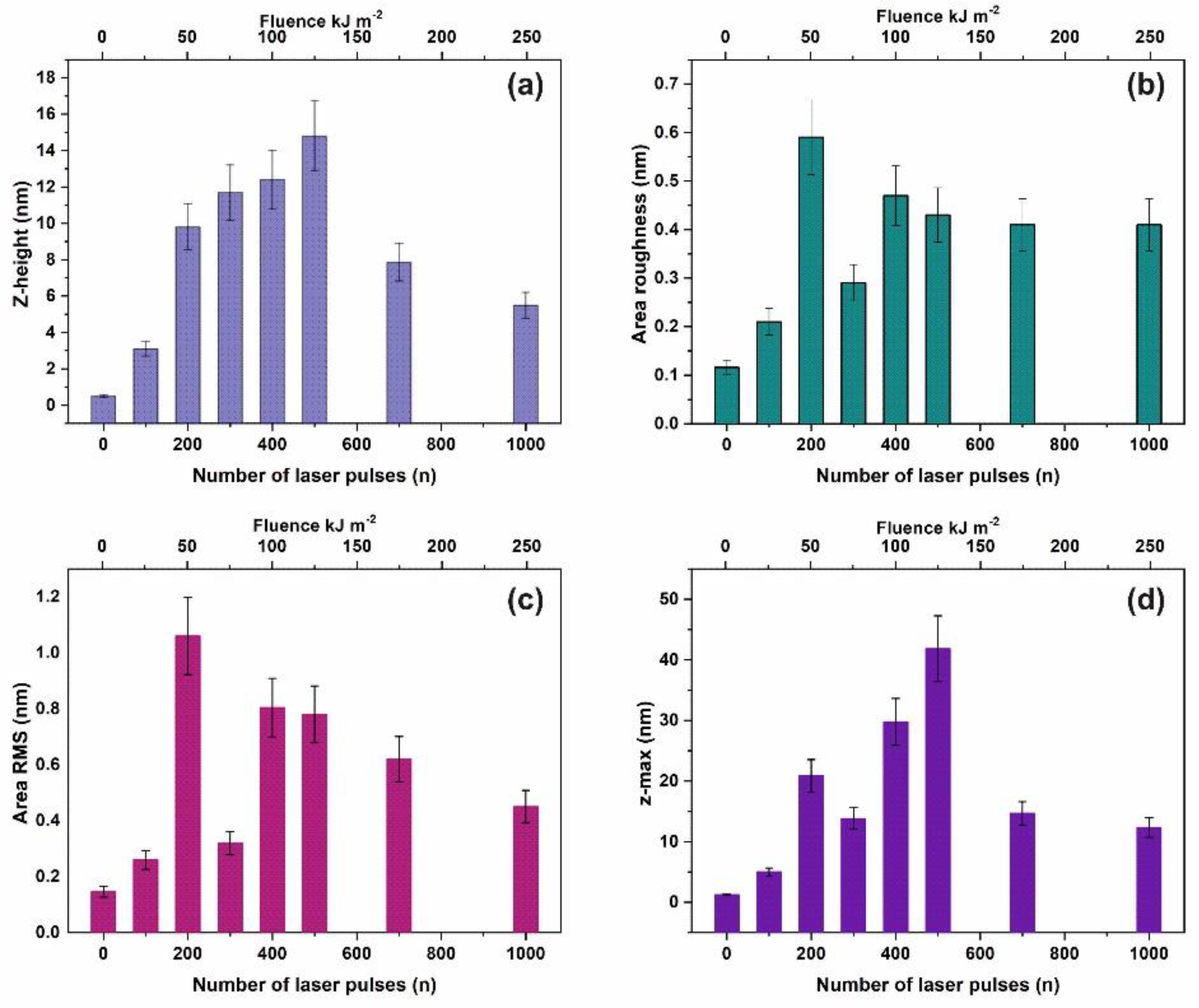
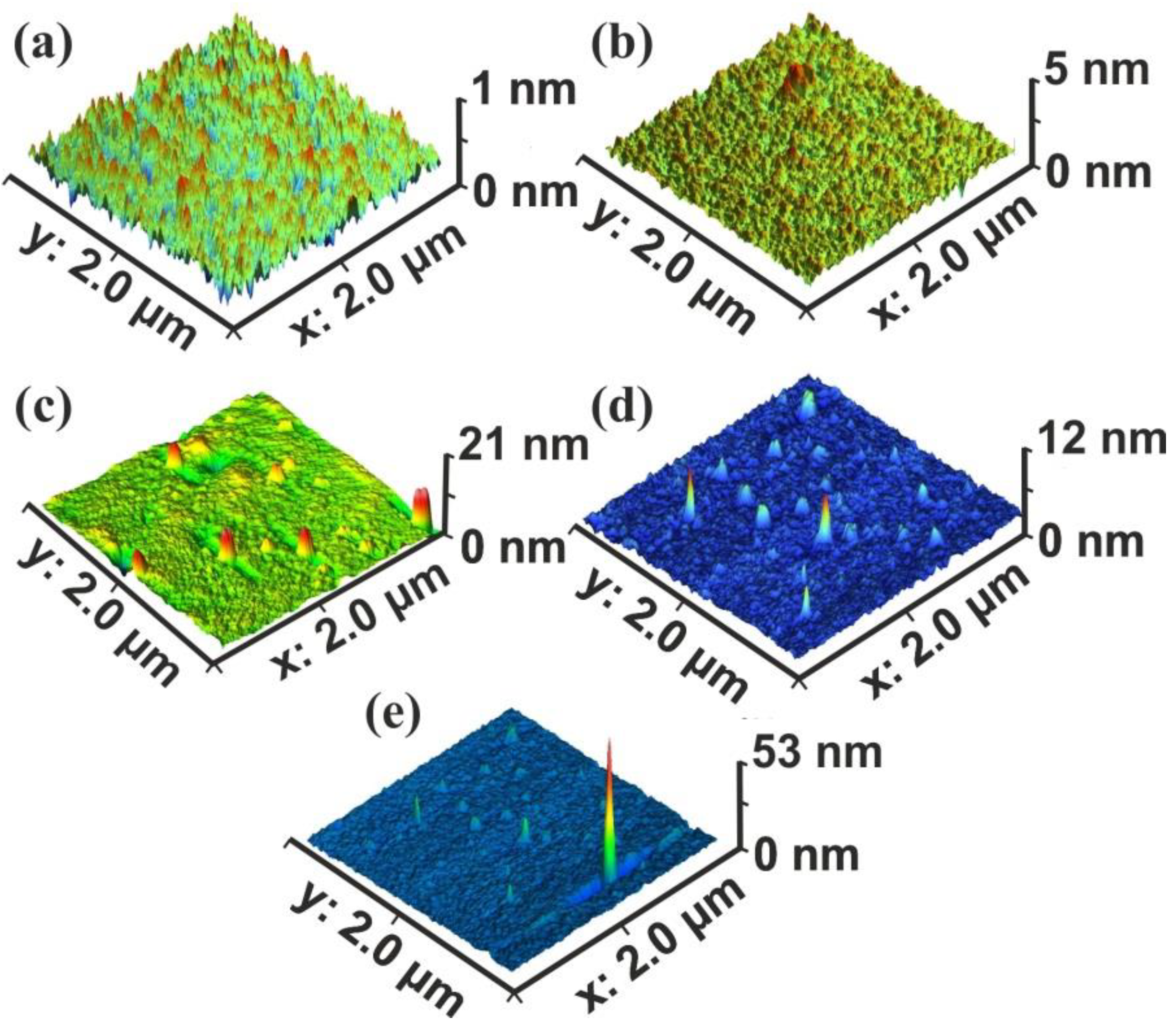
3.1. Surface Analysis
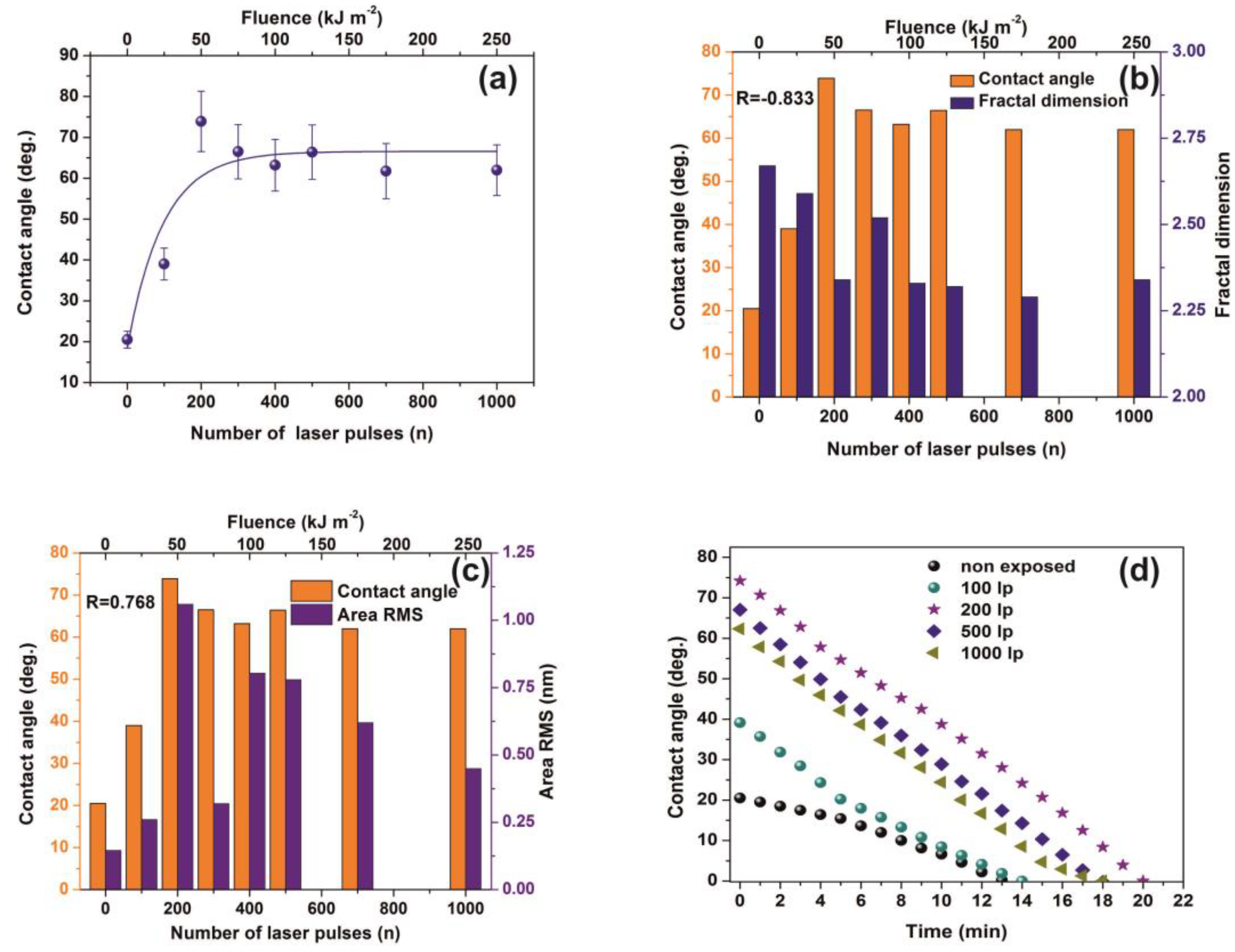
3.2. Fractal Analysis of 157 nm Photon Processed PAM Polymeric Matrixes
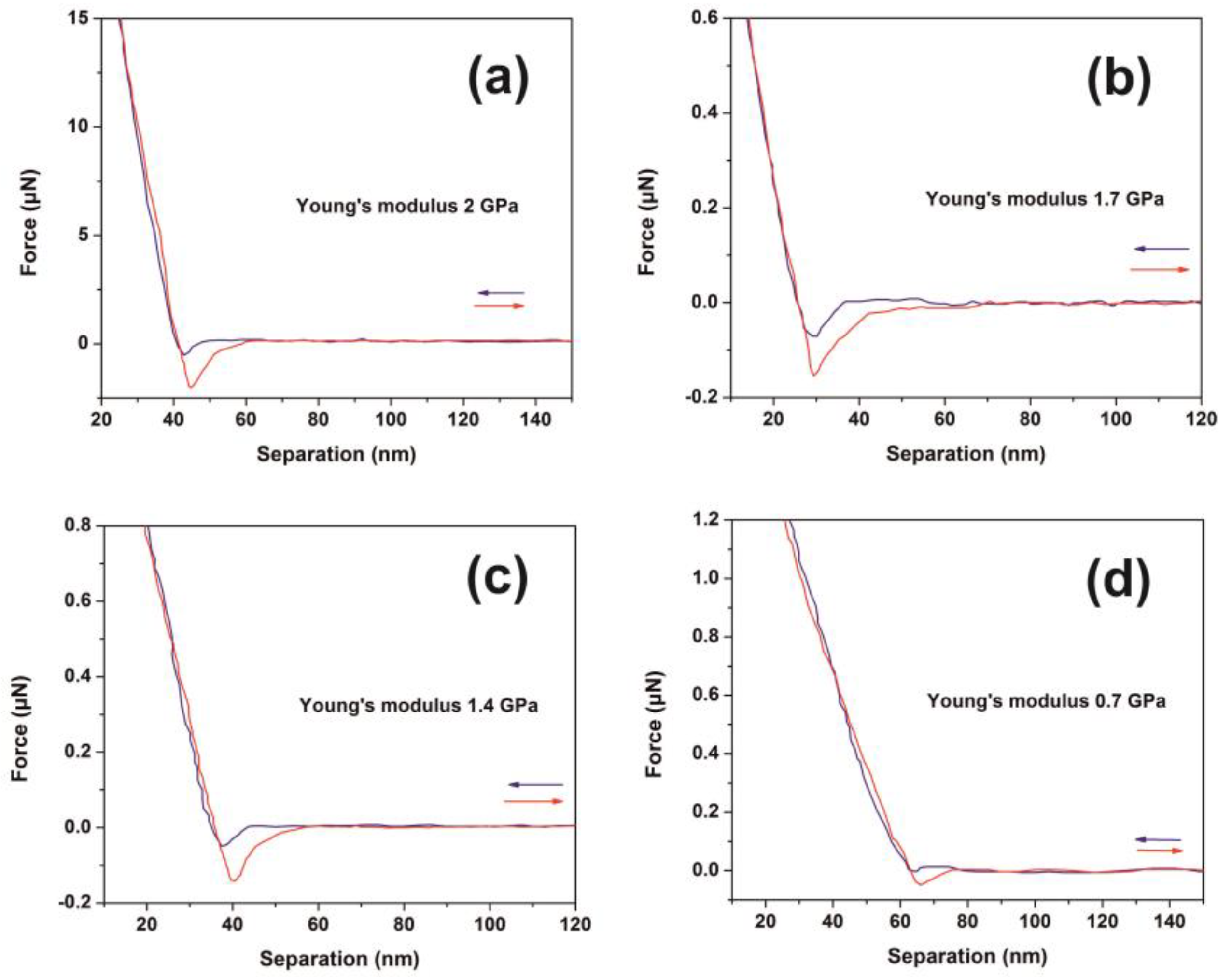
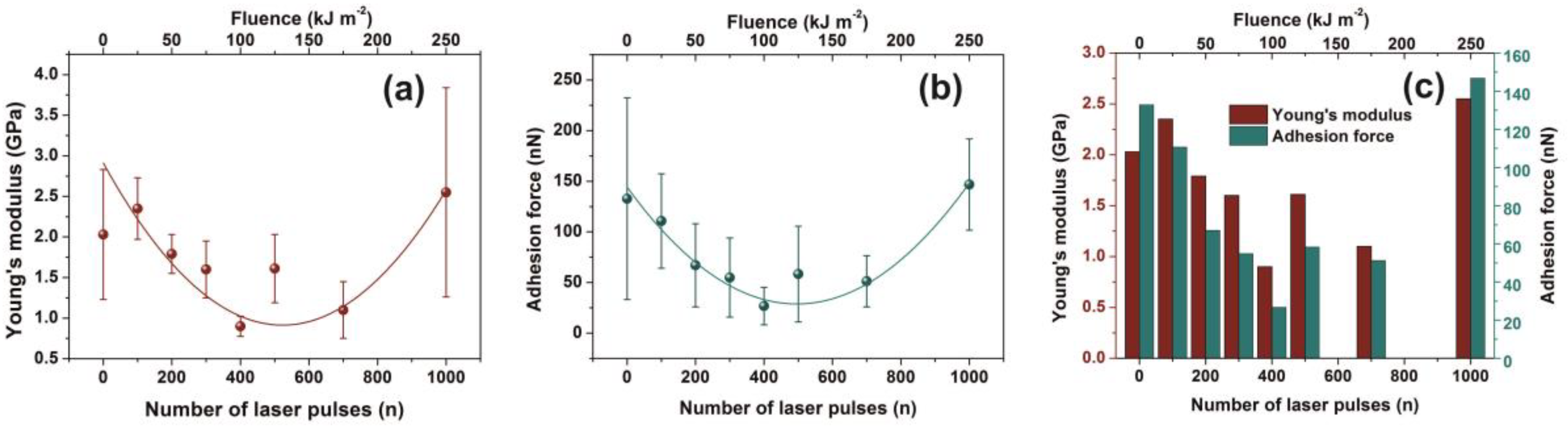
3.3. AFM-NI
3.4. Water Contact Angle (CA)
3.5. White Light Reflectance Spectroscopy (WLRS)
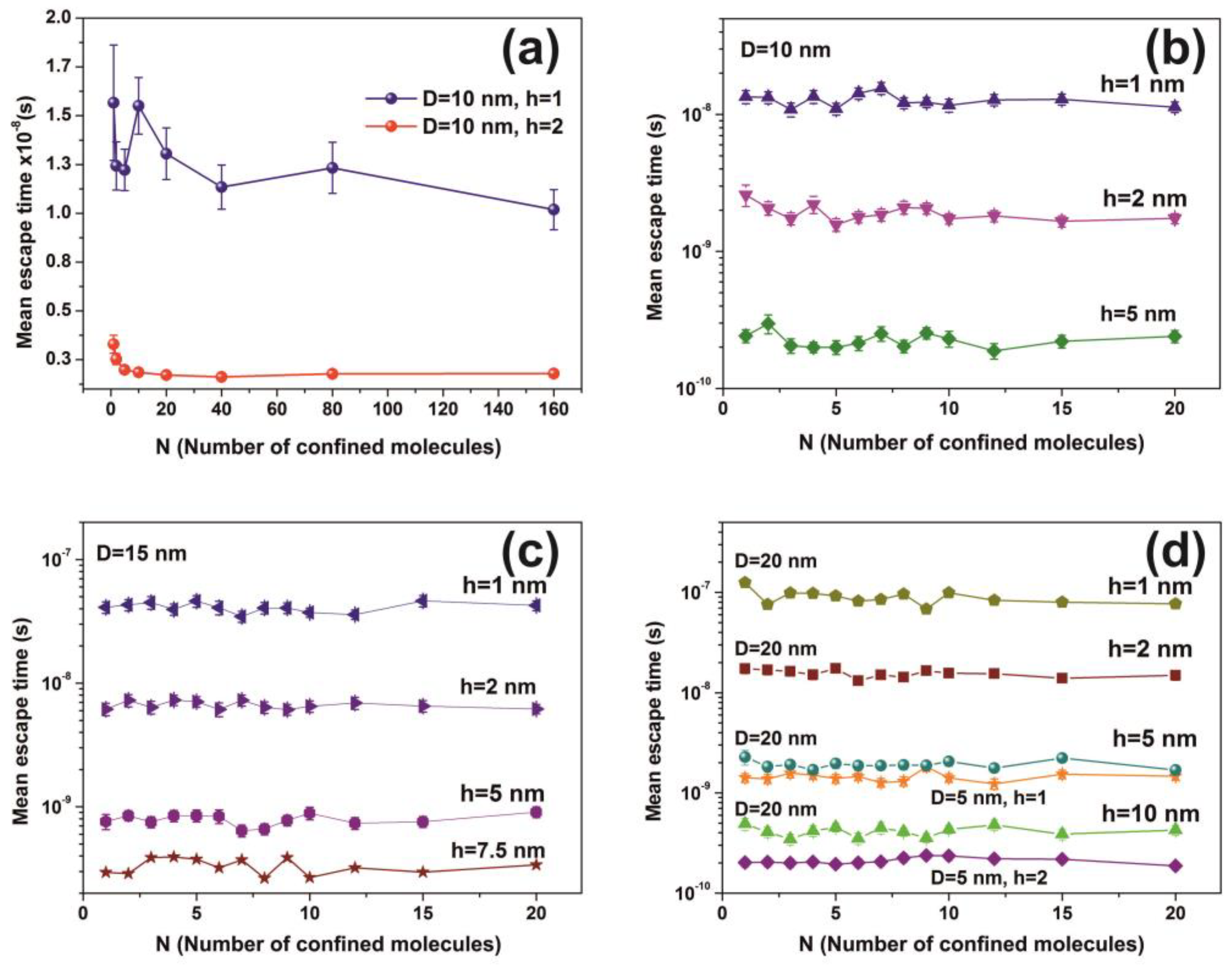
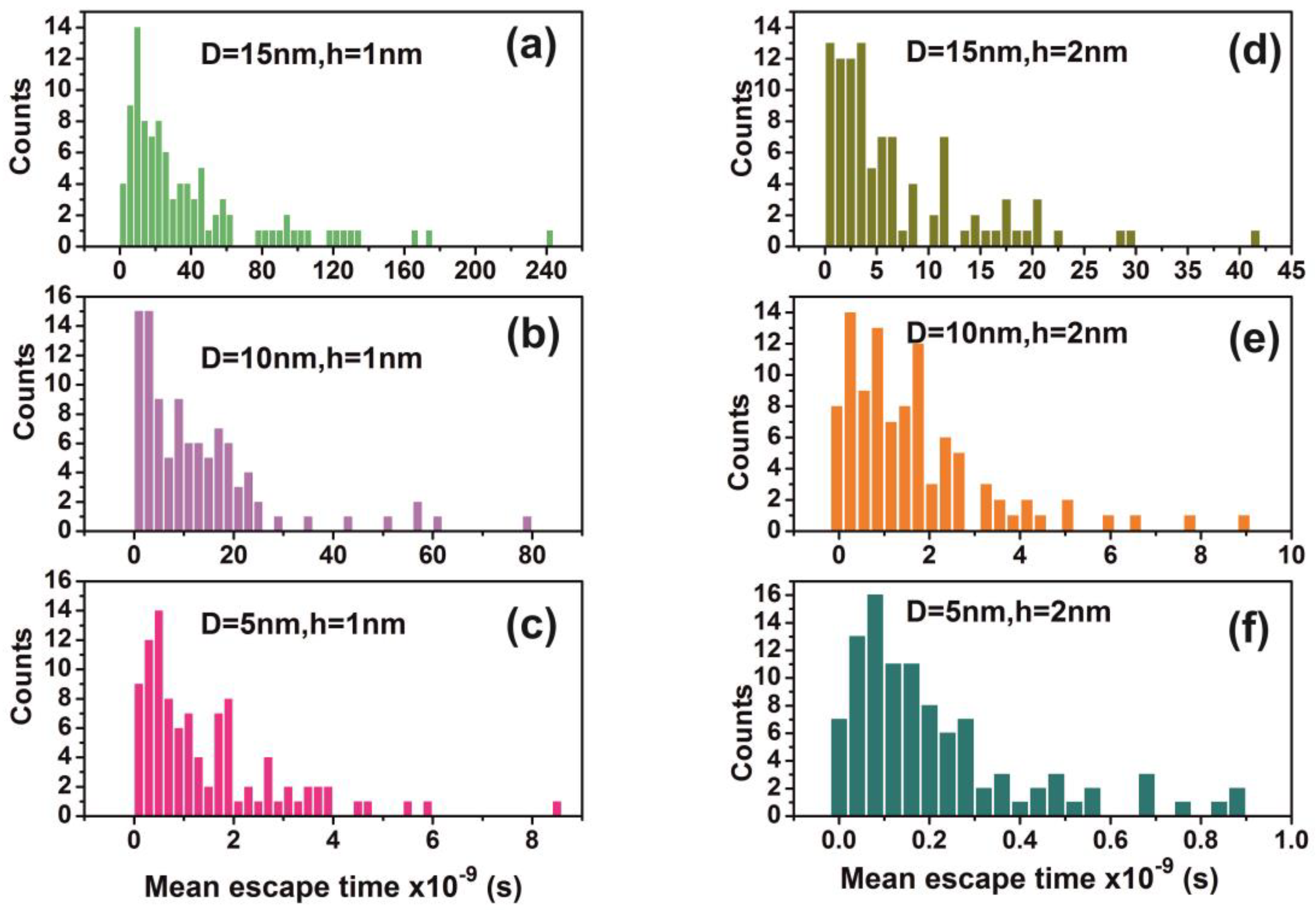
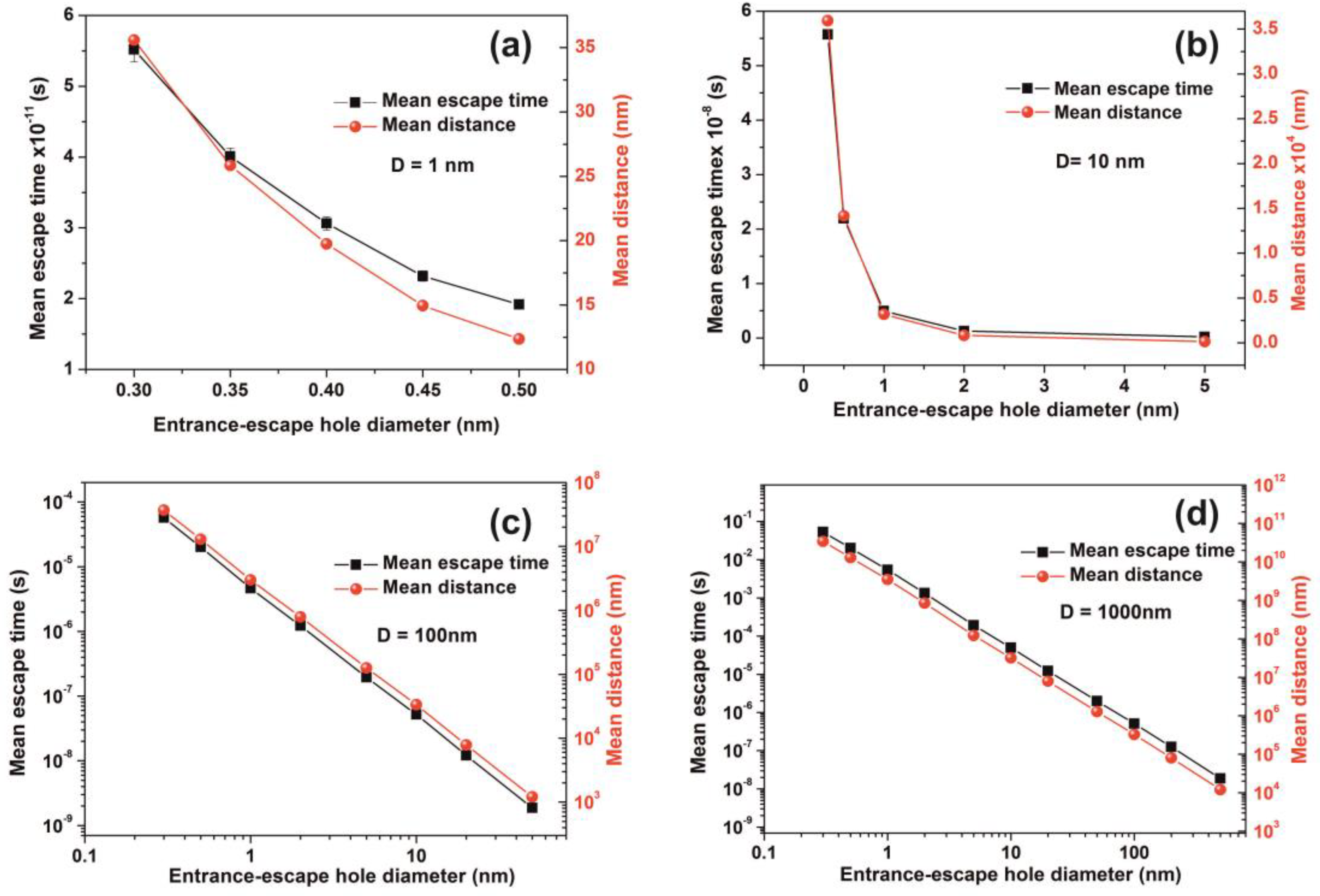
3.6. Random Walk Model
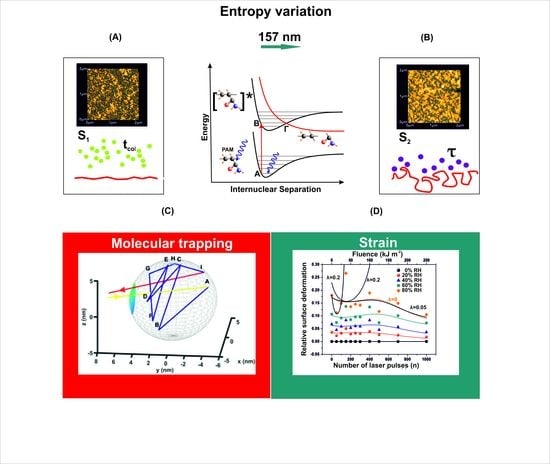
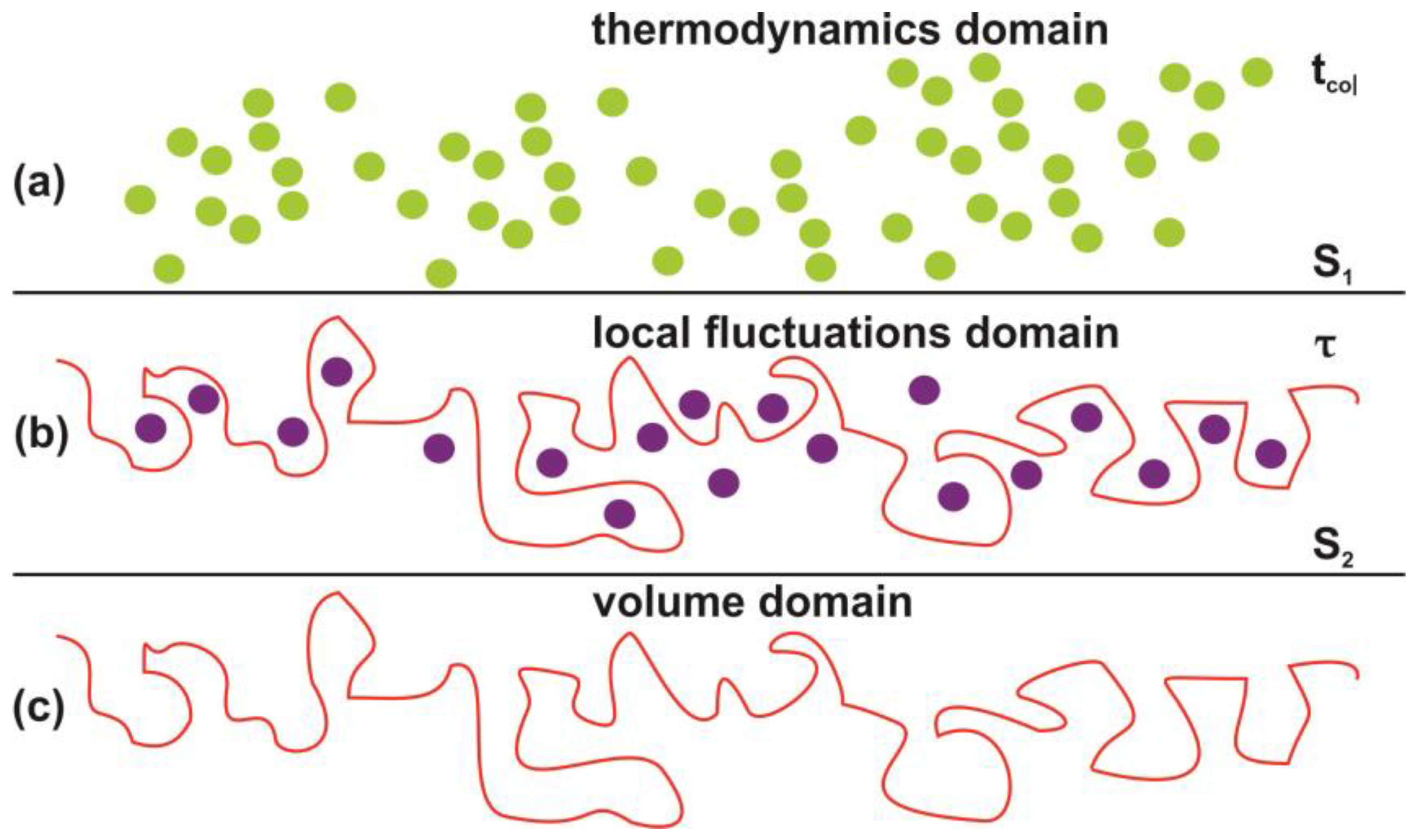
4. Discussion
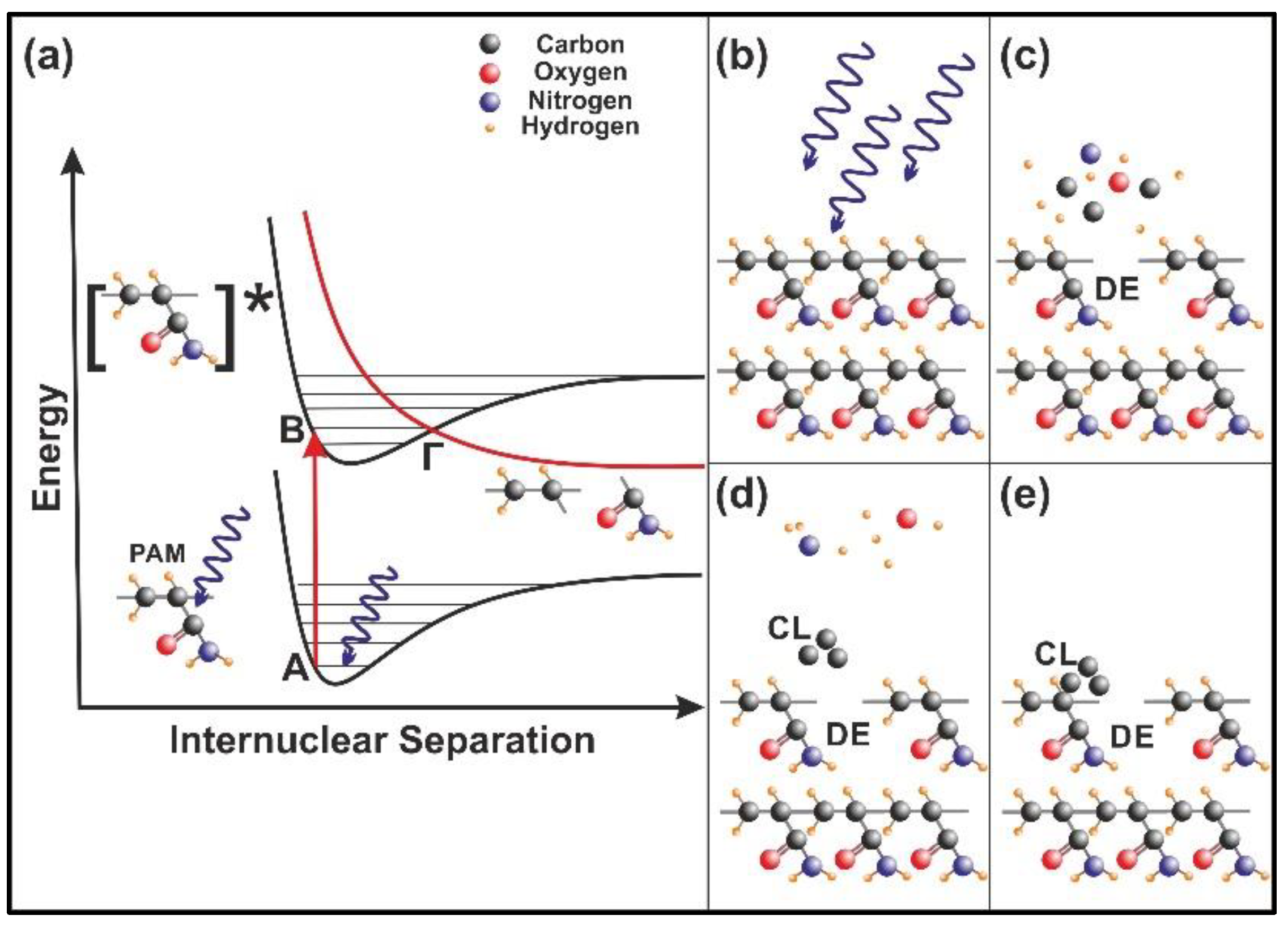
4.1. 157 nm Molecular Photodissociation of PAM Polymeric Chains
4.2. Trapping of Water Molecules in Nanocavities
4.3. Stress-Strain Response in Polymeric Matrixes-A Relation between Physics and Mechanics
4.4. Internal Energy Variation during Molecular Water Confinement
4.5. Entropic Energy Variation during Molecular Confinement
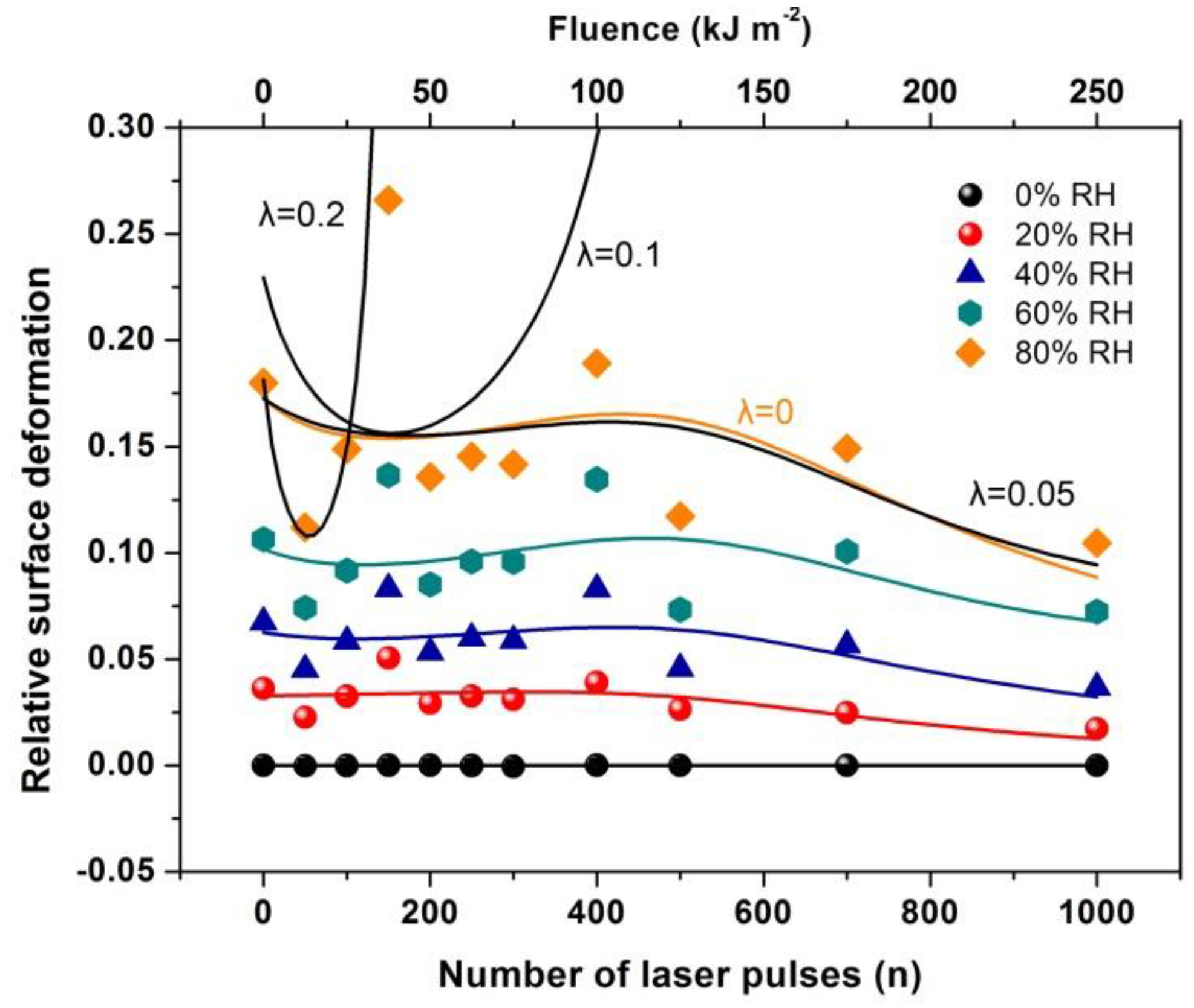
4.6. Surface Strain from the Confinement of Water Molecules
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| h (nm) | Cavity Diameter D = 1 nm | Cavity Diameter D = 10 nm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diffusion | Random Walk | Diffusion | Random Walk | |||||||
| τ (s) | τ (s) | Error (s) | Distance (nm) | Error (nm) | τ(s) | τ (s) | Error (s) | Distance (nm) | Error (nm) | |
| 0.3 | 3.98 × 10−14 | 5.51 × 10−11 | 1.7 × 10−12 | 35.5 | 1.1 | 3.98 × 10−11 | 5.57 × 10−8 | 1.7 × 10−9 | 35,931 | 1133 |
| 0.5 | 2.39 × 10−14 | 1.91 × 10−11 | 5 × 10−13 | 12.4 | 0.3 | 2.39 × 10-11 | 2.19 × 10−8 | 7 × 10−10 | 14,151 | 465 |
| 1 | 1.19 × 10-11 | 4.93 × 10−9 | 1.6 × 10−10 | 3182 | 107 | |||||
| 2 | 5.98 × 10-12 | 1.28 × 10−9 | 4 × 10−11 | 822 | 26 | |||||
| 5 | 2.39 × 10−12 | 1.90 × 10−10 | 5 × 10−12 | 128 | 4 | |||||
| h (nm) | Cavity Diameter D = 102 nm | Cavity Diameter D = 103 nm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diffusion | Random Walk | Diffusion | Random Walk | |||||||
| τ (s) | τ (s) | Error (s) | Distance (nm) | Error (nm) | τ (s) | τ (s) | Error (s) | Distance (nm) | Error (nm) | |
| 0.3 | 3.98 × 10−8 | 5.71 × 10−5 | 1.8 × 10−6 | 3.68 × 107 | 1.2 × 106 | 3.98 × 10−5 | 5.3 × 10−2 | 1.7 × 10−3 | 3.42 × 1010 | 1.1 × 109 |
| 0.5 | 2.39 × 10−8 | 2.00 × 10−5 | 6 × 10−7 | 1.29 × 107 | 4.1 × 105 | 2.39 × 10−5 | 2.01 × 10−2 | 6.3 × 10−4 | 1.3 × 1010 | 4.1 × 108 |
| 1 | 1.19 × 10−8 | 4.63 × 10−6 | 1.4 × 10−7 | 2.99 × 106 | 9 × 104 | 1.19 × 10−5 | 5.43 × 10−3 | 1.6 × 10−4 | 3.5 × 109 | 1.1 × 108 |
| 2 | 5.98 × 10−9 | 1.22 × 10−6 | 4 × 10−8 | 7.89 × 105 | 2.5 × 104 | 5.98 × 10−6 | 1.33 × 10−3 | 4.1 × 10−5 | 8.56 × 108 | 2.7 × 107 |
| 5 | 2.39 × 10−9 | 1.95 × 10−7 | 6 × 10−9 | 1.26 × 105 | 4 × 103 | 2.39 × 10−6 | 1.92 × 10−4 | 6.7 × 10−6 | 1.24 × 108 | 4.3 × 106 |
| 10 | 1.19 × 10−9 | 5.18 × 10−8 | 1.6 × 10−9 | 3.34 × 104 | 1060 | 1.19 × 10−6 | 4.99 × 10−5 | 1.6 × 10−6 | 3.22 × 107 | 1.1 × 106 |
| 20 | 5.97 × 10−10 | 1.21 × 10−8 | 3 × 10−10 | 7821 | 244 | 5.97 × 10−7 | 1.23 × 10−5 | 4.1 × 10−7 | 7.93 × 107 | 2.6 × 105 |
| 50 | 2.39 × 10−10 | 1.87 × 10−9 | 5 × 10−11 | 1204 | 35 | 2.39 × 10−7 | 1.99 × 10−6 | 6.4 × 10−8 | 1.28 × 106 | 4.1 × 104 |
| 100 | 1.19 × 10−7 | 5.07 × 10−7 | 1.5 × 10−8 | 3.27 × 105 | 9.8 × 103 | |||||
| 200 | 5.97 × 10−8 | 1.25 × 10−7 | 3.7 × 10−9 | 8.05 × 104 | 2.4 × 103 | |||||
| 500 | 2.39 × 10−8 | 1.88 × 10−8 | 5.6 × 10−10 | 1.21 × 104 | 3.6 × 102 | |||||
| Cavity Diameter = 5 nm | ||||
|---|---|---|---|---|
| N (Number of Molecules) | h = 1 nm | h = 2 nm | ||
| τ (s) | Error (s) | τ (s) | Error (s) | |
| 1 | 1.41 × 10−9 | 1.4 × 10−10 | 2.02 × 10−10 | 2.0 × 10−11 |
| 2 | 1.38 × 10−9 | 1.4 × 10−10 | 2.04 × 10−10 | 2.2 × 10−11 |
| 3 | 1.57 × 10−9 | 1.6 × 10−10 | 2.00 × 10−10 | 2.1 × 10−11 |
| 4 | 1.50 × 10−9 | 1.4 × 10−10 | 2.05 × 10−10 | 1.9 × 10−11 |
| 5 | 1.39 × 10−9 | 1.4 × 10−10 | 1.95 × 10−10 | 1.8 × 10−11 |
| 6 | 1.46 × 10−9 | 1.3 × 10−10 | 2.01 × 10−10 | 2.2 × 10−11 |
| 7 | 1.27 × 10−9 | 1.2 × 10−10 | 2.06 × 10−10 | 2.1 × 10−11 |
| 8 | 1.30 × 10−9 | 1.4 × 10−10 | 2.25 × 10−10 | 2.4 × 10−11 |
| 9 | 1.82 × 10−9 | 1.8 × 10−10 | 2.37 × 10−10 | 2.1 × 10−11 |
| 10 | 1.41 × 10−9 | 1.4 × 10−10 | 2.35 × 10−10 | 2.4 × 10−11 |
| 12 | 1.23 × 10−9 | 1.5 × 10−10 | 2.20 × 10−10 | 2.1 × 10−11 |
| 15 | 1.53 × 10−9 | 1.5 × 10−10 | 2.18 × 10−10 | 2.0 × 10−11 |
| 20 | 1.47 × 10−9 | 1.3 × 10−10 | 1.87 × 10−10 | 1.9 × 10−11 |
| Cavity Diameter = 10 nm | ||||||
|---|---|---|---|---|---|---|
| N (Number of Molecules) | h = 1 nm | h = 2 nm | h = 5 nm | |||
| τ (s) | Error (s) | τ (s) | Error (s) | τ (s) | Error (s) | |
| 1 | 1.35 × 10−8 | 1.5 × 10−9 | 2.59 × 10−9 | 4.6 × 10−10 | 2.42 × 10−10 | 2.7 × 10−11 |
| 2 | 1.33 × 10−8 | 1.3 × 10−9 | 2.07 × 10−9 | 2.3 × 10−10 | 2.97 × 10−10 | 4.7 × 10−11 |
| 3 | 1.09 × 10−8 | 1.3 × 10−9 | 1.74 × 10−9 | 1.7 × 10−10 | 2.06 × 10−10 | 2.5 × 10−11 |
| 4 | 1.35 × 10−8 | 1.5 × 10−9 | 2.21 × 10−9 | 3.2 × 10−10 | 2.00 × 10−10 | 1.8 × 10−11 |
| 5 | 1.10 × 10−8 | 1.1 × 10−9 | 1.57 × 10−9 | 1.7 × 10−10 | 2.00 × 10−10 | 2.4 × 10−11 |
| 6 | 1.43 × 10−8 | 1.4 × 10−9 | 1.78 × 10−9 | 1.7 × 10−10 | 2.14 × 10−10 | 2.5 × 10−11 |
| 7 | 1.55 × 10−8 | 1.6 × 10−9 | 1.85 × 10−9 | 1.9 × 10−10 | 2.51 × 10−10 | 3.1 × 10−11 |
| 8 | 1.21 × 10−8 | 1.1 × 10−9 | 2.10 × 10−9 | 2.2 × 10−10 | 2.03 × 10−10 | 2.1 × 10−11 |
| 9 | 1.23 × 10−8 | 1.1 × 10−9 | 2.07 × 10−9 | 2.0 × 10−10 | 2.54 × 10−10 | 2.4 × 10−11 |
| 10 | 1.17 × 10−8 | 1.3 × 10−9 | 1.73 × 10−9 | 1.5 × 10−10 | 2.31 × 10−10 | 3.1 × 10−11 |
| 12 | 1.28 × 10−8 | 1.2 × 10−9 | 1.82 × 10−9 | 1.7 × 10−10 | 1.88 × 10−10 | 2.4 × 10−11 |
| 15 | 1.29 × 10−8 | 1.2 × 10−9 | 1.66 × 10−9 | 1.6 × 10−10 | 2.21 × 10−10 | 2.3 × 10−11 |
| 20 | 1.13 × 10−8 | 1.0 × 10−9 | 1.74 × 10−9 | 1.5 × 10−10 | 2.40 × 10−10 | 2.5 × 10−11 |
| Cavity Diameter = 15 nm | ||||||||
|---|---|---|---|---|---|---|---|---|
| N (Number of Molecules) | h = 1 nm | h = 2 nm | H = 5 nm | h = 7.5 nm | ||||
| τ | Error (s) | τ (s) | Error (s) | τ (s) | Error (s) | τ (s) | Error (s) | |
| 1 | 1.41 × 10−9 | 1.4 × 10−10 | 6.17 × 10−9 | 7.0 × 10−10 | 7.61 × 10−10 | 1.1 × 10−10 | 2.95 × 10−10 | 3.6 × 10−11 |
| 2 | 1.38 × 10−9 | 1.4 × 10−10 | 7.26 × 10−9 | 8.3 × 10−10 | 8.49 × 10−10 | 8.1 × 10−11 | 2.88 × 10−10 | 2.7 × 10−11 |
| 3 | 1.57 × 10−9 | 1.6 × 10−10 | 6.39 × 10−9 | 7.5 × 10−10 | 7.52 × 10−10 | 7.7 × 10−11 | 3.88 × 10−10 | 5.9 × 10−11 |
| 4 | 1.50 × 10−9 | 1.4 × 10−10 | 7.29 × 10−9 | 6.8 × 10−10 | 8.47 × 10−10 | 8.8 × 10−11 | 3.93 × 10−10 | 5.2 × 10−11 |
| 5 | 1.39 × 10−9 | 1.4 × 10−10 | 7.09 × 10−9 | 6.8 × 10−10 | 8.47 × 10−10 | 9.2 × 10−11 | 3.77 × 10−10 | 4.3 × 10−11 |
| 6 | 1.46 × 10−9 | 1.3 × 10−10 | 6.13 × 10−9 | 7.7 × 10−10 | 8.37 × 10−10 | 1.1 × 10−10 | 3.21 × 10−10 | 4.2 × 10−11 |
| 7 | 1.27 × 10−9 | 1.2 × 10−10 | 7.26 × 10−9 | 7.4 × 10−10 | 6.41 × 10−10 | 7.0 × 10−11 | 3.72 × 10−10 | 4.3 × 10−11 |
| 8 | 1.30 × 10−9 | 1.4 × 10−10 | 6.37 × 10−9 | 6.8 × 10−10 | 6.60 × 10−10 | 6.8 × 10−11 | 2.65 × 10−10 | 3.3 × 10−11 |
| 9 | 1.82 × 10−9 | 1.8 × 10−10 | 6.11 × 10−9 | 6.1 × 10−10 | 7.77 × 10−10 | 7.6 × 10−11 | 3.88 × 10−10 | 4.1 × 10−11 |
| 10 | 1.41 × 10−9 | 1.4 × 10−10 | 6.49 × 10−9 | 6.9 × 10−10 | 8.88 × 10−10 | 1.0 × 10−10 | 2.67 × 10−10 | 3.3 × 10−11 |
| 12 | 1.23 × 10−9 | 1.5 × 10−10 | 6.90 × 10−9 | 7.8 × 10−10 | 7.38 × 10−10 | 8.1 × 10−11 | 3.21 × 10−10 | 4.0 × 10−11 |
| 15 | 1.53 × 10−9 | 1.5 × 10−10 | 6.52 × 10−9 | 6.9 × 10−10 | 7.58 × 10−10 | 7.7 × 10−11 | 2.96 × 10−10 | 3.2 × 10−11 |
| 20 | 1.47 × 10−9 | 1.3 × 10−10 | 6.19 × 10−9 | 5.3 × 10−10 | 9.07 × 10−10 | 8.9 × 10−11 | 3.39 × 10−10 | 4.5 × 10−11 |
| Cavity Diameter = 20 nm | ||||||||
|---|---|---|---|---|---|---|---|---|
| N (Number of Molecules) | h = 1 nm | h = 2 nm | h = 5 nm | h = 10 nm | ||||
| τ (s) | Error (s) | τ (s) | Error (s) | τ (s) | Error (s) | τ (s) | Error (s) | |
| 1 | 1.26 × 10−7 | 1.6 × 10−8 | 1.74 × 10−8 | 2.0 × 10−9 | 2.27 × 10−9 | 3.85 × 10−10 | 4.89 × 10−10 | 7.03 × 10−11 |
| 2 | 7.59 × 10−8 | 7.5 × 10−9 | 1.69 × 10−8 | 1.8 × 10−9 | 1.82 × 10−9 | 2.24 × 10−10 | 4.07 × 10−10 | 4.78 × 10−11 |
| 3 | 9.88 × 10−8 | 9.5 × 10−9 | 1.63 × 10−8 | 1.7 × 10−9 | 1.91 × 10−9 | 2.04 × 10−10 | 3.46 × 10−10 | 4.19 × 10−11 |
| 4 | 9.80 × 10−8 | 8.5 × 10−9 | 1.51 × 10−8 | 1.7 × 10−9 | 1.70 × 10−9 | 1.85 × 10−10 | 4.17 × 10−10 | 5.17 × 10−11 |
| 5 | 9.22 × 10−8 | 9.6 × 10−9 | 1.75 × 10−8 | 1.8 × 10−9 | 1.96 × 10−9 | 2.24 × 10−10 | 4.54 × 10−10 | 4.66 × 10−11 |
| 6 | 8.20 × 10−8 | 7.7 × 10−9 | 1.32 × 10−8 | 1.3 × 10−9 | 1.87 × 10−9 | 2.11 × 10−10 | 3.51 × 10−10 | 4.63 × 10−11 |
| 7 | 8.51 × 10−8 | 8.3 × 10−9 | 1.51 × 10−8 | 1.2 × 10−9 | 1.87 × 10−9 | 1.87 × 10−10 | 4.48 × 10−10 | 5.82 × 10−11 |
| 8 | 9.64 × 10−8 | 8.5 × 10−9 | 1.43 × 10−8 | 1.5 × 10−9 | 1.90 × 10−9 | 2.05 × 10−10 | 4.10 × 10−10 | 4.13 × 10−11 |
| 9 | 6.85 × 10−8 | 5.9 × 10−9 | 1.66 × 10−8 | 1.6 × 10−9 | 1.88 × 10−9 | 2.15 × 10−10 | 3.56 × 10−10 | 3.69 × 10−11 |
| 10 | 9.94 × 10−8 | 9.6 × 10−9 | 1.56 × 10−8 | 1.5 × 10−9 | 2.05 × 10−9 | 2.18 × 10−10 | 4.32 × 10−10 | 4.07 × 10−11 |
| 12 | 8.36 × 10−8 | 9.8 × 10−9 | 1.55 × 10−8 | 1.5 × 10−9 | 1.77 × 10−9 | 1.81 × 10−10 | 4.77 × 10−10 | 5.87 × 10−11 |
| 15 | 8.01 × 10−8 | 7.7 × 10−9 | 1.40 × 10−8 | 1.4 × 10−9 | 2.23 × 10−9 | 2.01 × 10−10 | 3.88 × 10−10 | 4.80 × 10−11 |
| 20 | 7.68 × 10−8 | 7.8 × 10−9 | 1.49 × 10−8 | 1.6 × 10−9 | 1.69 × 10−9 | 1.89 × 10−10 | 4.26 × 10−10 | 4.87 × 10−11 |
References
- Levinger, N.E. Water in confinement. Science 2002, 298, 1722–1723. [Google Scholar] [CrossRef] [PubMed]
- Martin, D.R.; Forsmo, J.E.; Matyushov, D.V. Complex Dynamics of Water in Protein Confinement. J. Phys. Chem. 2018, 122, 3418–3425. [Google Scholar] [CrossRef]
- Rasaiah, J.C.; Garde, S.; Hummer, G. Water in nonpolar confinment: From Natotubes to Proteins and Beyond. Annu. Rev. Phys. Chem. 2008, 59, 713–740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hummer, G.; Garde, S. Cavity expulsion and weak dewetting of hydrophobic soluts in water. Phys. Rev. Lett. 1998, 80, 4193–4196. [Google Scholar] [CrossRef]
- Muñoz-Santiburcio, D.; Marx, D. Nanoconfinement in Slit Pores Enhances Water Self-Dissociation. Phys. Rev. Lett. 2017, 119, 056002. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.; Acharya, S.; Bagchi, B. Altered polar character of nanoconfined liquid water. Phys. Rev. Res. 2019, 1, 033145. [Google Scholar] [CrossRef] [Green Version]
- Gladovic, M.; Bren, U.; Urbic, T. Thermodynamic properties of water in confined environments: A Monte Carlo study. Mol. Phys. 2018, 116, 1133–1144. [Google Scholar] [CrossRef]
- Ball, P. Water is an active matrix of life for cell and molecular biology. Proc. Natl. Acad. Sci. USA 2017, 114, 13327–13335. [Google Scholar] [CrossRef] [Green Version]
- Moscatelli, A. The power of one atom. Nat. Nanotech. 2016. [Google Scholar] [CrossRef]
- Lucia, U.A. Link between Nano- and Classical Thermodynamics: Dissipation Analysis (The Entropy Generation Approach in Nano-Thermodynamics). Entropy 2015, 17, 1309–1328. [Google Scholar] [CrossRef]
- Ernst, J.A.; Clubb, R.T.; Zhou, H.X.; Gronenborn, A.M.; Clore, G.M. Demonstration of positionally disordered water within a protein hydrophobic cavity by NMR. Science 1995, 267, 1813–1817. [Google Scholar] [CrossRef] [PubMed]
- Chaban, V.V.; Prezhdo, V.V.; Prezhdo, O.V. Confinement by Carbon Nanotubes Drastically Alters the Boiling and Critical Behavior of Water Droplets. ACS Nano 2012, 6, 2766–2773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cefalas, A.C.; Sarantopoulou, E.; Kollia, Z.; Kitsara, M.; Raptis, I.; Bakalis, E. Entropic nanothermodynamic potential from molecular trapping within photon induced nano-voids in photon processed PDMS layers. Soft Matter 2012, 8, 5561–5574. [Google Scholar] [CrossRef]
- Hill, T.L. A Different Approach to Nanothermodynamics. Nano Lett. 2001, 1, 273–275. [Google Scholar] [CrossRef]
- Giebultowicz, T. Nanothermodynamics: Breathing life into an old model. Nature 2000, 408, 299–301. [Google Scholar] [CrossRef]
- Li, Z.H.; Truhlar, D.G. Nanothermodynamics of metal nanoparticles. Chem. Sci. 2014, 5, 2605–2624. [Google Scholar] [CrossRef]
- Wang, C.X.; Yang, G.W. Thermodynamics of metastable phase nucleation at the nanoscale. Mater. Sci. Eng. R. 2005, 49, 157–202. [Google Scholar] [CrossRef]
- Hill, T.L. Extension of Nanothermodynamics to Include a One-Dimensional Surface Excess. Nano Lett. 2001, 1, 159–160. [Google Scholar] [CrossRef]
- Schnell, S.K.; Liu, X.; Simon, J.M.; Bardow, A.; Bedeaux, D.; Vlugt, T.J.H.; Kjelstrup, S. Calculating Thermodynamic Properties from Fluctuations at Small Scales. J. Phys. Chem. 2011, 115, 10911–10918. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, Q.; Emrick, T.; Balazs, A.C.; Russell, T.P. Entropy-driven segregation of nanoparticles to cracks in multilayered composite polymer structures. Nat. Mater. 2006, 5, 229–233. [Google Scholar] [CrossRef]
- Ruggeri, F.; Krishnan, M. Entropic Trapping of a Singly Charged Molecule in Solution. Nano Lett. 2018, 18, 3773–3779. [Google Scholar] [CrossRef] [PubMed]
- Guisbiers, G. Advances in thermodynamic modelling of nanoparticles. Adv. PhysX 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Dai, X.; Hou, C.; Xu, Z.; Yang, Y.; Zhu, G.; Chen, P.; Huang, Z.; Yan, L.T. Entropic Effects in Polymer Nanocomposites. Entropy 2019, 21, 186. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Morales, G.; Cervera, J.; Manzanares, J.A. Nanothermodynamcis. In Handbook of Nanophysics: Principles and Methods, 1st ed.; Sattler, K.D., Ed.; CRC Press Taylor & Francis Group: Boca Raton Florida, FL, USA, 2011. [Google Scholar] [CrossRef]
- Gavriil, V.; Chatzichristidi, M.; Kollia, Z.; Cefalas, A.C.; Spyropoulos-Antonakakis, N.; Semashko, V.V.; Sarantopoulou, E. Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities. Entropy 2018, 20, 545. [Google Scholar] [CrossRef] [Green Version]
- Huber, P. Soft matter in hard confinement: Phase transition thermodynamics, structure, texture, diffusion and flow in nanoporous media. J. Phys. Condens. Matter 2015, 27, 103102. [Google Scholar] [CrossRef] [Green Version]
- Galteland, O.; Bedeaux, D.; Kjelstrup, S. Pressures Inside a Nano-Porous Medium. The Case of a Single Phase Fluid. Front. Phys. 2019, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Stefi, A.L.; Sarantopoulou, E.; Kollia, Z.; Spyropoulos-Antonakakis, N.; Bourkoula, A.; Petrou, P.S.; Kakabakos, S.; Soras, G.; Trohopoulos, P.N.; Nizamutdinov, A.S.; et al. Nanothermodynamics Mediates Drug Delivery. In GeNeDis 2014 Neurodegeneration; Vlamos, P., Alexiou, A., Eds.; Springer: Cham, Switzerland, 2015; Volume 822, pp. 213–220. [Google Scholar] [CrossRef]
- Cefalas, A.C.; Kollia, Z.; Spyropoulos-Antonakakis, N.; Gavriil, V.; Christofilos, D.; Kourouklis, G.; Shemashko, V.V.; Pavlov, V.; Sarantopoulou, E. Surface profile gradient in amorphous Ta2O5 semi conductive layers regulates nanoscale electric current stability. Appl. Surf. Sci. 2017, 396, 1000–1019. [Google Scholar] [CrossRef] [Green Version]
- Tranchida, D.; Sperotto, E.; Chateauminois, A.; Schönherr, H. Entropic Effects on the Mechanical Behavior of Dry Polymer Brushes During Nanoindentation by Atomic Force Microscopy. Macromolecules 2011, 44, 368–374. [Google Scholar] [CrossRef]
- Nicolis, S.J. Dynamics of Hierarchical Systems: An. Evolutionary Approach, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1986; ISBN 978-3-642-69694-7. [Google Scholar]
- Nash, T. The Role of Entropy in Molecular Self-Assembly. J. Nanomed. Res. 2017, 5, 00126. [Google Scholar] [CrossRef] [Green Version]
- Cefalas, A.C.; Kobe, S.; Dražic, G.; Sarantopoulou, E.; Kollia, Z.; Stražišar, J.; Medend, A. Nanocrystallization of CaCO3 at solid/liquid interfaces in magnetic field: A quantum approach. Appl. Surf. Sci. 2008, 254, 6715–6724. [Google Scholar] [CrossRef]
- Grzybowski, B.A.; Wilmer, C.E.; Kim, J.; Browne, K.P.; Bishop, K.J.M. Self-assembly: From crystals to cells. Soft Matter 2009, 5, 1110–1128. [Google Scholar] [CrossRef]
- Dauenhauer, P.J.; Abdelrahman, O.A. A Universal Descriptor for the Entropy of Adsorbed Molecules in Confined Spaces. ACS Cent. Sci. 2018, 4, 1235–1243. [Google Scholar] [CrossRef]
- Campbell, C.T.; Sellers, J.R.V. The Entropies of Adsorbed Molecules. J. Am. Chem. Soc. 2012, 134, 18109–18115. [Google Scholar] [CrossRef] [PubMed]
- Sarantopoulou, E.; Petrou, P.S.; Kollia, Z.; Palles, D.; Spyropoulos-Antonakakis, N.; Kakabakos, S.; Cefalas, A.C. Protein immobilization and detection on laser processed polystyrene surfaces. J. Appl. Phys. 2011, 110, 064309-17. [Google Scholar] [CrossRef]
- Nguyen, A.K.; Narayan, R.J. Two-photon polymerization for biological applications. Mater. Today 2017, 20, 314–322. [Google Scholar] [CrossRef]
- Zheng, L.; Kurselis, K.; El-Tamer, A.; Hinze, U.; Reinhardt, C.; Overmeyer, L.; Chichkov, B. Nanofabrication of High-Resolution Periodic Structures with a Gap Size Below 100 nm by Two-Photon Polymerization. Nanoscale Res. Lett. 2019, 14, 134. [Google Scholar] [CrossRef]
- Yang, T.H.; Kao, C.R.; Shigetou, A. Organic-Inorganic Solid-State Hybridization with High-Strength and Anti-Hydrolysis Interface. Sci. Rep. 2019, 9, 504. [Google Scholar] [CrossRef]
- Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C.; Siokou, A.E.; Argitis, P.; Bellas, V.; Kobe, S. Surface modification of polyhedral oligomeric silsesquioxane block copolymer films by 157 nm laser light. J. Appl. Phys. 2009, 105, 114305. [Google Scholar] [CrossRef]
- Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C.; Manoli, K.; Sanopoulou, M.; Goustouridis, D.; Chatzandroulis, S.; Raptis, I. Surface nano/micro functionalization of PMMA thin films by 157 nm irradiation for sensing applications. Appl. Surf. Sci. 2008, 254, 1710–1719. [Google Scholar] [CrossRef]
- Douvas, A.M.; Petrou, P.S.; Kakabakos, S.E.; Misiakos, K.; Argitis, P.; Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C. 157-nm Laser ablation of polymeric layers for fabrication of biomolecule microarrays. Anal. Bioanal. Chem. 2005, 381, 1027–1032. [Google Scholar] [CrossRef]
- Wu, C.T.; Soliman, A.I.A.; Utsunomiya, T.; Ichii, T.; Sugimura, H. Formation of submicron-sized silica patterns on flexible polymer substrates based on vacuum ultraviolet photo-oxidation. RSC Adv. 2019, 9, 32313–32322. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.J.; Sugimura, H. Effects of irradiation atmosphere on vacuum ultraviolet-induced surface modification of cyclo-olefin polymer substrates. Appl. Phys. Express 2019, 12, 101002. [Google Scholar] [CrossRef]
- Kirchner, R.; Chidambaram, N.; Schift, H. Benchmarking surface selective vacuum ultraviolet and thermal postprocessing of thermoplastics for ultrasmooth 3-D-printed micro-optics. Opt. Eng. 2018, 57, 041403. [Google Scholar] [CrossRef]
- Kumar, K.V.; Srinivas, G.; Wood, B.; Ramisetty, K.A.; Stewart, A.A.; Howard, C.A.; Brett, D.J.L.; Rodriguez-Reinoso, F. Characterization of adsorption site energies and heterogeneous surfaces of porous materials. J. Mater. Chem. 2019, 7, 10104–10137. [Google Scholar] [CrossRef] [Green Version]
- Lorzing, G.R.; Gosselin, E.J.; Trump, B.A.; York, A.H.P.; Sturluson, A.; Casey, R.; Glenn, P.A.; Brown, C.M.; Simon, C.M.; Bloch, E. Understanding Gas Storage in Cuboctahedral Porous Coordination Cages. J. Am. Chem. Soc. 2019, 141, 12128–12138. [Google Scholar] [CrossRef]
- Sadasivuni, K.K.; Cabibihan, J.J.; Deshmukh, K.; Goutham, S.; Abubasha, M.K.; Gogoi, J.P.; Klemenoks, I.; Sakale, G.; Sekhar, B.S.; Sreekanth, P.S.R.; et al. A review on porous polymer composite materials for multifunctional electronic applications. Polymer Plast. Tech. Eng. 2019, 58, 1253–1294. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Jiang, D. Conjugated Microporous Polymers as Molecular Sensing Devices: Microporous Architecture Enables Rapid Response and Enhances Sensitivity in Fluorescence-On and Fluorescence-Off Sensing. J. Am. Chem. Soc. 2012, 134, 8738–8741. [Google Scholar] [CrossRef]
- Reguera, D.; Luque, A.; Burada, P.S.; Schmid, G.; Rubi, J.M.; Hänggi, P. Entropic splitter for particle separation. Phys. Rev. Lett. 2012, 108, 020604-5. [Google Scholar] [CrossRef]
- Zwanzig, R. Diffusion past an entropy barrier. J. Phys. Chem. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Pullumbi, P.; Brandani, F.; Brandani, S. Gas separation by adsorption: Technological drivers and opportunities for improvement. Curr. Opin. Chem. Eng. 2019, 24, 131–142. [Google Scholar] [CrossRef]
- Chena, X.Y.; Kaliaguinea, S.; Rodriguea, D. Polymer hollow fiber membranes for gas separation: A comparison between three commercial resins. AIP Conf. Proc. 2019, 2139, 070003. [Google Scholar] [CrossRef]
- Szałaj, U.; Świderska-Środa, A.; Chodara, A.; Gierlotka, S.; Łojkowski, W. Nanoparticle Size Effect on Water Vapour Adsorption by Hydroxyapatite. Nanomaterials 2019, 9, 1005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zainuddin, T.; Chirila, T.V.; Barnard, Z.; Watson, G.S.; Toh, C.; Blakey, I.; Whittaker, A.K.; Hill, D.J.T. F2 excimer laser (157nm) radiation modification and surface ablation of PHEMA hydrogels and the effects on bioactivity: Surface attachment and proliferation of human corneal epithelial cells. Rad. Phys. Chem. 2011, 80, 219–229. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, H.; Tang, D.; Li, Y.; Li, X.J.; Xu, F. Bioactuators based on stimulus-responsive hydrogels and their emerging biomedical applications. NPG Asia Mater. 2019, 11, 64. [Google Scholar] [CrossRef] [Green Version]
- Spyropoulos-Antonakakis, N.; Sarantopoulou, E.; Trohopoulos, P.N.; Stefi, A.L.; Kollia, Z.; Gavriil, V.E.; Bourkoula, A.; Petrou, P.S.; Kakabakos, S.; Semashko, V.V.; et al. Selective aggregation of PAMAM dendrimernanocarriers and PAMAM/ZnPc nanodrugs on human atheromatous carotid tissues: A photodynamic therapy for atherosclerosis. Nanoscale Res. Lett. 2015, 10, 210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muzzio, M.; Li, J.; Yin, Z.; Delahunty, I.; Xie, J.; Sun, S. Monodisperse nanoparticles for catalysis and nanomedicine. Nanoscale 2019, 11, 18946–18967. [Google Scholar] [CrossRef]
- Sanzari, I.; Callisti, M.; Grazia, A.; Evans, D.J.; Polcar, T.; Prodromakis, T. Parylene topographic micropattern as a template for patterning PDMS and Polyacrylamide hydrogel. Sci. Rep. 2017, 7, 5764. [Google Scholar] [CrossRef] [Green Version]
- Xiong, B.; Loss, R.D.; Shields, D.; Pawlik, T.; Hochreiter, R.; Zydney, A.L.; Kumar, M. Polyacrylamide degradation and its implications in environmental systems. NPJ Clean Water 2018, 1, s41545-18. [Google Scholar] [CrossRef]
- Kundu, B.; Kundu, S.C. Silk sericin/polyacrylamide in situ forming hydrogels for dermal reconstruction. Biomaterials 2012, 33, 7456–7467. [Google Scholar] [CrossRef]
- Ahad, I.U.; Bartnik, A.; Fiedorowicz, H.; Kostecki, J.; Korczyc, B.; Ciach, T.; Brabazon, D. Surface modification of polymers for biocompatibility via exposure to extreme ultraviolet radiation. J. Biomed. Mater. Res. 2014, 102, 3298–3310. [Google Scholar] [CrossRef] [Green Version]
- Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C.; Douvas, A.M.; Chatzichristidi, M.; Argitis, P.; Kobe, S. Nano-scale spatial control over surface morphology of biocompatible fluoropolymers at 157 nm. Mater. Sci. Eng. 2007, 27, 1191–1196. [Google Scholar] [CrossRef]
- Tran, K.T.M.; Nguyen, T.D. Lithography-based methods to manufacture biomaterials at small scales. J.Sci. Adv. Mater. Dev. 2017, 2, 1–14. [Google Scholar] [CrossRef]
- Nzenguet, A.M.; Aqlil, M.; Essamlali, Y.; Amadine, O.; Snik, A.; Larzek, M.; Zahouily, M. Novel bionanocomposite films based on graphene oxide filled starch/polyacrylamide polymer blend: Structural, mechanical and water barrier properties. J. Polym. Res. 2018, 25, 86. [Google Scholar] [CrossRef]
- Smithson, R.L.W.; Evans, D.F.; Monfils, J.D.; Guire, P.E. Ultrathin film characterization: Photoreactive polyacrylamide. Colloids Surf. Biointerfaces 1993, 1, 349–355. [Google Scholar] [CrossRef]
- Vijayalakshmi, S.P.; Senapati, D.; Madras, G. Pulsed laser degradation of polyethylene oxide and polyacrylamide in aqueous solution. Polym. Degrad. Stab. 2005, 87, 521–526. [Google Scholar] [CrossRef]
- Rong, J.; Zhu, K.; Chen, M. Study on purification technology of polyacrylamide wastewater by non-thermal plasma. Plasma Sci. Technol. 2019, 21, 054008. [Google Scholar] [CrossRef]
- Song, W.; Zhang, Y.; Yu, J.; Gao, Y.; Naitoc, T.; Oinumac, G.; Inanagac, Y.; Yang, M. Rapid removal of polyacrylamide from wastewater by plasma in the gas–liquid interface. J. Environ. Sci. 2019, 83, 1–7. [Google Scholar] [CrossRef]
- Caulfield, M.J.; Hao, X.; Qiao, G.G.; Solomon, D.H. Degradation of polyacrylamides. Part, I. Linear polyacrylamide. Polymer 2003, 44, 1331–1337. [Google Scholar] [CrossRef]
- Timoshenko, S. Theory of Elasticity, 1st ed.; McCraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1934; p. 7. [Google Scholar]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Zahn, W.; Zösch, A. Characterization of thin film surfaces by fractal geometry. Fresenius J. Anal. Chem. 1997, 358, 119–121. [Google Scholar] [CrossRef]
- Raptis, I.; Kovač, J.; Chatzichristidi, M.; Sarantopoulou, E.; Kollia, Z.; Kobe, S.; Cefalas, A.C. Enhancement of sensing properties of thin poly(methyl methacrylate) films by VUV modification. J. Laser Micro Nanoeng. 2007, 2, 200–205. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, J. Accelerated Plasma-Aging of Polymers. In The Plasma Chemistry of Polymer Surfaces: Advance Techniques for Surface Design, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; pp. 239–248. [Google Scholar] [CrossRef]
- Park, C.S.; Jung, E.Y.; Jang, H.J.; Bae, G.T.; Shin, B.J.; Tae, H.S. Synthesis and Properties of Plasma-Polymerized Methyl Methacrylate via the Atmospheric Pressure Plasma Polymerization Technique. Polymers 2019, 11, 396. [Google Scholar] [CrossRef] [Green Version]
- Denisin, A.K.; Pruitt, B.L. Tuning the Range of Polyacrylamide Gel Stiffness for Mechanobiology Applications. ACS Appl. Mater. Interfaces 2016, 8, 21893–21902. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, N. Materials Characterization Modern Methods and Applications, 1st ed.; CRC Press, Taylor & Francis Group: New York, NY, USA, 2015; ISBN 978-9814613064. [Google Scholar]
- Constantinides, G.; Kalcioglu, Z.I.; McFarland, M.; Smith, J.F.; Van Vliet, K.J. Probing mechanical properties of fully hydrated gels and biological tissues. J. Biomech. 2008, 41, 3285–3289. [Google Scholar] [CrossRef] [PubMed]
- An, M.; Demir, B.; Wan, X.; Meng, H.; Yang, N.; Walsh, T.R. Predictions of Thermo-Mechanical Properties of Cross-Linked Polyacrylamide Hydrogels Using Molecular Simulations. Adv. Theory Simul. 2019, 2, 1800153. [Google Scholar] [CrossRef]
- Grigoriev, I.V.; Makhnovskii, Y.A.; Berezhkovskii, A.M.; Zitserman, V.Y. Kinetics of escape through a small hole. J. Chem. Phys. 2002, 116, 9574–9577. [Google Scholar] [CrossRef]
- Wohlfromm, T.; Vogel, M. On the coupling of protein and water dynamics in confinement: Spatially resolved molecular dynamics simulation studies. J. Chem. Phys. 2019, 150, 245101. [Google Scholar] [CrossRef]
- Jonchhe, S.; Pandey, S.; Emura, T.; Hidaka, K.; Hossain, M.A.; Shrestha, P.; Sugiyama, H.; Endo, M.; Mao, H. Decreased water activity in nanoconfinement contributes to the folding of G-quadruplex and i-motif structures. Proc. Natl. Acad. Sci. USA 2018, 115, 9539–9544. [Google Scholar] [CrossRef] [Green Version]
- Biswas, R.; Bagchi, B. Anomalous water dynamics at surfaces and interfaces: Synergistic effects of confinement and surface interactions. J. Phys. Condens. Matter 2018, 30, 013001. [Google Scholar] [CrossRef]
- Gorshunov, B.P.; Zhukova, E.S.; Torgashev, V.I.; Lebedev, V.V.; Shakurov, G.S.; Kremer, R.K.; Pestrjakov, E.V.; Thomas, G.; Fursenko, D.A.; Dressel, M. Quantum Behavior of Water Molecules Confined to Nanocavities in Gemstones. J. Phys. Chem. Lett. 2013, 4, 2015–2020. [Google Scholar] [CrossRef]
- Oh, M.I.; Gupta, M.; Oh, C.I.; Weaver, D.F. Understanding the effect of nanoconfinement on the structure of water hydrogen bond networks. Phys. Chem. Chem. Phys. 2019, 21, 26237–26250. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Guo, Y.; Diao, D. Structure and dynamics of water confined in a graphene nanochannel under gigapascal high pressure: Dependence of friction on pressure and confinement. Phys. Chem. Chem. Phys. 2017, 19, 14048. [Google Scholar] [CrossRef] [PubMed]
- Strøm, B.A.; Simon, J.M.; Schnell, S.K.; Kjelstrup, S.; He, J.; Bedeaux, D. Size and shape effects on the thermodynamic properties of nanoscale volumes of water. Phys. Chem. Chem. Phys. 2017, 19, 9016. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Kumar, H.; Dasgupta, C.; Maiti, P.K. Confined Water: Structure, Dynamics, and Thermodynamics. Acc. Chem. Res. 2017, 50, 2139–2146. [Google Scholar] [CrossRef] [PubMed]
- Leoni, F.; Franzese, G. Effects of confinement between attractive and repulsive walls on the thermodynamics of an anomalous fluid. Phys. Rev. 2016, 94, 062604. [Google Scholar] [CrossRef] [Green Version]
- Firat, C.; Sisman, A.; Ozturk, Z.F. Thermodynamics of gases in nano cavities. Energy 2010, 35, 814–819. [Google Scholar] [CrossRef]
- Boyer, T.H. Quantum electromagnetic zero point energy of a conducting spherical cell and the Casimir model for a charged particle. Phys. Rev. 1968, 174, 1764. [Google Scholar] [CrossRef]
- Cheng, K.L.; Sheng, Y.J.; Tsao, H.K. Brownian escape and force-driven transport through entropic barriers: Particle size effect. J. Chem. Phys. 2008, 129, 184901. [Google Scholar] [CrossRef]
- Pascal, T.A.; Goddard, W.A.; Junga, Y. Entropy and the driving force for the filling of carbon nanotubes with water. Proc. Natl. Acad. Sci. USA 2011, 108, 11794–11798. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.X.; Zwanzig, R. A rate process with an entropy barrier. J. Chem. Phys. 1991, 94, 6147–6152. [Google Scholar] [CrossRef]
- Hetnarski, R.B.; Eslami, M.R. Thermal Stresses-Advanced Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2009; ISBN 978-3-030-10436-8. [Google Scholar]
- Grosman, A.; Ortega, C. Influence of elastic deformation of porous materials in adsorption-desorption process: A thermodynamic approach. Phys. Rev. 2008, 78, 085433. [Google Scholar] [CrossRef] [Green Version]
- Pathria, R.K.; Beale, P.B. Statistical Mechanics, 3rd ed.; Academic Press: Burlington, MA, USA, 2011; ISBN 978-0-12-382188-1. [Google Scholar]
- Montroll, E.W.; Weiss, G.H. Random Walks on Lattices II. J. Math. Phys. 1965, 6, 167. [Google Scholar] [CrossRef]
- Montroll, E.W.; Scher, H. Random Walks on Lattices. IV. Continuous-Time walks and influence of Absorbing Boundaries. J. Stat. Phys. 1973, 9, 101–135. [Google Scholar] [CrossRef]
- Blumen, A.; Klafter, J.; White, B.S.; Zumofen, G. Continuous-Time Random Walks on fractals. Phys. Rev. Lett. 1984, 53, 1301. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavriil, V.; Chatzichristidi, M.; Christofilos, D.; Kourouklis, G.A.; Kollia, Z.; Bakalis, E.; Cefalas, A.-C.; Sarantopoulou, E. Entropy and Random Walk Trails Water Confinement and Non-Thermal Equilibrium in Photon-Induced Nanocavities. Nanomaterials 2020, 10, 1101. https://doi.org/10.3390/nano10061101
Gavriil V, Chatzichristidi M, Christofilos D, Kourouklis GA, Kollia Z, Bakalis E, Cefalas A-C, Sarantopoulou E. Entropy and Random Walk Trails Water Confinement and Non-Thermal Equilibrium in Photon-Induced Nanocavities. Nanomaterials. 2020; 10(6):1101. https://doi.org/10.3390/nano10061101
Chicago/Turabian StyleGavriil, Vassilios, Margarita Chatzichristidi, Dimitrios Christofilos, Gerasimos A. Kourouklis, Zoe Kollia, Evangelos Bakalis, Alkiviadis-Constantinos Cefalas, and Evangelia Sarantopoulou. 2020. "Entropy and Random Walk Trails Water Confinement and Non-Thermal Equilibrium in Photon-Induced Nanocavities" Nanomaterials 10, no. 6: 1101. https://doi.org/10.3390/nano10061101
APA StyleGavriil, V., Chatzichristidi, M., Christofilos, D., Kourouklis, G. A., Kollia, Z., Bakalis, E., Cefalas, A.-C., & Sarantopoulou, E. (2020). Entropy and Random Walk Trails Water Confinement and Non-Thermal Equilibrium in Photon-Induced Nanocavities. Nanomaterials, 10(6), 1101. https://doi.org/10.3390/nano10061101