Comprehensive Electrostatic Modeling of Exposed Quantum Dots in Graphene/Hexagonal Boron Nitride Heterostructures
Abstract
1. Introduction
2. Materials and Methods
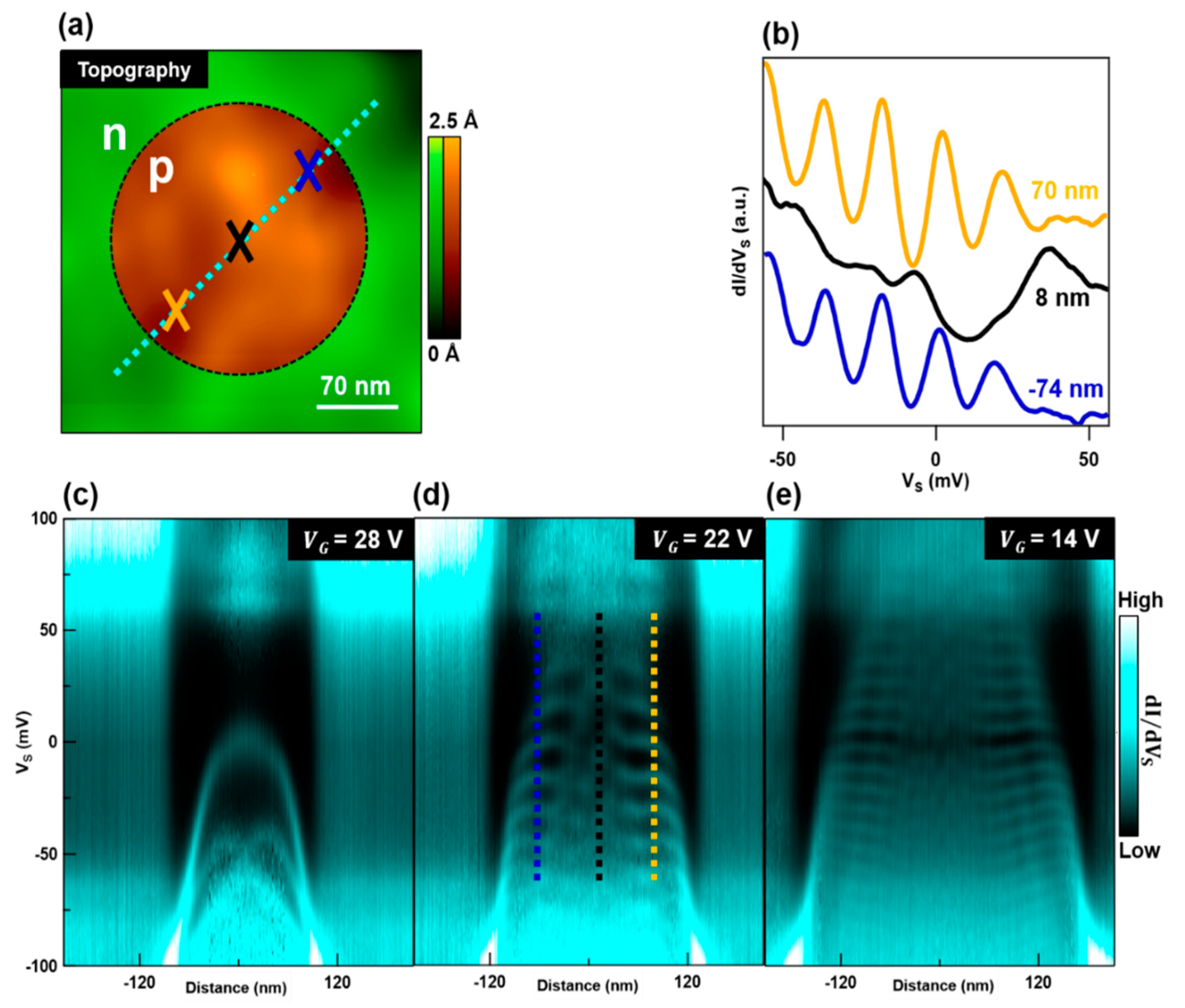
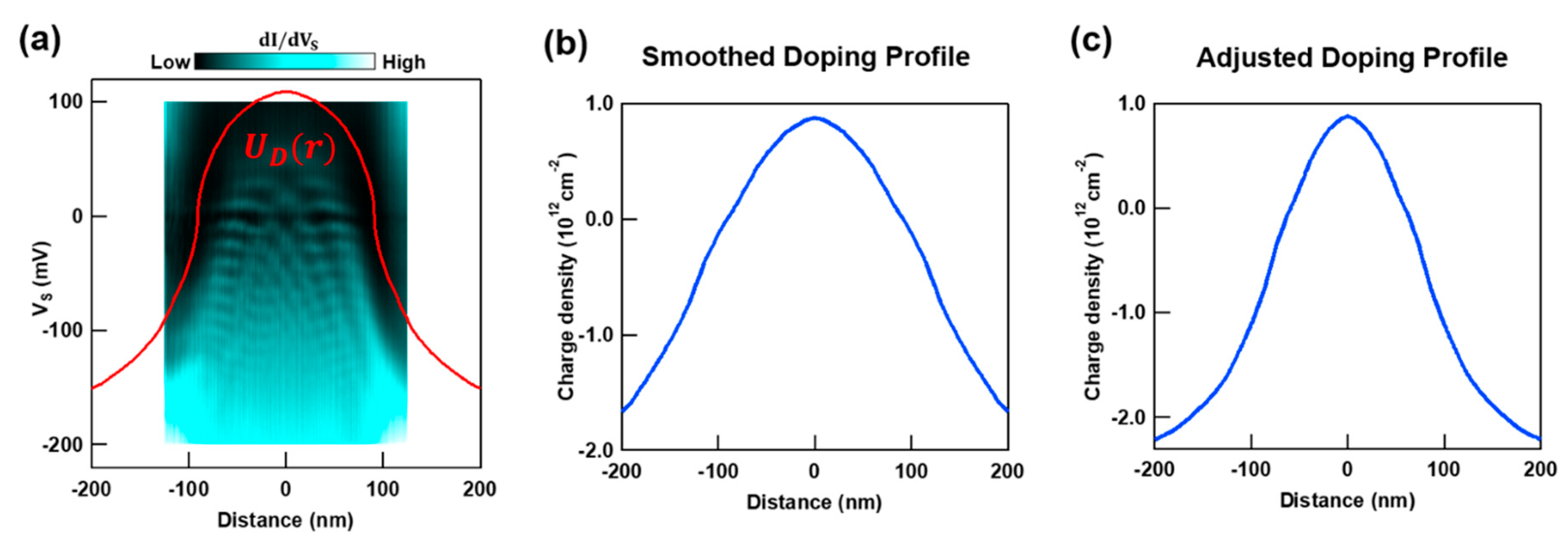
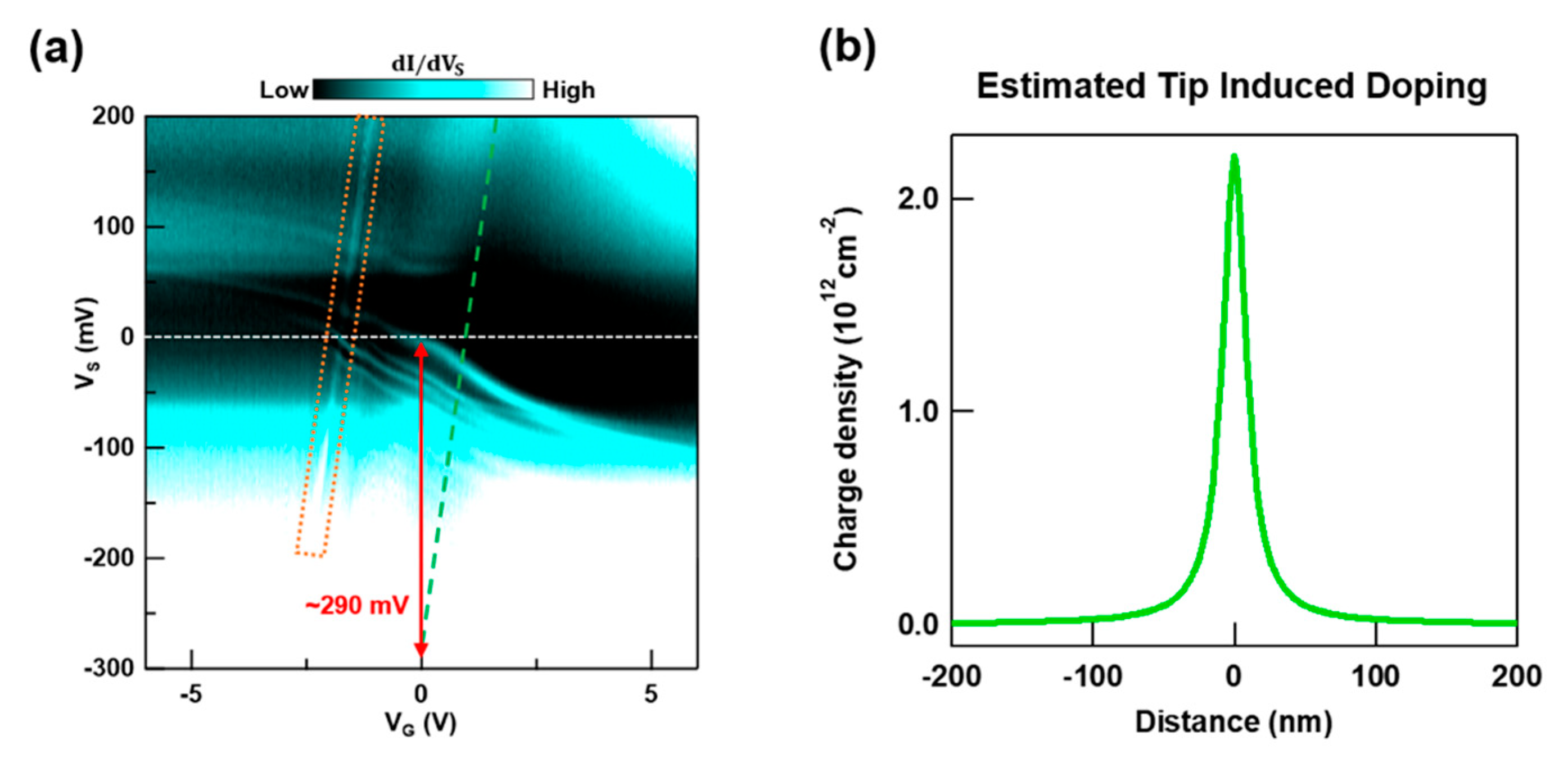
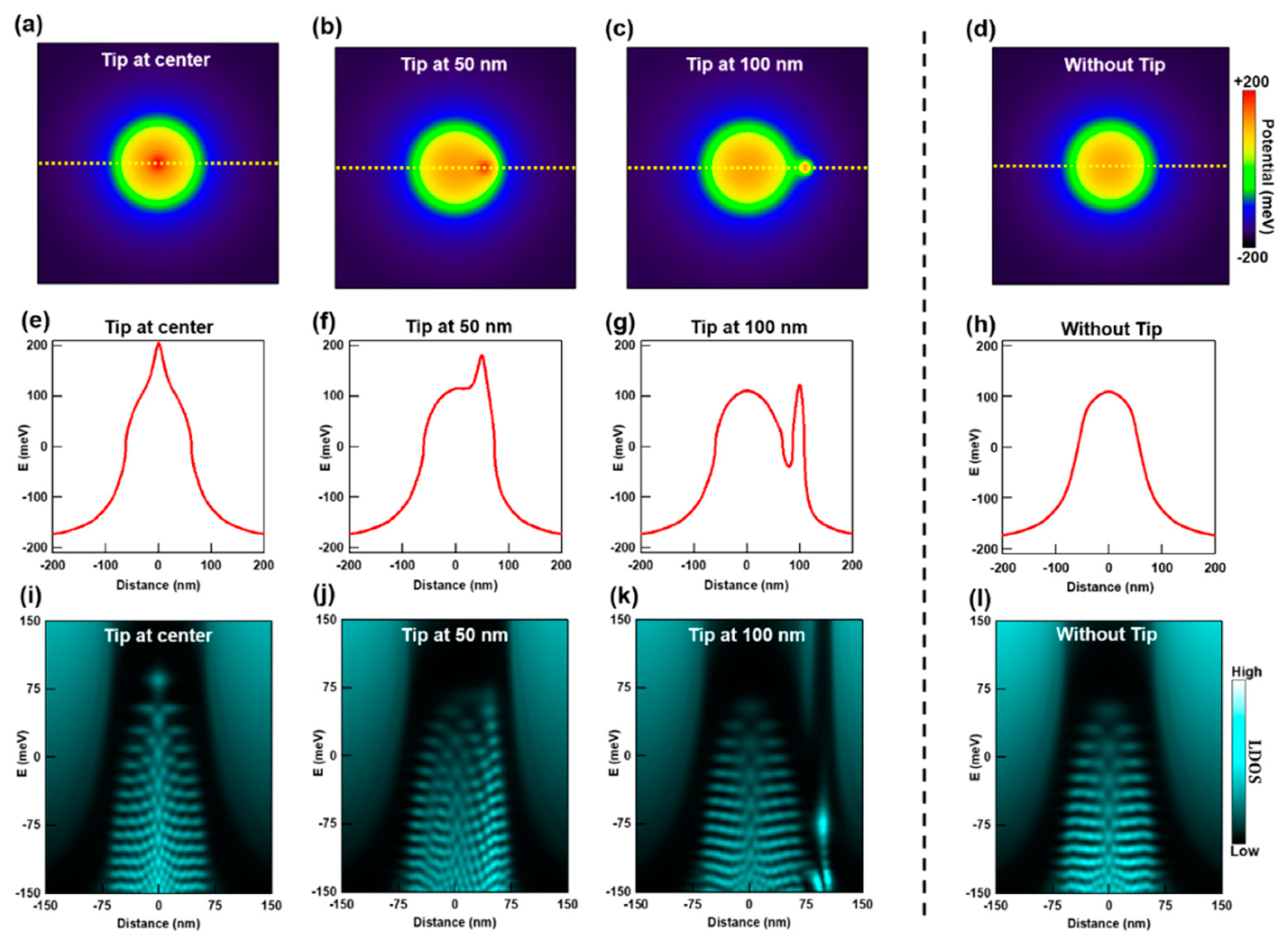
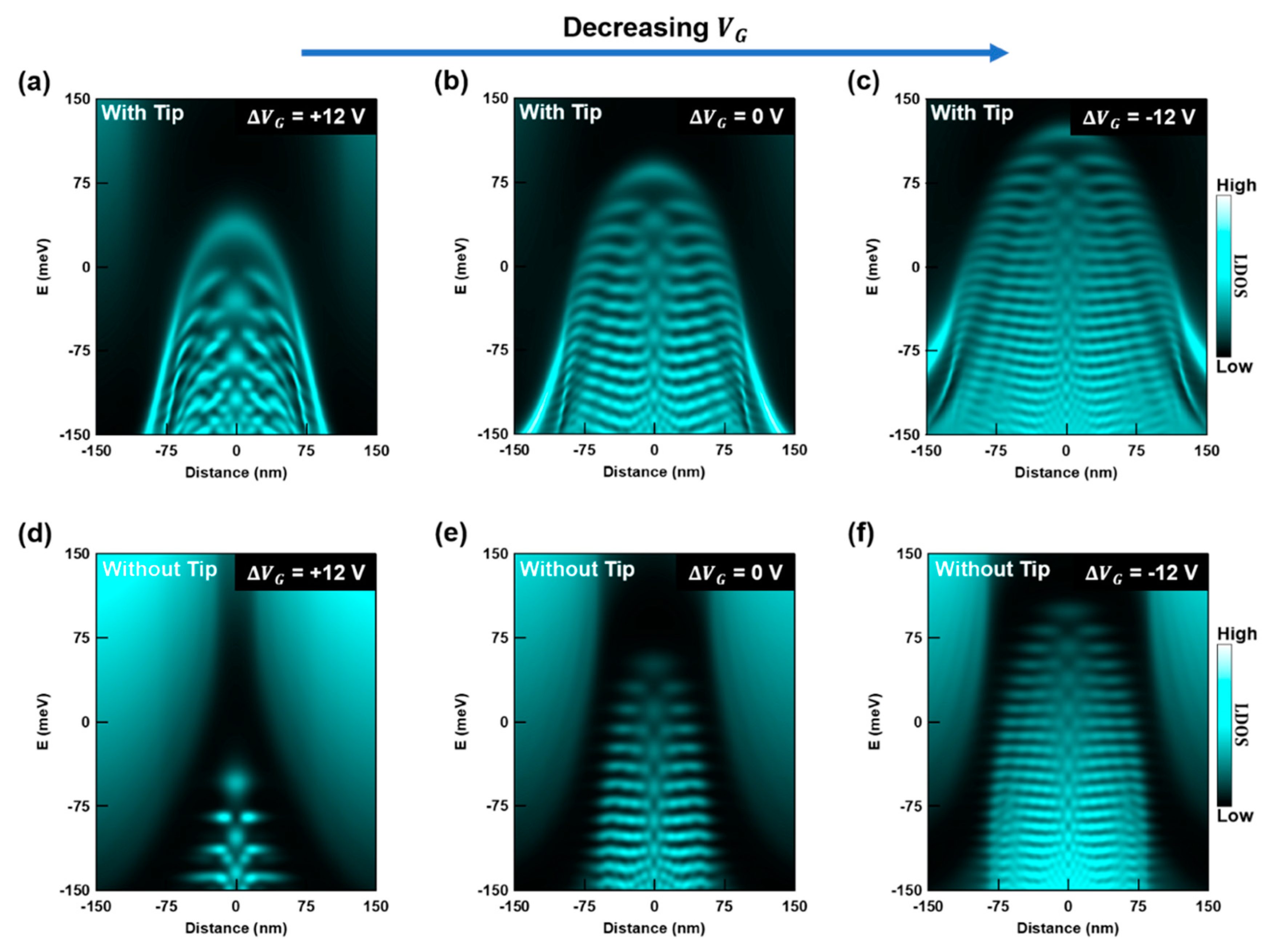
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ponomarenko, L.A.; Schedin, F.; Katsnelson, M.I.; Yang, R.; Hill, E.W.; Novoselov, K.S.; Geim, A.K. Chaotic Dirac Billiard in Graphene Quantum Dots. Science 2008, 320, 356–358. [Google Scholar] [CrossRef] [PubMed]
- Schnez, S.; Güttinger, J.; Huefner, M.; Stampfer, C.; Ensslin, K.; Ihn, T. Imaging Localized States in Graphene Nanostructures. Phys. Rev. B 2010, 82, 165445. [Google Scholar] [CrossRef]
- Todd, K.; Chou, H.T.; Amasha, S.; David, G.G. Quantum Dot Behavior in Graphene Nanoconstrictions. Nano Lett. 2009, 9, 416–421. [Google Scholar] [CrossRef]
- Han, M.Y.; Özyilmaz, B.; Zhang, Y.; Kim, P. Energy Band-Gap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef]
- Subramaniam, D.; Libisch, F.; Li, Y.; Pauly, C.; Geringer, V.; Reiter, R.; Mashoff, T.; Liebmann, M.; Burgdörfer, J.; Busse, C.; et al. Wave-Function Mapping of Graphene Quantum Dots with Soft Confinement. Phys. Rev. Lett. 2012, 108, 046801. [Google Scholar] [CrossRef] [PubMed]
- Hämäläinen, S.K.; Sun, Z.; Boneschanscher, M.P.; Uppstu, A.; Ijäs, M.; Harju, A.; Vanmaekelbergh, D.; Liljeroth, P. Quantum-Confined Electronic States in Atomically Well-Defined Graphene Nanostructures. Phys. Rev. Lett. 2011, 107, 236803. [Google Scholar] [CrossRef]
- Phark, S.H.; Borme, J.; Vanegas, A.L.; Corbetta, M.; Sander, D.; Kirschner, J. Direct Observation of Electron Confinement in Epitaxial Graphene Nanoislands. ACS Nano 2011, 5, 8162–8166. [Google Scholar] [CrossRef]
- Lu, J.; Yeo, P.S.E.; Gan, C.K.; Wu, P.; Loh, K.P. Transforming C 60 Molecules into Graphene Quantum Dots. Nat. Nanotechnol. 2011, 6, 247–252. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, D.; Shytov, A.V.; Brar, V.W.; Choi, S.; Wu, Q.; Tsai, H.Z.; Regan, W.; Zettl, A.; Kawakami, R.K.; et al. Observing Atomic Collapse Resonances in Artificial Nuclei on Graphene. Science 2013, 340, 734–737. [Google Scholar] [CrossRef]
- Jung, S.; Rutter, G.M.; Klimov, N.N.; Newell, D.B.; Calizo, I.; Hight-Walker, A.R.; Zhitenev, N.B.; Stroscio, J.A. Evolution of Microscopic Localization in Graphene in a Magnetic Field from Scattering Resonances to Quantum Dots. Nat. Phys. 2011, 7, 245–251. [Google Scholar] [CrossRef]
- Freitag, N.M.; Chizhova, L.A.; Nemes-Incze, P.; Woods, C.R.; Gorbachev, R.V.; Cao, Y.; Geim, A.K.; Novoselov, K.S.; Burgdörfer, J.; Libisch, F.; et al. Electrostatically Confined Monolayer Graphene Quantum Dots with Orbital and Valley Splittings. Nano Lett. 2016, 16, 5798–5805. [Google Scholar] [CrossRef] [PubMed]
- Freitag, N.M.; Reisch, T.; Chizhova, L.A.; Nemes-Incze, P.; Holl, C.; Woods, C.R.; Gorbachev, R.V.; Cao, Y.; Geim, A.K.; Novoselov, K.S.; et al. Large Tunable Valley Splitting in Edge-Free Graphene Quantum Dots on Boron Nitride. Nat. Nanotechnol. 2018, 13, 392–397. [Google Scholar] [CrossRef] [PubMed]
- Velasco, J.; Ju, L.; Wong, D.; Kahn, S.; Lee, J.; Tsai, H.Z.; Germany, C.; Wickenburg, S.; Lu, J.; Taniguchi, T.; et al. Nanoscale Control of Rewriteable Doping Patterns in Pristine Graphene/Boron Nitride Heterostructures. Nano Lett. 2016, 16, 1620–1625. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Wong, D.; Velasco, J.; Rodriguez-Nieva, J.F.; Kahn, S.; Tsai, H.Z.; Taniguchi, T.; Watanabe, K.; Zettl, A.; Wang, F.; et al. Imaging Electrostatically Confined Dirac Fermions in Graphene Quantum Dots. Nat. Phys. 2016, 12, 1032–1036. [Google Scholar] [CrossRef]
- Ghahari, F.; Walkup, D.; Gutiérrez, C.; Rodriguez-Nieva, J.F.; Zhao, Y.; Wyrick, J.; Natterer, F.D.; Cullen, W.G.; Watanabe, K.; Taniguchi, T.; et al. An on/off Berry Phase Switch in Circular Graphene Resonators. Science 2017, 356, 845–849. [Google Scholar] [CrossRef]
- Gutiérrez, C.; Walkup, D.; Ghahari, F.; Lewandowski, C.; Rodriguez-Nieva, J.F.; Watanabe, K.; Taniguchi, T.; Levitov, L.S.; Zhitenev, N.B.; Stroscio, J.A. Interaction-Driven Quantum Hall Wedding Cake–like Structures in Graphene Quantum Dots. Science 2018, 361, 789–794. [Google Scholar] [CrossRef]
- Zhao, Y.; Wyrick, J.; Natterer, F.D.; Rodriguez-Nieva, J.F.; Lewandowski, C.; Watanabe, K.; Taniguchi, T.; Levitov, L.S.; Zhitenev, N.B.; Stroscio, J.A. Creating and Probing Electron Whispering-Gallery Modes in Graphene. Science 2015, 348, 672–675. [Google Scholar] [CrossRef]
- Jiang, Y.; Mao, J.; Moldovan, D.; Masir, M.R.; Li, G.; Watanabe, K.; Taniguchi, T.; Peeters, F.M.; Andrei, E.Y. Tuning a Circular P-N Junction in Graphene from Quantum Confinement to Optical Guiding. Nat. Nanotechnol. 2017, 12, 1045–1049. [Google Scholar] [CrossRef]
- Zomer, P.J.; Dash, S.P.; Tombros, N.; Van Wees, B.J. A Transfer Technique for High Mobility Graphene Devices on Commercially Available Hexagonal Boron Nitride. Appl. Phys. Lett. 2011, 99, 232104. [Google Scholar] [CrossRef]
- Goossens, A.M.; Calado, V.E.; Barreiro, A.; Watanabe, K.; Taniguchi, T.; Vandersypen, L.M.K. Mechanical Cleaning of Graphene. Appl. Phys. Lett. 2012, 100, 073110. [Google Scholar] [CrossRef]
- Velasco, J.; Lee, J.; Wong, D.; Kahn, S.; Tsai, H.Z.; Costello, J.; Umeda, T.; Taniguchi, T.; Watanabe, K.; Zettl, A.; et al. Visualization and Control of Single-Electron Charging in Bilayer Graphene Quantum Dots. Nano Lett. 2018, 18, 5104–5110. [Google Scholar] [CrossRef] [PubMed]
- Tersoff, J.; Hamann, D.R. Theory of the Scanning Tunneling Microscope. Phys. Rev. B 1985, 31, 805–813. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Chiral Tunnelling and the Klein Paradox in Graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef]
- Cheianov, V.V.; Fal’ko, V.I. Selective Transmission of Dirac Electrons and Ballistic Magnetoresistance of N-p Junctions in Graphene. Phys. Rev. B 2006, 74, 041403. [Google Scholar] [CrossRef]
- Shytov, A.V.; Rudner, M.S.; Levitov, L.S. Klein Backscattering and Fabry-Pérot Interference in Graphene Heterojunctions. Phys. Rev. Lett. 2008, 101, 156804. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.S.; Fogler, M.M. Scattering of Two-Dimensional Massless Dirac Electrons by a Circular Potential Barrier. Phys. Rev. B 2014, 90, 235402. [Google Scholar] [CrossRef]
- Schulz, C.; Heinisch, R.L.; Fehske, H. Scattering of Two-Dimensional Dirac Fermions on Gate-Defined Oscillating Quantum Dots. Phys. Rev. B 2015, 91, 045130. [Google Scholar] [CrossRef]
- Chen, H.Y.; Apalkov, V.; Chakraborty, T. Fock-Darwin States of Dirac Electrons in Graphene-Based Artificial Atoms. Phys. Rev. Lett. 2007, 98, 186803. [Google Scholar] [CrossRef]
- Matulis, A.; Peeters, F.M. Quasibound States of Quantum Dots in Single and Bilayer Graphene. Phys. Rev. B 2008, 77, 115423. [Google Scholar] [CrossRef]
- Bardarson, J.H.; Titov, M.; Brouwer, P.W. Electrostatic Confinement of Electrons in an Integrable Graphene Quantum Dot. Phys. Rev. Lett. 2009, 102, 226803. [Google Scholar] [CrossRef]
- Zhang, Y.; Brar, V.W.; Girit, C.; Zettl, A.; Crommie, M.F. Origin of Spatial Charge Inhomogeneity in Graphene. Nat. Phys. 2009, 5, 722–726. [Google Scholar] [CrossRef]
- Rutter, G.M.; Jung, S.; Klimov, N.N.; Newell, D.B.; Zhitenev, N.B.; Stroscio, J.A. Microscopic Polarization in Bilayer Graphene. Nat. Phys. 2011, 7, 649–655. [Google Scholar] [CrossRef]
- LeRoy, B.J.; Kong, J.; Pahilwani, V.K.; Dekker, C.; Lemay, S.G. Three-Terminal Scanning Tunneling Spectroscopy of Suspended Carbon Nanotubes. Phys. Rev. B 2005, 72, 075413. [Google Scholar] [CrossRef]
- Chae, J.; Jung, S.; Young, A.F.; Dean, C.R.; Wang, L.; Gao, Y.; Watanabe, K.; Taniguchi, T.; Hone, J.; Shepard, K.L.; et al. Renormalization of the Graphene Dispersion Velocity Determined from Scanning Tunneling Spectroscopy. Phys. Rev. Lett. 2012, 109, 116802. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Brar, V.W.; Wang, F.; Girit, C.; Yayon, Y.; Panlasigui, M.; Zettl, A.; Crommie, M.F. Giant Phonon-Induced Conductance in Scanning Tunnelling Spectroscopy of Gate-Tunable Graphene. Nat. Phys. 2008, 4, 627–630. [Google Scholar] [CrossRef]
- Holdman, G.R.; Krebs, Z.J.; Behn, W.A.; Smith, K.J.; Watanabe, K.; Taniguchi, T.; Brar, V.W. Dynamic Band Structure and Capacitance Effects in Scanning Tunneling Spectroscopy of Bilayer Graphene. Appl. Phys. Lett. 2019, 115, 181601. [Google Scholar] [CrossRef]
- Walkup, D.; Ghahari, F.; Gutiérrez, C.; Watanabe, K.; Taniguchi, T.; Zhitenev, N.B.; Stroscio, J.A. Tuning Single-Electron Charging and Interactions between Compressible Landau Level Islands in Graphene. Phys. Rev. B 2020, 101, 035428. [Google Scholar] [CrossRef]
- Moldovan, D.; Anđelković, M.; Peeters, F. pybinding v0.9.4: A Python package for tight-binding calculations. Zenodo 2017. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quezada-López, E.A.; Ge, Z.; Taniguchi, T.; Watanabe, K.; Joucken, F.; Velasco, J., Jr. Comprehensive Electrostatic Modeling of Exposed Quantum Dots in Graphene/Hexagonal Boron Nitride Heterostructures. Nanomaterials 2020, 10, 1154. https://doi.org/10.3390/nano10061154
Quezada-López EA, Ge Z, Taniguchi T, Watanabe K, Joucken F, Velasco J Jr. Comprehensive Electrostatic Modeling of Exposed Quantum Dots in Graphene/Hexagonal Boron Nitride Heterostructures. Nanomaterials. 2020; 10(6):1154. https://doi.org/10.3390/nano10061154
Chicago/Turabian StyleQuezada-López, Eberth A., Zhehao Ge, Takashi Taniguchi, Kenji Watanabe, Frédéric Joucken, and Jairo Velasco, Jr. 2020. "Comprehensive Electrostatic Modeling of Exposed Quantum Dots in Graphene/Hexagonal Boron Nitride Heterostructures" Nanomaterials 10, no. 6: 1154. https://doi.org/10.3390/nano10061154
APA StyleQuezada-López, E. A., Ge, Z., Taniguchi, T., Watanabe, K., Joucken, F., & Velasco, J., Jr. (2020). Comprehensive Electrostatic Modeling of Exposed Quantum Dots in Graphene/Hexagonal Boron Nitride Heterostructures. Nanomaterials, 10(6), 1154. https://doi.org/10.3390/nano10061154




