Probing the Nanostructure of Neutron-Irradiated Diamond Using Raman Spectroscopy
Abstract
:1. Introduction
2. Samples and Methods
3. Experiment and Discussion
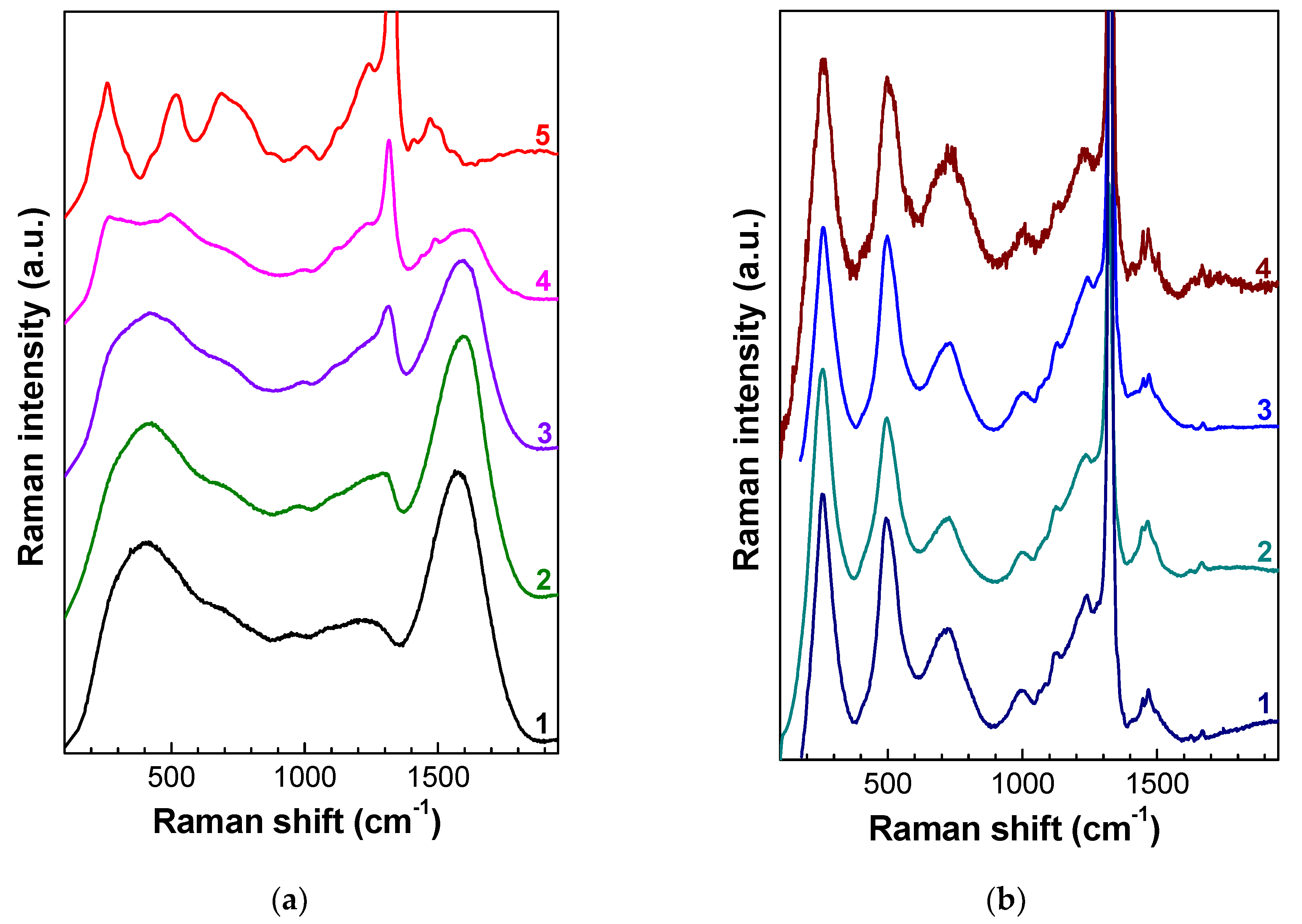
3.1. Raman Spectra of Neutron-Irradiated Diamonds
3.2. Phonon Confinement in Radiation-Damaged Crystals
3.3. Raman Spectra of Amorphous Diamond
3.4. Annealing Behavior of Fast Neutron-Irradiated Diamonds
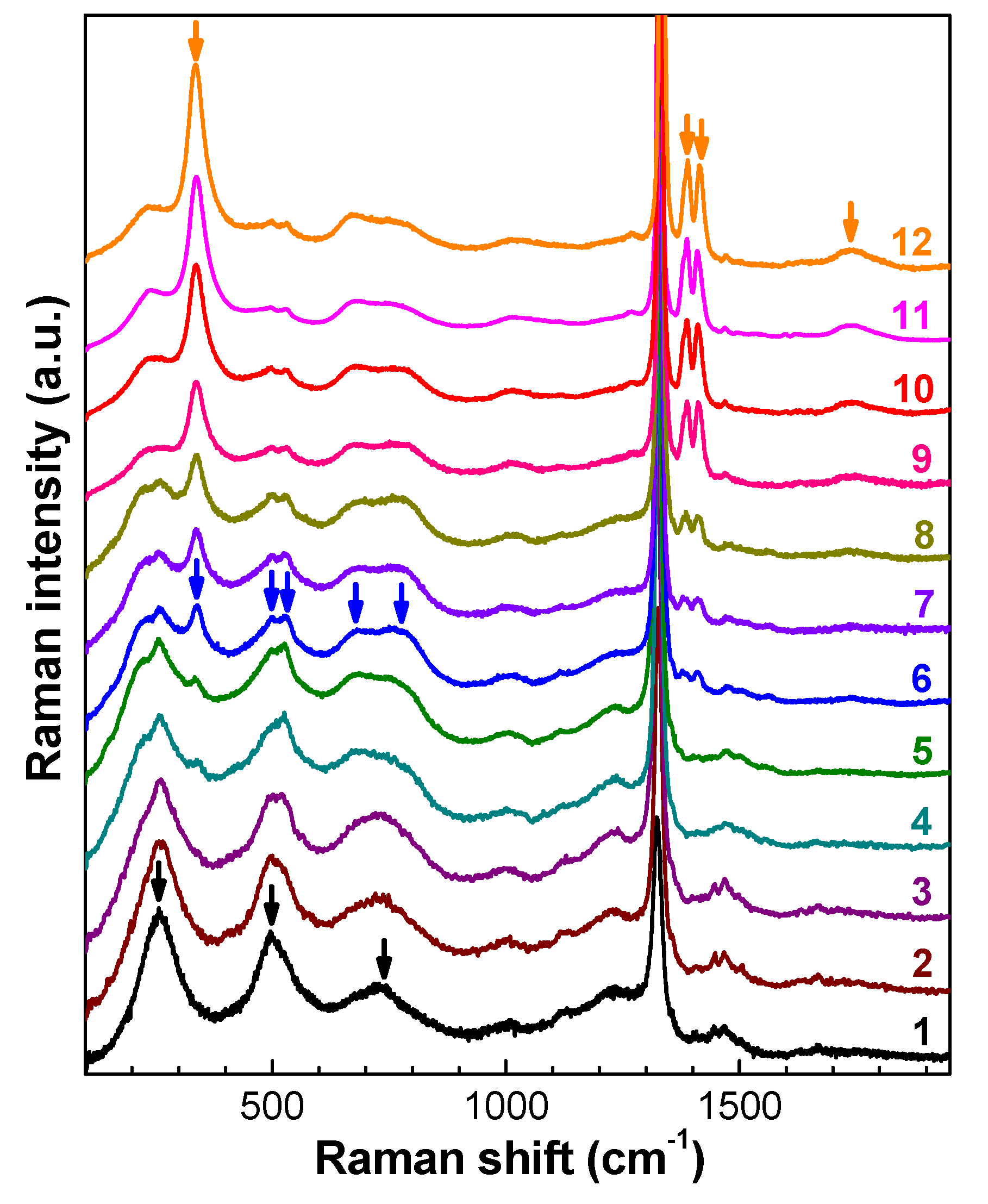
3.5. Evidence of New Raman Bands after High-Temperature Annealing of RD Diamonds
4. Conclusions
- (i)
- The shape of the Raman spectrum of diamonds irradiated by fast neutrons with a fluence of 3 × 1018 cm−2 or higher is determined by the phonon confinement effect due to the high concentration of intrinsic radiation defects. A measure of radiation damage in such samples is given by the phonon coherence length, Lph. A decrease in Lph to ~2 nm leads to the removal of the restriction that only phonons from the center of the Brillouin zone can contribute to the Raman spectra and gives rise to a band with a shape close to that of the PDOS of diamond in the Raman spectrum.
- (ii)
- The broad low-frequency band with a maximum near 400 cm−1 (the boson peak) in the Raman spectra of RD diamonds points to the formation of an amorphous sp3-phase with Lph~1 nm in RD diamonds. The boson peak persists in the Raman spectra of RD diamond up to annealing temperatures of 800–1000 °C, i.e., up to about the same temperatures at which di-interstitials (bands 1450, 1501, and 1814 cm−1) and the intrinsic defects responsible for the structural band near 1640 cm−1 are annealed. As the annealing temperature increases, the corresponding singularities in the Raman spectra are monotonically shifted to higher frequencies and approach the position of the bands in the PDOS spectra of diamond that correspond to the frequencies of optical and acoustic phonons at the singular points of the Brillouin zone.
- (iii)
- The fact that the Raman spectra of RD diamonds contain both the diamond and boson peaks confirms the hypothesis on the two-phase microstructure of RD diamond, in which nanosized amorphous regions are separated by crystalline regions with radiation defects and stabilized by the internal pressure.
- (iv)
- Annealing at high temperatures does not lead to the complete recrystallization of the diamond lattice. In the crystalline diamond phase, radiation defects represented in the Raman spectra by three groups of bands (first group = 260, 495, and 730 cm−1; second group = 230, 500, 530, 685, and 760 cm−1; and third group = 335, 1390, 1415, and 1740 cm−1), whose relative intensities synchronously change under annealing, experience restructuring during annealing. The maximum frequencies and FWHM of these bands are almost insensitive to their intensity, degree of RD, and the defect–impurity composition of the original diamond, and the bands themselves are attributable to vibrations of extended defects, which are stable in RD diamonds at least up to a temperature of 1700 °C.
Author Contributions
Funding
Conflicts of Interest
References
- Zamboni, I.; Pastuović, Ž.; Jakšić, M. Radiation hardness of single crystal CVD diamond detector tested with MeV energy ions. Diam. Relat. Mater. 2013, 31, 65–71. [Google Scholar] [CrossRef]
- Olivero, P.; Amato, G.; Bellotti, F.; Budnyk, O.; Colombo, E.; Jakšić, M.; Manfredotti, C.; Pastuović, Ž.; Picollo, F.; Skukan, N.; et al. Direct fabrication of three-dimensional buried conductive channels in single crystal diamond with ion microbeam induced graphitization. Diam. Relat. Mater. 2009, 18, 870–876. [Google Scholar] [CrossRef] [Green Version]
- Seki, Y.; Hoshino, Y.; Nakata, J. Remarkable p-type activation of heavily doped diamond accomplished by boron ion implantation at room temperature and subsequent annealing at relatively low temperatures of 1150 and 1300 °C. Appl. Phys. Lett. 2019, 115, 072103. [Google Scholar] [CrossRef]
- Dam, S.B.; Walsh, M.; Degen, M.J.; Bersin, E.; Mouradian, S.L.; Galiullin, A.; Ruf, M.; IJspeert, M.; Taminiau, T.H.; Hanson, R.; et al. Optical coherence of diamond nitrogen-vacancy centers formed by ion implantation and annealing. Phys. Rev. B 2009, 99, 161203. [Google Scholar]
- Orwa, J.O.; Aharonovich, I.; Jelezko, F.; Balasubramanian, G.; Balog, P.; Markham, M.; Twitchen, D.J.; Greentree, A.D.; Prawer, S. Nickel related optical centres in diamond created by ion implantation. J. Appl. Phys. 2010, 107, 093512. [Google Scholar] [CrossRef] [Green Version]
- Lühmann, T.; John, R.; Wunderlich, R.; Meijer, J.; Pezzagna, S. Coulomb-driven single defect engineering for scalable qubits and spin sensors in diamond. Nature Commun. 2019, 10, 4956. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.M.; Meynell, S.A.; Bleszynski Jayich, A.C.; Meijer, J. Colour centre generation in diamond for quantum technologies. Nanophotonics 2019, 8, 11. [Google Scholar] [CrossRef]
- Alghannam, F.; Hemmer, P. Engineering of shallow layers of nitrogen vacancy colour centres in diamond using plasma immersion ion implantation. Scientific Rep. 2019, 9, 5870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKenzie, W.R.; Quadir, M.Z.; Gass, M.H.; Munro, P.R. Focused ion beam implantation of diamond. Diam. Relat. Mater. 2011, 20, 1125–1128. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Steeds, J.W.; Li, Z.; Wang, H. Annealing and lateral migration of defects in IIa diamond created by near-threshold electron irradiation. Appl. Phys. Lett. 2017, 110, 152101. [Google Scholar] [CrossRef]
- Hei, L.; Zhao, Y.; Wei, J.; Liu, J.; Li, C.; Lü, F.X. Optical characterization of single-crystal diamond grown by DC arc plasma jet CVD. Int. J. Miner. Metall. Mater. 2017, 24, 1424–1429. [Google Scholar] [CrossRef]
- Mainwood, A. CVD diamond particle detectors. Diam. Relat. Mater. 1998, 7, 504–509. [Google Scholar] [CrossRef]
- Poklonskaya, O.N.; Vyrko, S.A.; Khomich, A.A.; Averin, A.A.; Khomich, A.V.; Khmelnitsky, R.A.; Poklonski, N.A. Raman scattering in natural diamond crystals implanted with high-energy ions and irradiated with fast neutrons. J. Appl. Spectrosc. 2014, 81, 969–977. [Google Scholar] [CrossRef]
- Poklonskaya, O.N.; Khomich, A.A. Raman scattering in a diamond crystal implanted by high-energy nickel ions. J. Appl. Spectrosc. 2013, 80, 715–720. [Google Scholar] [CrossRef]
- Ralchenko, V.G.; Pimenov, S.M.; Konov, V.I.; Khomich, A.V.; Saveliev, A.; Popovich, A.F.; Vlasov, I.I.; Zavedeev, E.; Bozhko, A.; Loubnin, E.; et al. Nitrogenated nanocrystalline diamond films: Thermal and optical properties. Diam. Relat. Mater. 2007, 16, 2067–2073. [Google Scholar] [CrossRef]
- Sukhadolau, A.V.; Ivakin, E.V.; Ralchenko, V.G.; Khomich, A.V.; Vlasov, A.V.; Popovich, A.F. Thermal conductivity of CVD diamond at elevated temperatures. Diam. Relat. Mater. 2005, 14, 589–593. [Google Scholar] [CrossRef]
- Nistor, S.V.; Stefan, M.; Ralchenko, V.G.; Khomich, A.V.; Schoemaker, D. Nitrogen and hydrogen in thick diamond films grown by microwave plasma enhanced chemical vapor deposition at variable H2 flow rates. J. Appl. Phys. 2000, 87, 8741–8746. [Google Scholar] [CrossRef]
- Khomich, A.A.; Dzeraviaha, A.N.; Poklonskaya, O.N.; Khomich, A.V.; Khmelnitsky, R.A.; Poklonski, N.A.; Ralchenko, V.G. Effect of neutron irradiation on the hydrogen state in CVD diamond films. J. Phys.: Conf. Ser. 2018, 1135, 012019. [Google Scholar] [CrossRef]
- Karkin, A.E.; Voronin, V.I.; Berger, I.F.; Kazantsev, V.A.; Ponosov, Y.S.; Ralchenko, V.G.; Konov, V.I.; Goshchitskii, B.N. Neutron irradiation effects in chemical-vapor-deposited diamond. Phys. Rev. B 2008, 78, 033204. [Google Scholar] [CrossRef]
- Nikolaenko, V.A.; Gordeev, V.G. Diamond amorphization in neutron irradiation. Radiat. Eff. Def. Sol. 1996, 139, 183–188. [Google Scholar] [CrossRef]
- Orwa, J.O.; Nugent, K.W.; Jamieson, D.N.; Prawer, S. Raman investigation of damage caused by deep ion implantation in diamond. Phys. Rev. B. 2000, 62, 5461–5472. [Google Scholar] [CrossRef]
- Khomich, A.A.; Averin, A.A.; Poklonskaya, O.N.; Bokova-Sirosh, S.N.; Dzeraviaha, A.N.; Khmelnitsky, R.A.; Vlasov, I.I.; Shenderova, O.; Poklonski, N.A.; Khomich, A.V. Features of the 1640 cm-1 band in the Raman spectra of radiation-damaged and nano-sized diamonds. J. Phys. Conf. Ser. 2019, 1400, 044017. [Google Scholar] [CrossRef]
- Zaitsev, A.M. Optical Properties of Diamond. A Data Handbook; Springer: Berlin, Germany, 2001. [Google Scholar]
- Klein, C.A.; Hartnett, T.M.; Robinson, J. Critical point phonon frequencies of diamond. Phys. Rev. B 1992, 45, 854–863. [Google Scholar] [CrossRef] [PubMed]
- Nazare, M.H.; Neves, A.J. Properties, Growth and applications of diamond; The Institution of Electrical Engineers: London, UK, 2011. [Google Scholar]
- Bosak, A.; Krisch, M. Phonon density of states probed by inelastic x-ray scattering. Phys. Rev. B 2005, 72, 224305. [Google Scholar] [CrossRef]
- Khomich, A.V.; Khmelnitskii, R.A.; Hu, X.J.; Khomich, A.A.; Popovich, A.F.; Vlasov, I.I.; Dravin, V.A.; Chen, Y.G.; Karkin, A.E.; Ralchenko, V.G. Radiation damage effects on optical, electrical, and thermophysical properties of CVD diamond films. J. Appl. Spectrosc. 2013, 80, 707–714. [Google Scholar] [CrossRef]
- Casari, C.S.; Li Bassi, A.; Baserga, A.; Ravagnan, L.; Piseri, P.; Lenardi, C.; Tommasini, M.; Milani, A.; Fazzi, D.; Bottani, C.E.; et al. Low-frequency modes in the Raman spectrum of sp-sp2 nanostructured carbon. Phys. Rev. B 2008, 77, 195444. [Google Scholar] [CrossRef] [Green Version]
- Nikolaenko, V.A.; Krasikov, E.A. Effect of reactor radiation intensity on crystal lattice expansion in diamond. Atom. Energy 2014, 115, 267–276. [Google Scholar] [CrossRef]
- Broadway, D.A.; Johnson, B.C.; Barson, M.S.J.; Lillie, S.E.; Dontschuk, N.; McCloskey, D.J.; Tsai, A.; Teraji, T.; Simpson, D.A.; Stacey, A.; et al. Microscopic imaging of the stress tensor in diamond using in situ quantum sensors. Nano Lett. 2019, 19, 4543–4550. [Google Scholar] [CrossRef]
- Bosia, F.; Calusi, S.; Giuntini, L.; Lagomarsino, S.; Giudice, A.L.; Massi, M.; Olivero, P.; Picollo, F.; Sciortino, S.; Sordini, A.; et al. Finite element analysis of ion-implanted diamond surface swelling. Nucl. Instr. Meth. Phys. Res. B 2010, 268, 2991–2995. [Google Scholar] [CrossRef] [Green Version]
- Khmelnitsky, R.A.; Dravin, V.A.; Tal, A.A.; Zavedeev, E.V.; Khomich, A.A.; Khomich, A.V.; Alekseev, A.A.; Terentiev, S.A. Damage accumulation in diamond during ion implantation. J. Mater. Res. 2015, 30, 1583–1592. [Google Scholar] [CrossRef]
- Koyanagi, T.; Katoh, Y.; Lance, M.J. Raman spectroscopy of neutron irradiated silicon carbide: Correlation among Raman spectra, swelling, and irradiation temperature. J. Raman Spectr. 2018, 49, 1686–1692. [Google Scholar] [CrossRef]
- Newton, M.E.; Campbell, B.A.; Twitchen, D.J.; Baker, J.M.; Anthony, T.R. Recombination-enhanced diffusion of selfinterstitial atoms and vacancy-interstitial recombination in diamond. Diam. Relat. Mater. 2002, 11, 618–622. [Google Scholar] [CrossRef]
- Hines, R.L. Radiation Damage of Diamond by 20-keV Carbon Ions. Phys. Rev. 1965, 138, 1747–1751. [Google Scholar] [CrossRef]
- Prawer, S.; Kalish, R. Ion-beam-induced transformation of diamond. Phys. Rev. B 1995, 51, 15711–15722. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM – The stopping and range of ions in matter. Nucl. Instrum. Methods B 2010, 268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Khomich, A.; Khmelnitskiy, R.; Dravin, V.; Gippius, A.; Zavedeev, E.; Vlasov, I. Radiation damage in diamonds subjected to helium implantation. Phys. Sol. St. 2007, 49, 1661–1665. [Google Scholar] [CrossRef]
- Khmelnitsky, R.A.; Dravin, V.A.; Tal, A.A.; Latushko, M.I.; Khomich, A.A.; Khomich, A.V.; Trushin, A.S.; Alekseev, A.A.; Terentiev, S.A. Mechanical stresses and amorphization of ion-implanted diamond. Nucl. Instr. Meth. Phys. Res. B 2013, 304, 5–10. [Google Scholar] [CrossRef]
- Khasawinah, S.A.; Popovici, G.; Farmer, J.; Sung, T.; Prelas, M.A.; Chamberlain, J.; White, H. Neutron irradiation and annealing of 10B doped chemical vapor deposited diamond films. J. Mater. Res. 1995, 10, 2523. [Google Scholar] [CrossRef]
- Prawer, S.; Nugent, K.W.; Jamieson, D.N. The Raman spectrum of amorphous diamond. DRM 1998, 7, 106–110. [Google Scholar] [CrossRef]
- Wang, C.Z.; Ho, K.M. Structure, dynamics, and electronic properties of diamondlike amorphous carbon. Phys. Rev. Lett. 1993, 71, 1184. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Montroll, E.W.; Weiss, G.H. Theory of Lattice Dynamics in the Harmonic Approximation; Academic: New York, NY, USA, 1963. [Google Scholar]
- Richter, H.; Wang, Z.P.; Ley, L. The one phonon Raman spectrum in microcrystalline silicon. Sol. Stat. Com. 1981, 39, 625–629. [Google Scholar] [CrossRef]
- Osswald, S.; Mochalin, V.N.; Havel, M.; Yushin, G.; Gogotsi, Y. Phonon confinement effects in the Raman spectrum of nanodiamond. Phys. Rev. B 2009, 80, 075419. [Google Scholar] [CrossRef]
- Ager, J.W.; Veirs, D.K.; Rosenblatt, G.M. Spatially resolved Raman studies of diamond films grown by chemical vapor deposition. Phys. Rev. B 1991, 43, 6491–6499. [Google Scholar] [CrossRef] [PubMed]
- Shtyrkov, E.I.; Klimovitskii, A.; Hartog, H.W.D.; Vainshtein, D.I. Raman scattering and quantum confinement in heavily electron-irradiated alkali halides. J. Phys. Cond. Mat. 2002, 14, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Saikiran, V.; Srinivasa Rao, N.; Devaraju, G.; Chang, G.S.; Pathak, A.P. Ion beam irradiation effects on Genanocrystals synthesized by using RF sputtering followed by RTA. Nucl. Instr. Meth. Phys. Res. B 2013, 315, 161–164. [Google Scholar] [CrossRef]
- Mishra, S.; Kabiraj, D.; Roya, A.; Ghosh, S. Effect of high-energy light-ion irradiation on Si-GaAs and GaAs:Cr as observed by Raman spectroscopy. J. Raman Spectrosc. 2012, 43, 344–350. [Google Scholar] [CrossRef]
- Liang, J.H.; Wu, C.H. Characterization of damage behavior induced by low-temperature BGe molecular ion implantation in silicon. Vacuum 2013, 89, 86–89. [Google Scholar] [CrossRef]
- Mignuzzi, S.; Pollard, A.J.; Bonini, N.; Brennan, B.; Gilmore, I.S.; Pimenta, M.A.; Richards, D.; Roy, D. Effect of disorder on Raman scattering of single-layer MoS2. Phys. Rev. B 2015, 91, 195411. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.F.; Huang, L.; Zhu, W.; Ruan, Y.F. Raman scattering of neutron irradiated 6H-SiC. Sol. Stat. Com. 2012, 152, 887–890. [Google Scholar] [CrossRef]
- Prawer, S.; Nugent, K.W.; Jamieson, D.N.; Orwa, J.O.; Bursill, L.A.; Peng, J.L. The Raman spectrum of nanocrystalline diamond. Chem. Phys. Lett. 2000, 332, 93–97. [Google Scholar] [CrossRef]
- Ovsyuk, N.N.; Novikov, V.N. The influence of the degree of disorder of amorphous solids on the intensity of light scattering by acoustic phonons. J. Exper. Theor. Phys. 1998, 114, 315–321. [Google Scholar] [CrossRef]
- Grigera, T.S.; Martín-Mayor, V.; Parisi, G.; Verrocchio, P. Phonon interpretation of the ’boson peak’ in supercooled liquids. Nature 2003, 422, 289–292. [Google Scholar] [CrossRef]
- Klinger, M.I.; Kosevich, A.M. Soft-mode-dynamics model of acoustic-like high-frequency excitations in boson-peak spectra of glasses. Phys. Lett. A 2001, 280, 365–370. [Google Scholar] [CrossRef]
- Parshin, D.A.; Schober, H.R.; Gurevich, V.L. Vibrational instability, two-level systems, and the boson peak in glasses. Phys. Rev. B 2007, 76, 064206. [Google Scholar] [CrossRef] [Green Version]
- Chumakov, A.I.; Monaco, G.; Monaco, A.; Crichton, W.A.; Bosak, A.; Rüffer, R.; Meyer, A.; Kargl, F.; Comez, L.; Fioretto, D.; et al. Equivalence of the boson peak in glasses to the transverse acoustic van Hove singularity in crystals. Phys. Rev. Lett. 2011, 106, 225501. [Google Scholar] [CrossRef] [PubMed]
- Zorn, R. Viewpoint: The boson peak demystified? Physics 2011, 4, 44. [Google Scholar] [CrossRef] [Green Version]
- Chumakov, A.I.; Monaco, G.; Han, X.; Xi, L.; Bosak, A.; Paolasini, L.; Chernyshov, D.; Dyadkin, V. Relation between the boson peak in glasses and van Hove singularity in crystals. Philos. Mag. 2016, 96, 743–753. [Google Scholar] [CrossRef]
- Niu, L.; Zhu, J.; Gao, W.; Liu, A.; Han, X.; Du, S. First-principles calculation of vibrational Raman spectra of tetrahedral amorphous carbon. Phys. B Cond. Mat. 2008, 403, 3559–3562. [Google Scholar] [CrossRef]
- Sopu, D.; Kotakoski, J.; Albe, K. Finite-size effects in the phonon density of states of nanostructured germanium: A comparative study of nanoparticles, nanocrystals, nanoglasses, and bulk phases. Phys. Rev. B 2011, 83, 245416. [Google Scholar] [CrossRef]
- Sopu, D.; Albe, K.; Ritter, Y.; Gleiter, H. From nanoglasses to bulk massive glasses. Appl. Phys. Lett. 2009, 94, 191911. [Google Scholar] [CrossRef]
- Araujo, L.L.; Giulian, R.; Sprouster, D.J.; Schnohr, C.S.; Llewellyn, D.J.; Kluth, P.; Cookson, D.J.; Foran, G.J.; Ridgway, M.C. Size-dependent characterization of embedded Ge nanocrystals: Structural and thermal properties. Phys. Rev. B 2008, 78, 094112. [Google Scholar] [CrossRef] [Green Version]
- Korepanov, V.I.; Witek, H.; Okajima, H.; Ōsawa, E.; Hamaguchi, H. Three-dimensional model for phonon confinement in small particles: Quantitative band shape analysis of size-dependent Raman spectra of nanodiamonds. J. Chem. Phys. 2014, 140, 041107. [Google Scholar] [CrossRef] [PubMed]
- Prawer, S.; Rosenblum, I.; Orwa, J.O.; Adler, J. Identification of the point defects in diamond as measured by Raman spectroscopy: Comparison between experiment and computation. Chem. Phys. Lett. 2004, 390, 458–461. [Google Scholar] [CrossRef]
- Woods, G.S. Infrared absorption studies of the annealing of irradiated diamonds. Philos. Mag. B 1984, 50, 673–688. [Google Scholar] [CrossRef]
- Lin-Chung, P.J. Local vibrational modes of impurities in diamond. Phys. Rev. B 1994, 50, 16905–16913. [Google Scholar] [CrossRef]
- Agulló-Rueda, F.; Gordillo, N.; Ynsa, M.D.; Maira, A.; Cañas, J.; Ramos, M.A. Lattice damage in 9-MeV-carbon irradiated diamond and its recovery after annealing. Carbon 2017, 123, 334–343. [Google Scholar] [CrossRef] [Green Version]
- Sansone, G.; Salustro, S.; Noël, Y.; Maschio, L.; Mackrodt, W.C.; Dovesi, R. Looking for sp2 carbon atoms in diamond: A quantum mechanical study of interacting vacancies. Theor. Chem. Accounts 2018, 137, 29. [Google Scholar] [CrossRef]
- DeLaPierre, M.; Orlando, R.; Maschio, L.; Doll, K.; Ugliengo, P.; Dovesi, R. Performance of six functionals (LDA, PBE, PBESOL, B3LYP, PBE0, and WC1LYP) in the simulation of vibrational and dielectric properties of crystalline compounds. The case of forsterite Mg2SiO4. J. Comput. Chem. 2011, 32, 1775–1784. [Google Scholar] [CrossRef] [Green Version]
- Goss, J.P.; Coomer, B.J.; Jones, R.; Shaw, T.D.; Briddon, P.R.; Rayson, M.; Öberg, S. Self-interstitial aggregation in diamond. Phys. Rev. B 2001, 63, 195208. [Google Scholar] [CrossRef] [Green Version]
- Blank, V.D.; Aksenenkov, V.V.; Popov, M.Y.; Perfilov, S.A.; Kulnitskiy, B.A.; Tatyanin, Y.V.; Zhigalina, O.M.; Mavrin, B.N.; Denisov, V.N.; Ivlev, A.N.; et al. A new carbon structure formed at MeV neutron irradiation of diamond: Structural and spectroscopic investigations. Diam. Relat. Mater. 1999, 8, 1285–1290. [Google Scholar] [CrossRef]
- Popov, M. Stress-induced phase transitions in diamond. High Pressure Res. 2010, 30, 670–678. [Google Scholar] [CrossRef]
- Khmelnitsky, R.A.; Gippius, A.A. Transformation of diamond to graphite under heat treatment at low pressure. Phase Trans. 2014, 87, 175–192. [Google Scholar] [CrossRef]
- Khomich, A.A.; Khmelnitskii, R.A.; Poklonskaya, O.N.; Averin, A.A.; Bokova-Sirosh, S.N.; Poklonski, N.A.; Ralchenko, V.G.; Khomich, A.V. Photoluminescence Spectra of the 580-nm Center in Irradiated Diamonds. J. Appl. Spectrosc. 2019, 86, 597–605. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.C.; Robertson, J. Raman spectroscopy of amorphous, nanostructured, diamond-like carbon, and nanodiamond. Phil. Trans. R. Soc. Lond. A 2004, 362, 2477–2512. [Google Scholar] [CrossRef]
- Fairchild, B.A.; Rubanov, S.; Lau, D.W.M.; Robinson, M.; Suarez-Martinez, I.; Marks, N.; Greentree, A.D.; McCulloch, D.; Prawer, S. Mechanism for the amorphisation of diamond. Adv. Mater. 2012, 24, 2024–2029. [Google Scholar]
- Deslandes, A.; Guenette, M.C.; Belay, K.; Elliman, R.G.; Karatchevtseva, I.; Thomsen, L.; Riley, D.P.; Lumpkin, G.R. Diamond structure recovery during ion irradiation at elevated temperatures. Nucl. Instr. Meth. Phys. Res. B 2015, 365, 331–335. [Google Scholar] [CrossRef]
- Nshingabigwi, E.K.; Derry, T.E.; Naidoo, S.R.; Neethling, J.H.; Olivier, E.J.; O’Connell, J.H.; Levitt, C.M. Electron microscopy profiling of ion implantation damage in diamond: Dependence on fluence and annealing. Diam. Relat. Mater. 2014, 49, 1–8. [Google Scholar] [CrossRef]
- Hickey, D.P.; Jones, K.S.; Elliman, R.G. Amorphization and graphitization of single-crystal diamond—A transmission electron microscopy study. Diam. Relat. Mater. 2009, 18, 1353–1359. [Google Scholar] [CrossRef]
- Prins, J.F. Using ion implantation to dope diamond — an update on selected issues. Diam. Relat. Mater. 2001, 10, 1756–1764. [Google Scholar] [CrossRef]
- Salisbury, I.G.; Loretto, M.H. {113} Loops in electron-irradiated silicon. Philos. Mag. A 1979, 39, 317–323. [Google Scholar] [CrossRef]
- Jones, K.S.; Prussin, S.; Weber, E.R. A systematic analysis of defects in ion-implanted silicon. Appl. Phys. A-Mater. Sci. Proces. 1988, 45, 1–34. [Google Scholar] [CrossRef]
- Pasemann, M.; Hoehl, D.; Aseev, A.L.; Pchelyakov, O.P. Analysis of rod-like defects in silicon and germanium by means of high-resolution electron microscopy. Phys. Stat. Sol. A 1983, 80, 135–139. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khomich, A.A.; Khmelnitsky, R.A.; Khomich, A.V. Probing the Nanostructure of Neutron-Irradiated Diamond Using Raman Spectroscopy. Nanomaterials 2020, 10, 1166. https://doi.org/10.3390/nano10061166
Khomich AA, Khmelnitsky RA, Khomich AV. Probing the Nanostructure of Neutron-Irradiated Diamond Using Raman Spectroscopy. Nanomaterials. 2020; 10(6):1166. https://doi.org/10.3390/nano10061166
Chicago/Turabian StyleKhomich, Andrey A., Roman A. Khmelnitsky, and Alexander V. Khomich. 2020. "Probing the Nanostructure of Neutron-Irradiated Diamond Using Raman Spectroscopy" Nanomaterials 10, no. 6: 1166. https://doi.org/10.3390/nano10061166
APA StyleKhomich, A. A., Khmelnitsky, R. A., & Khomich, A. V. (2020). Probing the Nanostructure of Neutron-Irradiated Diamond Using Raman Spectroscopy. Nanomaterials, 10(6), 1166. https://doi.org/10.3390/nano10061166




