Magnetocrystalline and Surface Anisotropy in CoFe2O4 Nanoparticles
Abstract
1. Introduction
2. Materials and Methods
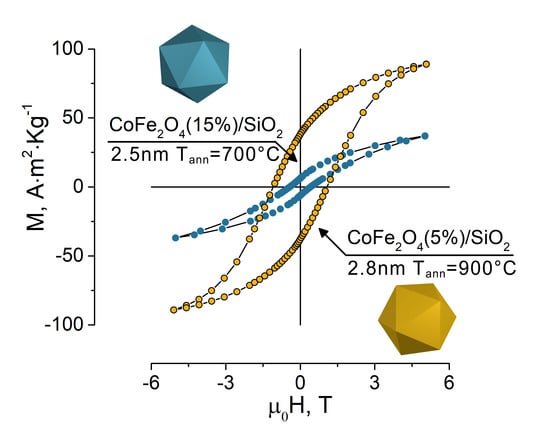
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gomes, J.D.A.; Sousa, M.H.; Tourinho, F.A.; Aquino, R.; Da Silva, G.J.; Depeyrot, J.; Dubois, E.; Perzynski, R. Synthesis of core-shell ferrite nanoparticles for ferrofluids: Chemical and magnetic analysis. J. Phys. Chem. C 2008, 112, 6220–6227. [Google Scholar] [CrossRef]
- Pardavi-Horvath, M. Microwave applications of soft ferrites. J. Magn. Magn. Mater. 2000, 216, 171–183. [Google Scholar] [CrossRef]
- Song, G.; Kenney, M.; Chen, Y.S.; Zheng, X.; Deng, Y.; Chen, Z.; Wang, S.X.; Gambhir, S.S.; Dai, H.; Rao, J. Carbon-coated FeCo nanoparticles as sensitive magnetic-particle-imaging tracers with photothermal and magnetothermal properties. Nat. Biomed. Eng. 2020, 4, 325–334. [Google Scholar] [CrossRef]
- Cardoso, V.F.; Francesko, A.; Ribeiro, C.; Bañobre-López, M.; Martins, P.; Lanceros-Mendez, S. Advances in Magnetic Nanoparticles for Biomedical Applications. Adv. Healthc. Mater. 2018, 7, 1700845. [Google Scholar] [CrossRef] [PubMed]
- Waag, F.; Gökce, B.; Kalapu, C.; Bendt, G.; Salamon, S.; Landers, J.; Hagemann, U.; Heidelmann, M.; Schulz, S.; Wende, H.; et al. Adjusting the catalytic properties of cobalt ferrite nanoparticles by pulsed laser fragmentation in water with defined energy dose. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rizzuti, A.; Dassisti, M.; Mastrorilli, P.; Sportelli, M.C.; Cioffi, N.; Picca, R.A.; Agostinelli, E.; Varvaro, G.; Caliandro, R. Shape-control by microwave-assisted hydrothermal method for the synthesis of magnetite nanoparticles using organic additives. J. Nanoparticle Res. 2015, 17, 1–16. [Google Scholar] [CrossRef]
- da Silva, F.G.; Depeyrot, J.; Campos, A.F.C.; Aquino, R.; Fiorani, D.; Peddis, D. Structural and Magnetic Properties of Spinel Ferrite Nanoparticles. J. Nanosci. Nanotechnol. 2019, 19, 4888–4902. [Google Scholar] [CrossRef]
- Cannas, C.; Musinu, A.; Piccaluga, G.; Fiorani, D.; Peddis, D.; Rasmussen, H.K.; Mørup, S. Magnetic properties of cobalt ferrite-silica nanocomposites prepared by a sol-gel autocombustion technique. J. Chem. Phys. 2006, 125, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Jovanović, S.; Spreitzer, M.; Otoničar, M.; Jeon, J.-H.; Suvorov, D. pH control of magnetic properties in precipitation-hydrothermal-derived CoFe2O4. J. Alloys Compd. 2014, 589, 271–277. [Google Scholar] [CrossRef]
- Albino, M.; Fantechi, E.; Innocenti, C.; López-Ortega, A.; Bonanni, V.; Campo, G.; Pineider, F.; Gurioli, M.; Arosio, P.; Orlando, T.; et al. Role of Zn2+ Substitution on the Magnetic, Hyperthermic, and Relaxometric Properties of Cobalt Ferrite Nanoparticles. J. Phys. Chem. C 2019, 123, 6148–6157. [Google Scholar] [CrossRef]
- Martínez, B.; Obradors, X.; Balcells, L.; Rouanet, A.; Monty, C. Low Temperature Surface Spin-Glass Transition in -gFe2O3 Nanoparticles. Phys. Rev. Lett. 1998, 80, 181–184. [Google Scholar] [CrossRef]
- Coey, J.M.D. Non-collinear Spin Arrangement in Ultrafine Ferrimagnetic Crystallites. Phys. Rev. Lett. 1971, 27, 1140. [Google Scholar] [CrossRef]
- Lin, D.; Nunes, A.C.; Majkrzak, C.F.; Berkowitz, A.E. Polarized neutron study of the magnetization density distribution within a CoFe2O4 colloidal particle II. J. Magn. Magn. Mater. 1995, 145, 343–348. [Google Scholar] [CrossRef]
- Peddis, D.; Mansilla, M.V.; Mørup, S.; Cannas, C.; Musinu, A.; Piccaluga, G.; D’Orazio, F.; Lucari, F.; Fiorani, D. Spin-canting and magnetic anisotropy in ultrasmall CoFe2O4 nanoparticles. J. Phys. Chem. B 2008, 112, 8507–8513. [Google Scholar] [CrossRef]
- Peddis, D.; Yaacoub, N.; Ferretti, M.; Martinelli, A.; Piccaluga, G.; Musinu, A.; Cannas, C.; Navarra, G.; Greneche, J.M.; Fiorani, D. Cationic distribution and spin canting in CoFe2O4 nanoparticles. J. Phys. Condens. Matter 2011, 23, 426004. [Google Scholar] [CrossRef]
- Peddis, D. Magnetic Properties of Spinel Ferrite Nanoparticles: Influence of the Magnetic Structure. In Magnetic Nanoparticle Assemblies; Trohidou, K.N., Ed.; Pan Stanford Publishing: Singapore, 2014; Volume 7, pp. 978–981. ISBN 9789814411967. [Google Scholar]
- Cannas, C.; Musinu, A.; Peddis, D.; Piccaluga, G. Synthesis and Characterization of CoFe2O4 Nanoparticles Dispersed in a Silica Matrix by a Sol−Gel Autocombustion Method. Chem. Mater. 2006, 18, 3835–3842. [Google Scholar] [CrossRef]
- Muscas, G.; Singh, G.; Glomm, W.R.; Mathieu, R.; Kumar, P.A.; Concas, G.; Agostinelli, E.; Peddis, D. Tuning the size and shape of oxide nanoparticles by controlling oxygen content in the reaction environment: Morphological analysis by aspect maps. Chem. Mater. 2015, 27, 1982–1990. [Google Scholar] [CrossRef]
- Peddis, D.; Jönsson, P.E.; Laureti, S.; Varvaro, G. Magnetic Interactions: A Tool to Modify the Magnetic Properties of Materials Based on Nanoparticles; Elsevier: Amsterdam, The Netherlands, 2014; Volume 6. [Google Scholar]
- Knobel, M.; Nunes, W.C.; Socolovsky, L.M.; De Biasi, E.; Vargas, J.M.; Denardin, J.C. Superparamagnetism and other magnetic features in granular materials: A review on ideal and real systems. J. Nanosci. Nanotechnol. 2008, 8, 2836–2857. [Google Scholar] [CrossRef]
- Dormann, J.L.; Fiorani, D.; Tronc, E. Magnetic Relaxation in Fine-Particle Systems. Adv. Chem. Phys. 1997, 98, 283–494. [Google Scholar]
- Gittleman, J.I.; Abeles, B.; Bozowski, S. Superparamagnetism and relaxation effects in granular Ni-SiO2 and Ni-Al2O3 films. Phys. Rev. B 1974, 9, 3891–3897. [Google Scholar] [CrossRef]
- Chantrell, R.W.; El-Hilo, M.; O’Grady, K. Spin-Glass behaviour in fine particle system. IEEE Trans. Magn. 1991, 27, 3570–3578. [Google Scholar] [CrossRef]
- Lavorato, G.C.; Peddis, D.; Lima, E.; Troiani, H.E.; Agostinelli, E.; Fiorani, D.; Zysler, R.D.; Winkler, E.L. Magnetic Interactions and Energy Barrier Enhancement in Core/Shell Bimagnetic Nanoparticles. J. Phys. Chem. C 2015, 119, 15755–15762. [Google Scholar] [CrossRef]
- Liu, C.; Zou, B.; Rondinone, A.J.; Zhang, Z.J. Chemical Control of Superparamagnetic Properties of Magnesium and Cobalt Spinel Ferrite Nanoparticles through Atomic Level Magnetic Couplings. J. Am. Chem. Soc. 2000, 122, 6263–6267. [Google Scholar] [CrossRef]
- Rondinone, A.J.; Liu, C.; Zhang, Z.J. Determination of Magnetic Anisotropy Distribution and Anisotropy Constant of Manganese Spinel Ferrite Nanoparticles. J. Phys. Chem. B 2001, 105, 7967–7971. [Google Scholar] [CrossRef]
- Hansen, M.F.; Mørup, S. Estimation of blocking temperatures from ZFC/FC curves. J. Magn. Magn. Mater. 1999, 203, 214–216. [Google Scholar] [CrossRef]
- Cannas, C.; Gatteschi, D.; Musinu, A.; Piccaluga, G.; Sangregorio, C. Structural and Magnetic Properties of Fe2O3 Nanoparticles Dispersed over a Silica Matrix. J. Phys. Chem. B 1998, 102, 7721–7726. [Google Scholar] [CrossRef]
- Pacakova, B.; Kubickova, S.; Reznickova, A.; Niznansky, D.; Vejpravova, J. Spinel Ferrite Nanoparticles: Correlation of Structure and Magnetism. In Magnetic Spinels—Synthesis, Properties and Applications; InTech: London, UK, 2017; ISBN 9789537619824. [Google Scholar]
- Dormann, J.L.; Bessais, L.; Fiorani, D. A dynamic study of small interacting particles: Superparamagnetic model and spin-glass laws. J. Phys. C Solid State Phys. 1988, 21, 2015. [Google Scholar] [CrossRef]
- del Castillo, V.L.C.D.; Rinaldi, C. Effect of sample concentration on the determination of the anisotropy constant of magnetic nanoparticles. IEEE Trans. Magn. 2010, 46, 852–859. [Google Scholar] [CrossRef]
- Sharifi, I.; Shokrollahi, H.; Amiri, S. Ferrite-based magnetic nanofluids used in hyperthermia applications. J. Magn. Magn. Mater. 2012, 324, 903–915. [Google Scholar] [CrossRef]
- Sharifi, I. Magnetic and structural studies on CoFe2O4 nanoparticles synthesized by co-precipitation, normal micelles and reverse micelles methods. J. Magn. Magn. Mater. 2012, 324, 1854–1861. [Google Scholar] [CrossRef]
- Omelyanchik, A.; Knezevic, N.; Rodionova, V.; Salvador, M.; Peddis, D.; Varvaro, G.; Laureti, S.; Mrakovic, A.; Kusigerski, V.; Illes, E. Experimental Protocols for Measuring Properties of Nanoparticles Dispersed in Fluids. In Proceedings of the 2018 IEEE 8th International Conference Nanomaterials: Application & Properties (NAP), Zatoka, Ukraine, 9–14 September 2018; pp. 1–5. [Google Scholar]
- Morrish, A.H. The Physical Principles of Magnetism; Wiley: Hoboken, NJ, USA, 1965; Volume 1, ISBN 0-7803-6029-X. [Google Scholar]
- Muscas, G.; Concas, G.; Cannas, C.; Musinu, A.; Ardu, A.; Orru, F.; Fiorani, D.; Laureti, S.; Rinaldi, D.; Piccaluga, G.; et al. Magnetic Properties of Small Magnetite Nanocrystals. J. Phisical Chem. C 2013, 114, 23378–23384. [Google Scholar] [CrossRef]
- Peddis, D.; Cannas, C.; Piccaluga, G.; Agostinelli, E.; Fiorani, D. Spin-glass-like freezing and enhanced magnetization in ultra-small CoFe2O4 nanoparticles. Nanotechnology 2010, 21, 125705. [Google Scholar] [CrossRef] [PubMed]
- Pérez, N.; Guardia, P.; Roca, A.G.; Morales, M.P.; Serna, C.J.; Iglesias, O.; Bartolomé, F.; García, L.M.; Batlle, X.; Labarta, A. Surface anisotropy broadening of the energy barrier distribution in magnetic nanoparticles. Nanotechnology 2008, 19, 475704. [Google Scholar] [CrossRef] [PubMed]
- Chantrell, R.W.; O’Grady, K. The Magnetic Properties of Fine Particles. In Applied Magnetism; Springer: Dordrecht, The Netherlands, 1994; pp. 113–164. [Google Scholar]
- El-Hilo, M.; Bsoul, I. Interaction effects on the coercivity and fluctuation field in granular powder magnetic systems. Phys. B Condens. Matter 2007, 389, 311–316. [Google Scholar] [CrossRef]




| Sample | dTEM | Tmax | Tirr | <TB>CH.2 | PDCH. | <TB>H.M. 2 | PDH.M. |
|---|---|---|---|---|---|---|---|
| (nm) | (K) | (K) | (K) | (%) | (K) | (%) | |
| N15T700 | 2.5(2) 1 | 29(1) | 57(5) | 18(1) | 3.26 | 16(1) | 4.56 |
| N15T800 | 5.3(5) | 43(1) | 70(5) | 22(2) | 2.86 | 25(2) | 2.44 |
| N15T900 | 6.6(5) | 53(1) | 82(3) | 29(1) | 2.41 | 31(2) | 2.45 |
| Sample | Néel−Arrhenius 1 | Vogel−Fulcher 2 | ||
|---|---|---|---|---|
| (J m−3) | (s) | (J m−3) | (K) | |
| N15T700 | 7.9(4) × 105 | 1.9 × 10−9 | 11(1) × 105 | −1(3) |
| N15T800 | 2.3(2) × 105 | 8.2 × 10−14 | 1.3(1) × 105 | 14(2) |
| N15T900 | 1.9(2) × 105 | 1.5 × 10−14 | 0.92(1) × 105 | 32(3) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omelyanchik, A.; Salvador, M.; D’Orazio, F.; Mameli, V.; Cannas, C.; Fiorani, D.; Musinu, A.; Rivas, M.; Rodionova, V.; Varvaro, G.; et al. Magnetocrystalline and Surface Anisotropy in CoFe2O4 Nanoparticles. Nanomaterials 2020, 10, 1288. https://doi.org/10.3390/nano10071288
Omelyanchik A, Salvador M, D’Orazio F, Mameli V, Cannas C, Fiorani D, Musinu A, Rivas M, Rodionova V, Varvaro G, et al. Magnetocrystalline and Surface Anisotropy in CoFe2O4 Nanoparticles. Nanomaterials. 2020; 10(7):1288. https://doi.org/10.3390/nano10071288
Chicago/Turabian StyleOmelyanchik, Alexander, María Salvador, Franco D’Orazio, Valentina Mameli, Carla Cannas, Dino Fiorani, Anna Musinu, Montserrat Rivas, Valeria Rodionova, Gaspare Varvaro, and et al. 2020. "Magnetocrystalline and Surface Anisotropy in CoFe2O4 Nanoparticles" Nanomaterials 10, no. 7: 1288. https://doi.org/10.3390/nano10071288
APA StyleOmelyanchik, A., Salvador, M., D’Orazio, F., Mameli, V., Cannas, C., Fiorani, D., Musinu, A., Rivas, M., Rodionova, V., Varvaro, G., & Peddis, D. (2020). Magnetocrystalline and Surface Anisotropy in CoFe2O4 Nanoparticles. Nanomaterials, 10(7), 1288. https://doi.org/10.3390/nano10071288