Abstract
A coupled graphene structure (CGS) is proposed to obtain an electrically tunable sub-femtometer (sub-fm) dimensional resolution. According to analytical and numerical investigations, the CGS can support two branches of localized surface plasmon resonances (LSPRs), which park at the dielectric spacer between two pieces of graphene. The coupled efficiencies of the odd-order modes are even four orders of magnitude higher than that of the even-order modes. In particular, a sub-fm resolution for detecting the change in the spacer thickness can be reached using the lowest order LSPR mode. The LSPR wavelength and the dimensional differential resolution can be electrically-tuned from 9.5 to 33 μm and from 4.3 to 15 nm/pm, respectively, by modifying the chemical potential of the graphene via the gate voltage. Furthermore, by replacing the graphene ribbon (GR) at the top of the CGS with multiple GRs of different widths, a resonant frequency comb in the absorption spectrum with a tunable frequency interval is generated, which can be used to detect the changes in spacer thicknesses at different locations with sub-fm resolution.
1. Introduction
The ultra-precise detection on extremely weak biological and physical processes occurring at the nanoscale has always been a strong desire, which can find important applications in probing DNA hybridization [1,2], molecule assembly [3,4], thermal expansion [5,6], and photomechanical effects [7,8]. On the road towards extra-high dimensional resolution, localized surface plasmon resonances (LSPRs) parking at the deep subwavelength nanocavity between coupled plasmonic nanostructures have attracted great attention [9,10,11,12]. The far-field absorption spectrum amplified by non-radiative decay of LSPRs depends intensely on the morphology, dimension, and material of the nanocavity [13,14,15,16,17]. Thus, it is possible to monitor awfully weak changes in the dimension of the nanocavity by measuring the shift of the LSPR frequency, or the equivalent LSPR wavelength. So far, various coupled plasmonic nanostructures that can support cavity plasmons have been reported, such as gold nanoparticle dimers [18], metallic nanocube on metallic film [19,20], metallic nanocube dimers [21,22,23], and gold/silver nanowire-on-mirror [24]. The dimensional resolutions of the coupled plasmonic nanostructures have reached the order of sub-picometer (sub-pm) theoretically and experimentally [23,24]. However, the sub-femtometer (sub-fm) dimensional resolution has yet to be attained, owing to the LSPR of coupled metallic nanostructures resonating at relatively short wavelengths. Moreover, the limited tunability restricted by the fixed material properties is also a stumbling block.
To tackle the aforementioned limits, a coupled graphene structure (CGS) is proposed to obtain electrically tunable sub-fm dimensional resolution, in which a graphene ribbon (GR) is tightly adhered to the upper surface of a dielectric spacer, and the lower surface of the spacer is attached to a graphene-pasted silver film. An analytical model is deduced to calculate the LSPR wavelength of the CGS. According to the calculated results, the CGS can support two branches of LSPRs parking at the dielectric spacer between two pieces of graphene, i.e., odd-order and even-order modes. The coupled efficiencies of the odd-order modes are four orders of magnitude higher than that of the even-order modes. Moreover, the coupled efficiencies of the odd-order modes decrease rapidly as the increase of mode orders. In particular, the resolution for detecting the change in thickness of the spacer can reach the sub-fm scale, which is dozens of times higher than the recently reported resolution [23,24]. The LSPR wavelength and the dimensional differential resolution (DDR) can be electrically tuned from 9.5 to 33 μm and from 4.3 to 15 nm/pm, respectively, by modifying the chemical potential of the graphene via the gate voltage. Furthermore, the sensitivity for monitoring the change in the refractive index (RI) of the spacer is 9.7 μm/RI unit (RIU), which means that the smallest change in the RI of the spacer that can be identified is on the order of 10−6 RIU. The greatest figure of merit (FoM) obtained can reach as high as 440, which is several times higher than previously reported values [21]. Significantly, a resonant frequency comb in the absorption spectrum with a tunable frequency interval is generated using a CGS with multiple GRs of different widths at the top. The electrically tunable sub-fm dimensional resolution facilitates the ultra-precise detection on extremely weak physical processes occurring at the nanoscale, such as thermal expansion, piezoelectric effects, and photomechanical effects.
2. Theoretical Model and Method
The schematic diagram of the proposed CGS is shown in Figure 1a. The lower surface of the dielectric spacer is in contact with a graphene-pasted silver film, and the upper surface is covered by another piece of GR. The chemical potential of the graphene can be actively tuned by modifying the gate voltage [25,26,27], temperature [28], chemical doping [29], electric field [30], and so on [31,32]. The cross section of the simulated structure modeled by using the commercially available software COMSOL Multiphysics (Stockholm, Sweden) is shown in Figure 1b. The entire system is placed in the air with a relative permittivity of ε1 = 1, which is illuminated by a linearly polarized plane wave from the top. The silver film is treated as a half-infinity-extended body, and its relative permittivity is modeled using the Drude model, ε4 = 1 − ωp2/(ω2 + iωγ), where ω is the angular frequency of the incident wave. ωp = 9.014 eV and γ = 0.018 eV [33] are the plasma frequency and damping constant, respectively. To prevent unrealistically sharp edges, both ends of the GR are semicircular with a curvature, δ/2, where δ = 0.34 nm is the thickness of the graphene. The relative permittivity of the graphene, ε2, can be calculated using ε2 = iσg/(ωε0δ) [34,35], where ε0 is the permittivity of vacuum. The surface conductivity of the graphene, σg, can be evaluated using the Kubo formula as follows [28,36]:
where σintra and σinter represent the intra-band and inter-band terms of surface conductivity, respectively. −e is the charge of an electron, ћ = h/(2π) is the reduced Planck’s constant, kB is Boltzmann’s constant, and μc is chemical potential of graphene. The temperature and charged particle scattering rate are set as T = 300 K and Г = 0.1 meV, respectively.
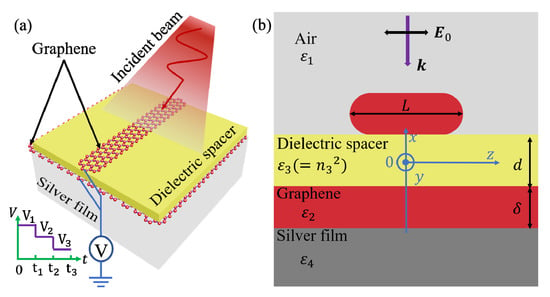
Figure 1.
(a) The schematic diagram and (b) cross section of the coupled graphene structure (CGS). The adopted Cartesian coordinate system is shown in (b).
When the length of the GR in the y direction is regarded as infinite, the CGS in Figure 1b can be reduced to a five-layer slab waveguide for surface plasmon polaritons (SPPs) propagating along the z direction. The SPPs are transverse magnetic (TM) modes [37], so the magnetic field component can be written as:
where Aj (j = 1, 2, 3, 4, or 5) and Bl (l = 2, 3, or 4) are undetermined mode coefficients, and d is the thickness of the dielectric spacer. ϕ = e−i(ωt−βz) and kq2 = β2 − μ0μqε0εqω2 (q = 1, 2, 3, or 4), respectively, where β is the complex propagation constant, μ0 is the permeability of vacuum, μq = 1 for the considered nonmagnetic materials, and εq are the relative permittivity. Based on the expression of Hy and the relationship between electric and magnetic field components, the electric field components Ex and Ez can be solved [38]. By further employing the continuities of the tangential field components Hy and Ez at interfaces x = d/2 + δ, d/2, − d/2, and − d/2 − δ, we obtain the following dispersion equation:
Owing to the finite width of the GR, electromagnetic waves are confined within the lateral range covered by the GR, thus some standing-waves with specific propagation constants can be supported by the CGS. The resonant condition of the standing-waves can be written as [23]:
where m is a positive integer characterizing the number of wave-nodes in the z direction, and L is the width of the GR. φ = arctan[Re(r)/Im(r)] is a phase shift from scattering at the boundaries [39], where the complex reflection coefficient r = [(1 − G)/(1 + G)]*. The intermediate variable G can be written as [40,41]:
where λ is the wavelength of the incident wave and k0 = 2π/λ is the wavenumber in vacuum. By solving Equations (5) and (6), the resonance wavelength can be quantitatively determined.
3. Results and Discussion
When the wave vector of incident wave matches the oscillation frequency of free electrons of the CGS, the plasmons around the graphene are strongly coupled together at the dielectric spacer. The normalized absorption spectrum was calculated using COMSOL Multiphysics, as shown by the black line in Figure 2a. The coupled LSPRs supported by the CGS can be divided into two branches: odd-order and even-order modes. The coupled efficiencies of the even-order modes are even four orders of magnitude lower than that of the odd-order modes, so they are difficult to be observed from the absorption spectrum. The coupled efficiencies of odd-order modes decrease rapidly as the increased mode order. The positions of the resonance wavelengths calculated using the analytical model are shows by the downward dashed blue arrows in Figure 2a, which are consistent with the numerical calculation results. The first four modes labeled m1, m2, m3, and m4, correspond to electric field distributions with 1, 2, 3, and 4 zero wave-nodes at the dielectric spacer, as shown in Figure 2b. For the odd-order modes, the proportion of the electric field leaked into the free space gradually increased as the mode order increased, which corresponded to the decrease of the coupled efficiency. However, for even-order modes the percentage of the electric field diffused into the free space gradually decreased with the increase of the mode order, corresponding to the increase of coupled efficiency. Moreover, the percentage of the electric field of the even-order modes diffused into free space is much larger than that of the odd-order modes.
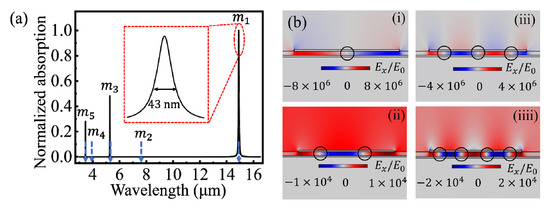
Figure 2.
(a) Normalized absorption spectrum of the CGS (black line) and the positions of resonance wavelengths solved by using the analytical model (downward dashed blue arrows). The inset in (a) shows that the full width at half maximum (FWHM) of the m1 peak is 43 nm. (b) Electric field distributions corresponding to the coupled localized surface plasmon resonances (LSPRs) labeled (i) m1, (ii) m2, (iii) m3, and (iiii) m4 in (a). The chemical potential of graphene is μc = 0.5 eV. The width of GR is L = 40 nm. The thickness and refractive index (RI) of the dielectric spacer are d = 1.0 nm and n3 = 1.5, respectively.
The coupled efficiency of the first-order mode, the lowest frequency standing wave at the dielectric spacer, was larger than that of higher-order modes. Thus, it was easier to be detected on the absorption spectrum. Moreover, the first-order mode was far away from the higher-order modes, which facilitated the monitoring of the spectral shift. Thus, our research was focused on the first-order mode hereafter. The spectral behavior of the coupled LSPR was studied in the range of the spacer thickness d ≥ 0.7 nm, in which the quantum tunneling effect was negligible [18,23]. As shown in Figure 3a, when d decreased, the LSPR wavelength, λr, occurred a red-shift obviously, due to the increase of the electromagnetic coupled strength of the plasmons at the dielectric spacer [16,18]. Based on the proposed analytical model, the dependences of the resonance wavelength λr on the spacer thickness d are quantitatively calculated, as shown by the blue line in Figure 3b. It is observed that λr increased exponentially-like with the decrease of d, which is consistent with the previous scale behavior in other coupled plasmonic nanostructures [9,16,24]. The numerical results obtained using COMSOL Multiphysics are shown as the blue rectangles in Figure 3b, which agreed well with the analytical results. The DDR was further calculated by solving the differentiation of λr to d, i.e., DDR = |∂λr/∂d|, as shown by the red line in Figure 3b. The maximum DDR is 12 nm/pm at d = 0.7 nm, which is dozens of times higher than the previous results of coupled metallic nanostructures [23,24]. Since the resolution limit of spectrometers used in experiments was usually 0.01 nm, a sub-fm thickness variation can be identified by monitoring the spectral shift of the first-order LSPR in CGS. Noteworthily, the resolution can be further improved by reducing the chemical potential of graphene or increasing the width of the GR.
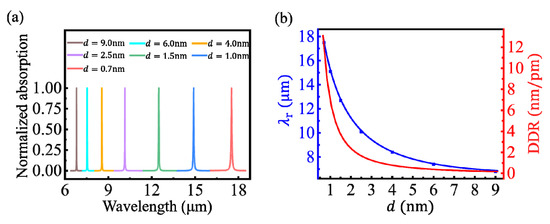
Figure 3.
(a) Normalized absorption spectrums of the CGS under different spacer thicknesses. (b) Dependences of the LSPR wavelength (blue line) and the dimensional differential resolution (DDR; red line), respectively, on the spacer thickness for μc = 0.5 eV, L = 40 nm, and n3 = 1.5. The blue rectangles are the numerical results obtained using COMSOL Multiphysics (this scheme is also used in Figure 4, Figure 5 and Figure 6).
The ultrahigh sensitivity of the LSPR in the CGS mainly results from several factors as follows. Compared with coupled metallic nanostructures, the CGS supports the LSPR resonating at a longer wavelength, which can increase electric near-field enhancement to higher orders of magnitude [42,43,44], and thus greatly improves the sensitivity. The electric near-field enhancement of the CGS beneficial for improving the sensitivity is also stronger than that of the non-coupled graphene [45,46,47]. Moreover, the CGS has a near-two-dimensional dielectric spacer, which can hold a purely coupled LSPR between two graphene, while the nanostructures with curved shapes typically contains near-degenerate plasmon modes that complicate the profile of the absorption spectrum and reduce the DDR [24].
The GR in the CGS is further replaced with a GR array (GRA) consisting of several GRs, as shown in Figure 4a, for obtaining more superior characteristics. According to the calculated results, when the widths of all GRs in the GRA are the same, the absorption efficiency can be greatly improved, which facilitates the observation of the resonance peaks in the absorption spectrum. When the separation between two adjacent GRs, s, is set as 10 nm, the coupled effect between the adjacent GRs is negligible. Thus, the absorption efficiency of resonance peaks increases linearly with the number of GRs, while the LSPR wavelength is independent on the GR number.
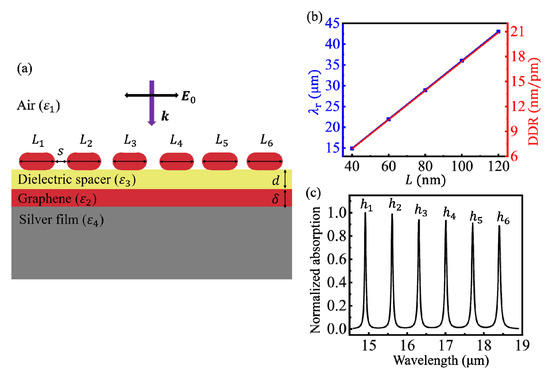
Figure 4.
(a) The cross section of the CGS with a graphene ribbon array (GRA). (b) Dependences of the LSPR wavelength (blue line) and the DDR (red line), respectively, on the graphene ribbon (GR) width. (c) A frequency comb in the absorption spectrum is generated using a CGS with six GRs under μc = 0.5 eV, n3 = 1.5, and d = 1.0 nm.
The resonance wavelength and the sensitivity for detecting the change in the spacer thickness were closely related to the width of the GR. The dependences of λr and DDR on L are shown by blue and red lines, respectively, in Figure 4b. The coupled LSPR can be regarded as a standing-wave mode, thus its resonance wavelength is proportional to the length of the resonant cavity, i.e., L. It is worth noting that the phase shift from scattering at the boundaries, φ, did not affect this major change trend. Moreover, the changing trends of DDR and λr with L are consistent for a given spacer thickness, which means that a larger GR width can make the sensitivity of the CGS higher.
Furthermore, multiple resonance peaks can be obtained simultaneously by using a GRA with GRs of different widths. Each resonance peak can be independently tuned by modifying the corresponding GR width. Thus, a frequency comb in the absorption spectrum can be generated by adjusting the width of each GR, as shown in Figure 4c. The wavelength intervals between adjacent resonance peaks were all 0.7 μm. The GR widths were L1 = 40 nm, L2 = 42 nm, L3 = 44 nm, L4 = 46 nm, L5 = 48 nm, and L6 = 50 nm, and the separation between adjacent GRs was s = 10 nm. The peaks labeled from h1 to h6 in the Figure 4c correspond to the width from L1 to L6, respectively. The wavelength interval can be tuned not only by the GR width, but also by μc, n3, and d. The resonant frequency comb in the absorption spectrum can be used to detect the changes in spacer thicknesses at different locations with sub-fm resolution.
Different from coupled nanostructures made of noble metals, the LSPR wavelength of the CGS can be controlled by tuning the chemical potential of graphene via the gate voltage. The relationship between the chemical potential, μc, and the voltage, V, can be written as , where vF is the Fermi velocity and n = Cg(V + V0)/e is the charge density. Cg and V0 are the gate capacitance and offset voltage, respectively [28]. The dependences of λr and DDR on μc were calculated, as shown by the blue and red lines, respectively, in Figure 5a. When μc decreases from 1.5 to 0.1 eV, the LSPR wavelength increased from 9.5 to 33 μm, corresponding to a res-shift, and the DDR increased from 4.3 to 15 nm/pm. The changing trends of λr and DDR with μc were highly coincident for a given spacer thickness. It is pointed out that the LSPR wavelength and the DDR can also be tuned in different ranges by changing the spacer thickness or the GR width. According to Equations (1)–(3), the relationship between σg and μc was very complicated. According to the calculations, the changing trends of λr and DDR were closely related to , so λm was used to describe the wavelength corresponding to the maximum value of ξ at a given chemical potential and the dependence of λm on μc was further calculated, as shown in Figure 5b. The changing trends of λr and λm with μc were very similar. However, λr and λm were not completely equal for a given μc, because λr was influenced by not only the graphene, but also the structure of the CGS, such as the GR width and the spacer thickness.
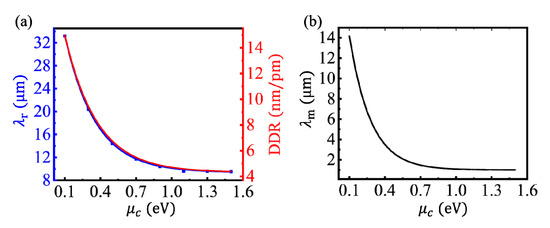
Figure 5.
(a) Dependences of the LSPR wavelength (blue line) and the DDR (red line), respectively, on the chemical potential of the graphene under L = 40 nm, n3 = 1.5, and d = 1.0 nm. (b) The dependence of λm on μc.
Besides the dimension detection, the CGS can also be used to detect the change in the RI of the dielectric spacer, n3. As shown in Figure 6, with the increase of n3 a linear red-shift occurred in the LSPR wavelength, which is accompanied by the increase of electromagnetic coupled strength of the plasmons [16]. The gradient of λr to n3 was 9.7 μm/RIU, thus the smallest change in the RI of the spacer that can be identified is on the order of 10−6 RIU by monitoring the spectral shift of the coupled LSPR. When n3 increased from 1.0 to 2.0, the FWHM of the resonance peak increased from 22 to 74 nm. Thus the FoM, defined as the ratio of the gradient of λr to n3 to the FWHM, i.e., FoM = |∂λr/∂n3|/FWHM, changed from 440 to 130, which is several times higher than the reported results of coupled metallic nanostructures [21]. Moreover, since the DDR increased linearly with the increase of n3, a dielectric spacer with a larger RI can make the dimensional resolution higher.
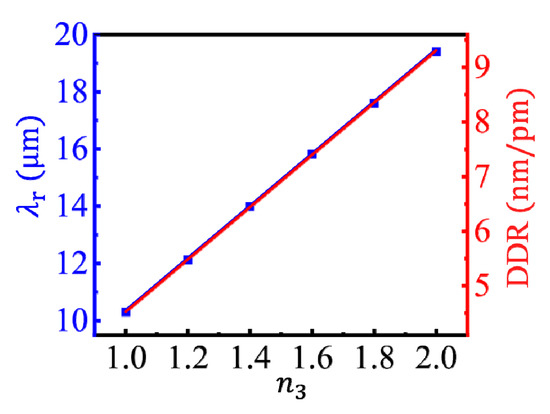
Figure 6.
Dependences of the LSPR wavelength (blue line) and the DDR (red line), respectively, on the RI of the dielectric spacer under μc = 0.5 eV, L = 40 nm, and d = 1.0 nm.
4. Conclusions
To conclude, a CGS was proposed to obtain electrically tunable sub-fm dimensional resolution. An analytical model was deduced for calculating the LSPR wavelength of the CGS. Analytical and numerical studies show that the proposed CGS could support odd-order and even-order LSPR modes parking at the dielectric spacer between two pieces of graphene, and the coupled efficiencies of the odd-order modes were even four orders of magnitude higher than that of the even-order modes. The coupled efficiencies of the odd-order modes decreased rapidly as the mode order increased. In particular, the dimensional resolution could even reach the sub-fm scale by monitoring the shift of the first-order LSPR wavelength. The LSPR wavelength and the DDR could be tuned from 9.5 to 33 μm and from 4.3 to 15 nm/pm, respectively, by modifying the chemical potential of the graphene via the gate voltage. Furthermore, the sensitivity for monitoring the change in the RI of the spacer was 9.7 μm/RIU, so the smallest identifiable change in the RI of the spacer was on the order of 10−6 RIU. Moreover, the greatest FoM obtained could reach as high as 440. Significantly, a resonant frequency comb in the absorption spectrum with a tunable frequency interval was generated by using a CGS with multiple GRs of different widths at the top. According to the obtained results, the proposed CGS may push the dimensional resolution of tunable plasmon sensors to a new level.
Author Contributions
Conceptualization, Z.W. and H.L.; Methodology, Z.W.; Validation, Z.W.; Formal Analysis, Z.W. and H.L.; Investigation, Z.W.; Resources, H.Z. and H.L., Writing—Original Draft Preparation, Z.W.; Writing—Review & Editing, H.L., L.Z., M.Z., and S.R.; Supervision, H.L.; Funding Acquisition, H.L., I.L.L., H.S., and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC) (11874270), Fund Project for Shenzhen Fundamental Research Program (JCYJ20180305125000525, JCYJ20190808143409787), and Fundamental Research Funds for the Central Universities of Xi’an Jiaotong University (Z201805196).
Acknowledgments
The authors acknowledge the useful discussions with Huilin Luo and the help on modeling using COMSOL Multiphysics from Shunping Zhang and Tong Fu in Wuhan University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sönnichsen, C.; Reinhard, B.M.; Liphardt, J.; Alivisatos, A.P. A molecular ruler based on plasmon coupling of single gold and silver nanoparticles. Nat. Biotechnol. 2005, 23, 741–745. [Google Scholar] [CrossRef]
- Chen, J.I.L.; Chen, Y.; Ginger, D.S. Plasmonic nanoparticle dimers for optical sensing of DNA in complex media. J. Am. Chem. Soc. 2010, 132, 9600–9601. [Google Scholar] [CrossRef] [PubMed]
- Reinhard, B.M.; Sheikholeslami, S.; Mastroianni, A.; Alivisatos, A.P.; Liphardt, J. Use of plasmon coupling to reveal the dynamics of DNA bending and cleavage by single EcoRV restriction enzymes. Proc. Natl. Acad. Sci. USA 2007, 104, 2667. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Reinhard, B.M. Monitoring Simultaneous Distance and Orientation Changes in Discrete Dimers of DNA Linked Gold Nanoparticles. J. Phys. Chem. C 2009, 113, 11215–11222. [Google Scholar] [CrossRef][Green Version]
- Tian, M.; Huang, Y.; Wang, W.; Li, R.; Liu, P.; Liu, C.; Zhang, Y. Temperature-dependent electrical properties of graphene nanoplatelets film dropped on flexible substrates. J. Mater. Res. 2014, 29, 1288–1294. [Google Scholar] [CrossRef]
- Zhao, X.; Long, Y.; Yang, T.; Li, J.; Zhu, H. Simultaneous high sensitivity sensing of temperature and humidity with Graphene Woven Fabrics. ACS Appl. Mater. Interfaces 2017, 9, 30171–30176. [Google Scholar] [CrossRef] [PubMed]
- Wie, J.J.; Wang, D.H.; Lee, K.M.; Tan, L.-S.; White, T.J. Molecular engineering of Azobenzene-Functionalized Polyimides to enhance both photomechanical work and motion. Chem. Mater. 2014, 26, 5223–5230. [Google Scholar] [CrossRef]
- Wang, H.; Song, S.; Zou, X.; Wang, F.; Zhang, Z.; Morozov, S.I.; Wang, X.; Reddy, K.M.; An, Q. Photomechanical effect leading to extraordinary ductility in covalent semiconductors. Phys. Rev. B 2019, 100, 094110. [Google Scholar] [CrossRef]
- Su, K.-H.; Wei, Q.-H.; Zhang, X.; Mock, J.; Smith, D.R.; Schultz, S. Interparticle coupling effects on plasmon resonances of nanogold particles. Nano Lett. 2003, 3, 1087–1090. [Google Scholar] [CrossRef]
- Gunnarsson, L.; Rindzevicius, T.; Prikulis, J.; Kasemo, B.; Käll, M.; Zou, S.; Schatz, G.C. Confined plasmons in nanofabricated single silver particle pairs: Experimental observations of strong interparticle interactions. J. Phys. Chem. B 2005, 109, 1079–1087. [Google Scholar] [CrossRef]
- Hill, R.T.; Mock, J.J.; Hucknall, A.; Wolter, S.D.; Jokerst, N.M.; Smith, D.R.; Chilkoti, A. Plasmon ruler with angstrom length resolution. ACS Nano 2012, 6, 9237–9246. [Google Scholar] [CrossRef] [PubMed]
- Mubeen, S.; Zhang, S.; Kim, N.; Lee, S.; Krämer, S.; Xu, H.; Moskovits, M. Plasmonic properties of gold nanoparticles separated from a gold mirror by an ultrathin oxide. Nano Lett. 2012, 12, 2088–2094. [Google Scholar] [CrossRef] [PubMed]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Sönnichsen, C.; Franzl, T.; Wilk, T.; von Plessen, G.; Feldmann, J.; Wilson, O.; Mulvaney, P. Drastic reduction of plasmon damping in gold nanorods. Phys. Rev. Lett. 2002, 88, 077402. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.K.; Lee, K.S.; El-Sayed, I.H.; El-Sayed, M.A. Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: Applications in biological imaging and biomedicine. J. Phys. Chem. B 2006, 110, 7238–7248. [Google Scholar] [CrossRef]
- Jain, P.K.; Huang, W.; El-Sayed, M.A. On the universal scaling behavior of the distance decay of plasmon coupling in metal nanoparticle pairs: A plasmon ruler equation. Nano Lett. 2007, 7, 2080–2088. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L. Nanostructures for surface plasmons. Adv. Opt. Photonics 2012, 4, 157–321. [Google Scholar] [CrossRef]
- Esteban, R.N.; Aguirregabiria, G.; Borisov, A.G.; Wang, Y.M.; Nordlander, P.; Bryant, G.W.; Aizpurua, J. The morphology of narrow gaps modifies the plasmonic response. ACS Photonics 2015, 2, 295–305. [Google Scholar] [CrossRef]
- Powell, A.W.; Coles, D.M.; Taylor, R.A.; Watt, A.A.; Assender, H.E.; Smith, J.M. Plasmonic gas sensing using nanocube patch antennas. Adv. Opt. Mater. 2016, 4, 634–642. [Google Scholar] [CrossRef]
- Zhang, F.-L.; Yi, J.; Peng, W.; Radjenovic, P.M.; Zhang, H.; Tian, Z.-Q.; Li, J.-F. Elucidating molecule–plasmon interactions in nanocavities with 2 nm spatial resolution and at the single-molecule level. Angew. Chem. Int. Ed. 2019, 58, 12133–12137. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Xu, H. Tunable dark plasmons in a metallic nanocube dimer: Toward ultimate sensitivity nanoplasmonic sensors. Nanoscale 2016, 8, 13722–13729. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhang, S.; Xu, H. Closely packed metallic nanocuboid dimer allowing plasmomechanical strong coupling. Phys. Rev. A 2019, 99, 033815. [Google Scholar] [CrossRef]
- Yang, D.-J.; Zhang, S.; Im, S.-J.; Wang, Q.-Q.; Xu, H.; Gao, S. Analytical analysis of spectral sensitivity of plasmon resonances in a nanocavity. Nanoscale 2019, 11, 10977–10983. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, S.; Deng, Q.; Xu, H. Probing of sub-picometer vertical differential resolutions using cavity plasmons. Nat. Commun. 2018, 9, 801. [Google Scholar] [CrossRef]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef]
- Amanatiadis, S.; Kantartzis, N. Distortion of surface plasmon polariton propagation on graphene due to chemical potential variation. Appl. Phys. A 2016, 122, 313. [Google Scholar] [CrossRef]
- Bouzianas, G.D.; Kantartzis, N.; Tsiboukis, T.D. Plasmon mode excitation on graphene layers via obliquely-incident focused wideband pulses in rigorous time-domain algorithms. IEEE Trans. Magn. 2013, 49, 1773–1776. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Zhang, S.; Cao, T.; Alu, A.; Ruan, S.; Qiu, C.-W. Gate-programmable electro-optical addressing array of graphene-coated nanowires with sub-10 nm resolution. Acs Photonics 2016, 3, 1847–1853. [Google Scholar] [CrossRef]
- Mock, A. Padé approximant spectral fit for FDTD simulation of graphene in the near infrared. Opt. Mater. Express 2012, 2, 771–781. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Ma, Q.; Dai, J.; Luo, A.; Hong, W. Numerical and theoretical study of Tunable Plasmonically induced transparency effect based on bright–dark mode coupling in Graphene Metasurface. Nanomaterials 2020, 10, 232. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, H.; Wang, S.; Cai, M.; Zhang, H.; Qiao, Y. Electrical Phase Control Based on Graphene Surface Plasmon Polaritons in Mid-infrared. Nanomaterials 2020, 10, 576. [Google Scholar] [CrossRef] [PubMed]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Ning, T.; Li, J.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Tunable photonic-like modes in graphene-coated nanowires. Opt. Express 2019, 27, 35238–35244. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhang, L.; Yin, H.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Graphene-coated nanowires with a drop-shaped cross section for 10 nm confinement and 1 mm propagation. Opt. Lett. 2017, 42, 2078–2081. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Liang, H.W.; Ruan, S.C.; Zhang, M.; Su, H.; Li, I.L. Characteristics of modified surface plasmon polaritons on double-coated metal nanofilms. Laser Phys. Lett. 2014, 11, 115003. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Gordon, R. Light in a subwavelength slit in a metal: Propagation and reflection. Phys. Rev. B 2006, 73, 153405. [Google Scholar] [CrossRef]
- Chandran, A.; Barnard, E.S.; White, J.S.; Brongersma, M.L. Metal-dielectric-metal surface plasmon-polariton resonators. Phys. Rev. B 2012, 85, 085416. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.; Vasilevskiy, M.I. A primer on surface plasmon-polaritons in graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef]
- Strait, J.H.; Nene, P.; Chan, W.-M.; Manolatou, C.; Tiwari, S.; Rana, F.; Kevek, J.W.; McEuen, P.L. Confined plasmons in graphene microstructures: Experiments and theory. Phys. Rev. B 2013, 87, 241410. [Google Scholar] [CrossRef]
- Gonçalves, P.A.D.; Peres, N.M.R. An Introduction to Graphene Plasmonics; World Scientific: Singapore, 2016. [Google Scholar]
- Vasić, B.; Isić, G.; Gajić, R. Localized surface plasmon resonances in graphene ribbon arrays for sensing of dielectric environment at infrared frequencies. J. Appl. Phys. 2013, 113, 013110. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, X.; Chen, G.; Zhang, X.; Tan, Z.; Chen, J.; Ruoff, R.S.; Zhu, Y.; Lu, Y. Infrared biosensors based on graphene plasmonics: Modeling. Phys. Chem. Chem. Phys. 2013, 15, 17118–17125. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, C.; Yu, J.; Cao, H.; Li, S.; Jia, W. Design of infrared surface plasmon resonance sensors based on graphene ribbon arrays. Opt. Laser Technol. 2014, 59, 99–103. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).