Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods
Abstract
:1. Introduction
2. Structure Design and Simulation Method
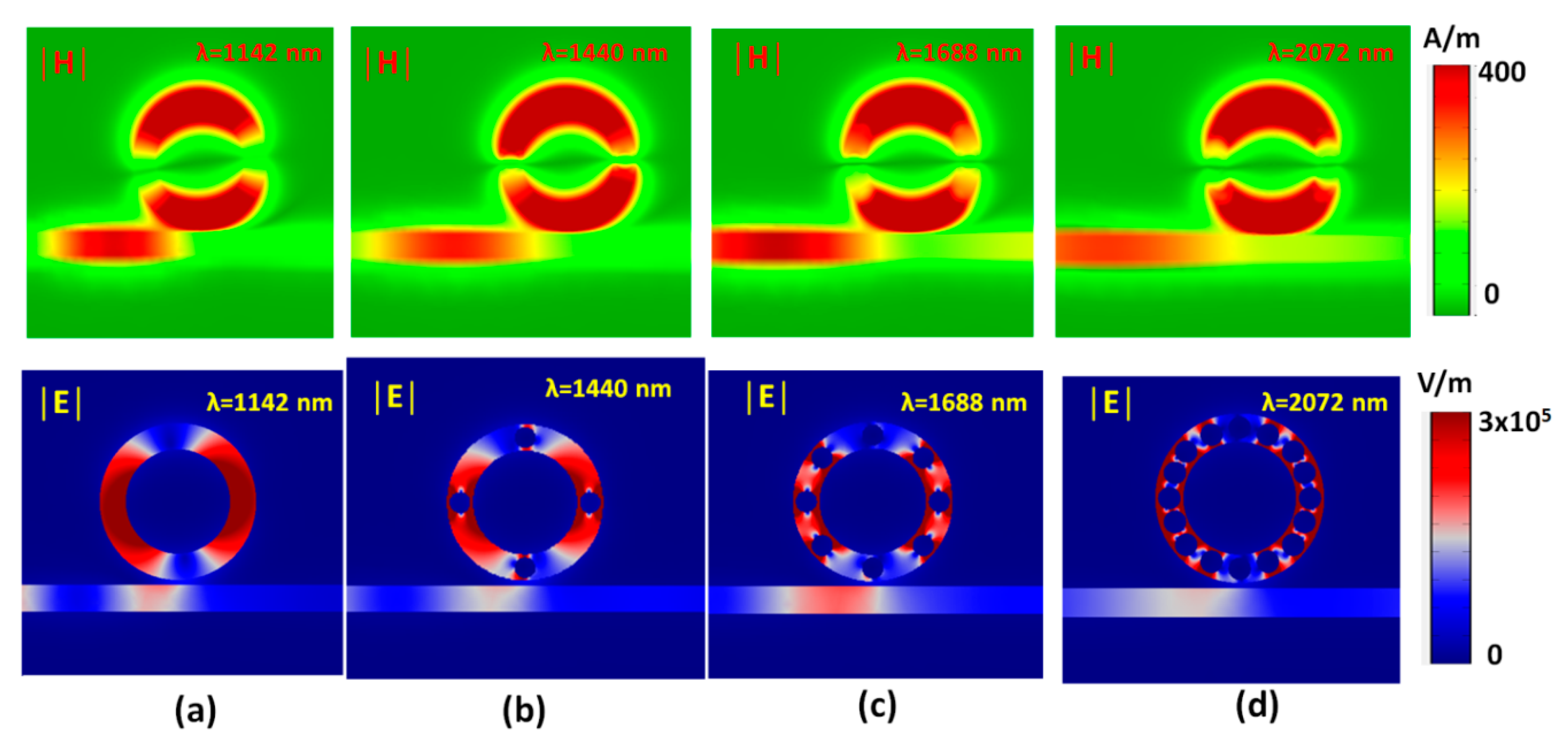
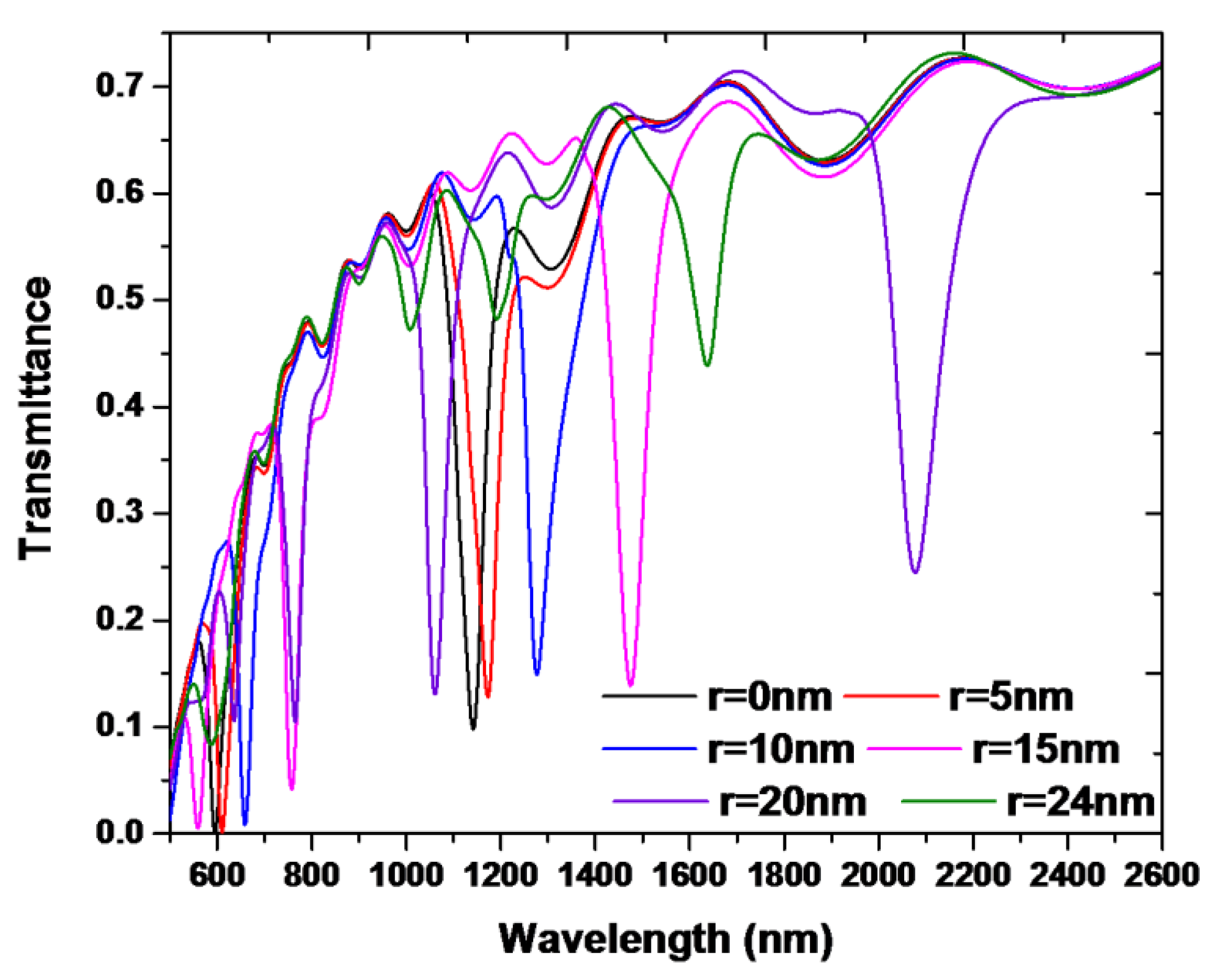
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haddouche, I.; Cherbi, L. Comparison of finite element and transfer matrix methods for numerical investigation of surface plasmon waveguides. Opt. Commun. 2017, 382, 132–137. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, R.B.; Tang, J.; Xue, C.Y.; Yan, S.B.; Zhang, W.D. Electromagnetically Induced Transparency and Refractive Index Sensing for a Plasmonic Waveguide with a Stub Coupled Ring Resonator. Plasmonics 2016, 12, 1007–1013. [Google Scholar] [CrossRef]
- Kumara, N.; Chau, Y.-F.C.; Huang, J.-W.; Huang, H.J.; Lin, C.-T.; Chiang, H.-P. Plasmonic spectrum on 1D and 2D periodic arrays of rod-shape metal nanoparticle pairs with different core patterns for biosensor and solar cell applications. J. Opt. 2016, 18, 115003. [Google Scholar] [CrossRef]
- Runowski, M.; Sobczak, S.; Marciniak, J.; Bukalska, I.; Lis, S.; Katrusiak, A. Gold nanorods as a high-pressure sensor of phase transitions and refractive-index gauge. Nanoscale 2019, 11, 8718–8726. [Google Scholar] [CrossRef]
- Barbillon, G. Latest Novelties on Plasmonic and Non-Plasmonic Nanomaterials for SERS Sensing. Nanomaterials 2020, 10, 1200. [Google Scholar] [CrossRef]
- Sun, R.-J.; Huang, H.J.; Hsiao, C.-N.; Lin, Y.-W.; Liao, B.-H.; Chau, Y.-F.C.; Chiang, H.-P. Reusable TiN Substrate for Surface Plasmon Resonance Heterodyne Phase Interrogation Sensor. Nanomaterials 2020, 10, 1325. [Google Scholar] [CrossRef]
- Sung, M.-J.; Ma, Y.-F.; Chau, Y.-F.C.; Huang, D.-W. Surface plasmon resonance in a hexagonal nanostructure formed by seven core shell nanocylinders. Appl. Opt. 2010, 49, 920–926. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Yang, T.-J.; Lee, W.-D. Coupling technique for efficient interfacing between silica waveguides and planar photonic crystal circuits. Appl. Opt. 2004, 43, 6656–6663. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Zhang, G.; Wang, Z.; Fan, G.; Yan, Y. Study on the Fano resonance of coupling M-type cavity based on surface plasmon polaritons. Opt. Commun. 2019, 433, 144–149. [Google Scholar] [CrossRef]
- Binfeng, Y.; Hu, G.; Zhang, R.; Yiping, C. Fano resonances in a plasmonic waveguide system composed of stub coupled with a square cavity resonator. J. Opt. 2016, 18, 055002. [Google Scholar] [CrossRef]
- Wang, G.; Lü, H.; Liu, X.M.; Gong, Y.; Wang, L. Optical bistability in metal-insulator-metal plasmonic waveguide with nanodisk resonator containing Kerr nonlinear medium. Appl. Opt. 2011, 50, 5287–5290. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Liu, Y.; Yu, Z.; Ye, H.; Peng, Y.; Shu, C.; Yang, C.; Zhang, W.; He, H. A nanometeric temperature sensor based on plasmonic waveguide with an ethanol-sealed rectangular cavity. Opt. Commun. 2015, 339, 1–6. [Google Scholar] [CrossRef]
- Tong, L.; Wei, H.; Zhang, S.; Xu, H. Recent Advances in Plasmonic Sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, J.; Zhao, Y.; Lu, N.; Xiong, Z. Numerical Investigation of a Branch-Shaped Filter Based on Metal-Insulator-Metal Waveguide. Plasmonics 2011, 6, 773–778. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef]
- Lee, K.-L.; Huang, J.-B.; Chang, J.-W.; Wu, S.-H.; Wei, P.-K. Ultrasensitive Biosensors Using Enhanced Fano Resonances in Capped Gold Nanoslit Arrays. Sci. Rep. 2015, 5, 8547. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Sun, C.; Gong, Q. Fano resonances in a single defect nanocavity coupled with a plasmonic waveguide. Opt. Lett. 2014, 39, 52–55. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Chao, C.-T.C.; Chiang, H.-P. Ultra-broad bandgap metal-insulator-metal waveguide filter with symmetrical stubs and defects. Results Phys. 2020, 17, 103116. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, F.; Chen, Y. Tunable Multichannel Plasmonic Filter Based on Coupling-Induced Mode Splitting. Plasmonics 2014, 10, 139–144. [Google Scholar] [CrossRef]
- Chau, Y.-F.C. Mid-infrared sensing properties of a plasmonic metal–insulator–metal waveguide with a single stub including defects. J. Phys. D Appl. Phys. 2020, 53, 115401. [Google Scholar] [CrossRef]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; Lei, L.; Guo, Z. Fano Resonance with Ultra-High Figure of Merits Based on Plasmonic Metal-Insulator-Metal Waveguide. Plasmonics 2014, 10, 27–32. [Google Scholar] [CrossRef]
- Akhavan, A.; Fard, H.G.; Abdolhosseini, S.; Habibiyan, H.; Ghafoorifard, H. Metal–insulator–metal waveguide-coupled asymmetric resonators for sensing and slow light applications. IET Optoelectron. 2018, 12, 220–227. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides. Appl. Phys. Lett. 2005, 87, 131102. [Google Scholar] [CrossRef]
- Khani, S.; Danaie, M.; Rezaei, P. Design of a Single-Mode Plasmonic Bandpass Filter Using a Hexagonal Resonator Coupled to Graded-Stub Waveguides. Plasmonics 2018, 14, 53–62. [Google Scholar] [CrossRef]
- Malmir, K.; Habibiyan, H.; Fard, H.G. An ultrasensitive optical label-free polymeric biosensor based on concentric triple microring resonators with a central microdisk resonator. Opt. Commun. 2016, 365, 150–156. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. Dual wavelength demultiplexer based on metal–insulator–metal plasmonic circular ring resonators. J. Mod. Opt. 2016, 63, 1078–1086. [Google Scholar] [CrossRef]
- Lü, H.; Wang, G.; Liu, X.M. Manipulation of light in MIM plasmonic waveguide systems. Chin. Sci. Bull. 2013, 58, 3607–3616. [Google Scholar] [CrossRef] [Green Version]
- Lü, H.; Liu, X.M.; Gong, Y.; Wang, L.; Mao, D. Multi-channel plasmonic waveguide filters with disk-shaped nanocavities. Opt. Commun. 2011, 284, 2613–2616. [Google Scholar] [CrossRef]
- Wang, G.; Lu, H. Unidirectional excitation of surface plasmon polaritons in T-shaped waveguide with nanodisk resonator. Opt. Commun. 2012, 285, 4190–4193. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.-Y.; Zhang, Z.-Y. Fano Resonance in a Gear-Shaped Nanocavity of the Metal–Insulator–Metal Waveguide. Plasmonics 2012, 8, 797–801. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.C.; Chao, C.-T.C.; Huang, H.J.; Kumara, N.; Lim, C.; Chiang, H.-P. Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects. Nanomaterials 2019, 9, 1433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Luo, L.; Xue, C.-Y.; Zhang, W.; Yan, S. Fano Resonance Based on Metal-Insulator-Metal Waveguide-Coupled Double Rectangular Cavities for Plasmonic Nanosensors. Sensors 2016, 16, 642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhan, S.; Li, H.; Cao, G.; He, Z.; Li, B.; Yang, H. Slow light based on plasmon-induced transparency in dual-ring resonator-coupled MDM waveguide system. J. Phys. D Appl. Phys. 2014, 47. [Google Scholar] [CrossRef]
- Ren, X.; Ren, K.; Cai, Y. Tunable compact nanosensor based on Fano resonance in a plasmonic waveguide system. Appl. Opt. 2017, 56. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Song, X.; Wang, Y.; Yu, L. Tunable triple Fano resonances based on multimode interference in coupled plasmonic resonator system. Opt. Express 2016, 24, 15351. [Google Scholar] [CrossRef]
- Zhao, T.; Yu, S. Ultra-High Sensitivity Nanosensor Based on Multiple Fano Resonance in the MIM Coupled Plasmonic Resonator. Plasmonics 2017, 13, 1115–1120. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yu, L. Independently Formed Multiple Fano Resonances for Ultra-High Sensitivity Plasmonic Nanosensor. Plasmonics 2016, 13, 107–113. [Google Scholar] [CrossRef]
- Wu, C.; Ding, H.; Huang, T.; Wu, X.; Chen, B.; Ren, K.; Fu, S. Plasmon-Induced Transparency and Refractive Index Sensing in Side-Coupled Stub-Hexagon Resonators. Plasmonics 2017, 13, 251–257. [Google Scholar] [CrossRef]
- Shi, X.; Ma, L.; Zhang, Z.; Tang, Y.; Zhang, Y.; Han, J.; Sun, Y. Dual Fano resonance control and refractive index sensors based on a plasmonic waveguide-coupled resonator system. Opt. Commun. 2018, 427, 326–330. [Google Scholar] [CrossRef]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; Lei, L.; Meng, Z. Single/Dual Fano Resonance Based on Plasmonic Metal-Dielectric-Metal Waveguide. Plasmonics 2015, 11, 315–321. [Google Scholar] [CrossRef]
- Sun, Y.-S.; Chau, Y.-F.C.; Yeh, H.-H.; Tsai, D.P. Highly Birefringent Index-Guiding Photonic Crystal Fiber with Squeezed Differently Sized Air-Holes in Cladding. Jpn. J. Appl. Phys. 2008, 47, 3755–3759. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.-Y.; Chau, Y.-F.C.; Huang, Y.-W.; Yeh, H.-Y.; Tsai, D.P. Design of high birefringence and low confinement loss photonic crystal fibers with five rings hexagonal and octagonal symmetry air-holes in fiber cladding. J. Appl. Phys. 2011, 109, 93103. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Theoretical investigation of compact couplers between dielectric slab waveguides and two-dimensional metal-dielectric-metal plasmonic waveguides. Opt. Express 2007, 15, 1211–1221. [Google Scholar] [CrossRef] [Green Version]
- Kuttge, M.; De Abajo, F.J.G.; Polman, A. Ultrasmall Mode Volume Plasmonic Nanodisk Resonators. Nano Lett. 2010, 10, 1537–1541. [Google Scholar] [CrossRef] [PubMed]
- Walther, C.; Scalari, G.; Amanti, M.I.; Beck, M.; Faist, J. Microcavity Laser Oscillating in a Circuit-Based Resonator. Science 2010, 327, 1495–1497. [Google Scholar] [CrossRef]
- Kamada, S.; Okamoto, T.; El-Zohary, S.E.; Haraguchi, M. Design optimization and fabrication of Mach- Zehnder interferometer based on MIM plasmonic waveguides. Opt. Express 2016, 24, 16224. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual. Available online: http://www.comsol.com (accessed on 3 October 2018).
- Bahramipanah, M.; Abrishamian, M.S.; Mirtaheri, S.A.; Liu, J.-M. Ultracompact plasmonic loop–stub notch filter and sensor. Sens. Actuators B Chem. 2014, 194, 311–318. [Google Scholar] [CrossRef]
- Chu, Y.; Schonbrun, E.; Yang, T.; Crozier, K.B. Experimental observation of narrow surface plasmon resonances in gold nanoparticle arrays. Appl. Phys. Lett. 2008, 93, 181108. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; He, H. The sensing characteristics of plasmonic waveguide with a single defect. Opt. Commun. 2014, 323, 44–48. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef] [PubMed]
- Min, C.; Wang, P.; Jiao, X.; Deng, Y.; Ming, H. Beam manipulating by metallic nano-optic lens containing nonlinear media. Opt. Express 2007, 15, 9541–9546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kekatpure, R.D.; Hryciw, A.; Barnard, E.S.; Brongersma, M.L. Solving dielectric and plasmonic waveguide dispersion relations on a pocket calculator. Opt. Express 2009, 17, 24112–24129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.T.; Wu, P.C.; Chen, C.J.; Chung, H.-Y.; Chau, Y.-F.C.; Kuan, C.H.; Tsai, D.P. Electromagnetic energy vortex associated with sub-wavelength plasmonic Taiji marks. Opt. Express 2010, 18, 19665–19671. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Yeh, H.-H.; Tsai, D.P. Surface plasmon effects excitation from three-pair arrays of silver-shell nanocylinders. Phys. Plasmas 2009, 16, 22303. [Google Scholar] [CrossRef]
- Ho, Y.Z.; Chen, W.T.; Huang, Y.-W.; Wu, P.C.; Tseng, M.L.; Wang, Y.T.; Chau, Y.-F.C.; Tsai, D.P. Tunable plasmonic resonance arising from broken-symmetric silver nanobeads with dielectric cores. J. Opt. 2012, 14, 114010. [Google Scholar] [CrossRef]
- Lin, C.-T.; Chang, M.-N.; Huang, H.J.; Chen, C.-H.; Sun, R.-J.; Liao, B.-H.; Chau, Y.-F.C.; Hsiao, C.-N.; Shiao, M.-H.; Tseng, F.-G. Rapid fabrication of three-dimensional gold dendritic nanoforests for visible light-enhanced methanol oxidation. Electrochim. Acta 2016, 192, 15–21. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Lim, C.; Lee, C.; Huang, H.J.; Lin, C.-T.; Kumara, N.; Yoong, V.N.; Chiang, H.-P. Tailoring surface plasmon resonance and dipole cavity plasmon modes of scattering cross section spectra on the single solid-gold/gold-shell nanorod. J. Appl. Phys. 2016, 120, 093110. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Syu, J.-Y.; Chao, C.-T.C.; Chiang, H.-P.; Lim, C. Design of crossing metallic metasurface arrays based on high sensitivity of gap enhancement and transmittance shift for plasmonic sensing applications. J. Phys. D Appl. Phys. 2016, 50, 045105. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Yeh, H.-H.; Liao, C.-C.; Ho, H.-F.; Liu, C.-Y.; Tsai, D.P. Controlling surface plasmon of several pair arrays of silver-shell nanocylinders. Appl. Opt. 2010, 49, 1163–1169. [Google Scholar] [CrossRef]
- Hsieh, L.-Z.; Chau, Y.-F.C.; Lim, C.; Lin, M.-H.; Huang, H.J.; Lin, C.-T.; Syafi’Ie, I.M.N. Metal nano-particles sizing by thermal annealing for the enhancement of surface plasmon effects in thin-film solar cells application. Opt. Commun. 2016, 370, 85–90. [Google Scholar] [CrossRef]
- Hu, C.-C.; Tsai, Y.-T.; Yang, W.; Chau, Y.-F.C. Effective Coupling of Incident Light Through an Air Region into an S-Shape Plasmonic Ag Nanowire Waveguide with Relatively Long Propagation Length. Plasmonics 2014, 9, 573–579. [Google Scholar] [CrossRef]
- Hu, C.; Yang, W.; Tsai, Y.T.; Chau, Y.F. Gap enhancement and transmittance spectra of a periodic bowtie nanoantenna array buried in a silica substrate. Opt. Commun. 2014, 324, 227–233. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Tsai, D.P. Three-dimensional analysis of silver nano-particles doping effects on super resolution near-field structure. Opt. Commun. 2007, 269, 389–394. [Google Scholar] [CrossRef]
- Nasirifar, R.; Danaie, M.; Dideban, A. Dual channel optical fiber refractive index sensor based on surface plasmon resonance. Optik 2019, 186, 194–204. [Google Scholar] [CrossRef]
- Zheng, G.; Su, W.; Chen, Y.; Zhang, C.; Lai, M.; Liu, Y. Band-stop filters based on a coupled circular ring metal–insulator–metal resonator containing nonlinear material. J. Opt. 2012, 14, 55001. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.; Yu, L.; Xiao, J. Sharp Trapped Resonances by Exciting the Anti-symmetric Waveguide Mode in a Metal-Insulator-Metal Resonator. Plasmonics 2014, 10, 131–137. [Google Scholar] [CrossRef]
- Rahmatiyar, M.; Danaie, M.; Afsahi, M. Employment of cascaded coupled resonators for resolution enhancement in plasmonic refractive index sensors. Opt. Quantum Electron. 2020, 52, 1–19. [Google Scholar] [CrossRef]
- Zhang, B.-H.; Wang, L.-L.; Li, H.-J.; Zhai, X.; Xia, S.-X. Two kinds of double Fano resonances induced by an asymmetric MIM waveguide structure. J. Opt. 2016, 18, 65001. [Google Scholar] [CrossRef]
- Luo, S.; Li, B.; Xiong, D.; Zuo, D.; Wang, X. A High Performance Plasmonic Sensor Based on Metal-Insulator-Metal Waveguide Coupled with a Double-Cavity Structure. Plasmonics 2016, 12, 223–227. [Google Scholar] [CrossRef]
- Guo, Z.; Wen, K.; Hu, Q.; Lai, W.; Lin, J.; Fang, Y. Plasmonic Multichannel Refractive Index Sensor Based on Subwavelength Tangent-Ring Metal–Insulator–Metal Waveguide. Sensors 2018, 18, 1348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chau, Y.-F.C.; Chao, C.T.C.; Huang, H.J.; Wang, Y.-C.; Chiang, H.-P.; Idris, M.N.S.M.; Masri, Z.; Lim, C.M. Strong and tunable plasmonic field coupling and enhancement generating from the protruded metal nanorods and dielectric cores. Results Phys. 2019, 13, 102290. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou Chao, C.-T.; Chou Chau, Y.-F.; Huang, H.J.; Kumara, N.T.R.N.; Kooh, M.R.R.; Lim, C.M.; Chiang, H.-P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials 2020, 10, 1399. https://doi.org/10.3390/nano10071399
Chou Chao C-T, Chou Chau Y-F, Huang HJ, Kumara NTRN, Kooh MRR, Lim CM, Chiang H-P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials. 2020; 10(7):1399. https://doi.org/10.3390/nano10071399
Chicago/Turabian StyleChou Chao, Chung-Ting, Yuan-Fong Chou Chau, Hung Ji Huang, N. T. R. N. Kumara, Muhammad Raziq Rahimi Kooh, Chee Ming Lim, and Hai-Pang Chiang. 2020. "Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods" Nanomaterials 10, no. 7: 1399. https://doi.org/10.3390/nano10071399
APA StyleChou Chao, C.-T., Chou Chau, Y.-F., Huang, H. J., Kumara, N. T. R. N., Kooh, M. R. R., Lim, C. M., & Chiang, H.-P. (2020). Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials, 10(7), 1399. https://doi.org/10.3390/nano10071399









