Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons
Abstract
:1. Introduction
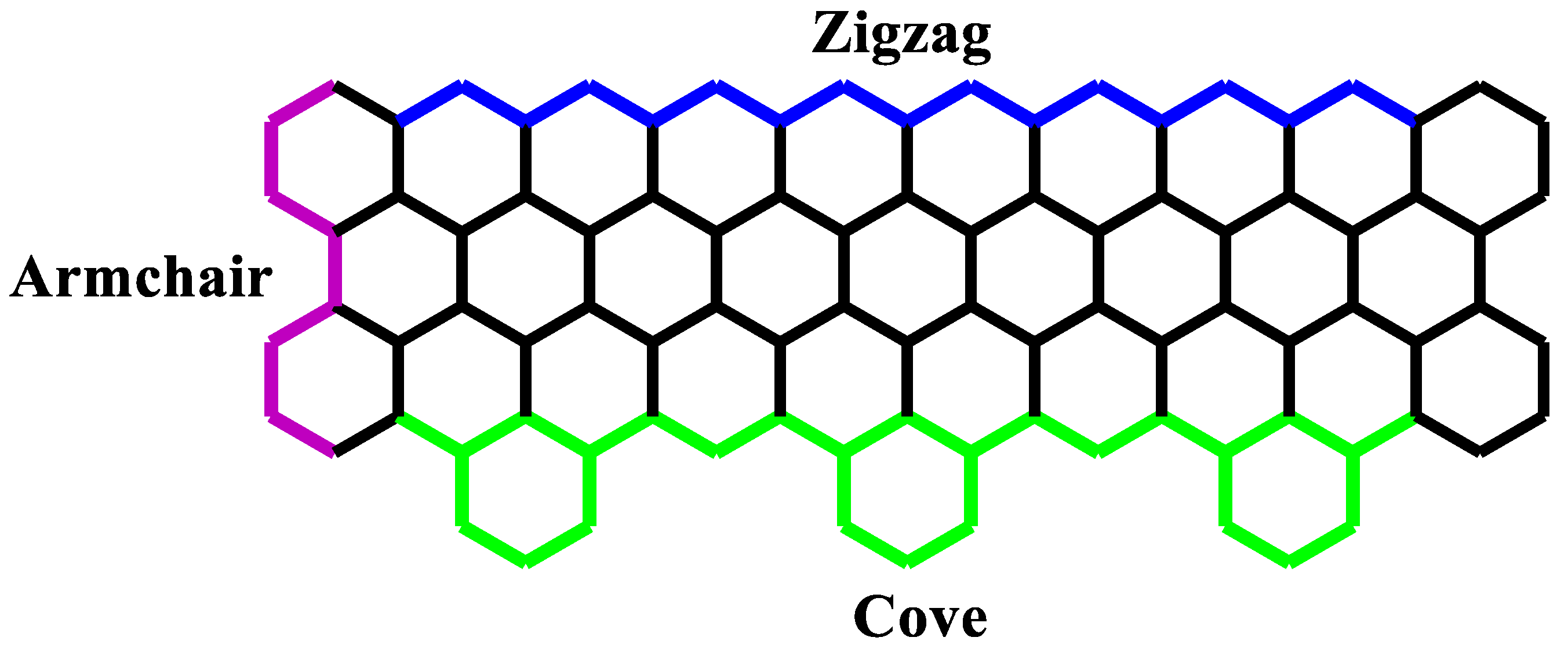
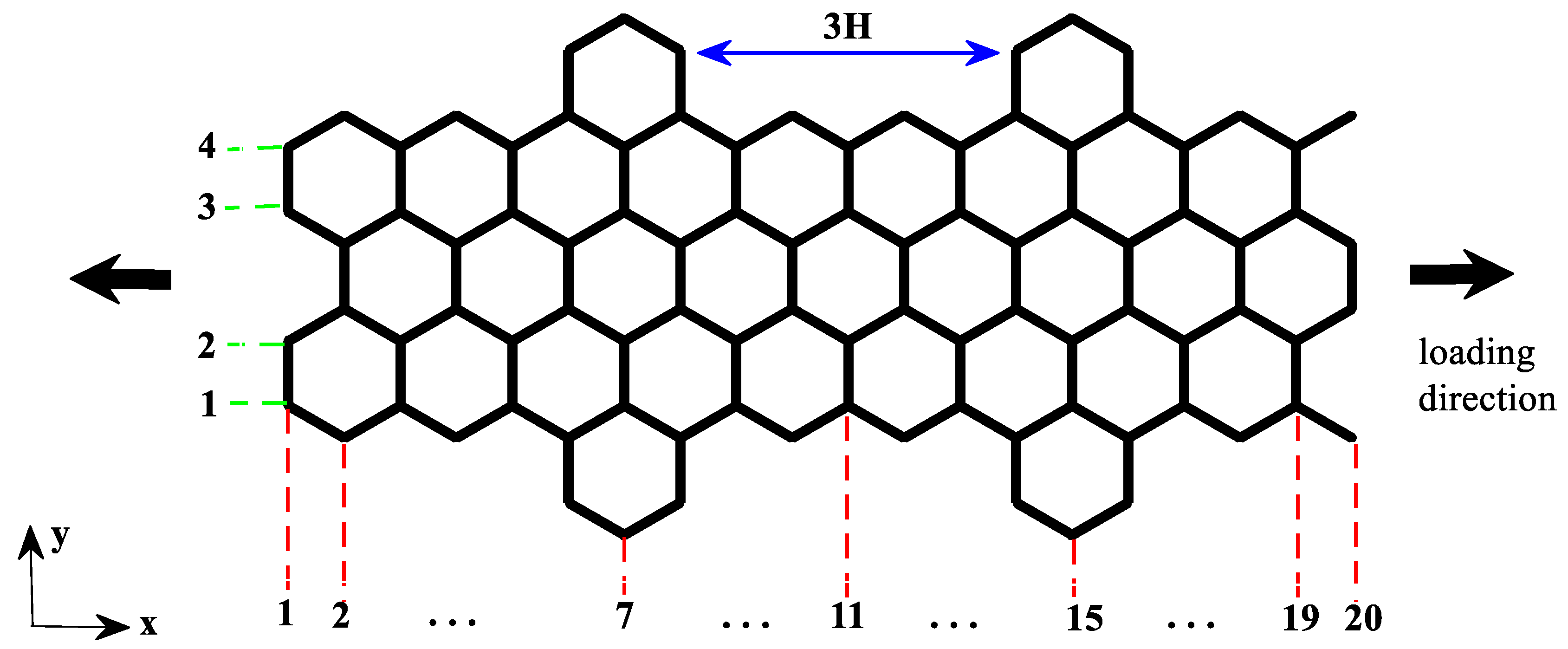
2. Methodology
3. Results and Discussion
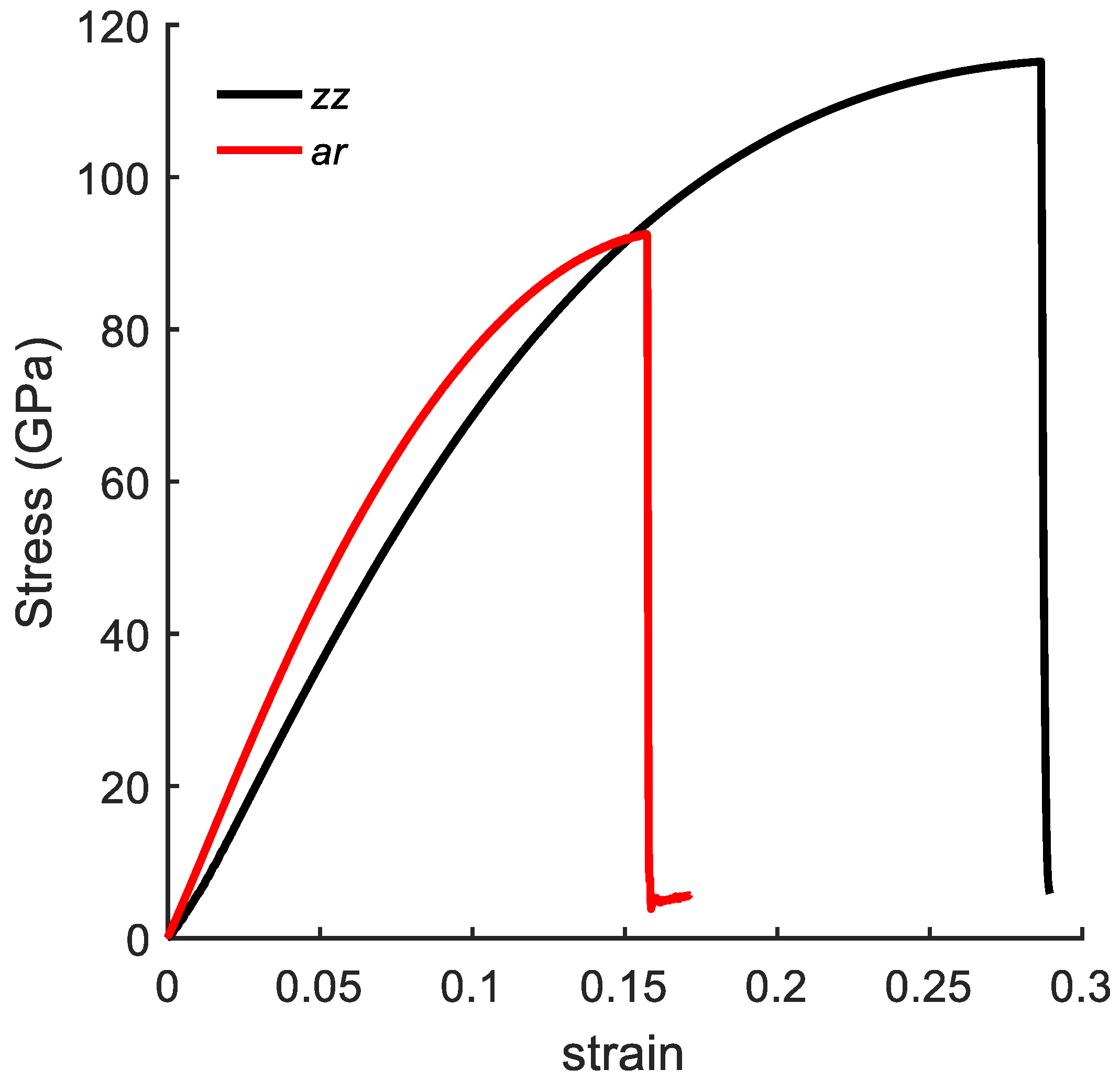
3.1. Validation of MD Simulation
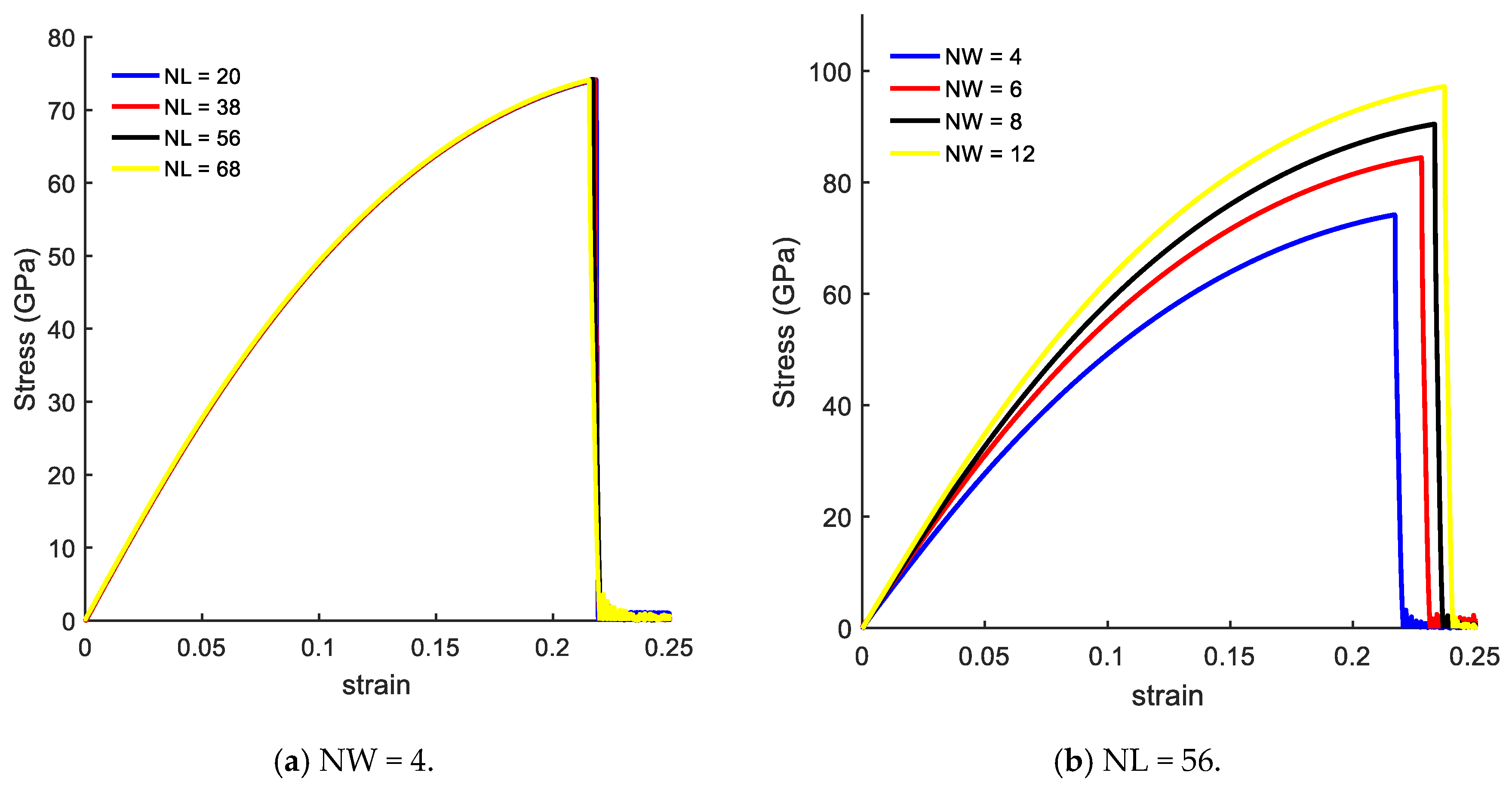
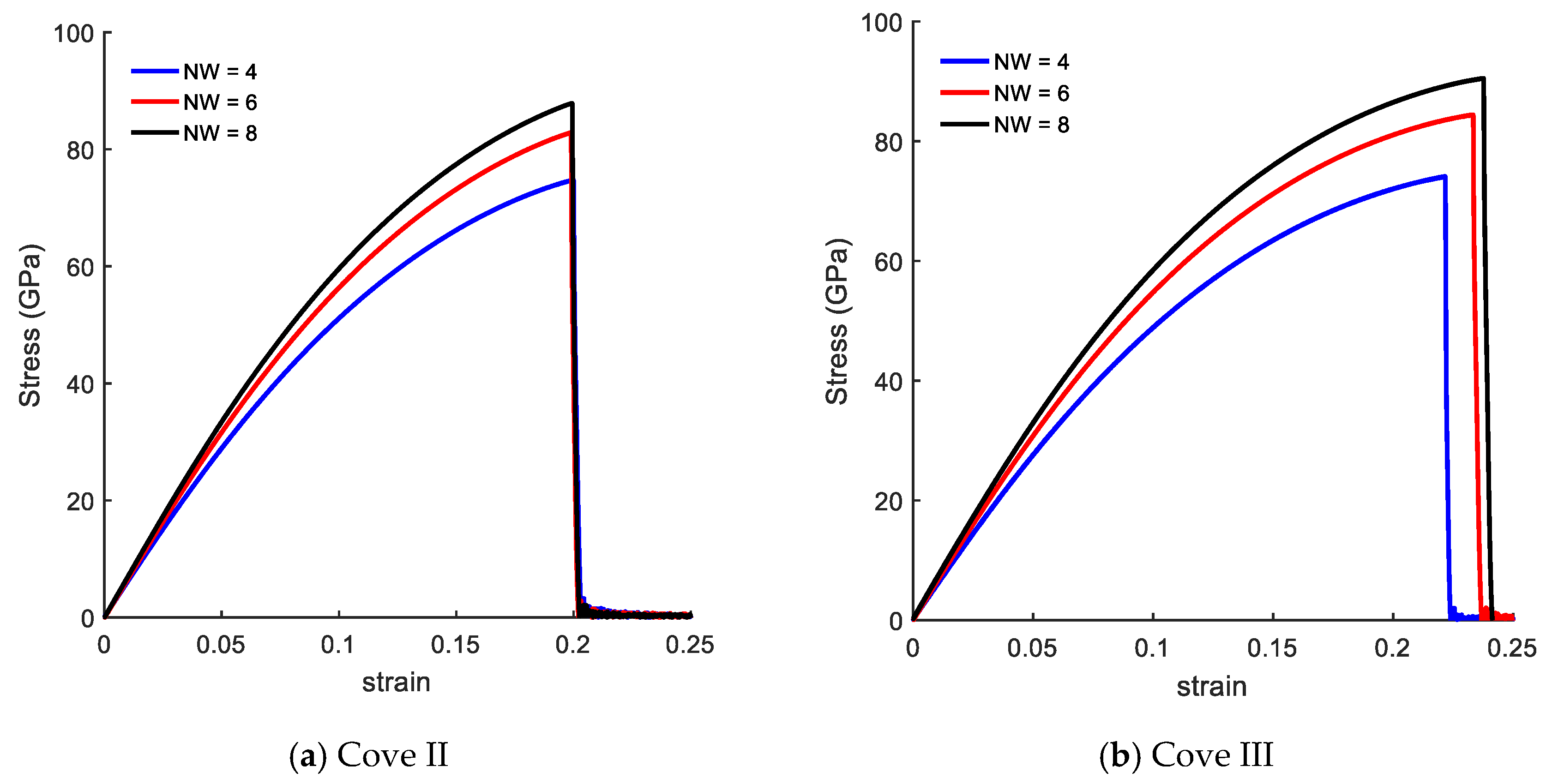
3.2. Size Effects on Mechanical Response of CGNR
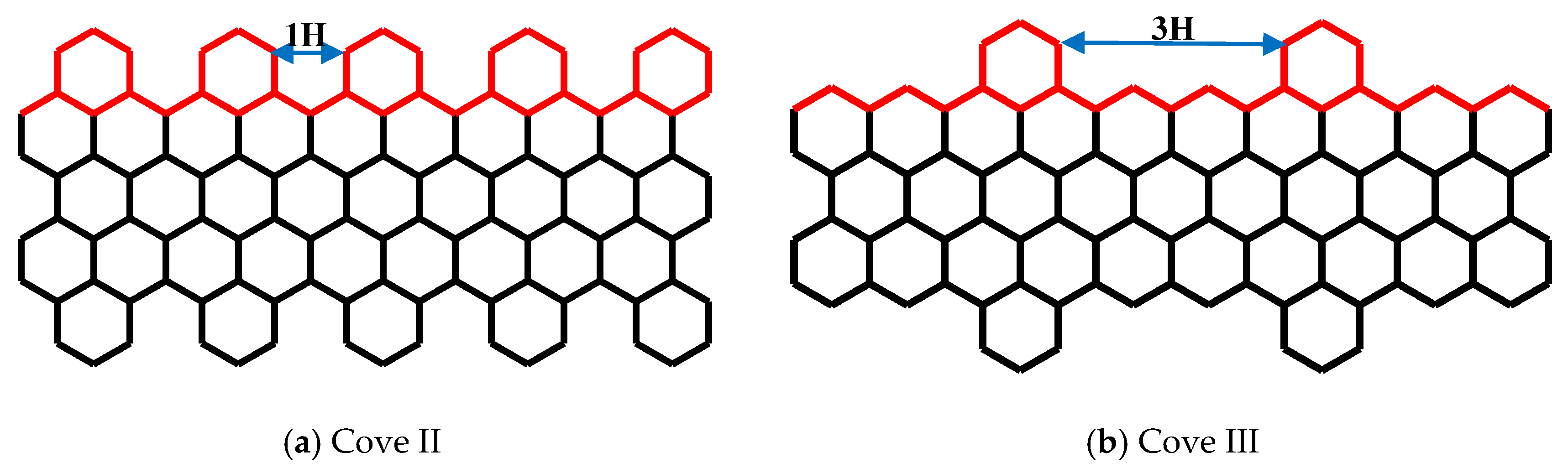
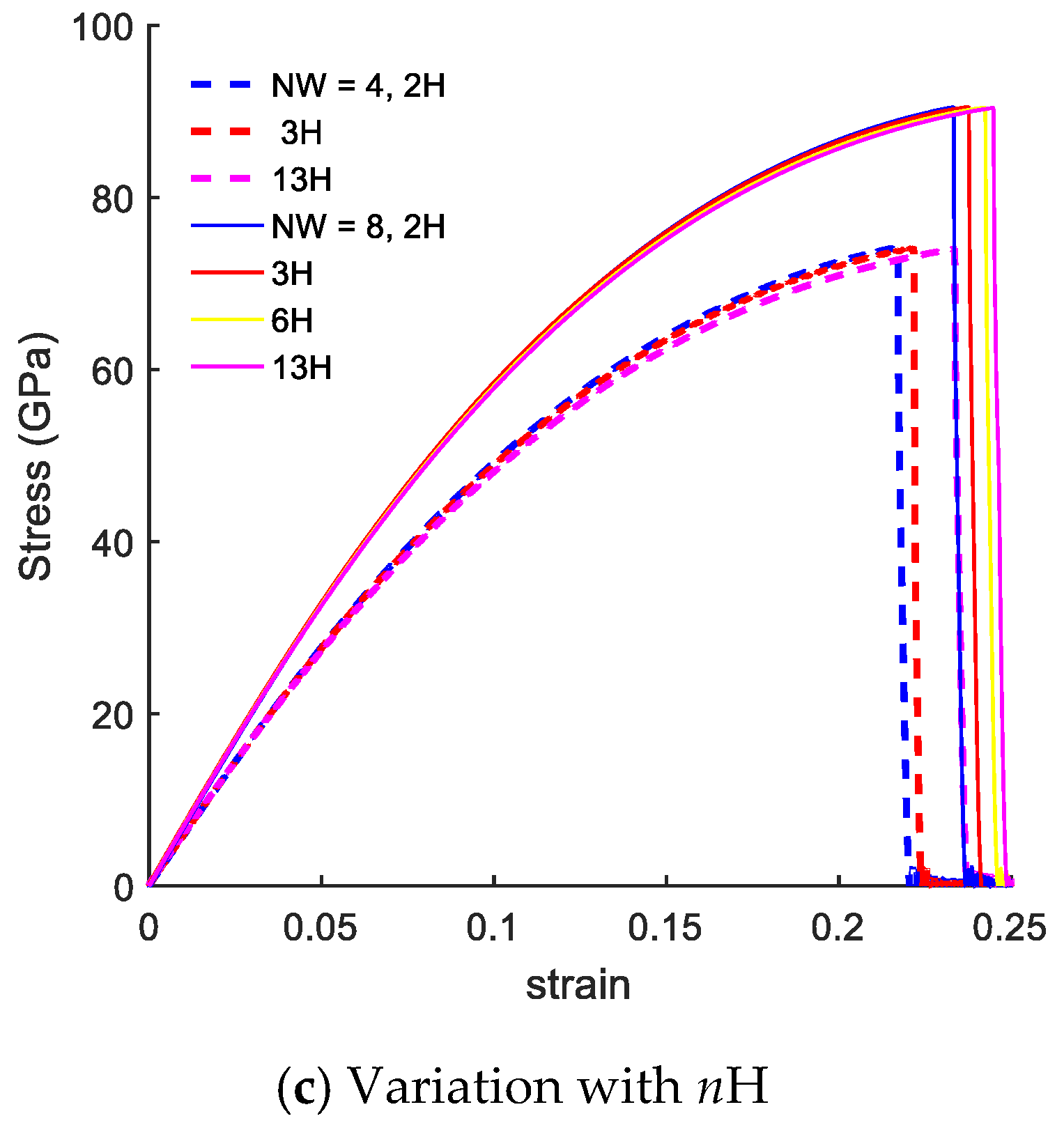
3.3. Edge Effects on the Mechanical Response of CGNR
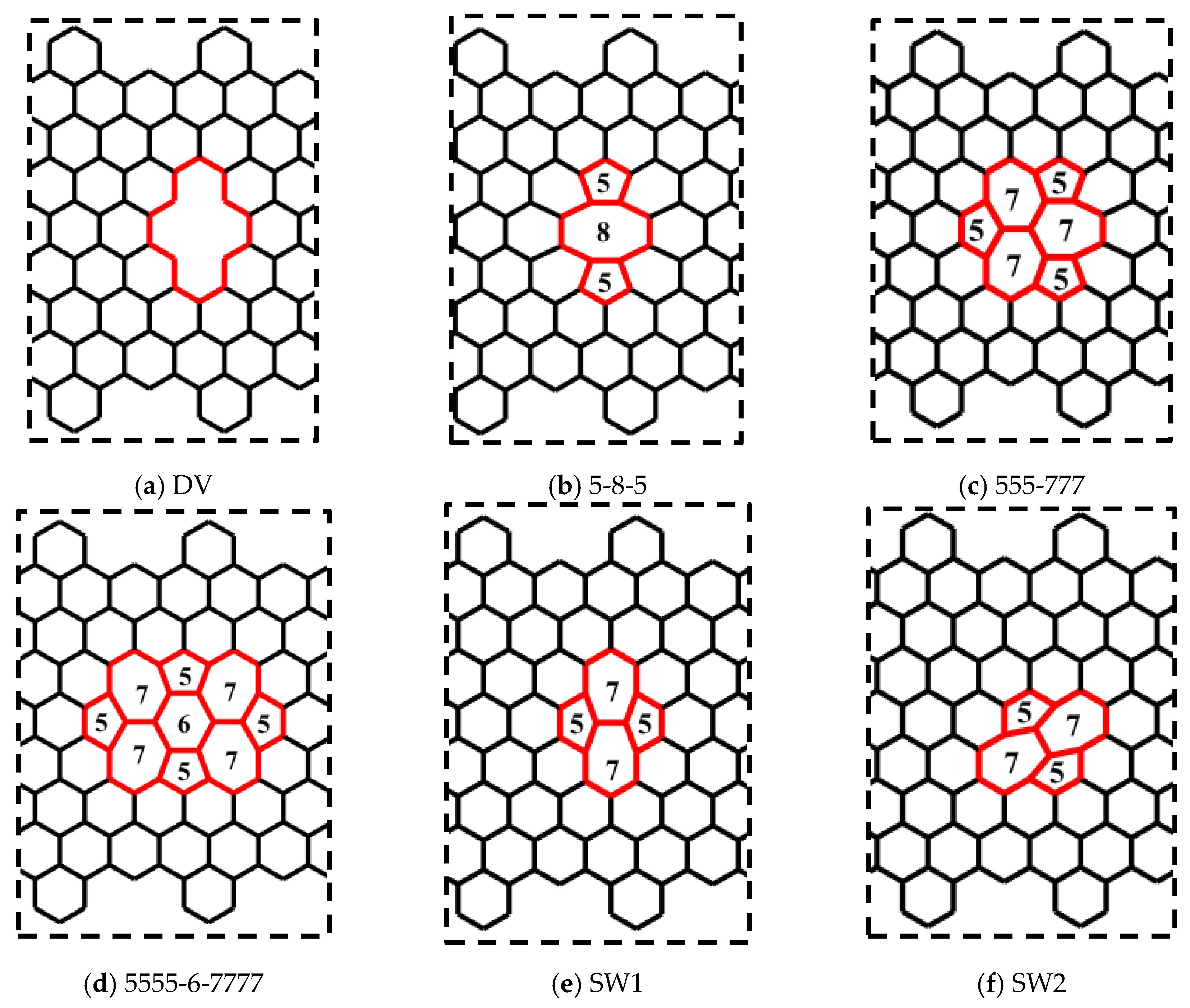
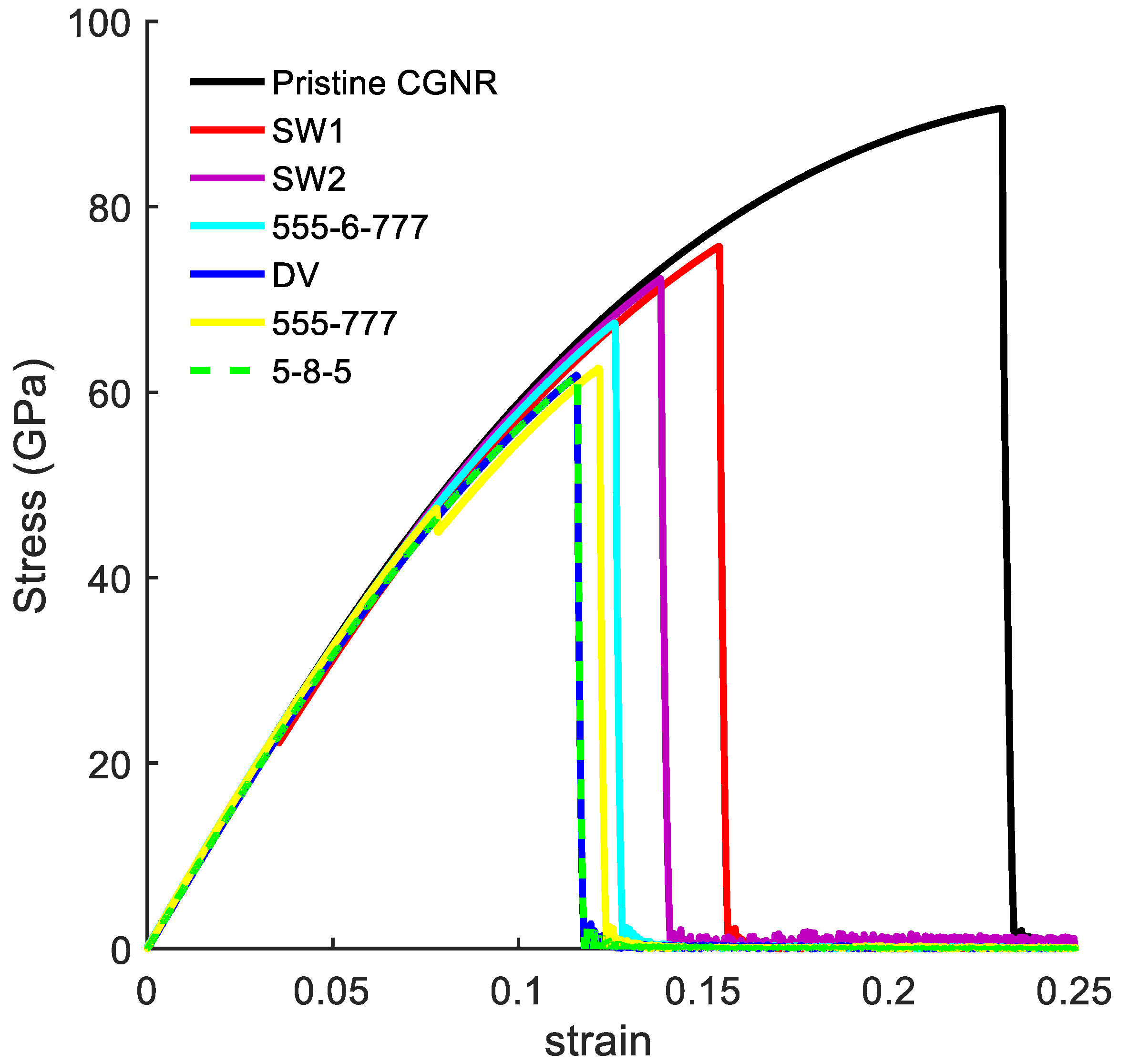
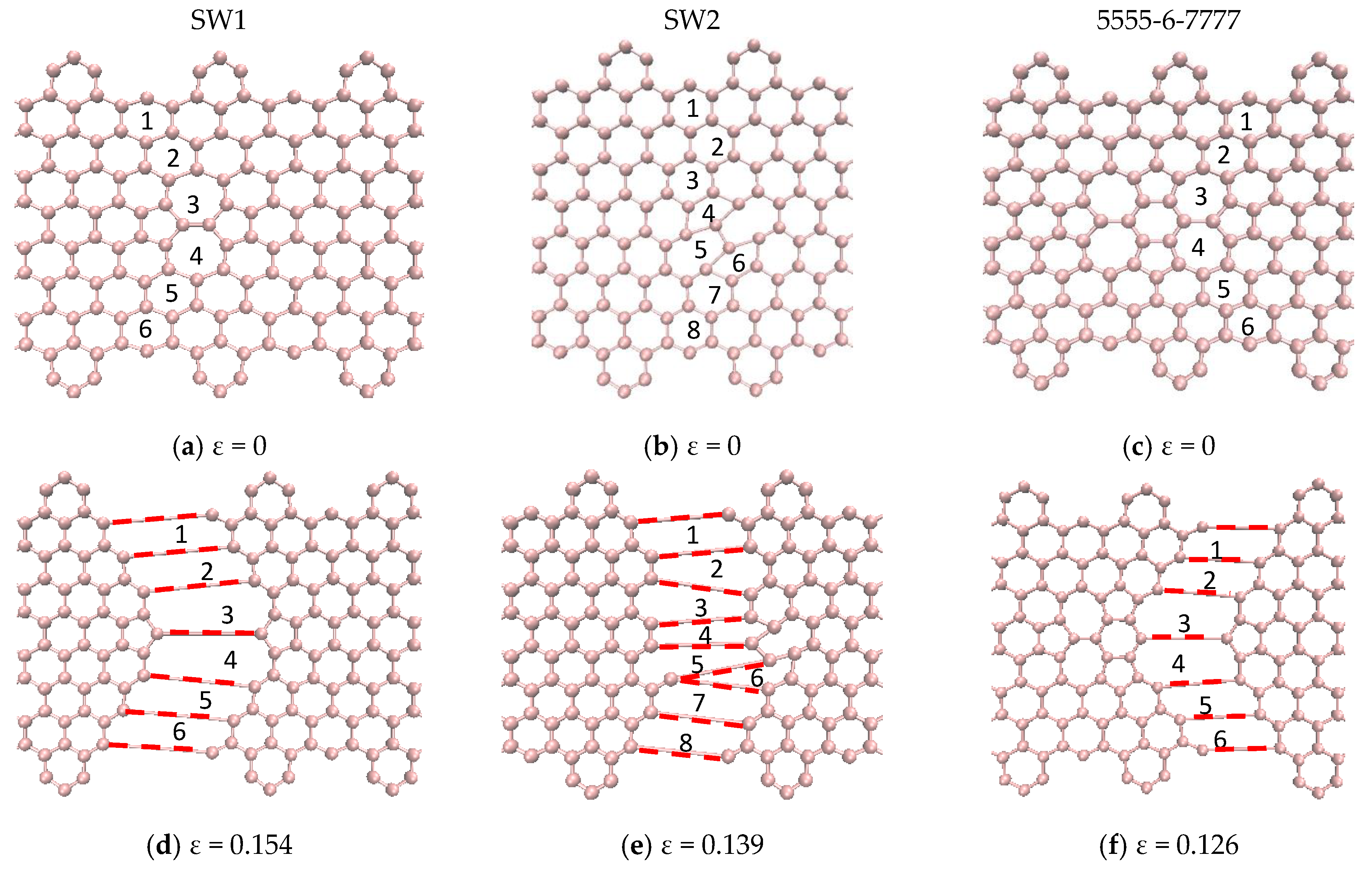
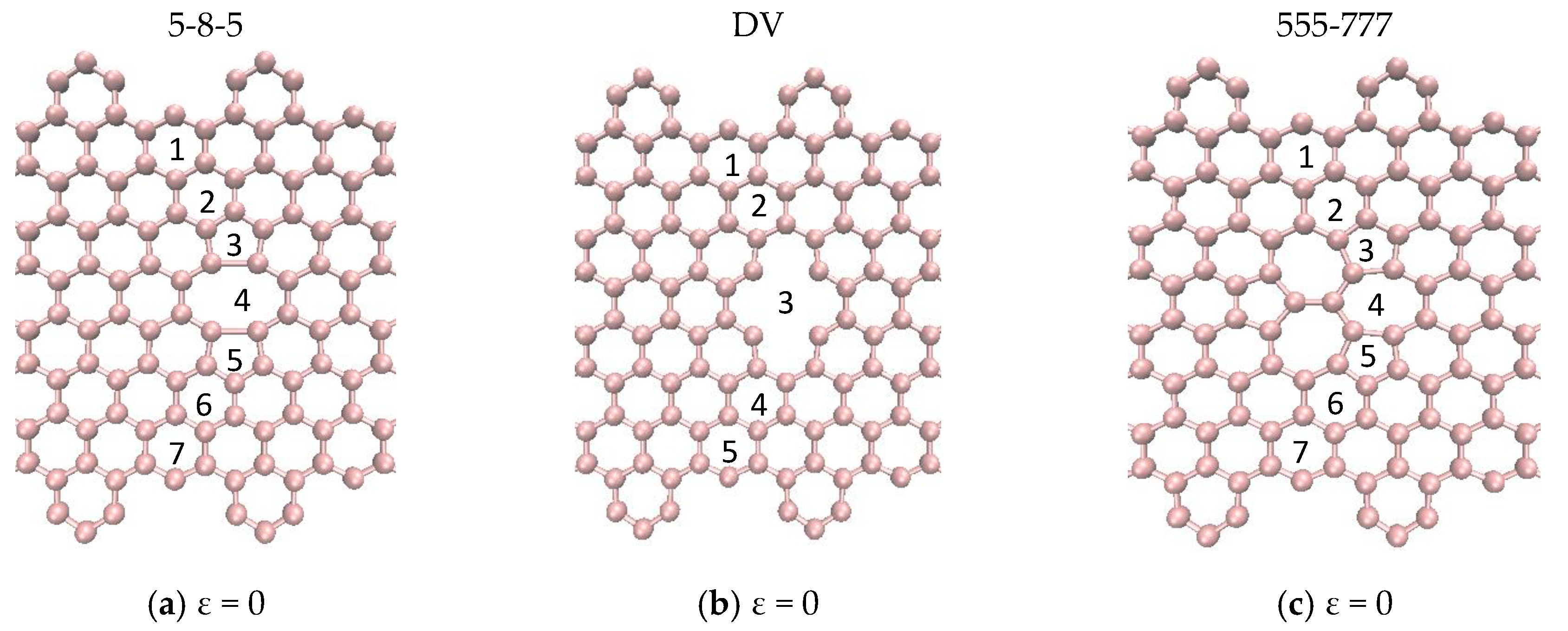
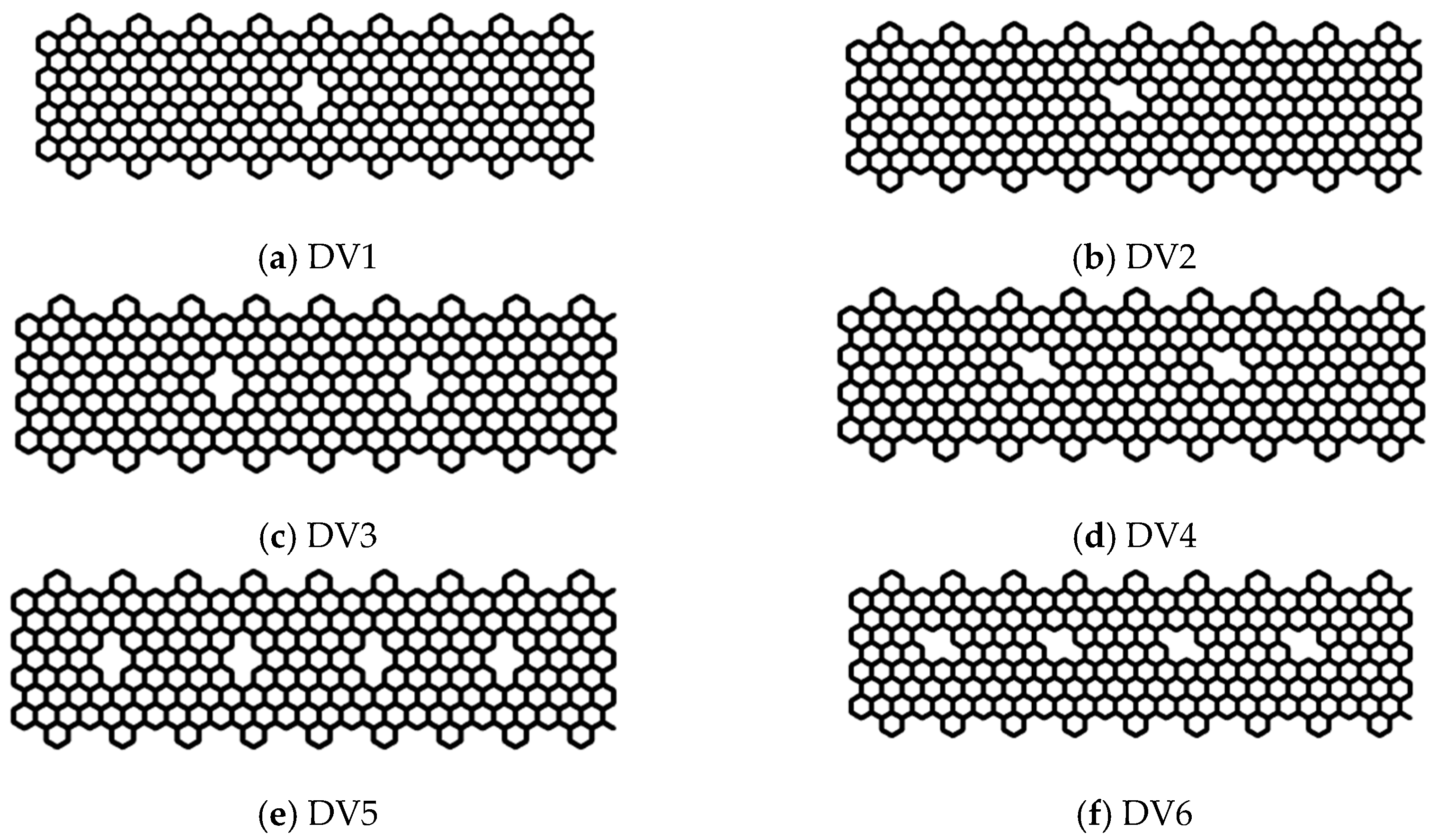
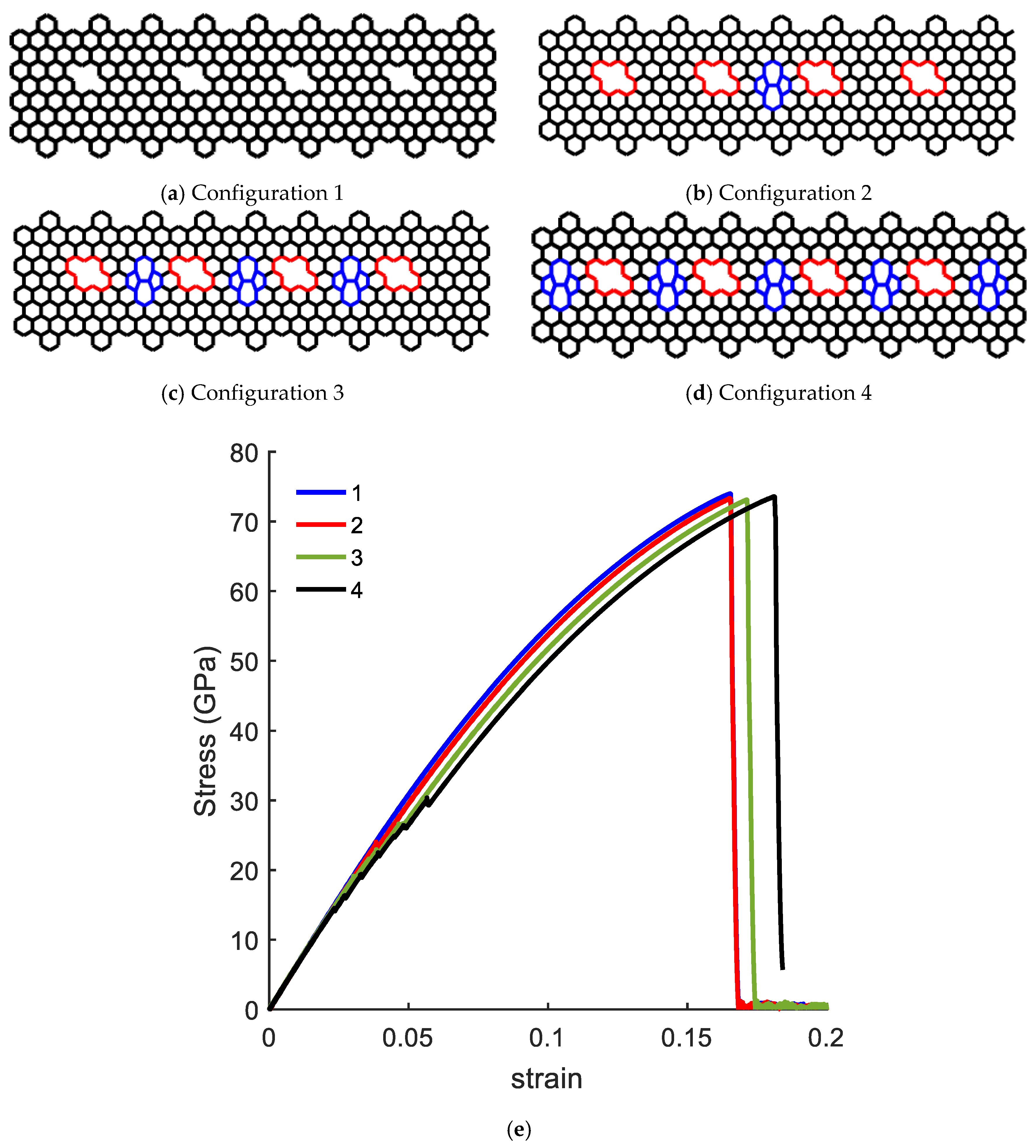
3.4. Topological and Vacancy Defects in CGNR
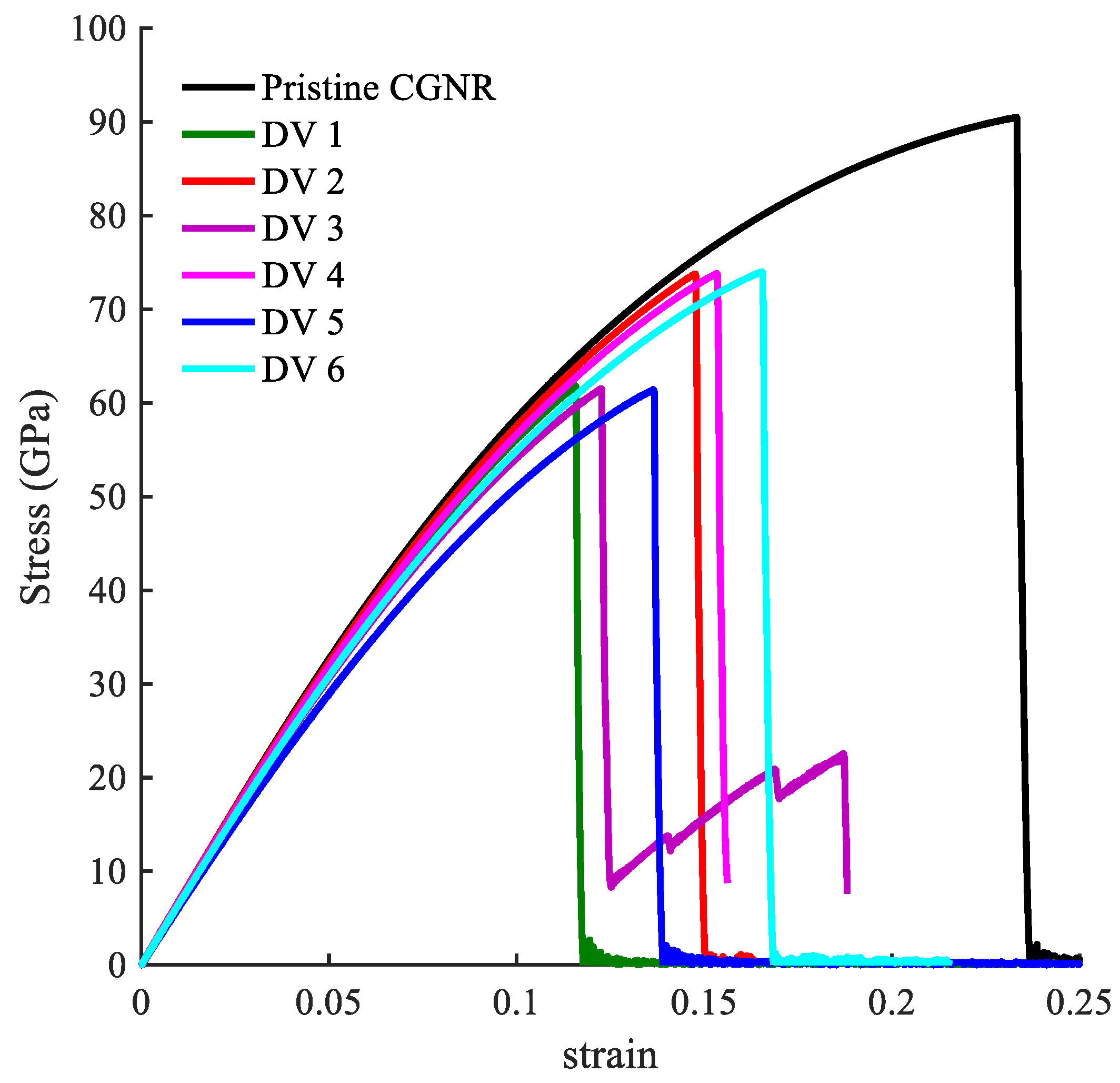
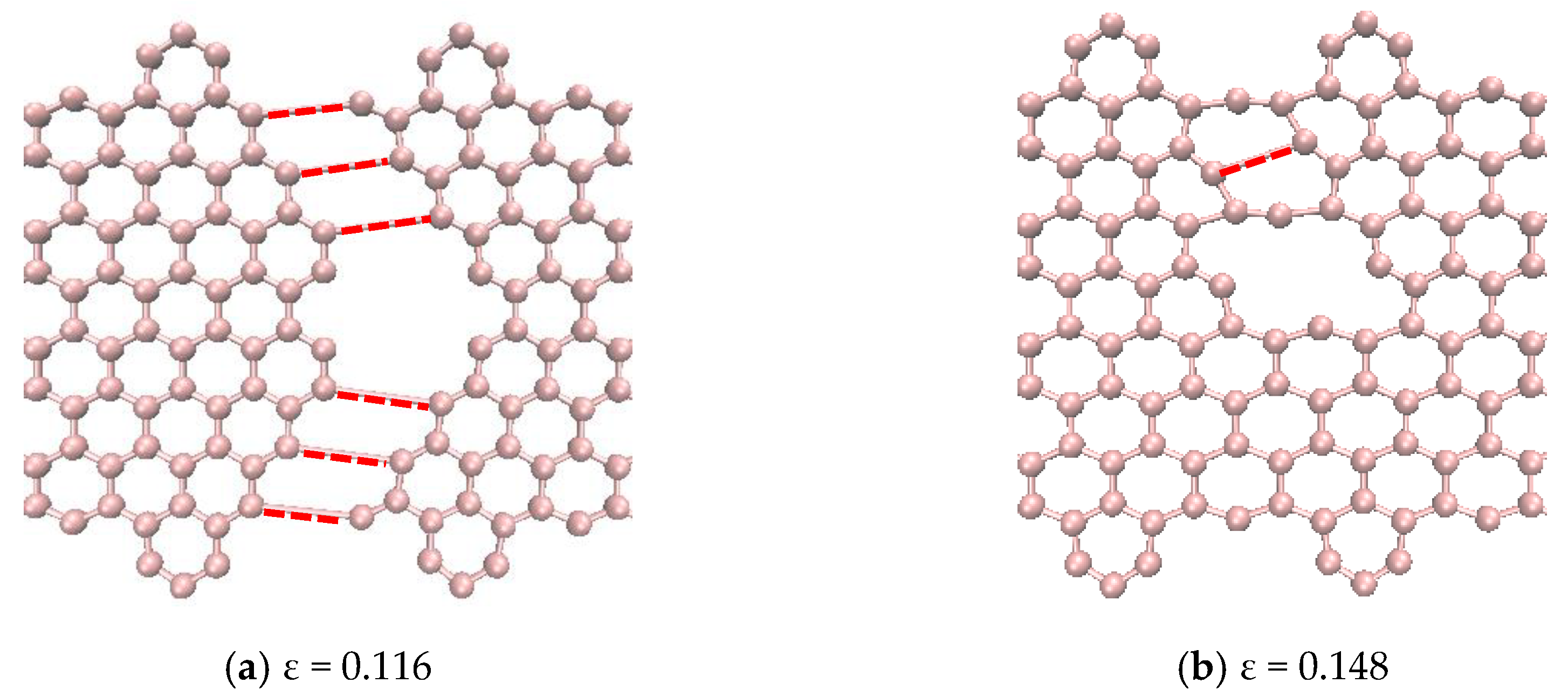
3.5. Vacancy Effects on the Mechanical Response of CGNR
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, B.W.; Tan, Y.Z.; Giannakopoulos, A.; Sanchez-Sanchez, C.; Beljonne, D.; Ruffieux, P.; Fasel, R.; Feng, X.; Müllen, K. Toward Cove-Edged Low Band Gap Graphene Nanoribbons. J. Am. Chem. Soc. 2015, 137, 6097–6103. [Google Scholar] [CrossRef] [Green Version]
- Talirz, L.; Söde, H.; Dumslaff, T.; Wang, S.; Sanchez-Valencia, J.R.; Liu, J.; Shinde, P.; Pignedoli, C.A.; Liang, L.; Meunier, V.; et al. On-Surface Synthesis and characterization of 9-atom wide armchair graphene nanoribbons. ACS Nano 2017, 11, 1380–1388. [Google Scholar] [CrossRef]
- Talirz, L.; Ruffieux, P.; Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 2016, 6222–6231. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Fukui, K.I.; Enoki, T.; Kusakabe, K.; Kaburagi, Y. Observation of zigzag and armchair edges of graphite using scanning tunneling microscopy and spectroscopy. Phys. Rev. B 2005, 71, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Ruffieux, P.; Cai, J.; Plumb, N.C.; Patthey, L.; Prezzi, D.; Ferretti, A.; Molinari, E.; Feng, X.; Müllen, K.; Pignedoli, C.A.; et al. Electronic structure of atomically precise graphene nanoribbons. ACS Nano 2012, 6, 6930–6935. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Ruffieux, P.; Jaafar, R.; Bieri, M.; Braun, T.; Blankenburg, S.; Muoth, M.; Seitsonen, A.P.; Saleh, M.; Feng, X.; et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 2010, 466, 470–473. [Google Scholar] [CrossRef]
- Zschieschang, U.; Klauk, H.; Müeller, I.B.; Strudwick, A.J.; Hintermann, T.; Schwab, M.G.; Narita, A.; Feng, X.; Müellen, K.; Weitz, R.T. Electrical characteristics of field-effect transistors based on chemically Synthesized graphene nanoribbons. Adv. Electron. Mater. 2015, 1, 1–5. [Google Scholar] [CrossRef]
- Rizzo, D.J.; Veber, G.; Cao, T.; Bronner, C.; Chen, T.; Zhao, F.; Rodriguez, H.; Louie, S.G.; Crommie, M.F.; Fischer, F.R. Topological band engineering of graphene nanoribbons. Nature 2018, 560, 204–208. [Google Scholar] [CrossRef] [PubMed]
- Puster, M.; Rodríguez-Manzo, J.A.; Balan, A.; Drndić, M. Toward sensitive graphene nanoribbon-nanopore devices by preventing electron beam-induced damage. ACS Nano 2013, 7, 11283–11289. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, K.; Yamanaka, A.; Okada, S. Mechanical properties of graphene nanoribbons under uniaxial tensile strain. Jpn. J. Appl. Phys. 2018, 57. [Google Scholar] [CrossRef]
- Narita, A.; Feng, X.; Hernandez, Y.; Jensen, S.A.; Bonn, M.; Yang, H.; Verzhbitskiy, I.A.; Casiraghi, C.; Hansen, M.R.; Koch, A.H.R.; et al. Synthesis of structurally well-defined and liquid-phase-processable graphene nanoribbons. Nat. Chem. 2014, 6, 126–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konnerth, R.; Cervetti, C.; Narita, A.; Feng, X.; Müllen, K.; Hoyer, A.; Burghard, M.; Kern, K.; Dressel, M.; Bogani, L. Tuning the deposition of molecular graphene nanoribbons by surface functionalization. Nanoscale 2015, 7, 12807–12811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vicarelli, L.; Heerema, S.J.; Dekker, C.; Zandbergen, H.W. Controlling defects in graphene for optimizing the electrical properties of graphene nanodevices. ACS Nano 2015, 9, 3428–3435. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.N.; Liu, G.; Narita, A.; Orosco, M.; Feng, X.; Müllen, K.; Zhou, C. Deposition, characterization, and thin-film-based chemical sensing of ultra-long chemically synthesized graphene nanoribbons. J. Am. Chem. Soc. 2014, 136, 7555–7558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanov, I.; Hu, Y.; Osella, S.; Beser, U.; Wang, H.I.; Beljonne, D.; Narita, A.; Müllen, K.; Turchinovich, D.; Bonn, M. Role of edge engineering in photoconductivity of graphene nanoribbons. J. Am. Chem. Soc. 2017, 139, 7982–7988. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.; Zhao, F.; Louie, S.G. Topological phases in graphene nanoribbons: Junction states, spin centers, and quantum spin chains. Phys. Rev. Lett. 2017, 119, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Narita, A.; Chen, Z.; Chen, Q.; Müllen, K. Solution and on-surface synthesis of structurally defined graphene nanoribbons as a new family of semiconductors. Chem. Sci. 2019, 10, 964–975. [Google Scholar] [CrossRef] [Green Version]
- Sisto, T.J.; Zhong, Y.; Zhang, B.; Trinh, M.T.; Miyata, K.; Zhong, X.; Zhu, X.Y.; Steigerwald, M.L.; Ng, F.; Nuckolls, C. Long, atomically precise donor-acceptor cove-edge nanoribbons as electron acceptors. J. Am. Chem. Soc. 2017, 139, 5648–5651. [Google Scholar] [CrossRef]
- Fu, Y.; Ragab, T.; Basaran, C. The effect of Stone-Wales defects on the mechanical behavior of graphene nano-ribbons. Comput. Mater. Sci. 2016, 124, 142–150. [Google Scholar] [CrossRef]
- Chu, Y.; Ragab, T.; Basaran, C. The size effect in mechanical properties of finite-sized graphene nanoribbon. Comput. Mater. Sci. 2014, 81, 269–274. [Google Scholar] [CrossRef]
- Zhang, J.; Ragab, T.; Basaran, C. Comparison of fracture behavior of defective armchair and zigzag graphene nanoribbons. Int. J. Damage Mech. 2019, 28, 325–345. [Google Scholar] [CrossRef] [Green Version]
- Bu, H.; Chen, Y.; Zou, M.; Yi, H.; Bi, K.; Ni, Z. Atomistic simulations of mechanical properties of graphene nanoribbons. Phys. Lett. A 2009, 373, 3359–3362. [Google Scholar] [CrossRef]
- Zhao, H.; Min, K.; Aluru, N.R. Size and chirality dependent elastic properties of graphene Nanoribbons under uniaxial tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, D.A.; Mesquita, E.; Rajapakse, R.K.N.D.; Pavanello, R. Atomic-scale finite element modelling of mechanical behaviour of graphene nanoribbons. Int. J. Mech. Mater. Des. 2018, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mazilova, T.I.; Sadanov, E.V.; Mikhailovskij, I.M. Tensile strength of graphene nanoribbons: An experimental approach. Mater. Lett. 2019, 242, 17–19. [Google Scholar] [CrossRef]
- Koch, M.; Li, Z.; Nacci, C.; Kumagai, T.; Franco, I.; Grill, L. How structural defects affect the mechanical and electrical properties of single molecular wires. Phys. Rev. Lett. 2018, 121, 47701. [Google Scholar] [CrossRef] [Green Version]
- Pincak, R.; Smotlacha, J.; Osipov, V.A. Electronic states of zigzag graphene nanoribbons with edges reconstructed with topological defects. Phys. B Condens. Matter 2015, 475, 61–65. [Google Scholar] [CrossRef] [Green Version]
- Smotlacha, J.; Pincak, R. Electronic properties of phosphorene and graphene nanoribbons with edge vacancies in magnetic field. Phys. Lett. A 2018, 382, 846–854. [Google Scholar] [CrossRef] [Green Version]
- Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related species. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Terrones, H.; Lv, R.; Terrones, M.; Dresselhaus, M.S. The role of defects and doping in 2D graphene sheets and 1D nanoribbons. Rep. Prog. Phys. 2012, 75. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An extended defect in graphene as a metallic wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef] [PubMed]
- Sahan, Z.; Berber, S. Divacancy in graphene nano-ribbons. Phys. E Low-Dimens. Syst. Nanostructures 2019, 106, 239–249. [Google Scholar] [CrossRef]
- Botello-Méndez, A.R.; Declerck, X.; Terrones, M.; Terrones, H.; Charlier, J.C. One-dimensional extended lines of divacancy defects in graphene. Nanoscale 2011, 3, 2868–2872. [Google Scholar] [CrossRef]
- Tang, G.P.; Zhou, J.C.; Zhang, Z.H.; Deng, X.Q.; Fan, Z.Q. A theoretical investigation on the possible improvement of spin-filter effects by an electric field for a zigzag graphene nanoribbon with a line defect. Carbon 2013, 60, 94–101. [Google Scholar] [CrossRef]
- Kaur, S.; Narang, S.B.; Randhawa, D.K.K. Influence of the pore shape and dimension on the enhancement of thermoelectric performance of graphene nanoribbons. J. Mater. Res. 2017, 32, 1149–1159. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, H.; Wei, J.; Li, B.; Xu, D. Atomistic simulations of divacancy defects in armchair graphene nanoribbons: Stability, electronic structure, and electron transport properties. Phys. Lett. A 2014, 378, 416–420. [Google Scholar] [CrossRef]
- Tabarraei, A.; Shadalou, S.; Song, J.-H. Mechanical properties of graphene nanoribbons with disordered edges. Comput. Mater. Sci. 2015, 96, 10–19. [Google Scholar] [CrossRef]
- Bizao, R.A.; Botari, T.; Perim, E.; Pugno, N.M.; Galvao, D.S. Mechanical properties and fracture patterns of graphene (graphitic) nanowiggles. Carbon 2017, 119, 431–437. [Google Scholar] [CrossRef] [Green Version]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, X. Mechanical properties of nanoporous graphene membrane. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Osella, S.; Narita, A.; Schwab, M.G.; Hernandez, Y.; Feng, X.; Müllen, K.; Beljonne, D. Graphene nanoribbons as low band gap donor materials for organic photovoltaics: Quantum chemical aided design. ACS Nano 2012, 6, 5539–5548. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Dewapriya, M.A.N.; Rajapakse, R.K.N.D.; Phani, A.S. Atomistic and continuum modelling of temperature-dependent fracture of graphene. Int. J. Fract. 2014, 187, 199–212. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Rajasekaran, G.; Narayanan, P.; Parashar, A. Effect of point and line defects on mechanical and thermal properties of graphene: A review. Crit. Rev. Solid State Mater. Sci. 2016, 41, 47–71. [Google Scholar] [CrossRef]
- Cao, G. Atomistic studies of mechanical properties of graphene. Polymers 2014, 6, 2404–2432. [Google Scholar] [CrossRef]
- Damasceno, D.A.; Rajapakse, R.K.N.D.; Mesquita, E.; Pavanello, R. Atomistic simulation of tensile strength properties of graphene with complex vacancy and topological defects. Acta Mech. 2020. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Dahanayaka, M.; Liu, B.; Korznikova, E.A.; Dmitriev, S.V.; Wu, M.S.; Zhou, K. Characterization of two carbon allotropes, cyclicgraphene and graphenylene, as semi-permeable materials for membranes. Mater. Sci. Eng. B 2020, 259, 114569. [Google Scholar] [CrossRef]
- Terrones, M.; Botello-Méndez, A.R.; Campos-Delgado, J.; López-Urías, F.; Vega-Cantú, Y.I.; Rodríguez-Macías, F.J.; Elías, A.L.; Muñoz-Sandoval, E.; Cano-Márquez, A.G.; Charlier, J.C.; et al. Graphene and graphite nanoribbons: Morphology, properties, synthesis, defects and applications. Nano Today 2010, 5, 351–372. [Google Scholar] [CrossRef]
- Traversi, F.; Raillon, C.; Benameur, S.M.; Liu, K.; Khlybov, S.; Tosun, M.; Krasnozhon, D.; Kis, A.; Radenovic, A. Detecting the translocation of DNA through a nanopore using graphene nanoribbons. Nat. Nanotechnol. 2013, 8, 939–945. [Google Scholar] [CrossRef] [PubMed]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damasceno, D.A.; Rajapakse, R.K.N.D.N.; Mesquita, E. Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons. Nanomaterials 2020, 10, 1422. https://doi.org/10.3390/nano10071422
Damasceno DA, Rajapakse RKNDN, Mesquita E. Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons. Nanomaterials. 2020; 10(7):1422. https://doi.org/10.3390/nano10071422
Chicago/Turabian StyleDamasceno, Daniela A., R.K.N.D. Nimal Rajapakse, and Euclides Mesquita. 2020. "Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons" Nanomaterials 10, no. 7: 1422. https://doi.org/10.3390/nano10071422
APA StyleDamasceno, D. A., Rajapakse, R. K. N. D. N., & Mesquita, E. (2020). Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons. Nanomaterials, 10(7), 1422. https://doi.org/10.3390/nano10071422




