Experimental and Theoretical Studies of Methyl Orange Uptake by Mn–Rich Synthetic Mica: Insights into Manganese Role in Adsorption and Selectivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
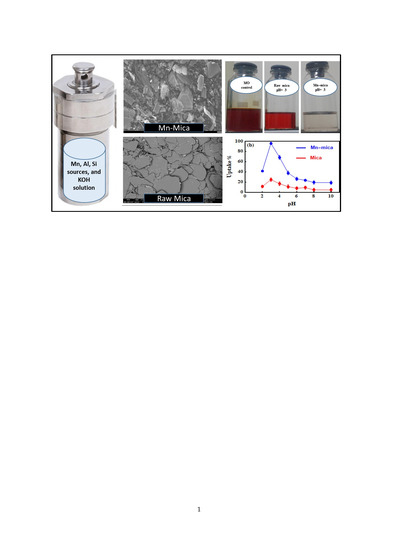
2.2. Synthesis of Mn–Rich Mica
2.3. Characterization of Mn–mica
2.4. Effect of pH on Methyl Orange (MO) Uptake by Mn–mica
2.5. MO Adsorption Kinetics Using Mn–mica
2.6. Equilibrium Studies of MO Adsorption on Mn–mica
2.7. Conventional and Advanced Dye Adsorption Modeling
- ❖
- Status 1: n and N2 are free adjustable parameters (i.e., multilayer).
- ❖
- Status 2: n is a free adjustable parameter and N2 = zero (fixed) (i.e., a monolayer).
- ❖
- Status 3: n is a free adjustable parameter and N2 =1 (fixed) (i.e., double–layer)
- ❖
- Status 4: n is a free adjustable parameter and N2 =2 (fixed) (i.e., triple–layer)
- ❖
- Status: n = unity (fixed) and N2 = zero (fixed) (i.e., Langmuir model)
3. Results and Discussions
3.1. Characterization of Mn–mica
3.2. Effect of pH on the MO Adsorption by Mn–mica
3.3. Contact Time Effect on MO Uptake by Mn–mica
3.4. MO Adsorption Kinetics
3.5. Dye Adsorption Modelling with Traditional Equations
3.6. Dye Adsorption Modelling with Advanced Equations
3.6.1. The n Parameter
3.6.2. The DM Parameter
3.6.3. Total Number of the Adsorbed MO Layers (Nt = 1 + N2)
3.6.4. Adsorption Capacity of MO at Saturation (Qsat = n·DM·Nt)
3.7. Dye Adsorption Energy (ΔE)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Komarneni, S.; Roy, R. Topotactic route to synthesis of novel hydroxylated phases: I. Trioctahedral micas. Clay Miner. 1986, 21, 125–131. [Google Scholar] [CrossRef]
- Choi, J.; Komarneni, S.; Grover, K.; Katasuki, H.; Park, M. Hydrothermal synthesis of Mn–mica. Appl. Clay Sci. 2009, 46, 69–72. [Google Scholar] [CrossRef]
- Komarneni, S.; Fregeau, E.; Breval, E.; Roy, R. Hydrothermal preparation of ultrafine ferrites and their sintering. J. Am. Ceram. Soc. 1998, 71, C26–C28. [Google Scholar] [CrossRef]
- Ishida, K.; Howthorne, F.C.; Hirowatari, F. Shirozulite, KMn2+(Si3Al)O10(OH)2, a new manganese-dominant trioctahedral mica: Description and crystal structure. Am. Mineral. 2004, 89, 232–238. [Google Scholar] [CrossRef]
- Selim, A.Q.; Mohamed, E.A.; Seliem, M.K.; Zayed, A.M. Synthesis of sole cancrinite phase from raw muscovite: Characterization and optimization. J. Alloy. Compd. 2018, 762, 653–667. [Google Scholar] [CrossRef]
- Yang, J.-S.; Lee, J.Y.; Park, Y.-T.; Baek, K.; Choi, J. Adsorption of As(III), As(V), Cd(II), Cu(II), and Pb(II) from Aqueous Solutions by Natural Muscovite. Sep. Sci. Technol. 2010, 45, 814–823. [Google Scholar] [CrossRef]
- Abukhadra, M.R.; Mostafa, M. Effective decontamination of phosphate and ammonium utilizing novel muscovite/phillipsite composite: Equilibrium investigation and realistic application. Sci. Total Environ. 2019, 667, 101–111. [Google Scholar] [CrossRef]
- Jalil, A.A.; Triwahyono, S.; Adam, S.H.; Rahim, N.D.; Aziz, M.A.A.; Hairom, N.H.H.; Razali, N.A.M.; Abidin, M.A.Z.; Mohamadiah, M.K.A. Adsorption of methyl orange from aqueous solution onto calcined Lapindo volcanic mud. J. Hazard. Mater. 2010, 181, 755–762. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, N.; Khani, H.; Gupta, V.K.; Amereh, E.; Agarwal, S. Adsorption process of methyl orange dye onto mesoporous carbon material–kinetic and thermodynamic studies. J. Colloid Interface Sci. 2011, 362, 457–462. [Google Scholar] [CrossRef]
- Sua, Y.; Jiaoa, Y.; Doua, C.; Hana, R. Biosorption of methyl orange from aqueous solutions using cationic surfactant-modified wheat straw in batch mode. Desalin. Water Treat. 2014, 52, 6145–6155. [Google Scholar] [CrossRef]
- Mobarak, M.; Selim, A.Q.; Mohamed, E.; Seliem, M.K. A superior adsorbent of CTAB/H2O2 solution−modified organic carbon rich-clay for hexavalent chromium and methyl orange uptake from solutions. Mol. Liq. J. 2018, 259, 384–397. [Google Scholar] [CrossRef]
- Mobarak, M.; Mohamed, E.A.; Selim, A.; Sellaoui, L.; Ben Lamine, A.; Erto, A.; Bonilla-Petriciolete, A.; Seliem, M.K. Surfactant–modified serpentine for fluoride and Cr(VI) adsorption in single and binary systems: Experimental studies and theoretical modeling. Chem. Eng. J. 2019, 360, 333–343. [Google Scholar] [CrossRef]
- Li, Z.; Sellaoui, L.; Dotto, G.L.; Lamine, A.B.; Petriciolet, A.B.; Hanafy, H.; Belmabrouk, H.; Matias, S.N.; Erto, A. Interpretation of the adsorption mechanism of reactive black 5 and Ponceau 4R dyes on chitosan/polyamide nanofibers via advanced statistical physics model. Mol. Liq. J. 2019, 285, 165–170. [Google Scholar] [CrossRef]
- Seliem, M.K.; Mobarak, M. Cr(VI) uptake by a new adsorbent of CTAB–modified carbonized coal: Experimental and advanced statistical physics studies. Mol. Liq. J. 2019, 294, 111676. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Selim, A.Q.; Ahmed, S.A.; Sellaou, L.; Bonilla-Petriciolet, A.; Ertoe, A.; Li, Z.; Li, Y.; Seliem, M.K. H2O2–activated anthracite impregnated with chitosan as a novel composite for Cr(VI) and methyl orange adsorption in single–compound and binary systems: Modeling and mechanism interpretation. Chem. Eng. J. 2020, 380, 122445. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Mobarak, M.; Kumar, R.; Barakat, M.A.; Bonilla-Petriciolet, A.; Seliem, M.K.; Selim, A.Q. Novel hybrid multifunctional composite of chitosan and altered basalt for barium adsorption: Experimental and theoretical studies. Colloids Surf. Physicochem. Eng. Asp. 2020, 593, 124613. [Google Scholar] [CrossRef]
- Li, Z.; Hanafy, H.; Zhang, L.; Sellaoui, L.; Netto, M.S.; Oliveira, M.L.S.; Seliem, M.K.; Dotto, G.L.; Bonilla-Petricioleti, A.; Li, Q. Adsorption of Congo red and methylene blue dyes on an ashitaba waste and a walnut shell-based activated carbon from aqueous solutions: Experiments, characterization and physical interpretations. Chem. Eng. J. 2020, 388, 124263. [Google Scholar] [CrossRef]
- Al-Ghouti, M.A.; Al-Degs, Y.S.; Khraisheh, M.A.M.; Ahmad, M.N.; Allen, S.J. Mechanisms and chemistry of dye adsorption on manganese oxides-modified diatomite. J. Environ. Manag. 2009, 90, 3520–3527. [Google Scholar] [CrossRef]
- Islam, M.A.; Ali, I.; Abdul Karim, S.M.; Firoz, M.S.H.; Chowdhury, A.-N.; Morton, D.W.; Angove, M.J. Removal of dye from polluted water using novel nano manganese oxide based Materials. J. Water Process Eng. 2019, 32, 100911. [Google Scholar] [CrossRef]
- Higashi, S.; Miki, H.; Komarneni, S. Mn-smectites: Hydrothermal synthesis and characterization. Appl. Clay Sci. 2007, 38, 104–112. [Google Scholar] [CrossRef] [Green Version]
- Komarneni, S.; Newalkar, B.L. Low temperature synthesis of micas under conventional-and microwave-hydrothermal conditions. Clays Clay Miner. 2003, 51, 693–700. [Google Scholar] [CrossRef]
- Eberl, D.D. Alkali cation selectivity and fixation by clay minerals. Clays Clay Miner. 1980, 28, 161–172. [Google Scholar] [CrossRef]
- Seliem, M.K.; Barczak, M.; Anastopoulos, I.; Giannakoudakis, D.A. A Novel Nanocomposite of Activated Serpentine Mineral Decorated with Magnetic Nanoparticles for Rapid and Elective Adsorption of Hazardous Cationic Dyes: Kinetics and Equilibrium Studies. Nanomaterials 2020, 10, 684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lagergren, S.; Svenska, B.K. Veternskapsakad, Zur theorie der sogenannten adsorption geloester stoffe. Handlingar 1898, 24, 1–39. [Google Scholar]
- Ho, Y.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Weber, J.C.; Morris, W.J. Proceedings of International Conference on Water Pollution Symposium. Pergamon 1962, 2, 231–266. [Google Scholar]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef] [Green Version]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Dubinin, M.M.; Radushkevich, L.V. The equation of the characteristic curve of the activated charcoal, Proceedings of the Academy of Sciences of the USSR. Phys. Chem. Sect. 1947, 55, 331–337. [Google Scholar]
- Li, F.; Wu, J.; Qin, Q.; Li, Z.; Huang, X. Facile synthesis of γ-MnOOH micro/nanorods and their conversion to β-MnO2, Mn3O4. J. Alloy. Compd. 2010, 492, 339–346. [Google Scholar] [CrossRef]
- Wang, G.; Hua, Y.; Su, X.; Komarneni, S.; Ma, S.; Wang, Y. Cr(VI) adsorption by montmorillonite nanocomposites. Appl. Clay Sci. 2016, 124–125, 111–118. [Google Scholar] [CrossRef]
- Hassan, H.; Hameed, B.H. Fe–clay as effective heterogeneous Fenton catalyst for the decolorization of Reactive Blue 4. Chem. Eng. J. 2011, 171, 912–918. [Google Scholar] [CrossRef]
- Selim, A.Q.; Sellaoui, L.; Ahmed, S.A.; Mobarak, M.; Mohamed, E.A.; Ben Lamine, A.; Erto, A.; Petriciolet, A.B.; Seliem, M.K. Statistical physics-based analysis of the adsorption of Cu2+ and Zn2+ onto synthetic cancrinite in single-compound and binary systems. J. Environ. Chem. Eng. 2019, 7, 103217. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, M.; Liu, Z.-H.; Ooi, K. IR spectra of manganese oxides with either layered or tunnel structures. Spectrochim. Acta Part A 2007, 67, 864–869. [Google Scholar] [CrossRef]
- Asuha, S.; Zhou, X.G.; Zhao, S. Adsorption of methyl orange and Cr(VI) on mesoporous TiO2 prepared by hydrothermal method. J. Hazard. Mater. 2010, 181, 204–210. [Google Scholar] [CrossRef]
- Seliem, M.K.; Komarneni, S. Equilibrium and kinetic studies for adsorption of iron from aqueous solution by synthetic Na-A zeolites: Statistical modeling and optimization. Microporous Mesoporous Mater. 2016, 228, 266–274. [Google Scholar] [CrossRef]
- Seliem, M.K.; Komarneni, S.; Byrne, T.; Cannon, F.S.; Shahien, M.G.; Khalil, A.A.; Abd El-Gaid, I.M. Removal of nitrate by synthetic organosilicas and organoclay: Kinetic and isotherm studies. Sep. Purif. Technol. 2013, 110, 181–187. [Google Scholar] [CrossRef]
- Seliem, M.K.; Komarneni, S.; AbuKhadra, M.R. Phosphate removal from solution by composite of MCM-41 silica with rice husk: Kinetic and equilibrium studies. Microporous Mesoporous Mater. 2016, 224, 51–57. [Google Scholar] [CrossRef]
- Seliem, M.K.; Komarneni, S.; Byrne, T.; Cannon, F.S.; Shahien, M.G.; Khalil, A.A.; Abd El-Gaid, I.M. Removal of perchlorate by synthetic organosilicas and organoclay: Kinetics and isotherm studies. Appl. Clay Sci. 2013, 71, 21–26. [Google Scholar] [CrossRef]
- Zayed, A.M.; Selim, A.Q.; Mohamed, E.A.; Abdel Wahed, M.S.M.; Seliem, M.K.; Sillanpaa, M. Adsorption characteristics of Na-A zeolites synthesized from Egyptian kaolinite for manganese in aqueous solutions: Response surface modeling and optimization. Appl. Clay Sci. 2017, 140, 17–24. [Google Scholar] [CrossRef]
- Marrakchi, F.; Hameed, B.H.; Hummadi, E.H. Mesoporous biohybrid epichlorohydrin crosslinked chitosan/carbon–clay adsorbent for effective cationic and anionic dyes adsorption. Int. J. Biol. Macromol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Lee, J.; Park, S.-M.; Alessi, D.S.; Baek, K. Adsorption Characteristics of Cesium onto Calcium-Silicate-Hydrate in Concrete Powder and Block. Chemosphere 2020, 259, 127494. [Google Scholar] [CrossRef]
- Tran, H.N.; You, S.-J.; Chao, H.-P. Thermodynamic parameters of cadmium adsorption onto orange peel calculated from various methods: A comparison study. J. Environ. Chem. Eng. 2016, 4, 2671–2682. [Google Scholar] [CrossRef]
- Zhang, L.; Sellaoui, L.; Franco, D.; Dotto, G.L.; Bajahzar, A.; Belmabrouk, H.; Bonilla-Petriciolet, A.; Oliveira, M.L.S.; Li, Z. Adsorption of dyes brilliant blue, sunset yellow and tartrazine from aqueous solution on chitosan: Analytical interpretation via multilayer statistical physics model. Chem. Eng. J. 2020, 382, 122952. [Google Scholar] [CrossRef]
- Wu, Q.; Liang, H.; Li, M.; Liu, B.; Xu, Z. Hierarchically Porous Carbon Membranes Derived from PAN and Their Selective Adsorption of Organic Dyes. Chin. J. Polym. Sci. 2016, 34, 23–33. [Google Scholar] [CrossRef]
- Hua, P.; Sellaoui, L.; Franco, D.; Netto, M.S.; Dotto, G.L.; Bajahzar, A.; Belmabrouk, H.; Bonilla-Petriciolet, A.; Li, Z. Adsorption of acid green and procion red on a magnetic geopolymer based adsorbent: Experiments, characterization and theoretical treatment. Chem. Eng. J. 2020, 383, 123113. [Google Scholar] [CrossRef]





| Gel Composition (Moles) | Temperature (°C) | Time (h) | XRD Result |
|---|---|---|---|
| (1)156 K2O, 13.05 MnO, 16.01 SiO2, 1.00 Al2O3, 1388 H2O | 200 | 96 | Sharp Mn–mica peak |
| (2)104 K2O, 13.05 MnO, 16.01 SiO2, 1.00 Al2O3, 1388 H2O | 200 | 96 | Weak Mn–mica peak |
| (3)78 K2O, 13.05 MnO, 16.01 SiO2, 1.00 Al2O3, 1388 H2O | 200 | 96 | Weak Mn–mica peak |
| (4)52 K2O, 13.05 MnO, 16.01 SiO2, 1.00 Al2O3, 1388 H2O | 200 | 96 | No Mn–mica peak |
| (5)19.5 K2O, 13.05 MnO, 16.01 SiO2, 1.00 Al2O3, 1388 H2O | 200 | 96 | No Mn–mica peak |
| Kinetic Model | Equation | Parameters | Refs. |
|---|---|---|---|
| Pseudo-first-order | (mg·g−1): removed amount of MO at time .(mg·g−1): equilibrium adsorption uptake (min−1): rate constant of the first-order adsorption. | [24] | |
| Pseudo-second-order | (g mg−1 min−1): rate constant of the second-order adsorption | [25] | |
| Intra-particle diffusion | (mg·g−1 min0.5): intraparticle diffusion rate constant. C (mg·g−1): intercept of the line. | [26] |
| Isotherm Model | Equation | Parameters | Refs. |
|---|---|---|---|
| Langmuir | (mg·L−1): equilibrium concentration of the MO in the solution (mg·g−1): removed amount of MO at equilibrium. (mg·g−1): maximum adsorption capacity (L·mg−1): Langmuir constant | [27] | |
| Freundlich | (mg/g)/(mg/L)1/n: MO adsorption capacity. n: heterogeneity factor. | [28] | |
| Dubinin–Radushkevich | (mol2/kJ2): D-R constant (kJ2/mol2):Polanyil potential, equal to . : universal gas constant (8.31 J/mol·K).T (K): absolute temperature. (mg·g−1): theoretical adsorption capacity. Experimental adsorption capacity (mg·g−1) : Calculated adsorption capacity (mg·g−1) | [29] |
| Kinetic Model | T = 25 °C | T = 40 °C | T = 55 °C |
|---|---|---|---|
| Pseudo-first-order | |||
| () | 47.71 | 46.73 | 44.83 |
| () | 44.096 | 45.659 | 44.171 |
| (min−1) | 0.149 | 0.039 | 0.029 |
| 0.9839 | 0.9797 | 0.9819 | |
| Pseudo-second-order | |||
| () | 47.355 | 46.927 | 46.309 |
| (g (mg·min)−1) | 0.0033 | 0.0021 | 0.0013 |
| 0.9934 | 0.99 | 0.9883 | |
| Intra-particle diffusion | |||
| (mg/g·min0.5) | 1.102 | 1.252 | 1.371 |
| C (mg/g) | 28.109 | 24.258 | 19.878 |
| 0.743 | 0.7709 | 0.8036 |
| Isotherm Model | T = 25 °C | T = 40 °C | T = 55 °C |
|---|---|---|---|
| Langmuir | |||
| () | 107.298 | 97.36 | 92.76 |
| ( | 0.044 | 0.018 | 0.012 |
| 0.9979 | 0.9975 | 0.999 | |
| 1.36 | 0.762 | 0.301 | |
| Freundlich | |||
| (mg/g)/(mg/L)1/n | 9.726 | 3.894 | 2.426 |
| 0.532 | 0.628 | 0.679 | |
| 0.9982 | 0.9971 | 0.9998 | |
| 0.571 | 0.542 | 0.067 | |
| D − R | |||
| 140.255 | 107.442 | 91.642 | |
| 6.753 | 5.972 | 5.822 | |
| 0.9985 | 0.9974 | 0.9989 | |
| 0.716 | 0.731 | 0.309 |
| T (°C) | ||||||
|---|---|---|---|---|---|---|
| 25 | 1.83 | 59.34 | 1.75 | 29.116 | 20.77 | 190.44 |
| 40 | 1.54 | 60.85 | 1.65 | 13.38 | 12.01 | 154.99 |
| 55 | 1.32 | 69.18 | 1.53 | 13.24 | 10.66 | 140.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barakat, M.A.; Selim, A.Q.; Mobarak, M.; Kumar, R.; Anastopoulos, I.; Giannakoudakis, D.; Bonilla-Petriciolet, A.; Mohamed, E.A.; Seliem, M.K.; Komarneni, S. Experimental and Theoretical Studies of Methyl Orange Uptake by Mn–Rich Synthetic Mica: Insights into Manganese Role in Adsorption and Selectivity. Nanomaterials 2020, 10, 1464. https://doi.org/10.3390/nano10081464
Barakat MA, Selim AQ, Mobarak M, Kumar R, Anastopoulos I, Giannakoudakis D, Bonilla-Petriciolet A, Mohamed EA, Seliem MK, Komarneni S. Experimental and Theoretical Studies of Methyl Orange Uptake by Mn–Rich Synthetic Mica: Insights into Manganese Role in Adsorption and Selectivity. Nanomaterials. 2020; 10(8):1464. https://doi.org/10.3390/nano10081464
Chicago/Turabian StyleBarakat, Mohamed A., Ali Q. Selim, Mohamed Mobarak, Rajeev Kumar, Ioannis Anastopoulos, Dimitrios Giannakoudakis, Adrián Bonilla-Petriciolet, Essam A. Mohamed, Moaaz K. Seliem, and Sridhar Komarneni. 2020. "Experimental and Theoretical Studies of Methyl Orange Uptake by Mn–Rich Synthetic Mica: Insights into Manganese Role in Adsorption and Selectivity" Nanomaterials 10, no. 8: 1464. https://doi.org/10.3390/nano10081464
APA StyleBarakat, M. A., Selim, A. Q., Mobarak, M., Kumar, R., Anastopoulos, I., Giannakoudakis, D., Bonilla-Petriciolet, A., Mohamed, E. A., Seliem, M. K., & Komarneni, S. (2020). Experimental and Theoretical Studies of Methyl Orange Uptake by Mn–Rich Synthetic Mica: Insights into Manganese Role in Adsorption and Selectivity. Nanomaterials, 10(8), 1464. https://doi.org/10.3390/nano10081464