Mechanism-Independent Manipulation of Single-Wall Carbon Nanotubes with Atomic Force Microscopy Tip
Abstract
:1. Introduction
2. Materials and Methods
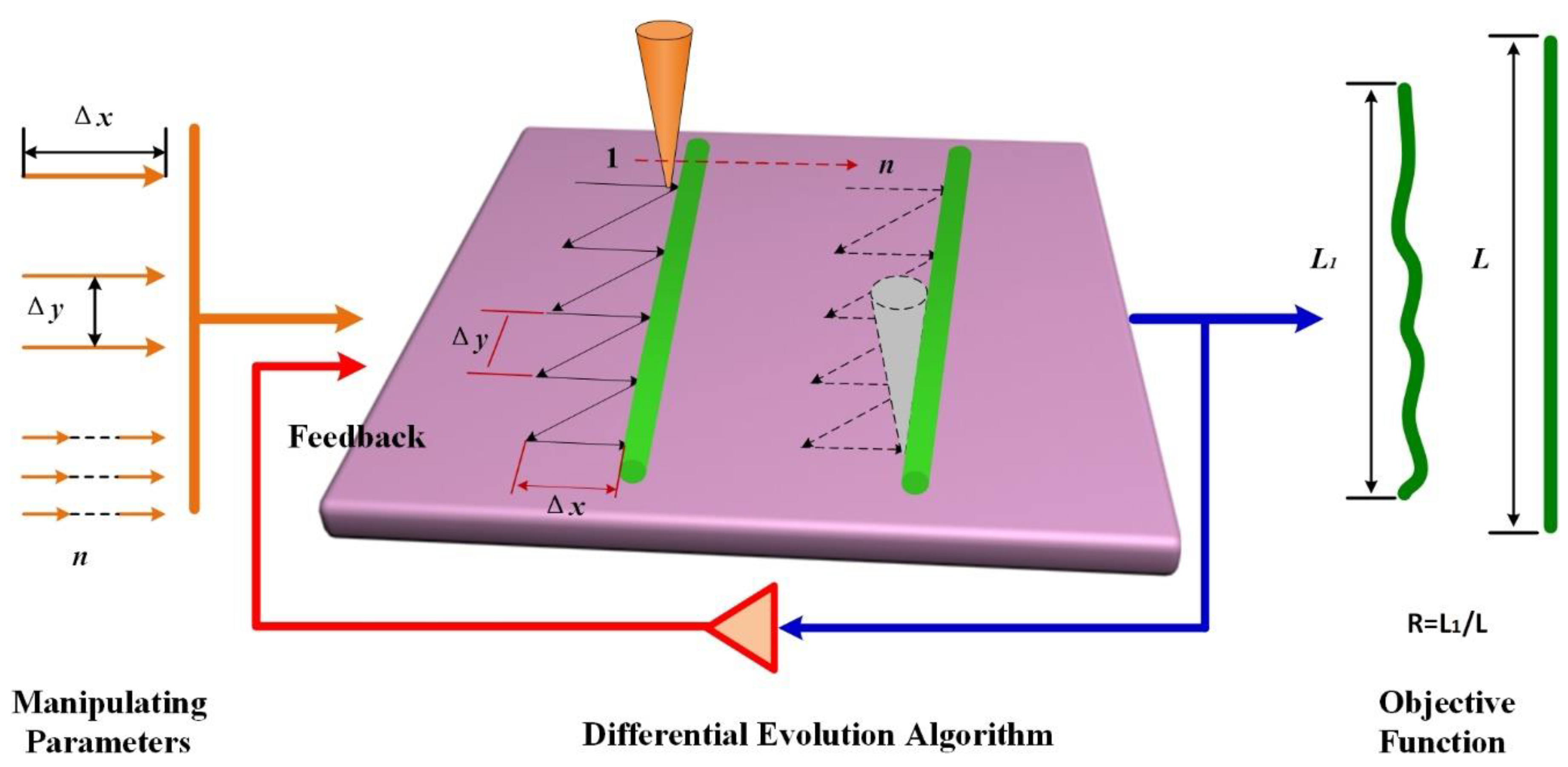
2.1. Manipulating Scheme
2.2. DE Algorithm
2.2.1. Initialization
2.2.2. Mutation
2.2.3. Crossover
2.2.4. Selection
2.3. AFM Experiments
3. Results and Discussion
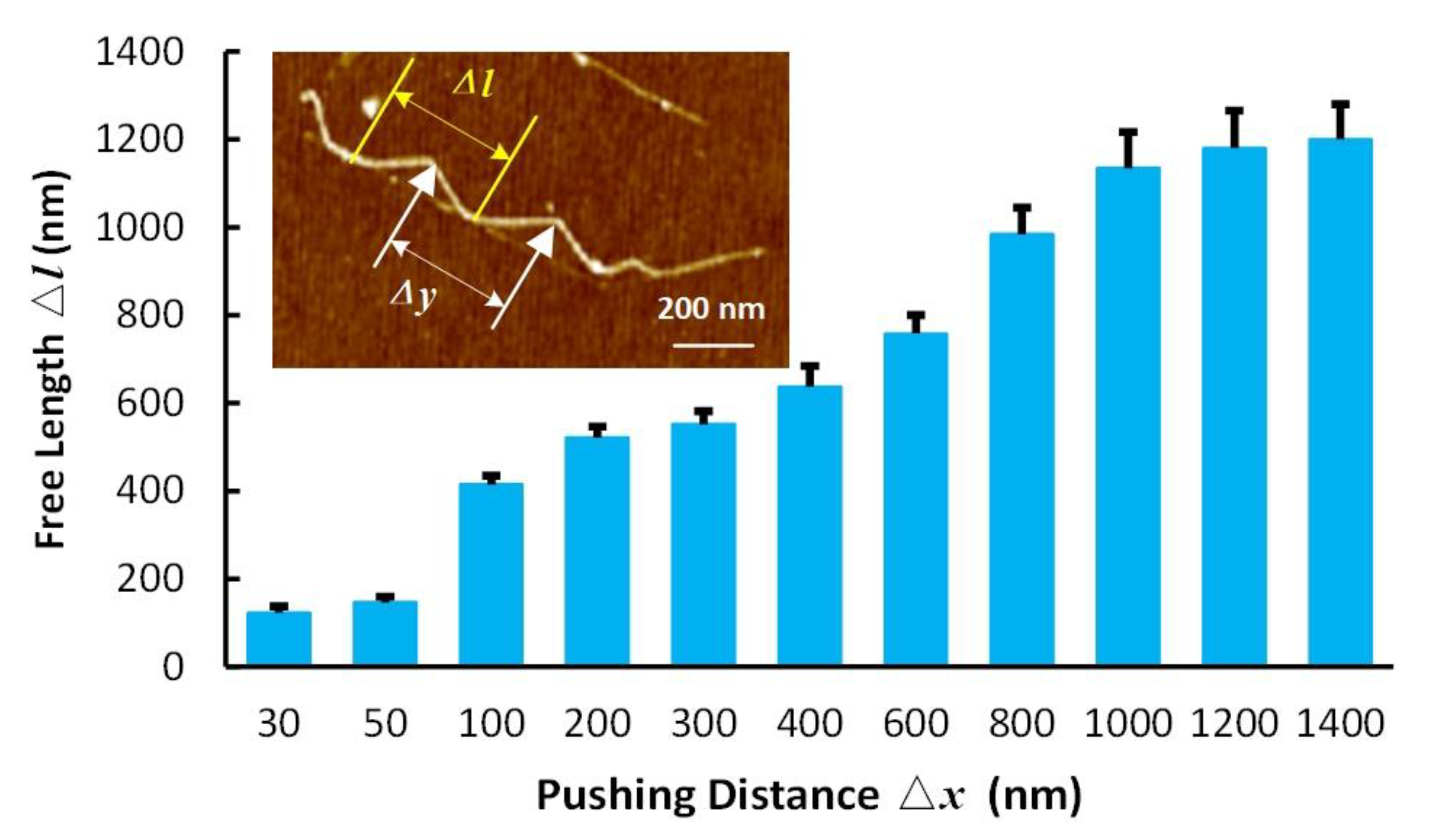
3.1. Parameters Space Optimization
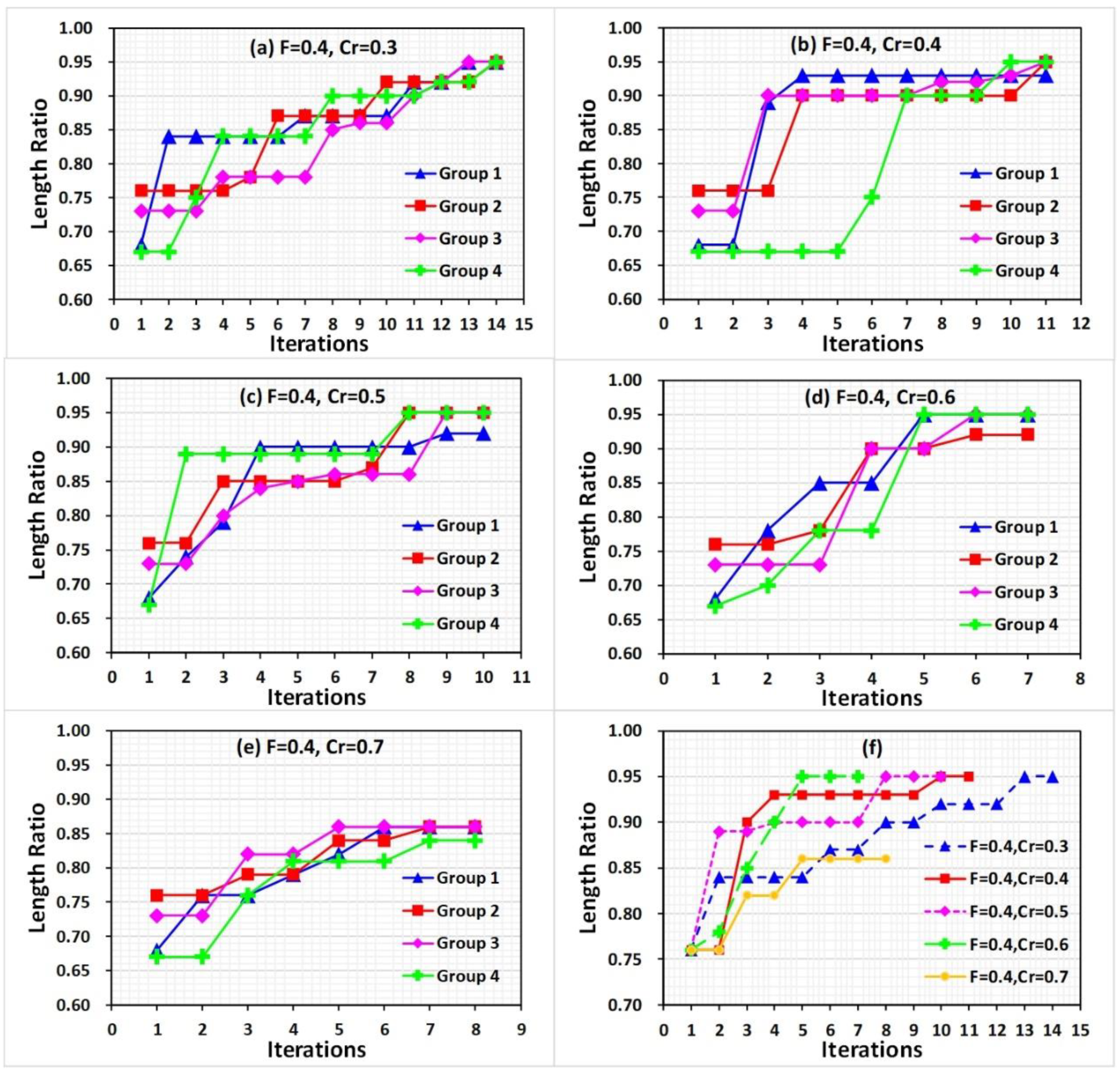
3.2. Intrinsic Parameters of DE Optimization
3.2.1. F Value Optimization
3.2.2. Cr Value Optimization
3.3. Pushing Parameter Combination
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Park, S.; Vosguerichian, M.; Bao, Z. A Review of Fabrication and Applications of Carbon Nanotube Film-Based Flexible Electronics. Nanoscale 2013, 5, 1727–1752. [Google Scholar] [CrossRef] [PubMed]
- Bezryadin, A.; Lau, C. Quantum Suppression of Superconductivity in Ultrathin Nanowires. Nature 2000, 404, 971–974. [Google Scholar] [CrossRef] [PubMed]
- Postma, H.W.C.; Teepen, T.; Yao, Z.; Grifoni, M.; Dekker, C. Carbon Nanotube Single-Electron Transistors at Room Temperature. Science 2001, 293, 76–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishikawa, F.N.; Curreli, M.; Olson, C.A.; Liao, H.-I.; Sun, R.; Roberts, R.W.; Cote, R.J.; Thompson, M.E.; Zhou, C. Importance of Controlling Nanotube Density for Highly Sensitive and Reliable Biosensors Functional in Physiological Conditions. ACS Nano 2010, 4, 6914–6922. [Google Scholar] [CrossRef]
- Deshpande, V.V.; Chiu, H.-Y.; Postma, H.W.C.; Miko, C.; Forr, L.; Bockrath, M. Carbon Nanotube Linear Bearing Nanoswitches. Nano Lett. 2006, 6, 1092–1095. [Google Scholar] [CrossRef]
- Cao, Q.; Kim, H.; Pimparkar, N.; Kulkarni, J.P.; Wang, C.; Shim, M.; Roy, K.; Alam, M.A.; Rogers, J.A. Medium-Scale Carbon Nanotube Thin-Film Integrated Circuits on Flexible Plastic Substrates. Nature 2008, 454, 495–500. [Google Scholar] [CrossRef]
- Tran, C.; Lecao, K.; Bui, T.T.; Dau, V.T. Dielectrophoresis Can Control the Density of CNT Membranes as Confirmed by Experiment and Dissipative Particle Simulation. Carbon 2019, 155, 279–286. [Google Scholar] [CrossRef]
- Papadopoulos, C.; Omrane, B. Nanometer-Scale Catalyst Patterning for Controlled Growth of Individual Single-Walled Carbon Nanotubes. Adv. Mater. 2008, 20, 1344–1347. [Google Scholar] [CrossRef]
- Rao, S.; Huang, L.; Setyawan, W.; Hong, S. Nanotube Electronics: Large-Scale Assembly of Carbon Nanotubes. Nature 2003, 425, 36–37. [Google Scholar] [CrossRef]
- Binnig, G.K.; Quate, C.F.; Gerber, C. The Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Shan, Z.; Huang, H. The Mechanical Properties of Nanowires. Adv. Sci. 2017, 4, 1600332. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Kang, K.H.; Kim, D.E. Sliding and Rolling Frictional Behavior of a Single ZnO Nanowire during Manipulation with an AFM. Nanoscale 2013, 5, 6081–6087. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Dong, M.; Jiang, D.; Li, S.; Shang, Y. The Effect of Surface Roughness on Normal Restitution Coefficient, Adhesion Force and Friction Coefficient of the Particle-Wall Collision. Power Technol. 2020, 362, 17–25. [Google Scholar] [CrossRef]
- Gui, X.; Xing, Y.; Rong, G.; Cao, Y.; Liu, J. Interaction Forces between Coal and Kaolinite Particles Measured by Atomic Force Microscopy. Powder Technol. 2016, 301, 349–355. [Google Scholar] [CrossRef]
- Li, M.; Xi, N.; Wang, Y.; Liu, L. Nanotopographical Surfaces for Regulating Cellular Mechanical Behaviors Investigatedb by Atomic Force Microscopy. ACS Biomate Sci. Eng. 2019, 5, 5036–5050. [Google Scholar] [CrossRef]
- Li, M.; Xi, N.; Wang, Y.; Liu, L. Tunable Hybrid Biopolymeric Hydrogel Scaffolds Based on Atomic Force Microscopy Characterizations for Tissue Engineering. IEEE Trans. Nanotechnol. 2019, 18, 315–328. [Google Scholar] [CrossRef]
- Wen, Y.; Lu, H.; Shen, Y.; Xie, H. Nanorobotic Manipulation System for 360° Characterization Atomic Force Microscopy. IEEE Trans. Ind. Electron. 2019, 67, 2916–2924. [Google Scholar] [CrossRef]
- Miriam, M.; Pablo, A.; Zamora, F.; Cristina, G.; Julio, G. AFM Manipulation of Gold Nanowires to Build Electrical Circuits. Nano Lett. 2019, 19, 5459–5468. [Google Scholar]
- Neugirg, B.R.; Koebley, S.R.; Schniepp, H.C.; Fery, A. AFM-Based Mechanical Characterization of Single Nanofibres. Nanoscale 2016, 8, 8414–8426. [Google Scholar] [CrossRef] [Green Version]
- Shi, Q.; Yang, Z.; Guo, Y.; Wang, H.; Sun, L.; Huang, Q.; Fukuda, T. A Vision-Based Automated Manipulation System for the Pick-Up of Carbon Nanotubes. IEEE/ASME Trans. Mech. 2017, 22, 845–854. [Google Scholar] [CrossRef]
- Lu, H.; Shang, W.; Xie, H.; Shen, Y. Ultrahigh-Precision Rotational Positioning under a Microscope: Nanorobotic System, Modeling, Control. IEEE Trans. Robot. 2018, 34, 497–507. [Google Scholar] [CrossRef]
- Bolopion, A.; Régnier, S. A Review of Haptic Feedback Teleoperation Systems for Micromanipulation and Microassembly. IEEE Trans. Autom. Sci. Eng. 2013, 10, 496–502. [Google Scholar] [CrossRef] [Green Version]
- Onal, C.D.; Ozcan, O.; Sitti, M. Automated 2-D Nanoparticle Manipulation Force Microscopy. IEEE Trans. Nanotechnol. 2011, 10, 472–481. [Google Scholar] [CrossRef]
- Korayem, M.H.; Saraie, M.B.; Saraee, M.B. Analysis the Effect of Different Geometries of AFM’s Cantilever on the Dynamic Behavior and the Critical Forces of Three-Dimensional Manipulation. Ultramicroscopy 2017, 175, 9–24. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Xi, N.; Yu, M.; Fung, W. Development of Augmented Reality System for AFM-Based Nanomanipulation. IEEE/ASME Trans. Mech. 2004, 9, 358–365. [Google Scholar] [CrossRef]
- Li, G.; Xi, N.; Chen, H.; Pomeroy, C.; Prokos, M. “Videolized” Atomic Force Microscopy for Interactive Nanomanipulation and Nanoassembly. IEEE Trans. Nanotechnol. 2005, 4, 605–615. [Google Scholar] [CrossRef]
- Liu, L.; Luo, Y.; Xi, N.; Wang, Y.; Zhang, J.; Li, G. Sensor Referenced Real-Time Videolization of Atomic Force Microscopy for Nanomanipulations. IEEE/ASME Trans. Mech. 2008, 13, 76–85. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Liu, L.; Wang, Z.; Wang, Z.; Xi, N.; Wang, Y.; Wu, C.; Dong, Z.; Yuan, S. AFM-Based Robotic Nano-Hand for Stable Manipulation at Nanoscale. IEEE Trans. Autom. Sci. Eng. 2013, 10, 285–295. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, Z.; Xi, N.; Wang, Y.; Liu, L. AFM Tip Position Control in situ for Effective Nano-Manipulation. IEEE/ASME Trans. Mech. 2018, 23, 2825–2836. [Google Scholar] [CrossRef]
- Korayem, M.H.; Khaksar, H. Investigating the Impact Models for Nanoparticles Manipulation Based on Atomic Force Microscope (According To Contact Mechanics). Powder Technol. 2019, 344, 17–26. [Google Scholar] [CrossRef]
- Saraee, M.B.; Korayem, M.H. Dynamic Modeling and Simulation of 3D Manipulation on Rough Surfaces Based on Developed Adhesion Models. Int. J. Adv. Manuf. Technol. 2017, 88, 529–545. [Google Scholar] [CrossRef]
- Hou, L.; Wang, S.; Huang, H. A Simple Criterion for Determining the Static Friction Force between Nanowires and Flat Substrates Using the Most-Bent-State Method. Nanotechnology 2015, 26, 165702. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wu, S.; Zhang, J.; Bai, H.; Jin, F.; Pang, H.; Hu, X. Strategies for the AFM Based Manipulation of Silver Nanowires on a Flat Surface. Nanotechnology 2017, 28, 365301. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W. Mechanical Properties of Suspended Individual Carbon Nanotube Studied by Atomic Force Microscope. Synth. Met. 2016, 216, 88–92. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, S.; Fu, X. Automated Manipulation of Carbon Nanotubes Using Atomic Force Microscopy. J. Nanosci. Nanotechnol. 2013, 13, 598–602. [Google Scholar] [CrossRef]
- Yang, S.C.; Qian, X. Controlled Manipulation of Flexible Carbon Nanotubes through Shape-Dependent Pushing by Atomic Force Microscopy. Langmuir 2013, 29, 11793–11801. [Google Scholar] [CrossRef]
- Zhang, X.C.; Myers, E.B.; Sader, J.E.; Roukes, M.L. Nanomechanical Torsional Resonators for Frequency-Shift Infrared Thermal Sensing. Nano Lett. 2013, 13, 1528–1534. [Google Scholar] [CrossRef] [Green Version]
- Storn, R.; Hall, A.R.; Falvo, M.R.; Superfine, R.; Washburn, S. Electromechanical response of single-walled carbon nanotubes to torsional strain in a self-contained device. Nature Nanotechnol. 2007, 2, 413–416. [Google Scholar]
- Mazzoni, M.S.; Chacham, H. Bandgap closure of a flattened semiconductor carbon nanotube: A first-principles study. Appl. Phys. Lett. 2000, 76, 1561–1563. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Maiti, A.; Alexei, S.; Anantram, M.P. Electronic transport through carbon nanotubes: Effects of structural deformation and tube chirality. Phys. Rev. Lett. 2002, 88, 126805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rochefort, A.; Avouris, P.; Lesage, F.; Salahub, D.R. Electrical and mechanical properties of distorted carbon nanotubes. Phys. Rev. B 1999, 60, 13824–13830. [Google Scholar] [CrossRef] [Green Version]
- Charlier, J.; Blase, X.; Roche, S. Electronic and transport properties of nanotubes. Rev. Mod. Phys. 2007, 79, 677–732. [Google Scholar] [CrossRef] [Green Version]


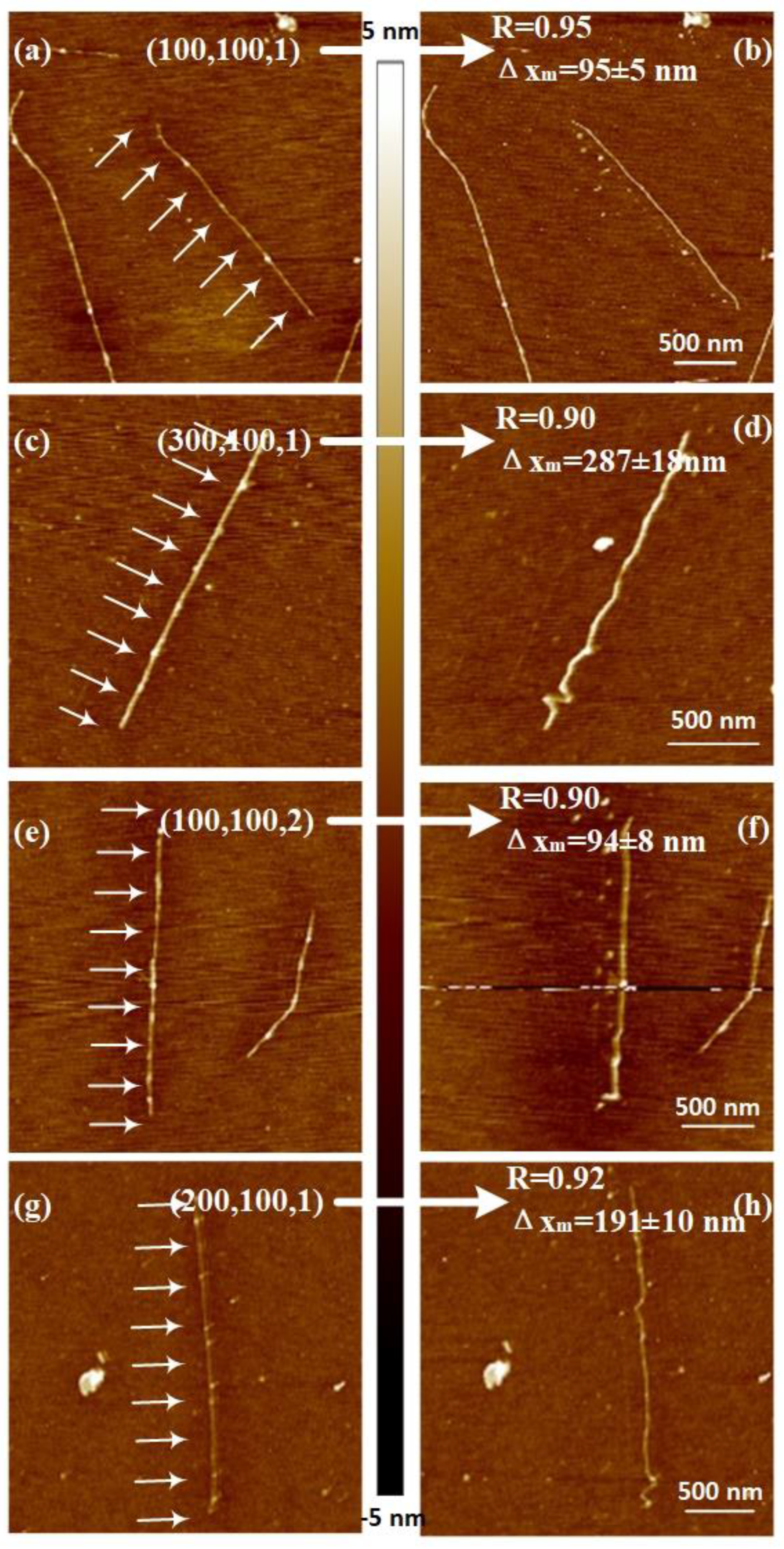

| R | 0.90 | 0.92 | 0.93 | 0.95 | |
|---|---|---|---|---|---|
| No. | |||||
| 1 | (100, 200, 2) | (50, 200, 1) | (200, 50, 1) | (30, 50, 1) | |
| 2 | (200, 200, 1) | (100, 200, 1) | - | (30, 100, 1) | |
| 3 | (300, 100, 1) | (200, 100, 1) | - | (50, 50, 1) | |
| 4 | (400, 50, 1) | - | - | (50, 100, 1) | |
| 5 | (100,100,2) | - | - | (100, 100, 1) | |
| 6 | - | - | - | (100, 50, 1) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, D.; Zhang, Y.; Li, R.; Liu, S.; Li, L.; Chen, H. Mechanism-Independent Manipulation of Single-Wall Carbon Nanotubes with Atomic Force Microscopy Tip. Nanomaterials 2020, 10, 1494. https://doi.org/10.3390/nano10081494
Ju D, Zhang Y, Li R, Liu S, Li L, Chen H. Mechanism-Independent Manipulation of Single-Wall Carbon Nanotubes with Atomic Force Microscopy Tip. Nanomaterials. 2020; 10(8):1494. https://doi.org/10.3390/nano10081494
Chicago/Turabian StyleJu, Dianming, Ying Zhang, Rui Li, Shuang Liu, Longhai Li, and Haitao Chen. 2020. "Mechanism-Independent Manipulation of Single-Wall Carbon Nanotubes with Atomic Force Microscopy Tip" Nanomaterials 10, no. 8: 1494. https://doi.org/10.3390/nano10081494
APA StyleJu, D., Zhang, Y., Li, R., Liu, S., Li, L., & Chen, H. (2020). Mechanism-Independent Manipulation of Single-Wall Carbon Nanotubes with Atomic Force Microscopy Tip. Nanomaterials, 10(8), 1494. https://doi.org/10.3390/nano10081494








