Design and Tuning of Nanofluids Applied to Chemical Enhanced Oil Recovery Based on the Surfactant–Nanoparticle–Brine Interaction: From Laboratory Experiments to Oil Field Application
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Surfactant and Nanoparticle Characterization
2.2.2. Surfactant–Nanoparticle–Brine Tuning
2.2.3. Batch Adsorption Tests
2.2.4. Rheological Measurements
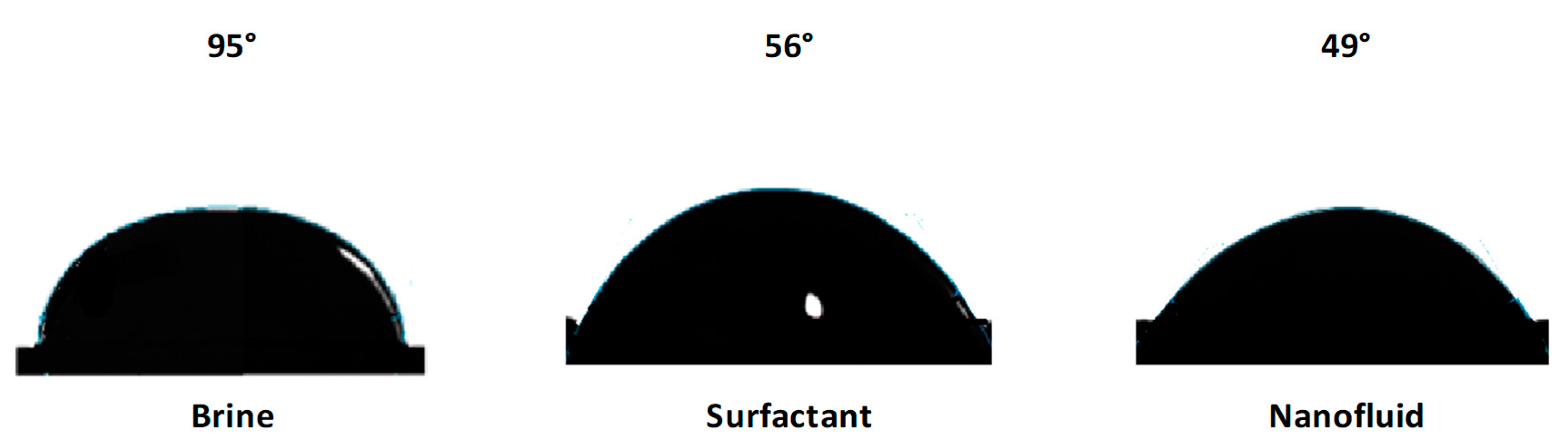
2.2.5. Contact Angle Measurements
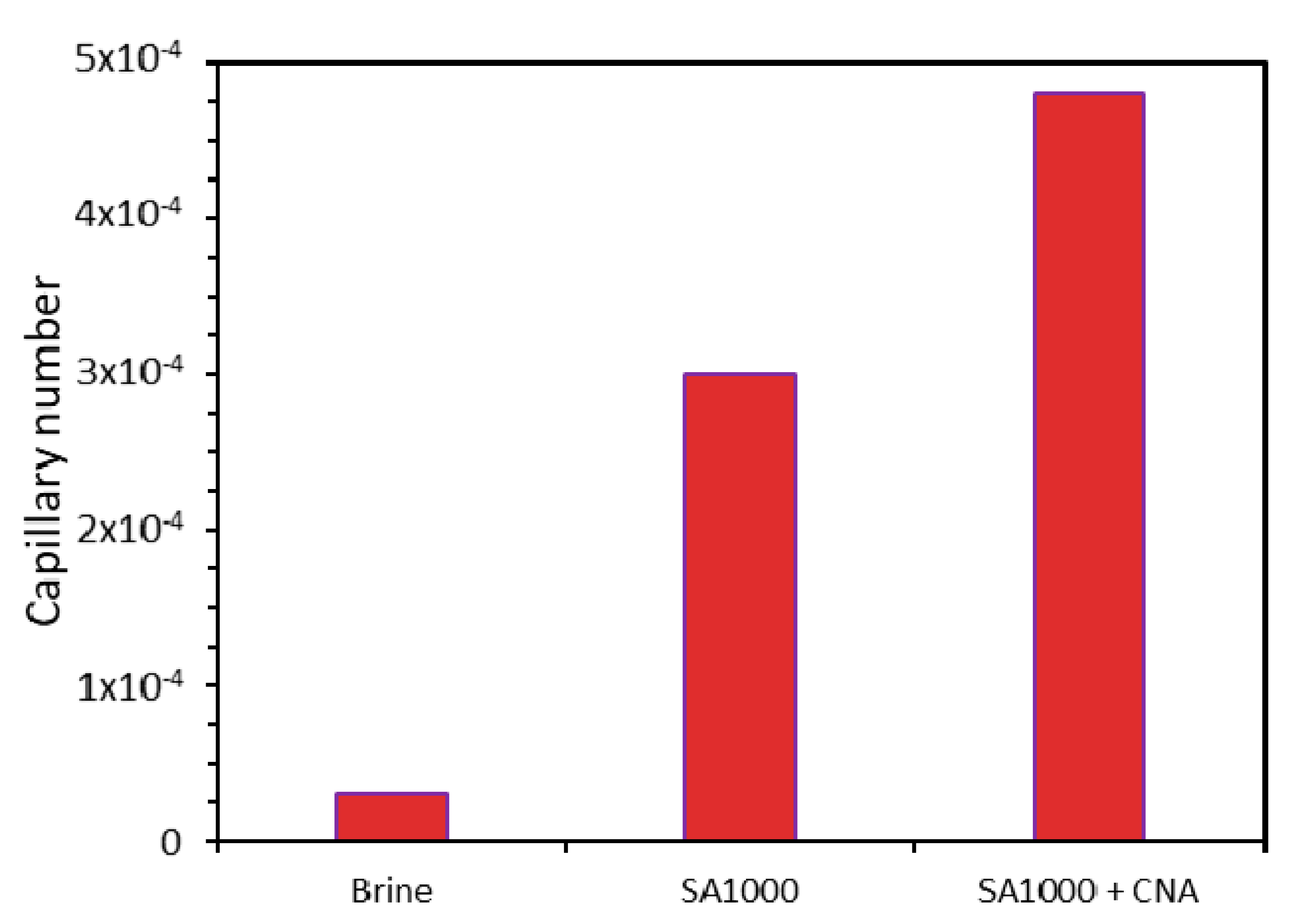
2.2.6. Capillary Number Estimation
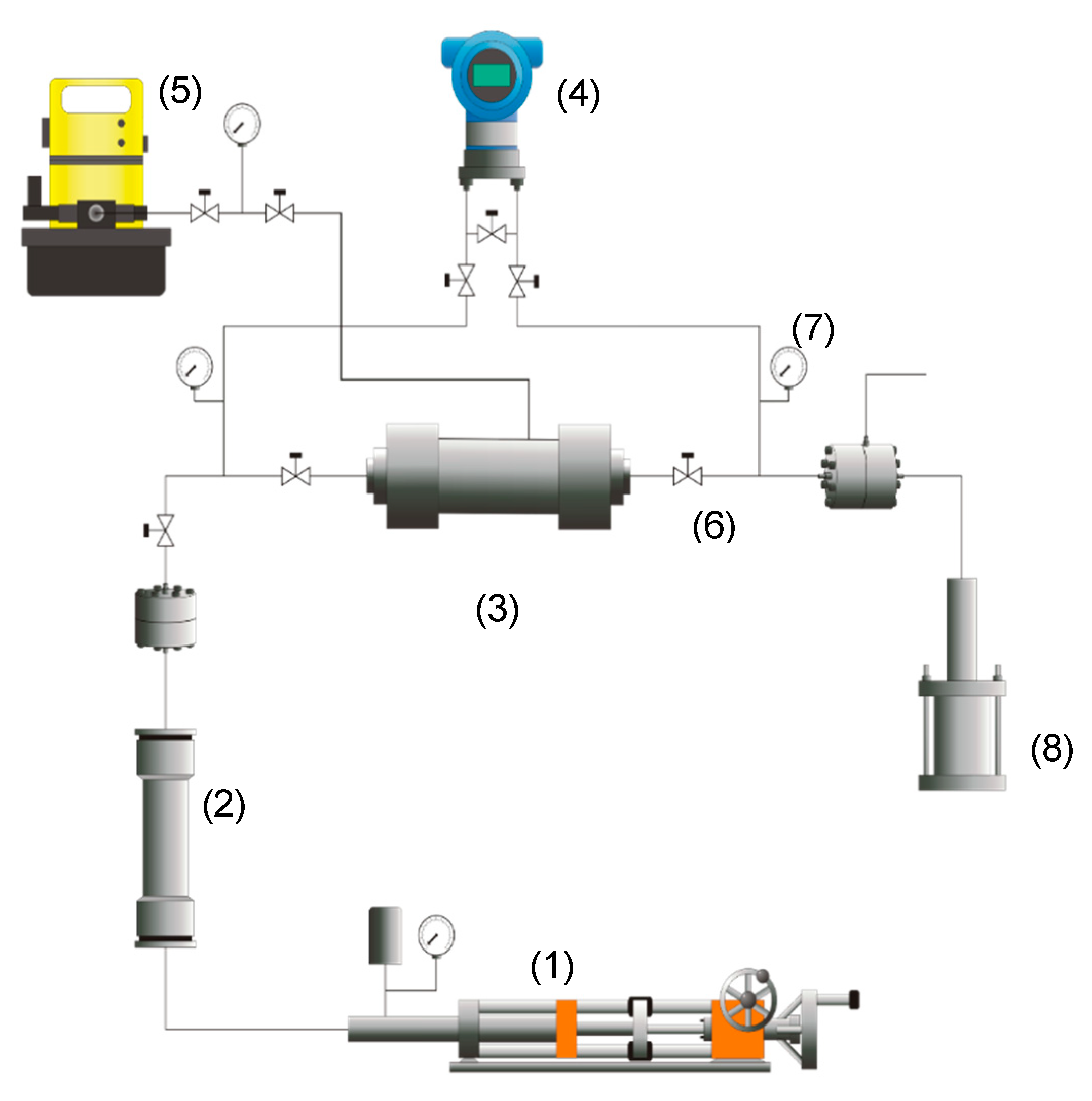
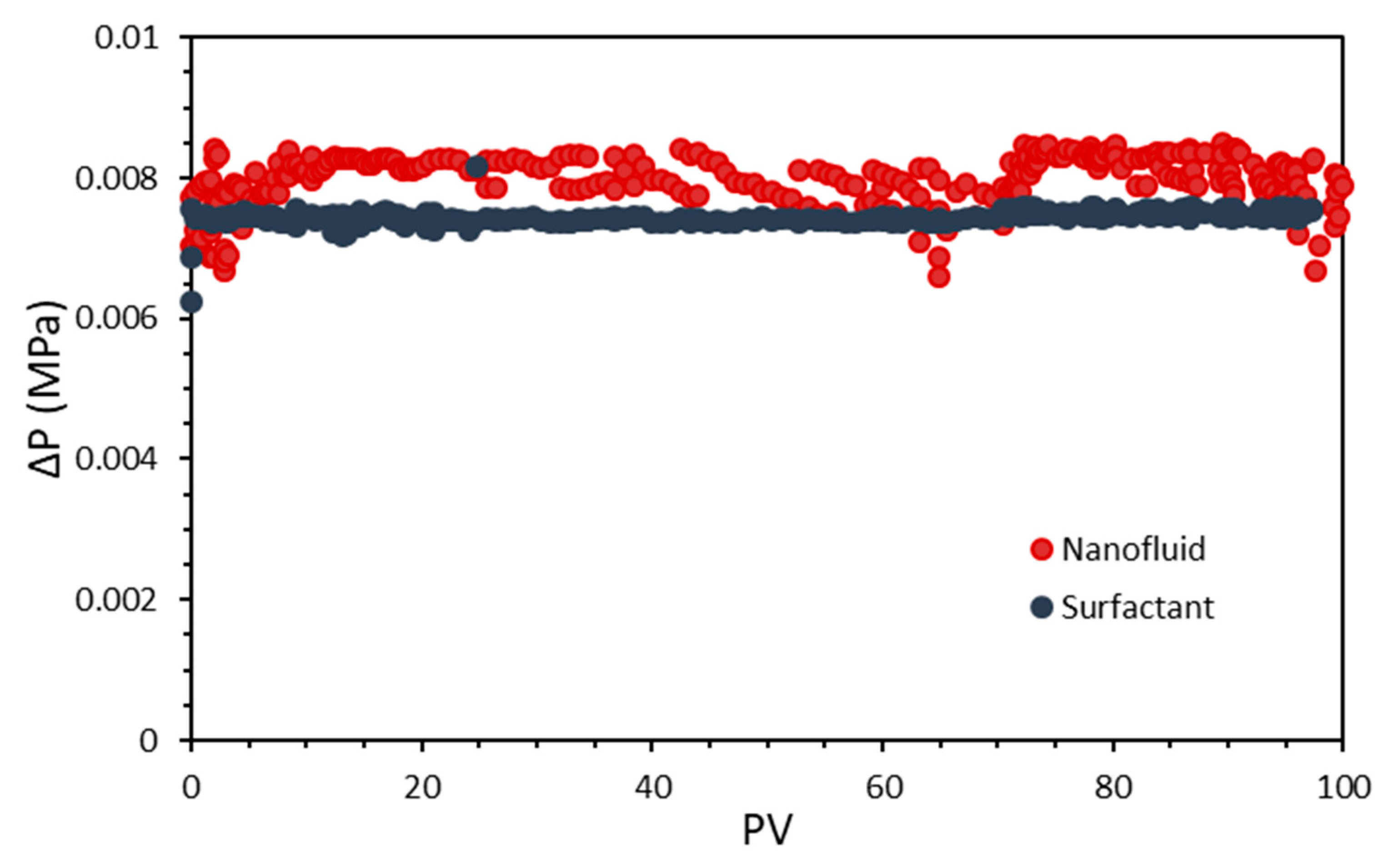
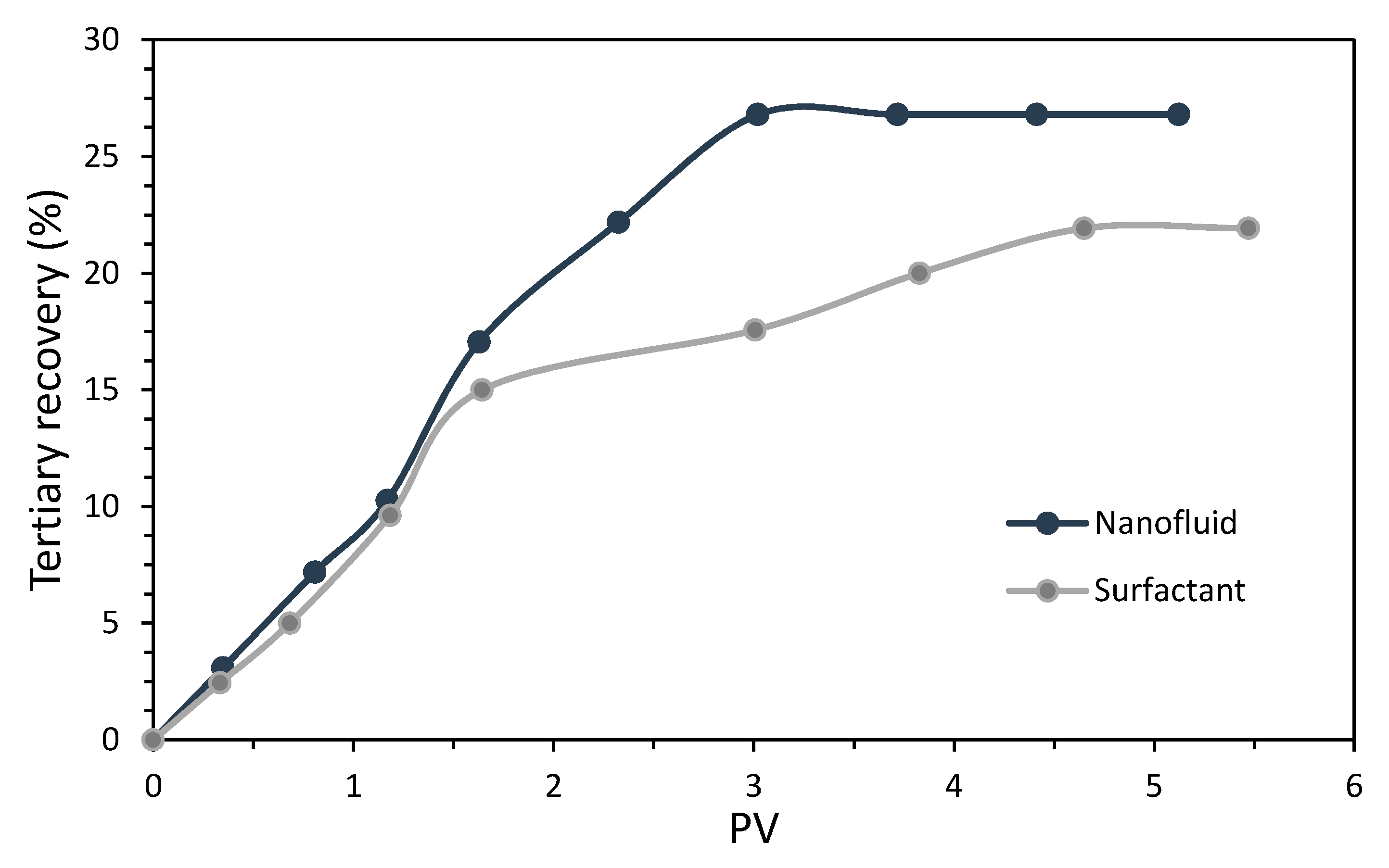
2.2.7. Coreflooding Tests
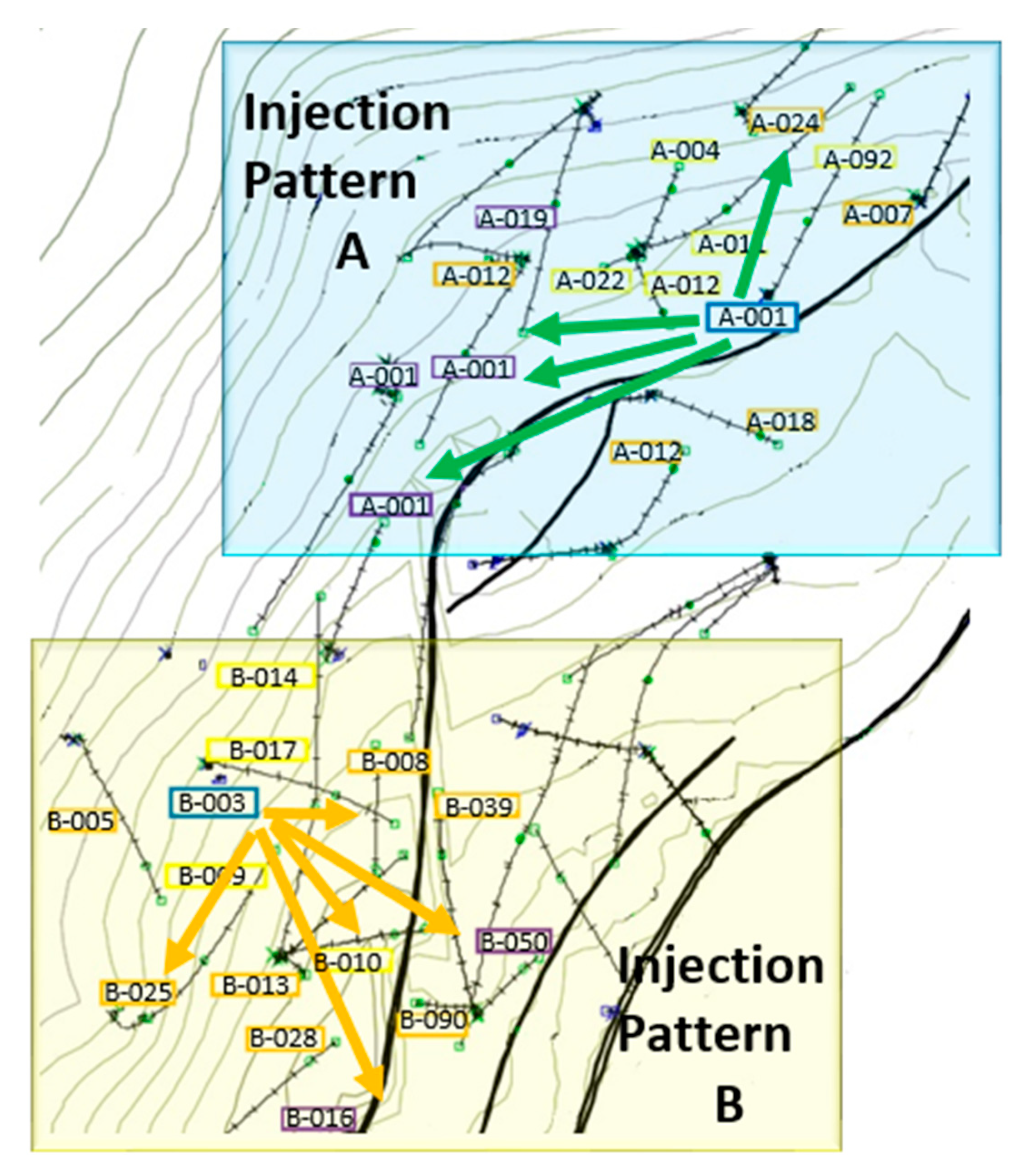
2.2.8. Field Test
3. Results
3.1. Materials Characterization
3.1.1. Surfactants
3.1.2. Nanoparticles
3.2. Surfactant–Nanoparticle–Brine Tuning
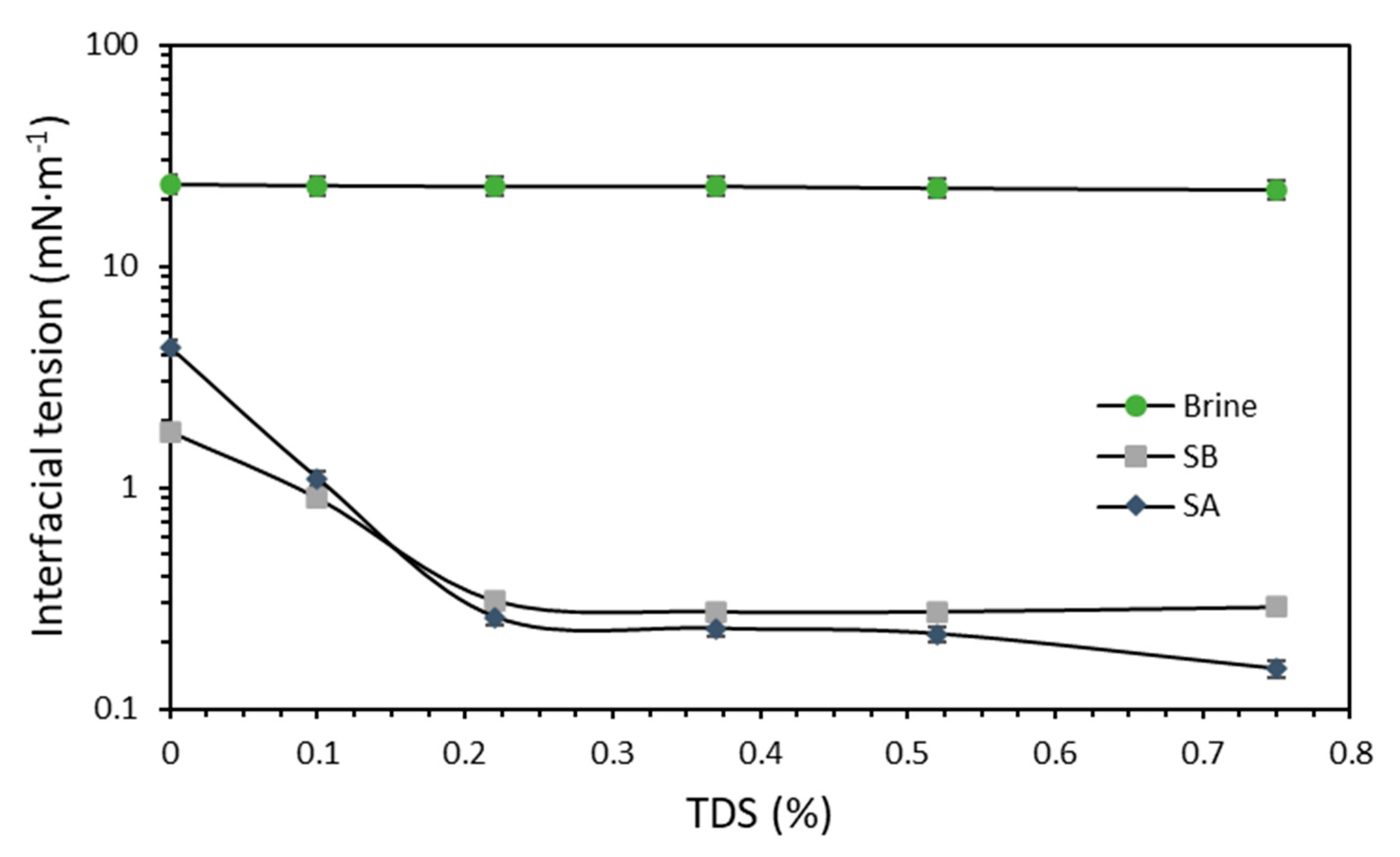
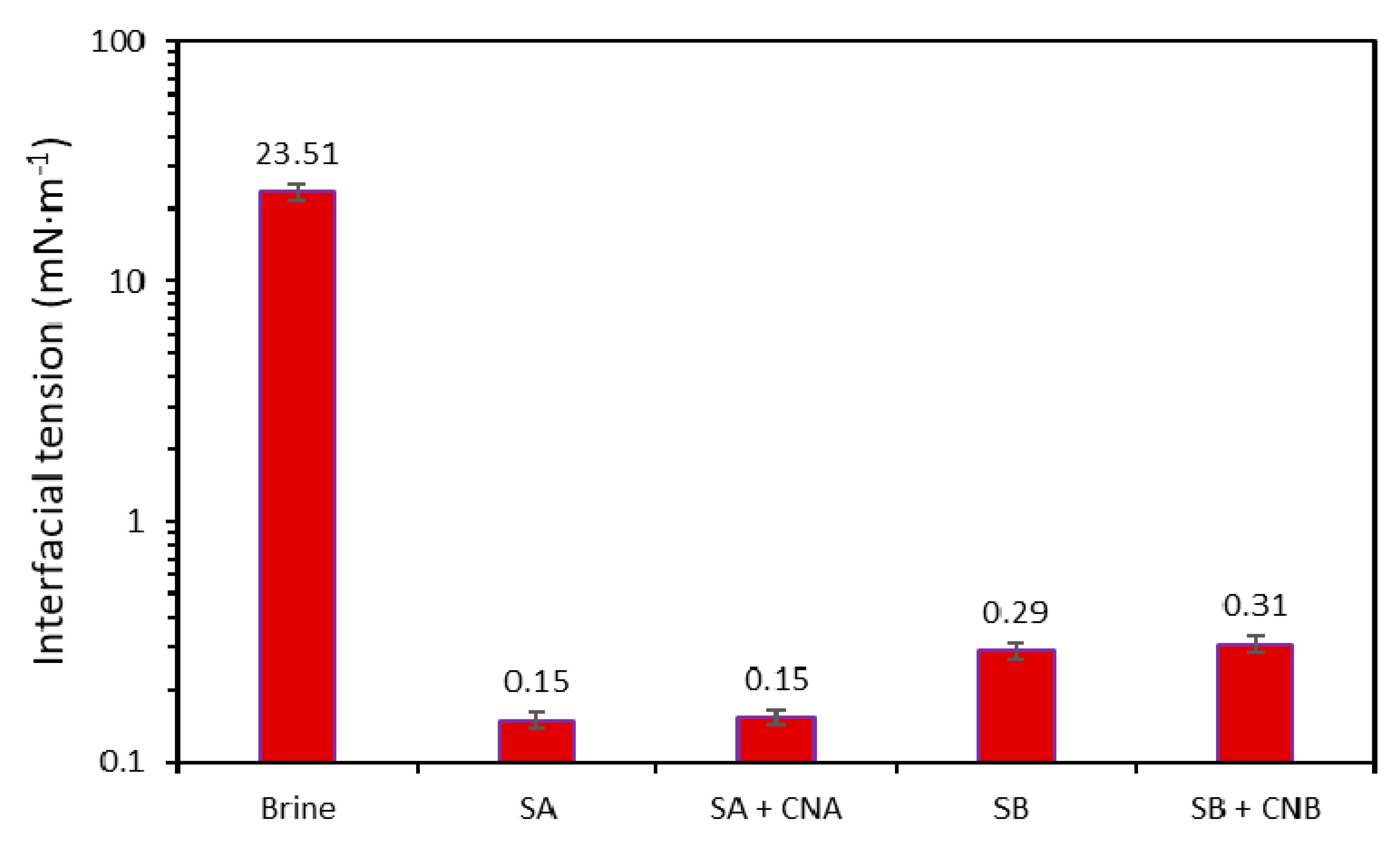
3.2.1. Salinity Effect on IFT
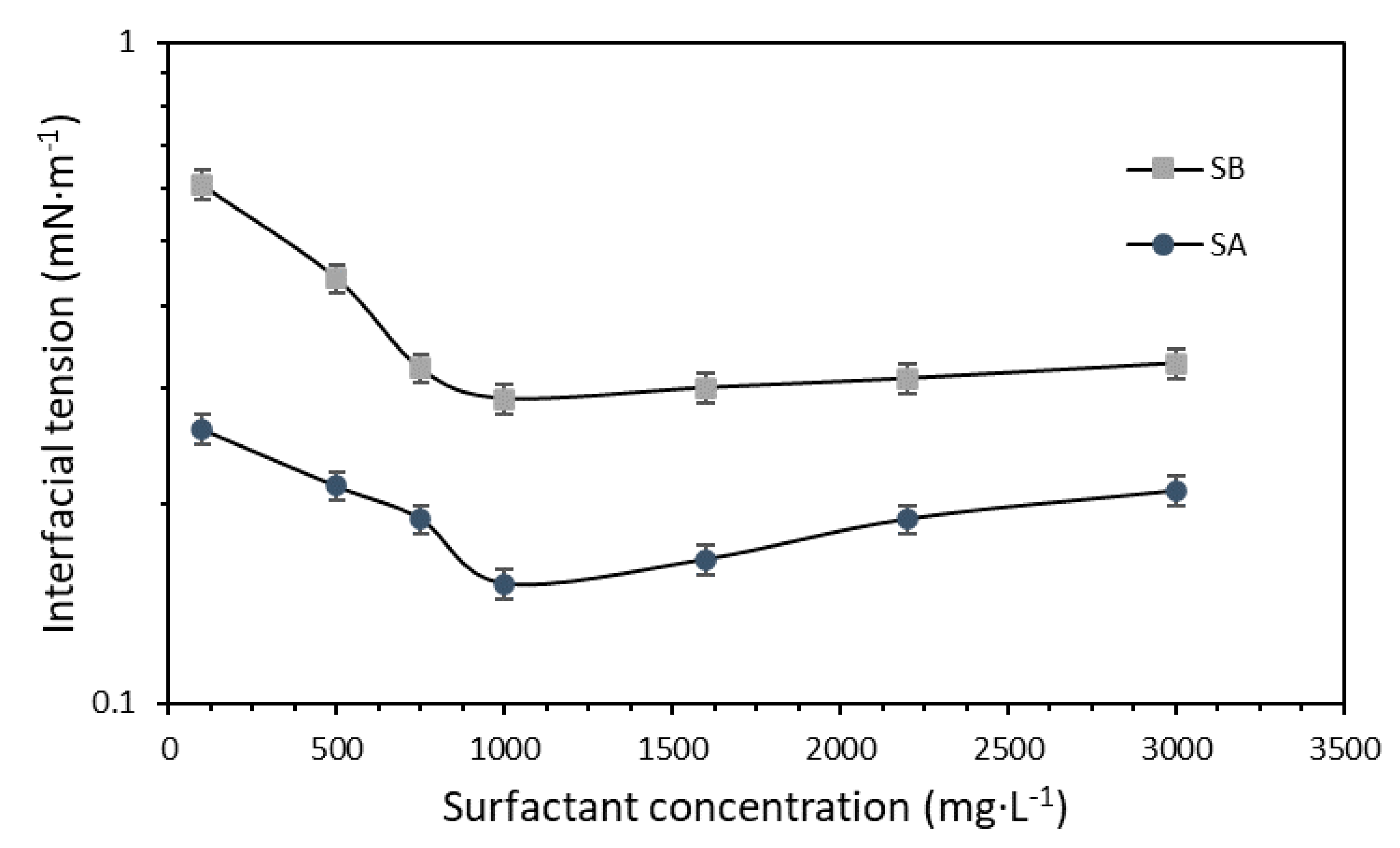
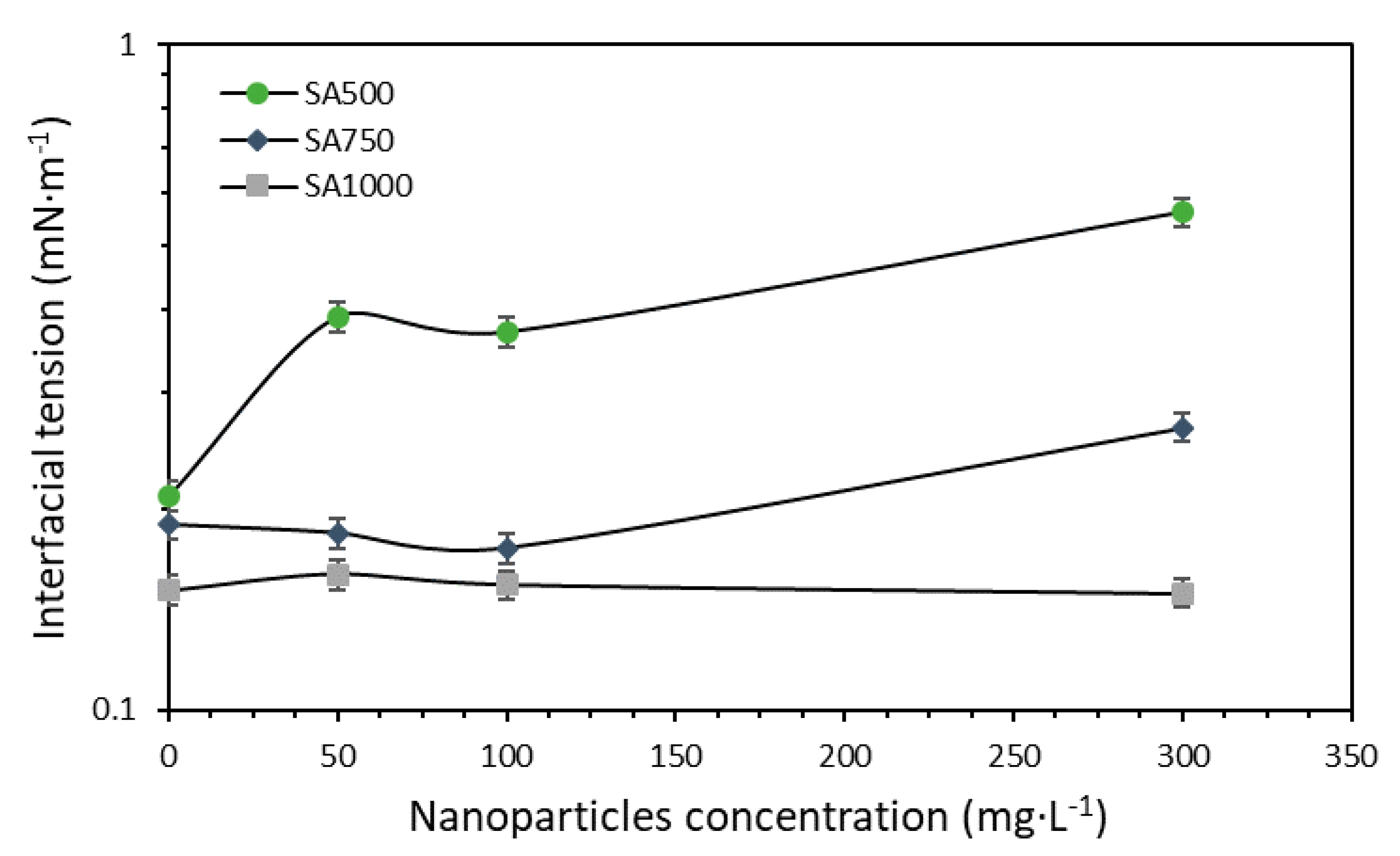
3.2.2. Surfactant and Nanoparticles Dosage Evaluation
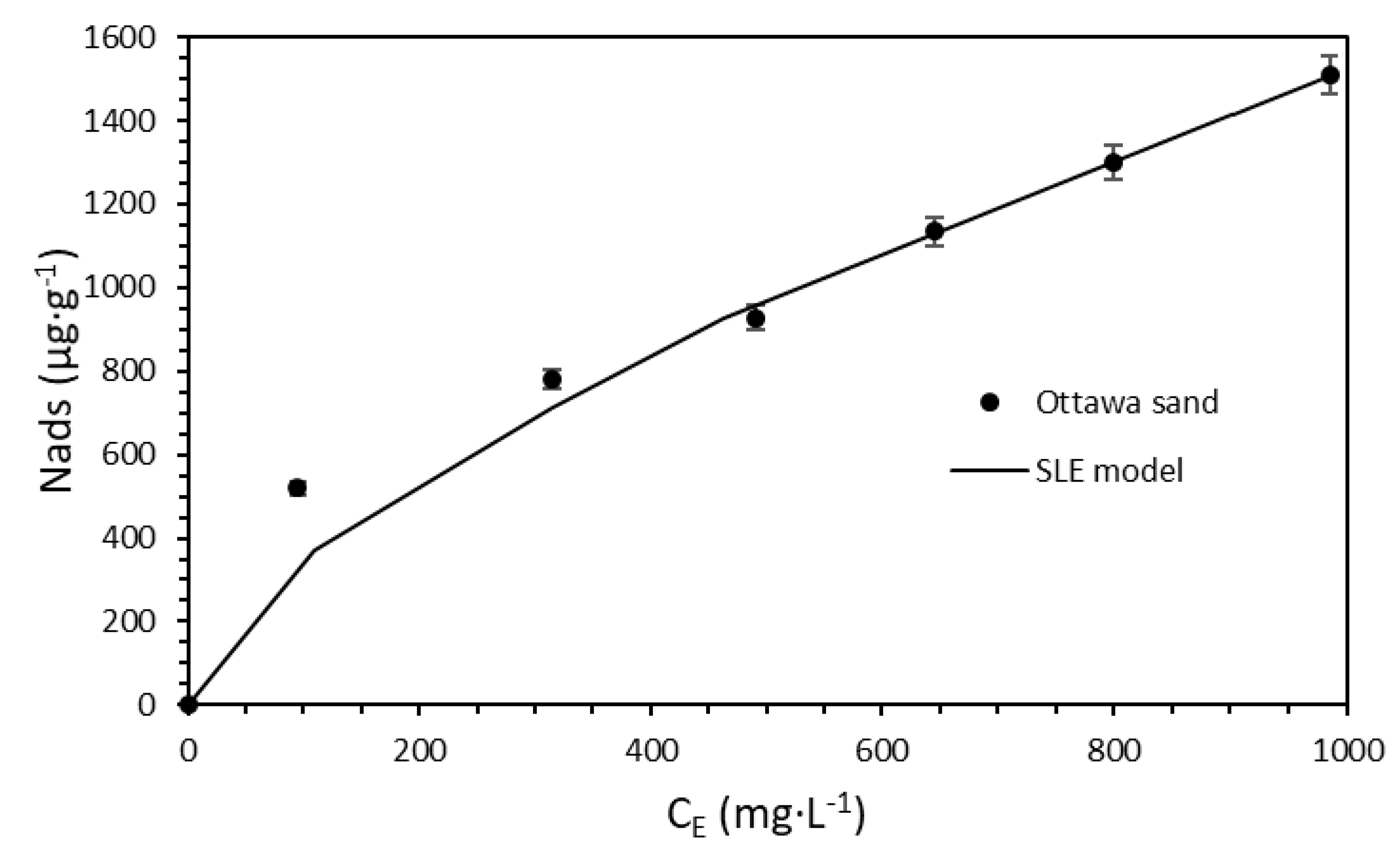
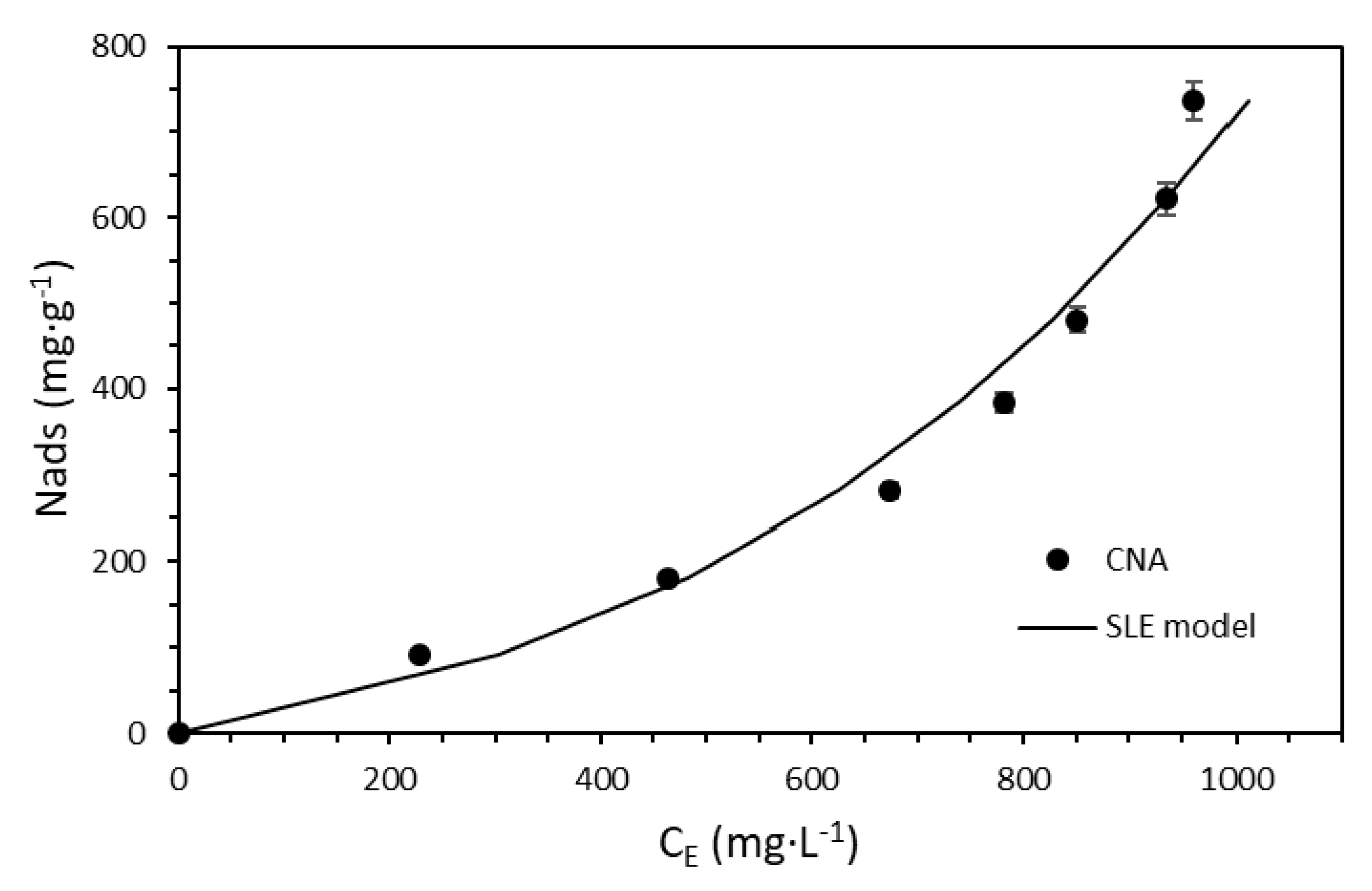
3.3. The Effect of Nanoparticles on Surfactant Adsorption
3.4. Capillary Number Estimation
3.5. Coreflooding Tests
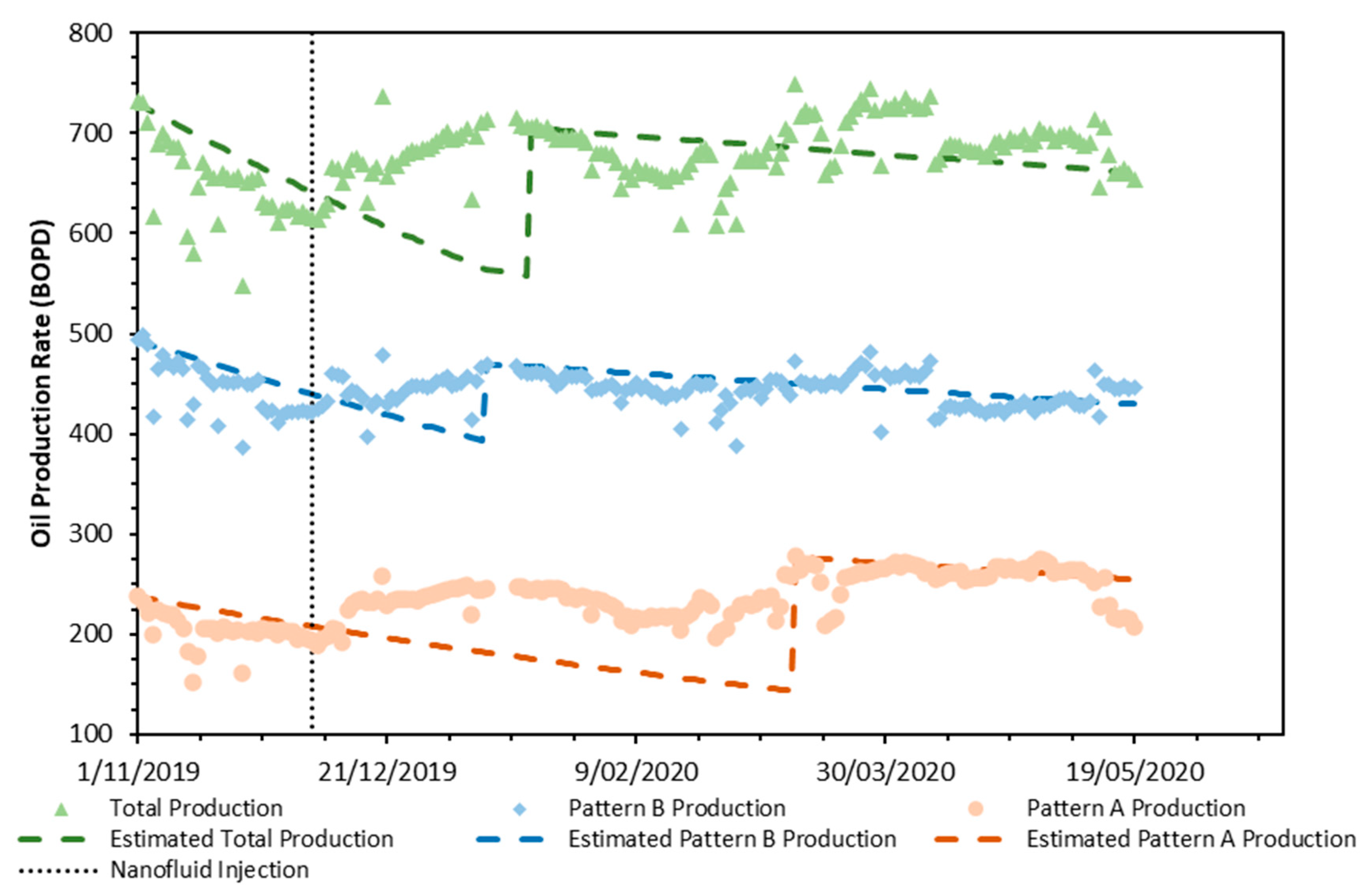
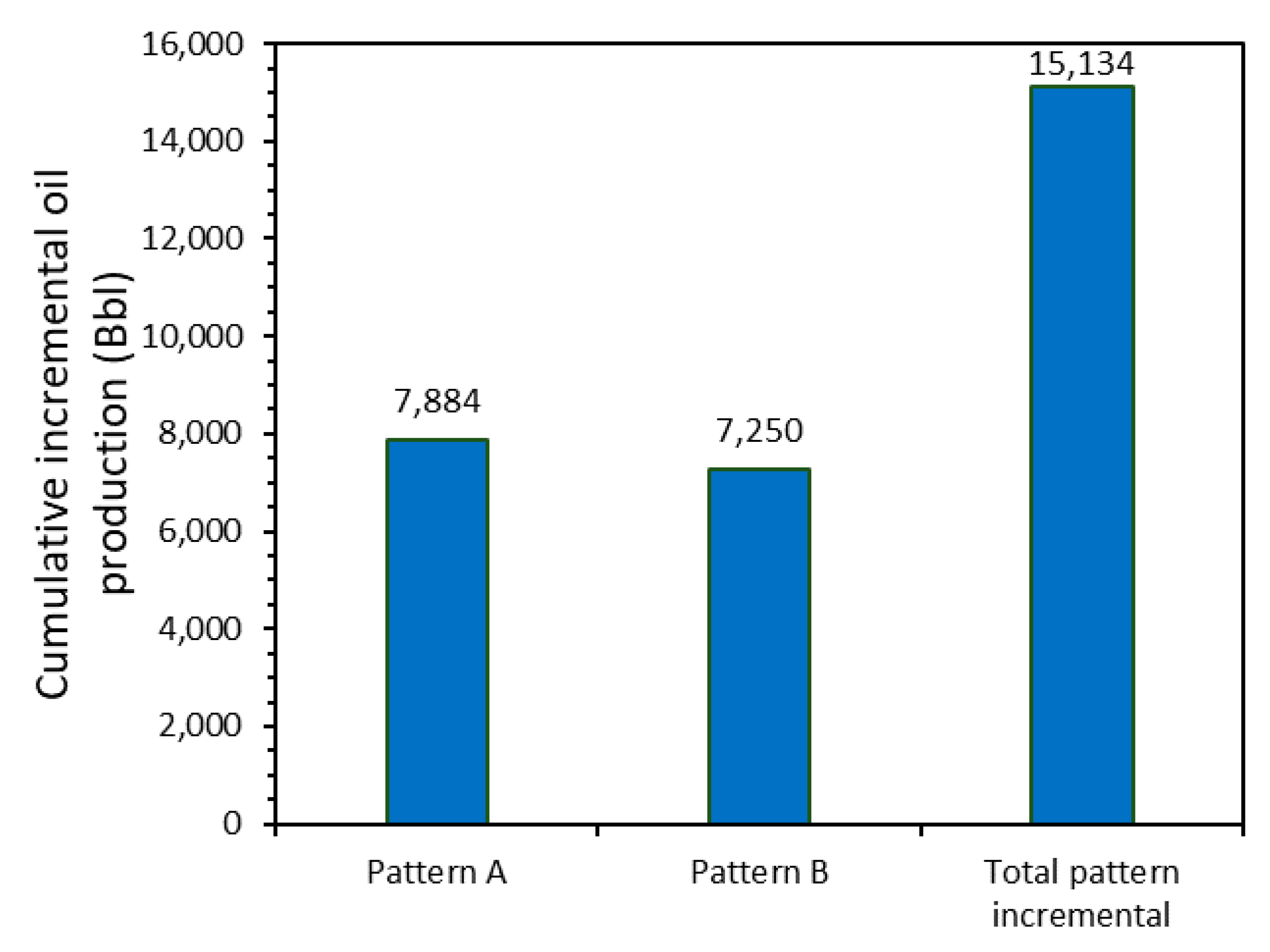
3.6. Field Application
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Franco, C.A.; Montoya, T.; Nassar, N.N.; Pereira-Almao, P.; Cortés, F.B. Adsorption and subsequent oxidation of colombian asphaltenes onto nickel and/or palladium oxide supported on fumed silica nanoparticles. Energy Fuels 2013, 27, 7336–7347. [Google Scholar] [CrossRef]
- Mozo, I.; Mejia, J.; Cortes, F.; Zabala, R. A Robust Mathematical Model for Heavy-Oil Well Stimulations Using Nanofluids: Modelling, Simulation and Validation at La. In Proceedings of the ECMOR XVI-16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3–6 September 2018. [Google Scholar]
- Nassar, N.N.; Hassan, A.; Pereira-Almao, P. Metal oxide nanoparticles for asphaltene adsorption and oxidation. Energy Fuels 2011, 25, 1017–1023. [Google Scholar] [CrossRef]
- Taborda, E.A.; Alvarado, V.; Cortés, F.B. Effect of SiO2-based nanofluids in the reduction of naphtha consumption for heavy and extra-heavy oils transport: Economic impacts on the Colombian market. Energy Convers. Manag. 2017, 148, 30–42. [Google Scholar] [CrossRef]
- Zabala, R.; Franco, C.; Cortés, F. Application of Nanofluids for Improving Oil Mobility in Heavy Oil and Extra-Heavy Oil: A Field Test. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 11–13 April 2016. [Google Scholar]
- Zabala, R.; Mora, E.; Botero, O.; Cespedes, C.; Guarin, L.; Franco, C.; Cortes, F.; Patino, J.; Ospina, N. Nano-technology for asphaltenes inhibition in Cupiagua South Wells. In Proceedings of the IPTC 2014: International Petroleum Technology Conference, Doha, Qatar, 19–22 January 2014. [Google Scholar]
- Giraldo, L.J.; Giraldo, M.A.; Llanos, S.; Maya, G.; Zabala, R.D.; Nassar, N.N.; Franco, C.A.; Alvarado, V.; Cortés, F.B. The effects of SiO2 nanoparticles on the thermal stability and rheological behavior of hydrolyzed polyacrylamide based polymeric solutions. J. Pet. Sci. Eng. 2017, 159, 841–852. [Google Scholar] [CrossRef]
- Llanos, S.n.; Giraldo, L.J.; Santamaria, O.; Franco, C.A.; Cortés, F.B. Effect of Sodium Oleate Surfactant Concentration Grafted onto SiO2 Nanoparticles in Polymer Flooding Processes. ACS Omega 2018, 3, 18673–18684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giraldo, J.; Benjumea, P.; Lopera, S.; Cortés, F.B.; Ruiz, M.A. Wettability alteration of sandstone cores by alumina-based nanofluids. Energy Fuels 2013, 27, 3659–3665. [Google Scholar] [CrossRef]
- Hendraningrat, L.; Torsæter, O. Metal oxide-based nanoparticles: Revealing their potential to enhance oil recovery in different wettability systems. Appl. Nanosci. 2015, 5, 181–199. [Google Scholar] [CrossRef] [Green Version]
- Ju, B.; Fan, T.; Ma, M. Enhanced oil recovery by flooding with hydrophilic nanoparticles. China Particuology 2006, 4, 41–46. [Google Scholar] [CrossRef]
- Giraldo, L.J.; Gallego, J.; Villegas, J.P.; Franco, C.A.; Cortés, F.B. Enhanced waterflooding with NiO/SiO2 0-D Janus nanoparticles at low concentration. J. Pet. Sci. Eng. 2019, 174, 40–48. [Google Scholar] [CrossRef]
- Cheraghian, G.; Hendraningrat, L. A review on applications of nanotechnology in the enhanced oil recovery part B: Effects of nanoparticles on flooding. Int. Nano Lett. 2016, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Striolo, A. Nanoparticle effects on the water-oil interfacial tension. Phys. Rev. E 2012, 86, 051610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeyghami, M.; Kharrat, R.; Ghazanfari, M. Investigation of the applicability of nano silica particles as a thickening additive for polymer solutions applied in EOR processes. Energy Sources Part A Recovery Util. Environ. Eff. 2014, 36, 1315–1324. [Google Scholar] [CrossRef]
- Zhu, D.; Han, Y.; Zhang, J.; Li, X.; Feng, Y. Enhancing rheological properties of hydrophobically associative polyacrylamide aqueous solutions by hybriding with silica nanoparticles. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Gbadamosi, A.O.; Junin, R.; Manan, M.A.; Yekeen, N.; Agi, A.; Oseh, J.O. Recent advances and prospects in polymeric nanofluids application for enhanced oil recovery. J. Ind. Eng. Chem. 2018, 66, 1–19. [Google Scholar] [CrossRef]
- Bryan, J.L.; Kantzas, A. Enhanced heavy-oil recovery by alkali-surfactant flooding. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007. [Google Scholar]
- Krumrine, P.H.; Falcone, J.S., Jr.; Campbell, T.C. Surfactant flooding 1: The effect of alkaline additives on IFT, surfactant adsorption, and recovery efficiency. Soc. Pet. Eng. J. 1982, 22, 503–513. [Google Scholar] [CrossRef]
- Larson, R. Analysis of the physical mechanisms in surfactant flooding. Soc. Pet. Eng. J. 1978, 18, 42–58. [Google Scholar] [CrossRef]
- Kamal, M.S.; Hussein, I.A.; Sultan, A.S. Review on surfactant flooding: Phase behavior, retention, IFT, and field applications. Energy Fuels 2017, 31, 7701–7720. [Google Scholar] [CrossRef]
- Rosen, M.J.; Wang, H.; Shen, P.; Zhu, Y. Ultralow interfacial tension for enhanced oil recovery at very low surfactant concentrations. Langmuir 2005, 21, 3749–3756. [Google Scholar] [CrossRef]
- Harbert, L. Low interfacial tension relative permeability. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. [Google Scholar]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions: III. Di and tri n-alkylbenzenesulfonates. J. Am. Oil Chem. Soc. 1978, 55, 513–520. [Google Scholar] [CrossRef]
- Desai, F.; Demond, A.; Hayes, K. Influence of Surfactant Sorption on Capillary Pressure—Saturation Relationships; ACS Publications: Washington, DC, USA, 1992. [Google Scholar]
- Gdanski, R.D. Modeling the impact of capillary pressure reduction by surfactants. In Proceedings of the International Symposium on Oilfield Chemistry, Houston, TX, USA, 28 February–2 March 2007. [Google Scholar]
- Kumar, N.; Mandal, A. Surfactant stabilized oil-in-water nanoemulsion: Stability, interfacial tension, and rheology study for enhanced oil recovery application. Energy Fuels 2018, 32, 6452–6466. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.M.; Bullón, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 1. Optimum formulation for simple surfactant–oil–water ternary systems. J. Surfactants Deterg. 2013, 16, 449–472. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.M.; Márquez, L.; Manchego, L.; Bullón, J. How to attain an ultralow interfacial tension and a three-phase behavior with a surfactant formulation for enhanced oil recovery: A review. Part 2. Performance improvement trends from Winsor’s premise to currently proposed inter-and intra-molecular mixtures. J. Surfactants Deterg. 2013, 16, 631–663. [Google Scholar] [PubMed] [Green Version]
- Alvarado, V.; Manrique, E. Enhanced oil recovery: An update review. Energies 2010, 3, 1529–1575. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Shadizadeh, S.R. Experimental investigation of a natural surfactant adsorption on shale-sandstone reservoir rocks: Static and dynamic conditions. Fuel 2015, 159, 15–26. [Google Scholar] [CrossRef]
- Bera, A.; Kumar, T.; Ojha, K.; Mandal, A. Adsorption of surfactants on sand surface in enhanced oil recovery: Isotherms, kinetics and thermodynamic studies. Appl. Surf. Sci. 2013, 284, 87–99. [Google Scholar] [CrossRef]
- Curbelo, F.D.; Santanna, V.C.; Neto, E.L.B.; Dutra, T.V., Jr.; Dantas, T.N.C.; Neto, A.A.D.; Garnica, A.I. Adsorption of nonionic surfactants in sandstones. Colloids Surf. A Physicochem. Eng. Asp. 2007, 293, 1–4. [Google Scholar] [CrossRef]
- Wesson, L.L.; Harwell, J.H. Surfactant adsorption in porous media. Surfactants Fundam. Appl. Pet. Ind. 2000, 121–158. [Google Scholar] [CrossRef]
- Amirianshoja, T.; Junin, R.; Idris, A.K.; Rahmani, O. A comparative study of surfactant adsorption by clay minerals. J. Pet. Sci. Eng. 2013, 101, 21–27. [Google Scholar] [CrossRef]
- Azam, M.R.; Tan, I.M.; Ismail, L.; Mushtaq, M.; Nadeem, M.; Sagir, M. Static adsorption of anionic surfactant onto crushed Berea sandstone. J. Pet. Explor. Prod. Technol. 2013, 3, 195–201. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, R.G.; Paria, S. Dynamic contact angles on PTFE surface by aqueous surfactant solution in the absence and presence of electrolytes. J. Colloid Interphase Sci. 2009, 337, 555–562. [Google Scholar] [CrossRef]
- Maurya, N.K.; Mandal, A. Investigation of synergistic effect of nanoparticle and surfactant in macro emulsion based EOR application in oil reservoirs. Chem. Eng. Res. Des. 2018, 132, 370–384. [Google Scholar] [CrossRef]
- Sharma, T.; Kumar, G.S.; Sangwai, J.S. Comparative effectiveness of production performance of Pickering emulsion stabilized by nanoparticle–surfactant–polymerover surfactant–polymer (SP) flooding for enhanced oil recoveryfor Brownfield reservoir. J. Pet. Sci. Eng. 2015, 129, 221–232. [Google Scholar] [CrossRef]
- Xu, D.; Bai, B.; Meng, Z.; Zhou, Q.; Li, Z.; Lu, Y.; Wu, H.; Hou, J.; Kang, W. A Novel Ultra-Low Interfacial Tension Nanofluid for Enhanced Oil Recovery in Super-Low Permeability Reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23–25 October 2018. [Google Scholar]
- Suleimanov, B.A.; Ismailov, F.; Veliyev, E. Nanofluid for enhanced oil recovery. J. Pet. Sci. Eng. 2011, 78, 431–437. [Google Scholar] [CrossRef]
- Zargartalebi, M.; Kharrat, R.; Barati, N. Enhancement of surfactant flooding performance by the use of silica nanoparticles. Fuel 2015, 143, 21–27. [Google Scholar] [CrossRef]
- Zhao, M.; Lv, W.; Li, Y.; Dai, C.; Wang, X.; Zhou, H.; Zou, C.; Gao, M.; Zhang, Y.; Wu, Y. Study on the synergy between silica nanoparticles and surfactants for enhanced oil recovery during spontaneous imbibition. J. Mol. Liq. 2018, 261, 373–378. [Google Scholar] [CrossRef]
- Cortés, F.B.; Lozano, M.; Santamaria, O.; Betancur Marquez, S.; Zapata, K.; Ospina, N.; Franco, C.A. Development and evaluation of surfactant nanocapsules for chemical Enhanced Oil Recovery (EOR) applications. Molecules 2018, 23, 1523. [Google Scholar] [CrossRef] [Green Version]
- Betancur, S.A.; Carrasco-Marín, F.; Franco, C.A.; Cortés, F.B. Development of composite materials based on the interaction between nanoparticles and surfactants for application in chemical enhanced oil recovery. Ind. Eng. Chem. Res. 2018, 57, 12367–12377. [Google Scholar] [CrossRef]
- Rezaei, A.; Riazi, M.; Escrochi, M.; Elhaei, R. Integrating surfactant, alkali and nano-fluid flooding for enhanced oil recovery: A mechanistic experimental study of novel chemical combinations. J. Mol. Liq. 2020, 308, 113106. [Google Scholar] [CrossRef]
- Betancur, S.; Giraldo, L.J.; Carrasco-Marín, F.; Riazi, M.; Manrique, E.J.; Quintero, H.; García, H.A.; Franco-Ariza, C.A.; Cortés, F.B. Importance of the Nanofluid Preparation for Ultra-Low Interfacial Tension in Enhanced Oil Recovery Based on Surfactant–Nanoparticle–Brine System Interaction. ACS Omega 2019, 4, 16171–16180. [Google Scholar] [CrossRef] [Green Version]
- Sheng, J.J. Status of surfactant EOR technology. Petroleum 2015, 1, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Al-Oweini, R.; El-Rassy, H. Synthesis and characterization by FTIR spectroscopy of silica aerogels prepared using several Si (OR) 4 and R′′ Si (OR′) 3 precursors. J. Mol. Struct. 2009, 919, 140–145. [Google Scholar] [CrossRef]
- Garcia-Mateos, I.; Mercedes Velazquez, M.; Rodriguez, L.J. Critical micelle concentration determination in binary mixtures of ionic surfactants by deconvolution of conductivity/concentration curves. Langmuir 1990, 6, 1078–1083. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, M.; Prieto, G.; Rega, C.; Varela, L.M.; Sarmiento, F.; Mosquera, V. A comparative study of the determination of the critical micelle concentration by conductivity and dielectric constant measurements. Langmuir 1998, 14, 4422–4426. [Google Scholar] [CrossRef]
- Rosen, M.J.; Aronson, S. Standard free energies of adsorption of surfactants at the aqueous solution/air interphase from surface tension data in the vicinity of the critical micelle concentration. Colloids Surf. 1981, 3, 201–208. [Google Scholar] [CrossRef]
- Shinoda, K.; Yamaguchi, T.; Hori, R. The surface tension and the critical micelle concentration in aqueous solution of β-D-alkyl glucosides and their mixtures. Bull. Chem. Soc. Jpn. 1961, 34, 237–241. [Google Scholar] [CrossRef]
- Lunkenheimer, K.; Wantke, K.-D. Determination of the surface tension of surfactant solutions applying the method of Lecomte du Noüy (ring tensiometer). Colloid Polym. Sci. 1981, 259, 354–366. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Demissie, H.; Duraisamy, R. Effects of electrolytes on the surface and micellar characteristics of Sodium dodecyl sulphate surfactant solution. J. Sci. Innov. Res. 2016, 5, 208–214. [Google Scholar]
- Pfeiffer, C.; Rehbock, C.; Hühn, D.; Carrillo-Carrion, C.; de Aberasturi, D.J.; Merk, V.; Barcikowski, S.; Parak, W.J. Interaction of colloidal nanoparticles with their local environment: The (ionic) nanoenvironment around nanoparticles is different from bulk and determines the physico-chemical properties of the nanoparticles. J. R. Soc. Interphase 2014, 11, 20130931. [Google Scholar] [CrossRef] [Green Version]
- Elmendorp, J.; De Vos, G. Measurement of interfacial tensions of molten polymer systems by means of the spinning drop method. Polym. Eng. Sci. 1986, 26, 415–417. [Google Scholar] [CrossRef]
- Verdier, C.; Vinagre, H.T.; Piau, M.; Joseph, D.D. High temperature interfacial tension measurements of PA6/PP interphases compatibilized with copolymers using a spinning drop tensiometer. Polymer 2000, 41, 6683–6689. [Google Scholar] [CrossRef] [Green Version]
- Montoya, T.; Coral, D.; Franco, C.A.; Nassar, N.N.; Cortés, F.B. A novel solid–liquid equilibrium model for describing the adsorption of associating asphaltene molecules onto solid surfaces based on the “Chemical Theory”. Energy Fuels 2014, 28, 4963–4975. [Google Scholar] [CrossRef]
- Montes, D.; Henao, J.; Taborda, E.A.; Gallego, J.; Cortés, F.B.; Franco, C.A. Effect of Textural Properties and Surface Chemical Nature of Silica Nanoparticles from Different Silicon Sources on the Viscosity Reduction of Heavy Crude Oil. ACS Omega 2020, 5, 5085–5097. [Google Scholar] [CrossRef] [PubMed]
- Montes, D.; Taborda, E.A.; Minale, M.; Cortés, F.B.; Franco-Ariza, C.A. Effect of the NiO/SiO2 Nanoparticles-Assisted Ultrasound Cavitation Process on the Rheological Properties of Heavy Crude Oil: Steady State Rheometry and Oscillatory Tests. Energy Fuels 2019, 33, 9671–9680. [Google Scholar] [CrossRef]
- Franco-Aguirre, M.; Zabala, R.D.; Lopera, S.H.; Franco, C.A.; Cortés, F.B. Interaction of anionic surfactant-nanoparticles for gas-Wettability alteration of sandstone in tight gas-condensate reservoirs. J. Nat. Gas Sci. Eng. 2018, 51, 53–64. [Google Scholar] [CrossRef]
- Villegas, J.P.; Moncayo-Riascos, I.; Galeano-Caro, D.; Riazi, M.; Franco, C.A.; Cortés, F.B. Functionalization of γ-Alumina and Magnesia Nanoparticles with a Fluorocarbon Surfactant to Promote Ultra-Gas-Wet Surfaces: Experimental and Theoretical Approach. ACS Appl. Mater. Interphases 2020, 12, 13510–13520. [Google Scholar] [CrossRef]
- Gupta, S.P.; Trushenski, S.P. Micellar flooding-compositional effects on oil displacement. Soc. Pet. Eng. J. 1979, 19, 116–128. [Google Scholar] [CrossRef]
- Johannesen, E.B.; Graue, A. Mobilization of remaining oil-emphasis on capillary number and wettability. In Proceedings of the International Oil Conference and Exhibition in Mexico, Veracruz, Mexico, 27–30 June 2007. [Google Scholar]
- Xia, H.; Wang, D.; Wu, W.; Jiang, H. Effect of the visco-elasticity of displacing fluids on the relationship of capillary number and displacement efficiency in weak oil-wet cores. In Proceedings of the Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 30 October–1 November 2007. [Google Scholar]
- Carvalho, M.S.; Alvarado, V. Oil recovery modeling of macro-emulsion flooding at low capillary number. J. Pet. Sci. Eng. 2014, 119, 112–122. [Google Scholar]
- Bashiri, A.; Kasiri, N. Properly use effect of capillary number on residual oil saturation. In Proceedings of the Nigeria annual international conference and exhibition, Abuja, Nigeria, 1–3 August 2011. [Google Scholar]
- Moore, T.; Slobod, R. Displacement of oil by water-effect of wettability, rate, and viscosity on recovery. In Proceedings of the Fall Meeting of the Petroleum Branch of AIME, New Orleans, LA, USA, 2–5 October 1955. [Google Scholar]
- Taborda, E.A.; Franco, C.A.; Lopera, S.H.; Alvarado, V.; Cortés, F.B. Effect of nanoparticles/nanofluids on the rheology of heavy crude oil and its mobility on porous media at reservoir conditions. Fuel 2016, 184, 222–232. [Google Scholar] [CrossRef]
- Mermoux, M.; Chabre, Y.; Rousseau, A. FTIR and 13C NMR study of graphite oxide. Carbon 1991, 29, 469–474. [Google Scholar] [CrossRef]
- Montes, D.; Cortés, F.B.; Franco, C.A. Reduction of heavy oil viscosity through ultrasound cavitation assisted by NiO nanocrystals-functionalized SiO2 nanoparticles. Dyna 2018, 85, 153–160. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press: Cambridge, MA, USA, 2013; Volume 2. [Google Scholar]
- Montes, D.; Orozco, W.; Taborda, E.A.; Franco, C.A.; Cortés, F.B. Development of Nanofluids for Perdurability in Viscosity Reduction of Extra-Heavy Oils. Energies 2019, 12, 1068. [Google Scholar] [CrossRef] [Green Version]
- Brinker, C.J.; Scherer, G.W. Sol-Gel Science: The Physics and Chemistry of Sol-Gel Processing; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Jung, K.Y.; Park, S.B. Enhanced photoactivity of silica-embedded titania particles prepared by sol–gel process for the decomposition of trichloroethylene. Appl. Catal. B Environ. 2000, 25, 249–256. [Google Scholar] [CrossRef]
- Fuseni, A.; Han, M.; Al-Mobith, A. Phase behavior and interfacial tension properties of an amphoteric surfactant for EOR application. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 19–22 May 2013. [Google Scholar]
- Huh, C. Interfacial tensions and solubilizing ability of a microemulsion phase that coexists with oil and brine. J. Colloid Interphase Sci. 1979, 71, 408–426. [Google Scholar] [CrossRef]
- Morini, M.A.; Messina, P.V.; Schulz, P.C. The interaction of electrolytes with non-ionic surfactant micelles. Colloid Polym. Sci. 2005, 283, 1206–1218. [Google Scholar] [CrossRef]
- Kundu, P.; Agrawal, A.; Mateen, H.; Mishra, I.M. Stability of oil-in-water macro-emulsion with anionic surfactant: Effect of electrolytes and temperature. Chem. Eng. Sci. 2013, 102, 176–185. [Google Scholar] [CrossRef]
- Para, G.; Jarek, E.; Warszyński, P.; Adamczyk, Z. Effect of electrolytes on surface tension of ionic surfactant solutions. Colloids Surf. A Physicochem. Eng. Asp. 2003, 222, 213–222. [Google Scholar] [CrossRef]
- Betancur, S.a.; Carrasco-Marín, F.; Pérez-Cadenas, A.n.F.; Franco, C.A.; Jiménez, J.; Manrique, E.J.; Quintero, H.; Cortés, F.B. Effect of Magnetic Iron Core–Carbon Shell Nanoparticles in Chemical Enhanced Oil Recovery for Ultralow Interfacial Tension Region. Energy Fuels 2019, 33, 4158–4168. [Google Scholar] [CrossRef]
- BARUT, K.D.; ARI, F.F.C.; Öner, F. Development and characterization of a cationic emulsion formulation as a potential pDNA carrier system. Turk. J. Chem. 2005, 29, 27–40. [Google Scholar]
- Bai, G.; Nichifor, M.; Lopes, A.; Bastos, M. Thermodynamic characterization of the interaction behavior of a hydrophobically modified polyelectrolyte and oppositely charged surfactants in aqueous solution: Effect of surfactant alkyl chain length. J. Phys. Chem. B 2005, 109, 518–525. [Google Scholar] [CrossRef]
- Mirchi, V.; Saraji, S.; Akbarabadi, M.; Goual, L.; Piri, M.J.I.; Research, E.C. A systematic study on the impact of surfactant chain length on dynamic interfacial properties in porous media: Implications for enhanced oil recovery. Ind. Eng. Chem. Res. 2017, 56, 13677–13695. [Google Scholar] [CrossRef]
- Chen, L.-J.; Lin, S.-Y.; Huang, C.-C. Effect of hydrophobic chain length of surfactants on enthalpy− entropy compensation of micellization. J. Phys. Chem. B 1998, 102, 4350–4356. [Google Scholar] [CrossRef]
- Hirasaki, G.J.; Miller, C.A.; Puerto, M. Recent advances in surfactant EOR. In Proceedings of the IPTC 2008: International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 3–5 December 2008. [Google Scholar]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Guzmán, J.D.; Betancur, S.; Carrasco-Marín, F.; Franco, C.A.; Nassar, N.N.; Cortés, F.B. Importance of the adsorption method used for obtaining the nanoparticle dosage for asphaltene-related treatments. Energy Fuels 2016, 30, 2052–2059. [Google Scholar] [CrossRef]
- Wu, C.; Li, N.J.; Chen, K.C.; Hsu, H.-F. Determination of critical micelle concentrations of ionic and nonionic surfactants based on relative viscosity measurements by capillary electrophoresis. Res. Chem. Intermed. 2014, 40, 2371–2379. [Google Scholar] [CrossRef]
- Bielawska, M.; Chodzińska, A.; Jańczuk, B.; Zdziennicka, A. Determination of CTAB CMC in mixed water+ short-chain alcohol solvent by surface tension, conductivity, density and viscosity measurements. Colloids Surf. A Physicochem. Eng. Asp. 2013, 424, 81–88. [Google Scholar] [CrossRef]
- Standnes, D.C.; Austad, T. Wettability alteration in chalk: 2. Mechanism for wettability alteration from oil-wet to water-wet using surfactants. J. Pet. Sci. Eng. 2000, 28, 123–143. [Google Scholar] [CrossRef]
- Somasundaran, P.; Zhang, L. Adsorption of surfactants on minerals for wettability control in improved oil recovery processes. J. Pet. Sci. Eng. 2006, 52, 198–212. [Google Scholar] [CrossRef]
- Betancur, S.; Olmos, C.M.; Pérez, M.; Lerner, B.; Franco, C.A.; Riazi, M.; Gallego, J.; Carrasco-Marín, F.; Cortés, F.B. A microfluidic study to investigate the effect of magnetic iron core-carbon shell nanoparticles on displacement mechanisms of crude oil for chemical enhanced oil recovery. J. Pet. Sci. Eng. 2020, 184, 106589. [Google Scholar] [CrossRef]
- Druetta, P.; Picchioni, F. Surfactant–Polymer Flooding: Influence of the Injection Scheme. Energy Fuels 2018, 32, 12231–12246. [Google Scholar] [CrossRef]




| Salts | Concentration (mg·L−1) |
|---|---|
| NaCl | 5.717 |
| CaCl2.2H2O | 13.525 |
| MgCl2.6H2O | 0.3833 |
| BaCl2.2H2O | 0.0996 |
| KCl | 7.4121 |
| Porous Media Properties | ||
|---|---|---|
| Property | Core 1 | Core 2 |
| Length (cm) | 7.1 | 17.5 |
| Diameter (cm) | 3.8 | 4.4 |
| Porosity (%) | 16 | 17 |
| Porous volume (cm3) | 13 | 43.5 |
| Mineralogy | 50% Ottawa sand−50% reservoir core cuts | |
| Surfactant Concentration (mg·L−1) | Total Treatment Injected (gal/d) | Date |
|---|---|---|
| Pattern A | ||
| 1000 | 54.6 | 6-Dec-19 |
| 500 | 48 | 23-Dec-19 |
| 300 | 29 | 8-Jan-20 |
| 350 | 33 | 28-Jan-20 |
| 350 | 31 | 3-Mar-20 |
| 400 | 37 | 20-Mar-20 |
| Pattern B | ||
| 1000 | 126 | 6-Dec-19 |
| 500 | 76 | 23-Dec-19 |
| 300 | 46 | 8-Jan-20 |
| 350 | 52 | 28-Jan-20 |
| 350 | 50 | 6-Apr-20 |
| Surfactant | Density (g·L−1) | CMC (mg·L−1) | HLB |
|---|---|---|---|
| SA | 0.94 | 250 | 11 |
| SB | 0.98 | 300 | 11 |
| Particle | dp50 (± 1 nm) | SBET (± 1 m2∙g−1) | pHIEP ± 0.1 |
|---|---|---|---|
| CNA | 71 | 192 | 2.0 |
| CNB | 70 | 221 | 2.2 |
| Adsorbent | H (mg·g−1) | K (g·g−1) | Nm (g·g−1) | RSME (%) |
|---|---|---|---|---|
| Ottawa sand | 0.00039 | 1.75 × 10−6 | 6042.51 | 4.58 |
| CNA | 5.16 | 2.64 | 4.22 | 4.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco, C.A.; Giraldo, L.J.; Candela, C.H.; Bernal, K.M.; Villamil, F.; Montes, D.; Lopera, S.H.; Franco, C.A.; Cortés, F.B. Design and Tuning of Nanofluids Applied to Chemical Enhanced Oil Recovery Based on the Surfactant–Nanoparticle–Brine Interaction: From Laboratory Experiments to Oil Field Application. Nanomaterials 2020, 10, 1579. https://doi.org/10.3390/nano10081579
Franco CA, Giraldo LJ, Candela CH, Bernal KM, Villamil F, Montes D, Lopera SH, Franco CA, Cortés FB. Design and Tuning of Nanofluids Applied to Chemical Enhanced Oil Recovery Based on the Surfactant–Nanoparticle–Brine Interaction: From Laboratory Experiments to Oil Field Application. Nanomaterials. 2020; 10(8):1579. https://doi.org/10.3390/nano10081579
Chicago/Turabian StyleFranco, Carlos A., Lady J. Giraldo, Carlos H. Candela, Karla M. Bernal, Fabio Villamil, Daniel Montes, Sergio H. Lopera, Camilo A. Franco, and Farid B. Cortés. 2020. "Design and Tuning of Nanofluids Applied to Chemical Enhanced Oil Recovery Based on the Surfactant–Nanoparticle–Brine Interaction: From Laboratory Experiments to Oil Field Application" Nanomaterials 10, no. 8: 1579. https://doi.org/10.3390/nano10081579
APA StyleFranco, C. A., Giraldo, L. J., Candela, C. H., Bernal, K. M., Villamil, F., Montes, D., Lopera, S. H., Franco, C. A., & Cortés, F. B. (2020). Design and Tuning of Nanofluids Applied to Chemical Enhanced Oil Recovery Based on the Surfactant–Nanoparticle–Brine Interaction: From Laboratory Experiments to Oil Field Application. Nanomaterials, 10(8), 1579. https://doi.org/10.3390/nano10081579







