Nanoparticle and Bioparticle Deposition Kinetics: Quartz Microbalance Measurements
Abstract
:1. Introduction
2. Kinetics of Particle Deposition—Theoretical Aspects
2.1. General Considerations
2.2. Limiting Solutions—Initial Deposition Rates
2.3. Surface Blocking Effects—Maximum Coverages
3. Modeling QCM Response—Heterogeneous (Particle-Like) Load
3.1. General Considerations
3.2. The Rigid Contact Regime
3.3. The Soft Contact Regime
4. Experimental Results
4.1. General Considerations
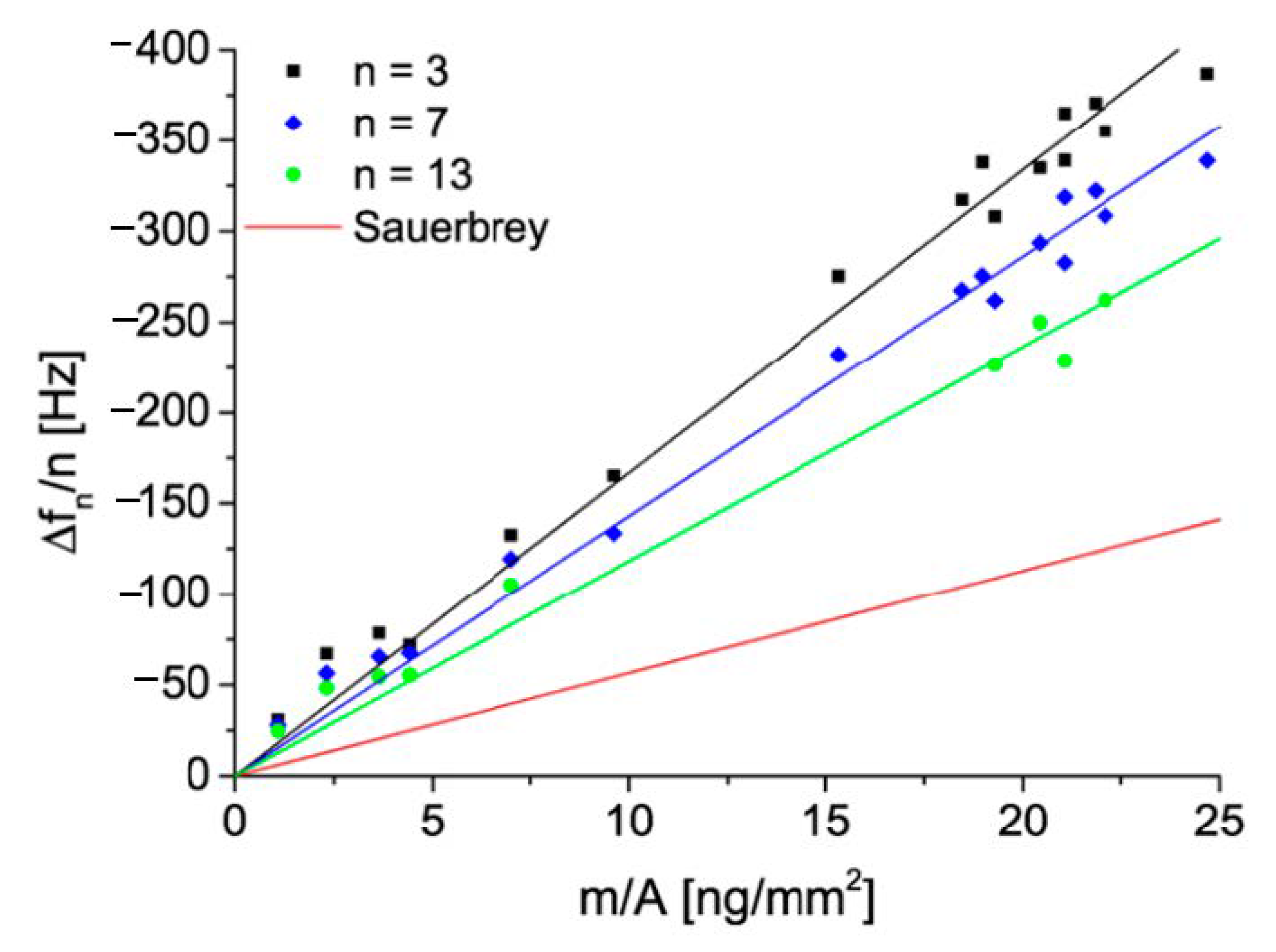
4.2. Reference Results for Nanoparticles
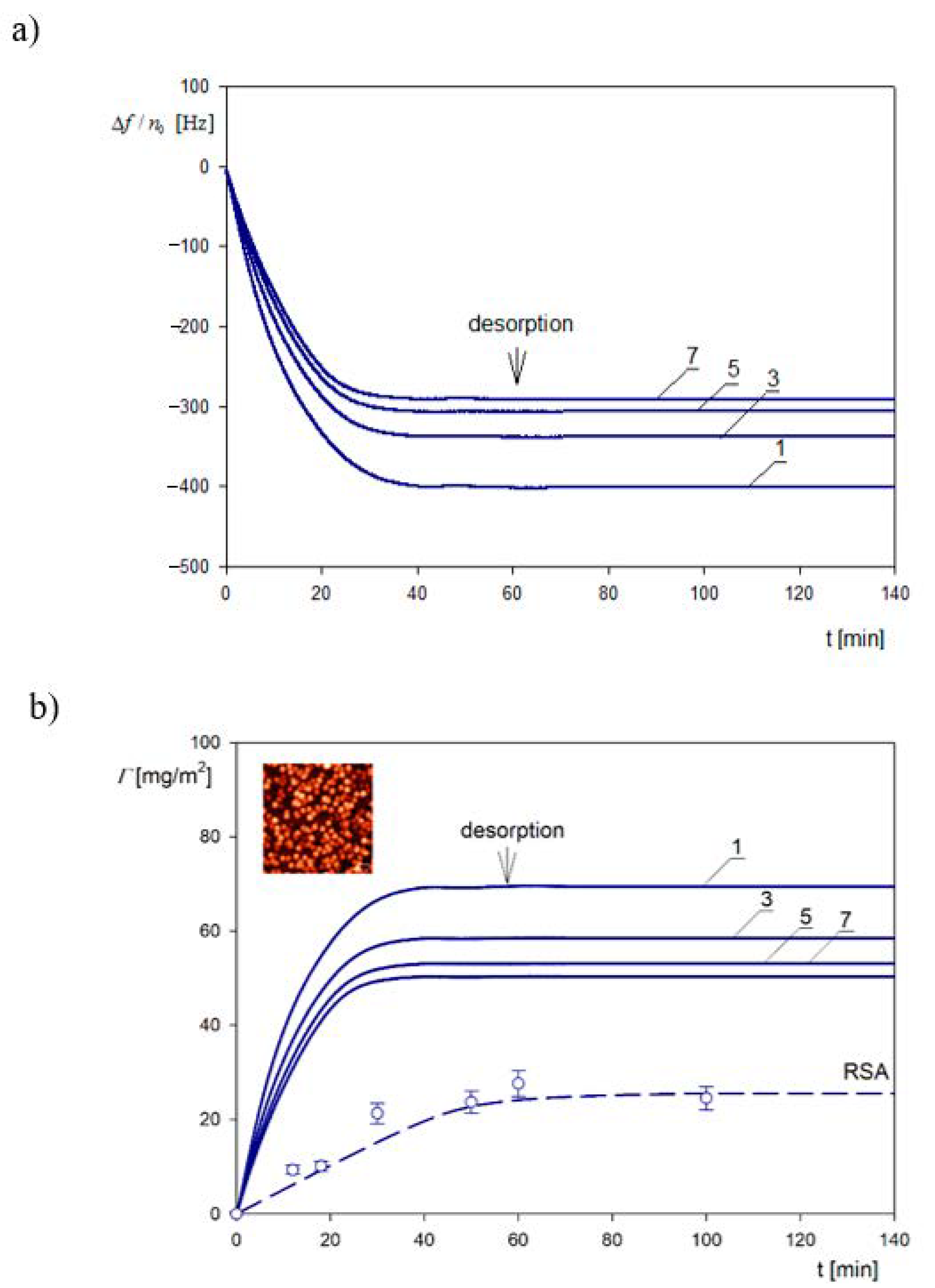
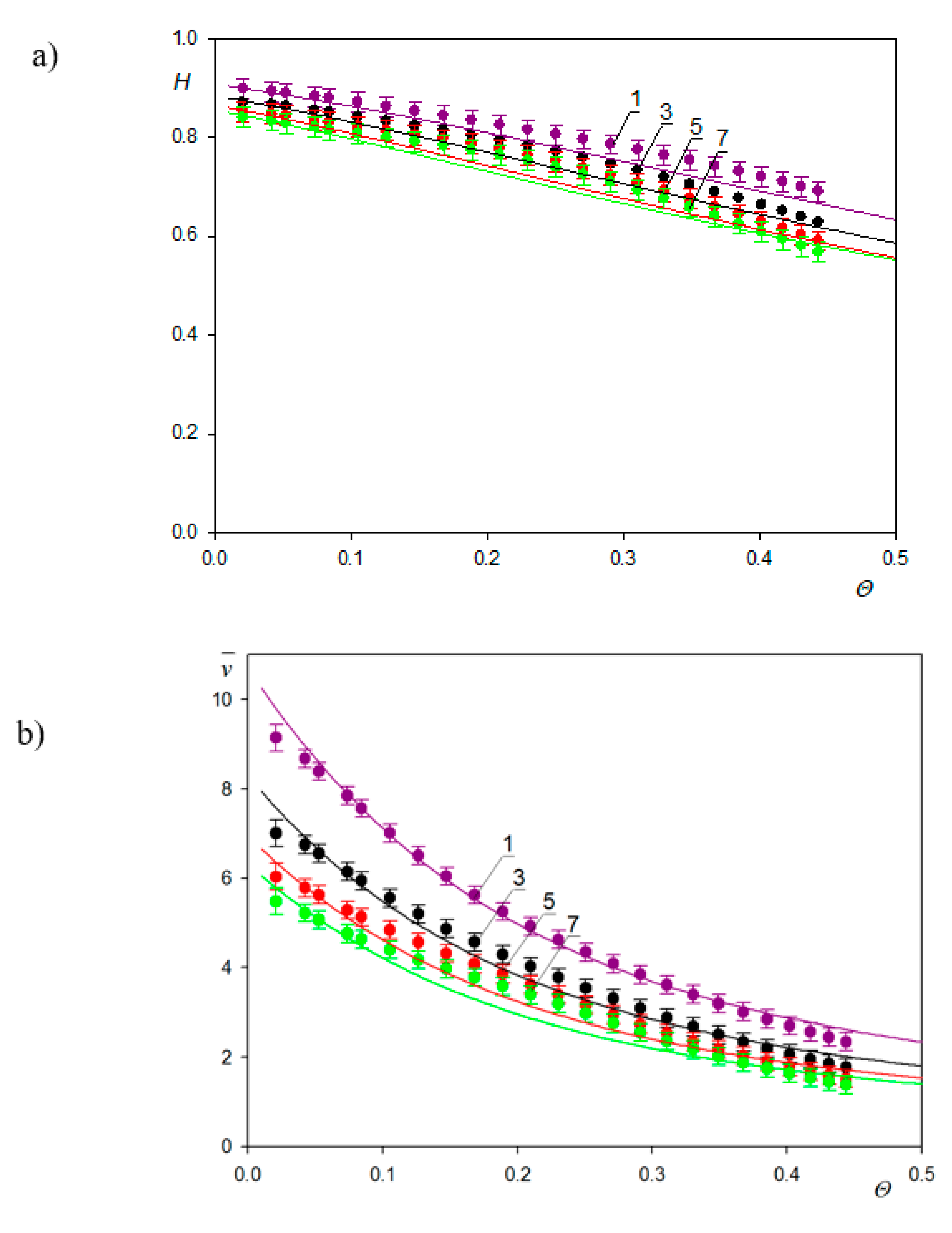
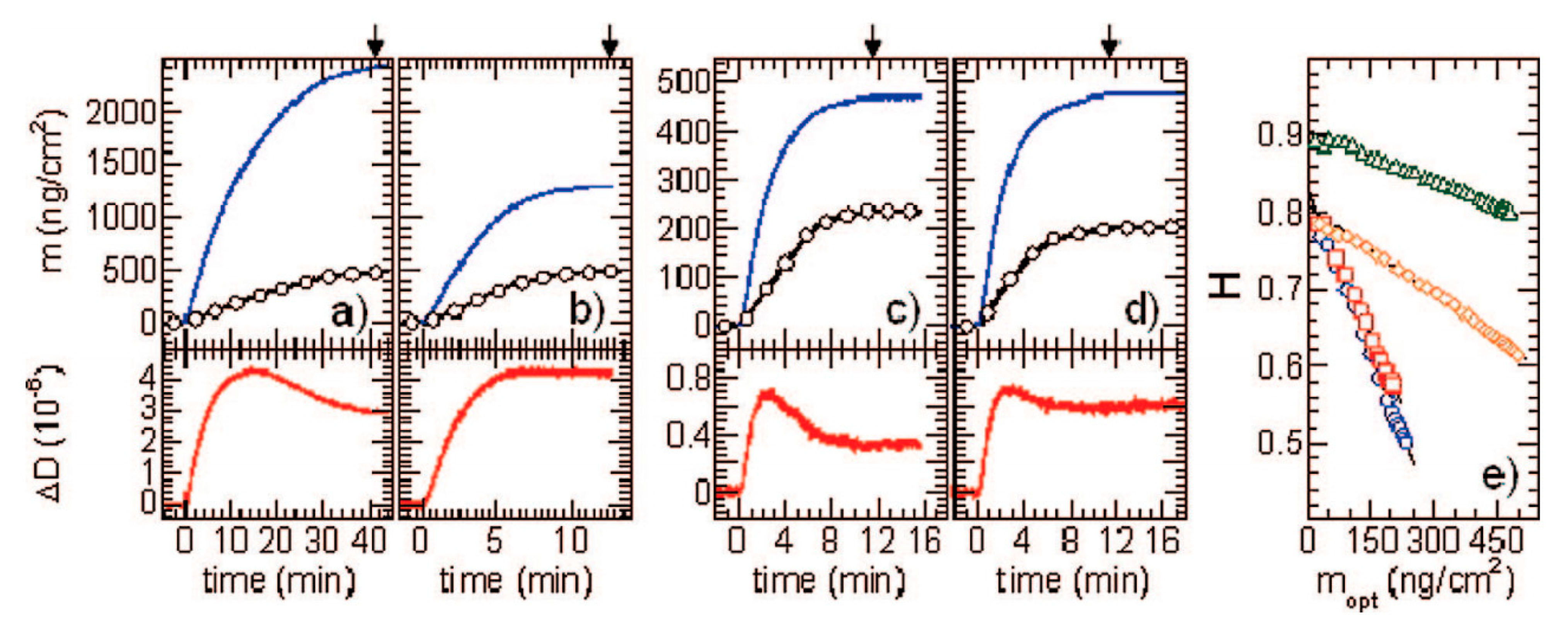
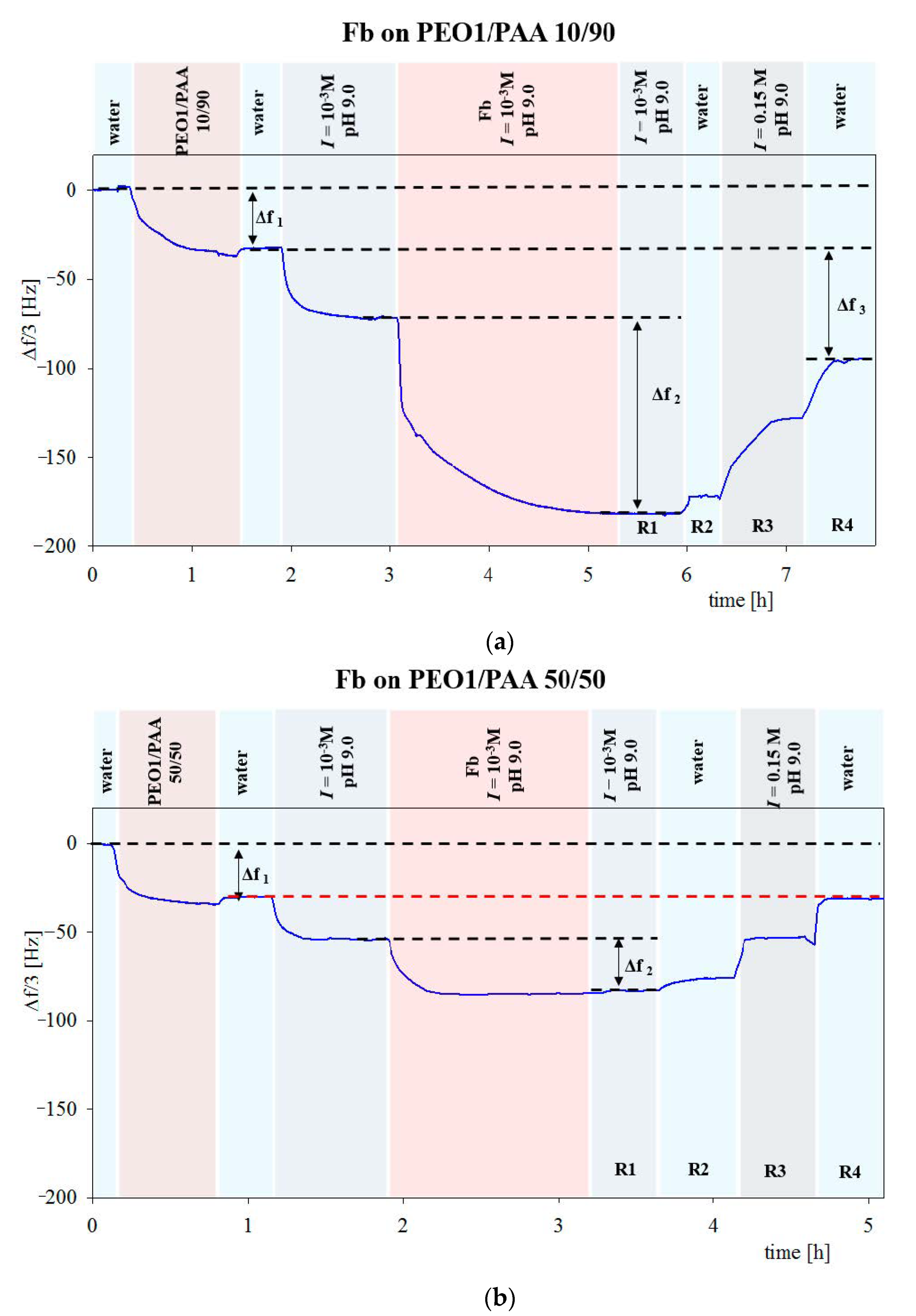
4.3. Bioparticle Deposition Kinetics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sau, T.K.; Rogach, A.L.; Jäckel, F.; Klar, T.A.; Feldmann, J. Properties and applications of colloidal nonspherical noble metal nanoparticles. Adv. Mater. 2010, 22, 1805–1825. [Google Scholar] [CrossRef]
- Yang, S.; Luo, X. Mesoporous nano/micro noble metal particles: Synthesis and applications. Nanoscale 2014, 6, 4438–4457. [Google Scholar] [CrossRef] [PubMed]
- Kubiak, K.; Adamczyk, Z.; Maciejewska, J.; Oćwieja, M. Gold nanoparticle monolayers of controlled coverage and structure. J. Phys. Chem. 2016, 120, 11807–11819. [Google Scholar] [CrossRef]
- Oćwieja, M.; Adamczyk, Z.; Morga, M.; Kubiak, K. Silver particle monolayers—Formation, stability, applications. Adv. Colloid Interface Sci. 2015, 222, 530–563. [Google Scholar] [CrossRef] [PubMed]
- Maciejewska-Prończuk, J. Mechanism of Formation of Noble Nanoparticle Layers at the Solid/Electrolyte Interface. Ph.D. Thesis, J. Haber Institute of Catalysis and Surface Chemistry, Polish Academy of Sciences, Kraków, Poland, 2019. [Google Scholar]
- Miah, M.; Pavey, K.D.; Gun’ko, M.; Sheehan, R.; Cragg, P.J. Observation of transient alkali metal inclusion in oxacalix[3] arenes. Supramol. Chem. 2004, 16, 185–192. [Google Scholar] [CrossRef]
- Konop, M.; Damps, T.; Misicka, A.; Rudnicka, L. Certain aspects of silver and silver nanoparticles in wound care. A Minireview. J. Nanomater. 2016, 7614753, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Lara, H.H.; Ixtepan-Turrent, L.; Jose Yacaman, M.; Lopez-Ribot, J. Inhibition of Candida auris biofilm formation on medical and environmental surfaces by silver nanoparticles. ACS Appl. Mater. Interfaces 2020, 12, 21183–21191. [Google Scholar] [CrossRef]
- Jeong, Y.; Kook, Y.; Leea, K.; Koh, W. Metal enhanced fluorescence (MEF) for biosensors: General approaches and a review of recent developments. Biosens. Bioelectron. 2018, 111, 102–116. [Google Scholar] [CrossRef]
- Badshah, M.A.; Koh, N.Y.; Zia, A.W.; Abbas, N.; Zahra, Z.; Saleem, M.W. Recent developments in plasmonic nanostructures for metal enhanced fluorescence-based biosensing. Nanomaterials 2020, 10, 1749. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, S.; Liu, Q.; Masliyah, J.; Xu, Z. QCM-D study of nanoparticle interactions. Adv. Colloid Interface Sci. 2016, 233, 94–114. [Google Scholar] [CrossRef] [Green Version]
- Astruc, D. Introduction: Nanoparticles in catalysis. Chem. Rev. 2020, 120, 461–463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yousefi, N.; Tufenkji, N. Probing the Interaction between nanoparticles and lipid membranes by quartz crystal microbalance with dissipation monitoring. Front. Chem. 2016, 4, 46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zembala, M.; Adamczyk, Z. Measurements of streaming potential for mica covered by colloid particles. Langmuir 2000, 16, 1593–1601. [Google Scholar] [CrossRef]
- Zembala, M.; Adamczyk, Z.; Warszyński, P. Influence of adsorbed particles on streaming potential of mica. Colloids Surf. A. 2001, 195, 3–15. [Google Scholar] [CrossRef]
- Nattich-Rak, M.; Dąbkowska, M.; Adamczyk, Z. Microparticle deposition on human serum albumin layers: Unraveling anomalous adsorption mechanism. Colloids Interfaces 2020, 4, 51. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Bratek, A.; Szelag, E.; Bastrzyk, A.; Michna, A.; Barbasz, J. Colloid particle deposition on heterogeneous surfaces produces by electrolyte adsorption. Colloids Surf. A: Physicochem. Eng. Asp. 2009, 343, 111–117. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Bratek-Skicki, A.; Żeliszewska, P.; Wasilewska, M. Mechanisms of fibrinogen adsorption at solid substrates. Curr. Top. Med. Chem. 2014, 14, 702–729. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Glawdel, T.; Ren, C.L.; Emelko, M.B. Non-linear, non-monotonic effect of nano-scale roughness on particle deposition in absence of an energy barrier: Experiments and modeling. Sci. Rep. 2015, 5, 17747. [Google Scholar] [CrossRef] [Green Version]
- Bratek-Skicki, A.; Zeliszewska, P.; Adamczyk, Z. Human fibrinogen adsorption on latex particles at pH 7.4 studied by electrophoretic mobility and AFM measurements. Curr. Top. Med. Chem. 2014, 14, 640–648. [Google Scholar] [CrossRef]
- Bratek-Skicki, A.; Żeliszewska, P.; Ruso, J.M. Fibrinogen: A journey into biotechnology. Soft Matter 2016, 12, 8639–8653. [Google Scholar] [CrossRef]
- Cross, W.M.; Ma, S.; Winter, R.M.; Kellar, J.J. FT-IR and SEM study of colloidal particle deposition. Colloids Surf. A Physicochem. Eng. Asp. 1999, 154, 115–125. [Google Scholar] [CrossRef]
- Kollmer, M.; Meinhardt, K.; Haupt, C.; Liberta, F.; Wulff, M.; Linder, J.; Handl, L.; Heinrich, L.; Loos, C.; Schmidt, M.; et al. Electron tomography reveals the fibril structure and lipid interactions in amyloid deposits. Proc. Natl. Acad. Sci. USA 2016, 113, 5604–5609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kleimann, J.; Lecoultre, G.; Papastavrou, G.; Jeanneret, S.; Galletto, P.; Koper, G.J.; Borkovec, M. Deposition of nanosized latex particles onto silica and cellulose surfaces studied by optical reflectometry. J. Colloid Interface Sci. 2006, 303, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Toccafondi, C.; Prato, M.; Maidecchi, G.; Penco, A.; Bisio, F.; Cavalleri, O.; Canepa, M. Optical properties of Yeast Cytochrome c monolayer on gold: An in situ spectroscopic ellipsometry investigation. J. Colloid Interface Sci. 2011, 364, 125–132. [Google Scholar] [CrossRef]
- Höök, F.; Vörös, J.; Rodahl, M.; Kurrat, R.; Böni, P.; Ramsden, J.J.; Textor, M.; Spencer, N.D.; Tengvall, P.; Gold, J.; et al. A comparative study of protein adsorption on titanium oxide surfaces using in situ ellipsometry, optical waveguide lightmode spectroscopy, and quartz crystal microbalance/dissipation. Colloids Surf. B. 2002, 24, 155–170. [Google Scholar] [CrossRef]
- Sander, M.; Madliger, M.; Schwarzenbach, R.P. Adsorption of transgenic insecticidal Cry1Ab protein to SiO2. 1. Forces driving adsorption. Environ. Sci. Technol. 2010, 44, 8870–8876. [Google Scholar] [CrossRef]
- Wasilewska, M.; Adamczyk, Z.; Sadowska, M.; Boulmedais, F.; Cieśla, M. Mechanisms of fibrinogen adsorption on silica sensors at various pHs: Experiments and theoretical modeling. Langmuir 2019, 35, 11275–11284. [Google Scholar] [CrossRef]
- Michna, A.; Pomorska, A.; Nattich-Rak, M.; Wasilewska, M.; Adamczyk, Z. Hydrodynamic solvation of poly(amido amine) dendrimer monolayers on silica. J. Phys. Chem. C. 2020, 124, 17684–17695. [Google Scholar] [CrossRef]
- Reimhult, E.; Larsson, C.; Kasemo, B.; Höök, F. Simultaneous surface plasmon resonance and quartz crystal microbalance with dissipation monitoring measurements of biomolecular adsorption events involving structural transformations and variations in coupled water. Anal. Chem. 2004, 76, 7211–7220. [Google Scholar] [CrossRef]
- Tokarczyk, K.; Jachimska, B. Quantitative interpretation of PAMAM dendrimers adsorption on silica surface. J. Colloids Interface Sci. 2017, 503, 86–94. [Google Scholar] [CrossRef]
- Bratek-Skicki, A.; Zeliszewska, P.; Adamczyk, Ż. Tuning conformations of fibrinogen monolayers on latex particles by pH of adsorption. Colloids Surf. B Biointerfaces 2013, 103, 482–488. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, Z.; Sadlej, K.; Wajnryb, E.; Nattich, M.; Ekiel-Jeżewska, M.L.; Bławzdziewicz, J. Streaming potential measurements of colloid, polyelectrolyte and protein deposition. Adv. Colloid Interface Sci. 2010, 153, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, Z.; Zaucha, M.; Zembala, M. Zeta potential of mica covered by colloid particles: A streaming potential study. Langmuir 2010, 26, 9368–9377. [Google Scholar] [CrossRef] [PubMed]
- Wasilewska, M.; Adamczyk, Z. Fibrinogen adsorption on mica studied by AFM and in situ streaming potential measurements. Langmuir 2011, 27, 686–696. [Google Scholar] [CrossRef] [PubMed]
- Tellechea, E.; Johannsmann, D.; Steinmetz, N.F.; Richter, R.P.; Reviakine, I. Model-independent analysis of QCM data on colloidal particle adsorption. Langmuir 2009, 25, 5177–5184. [Google Scholar] [CrossRef]
- Johannsmann, D.; Reviakine, I.; Richter, R.P. Dissipation in films of adsorbed nanospheres studied by quartz crystal microbalance (QCM). Anal. Chem. 2009, 81, 8167–8176. [Google Scholar] [CrossRef] [PubMed]
- Pomorska, A.; Shchukin, D.; Hammond, R.; Cooper, M.A.; Grundmeier, G.; Johannsmann, D. Positive frequency shifts observed upon adsorbing micron-sized solid objects to a quartz crystal microbalance from the liquid phase. Anal. Chem. 2010, 82, 2237–2242. [Google Scholar] [CrossRef]
- Olsson, A.L.J.; van der Mei, H.C.; Johansmann, D.; Busscher, H.J.; Sharma, P.K. Probing colloid-substratum contact stiffness by acoustic sensing in a liquid phase. Anal. Chem. 2012, 84, 4504–4512. [Google Scholar] [CrossRef]
- Olsson, A.L.; Quevedo, I.R.; He, D.; Basnet, M.; Tufenkji, N. Using the quartz crystal microbalance with dissipation monitoring to evaluate the size of nanoparticles deposited on surfaces. ACS Nano 2013, 7, 7833–7843. [Google Scholar] [CrossRef] [Green Version]
- Grunewald, C.; Schmudde, M.; Noufele, C.N.; Graf, C.; Risse, T. Ordered structures of functionalized silica nanoparticles on gold surfaces: Correlation of quartz crystal microbalance with structural characterization. Anal. Chem. 2015, 87, 10642–10649. [Google Scholar] [CrossRef]
- Kubiak, K.; Adamczyk, Z.; Oćwieja, M. Kinetics of silver nanoparticle deposition at PAH monolayers: Reference QCM results. Langmuir 2015, 31, 2988–2996. [Google Scholar] [CrossRef] [PubMed]
- Schmudde, M.; Grunewald, C.; Risse, T.; Graf, C. Controlling the interparticular distances of extended non-close-packed colloidal monolayers. Langmuir 2020, 36, 4827–4834. [Google Scholar] [CrossRef] [PubMed]
- Gillissen, J.J.J.; Jackman, J.A.; Tabaei, S.R.; Yoon, B.K.; Cho, N.J. Quartz crystal microbalance model for quantitatively probing the deformation of adsorbed particles at low surface coverage. Anal. Chem. 2017, 89, 11711–11718. [Google Scholar] [CrossRef] [PubMed]
- Gillissen, J.J.J.; Jackman, J.A.; Tabaei, S.R.; Cho, N.-J. Numerical study on the effect of particle surface coverage on the quartz crystal microbalance response. Anal. Chem. 2018, 90, 2238–2245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kananizadeh, N.; Rice, C.; Lee, J.; Rodenhausen, K.B.; Sekora, D.; Schubert, M.; Schubert, E.; Bartelt-Hunt, S.; Li, Y. Combined quartz crystal microbalance with dissipation (QCM-D) and generalized ellipsometry (GE) to characterize the deposition of titanium dioxide nanoparticles on model rough surfaces. J. Hazard. Mater. 2017, 322, 118–128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartelt-Hunt, S.; Schubert, E.; Zhang, J.; Li, Y. Deposition of titanium dioxide nanoparticles onto engineered rough surfaces with controlled heights and properties. Colloids Surf. B. 2019, 571, 125–133. [Google Scholar]
- Tarnapolsky, A.; Freger, V. Modeling QCM-D response to deposition and attachment of microparticles and living cells. Anal. Chem. 2018, 90, 13960–13968. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Sadowska, M. Hydrodynamic Solvent coupling effects in quartz crystal microbalance measurements of nanoparticle deposition kinetics. Anal. Chem. 2020, 92, 3896–3903. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Sadowska, M.; Żeliszewska, P. Applicability of QCM-D for quantitative measurements of nano- and microparticle deposition kinetics: Theoretical modeling and experiments. Anal. Chem. 2020, 92, 15087–15095. [Google Scholar] [CrossRef]
- Khopade, A.J.; Caruso, F. Electrostatically assembled polyelectrolyte/dendrimer multilayer films as ultrathin nanoreservoirs. Nano Lett. 2002, 2, 415–418. [Google Scholar] [CrossRef]
- Esumi, K.; Ichikawa, M.; Yoshimura, T. Adsorption characteristics of poly(amidoamine) and poly(propylene imine) dendrimers on gold. Colloids Surf. A. 2004, 232, 415–418. [Google Scholar] [CrossRef]
- Porus, M.; Clerc, F.; Maroni, P.; Borkovec, M. Ion-specific responsiveness of polyamidoamine (PAMAM) dendrimers adsorbed on silica substrates. Macromolecules 2012, 45, 3919–3927. [Google Scholar] [CrossRef]
- Rechendorff, K.; Hovgaard, M.B.; Foss, M.; Zhdanov, V.P.; Besenbacher, F. Enhancement of protein adsorption induced by surface roughness. Langmuir 2006, 22, 10885–10888. [Google Scholar] [CrossRef] [PubMed]
- Johannsmann, D.; Reviakine, I.; Rojas, E.; Gallego, M. Effect of sample heterogeneity on the interpretation of QCM(-D) data: Comparison of combined quartz crystal microbalance/atomic force microscopy measurements with finite element method modeling. Anal. Chem. 2008, 80, 8891–8899. [Google Scholar] [CrossRef] [PubMed]
- Bingen, P.; Wang, G.; Steinmetz, N.F.; Rodahl, M.; Richter, R.P. Solvation effects in the quartz crystal microbalance with dissipation monitoring response to biomolecular adsorption. A phenomenological approach. Anal. Chem. 2008, 80, 8880–8890. [Google Scholar] [CrossRef]
- Carton, I.; Brisson, A.R.; Richter, R.P. Label-free detection of clustering of membrane-bound proteins. Anal. Chem. 2010, 82, 9275–9281. [Google Scholar] [CrossRef]
- Wolny, P.M.; Spatz, J.P.; Richter, R.P. On the adsorption behavior of biotin-binding proteins on gold and silica. Langmuir 2010, 26, 1029–1034. [Google Scholar] [CrossRef]
- Reviakine, I.; Johannsmann, D.; Richter, R.P. Hearing what you cannot see and visualizing what you hear: Interpreting quartz crystal microbalance data from solvated interfaces. Anal. Chem. 2011, 83, 8838–8848. [Google Scholar] [CrossRef]
- Kubiak, K.; Adamczyk, Z.; Wasilewska, M. Mechanisms of fibrinogen adsorption at the silica substrate determined by QCM-D measurements. J. Colloid Interface Sci. 2015, 457, 378–387. [Google Scholar] [CrossRef] [PubMed]
- Kubiak, K.; Adamczyk, Z.; Cieśla, M. Fibrinogen adsorption mechanism at the gold substrate determined by QCM-D measurementsand RSA modelling. Colloids Surf. B. 2016, 139, 123–131. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Pomorska, A.; Nattich-Rak, M.; Wytrwal-Sarna, M.; Bernasik, A. Protein adsorption mechanisms at rough surfaces: Serum albumin at a gold substrate. J. Colloid Interface Sci. 2018, 530, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Bratek-Skicki, A.; Eloy, P.; Morga, M.; Dupont-Gillain, C. Reversible Protein adsorption on mixed PEO/PAA Polymer brushes: Role of Ionic strength and PEO content. Langmuir 2018, 34, 3037–3048. [Google Scholar] [CrossRef] [PubMed]
- Bratek-Skicki, A.; Cristaudo, V.; Savocco, J.; Nootens, S.; Morsomme, P.; Delcorte, A.; Dupont-Gillain, C. Mixed polymer brushes for the selective capture and release of proteins. Biomacromolecules 2019, 20, 778–789. [Google Scholar] [CrossRef] [PubMed]
- Bratek-Skicki, A. Design of Ultra-Thin PEO/PDMAEMA polymer coatings for tunable protein adsorption. Polymers 2020, 12, 660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eun, A.J.; Huang, L.; Chew, F.T.; Li, S.F.; Wong, S.M. Detection of two orchid viruses using quartz crystal microbalance (QCM) immunosensors. J. Virol. Methods 2002, 99, 71–79. [Google Scholar] [CrossRef]
- Peduru Hewa, T.M.; Tannock, G.A.; Mainwaring, D.E.; Harrison, S.; Fecondo, J.V. The detection of influenza A and B viruses in clinical specimens using a quartz crystal microbalance. J. Virol. Methods 2009, 162, 14–21. [Google Scholar] [CrossRef]
- Chen, Y.S.; Hung, Y.C.; Chiou, J.C.; Wang, H.L.; Huang, H.S.; Huang, L.C.; Huang, G.S. Ultrasensitive detection of cymbidium mosaic potexvirus using a single-wall carbon nanotube-functionalized quartz crystal microbalance. Jpn. J. Appl. Phys. 2010, 49, 105103. [Google Scholar] [CrossRef]
- Gutierrez, L.; Mylon, S.E.; Nash, B.; Nguyen, T.H. Deposition and aggregation kinetics of rotavirus in divalent cation solutions. Environ. Sci. Technol. 2010, 44, 4552–4557. [Google Scholar] [CrossRef]
- Rayaprolu, V.; Manning, B.M.; Douglas, T.R.; Bothner, B. Virus particles as active nanomaterials that can rapidly change their viscoelastic properties in response to dilute solutions. Soft Matter 2010, 6, 5286–5288. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, D.; Hou, B. Determination of sulphate-reducing bacteria based on vancomycin-functionalized magnetic nanoparticles using a modification-free quartz crystal microbalance. Biosens. Bioelectron. 2010, 25, 1847–1850. [Google Scholar] [CrossRef]
- Zhang, F.; Li, H.; Wang, X.; Low, H.Y.; Li, X. Hierarchically imprinted polymer substrates for enhanced attachment of Escherichia coli. J. Colloids Interface Sci. 2010, 343, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Gabi, M.; Hefermehl, L.; Lukic, D.; Zahn, R.; Vörös, J.; Eberli, D. Electrical microcurrent to prevent conditioning film and bacterial adhesion to urological stents. Urol. Res. 2011, 39, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Olsson, A.L.; van der Mei, H.C.; Busscher, H.J.; Sharma, P.K. Novel analysis of bacterium-substratum bond maturation measured using a quartz crystal microbalance. Langmuir 2010, 26, 11113–11117. [Google Scholar] [CrossRef] [PubMed]
- Gutman, J.; Walker, S.L.; Freger, V.; Herzberg, M. Bacterial attachment and viscoelasticity: Physicochemical and motility effects analyzed using quartz crystal microbalance with dissipation (QCM-D). Environ. Sci. Technol. 2013, 47, 398–404. [Google Scholar] [CrossRef] [PubMed]
- Fulgione, A.; Cimafonte, M.; Della Ventura, B.; Iannaccone, M.; Ambrosino, C.; Capuano, F.; Proroga, Y.T.R.; Velotta, R.; Capparelli, R. QCM-based immunosensor for rapid detection of Salmonella Typhimurium in food. Sci. Rep. 2018, 8, 16137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shan, Y.; Liu, L.; Liu, Y.; Harms, H.; Wick, L.Y. Effects of electrokinetic phenomena on bacterial deposition monitored by quartz crystal microbalance with dissipation monitoring. Environ. Sci. Technol. 2020, 54, 14036–14045. [Google Scholar] [CrossRef]
- Cama, G.; Jacobs, T.; Dimaki, M.I.; Svendsen, W.E.; Hauptmann, P.; Naumann, M. Disposable micro-fluidic biosensor array for online parallelized cell adhesion kinetics analysis on quartz crystal resonators. Meas. Sci. Technol. 2010, 21, 085801. [Google Scholar] [CrossRef]
- Chou, H.C.; Yan, T.R. Applying the quartz crystal microbalance technique to detect the epithelial cell tight junction integrality of caco-2 cells. Anal. Lett. 2010, 43, 2009–2018. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Mikhalovska, L.I.; Savina, I.N.; Shevchenko, R.V.; James, P.E.; Tomlins, S.L.; Mikhalovsky, S.V. Characterization and performance of hydrogel tissue scaffolds. Soft Matter 2010, 6, 5351–5358. [Google Scholar] [CrossRef]
- Huang, X.; Zauscher, S.; Klitzman, B.; Truskey, G.A.; Reichert, W.M.; Kenan, D.J.; Grinstaff, M.W. Peptide interfacial biomaterials improve endothelial cell adhesion and spreading on synthetic polyglycolic acid materials. Ann. Biomed. Eng. 2010, 38, 1965–1976. [Google Scholar] [CrossRef] [Green Version]
- Xi, J.; Chen, J.Y.; Garcia, M.P.; Penn, L.S. Quartz crystal microbalance in cell biology studies. Biochip Tissue Chip 2013, S5, 1–9. [Google Scholar] [CrossRef]
- Johannsmann, D. Viscoelastic, mechanical, and dielectric measurements on complex samples with the quartz crystal microbalance. Phys. Chem. Chem. Phys. 2008, 10, 4516–4534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rechendorff, K.; Hovgaard, M.B.; Foss, M.; Besenbacher, F. Influence of surface roughness on quartz crystal microbalance measurements in liquids. J. Appl. Phys. 2007, 101, 114502. [Google Scholar] [CrossRef]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: Englewood Cliff, NJ, USA, 1962. [Google Scholar]
- Adamczyk, Z.; Warszyński, P. Role of electrostatic interactions in particle adsorption. Adv. Colloid Interface Sci. 1996, 63, 141–149. [Google Scholar] [CrossRef]
- Elimelech, M.; Gergory, J.; Jia, X.; Williams, K.A. Particle Deposition and Aggregation; Butterworth-Heinemann: Oxford, UK, 1995. [Google Scholar]
- Adamczyk, Z. Particle adsorption and deposition: Role of electrostatic interactions. Colloid Interface Sci. 2003, 100–102, 267–347. [Google Scholar] [CrossRef]
- Adamczyk, Z. Particles at Interfaces: Interactions, Deposition, Structure; Hubbard, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 100–102. [Google Scholar]
- Evans, J.W. Random and cooperative sequential adsorption. Rev. Mol. Phys. 1993, 65, 1281–1329. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Weroński, P. Random sequential adsorption of spheroidal particles: Kinetics and jamming limit. J. Chem. Phys. 1996, 105, 5562–5573. [Google Scholar] [CrossRef] [Green Version]
- Adamczyk, Z. Kinetics of diffusion-controlled adsorption of colloid particles and proteins. J. Colloid Interface Sci. 2000, 229, 477–489. [Google Scholar] [CrossRef]
- Talbot, J.; Tarjus, G.; Van Tassel, P.R.; Viot, P. From car parking to protein adsorption: An overview of sequential adsorption processes. Colloids Surf. A 2000, 165, 287–324. [Google Scholar]
- Weroński, P. Application of the extended RSA models in studies of particle deposition at partially covered surfaces. Adv. Colloid Interface Sci. 2005, 118, 1–24. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Drei vorträge fiber diffusion, Brownsche bewegung und koagulation von kolloidteilchen. Z. Phys. 1916, 17, 557–585. [Google Scholar]
- Bowen, B.D.; Levine, S.; Epstein, N. Fine particle deposition in laminar flow through parallel-plate and cylindrical channels. J. Colloid Interface Sci. 1976, 54, 375–390. [Google Scholar] [CrossRef]
- Zhang, M.; Soto-Rodriguez, J.; Chen, I.-C.; Akbulut, M. Adsorption and removal dynamics of polymeric micellar nanocarriers loaded with a therapeutic agent on silica surfaces. Soft Matter 2013, 9, 10155–10164. [Google Scholar] [CrossRef]
- Ruckenstein, E. Reversible rate of adsorption or coagulation of brownian particles—Effect of the shape of the interaction potential. J. Colloid Interface Sci. 1978, 66, 531–643. [Google Scholar] [CrossRef]
- Ricci, S.M.; Talbot, J.; Tarjus, G.; Viot, P. Random sequential adsorption of anisotropic particles. II. Low coverage kinetics. J. Chem. Phys. 1992, 97, 5219–5228. [Google Scholar] [CrossRef] [Green Version]
- Hinrichsen, E.L.; Feder, J.; Jossang, T. Geometry of random sequential adsorption. J. Stat. Phys. 1986, 44, 793–822. [Google Scholar] [CrossRef]
- Sauerbrey, G. Vervendung von Schwingquartzen zor Waegung duenner Schichten und zur Mikrowaegung. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Ekiel-Jeżewska, M.J.; Adamczyk, Z.; Bławzdziewicz, J. Streaming current and effective ζ-potential for particle-covered surfaces with random particle distributions. J. Phys. Chem. C 2019, 123, 3517–3631. [Google Scholar] [CrossRef]



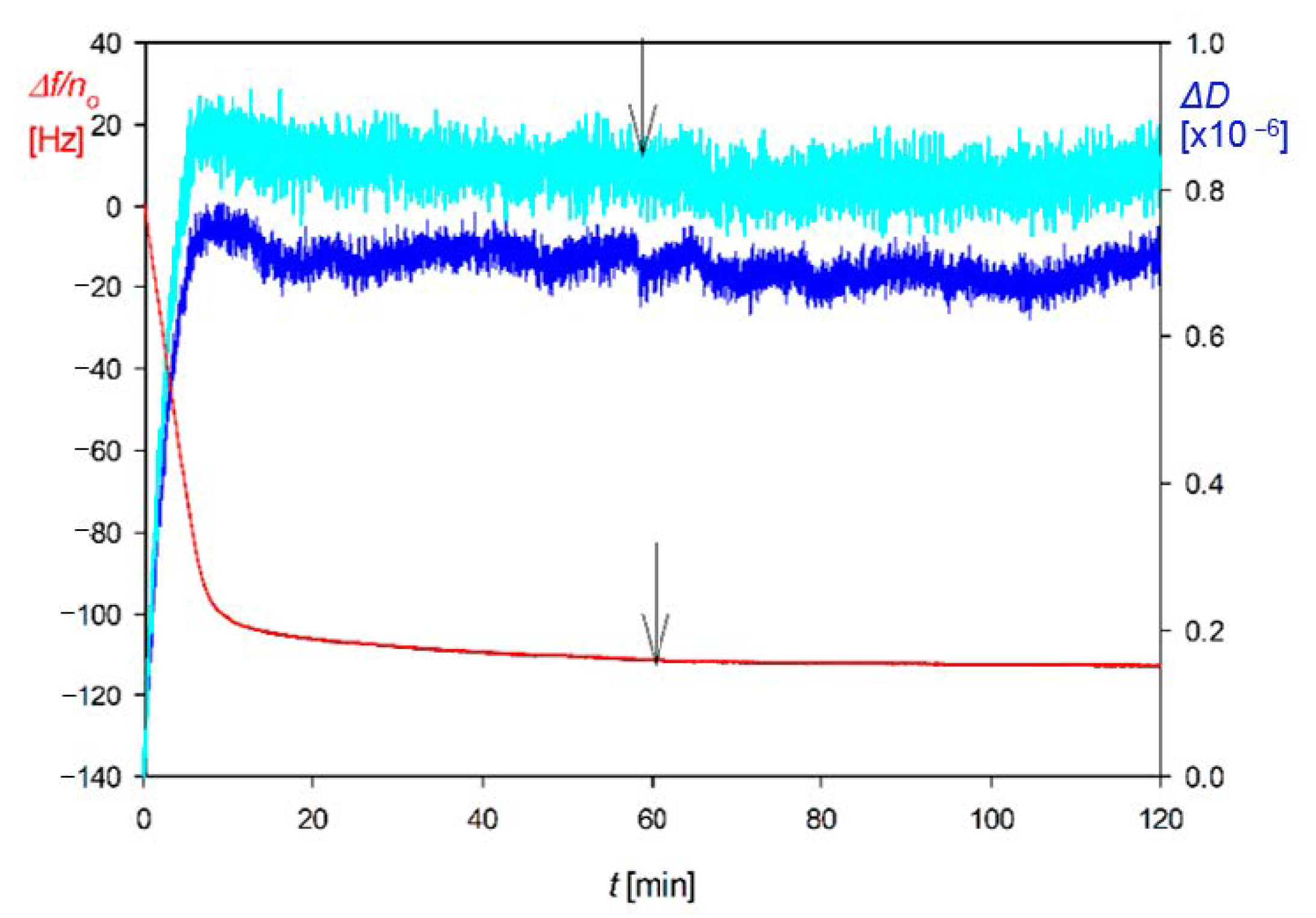
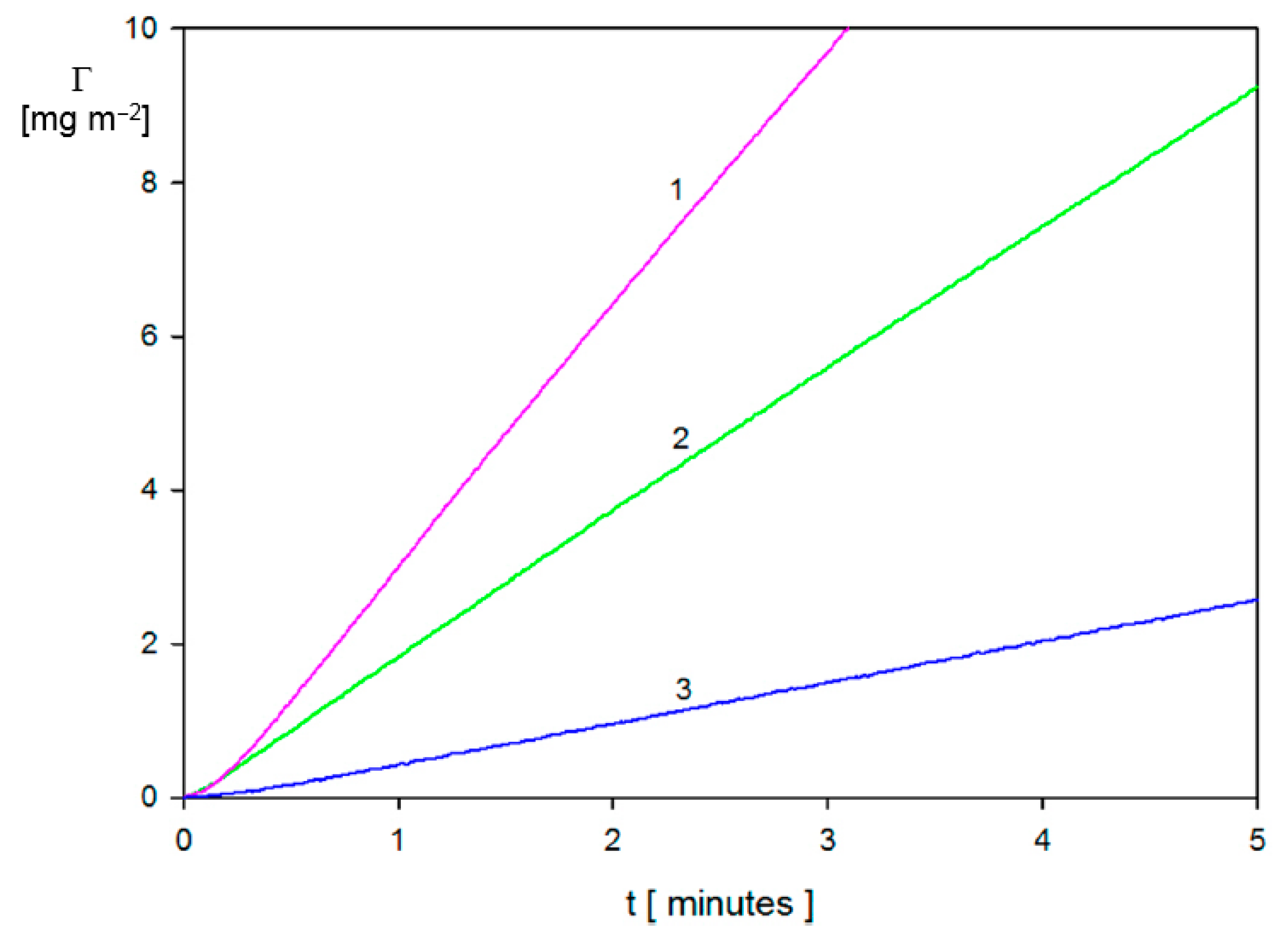

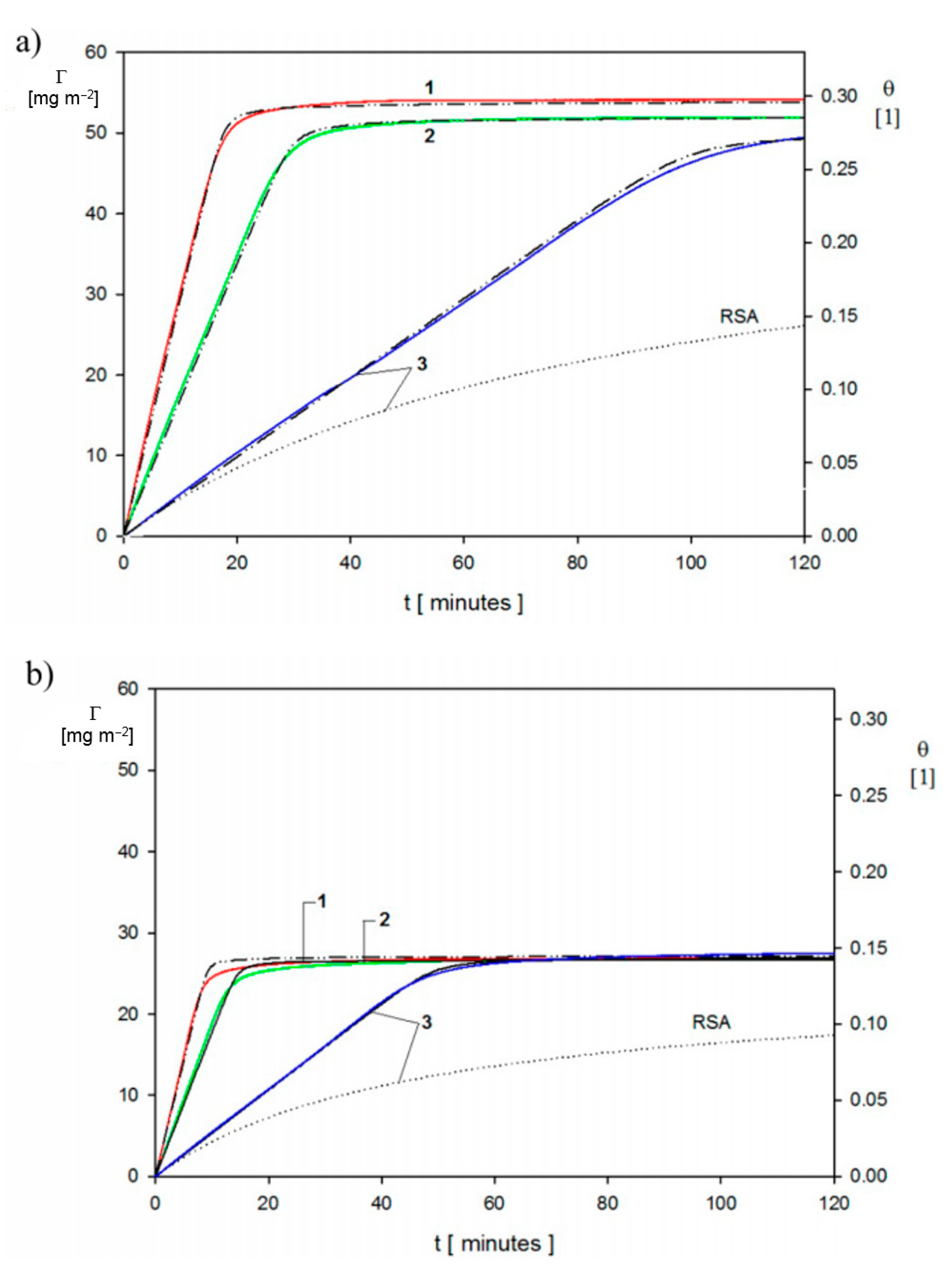

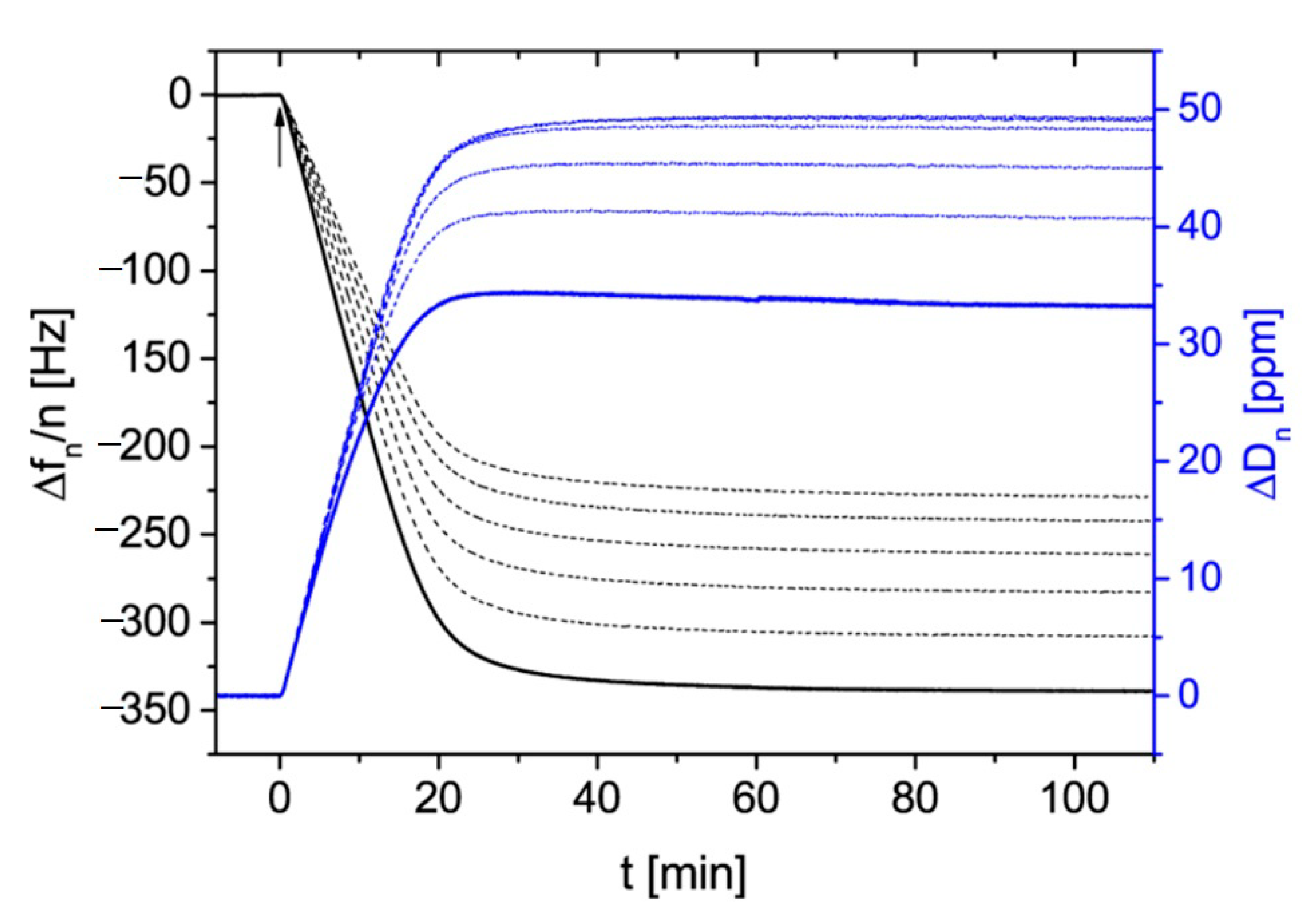


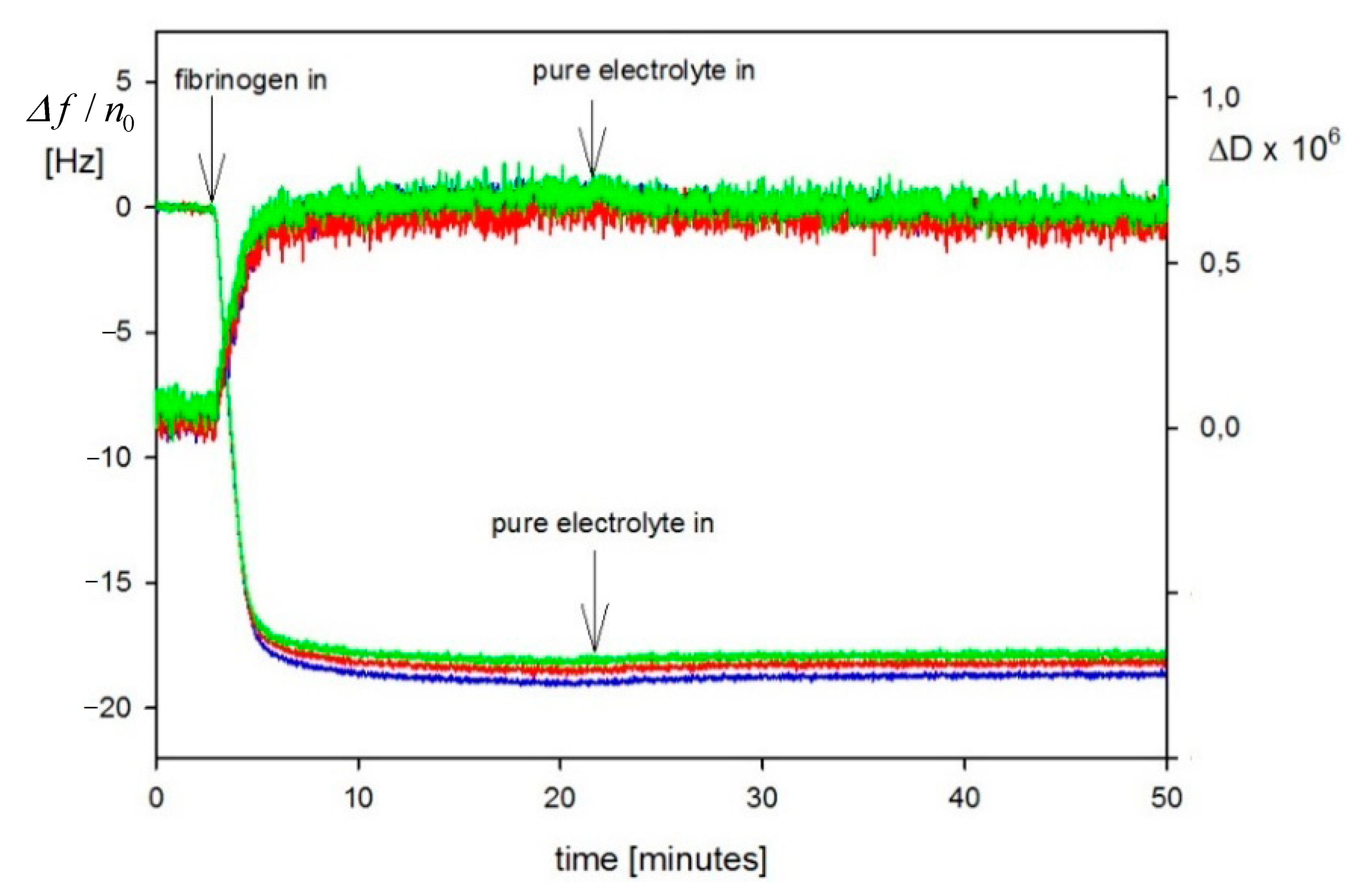
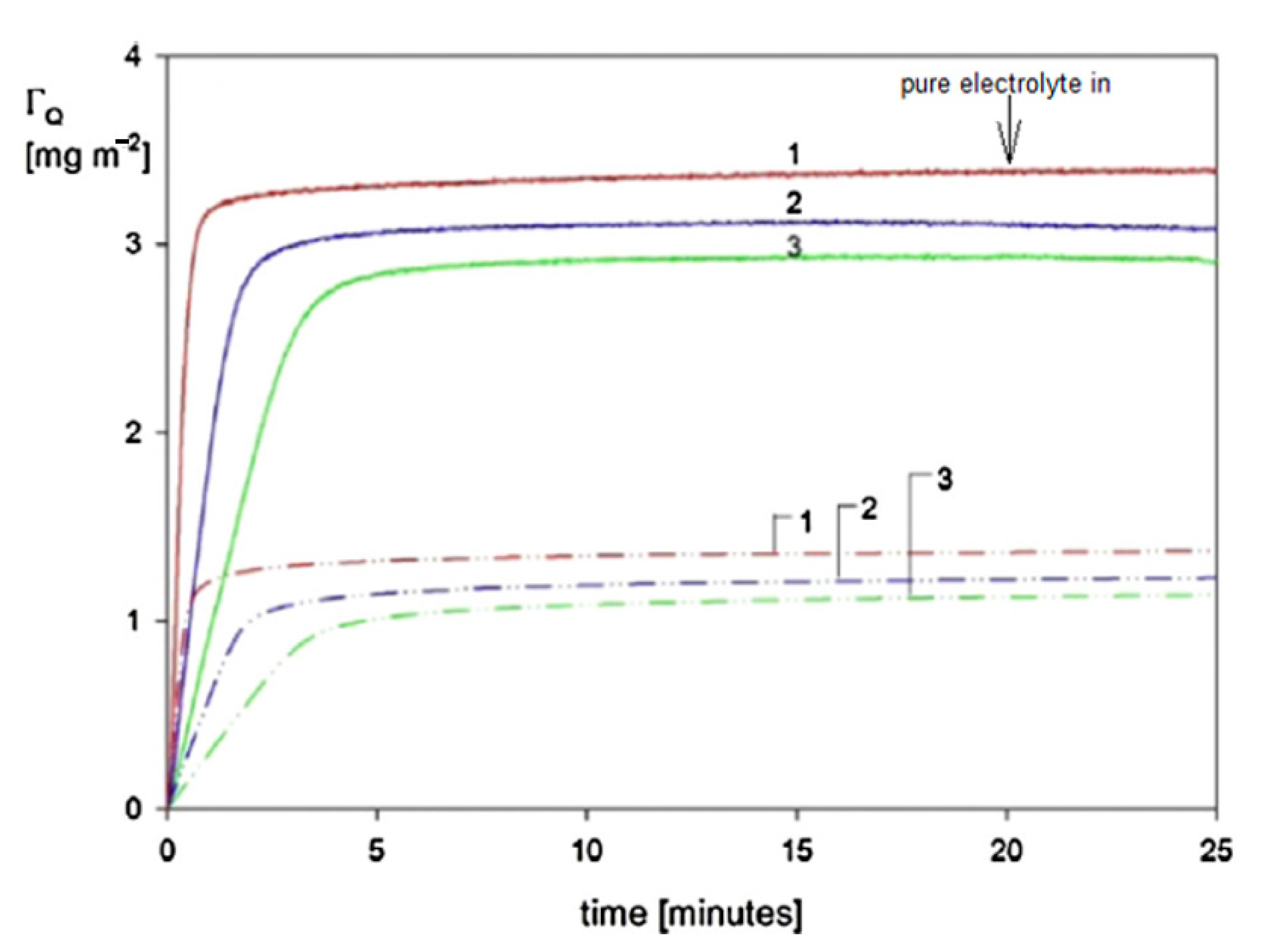
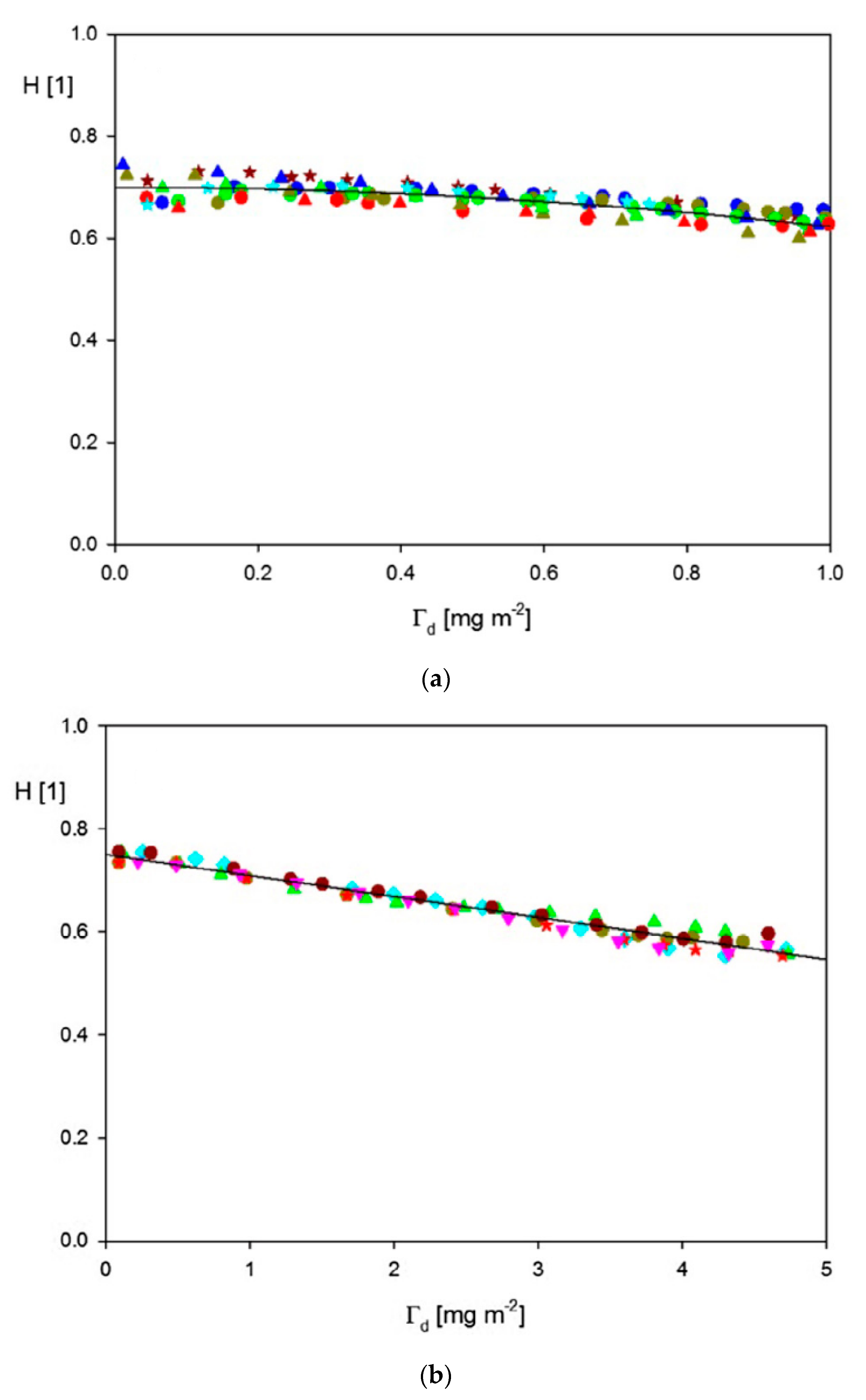
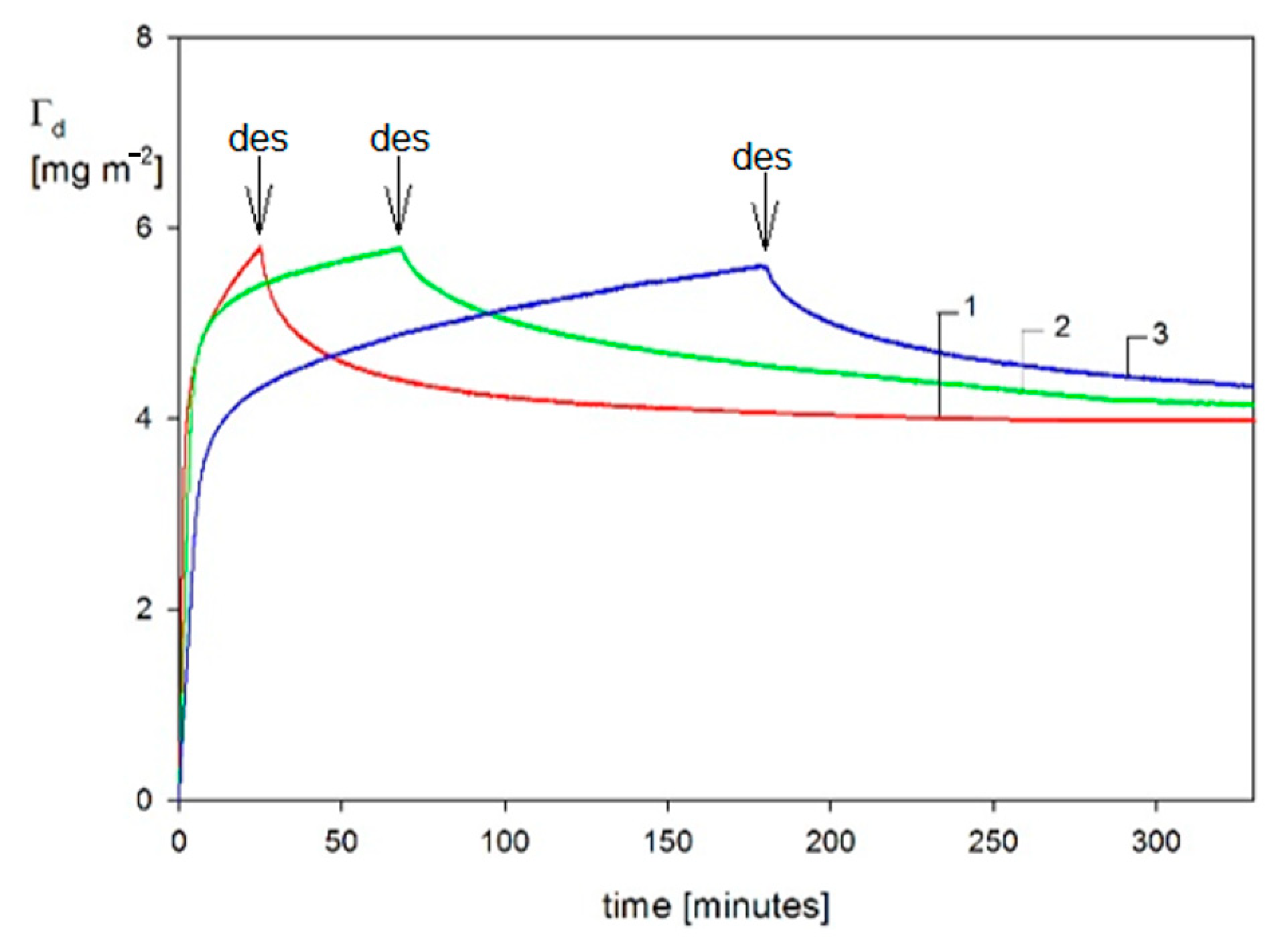

| Sample | Density [g cm−3] | Size [nm] | δ/a [1] | H0 Experiments | H0 Theory |
|---|---|---|---|---|---|
CPMV | 1.4 | 28 | 5.6 | 0.91 | 0.94 |
| SAv | 1.35 | 5.4 | 29 | 0.83 | 0.99 |
Av | 1.35 | 6.0 | 26 | 0.83 | 0.99 |
| SUVs | 1.01 | 30 | 5.3 | 0.81 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bratek-Skicki, A.; Sadowska, M.; Maciejewska-Prończuk, J.; Adamczyk, Z. Nanoparticle and Bioparticle Deposition Kinetics: Quartz Microbalance Measurements. Nanomaterials 2021, 11, 145. https://doi.org/10.3390/nano11010145
Bratek-Skicki A, Sadowska M, Maciejewska-Prończuk J, Adamczyk Z. Nanoparticle and Bioparticle Deposition Kinetics: Quartz Microbalance Measurements. Nanomaterials. 2021; 11(1):145. https://doi.org/10.3390/nano11010145
Chicago/Turabian StyleBratek-Skicki, Anna, Marta Sadowska, Julia Maciejewska-Prończuk, and Zbigniew Adamczyk. 2021. "Nanoparticle and Bioparticle Deposition Kinetics: Quartz Microbalance Measurements" Nanomaterials 11, no. 1: 145. https://doi.org/10.3390/nano11010145
APA StyleBratek-Skicki, A., Sadowska, M., Maciejewska-Prończuk, J., & Adamczyk, Z. (2021). Nanoparticle and Bioparticle Deposition Kinetics: Quartz Microbalance Measurements. Nanomaterials, 11(1), 145. https://doi.org/10.3390/nano11010145





