Heat Transport Control and Thermal Characterization of Low-Dimensional Materials: A Review
Abstract
:1. Introduction
2. Engineering the Phonon Thermal Conduction in Semiconductor Nanostructures and 2D Materials
2.1. Semiconductor Nanostructures
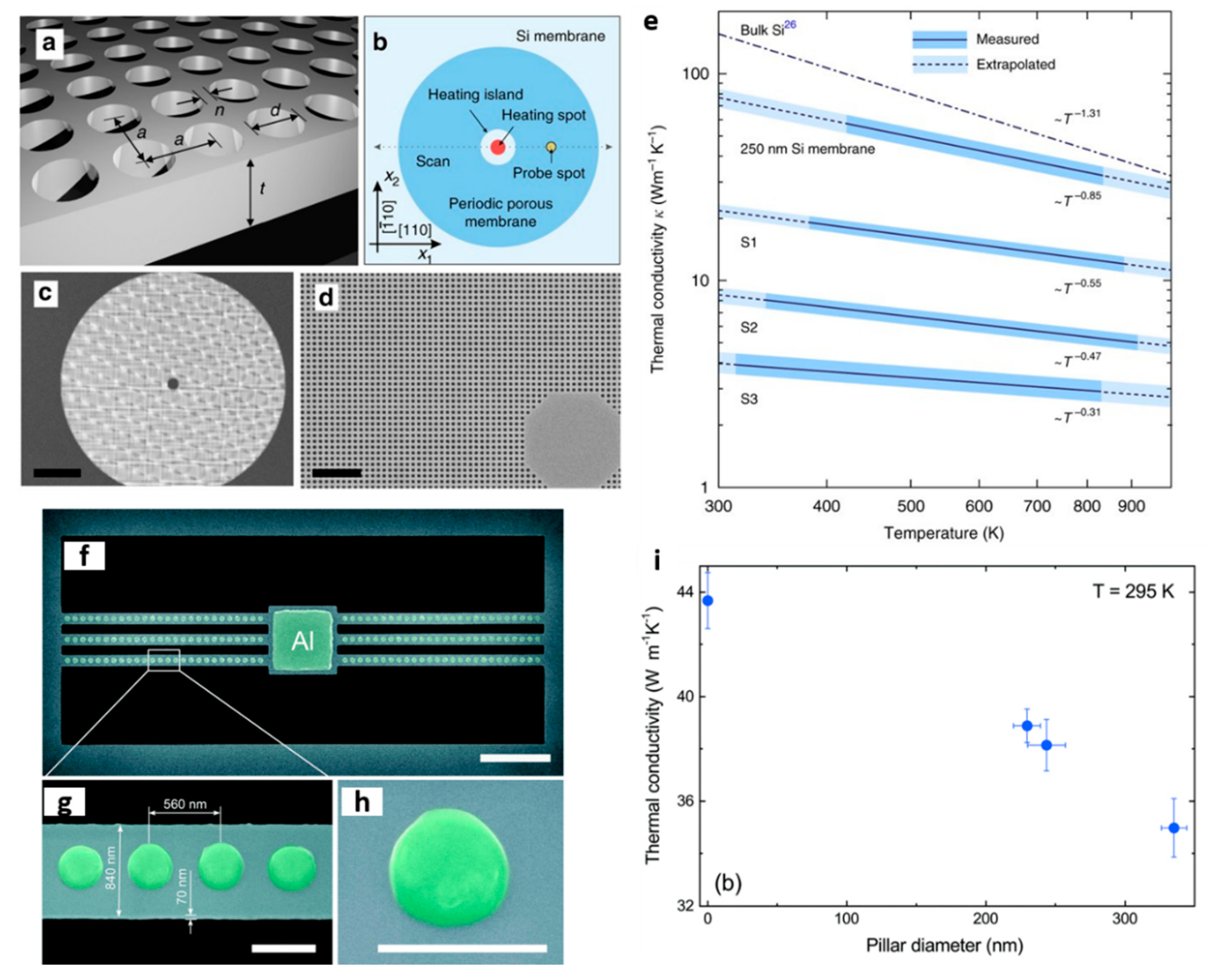
2.1.1. Membrane-Based Structures
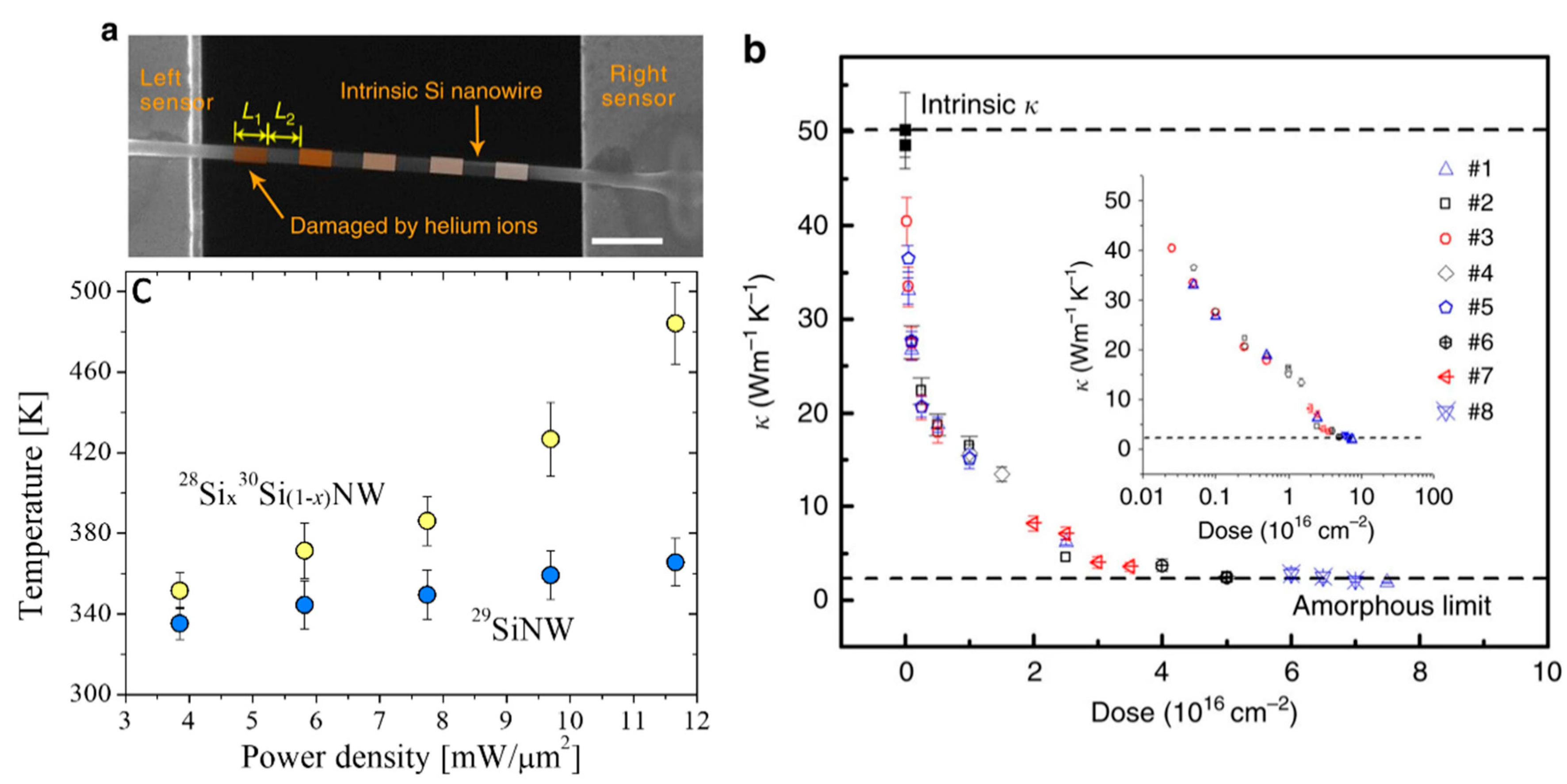
2.1.2. Nanowires
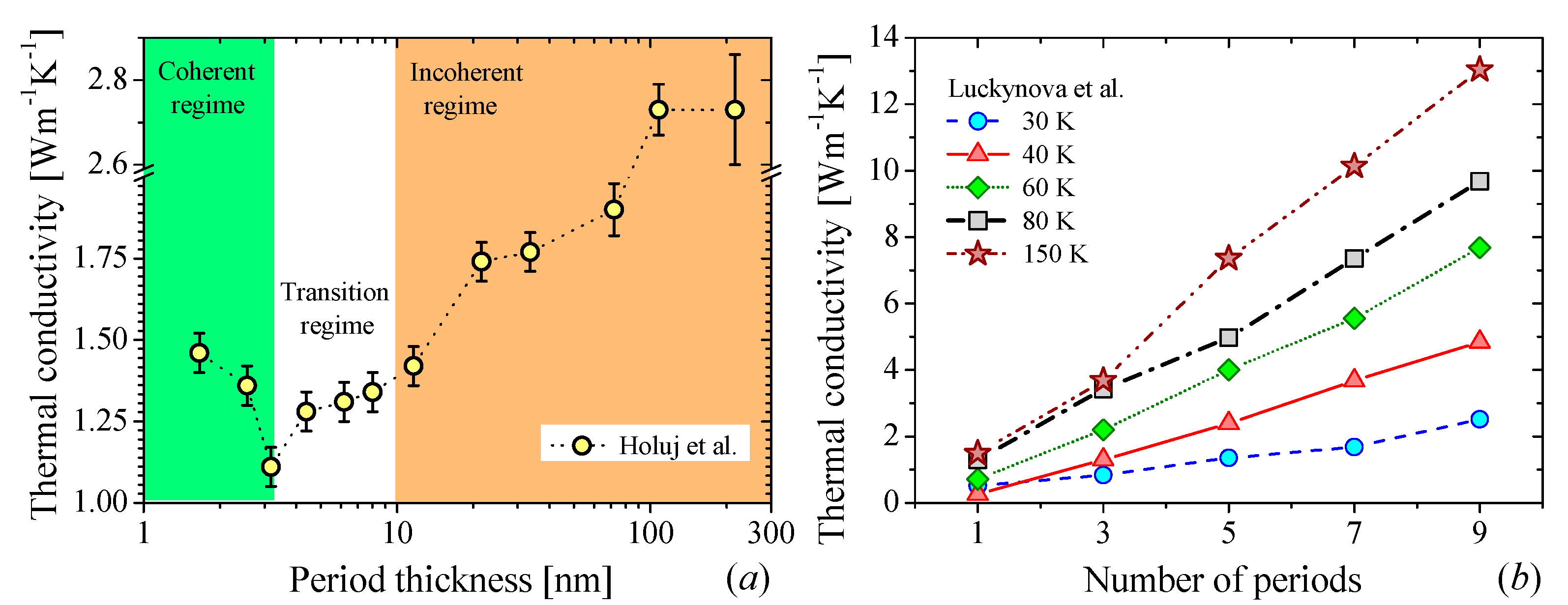
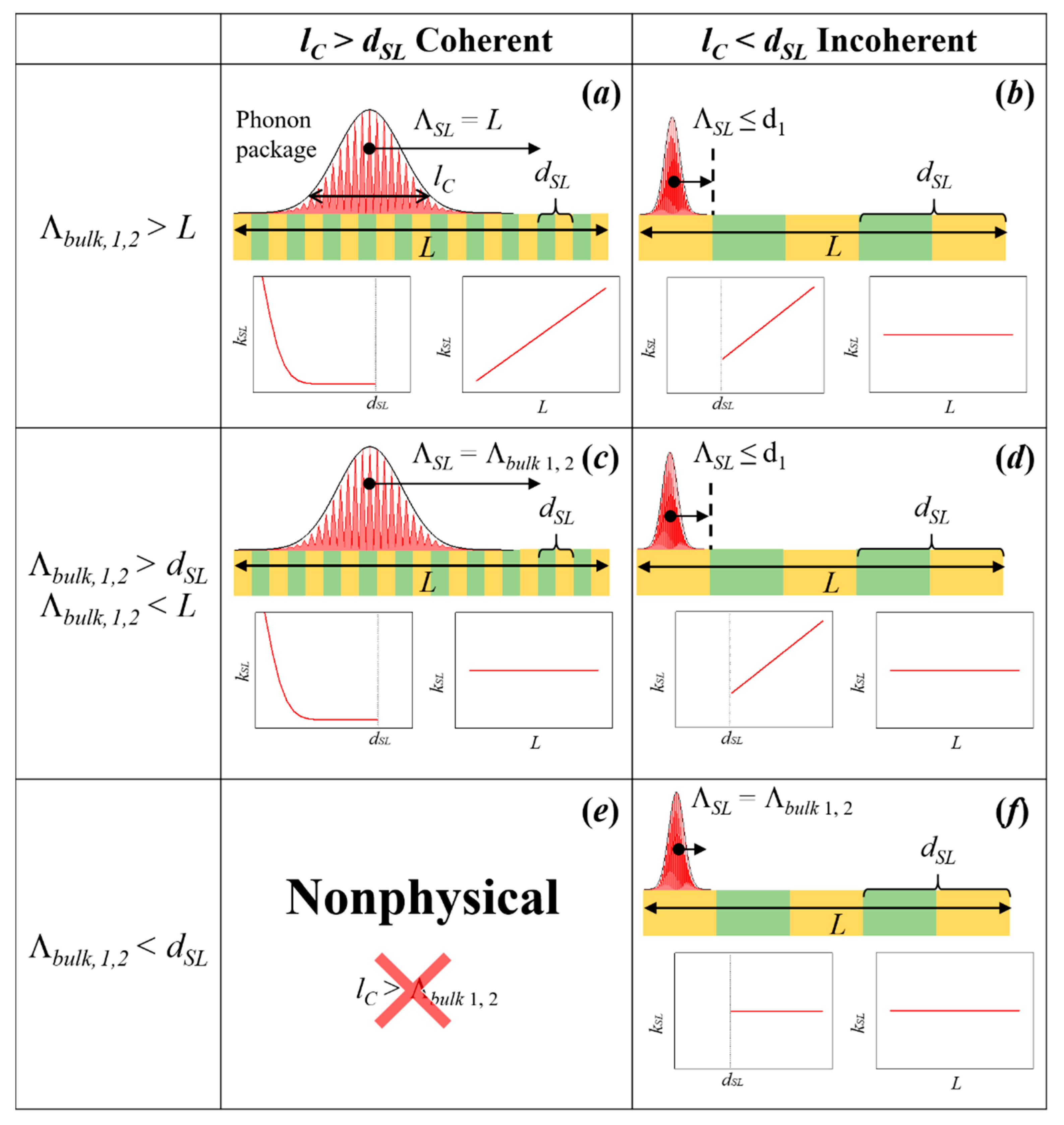
2.1.3. Superlattices
2.2. Two-Dimensional Materials
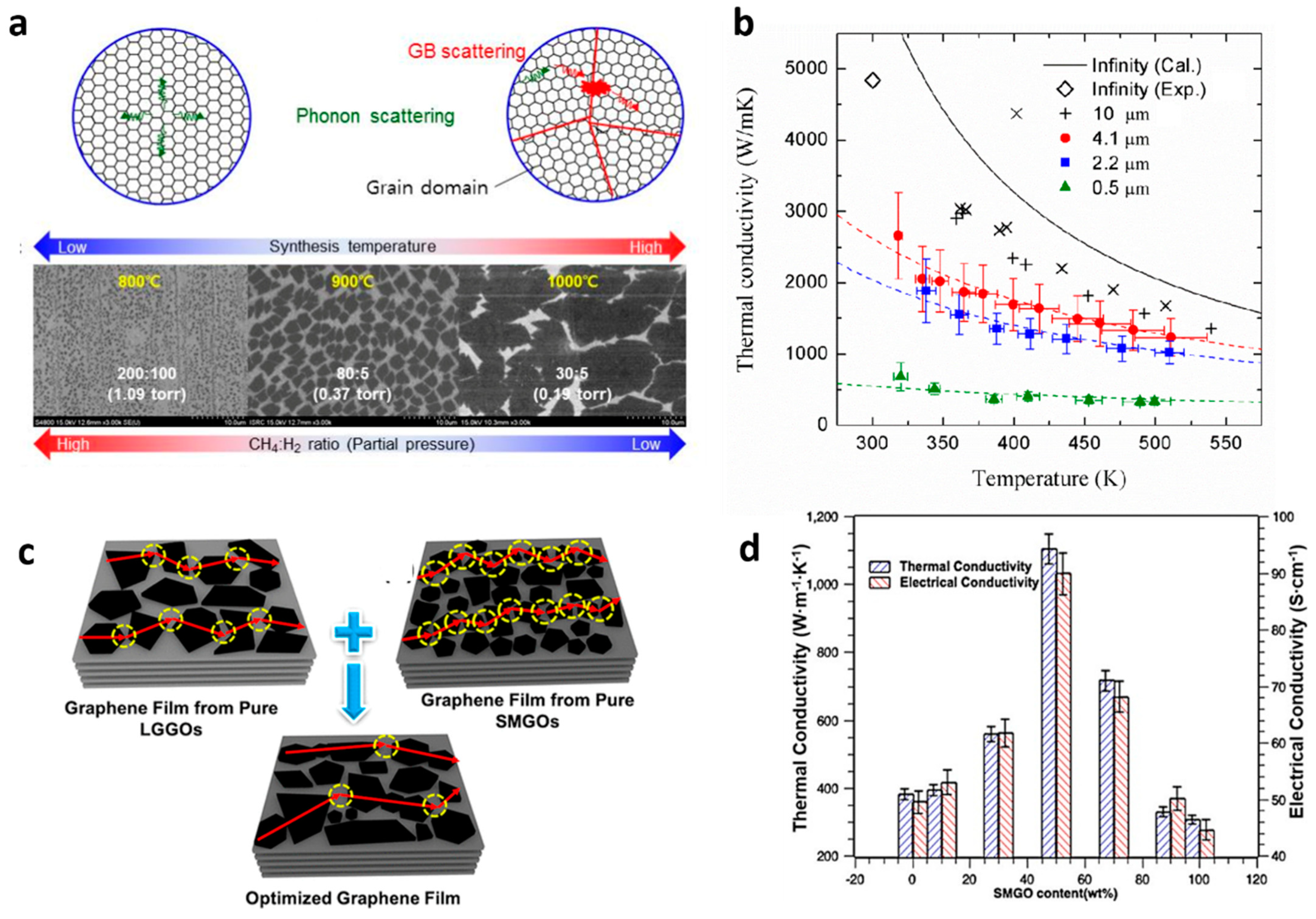
2.2.1. Graphene
2.2.2. Transition Metal Dichalcogenides and 2D Heterojunctions
3. Experimental Techniques for Thermal Characterization
3.1. Electro-Thermal Techniques
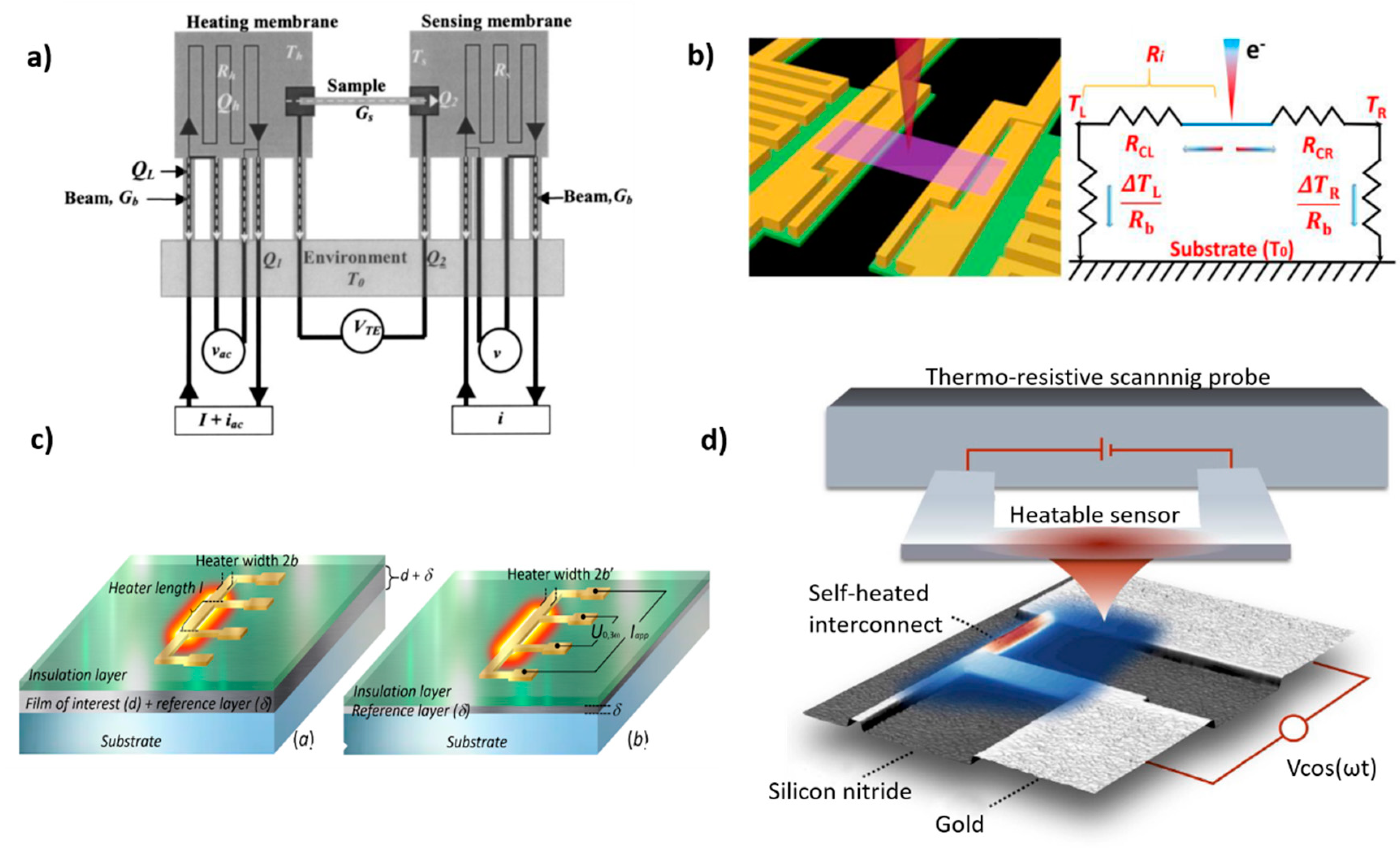
3.1.1. Suspended Thermal Bridge Method
3.1.2. Electron Beam Self-Heating Technique
3.1.3. Conventional Three-Omega Method
3.1.4. Scanning Thermal Microscopy
3.2. Optical Techniques
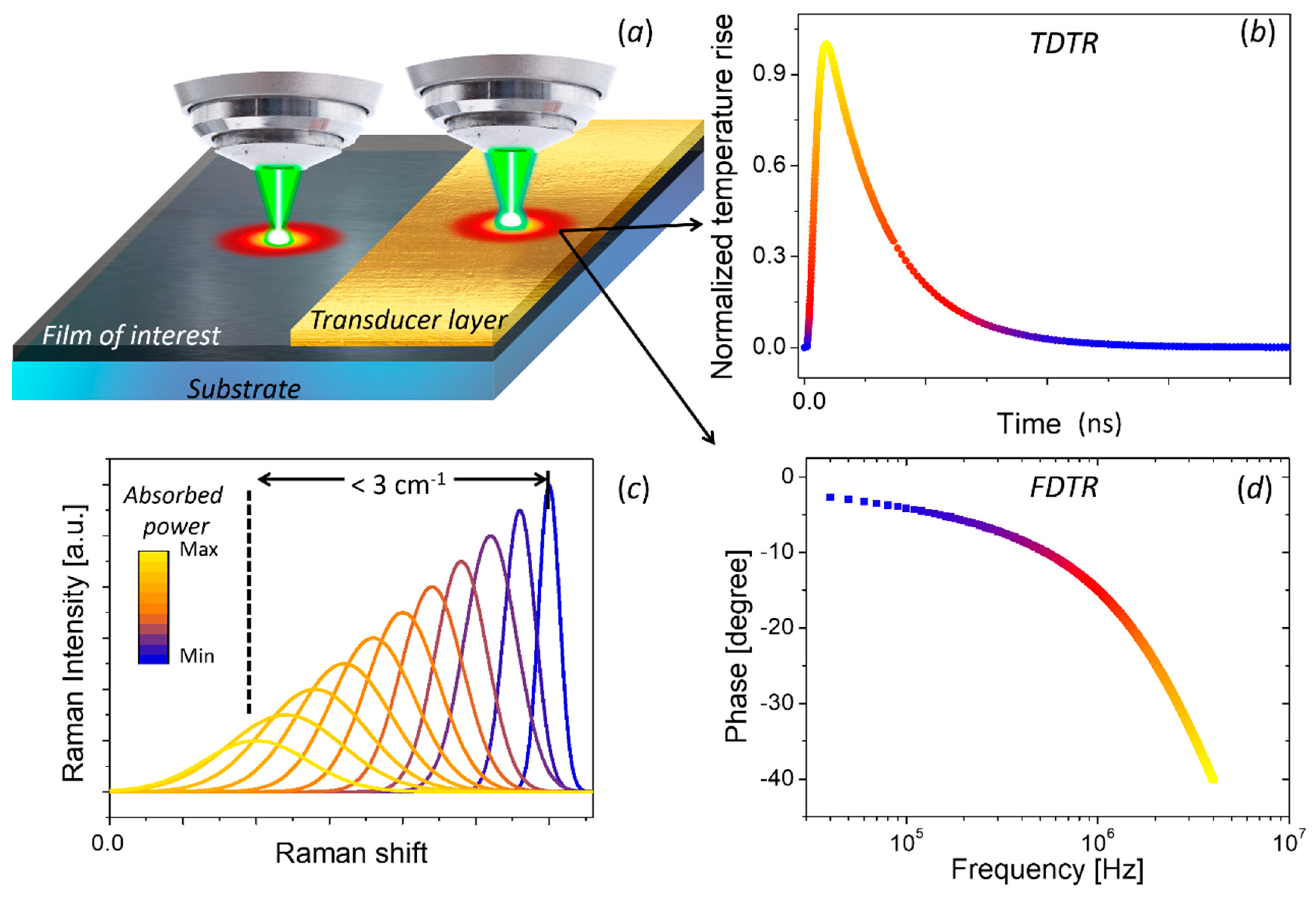
3.2.1. Opto-Thermal Raman Spectroscopy and Thermometry
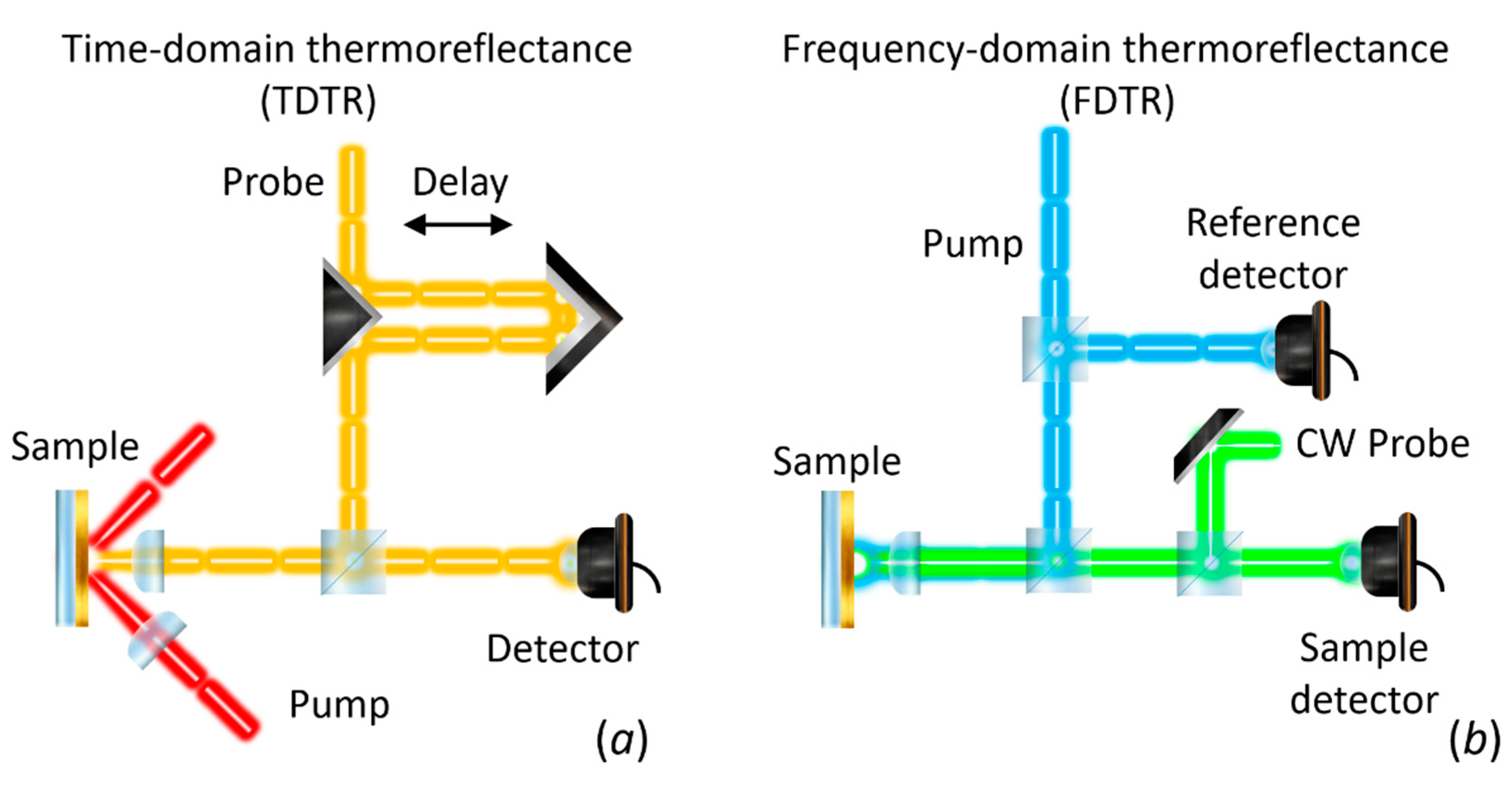
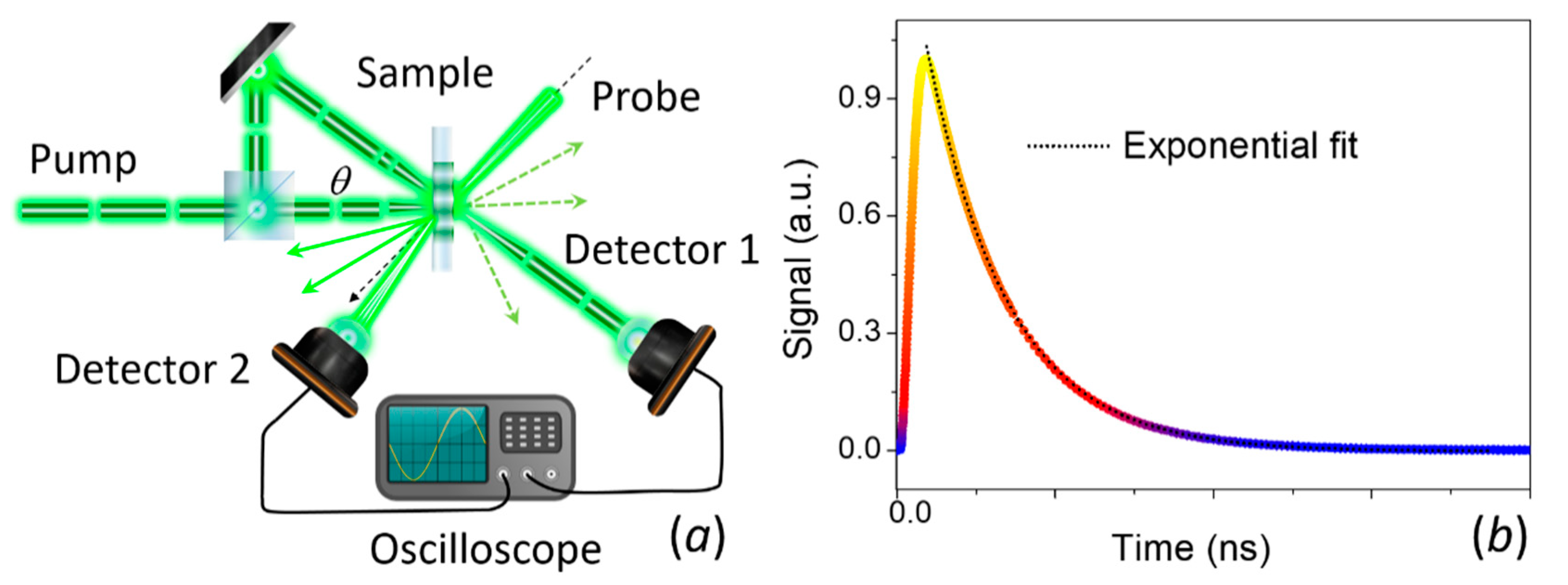
3.2.2. Thermoreflectance-Based Techniques
3.2.3. Thermal Transient Grating (TTG) Method
4. Summary and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Hamann, H.F.; Weger, A.; Lacey, J.A.; Hu, Z.; Bose, P.; Cohen, E.; Wakil, J. Hotspot-Limited Microprocessors: Direct Temperature and Power Distribution Measurements. IEEE J. Solid State Circuits 2007, 42, 56–65. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, Y.; Cheng, Y.; Chen, J.; Li, N.; Zhang, G. Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 2020, 860, 1–26. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Dong, L.; Aiyiti, A.; Xu, X.; Li, B. Superior thermal conductivity in suspended bilayer hexagonal boron nitride. Sci. Rep. 2016, 6, 25334. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Kim, K.; Jeong, W.; Zotti, L.A.; Pauly, F.; Cuevas, J.C.; Reddy, P. Heat dissipation in atomic-scale junctions. Nat. Cell Biol. 2013, 498, 209–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srivastava, G.P.; Kresin, V. The Physics of Phonons. Phys. Today 1991, 44, 75–76. [Google Scholar] [CrossRef] [Green Version]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Cuffe, J.; Chávez, E.; Shchepetov, A.; Chapuis, P.-O.; El Boudouti, E.H.; Alzina, F.; Kehoe, T.; Gomis-Bresco, J.; Dudek, D.; Pennec, Y.; et al. Phonons in Slow Motion: Dispersion Relations in Ultrathin Si Membranes. Nano Lett. 2012, 12, 3569–3573. [Google Scholar] [CrossRef] [Green Version]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: New York, NY, USA, 1960. [Google Scholar]
- Zou, J.; Balandin, A. Phonon heat conduction in a semiconductor nanowire. J. Appl. Phys. 2001, 89, 2932–2938. [Google Scholar] [CrossRef] [Green Version]
- Zou, J.; Lange, X.; Richardson, C. Lattice thermal conductivity of nanoscale AlN/GaN/AlN heterostructures: Effects of partial phonon spatial confinement. J. Appl. Phys. 2006, 100, 104309. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Significant decrease of the lattice thermal conductivity due to phonon confinement in a free-standing semiconductor quantum well. Phys. Rev. B 1998, 58, 1544–1549. [Google Scholar] [CrossRef] [Green Version]
- Malhotra, A.; Maldovan, M. Phononic pathways towards rational design of nanowire heat conduction. Nanotechnology 2019, 30, 372002. [Google Scholar] [CrossRef] [Green Version]
- Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Luckyanova, M.N.; Garg, J.; Esfarjani, K.; Jandl, A.; Bulsara, M.T.; Schmidt, A.J.; Minnich, A.J.; Chen, S.; Dresselhaus, M.S.; Ren, Z.; et al. Coherent Phonon Heat Conduction in Superlattices. Science 2012, 338, 936–939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravichandran, J.; Yadav, A.K.; Cheaito, R.; Rossen, P.B.; Soukiassian, A.; Suresha, S.J.; Duda, J.C.; Foley, B.M.; Lee, C.-H.; Zhu, Y.; et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 2014, 13, 168–172. [Google Scholar] [CrossRef] [PubMed]
- Maire, J.; Anufriev, R.; Yanagisawa, R.; Ramiere, A.; Volz, S.; Nomura, M. Heat conduction tuning by wave nature of phonons. Sci. Adv. 2017, 3, e1700027. [Google Scholar] [CrossRef] [Green Version]
- Anufriev, R.; Ramiere, A.; Maire, J.; Nomura, M. Heat guiding and focusing using ballistic phonon transport in phononic nanostructures. Nat. Commun. 2017, 8, 15505. [Google Scholar] [CrossRef]
- Asheghi, M.; Leung, Y.K.; Wong, S.S.; Goodson, K.E. Phonon-boundary scattering in thin silicon layers. Appl. Phys. Lett. 1997, 71, 1798–1800. [Google Scholar] [CrossRef] [Green Version]
- El Sachat, A. Characterization of Nanostructured Materials for Thermal Conduction and Heat Transfer Control. Ph.D. Thesis, Universitat Automona de Barcelona, Barcelona, Spain, 2017. [Google Scholar]
- Reparaz, J.S.; Chavez-Angel, E.; Wagner, M.R.; Graczykowski, B.; Gomis-Bresco, J.; Alzina, F.; Sotomayor Torres, C.M. A novel contactless technique for thermal field mapping and thermal conductivity determination: Two-Laser Raman Thermometry. Rev. Sci. Instrum. 2014, 85, 034901. [Google Scholar] [CrossRef] [Green Version]
- Marconnet, A.; Asheghi, M.; Goodson, K.E. From the Casimir Limit to Phononic Crystals: 20 Years of Phonon Transport Studies Using Silicon-on-Insulator Technology. J. Heat Transf. 2013, 135, 061601. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Peng, B.; Cong, C.; Shang, J.; Wu, L.; Yang, W.; Zhou, J.; Yu, P.; Zhang, H.; Wang, Y.; et al. In-Plane Anisotropic Thermal Conductivity of Few-Layered Transition Metal Dichalcogenide Td-WTe2. Adv. Mater. 2019, 31, e1804979. [Google Scholar] [CrossRef]
- Nomura, M.; Nakagawa, J.; Kage, Y.; Maire, J.; Moser, D.; Paul, O. Thermal phonon transport in silicon nanowires and two-dimensional phononic crystal nanostructures. Appl. Phys. Lett. 2015, 106, 143102. [Google Scholar] [CrossRef]
- Graczykowski, B.; El Sachat, A.; Reparaz, J.S.; Sledzinska, M.; Wagner, M.R.; Chavez-Angel, E.; Wu, Y.; Volz, S.; Alzina, F.; Sotomayor Torres, C.M. Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anufriev, R.; Maire, J.; Nomura, M. Reduction of thermal conductivity by surface scattering of phonons in periodic silicon nanostructures. Phys. Rev. B 2016, 93, 045411. [Google Scholar] [CrossRef]
- Yanagisawa, R.; Maire, J.; Ramiere, A.; Anufriev, R.; Nomura, M. Impact of limiting dimension on thermal conductivity of one-dimensional silicon phononic crystals. Appl. Phys. Lett. 2017, 110, 133108. [Google Scholar] [CrossRef]
- Iskandar, A.; Gwiazda, A.; Huang, Y.; Kazan, M.; Bruyant, A.; Tabbal, M.; Lerondel, G. Modification of the phonon spectrum of bulk Si through surface nanostructuring. J. Appl. Phys. 2016, 120, 095106. [Google Scholar] [CrossRef]
- Anufriev, R.; Yanagisawa, R.; Nomura, M. Aluminium nanopillars reduce thermal conductivity of silicon nanobeams. Nanoscale 2017, 9, 15083–15088. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Ohori, D.; Yanagisawa, R.; Anufriev, R.; Samukawa, S.; Nomura, M. Coherent and Incoherent Impacts of Nanopillars on the Thermal Conductivity in Silicon Nanomembranes. ACS Appl. Mater. Interfaces 2020, 12, 25478–25483. [Google Scholar] [CrossRef]
- Puurtinen, T.A.; Maasilta, I.J. Low-Temperature Coherent Thermal Conduction in Thin Phononic Crystal Membranes. Crystals 2016, 6, 72. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Puurtinen, T.A.; Geng, Z.; Maasilta, I.J. Minimizing Coherent Thermal Conductance by Controlling the Periodicity of Two-Dimensional Phononic Crystals. Phys. Rev. Appl. 2019, 12, 014008. [Google Scholar] [CrossRef] [Green Version]
- Zen, N.; Puurtinen, T.A.; Isotalo, T.J.; Chaudhuri, S.; Maasilta, I.J. Engineering thermal conductance using a two-dimensional phononic crystal. Nat. Commun. 2014, 5, 3435. [Google Scholar] [CrossRef]
- Wagner, M.R.; Graczykowski, B.; Reparaz, J.S.; El Sachat, A.; Sledzinska, M.; Alzina, F.; Sotomayor Torres, C.M. Two-Dimensional Phononic Crystals: Disorder Matters. Nano Lett. 2016, 16, 5661–5668. [Google Scholar] [CrossRef] [Green Version]
- Venkatasubramanian, R. Lattice thermal conductivity reduction and phonon localizationlike behavior in superlattice structures. Phys. Rev. B 2000, 61, 3091–3097. [Google Scholar] [CrossRef]
- Xie, G.; Ding, D.; Zhang, G. Phonon coherence and its effect on thermal conductivity of nanostructures. Adv. Phys. X 2018, 3, 1480417. [Google Scholar] [CrossRef]
- Lee, J.; Lee, W.; Wehmeyer, G.; Dhuey, S.; Olynick, D.L.; Cabrini, S.; Dames, C.; Urban, J.J.; Yang, P. Investigation of phonon coherence and backscattering using silicon nanomeshes. Nat. Commun. 2017, 8, 14054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, J.-K.; Mitrovic, S.; Tham, D.; Varghese, J.; Heath, J.R. Reduction of thermal conductivity in phononic nanomesh structures. Nat. Nanotechnol. 2010, 5, 718–721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hopkins, P.E.; Reinke, C.M.; Su, M.F.; Olsson, R.H.; Shaner, E.A.; Leseman, Z.C.; Serrano, J.R.; Phinney, L.M.; El-Kady, I. Reduction in the Thermal Conductivity of Single Crystalline Silicon by Phononic Crystal Patterning. Nano Lett. 2011, 11, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Alaie, S.; Goettler, D.F.; Su, M.; Leseman, Z.C.; Reinke, C.; El-Kady, I. Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature. Nat. Commun. 2015, 6, 7228. [Google Scholar] [CrossRef]
- Jain, A.; Yu, Y.-J.; McGaughey, A.J.H. Phonon transport in periodic silicon nanoporous films with feature sizes greater than 100 nm. Phys. Rev. B 2013, 87, 87. [Google Scholar] [CrossRef] [Green Version]
- Ravichandran, N.K.; Minnich, A.J. Coherent and incoherent thermal transport in nanomeshes. Phys. Rev. B 2014, 89, 89. [Google Scholar] [CrossRef] [Green Version]
- Latour, B.; Volz, S.; Chalopin, Y. Microscopic description of thermal-phonon coherence: From coherent transport to diffuse interface scattering in superlattices. Phys. Rev. B 2014, 90, 014307. [Google Scholar] [CrossRef] [Green Version]
- Sledzinska, M.; Graczykowski, B.; Maire, J.; Chavez-Angel, E.; Sotomayor Torres, C.M.; Alzina, F. 2D Phononic Crystals: Progress and Prospects in Hypersound and Thermal Transport Engineering. Adv. Funct. Mater. 2020, 30, 1904434. [Google Scholar] [CrossRef]
- Xiao, Y.; Xu, D.; Medina, F.J.; Wang, S.; Hao, Q. Thermal studies of nanoporous thin films with added periodic nanopores—A new approach to evaluate the importance of phononic effects. Mater. Today Phys. 2020, 12, 100179. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936. [Google Scholar] [CrossRef]
- Swinkels, M.Y.; Van Delft, M.R.; Oliveira, D.S.; Cavalli, A.A.; Zardo, I.; Van Der Heijden, R.W.; Bakkers, E.P.A.M. Diameter dependence of the thermal conductivity of InAs nanowires. Nanotechnology 2015, 26, 385401. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Zhu, X.; Han, J.; Xu, J.; Ma, L.; Li, H.; Zhuang, X.; Zhou, H.; Zhang, Q.; Xia, M.; et al. Synthesis and Diameter-dependent Thermal Conductivity of InAs Nanowires. Nano Micro Lett. 2014, 6, 301–306. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, W.; Lim, J.; Yu, Y.; Kong, Q.; Mattox, T.M.; Yang, P. Thermal Transport in Silicon Nanowires at High Temperature up to 700 K. Nano Lett. 2016, 16, 4133–4140. [Google Scholar] [CrossRef]
- Hsiao, T.-K.; Chang, H.-K.; Liou, S.-C.; Chu, M.-W.; Lee, S.-C.; Chang, C.-W. Observation of room-temperature ballistic thermal conduction persisting over 8.3 µm in SiGe nanowires. Nat. Nanotechnol. 2013, 8, 534–538. [Google Scholar] [CrossRef]
- Anufriev, R.; Gluchko, S.; Volz, S.; Nomura, M. Quasi-Ballistic Heat Conduction due to Lévy Phonon Flights in Silicon Nanowires. ACS Nano 2018, 12, 11928–11935. [Google Scholar] [CrossRef] [Green Version]
- Vakulov, D.; Gireesan, S.; Swinkels, M.Y.; Chavez, R.; Vogelaar, T.J.; Torres, P.; Campo, A.; De Luca, M.; Verheijen, M.A.; Koelling, S.; et al. Ballistic Phonons in Ultrathin Nanowires. Nano Lett. 2020, 20, 2703–2709. [Google Scholar] [CrossRef]
- Wang, L.; Li, B. Thermal Logic Gates: Computation with Phonons. Phys. Rev. Lett. 2007, 99, 177208. [Google Scholar] [CrossRef] [Green Version]
- Sklan, S.R. Splash, pop, sizzle: Information processing with phononic computing. AIP Adv. 2015, 5, 053302. [Google Scholar] [CrossRef] [Green Version]
- Wingert, M.C.; Chen, Z.C.Y.; Dechaumphai, E.; Moon, J.; Kim, J.-H.; Xiang, J.; Chen, R. Thermal Conductivity of Ge and Ge–Si Core–Shell Nanowires in the Phonon Confinement Regime. Nano Lett. 2011, 11, 5507–5513. [Google Scholar] [CrossRef] [PubMed]
- Juntunen, T.; Koskinen, T.; Khayrudinov, V.; Haggren, T.; Jiang, H.; Lipsanen, H.; Tittonen, I.J. Thermal conductivity suppression in GaAs–AlAs core–shell nanowire arrays. Nanoscale 2019, 11, 20507–20513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Liu, D.; Chen, J.; Zhu, L.; Belianinov, A.; Ovchinnikova, O.S.; Unocic, R.R.; Burch, M.J.; Kim, S.; Hao, H.; et al. Engineering the thermal conductivity along an individual silicon nanowire by selective helium ion irradiation. Nat. Commun. 2017, 8, 15919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mukherjee, S.; Givan, U.; Senz, S.; Bergeron, A.; Francoeur, S.; De La Mata, M.; Arbiol, J.; Sekiguchi, T.; Itoh, K.M.; Isheim, D.; et al. Phonon Engineering in Isotopically Disordered Silicon Nanowires. Nano Lett. 2015, 15, 3885–3893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mukherjee, S.; Givan, U.; Senz, S.; De La Mata, M.; Arbiol, J.; Moutanabbir, O. Reduction of Thermal Conductivity in Nanowires by Combined Engineering of Crystal Phase and Isotope Disorder. Nano Lett. 2018, 18, 3066–3075. [Google Scholar] [CrossRef] [PubMed]
- Narayanaamurti, V. Phonon Optics and Phonon Propagation in Semiconductors. Science 1981, 213, 717–723. [Google Scholar] [CrossRef]
- Hołuj, P.; Euler, C.; Balke, B.; Kolb, U.; Fiedler, G.; Müller, M.M.; Jaeger, T.; Angel, E.C.; Kratzer, P.; Jakob, G. Reduced thermal conductivity of TiNiSn/HfNiSn superlattices. Phys. Rev. B 2015, 92, 125436. [Google Scholar] [CrossRef] [Green Version]
- Qiu, B.; Chen, G.; Tian, Z. Effects of Aperiodicity and Roughness on Coherent Heat Conduction in Superlattices. Nanoscale Microscale Thermophys. Eng. 2015, 19, 272–278. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, C.; Ruan, X. Optimization of the random multilayer structure to break the random-alloy limit of thermal conductivity. Appl. Phys. Lett. 2015, 106, 073104. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, P.; Cao, L.; Wang, Y. Ultralow Lattice Thermal Conductivity of the Random Multilayer Structure with Lattice Imperfections. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Costescu, R.M.; Cahill, D.G.; Fabreguette, F.H.; Sechrist, Z.A.; George, S.M. Ultra-Low Thermal Conductivity in W/Al2O3 Nanolaminates. Science 2004, 303, 989–990. [Google Scholar] [CrossRef] [PubMed]
- Pernot, G.; Stoffel, M.; Savić, I.; Pezzoli, F.; Chen, P.; Savelli, G.; Jacquot, A.; Schumann, J.; Denker, U.; Mönch, I.; et al. Precise control of thermal conductivity at the nanoscale through individual phonon-scattering barriers. Nat. Mater. 2010, 9, 491–495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chavez-Angel, E.; Reuter, N.; Komar, P.; Heinz, S.; Kolb, U.; Kleebe, H.-J.; Jakob, G. Subamorphous Thermal Conductivity of Crystalline Half-Heusler Superlattices. Nanoscale Microscale Thermophys. Eng. 2018, 23, 1–9. [Google Scholar] [CrossRef]
- Niemelä, J.-P.; Giri, A.; Hopkins, P.E.; Karppinen, M. Ultra-low thermal conductivity in TiO2:C superlattices. J. Mater. Chem. A 2015, 3, 11527–11532. [Google Scholar] [CrossRef] [Green Version]
- Juntunen, T.; Vänskä, O.; Tittonen, I. Anderson Localization Quenches Thermal Transport in Aperiodic Superlattices. Phys. Rev. Lett. 2019, 122, 105901. [Google Scholar] [CrossRef] [Green Version]
- Luckyanova, M.N.; Mendoza, J.; Lu, H.; Song, B.; Huang, S.; Zhou, J.; Li, M.; Dong, Y.; Zhou, H.; Garlow, J.; et al. Phonon localization in heat conduction. Sci. Adv. 2018, 4, eaat9460. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Chen, J.; Li, B. Phonon thermal conduction in novel 2D materials. J. Phys. Condens. Matter 2016, 28, 483001. [Google Scholar] [CrossRef]
- Cepellotti, A.; Fugallo, G.; Paulatto, L.; Lazzeri, M.; Mauri, F.; Marzari, N. Phonon hydrodynamics in two-dimensional materials. Nat. Commun. 2015, 6, 6400. [Google Scholar] [CrossRef]
- Balandin, A.A. Phononics of Graphene and Related Materials. ACS Nano 2020, 14, 5170–5178. [Google Scholar] [CrossRef]
- Nika, D.L.; Balandin, A.A. Phonons and thermal transport in graphene and graphene-based materials. Rep. Prog. Phys. 2017, 80, 036502. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Hansson, J.; Liu, Y.; Chen, S.; Zehri, A.; Samani, M.K.; Wang, N.; Ni, Y.; Zhang, Y.; Zhang, Z.-B.; et al. Graphene related materials for thermal management. 2D Mater. 2019, 7, 012001. [Google Scholar] [CrossRef]
- Song, H.; Liu, J.; Liu, B.; Wu, J.; Cheng, H.-M.; Kang, F. Two-Dimensional Materials for Thermal Management Applications. Joule 2018, 2, 442–463. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wu, Q.; Mishra, C.; Kang, J.; Zhang, H.; Cho, K.; Cai, W.; Balandin, A.A.; Ruoff, R.S. Thermal conductivity of isotopically modified graphene. Nat. Mater. 2012, 11, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhu, L.; Chen, J.; Li, B.; Thong, J.T.L. Suppressing Thermal Conductivity of Suspended Tri-layer Graphene by Gold Deposition. Adv. Mater. 2013, 25, 6884–6888. [Google Scholar] [CrossRef] [PubMed]
- Malekpour, H.; Ramnani, P.; Srinivasan, S.; Balasubramanian, G.; Nika, D.L.; Mulchandani, A.; Lake, R.K.; Balandin, A.A. Thermal conductivity of graphene with defects induced by electron beam irradiation. Nanoscale 2016, 8, 14608–14616. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Wang, Y.; Wu, Z.; Wang, W.; Bi, K.; Liang, Z.; Yang, J.; Chen, Y.; Xu, Z.; Ni, Z. Defect-Engineered Heat Transport in Graphene: A Route to High Efficient Thermal Rectification. Sci. Rep. 2015, 5, 11962. [Google Scholar] [CrossRef] [Green Version]
- Anno, Y.; Imakita, Y.; Takei, K.; Akita, S.; Arie, T. Enhancement of graphene thermoelectric performance through defect engineering. 2D Mater. 2017, 4, 025019. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.; Liu, Z.; Wen, J.; Gao, Y.; Ren, X.; Chen, H.; Jin, C.; Ma, X.-L.; Xu, N.; Cheng, H.-M.; et al. Tailoring the thermal and electrical transport properties of graphene films by grain size engineering. Nat. Commun. 2017, 8, 14486. [Google Scholar] [CrossRef]
- Lee, W.; Kihm, K.D.; Kim, H.G.; Shin, S.; Lee, C.; Park, J.S.; Cheon, S.; Kwon, O.M.; Lim, G.; Lee, W. In-Plane Thermal Conductivity of Polycrystalline Chemical Vapor Deposition Graphene with Controlled Grain Sizes. Nano Lett. 2017, 17, 2361–2366. [Google Scholar] [CrossRef]
- Limbu, T.B.; Hahn, K.R.; Mendoza, F.; Sahoo, S.; Razink, J.J.; Katiyar, R.S.; Weiner, B.R.; Morell, G. Grain size-dependent thermal conductivity of polycrystalline twisted bilayer graphene. Carbon 2017, 117, 367–375. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; Colombo, L.; Ruoff, R.S. Evolution of Graphene Growth on Ni and Cu by Carbon Isotope Labeling. Nano Lett. 2009, 9, 4268–4272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Magnuson, C.W.; Venugopal, A.; Tromp, R.M.; Hannon, J.B.; Vogel, E.M.; Colombo, L.; Ruoff, R.S. Large-Area Graphene Single Crystals Grown by Low-Pressure Chemical Vapor Deposition of Methane on Copper. J. Am. Chem. Soc. 2011, 133, 2816–2819. [Google Scholar] [CrossRef] [PubMed]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, B.; Ruan, X. Reduction of spectral phonon relaxation times from suspended to supported graphene. Appl. Phys. Lett. 2012, 100, 193101. [Google Scholar] [CrossRef] [Green Version]
- Jang, W.; Chen, Z.; Bao, W.; Lau, C.N.; Dames, C. Thickness-Dependent Thermal Conductivity of Encased Graphene and Ultrathin Graphite. Nano Lett. 2010, 10, 3909–3913. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Yi, H.; Yao, Y.; Li, C.; Li, Z. Thermally Conductive Graphene Films for Heat Dissipation. ACS Appl. Nano Mater. 2020, 3, 2149–2155. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L. Hierarchically hydrogen-bonded graphene/polymer interfaces with drastically enhanced interfacial thermal conductance. Nanoscale 2019, 11, 3656–3664. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, L. Polymeric Self-Assembled Monolayers Anomalously Improve Thermal Transport across Graphene/Polymer Interfaces. ACS Appl. Mater. Interfaces 2017, 9, 28949–28958. [Google Scholar] [CrossRef]
- Shahil, K.M.F.; Balandin, A.A. Graphene–Multilayer Graphene Nanocomposites as Highly Efficient Thermal Interface Materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Khan, M.E.; Ko, J.-H.; Kim, J.H.; Lee, E.-S.; Suh, J.; Wu, J.; Kim, Y.-H.; Park, J.Y.; Lyeo, H.-K. Bimodal Control of Heat Transport at Graphene–Metal Interfaces Using Disorder in Graphene. Sci. Rep. 2016, 6, 34428. [Google Scholar] [CrossRef] [Green Version]
- Hopkins, P.E.; Baraket, M.; Barnat, E.V.; Beechem, T.E.; Kearney, S.P.; Duda, J.C.; Robinson, J.T.; Walton, S.G. Manipulating Thermal Conductance at Metal–Graphene Contacts via Chemical Functionalization. Nano Lett. 2012, 12, 590–595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malekpour, H.; Chang, K.-H.; Chen, J.-C.; Lu, C.-Y.; Nika, D.L.; Novoselov, K.S.; Balandin, A.A. Thermal Conductivity of Graphene Laminate. Nano Lett. 2014, 14, 5155–5161. [Google Scholar] [CrossRef] [PubMed]
- Aiyiti, A.; Hu, S.; Wang, C.; Xi, Q.; Cheng, Z.; Xia, M.; Ma, Y.; Wu, T.D.A.J.; Guo, J.; Wang, Q.; et al. Thermal conductivity of suspended few-layer MoS2. Nanoscale 2018, 10, 2727–2734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhang, J.; Puretzky, A.A.; Yoshimura, A.; Sang, X.; Cui, Q.; Li, Y.; Liang, L.; Ghosh, A.W.; Zhao, H.; et al. Isotope-Engineering the Thermal Conductivity of Two-Dimensional MoS2. ACS Nano 2019, 13, 2481–2489. [Google Scholar] [CrossRef]
- Sledzinska, M.; Graczykowski, B.; Placidi, M.; Reig, D.S.; El Sachat, A.; Reparaz, J.S.; Alzina, F.; Mortazavi, B.; Quey, R.; Colombo, L.; et al. Thermal conductivity of MoS2 polycrystalline nanomembranes. 2D Mater. 2016, 3, 035016. [Google Scholar] [CrossRef] [Green Version]
- Sledzinska, M.; Quey, R.; Mortazavi, B.; Graczykowski, B.; Placidi, M.; Reig, D.S.; Navarro-Urrios, D.; Alzina, F.; Colombo, L.; Roche, S.; et al. Record Low Thermal Conductivity of Polycrystalline MoS2 Films: Tuning the Thermal Conductivity by Grain Orientation. ACS Appl. Mater. Interfaces 2017, 9, 37905–37911. [Google Scholar] [CrossRef] [Green Version]
- Peimyoo, N.; Shang, J.; Yang, W.; Wang, Y.; Cong, C.; Yu, D.Y.W. Thermal conductivity determination of suspended mono- and bilayer WS2 by Raman spectroscopy. Nano Res. 2014, 8, 1210–1221. [Google Scholar] [CrossRef]
- Chiritescu, C.; Cahill, D.G.; Nguyen, N.; Johnson, D.; Bodapati, A.; Keblinski, P.; Zschack, P. Ultralow Thermal Conductivity in Disordered, Layered WSe2 Crystals. Science 2007, 315, 351–353. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Jiang, C.; Pope, T.R.; Tsang, C.; Stickney, J.L.; Goli, P.; Renteria, J.; Salguero, T.T.; Balandin, A.A. Phonon and thermal properties of exfoliated TaSe2 thin films. J. Appl. Phys. 2013, 114, 204301. [Google Scholar] [CrossRef] [Green Version]
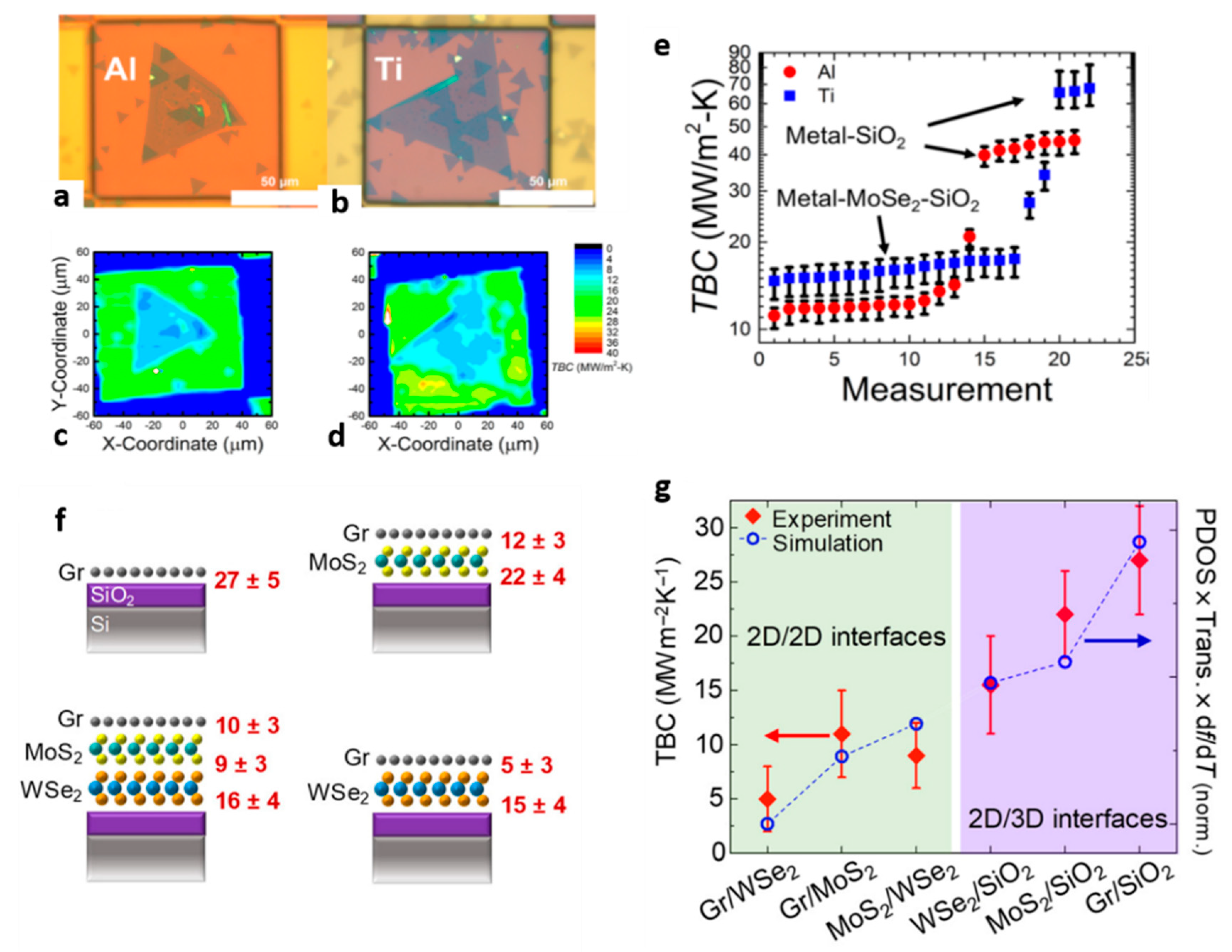
- Brown, D.B.; Shen, W.; Li, X.; Xiao, K.; Geohegan, D.B.; Kumar, S. Spatial Mapping of Thermal Boundary Conductance at Metal–Molybdenum Diselenide Interfaces. ACS Appl. Mater. Interfaces 2019, 11, 14418–14426. [Google Scholar] [CrossRef]
- Chen, C.-C.; Li, Z.; Shi, L.; Wang, B. Thermal interface conductance across a graphene/hexagonal boron nitride heterojunction. Appl. Phys. Lett. 2014, 104, 081908. [Google Scholar] [CrossRef] [Green Version]
- Vaziri, S.; Yalon, E.; Rojo, M.M.; Suryavanshi, S.V.; Zhang, H.; McClellan, C.J.; Bailey, C.S.; Smithe, K.K.H.; Gabourie, A.J.; Chen, V.; et al. Ultrahigh thermal isolation across heterogeneously layered two-dimensional materials. Sci. Adv. 2019, 5, eaax1325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, P.; Shi, L.; Majumdar, A.; McEuen, P.L. Thermal Transport Measurements of Individual Multiwalled Nanotubes. Phys. Rev. Lett. 2001, 87, 215502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, L.; Li, D.; Yu, C.; Jang, W.; Kim, D.; Yao, Z.; Kim, P.; Majumdar, A. Measuring Thermal and Thermoelectric Properties of One-Dimensional Nanostructures Using a Microfabricated Device. J. Heat Transf. 2003, 125, 881–888. [Google Scholar] [CrossRef]
- Mavrokefalos, A.; Pettes, M.T.; Zhou, F.; Shi, L. Four-probe measurements of the in-plane thermoelectric properties of nanofilms. Rev. Sci. Instrum. 2007, 78, 34901. [Google Scholar] [CrossRef] [PubMed]
- Alaie, S.; Goettler, D.F.; Abbas, K.; Su, M.F.; Reinke, C.M.; El-Kady, I.; Leseman, Z.C. Microfabricated suspended island platform for the measurement of in-plane thermal conductivity of thin films and nanostructured materials with consideration of contact resistance. Rev. Sci. Instrum. 2013, 84, 105003. [Google Scholar] [CrossRef]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Pereira, L.F.C.; Wang, Y.; Wu, J.; Zhang, K.; Zhao, X.; Bae, S.; Bui, C.T.; Xie, R.; Thong, J.T.L.; et al. Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Pettes, M.T.; Jo, I.; Yao, Z.; Shi, L. Influence of Polymeric Residue on the Thermal Conductivity of Suspended Bilayer Graphene. Nano Lett. 2011, 11, 1195–1200. [Google Scholar] [CrossRef]
- Jo, I.; Pettes, M.T.; Lindsay, L.; Ou, E.; Weathers, A.; Moore, A.L.; Yao, Z.; Shi, L. Reexamination of basal plane thermal conductivity of suspended graphene samples measured by electro-thermal micro-bridge methods. AIP Adv. 2015, 5, 053206. [Google Scholar] [CrossRef] [Green Version]
- Yarali, M.; Wu, X.; Gupta, T.; Ghoshal, D.; Xie, L.; Zhu, Z.; Brahmi, H.; Bao, J.; Chen, S.; Luo, T.; et al. Effects of Defects on the Temperature-Dependent Thermal Conductivity of Suspended Monolayer Molybdenum Disulfide Grown by Chemical Vapor Deposition. Adv. Funct. Mater. 2017, 27, 1704357. [Google Scholar] [CrossRef]
- Yu, C.; Saha, S.; Zhou, J.; Shi, L.; Cassell, A.M.; Cruden, B.A.; Ngo, Q.; Li, J. Thermal Contact Resistance and Thermal Conductivity of a Carbon Nanofiber. J. Heat Transf. 2005, 128, 234–239. [Google Scholar] [CrossRef]
- Demers, H.; Poirier-Demers, N.; Couture, A.R.; Joly, D.; Guilmain, M.; De Jonge, N.; Drouin, D. Three-dimensional electron microscopy simulation with the CASINO Monte Carlo software. Scanning 2011, 33, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Jo, I.; Pettes, M.T.; Ou, E.; Wu, W.; Shi, L. Basal-plane thermal conductivity of few-layer molybdenum disulfide. Appl. Phys. Lett. 2014, 104, 201902. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.M.; Jo, I.; Shi, L. Phonon-interface scattering in multilayer graphene on an amorphous support. Proc. Natl. Acad. Sci. USA 2013, 110, 16321–16326. [Google Scholar] [CrossRef] [Green Version]
- Jo, I.; Pettes, M.T.; Kim, J.; Watanabe, K.; Taniguchi, T.; Yao, Z.; Shi, L. Thermal Conductivity and Phonon Transport in Suspended Few-Layer Hexagonal Boron Nitride. Nano Lett. 2013, 13, 550–554. [Google Scholar] [CrossRef] [Green Version]
- Weathers, A.; Khan, Z.U.; Brooke, R.; Evans, D.; Pettes, M.T.; Andreasen, J.W.; Crispin, X.; Shi, L. Significant Electronic Thermal Transport in the Conducting Polymer Poly(3,4-ethylenedioxythiophene). Adv. Mater. 2015, 27, 2101–2106. [Google Scholar] [CrossRef] [Green Version]
- Hao, Q.; Xu, D.; Zhao, H.; Xiao, Y.; Medina, F.J. Thermal Studies of Nanoporous Si Films with Pitches on the Order of 100 nm -Comparison between Different Pore-Drilling Techniques. Sci. Rep. 2018, 8, 9056. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, A.J.; Chen, X.; Chen, G. Pulse accumulation, radial heat conduction, and anisotropic thermal conductivity in pump-probe transient thermoreflectance. Rev. Sci. Instrum. 2008, 79, 114902. [Google Scholar] [CrossRef] [Green Version]
- Feshchenko, A.V.; Casparis, L.; Khaymovich, I.M.; Maradan, D.; Saira, O.-P.; Palma, M.; Meschke, M.; Pekola, J.P.; Zumbühl, D.M. Tunnel-Junction Thermometry Down to Millikelvin Temperatures. Phys. Rev. Appl. 2015, 4, 4. [Google Scholar] [CrossRef]
- Aiyiti, A.; Bai, X.; Wu, J.; Xu, X.; Li, B. Measuring the thermal conductivity and interfacial thermal resistance of suspended MoS 2 using electron beam self-heating technique. Sci. Bull. 2018, 63, 452–458. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Xie, R.; Yang, N.; Li, B.; Thong, J.T.L. Profiling Nanowire Thermal Resistance with a Spatial Resolution of Nanometers. Nano Lett. 2014, 14, 806–812. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liu, X.; Rath, A.; Wu, J.; Li, B.; Zhou, W.; Xie, G.; Zhang, Y.-W.; Thong, J.T.L. Probing thermal transport across amorphous region embedded in a single crystalline silicon nanowire. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Cahill, D.G. Thermal conductivity measurement from 30 to 750 K: The 3ω method. Rev. Sci. Instrum. 1990, 61, 802–808. [Google Scholar] [CrossRef]
- Oh, D.-W.; Jain, A.; Eaton, J.K.; Goodson, K.E.; Lee, J.S. Thermal conductivity measurement and sedimentation detection of aluminum oxide nanofluids by using the 3ω method. Int. J. Heat Fluid Flow 2008, 29, 1456–1461. [Google Scholar] [CrossRef]
- Rodríguez-Laguna, M.D.R.; Castro-Alvarez, A.; Sledzinska, M.; Maire, J.; Costanzo, F.; Ensing, B.; Pruneda, M.; Ordejon, P.; Sotomayor Torres, C.M.; Gomez-Romero, P.; et al. Mechanisms behind the enhancement of thermal properties of graphene nanofluids. Nanoscale 2017, 10, 15402–15409. [Google Scholar] [CrossRef] [Green Version]
- Gauthier, S.; Giani, A.; Combette, P. Gas thermal conductivity measurement using the three-omega method. Sens. Actuators A Phys. 2013, 195, 50–55. [Google Scholar] [CrossRef]
- Cahill, D.G.; Katiyar, M.; Abelson, J.R. Thermal conductivity ofa-Si:H thin films. Phys. Rev. B 1994, 50, 6077–6081. [Google Scholar] [CrossRef]
- Kim, J.H.; Feldman, A.; Novotny, D.B. Application of the three omega thermal conductivity measurement method to a film on a substrate of finite thickness. J. Appl. Phys. 1999, 86, 3959–3963. [Google Scholar] [CrossRef]
- Borcatasciuc, T.; Kumar, A.R.; Chen, G. Data reduction in 3ω method for thin-film thermal conductivity determination. Rev. Sci. Instrum. 2001, 72, 2139–2147. [Google Scholar] [CrossRef]
- Völklein, F. Thermal conductivity and diffusivity of a thin film SiO2-Si3N4 sandwich system. Thin Solid Films 1990, 188, 27–33. [Google Scholar] [CrossRef]
- Sikora, A.; Ftouni, H.; Richard, J.; Hébert, C.; Eon, D.; Omnès, F.; Bourgeois, O. Highly sensitive thermal conductivity measurements of suspended membranes (SiN and diamond) using a 3ω-Völklein method. Rev. Sci. Instrum. 2012, 83, 054902. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Yi, W.; Zhang, D.L. 3ω method for specific heat and thermal conductivity measurements. Rev. Sci. Instrum. 2001, 72, 2996–3003. [Google Scholar] [CrossRef] [Green Version]
- Choi, T.Y.; Poulikakos, D.; Tharian, J.; Sennhauser, U. Measurement of thermal conductivity of individual multiwalled carbon nanotubes by the 3-ω method. Appl. Phys. Lett. 2005, 87, 13108. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Tang, D.-W.; Li, X.B.; Zheng, X.H.; Zhang, W.G.; Zheng, L.X.; Zhu, Y.; Jin, A.Z.; Yang, H.; Gu, C.Z. Length-dependent thermal conductivity of an individual single-wall carbon nanotube. Appl. Phys. Lett. 2007, 91, 123119. [Google Scholar] [CrossRef]
- Menges, F.; Riel, H.; Stemmer, A.; Gotsmann, B. Nanoscale thermometry by scanning thermal microscopy. Rev. Sci. Instrum. 2016, 87, 074902. [Google Scholar] [CrossRef]
- Sadat, S.; Meyhöfer, E.; Reddy, P. High resolution resistive thermometry for micro/nanoscale measurements. Rev. Sci. Instrum. 2012, 83, 84902. [Google Scholar] [CrossRef]
- Kim, K.; Jeong, W.; Lee, W.; Reddy, P. Ultra-High Vacuum Scanning Thermal Microscopy for Nanometer Resolution Quantitative Thermometry. ACS Nano 2012, 6, 4248–4257. [Google Scholar] [CrossRef]
- Yasaei, P.; Murthy, A.A.; Xu, Y.; Dos Reis, R.; Shekhawat, G.S.; Dravid, V.P. Spatial Mapping of Hot-Spots at Lateral Heterogeneities in Monolayer Transition Metal Dichalcogenides. Adv. Mater. 2019, 31, e1808244. [Google Scholar] [CrossRef]
- Choi, D.; Poudel, N.; Wang, B.; Shi, L. Effects of basal-plane thermal conductivity and interface thermal conductance on the hot spot temperature in graphene electronic devices. Appl. Phys. Lett. 2017, 110, 073104. [Google Scholar] [CrossRef] [Green Version]
- El Sachat, A.; Köeneman, F.; Menges, F.; Del Corro, E.; Garrido, J.A.; Sotomayor Torres, C.M.; Alzina, F.; Gotsmann, B. Crossover from ballistic to diffusive thermal transport in suspended graphene membranes. 2D Mater. 2019, 6, 025034. [Google Scholar] [CrossRef]
- El Sachat, A.; Spièce, J.; Evangeli, C.; Robson, A.J.; Kreuzer, M.; Rodríguez-Laguna, M.D.R.; Chavez-Angel, E.; Sledzinska, M.; Sotomayor Torres, C.M.; Kolosov, O.V.; et al. Nanoscale Mapping of Thermal and Mechanical Properties of Bare and Metal-Covered Self-Assembled Block Copolymer Thin Films. ACS Appl. Polym. Mater. 2019, 2, 487–496. [Google Scholar] [CrossRef]
- Pumarol, M.E.; Rosamond, M.C.; Tovee, P.; Petty, M.C.; Zeze, D.A.; Falko, V.; Kolosov, O.V. Direct Nanoscale Imaging of Ballistic and Diffusive Thermal Transport in Graphene Nanostructures. Nano Lett. 2012, 12, 2906–2911. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Chung, J.; Hwang, G.; Kwon, O.; Lee, J.S. Quantitative Measurement with Scanning Thermal Microscope by Preventing the Distortion Due to the Heat Transfer through the Air. ACS Nano 2011, 5, 8700–8709. [Google Scholar] [CrossRef]
- Menges, F.; Riel, H.; Stemmer, A.; Dimitrakopoulos, C.; Gotsmann, B. Thermal Transport into Graphene through Nanoscopic Contacts. Phys. Rev. Lett. 2013, 111, 205901. [Google Scholar] [CrossRef]
- Martinek, J.; Klapetek, P.; Campbell, A.C. Methods for topography artifacts compensation in scanning thermal microscopy. Ultramicroscopy 2015, 155, 55–61. [Google Scholar] [CrossRef] [Green Version]
- Hwang, G.; Chung, J.; Kwon, O. Enabling low-noise null-point scanning thermal microscopy by the optimization of scanning thermal microscope probe through a rigorous theory of quantitative measurement. Rev. Sci. Instrum. 2014, 85, 114901. [Google Scholar] [CrossRef]
- Bodzenta, J.; Kaźmierczak-Bałata, A.; Harris, K. Quantitative thermal measurement by the use of scanning thermal microscope and resistive thermal probes. J. Appl. Phys. 2020, 127, 031103. [Google Scholar] [CrossRef]
- Gomès, S.; Assy, A.; Chapuis, P.-O. Scanning thermal microscopy: A review. Phys. Status Solidi A 2015, 212, 477–494. [Google Scholar] [CrossRef]
- Saci, A.; Battaglia, J.-L.; De, I. Notice of Violation of IEEE Publication Principles: Accurate New Methodology in Scanning Thermal Microscopy. IEEE Trans. Nanotechnol. 2015, 14, 1035–1039. [Google Scholar] [CrossRef]
- Cahill, D.G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 2004, 75, 5119–5122. [Google Scholar] [CrossRef]
- Tortello, M.; Pasternak, I.; Żerańska-Chudek, K.; Strupinski, W.; Gonnelli, R.S.; Fina, A. Chemical-Vapor-Deposited Graphene as a Thermally Conducting Coating. ACS Appl. Nano Mater. 2019, 2, 2621–2633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoon, K.; Hwang, G.; Chung, J.; Kim, H.G.; Kwon, O.; Kihm, K.D.; Lee, J.S. Measuring the thermal conductivity of residue-free suspended graphene bridge using null point scanning thermal microscopy. Carbon 2014, 76, 77–83. [Google Scholar] [CrossRef]
- El Sachat, A.; Reparaz, J.S.; Spiece, J.; Alonso, M.I.; Goñi, A.R.; Garriga, M.; Vaccaro, P.O.; Wagner, M.R.; Kolosov, O.V.; Sotomayor Torres, C.M.; et al. Thermal transport in epitaxial Si1−xGex alloy nanowires with varying composition and morphology. Nanotechnology 2017, 28, 505704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puyoo, E.; Grauby, S.; Rampnoux, J.-M.; Rouvière, E.; Dilhaire, S. Scanning thermal microscopy of individual silicon nanowires. J. Appl. Phys. 2011, 109, 024302. [Google Scholar] [CrossRef]
- Menges, F.; Mensch, P.; Schmid, H.; Riel, H.; Stemmer, A.; Gotsmann, B. Temperature mapping of operating nanoscale devices by scanning probe thermometry. Nat. Commun. 2016, 7, 10874. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makris, A.; Haeger, T.; Heiderhoff, R.; Riedl, T. From diffusive to ballistic Stefan–Boltzmann heat transport in thin non-crystalline films. RSC Adv. 2016, 6, 94193–94199. [Google Scholar] [CrossRef] [Green Version]
- Juszczyk, J.; Kaźmierczak-Bałata, A.; Firek, P.; Bodzenta, J. Measuring thermal conductivity of thin films by Scanning Thermal Microscopy combined with thermal spreading resistance analysis. Ultramicroscopy 2017, 175, 81–86. [Google Scholar] [CrossRef]
- Tortello, M.; Colonna, S.; Bernal, M.; Gomez, J.; Pavese, M.; Novara, C.; Giorgis, F.; Maggio, M.; Guerra, G.; Saracco, G.; et al. Effect of thermal annealing on the heat transfer properties of reduced graphite oxide flakes: A nanoscale characterization via scanning thermal microscopy. Carbon 2016, 109, 390–401. [Google Scholar] [CrossRef] [Green Version]
- Yalon, E.; McClellan, C.J.; Smithe, K.K.H.; Rojo, M.M.; Xu, R.L.; Suryavanshi, S.V.; Gabourie, A.J.; Neumann, C.M.; Xiong, F.; Farimani, A.B.; et al. Energy Dissipation in Monolayer MoS2 Electronics. Nano Lett. 2017, 17, 3429–3433. [Google Scholar] [CrossRef] [Green Version]
- Harzheim, A.; Evangeli, C.; Kolosov, O.V.; Gehring, P. Direct mapping of local Seebeck coefficient in 2D material nanostructures via scanning thermal gate microscopy. 2D Mater. 2020, 7, 041004. [Google Scholar] [CrossRef]
- Harzheim, A.; Spiece, J.; Evangeli, C.; McCann, E.; Falko, V.; Sheng, Y.; Warner, J.H.; Briggs, G.A.D.; Mol, J.A.; Gehring, P.; et al. Geometrically Enhanced Thermoelectric Effects in Graphene Nanoconstrictions. Nano Lett. 2018, 18, 7719–7725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gächter, N.; Könemann, F.; Sistani, M.; Bartmann, M.G.; Sousa, M.; Staudinger, P.; Lugstein, A.; Gotsmann, B. Spatially resolved thermoelectric effects in operando semiconductor–metal nanowire heterostructures. Nanoscale 2020, 12, 20590–20597. [Google Scholar] [CrossRef] [PubMed]
- Campbell, I.; Fauchet, P. The effects of microcrystal size and shape on the one phonon Raman spectra of crystalline semiconductors. Solid State Commun. 1986, 58, 739–741. [Google Scholar] [CrossRef]
- Camassel, J.; Falkovsky, L.A.; Planes, N. Strain effect in silicon-on-insulator materials: Investigation with optical phonons. Phys. Rev. B 2000, 63, 035309. [Google Scholar] [CrossRef] [Green Version]
- Mishra, P.; Jain, K.P. Temperature-dependent Raman scattering studies in nanocrystalline silicon and finite-size effects. Phys. Rev. B 2000, 62, 14790–14795. [Google Scholar] [CrossRef]
- Chávez, E.; Fuentes, S.; Zarate, R.A.; Padilla-Campos, L.; Chavez-Angel, E. Structural analysis of nanocrystalline BaTiO3. J. Mol. Struct. 2010, 984, 131–136. [Google Scholar] [CrossRef]
- Hart, T.R.; Aggarwal, R.L.; Lax, B. Temperature Dependence of Raman Scattering in Silicon. Phys. Rev. B 1970, 1, 638–642. [Google Scholar] [CrossRef]
- Périchon, S.; Lysenko, V.; Remaki, B.; Barbier, D.; Champagnon, B. Measurement of porous silicon thermal conductivity by micro-Raman scattering. J. Appl. Phys. 1999, 86, 4700–4702. [Google Scholar] [CrossRef]
- Jaramillo-Fernandez, J.; O’Dwyer, C.; Sotomayor-Torres, C.M. Raman thermometry analysis: Modelling assumptions revisited. Appl. Therm. Eng. 2018, 130, 1175–1181. [Google Scholar] [CrossRef]
- Huang, S.; Ruan, X.-D.; Fu, X.; Yang, H.-Y. Measurement of the thermal transport properties of dielectric thin films using the micro-Raman method. J. Zhejiang Univ. A 2009, 10, 7–16. [Google Scholar] [CrossRef]
- Huang, S.; Ruan, X.; Zou, J.; Fu, X.; Yang, H. Thermal conductivity measurement of submicrometer-scale silicon dioxide films by an extended micro-Raman method. Microsyst. Technol. 2009, 15, 837–842. [Google Scholar] [CrossRef]
- Judek, J.; Gertych, A.P.; Świniarski, M.; Łapińska, A.; Dużyńska, A.; Zdrojek, M. High accuracy determination of the thermal properties of supported 2D materials. Sci. Rep. 2015, 5, srep12422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoib, B.; Filser, S.; Stötzel, J.; Greppmair, A.; Petermann, N.; Wiggers, H.; Schierning, G.; Stutzmann, M.; Brandt, M. Spatially resolved determination of thermal conductivity by Raman spectroscopy. Semicond. Sci. Technol. 2014, 29, 124005. [Google Scholar] [CrossRef] [Green Version]
- Palankovski, V.; Selberherr, S. Thermal models for semiconductor device simulation. In Proceedings of the HITEN 99. Third European Conference on High Temperature Electronics (IEEE Cat. No.99EX372), Berlin, Germany, 7 July 1999; pp. 25–28. [Google Scholar]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.K.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Sahoo, S.; Gaur, A.P.S.; Ahmadi, M.; Guinel, M.J.-F.; Katiyar, R.S. Temperature-Dependent Raman Studies and Thermal Conductivity of Few-Layer MoS2. J. Phys. Chem. C 2013, 117, 9042–9047. [Google Scholar] [CrossRef] [Green Version]
- Yan, R.; Simpson, J.R.; Bertolazzi, S.; Brivio, J.; Watson, M.; Wu, X.; Kis, A.; Luo, T.; Walker, A.R.H.; Xing, H.G. Thermal Conductivity of Monolayer Molybdenum Disulfide Obtained from Temperature-Dependent Raman Spectroscopy. ACS Nano 2014, 8, 986–993. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, D.; Li, Y.; Lee, G.-H.; Cui, X.; Chenet, D.; Hyoung, L.G.; Heinz, T.F.; Hone, J.C. Measurement of Lateral and Interfacial Thermal Conductivity of Single- and Bilayer MoS2 and MoSe2 Using Refined Optothermal Raman Technique. ACS Appl. Mater. Interfaces 2015, 7, 25923–25929. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Maassen, J.; Deng, Y.; Du, Y.; Garrelts, R.P.; Lundstrom, M.S.; Ye, P.D.; Xu, X. Anisotropic in-plane thermal conductivity observed in few-layer black phosphorus. Nat. Commun. 2015, 6, 8572. [Google Scholar] [CrossRef]
- Yalon, E.; Aslan Özgür, B.; Smithe, K.K.H.; McClellan, C.J.; Suryavanshi, S.V.; Xiong, F.; Sood, A.; Neumann, C.M.; Xu, X.; Goodson, K.E.; et al. Temperature-Dependent Thermal Boundary Conductance of Monolayer MoS2 by Raman Thermometry. ACS Appl. Mater. Interfaces 2017, 9, 43013–43020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, I.-K.; Pettes, M.T.; Aykol, M.; Chang, C.-C.; Hung, W.-H.; Theiss, J.; Shi, L.; Wang, B. Direct observation of heat dissipation in individual suspended carbon nanotubes using a two-laser technique. J. Appl. Phys. 2011, 110, 044328. [Google Scholar] [CrossRef] [Green Version]
- Fan, D.; Sigg, H.; Spolenak, R.; Ekinci, Y. Strain and thermal conductivity in ultrathin suspended silicon nanowires. Phys. Rev. B 2017, 96, 96. [Google Scholar] [CrossRef] [Green Version]
- Sett, S.; Aggarwal, V.K.; Singha, A.; Raychaudhuri, A. Temperature-dependent Thermal Conductivity of a Single Germanium Nanowire Measured by Optothermal Raman Spectroscopy. Phys. Rev. Appl. 2020, 13, 054008. [Google Scholar] [CrossRef]
- Doerk, G.S.; Carraro, C.; Maboudian, R. Single Nanowire Thermal Conductivity Measurements by Raman Thermography. ACS Nano 2010, 4, 4908–4914. [Google Scholar] [CrossRef]
- Wudil, Y.; Gondal, M.; Rao, S.; Kunwar, S. Thermal conductivity of PLD-grown thermoelectric Bi2Te2.7Se0.3 films using temperature-dependent Raman spectroscopy technique. Ceram. Int. 2020, 46, 7253–7258. [Google Scholar] [CrossRef]
- Shen, C.; Du, W.; Wu, Z.; Xing, J.; Ha, S.T.; Shang, Q.; Xu, W.; Xiong, Q.; Liu, X.-F.; Zhang, Q. Thermal conductivity of suspended single crystal CH 3 NH 3 PbI 3 platelets at room temperature. Nanoscale 2017, 9, 8281–8287. [Google Scholar] [CrossRef]
- Anaya, J.; Rossi, S.; AlOmari, M.; Kohn, E.; Tóth, L.; Pécz, B.; Kuball, M. Thermal conductivity of ultrathin nano-crystalline diamond films determined by Raman thermography assisted by silicon nanowires. Appl. Phys. Lett. 2015, 106, 223101. [Google Scholar] [CrossRef] [Green Version]
- Chávez-Ángel, E.; Reparaz, J.S.; Gomis-Bresco, J.; Wagner, M.R.; Cuffe, J.; Graczykowski, B.; Shchepetov, A.; Jiang, H.; Prunnila, M.; Ahopelto, J.; et al. Reduction of the thermal conductivity in free-standing silicon nano-membranes investigated by non-invasive Raman thermometry. APL Mater. 2014, 2, 012113. [Google Scholar] [CrossRef]
- Malekpour, H.; Balandin, A.A. Raman-based technique for measuring thermal conductivity of graphene and related materials. J. Raman Spectrosc. 2018, 49, 106–120. [Google Scholar] [CrossRef] [Green Version]
- Sandell, S.; Chavez-Angel, E.; El Sachat, A.; He, J.; Sotomayor Torres, C.M.; Maire, J. Thermoreflectance techniques and Raman thermometry for thermal property characterization of nanostructures. J. Appl. Phys. 2020, 128, 131101. [Google Scholar] [CrossRef]
- Ehrenreich, H.; Philipp, H.R. Optical Properties of Ag and Cu. Phys. Rev. 2002, 128, 1622–1629. [Google Scholar] [CrossRef]
- Paddock, C.A.; Eesley, G.L. Transient thermoreflectance from thin metal films. J. Appl. Phys. 1986, 60, 285–290. [Google Scholar] [CrossRef]
- Jiang, P.; Qian, X.; Yang, R. Tutorial: Time-domain thermoreflectance (TDTR) for thermal property characterization of bulk and thin film materials. J. Appl. Phys. 2018, 124, 161103. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, A.J.; Cheaito, R.; Chiesa, M. A frequency-domain thermoreflectance method for the characterization of thermal properties. Rev. Sci. Instruments 2009, 80, 094901. [Google Scholar] [CrossRef]
- Faugeras, C.; Faugeras, B.; Orlita, M.; Potemski, M.; Nair, R.R.; Geim, A.K. Thermal Conductivity of Graphene in Corbino Membrane Geometry. ACS Nano 2010, 4, 1889–1892. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Moore, A.L.; Zhu, Y.; Li, X.; Chen, S.; Shi, L.; Ruoff, R.S. Thermal Transport in Suspended and Supported Monolayer Graphene Grown by Chemical Vapor Deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef]
- Chen, S.; Li, Q.; Zhang, Q.; Qu, Y.; Ji, H.; Ruoff, R.S.; Cai, W. Thermal conductivity measurements of suspended graphene with and without wrinkles by micro-Raman mapping. Nanotechnology 2012, 23, 365701. [Google Scholar] [CrossRef]
- Eichler, H.J.; Salje, G.; Stahl, H. Thermal diffusion measurements using spatially periodic temperature distributions induced by laser light. J. Appl. Phys. 1973, 44, 5383–5388. [Google Scholar] [CrossRef]
- Skurk, H.; Maznev, A.A.; Matthias, E. Transient thermal gratings at surfaces for thermal characterization of bulk materials and thin films. Appl. Phys. A 1995, 61, 253–261. [Google Scholar] [CrossRef]
- Maznev, A.A.; Nelson, K.A.; Rogers, J.A. Optical heterodyne detection of laser-induced gratings. Opt. Lett. 1998, 23, 1319–1321. [Google Scholar] [CrossRef] [PubMed]
- Nelson, K.A.; Casalegno, R.; Miller, R.J.D.; Fayer, M.D. Laser-induced excited state and ultrasonic wave gratings: Amplitude and phase grating contributions to diffraction. J. Chem. Phys. 1982, 77, 1144–1152. [Google Scholar] [CrossRef]
- Johnson, J.A.; Maznev, A.A.; Cuffe, J.; Eliason, J.K.; Minnich, A.J.; Kehoe, T.; Sotomayor Torres, C.M.; Chen, G.; Nelson, K.A. Direct Measurement of Room-Temperature Nondiffusive Thermal Transport Over Micron Distances in a Silicon Membrane. Phys. Rev. Lett. 2013, 110, 025901. [Google Scholar] [CrossRef] [PubMed]
- Reddy, A.L.M.; Gowda, S.R.; Shaijumon, M.M.; Ajayan, P.M. Hybrid Nanostructures for Energy Storage Applications. Adv. Mater. 2012, 24, 5045–5064. [Google Scholar] [CrossRef]
- Machida, Y.; Subedi, A.; Akiba, K.; Miyake, A.; Tokunaga, M.; Akahama, Y.; Izawa, K.; Behnia, K. Observation of Poiseuille flow of phonons in black phosphorus. Sci. Adv. 2018, 4, eaat3374. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Lee, S. Crossover of ballistic, hydrodynamic, and diffusive phonon transport in suspended graphene. Phys. Rev. B 2019, 99, 085202. [Google Scholar] [CrossRef] [Green Version]
- Ziabari, A.; Torres, P.; Vermeersch, B.; Xuan, Y.; Cartoixà, X.; Torelló, A.; Bahk, J.-H.; Koh, Y.R.; Parsa, M.; Ye, P.D.; et al. Full-field thermal imaging of quasiballistic crosstalk reduction in nanoscale devices. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
| Resolution | |||||||
|---|---|---|---|---|---|---|---|
| Method | Material Geometry | Measurement | Temperature | Spatial | Temporal | Imaging | Limitations |
| Suspended thermal bridge | Suspended 2D materials, thin films, NWs, etc | k‖ | ~50 mK | Mean value | - | No | Difficult sample preparation, influence of extrinsic thermal contact resistances |
| Electron beam self-heating | Suspended 2D materials, thin films, NWs, etc | k‖, Rc, TBC | ~0.4 mK | ~20 nm (heating volume dependent) | - | No | Limited to thick samples, difficult sample preparation |
| 3w-method | Supported and suspended films | k‖, k⊥ | Mean value | Mean value | - | No | For electrical conductive films, electrical insulation is needed |
| SThM | Supported and suspended 2D materials, films, NWs, bulk etc. | Rts, T | <5 mK | <10 nm | 10–100 µs | Yes | No direct access to k, hard modelling is needed |
| Raman spectroscopy | Supported and suspended 2D materials, films, NWs, bulk, etc | k‖, k⊥, TBC | ~2 K | ~λ/2 nm | - | Yes | Assumptions to determine k, complex sample preparation for 2D materials |
| Two-laser Raman Themometry | Suspend membrane-based structures, 2D materials | k‖ | ~2 K | ~λ/2 nm | - | Yes | Limited to suspended structures |
| Frequency domain thermoreflectance | Supported 2D materials and films | k‖, k⊥, TBC | Sub-100 mK | ~λ/2 nm | Sub-ps | Yes | Deposition of a thin metal film (transducer) is required |
| Time domain thermoreflectance | Supported 2D materials and films | k‖, k⊥, TBC | Sub-100 mK | ~λ/2 nm | <1 ns | Yes | Deposition of a thin metal film (transducer) is required |
| Thermal transient grating | Supported and suspended fims | α‖ | Sub-100 mK | ~50 μm | 10’s ps | No | Limited to the efficiency of the diffraction pattern |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Sachat, A.; Alzina, F.; Sotomayor Torres, C.M.; Chavez-Angel, E. Heat Transport Control and Thermal Characterization of Low-Dimensional Materials: A Review. Nanomaterials 2021, 11, 175. https://doi.org/10.3390/nano11010175
El Sachat A, Alzina F, Sotomayor Torres CM, Chavez-Angel E. Heat Transport Control and Thermal Characterization of Low-Dimensional Materials: A Review. Nanomaterials. 2021; 11(1):175. https://doi.org/10.3390/nano11010175
Chicago/Turabian StyleEl Sachat, Alexandros, Francesc Alzina, Clivia M. Sotomayor Torres, and Emigdio Chavez-Angel. 2021. "Heat Transport Control and Thermal Characterization of Low-Dimensional Materials: A Review" Nanomaterials 11, no. 1: 175. https://doi.org/10.3390/nano11010175
APA StyleEl Sachat, A., Alzina, F., Sotomayor Torres, C. M., & Chavez-Angel, E. (2021). Heat Transport Control and Thermal Characterization of Low-Dimensional Materials: A Review. Nanomaterials, 11(1), 175. https://doi.org/10.3390/nano11010175








