Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media
Abstract
1. Introduction
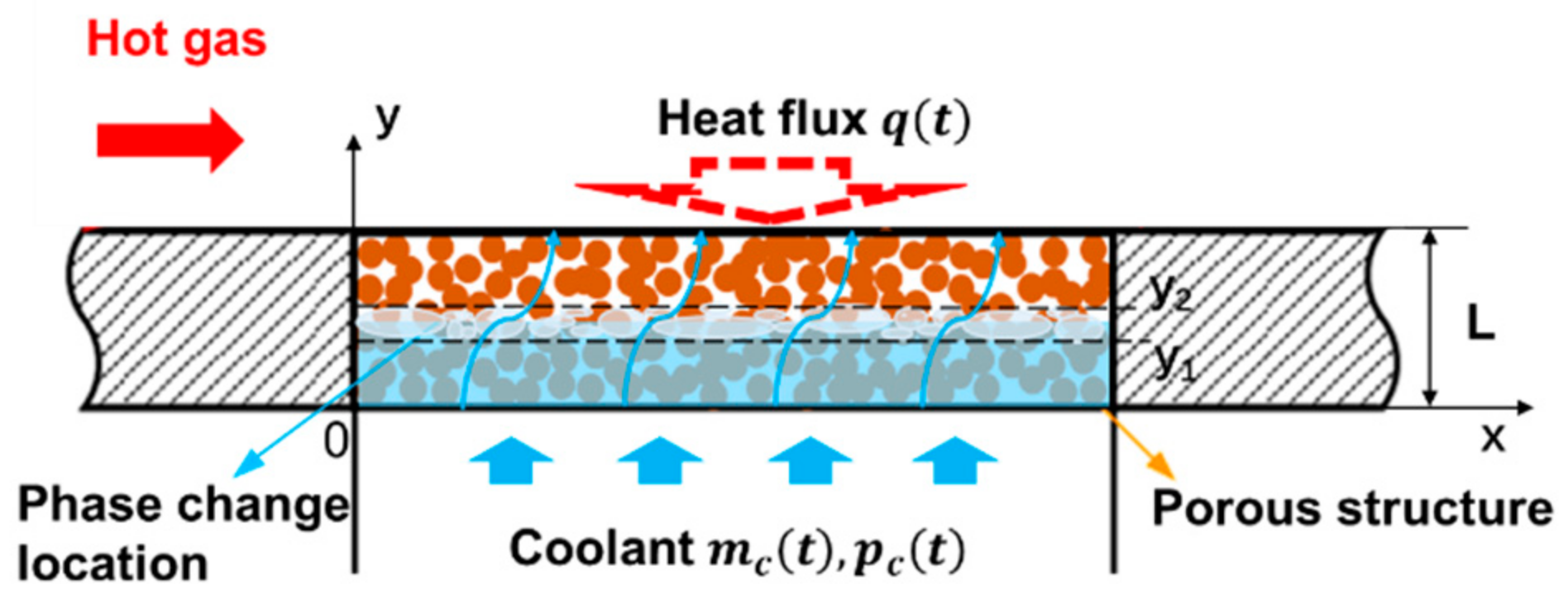
2. Mathematical Model and Theoretical Analysis
2.1. Mass Conservation Equation
2.2. Momentum Conservation Equation
2.3. Energy Conservation Equation
2.4. Constitutive Relations
3. Numerical Approach
3.1. Initial and Boundary Conditions
3.2. Solution Procedure
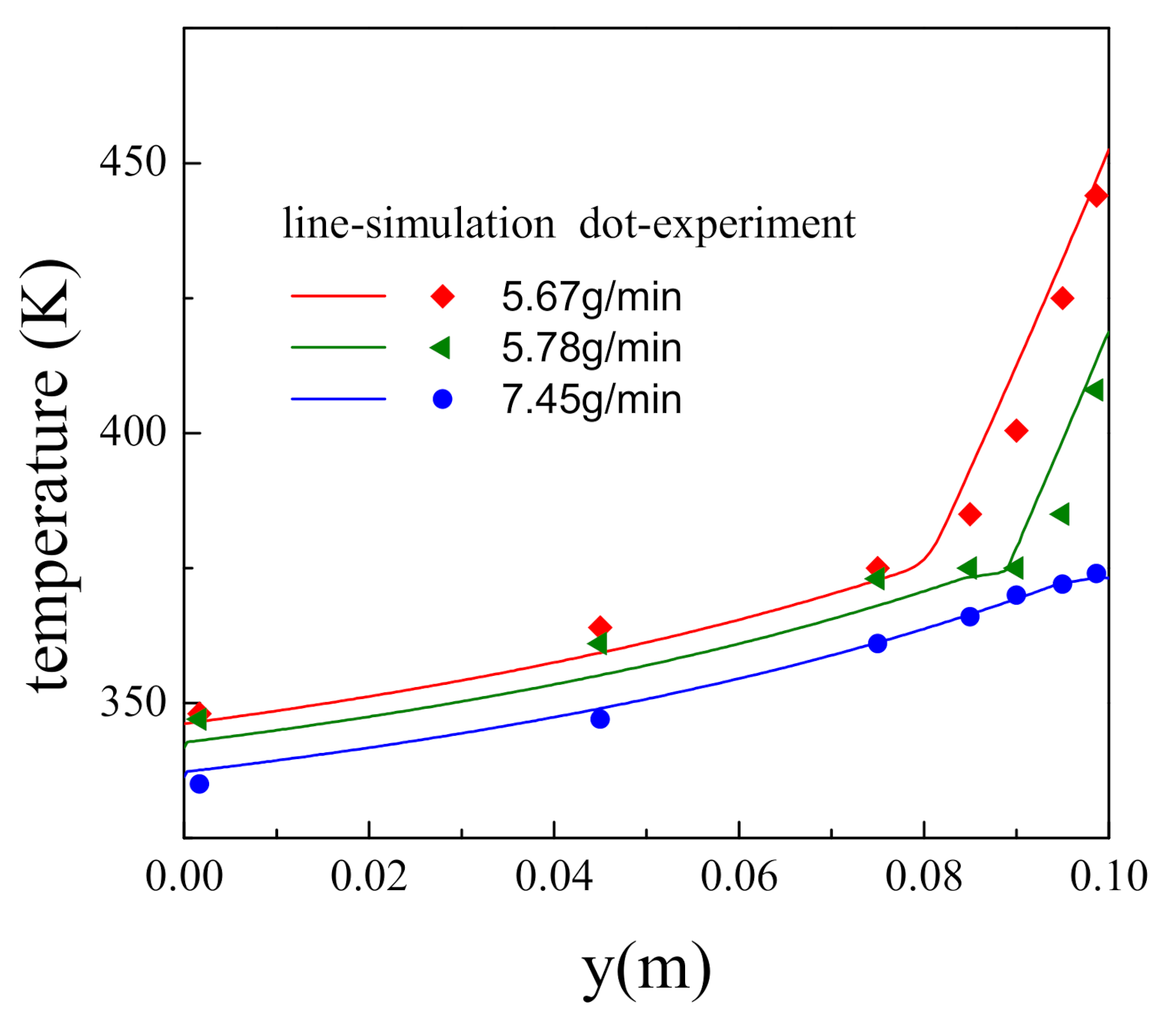
4. Experiment and Verification
5. Results and Discussions
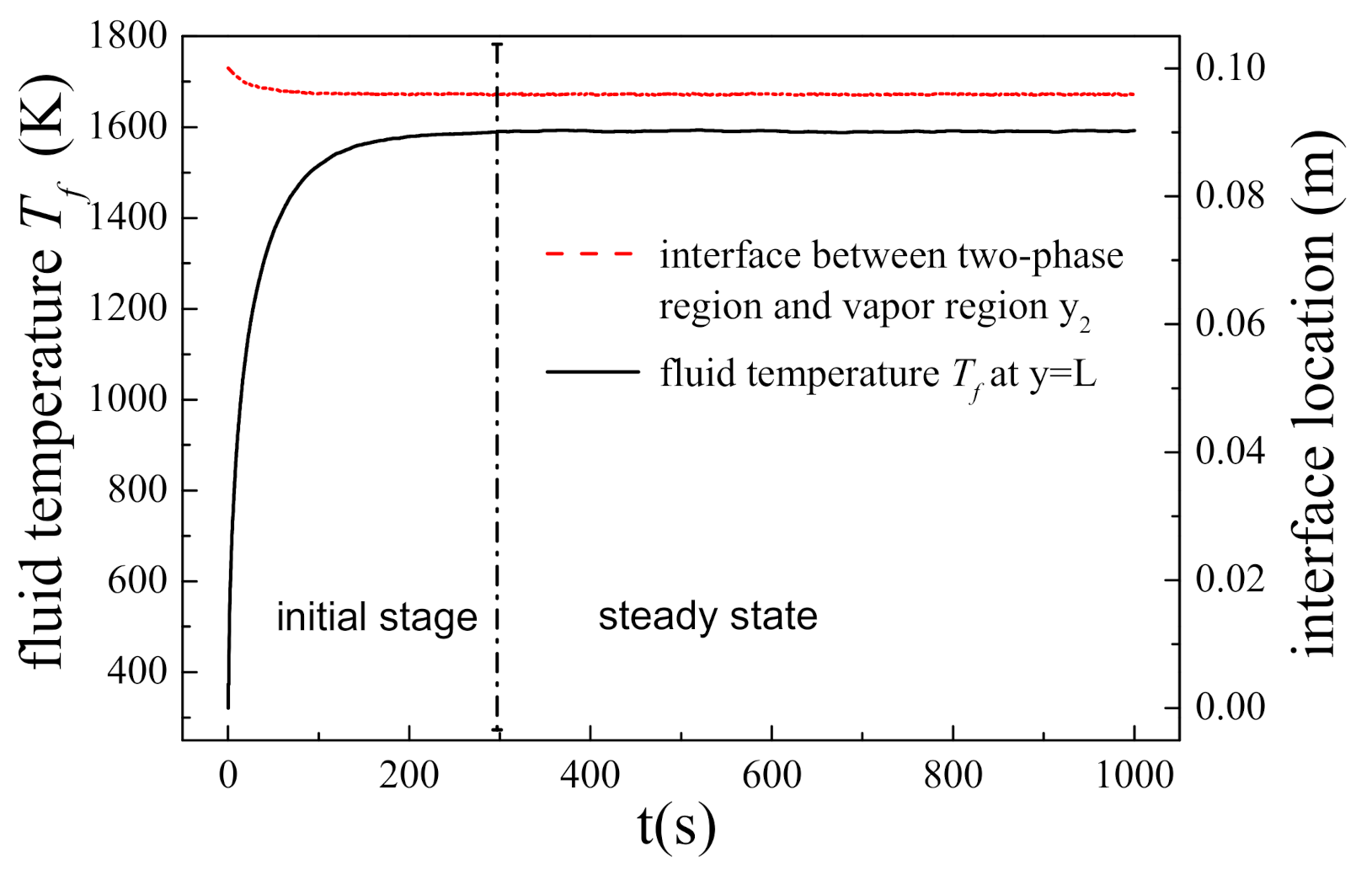
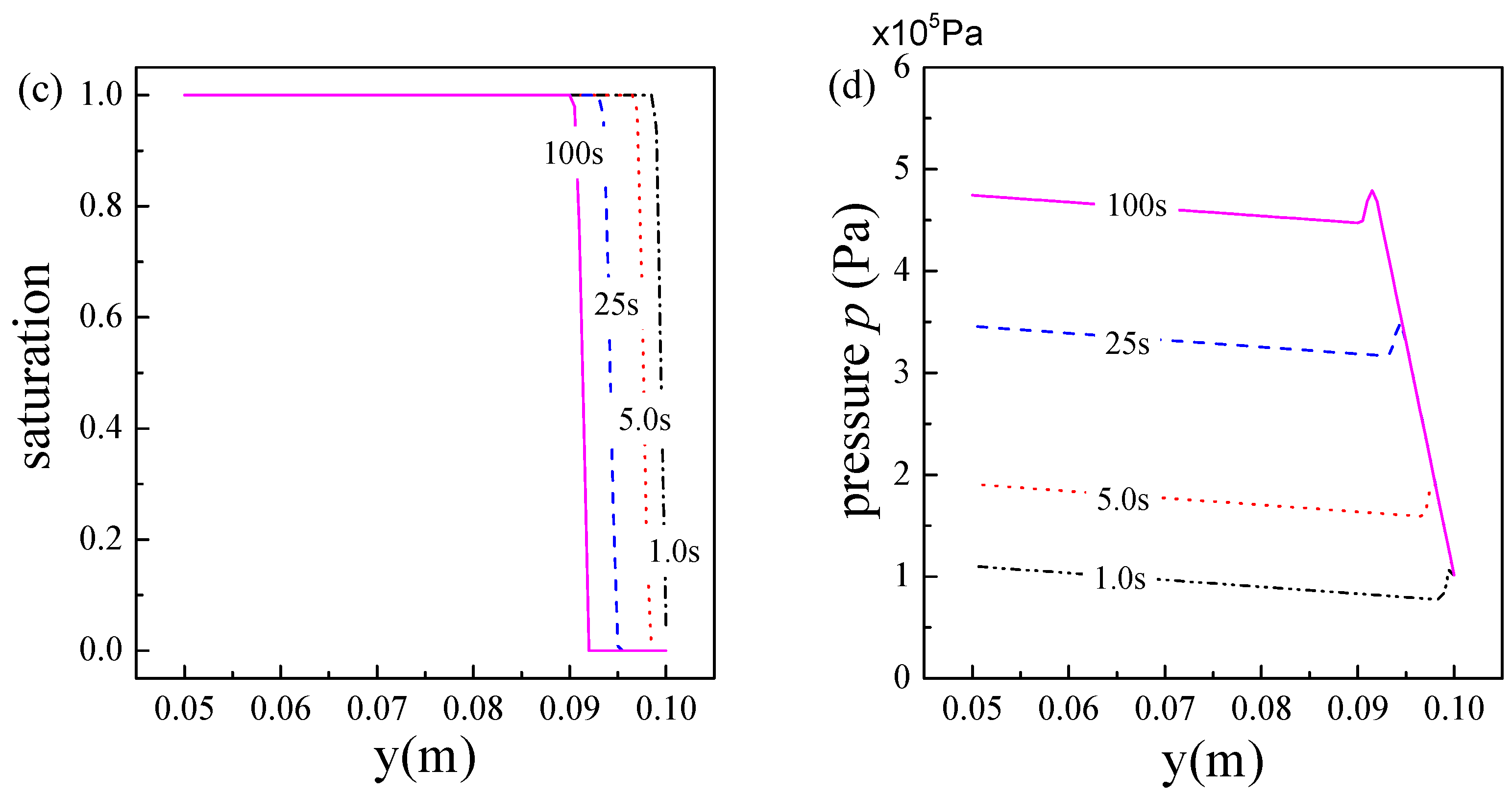
5.1. Transient Behavior of Two-Phase Flow with Phase Change in Porous Media
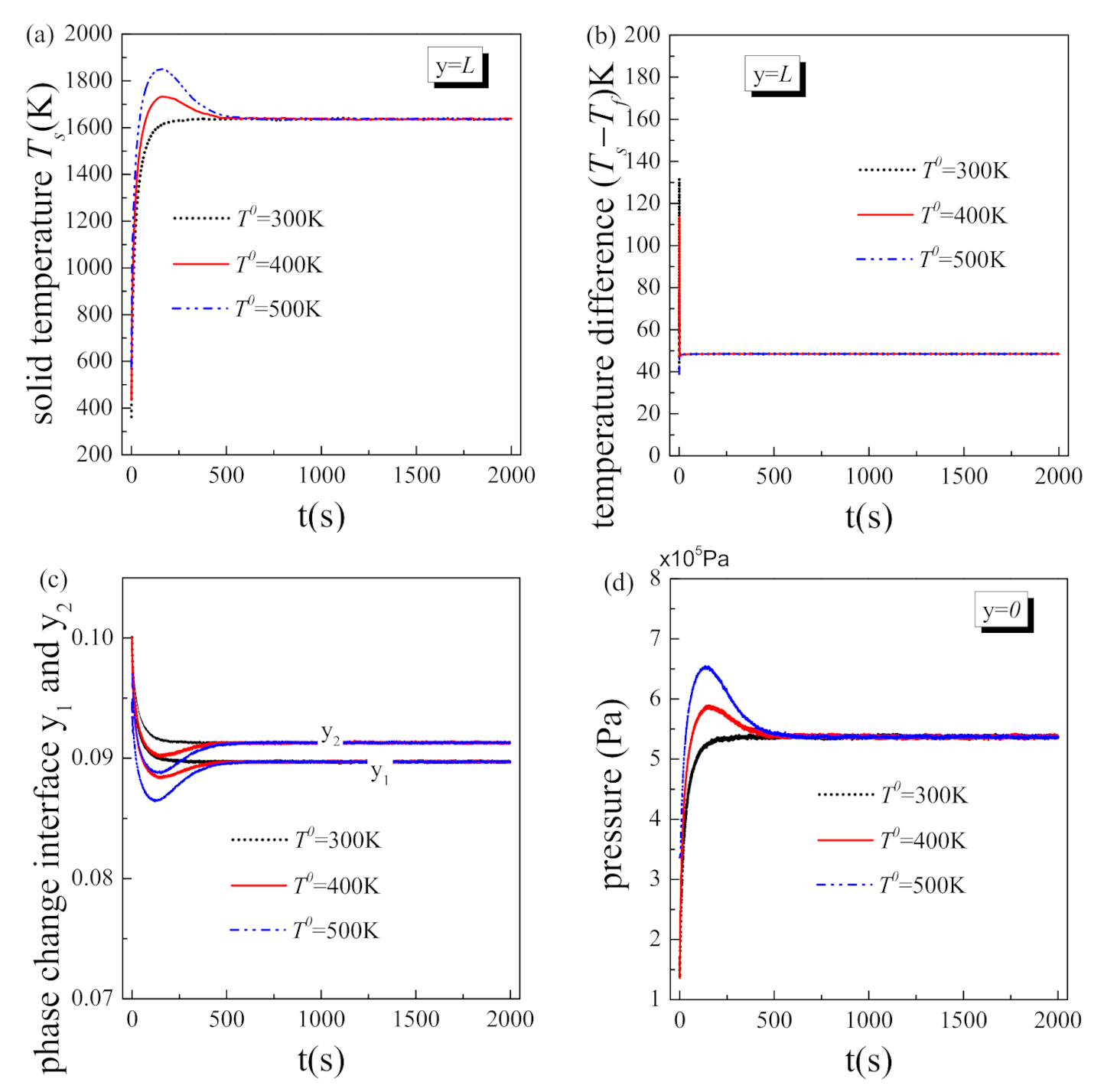
5.2. Effect of Initial Temperature
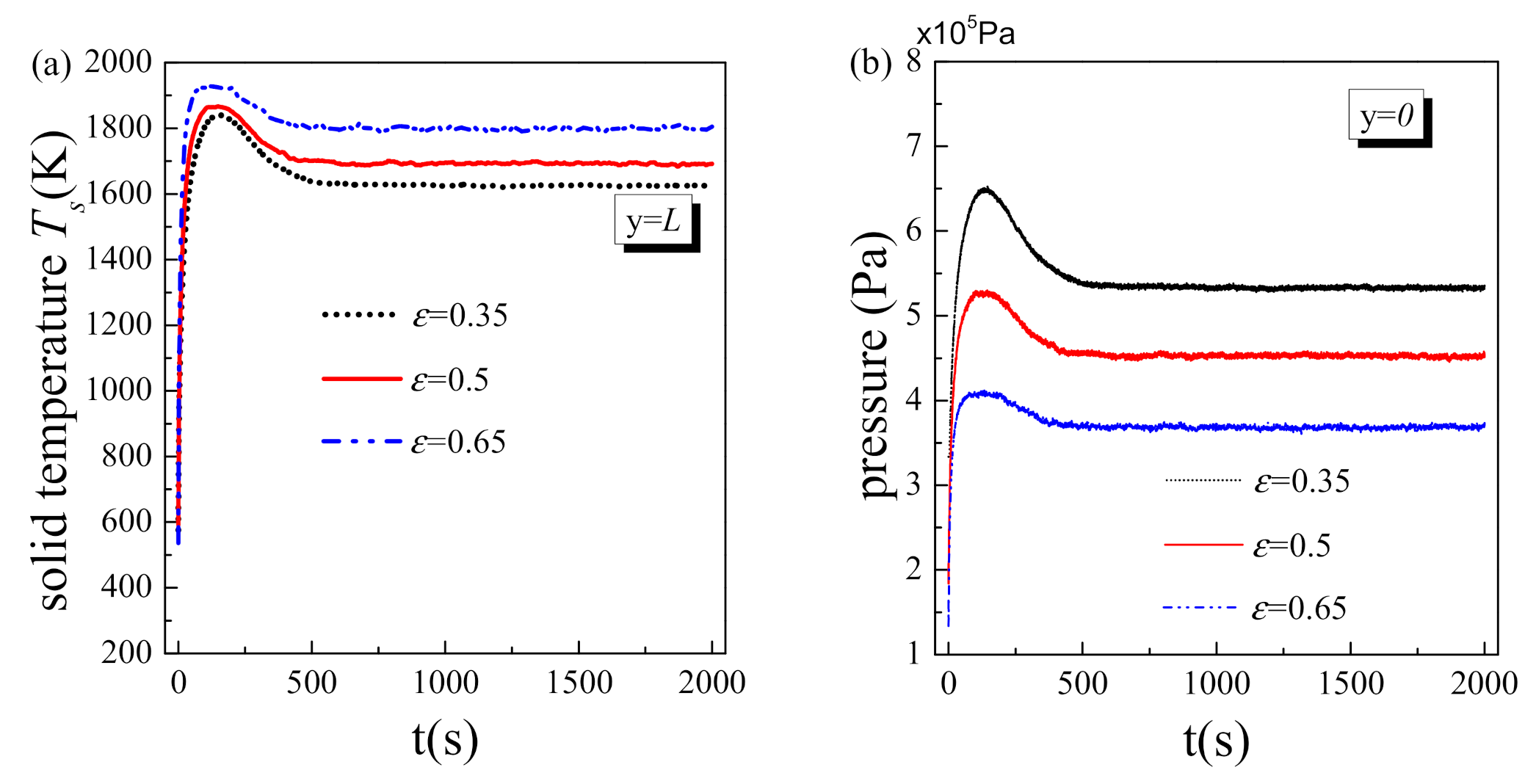
5.3. Effect of Porosity
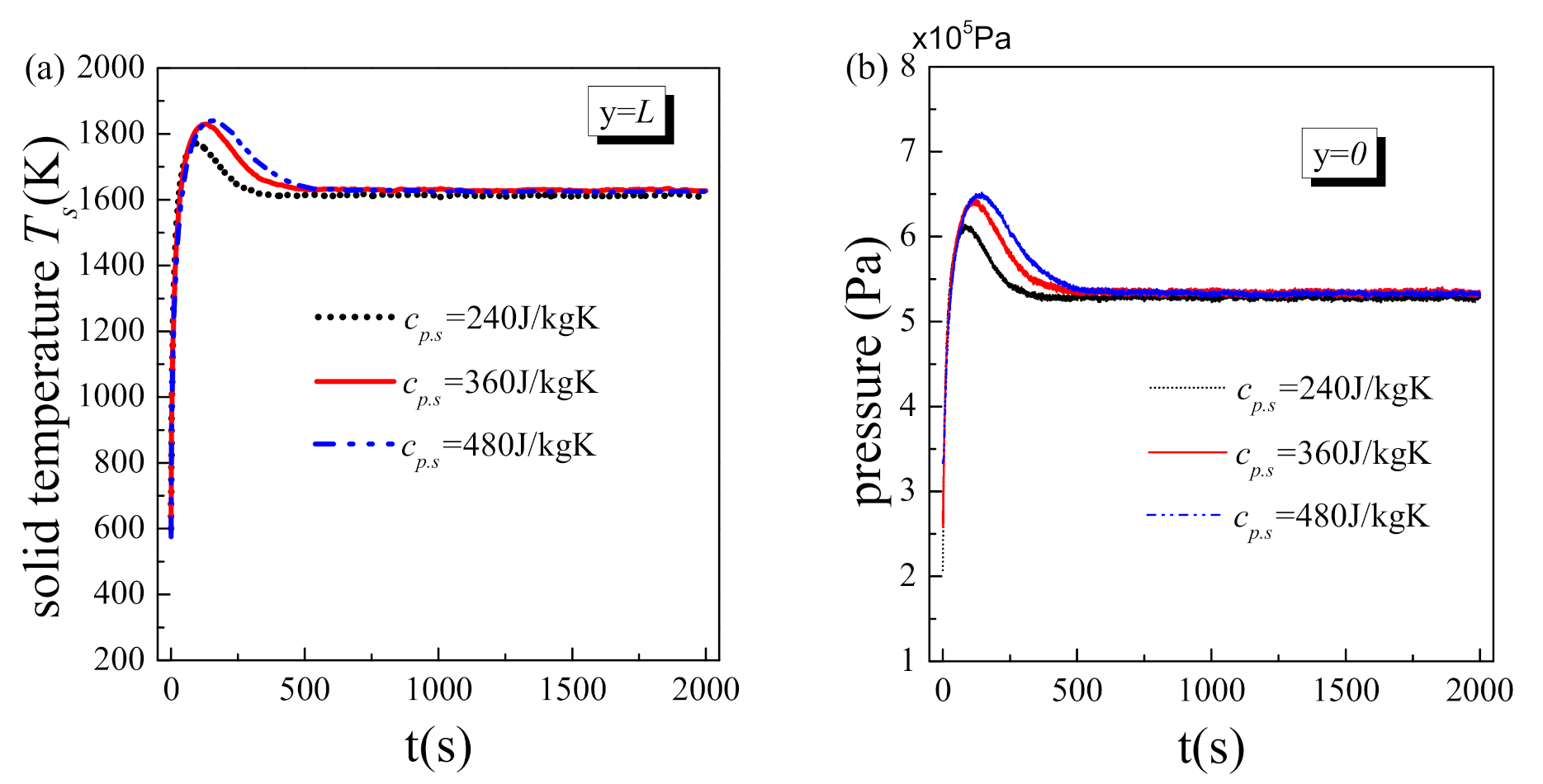
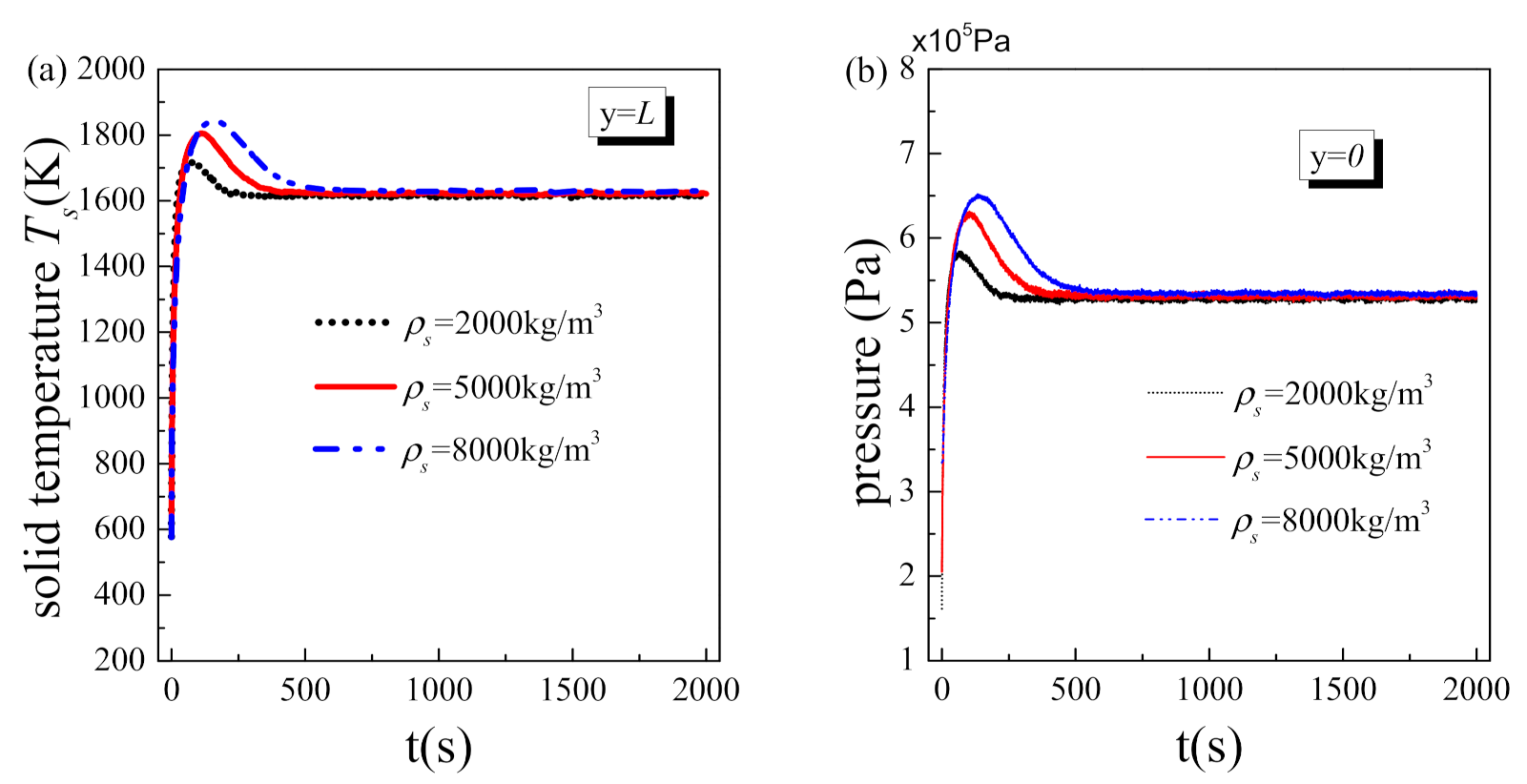
5.4. Effect of Material Properties
6. Conclusions
- (1)
- For the porous matrix with fixed microstructure, when the heat flux on the boundary and the fluid mass flow rate both keep unchanged, the two-phase flow with liquid phase change in porous media will eventually achieve equilibrium, which is known as the steady state. Before reaching steady state, the transient two-phase flow with liquid phase change in porous media goes through an initial stage, in which the physical parameters vary with time significantly;
- (2)
- The system initial temperature has no influence on the steady state of the two-phase flow with liquid phase change in porous media. However, when the initial system temperature is relatively high, distinct transient heat transfer deterioration and vapor block occur in the initial stage, which may cause unexpectedly premature cooling failure and structure ablation;
- (3)
- The porosity not only affects the transient variation of the physical parameter in the initial stage but also changes their steady values. Large porosity design could greatly reduce the fluid-driven force and impair the transient heat transfer deterioration and vapor block, but at the cost of increasing the system temperature;
- (4)
- As the heat capacity and the density of the solid material increases, the system spends more time reaching a steady state, and the transient heat transfer deterioration and vapor block effect in the initial stage are severer. Therefore, porous matrix made of a material with low heat capacity and density could reduce the transient heat transfer deterioration and the transient vapor block effect without affecting the steady state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| cp | specific heat, J∙kg−1∙K−1 |
| dp | particle diameter, m |
| g | gravity vector |
| h | heat transfer coefficient, W∙m−2∙K−1; or specific enthalpy, J∙kg−1 |
| hlv | latent heat of evaporation, J∙kg−1 |
| K | permeability, m2 |
| k | thermal conductivity, W∙m−1∙K−1 |
| L | length of the porous matrix, m |
| m | mass flow rate per unit area, kg∙m−2∙s−1 |
| m’ | interfacial mass transfer rate, kg∙m−3∙s−1 |
| p | pressure, Pa |
| q | heat flux, W∙m−2 |
| Rg | gas constant of air, J∙kg−1∙K−1 |
| s | liquid saturation |
| T | temperature, K |
| u | velocity vector |
| u, v | velocity components along x and y axes, m/s |
| x, y | Cartesian coordinate, m |
| Greek Symbols | |
| 𝜀 | porosity |
| μ | dynamic viscosity, N∙s∙m−2 |
| ρ | density, kg∙m−3 |
| σ | interfacial tension, N∙m−1 |
| Subscripts | |
| 0 | reference |
| c | coolant |
| eff | effective |
| i, f | fluid in a different region |
| l, v | liquid, vapor |
| s | solid |
| sat | saturated state |
| sf | fluid to solid |
| Superscripts | |
| 0 | initial |
References
- Tambue, A.; Berre, I.; Nordbotten, J.M. Efficient simulation of geothermal processes in heterogeneous porous media based on the exponential Rosenbrock-Euler and Rosenbrock-type Methods. Adv. Water Resour. 2013, 53, 250–262. [Google Scholar] [CrossRef]
- Khan, M.S.; Zou, R.; Yu, A. Computational simulation of air-side heat transfer and pressure drop performance in staggered mannered twisted oval tube bundle operating in crossflow. Int. J. Therm. Sci. 2020, 106748. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Z.R.; Jiao, K.; Du, Q. Sensitivity analysis of uncertain parameters based on an improved proton exchange membrane fuel analytical model. Energy Convers. Manag. 2018, 164, 639–654. [Google Scholar] [CrossRef]
- Zhang, S.Z.; Chen, B.; Shu, P.; Luo, M.J.; Xie, C.J.; Quan, S.H.; Tu, Z.K.; Yu, Y. Evaluation of performance enhancement by condensing the anode moisture in a proton exchange membrane fuel cell stack. Appl. Therm. Eng. 2017, 120, 115–120. [Google Scholar] [CrossRef]
- Bennai, F.; Abahri, K.; Belarbi, R.; Tahakourt, A. Periodic homogenization for heat, air, and moisture transfer of porous building materials. Numer. Heat Transf. Part B Fundam. 2016, 70, 420–440. [Google Scholar] [CrossRef]
- Bae, J.; Lee, S.Y.; Kim, S.J. Numerical investigation of effect of film dynamics on fluid motion and thermal performance in pulsating heat pipes. Energy Convers. Manag. 2017, 151, 296–310. [Google Scholar] [CrossRef]
- van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Wei, T. All-in-one design integrates microfluidic cooling into electronic chips. Nature 2020, 585, 188–189. [Google Scholar] [CrossRef]
- Fan, J.C.; Wu, H.A.; Wang, F.C. Evaporation-driven liquid flow through nanochannels. Phys. Fluids 2020, 32, 012001. [Google Scholar]
- Zhang, B.; Huang, H.; Lu, X.; Peng, J. Experimental investigation on transpiration cooling for porous ceramic with liquid water. Acta Astronaut. 2020, 167, 117–121. [Google Scholar] [CrossRef]
- Strauss, F.; Wößner, M.; Weißwange, M.; Manfletti, C.; Schlechtriem, S. Experiments on flow interaction in a transpiration cooled model scramjet. In Proceedings of the 7th European Conference for Aeronautics and Space Science, Mailand, Italy, 3–6 June 2017. [Google Scholar]
- Wu, N.; Wang, J.H.; He, F.; Chen, L.; Ai, B.C. Optimization transpiration cooling of nose cone with non-uniform permeability. Int. J. Heat Mass Transf. 2018, 127, 882–891. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, D.; Zhou, L.; Li, Z.; He, X. Experimental investigation on the distribution characteristics of bubble contact areas in the narrow channel. Int. J. Heat Mass Transf. 2019, 137, 876–881. [Google Scholar] [CrossRef]
- Huang, G.; Liao, Z.; Xu, R.; Zhu, Y.; Jiang, P.X. Self-pumping transpiration cooling with phase change for sintered porous plates. Appl. Therm. Eng. 2019, 159, 113870. [Google Scholar] [CrossRef]
- Bau, H.H.; Torrance, K. Boiling in low-permeability porous materials. Int. J. Heat Mass Transf. 1982, 25, 45–55. [Google Scholar] [CrossRef]
- He, F.; Wang, J.H.; Dong, W.J.; Wu, N. Model comparison, thermal nonequilibrium characteristic and boundary conditions discussion of two-phase flow with phase change in porous media. Numer. Heat Transf. Part B Fundam. 2019, 76, 88–105. [Google Scholar] [CrossRef]
- Wang, C.Y.; Beckermann, C. A two-phase mixture model of liquid-gas flow and heat transfer in capillary porous media- I. Formulation. Int. J. Heat Mass Transf. 1993, 36, 2747–2758. [Google Scholar]
- Shi, J.X.; Wang, J.H. A numerical investigation of transpiration cooling with liquid coolant phase change. Transp. Porous Media 2011, 87, 703–716. [Google Scholar] [CrossRef]
- Dong, W.J.; Wang, J.H. A new model and its application to investigate transpiration cooling with liquid coolant phase change. Transp. Porous Media 2018, 122, 575–593. [Google Scholar] [CrossRef]
- He, F.; Wang, J.H.; Xu, L.C.; Wang, X. Modeling and simulation of transpiration cooling with phase change. Appl. Therm. Eng. 2013, 58, 173–180. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mendes, M.A.; Trimis, D.; Ray, S. Simulation of complete liquid-vapour phase change process inside porous evaporator using local thermal non-equilibrium model. Int. J. Therm. Sci. 2015, 94, 228–241. [Google Scholar] [CrossRef]
- Ray, S.; Alomar, O.R. Simulation of liquid-vapour phase change process inside porous media using modified enthalpy formulation. Int. J. Therm. Sci. 2016, 105, 123–136. [Google Scholar] [CrossRef]
- Xin, C.; Rao, Z.; You, X.; Song, Z.; Han, D. Numerical investigation of vapor–liquid heat and mass transfer in porous media. Energy Convers. Manag. 2014, 78, 1–7. [Google Scholar] [CrossRef]
- Su, H.; He, F.; Wang, J.H.; Wu, N.; Yao, R.; Han, H.; Chu, M. Numerical investigation on the characteristics of coolant flow, heat absorption and phase change in transpiration cooling process. Int. J. Therm. Sci. 2019, 142, 68–76. [Google Scholar] [CrossRef]
- Alomar, O.R.; Mendes, M.A.; Trimis, D.; Ray, S. Numerical simulation of complete liquid-vapour phase change process inside porous media: A comparison between local thermal equilibrium and non-equilibrium models. Int. J. Therm. Sci. 2017, 112, 222–241. [Google Scholar] [CrossRef]
- Xiao, X.; Zhao, G.; Zhou, W. Numerical investigation of transpiration cooling for porous nose cone with liquid coolant. Int. J. Heat Mass Transf. 2018, 121, 1297–1306. [Google Scholar] [CrossRef]
- He, F.; Dong, W.J.; Wang, J.H.; Zhou, J.; Tang, L. Transient model and its application to investigate the injection mode and periodical operation of transpiration cooling with liquid coolant phase change. Appl. Therm. Eng. 2020, 181, 115956. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Y.; Liao, Z.; Ouyang, X.L.; Jiang, P.X. Experimental investigation of transpiration cooling with phase change for sintered porous plates. Int. J. Heat Mass Transf. 2017, 114, 1201–1213. [Google Scholar] [CrossRef]
- Luan, Y.; He, F.; Wang, J.H.; Wu, Y.D.; Zhu, G.S. An experimental investigation on instability of transpiration cooling with phase change. Int. J. Therm. Sci. 2020, 156, 106498. [Google Scholar] [CrossRef]
- Reza-E-Rabbi, S.; Arifuzzaman, S.M.; Sarkar, T.; Khan, M.S.; Ahmmed, S.F. Explicit finite difference analysis of an unsteady MHD flow of a chemically reacting Casson fluid past a stretching sheet with Brownian motion and thermophoresis effects. J. King Saud Univ. Sci. 2020, 32, 690–701. [Google Scholar] [CrossRef]
- Arifuzzaman, S.M.; Khan, M.S.; Al-Mamum, A.; Reza-E-Rabbi, S.; Biswas, P.; Karim, I. Hydrodynamic stability and heat and mass transfer flow analysis of MHD radiative fourth-grade fluid through porous plate with chemical reaction. J. King Saud Univ. Sci. 2019, 31, 1388–1398. [Google Scholar] [CrossRef]
- Hu, H.; Jiang, P.; Ouyang, X.; Zhao, C.; Xu, R. A modified energy equation model for flow boiling in porous media and its application to transpiration cooling at low pressures with transient effect. Int. J. Heat Mass Transf. 2020, 158, 119745. [Google Scholar] [CrossRef]

| Capillary pressure | |
| Relative permeability | |
| Effective thermal conductivity | |
| Fluid-to-solid heat transfer coefficient | |
| Specific surface | |
| Convective heat transfer of fluid-to-solid in pores | In the single-phase regions: In two-phase regions: |
| Specific enthalpy |
| Property (Units) | Liquid | Vapor |
|---|---|---|
| Density (kg∙m−3) | 957.85 | Ideal gas law |
| Specific heat (J∙kg−1∙K−1) | 4217 | 2029 |
| Thermal conductivity (10−3 W∙m−1∙K−1) | 680 | |
| Prandtl number | 0.984 | |
| Dynamic viscosity (10−6 N∙s∙m−2) | ||
| Specific enthalpy at T0 = 373.15 K, p0 = 1 atm(106 J∙kg−1) | 2.676 | 0.419 |
| Latent heat (106 J∙kg−1) | 2.257 | |
| Heat flux at the hot side (W m−2) | q = 1.5 × 106 |
| Liquid water mass flow rate (kg m−2 s−1) | m = 0.3 |
| Thickness of porous media (m) | L = 0.1 |
| Porosity | ε = 0.35 |
| Thermal conductivity of solid (W m−1 K−1) | ks = 13.4 |
| Particle diameter (m) | dp = 5 × 10−5 |
| Heat transfer coefficient at the cold side (W m−2 K−1) | hc = 31.4 |
| Liquid water temperature at the cold side (K) | Tc = 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Dong, W.; Wang, J. Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media. Nanomaterials 2021, 11, 183. https://doi.org/10.3390/nano11010183
He F, Dong W, Wang J. Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media. Nanomaterials. 2021; 11(1):183. https://doi.org/10.3390/nano11010183
Chicago/Turabian StyleHe, Fei, Wenjie Dong, and Jianhua Wang. 2021. "Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media" Nanomaterials 11, no. 1: 183. https://doi.org/10.3390/nano11010183
APA StyleHe, F., Dong, W., & Wang, J. (2021). Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media. Nanomaterials, 11(1), 183. https://doi.org/10.3390/nano11010183




