Friedel Oscillations Induced by Magnetic Skyrmions: From Scattering Properties to All-Electrical Detection
Abstract
:1. Introduction
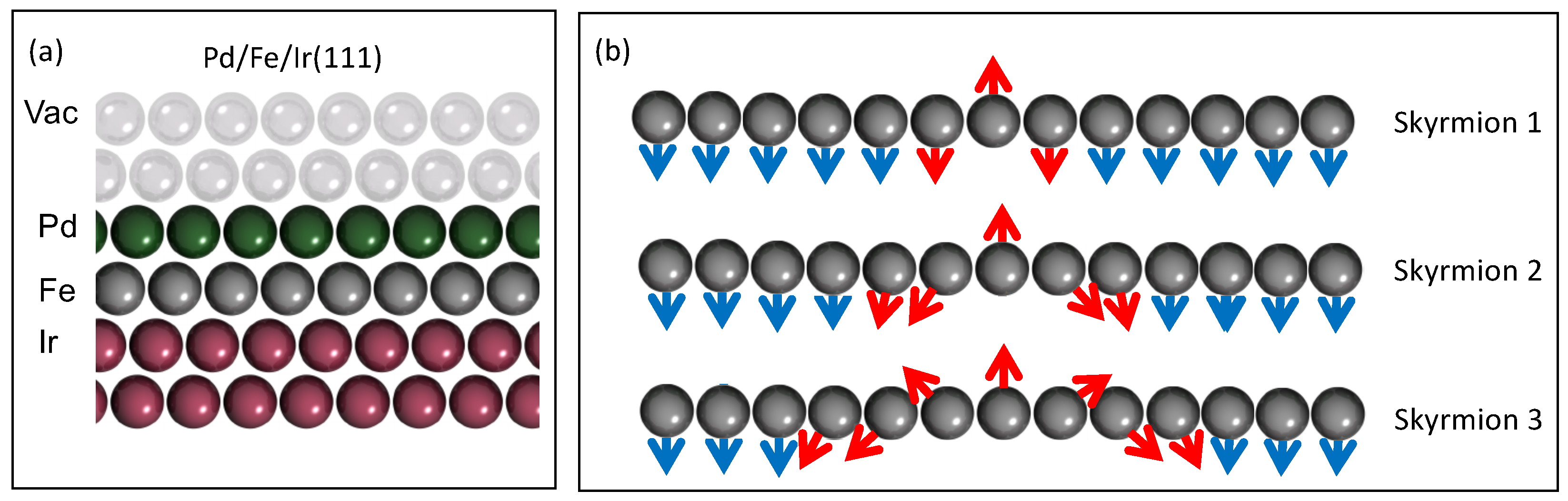
2. Materials and Methods
3. Results and Discussion
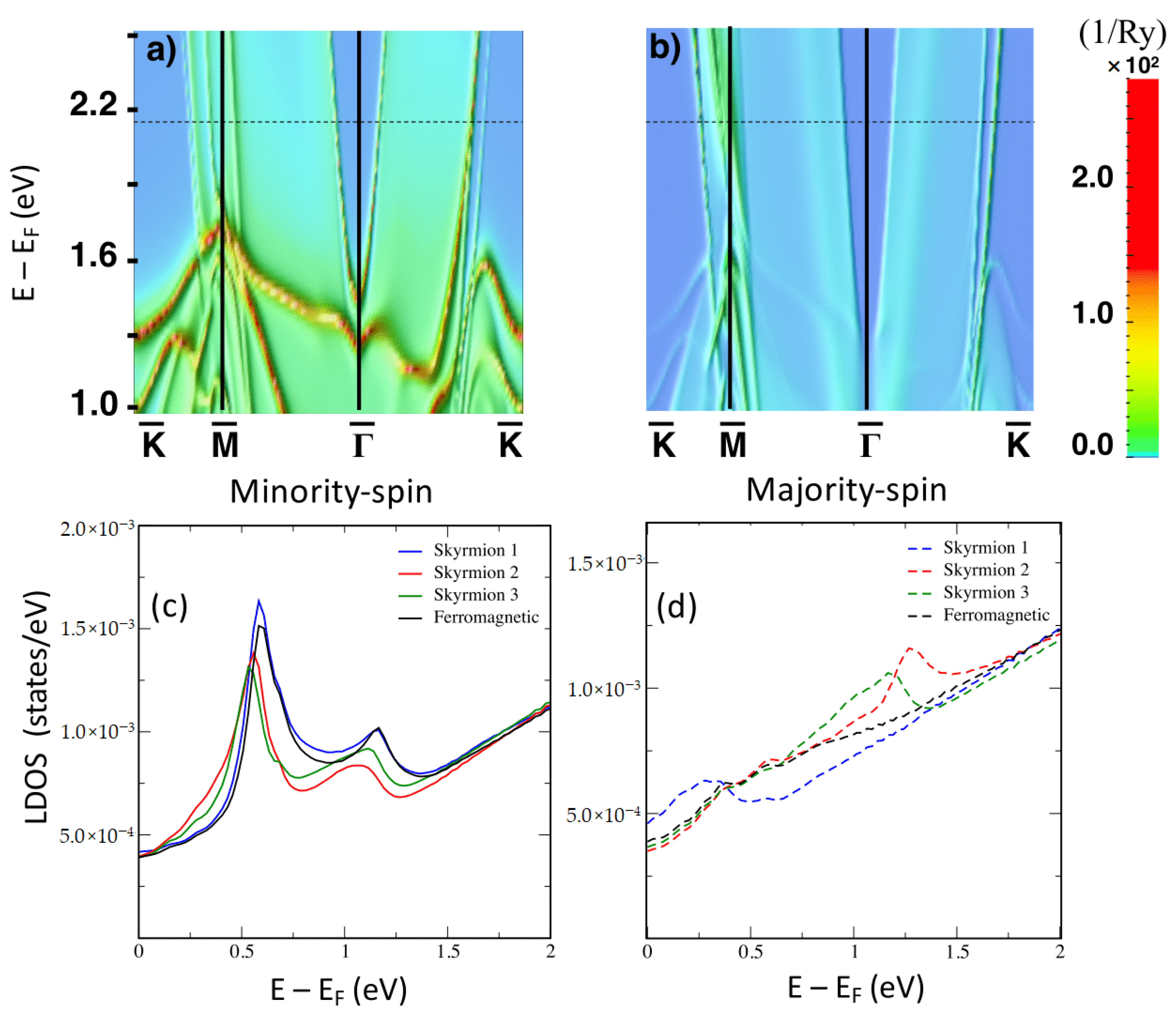
3.1. Interface State
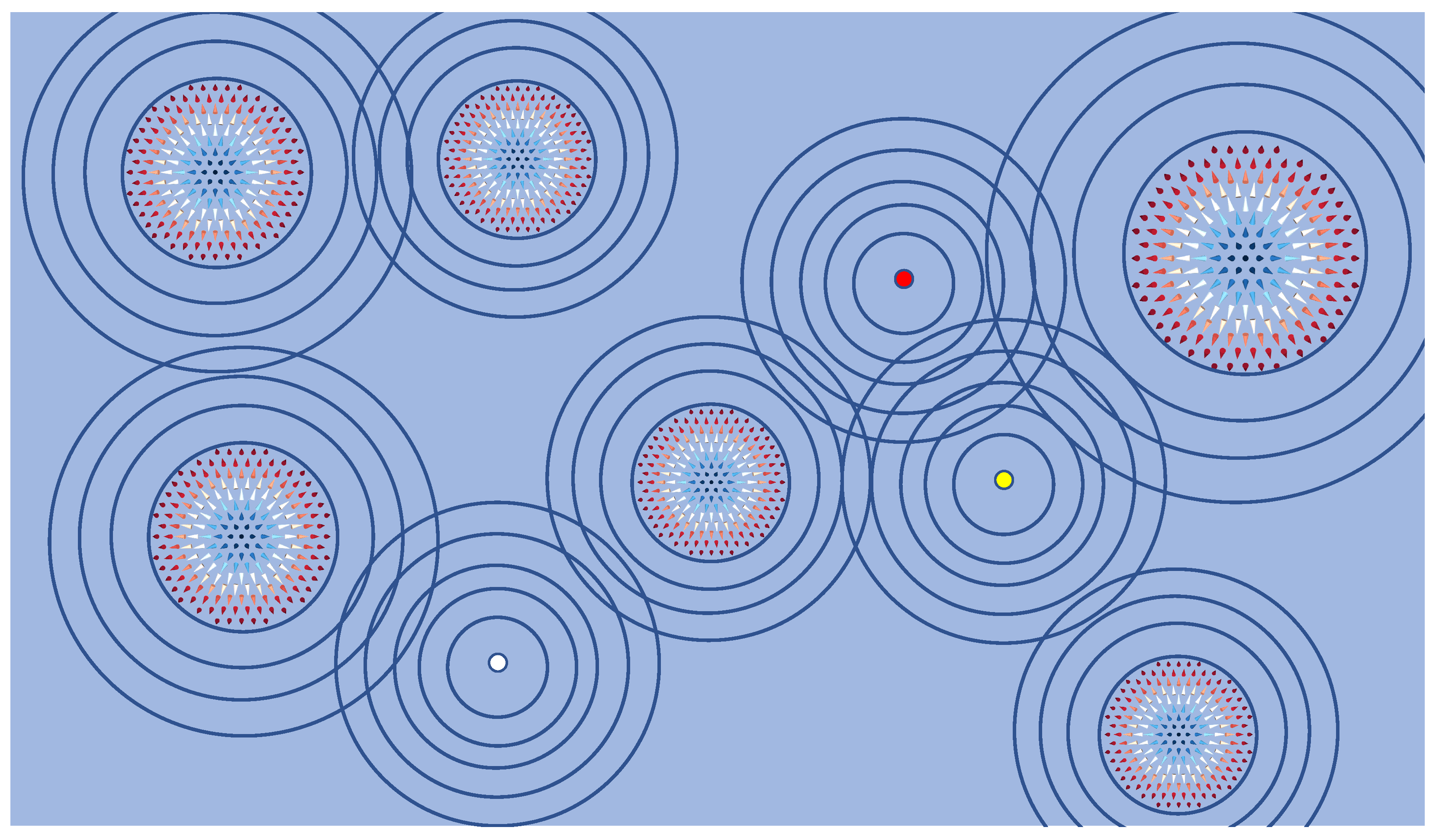
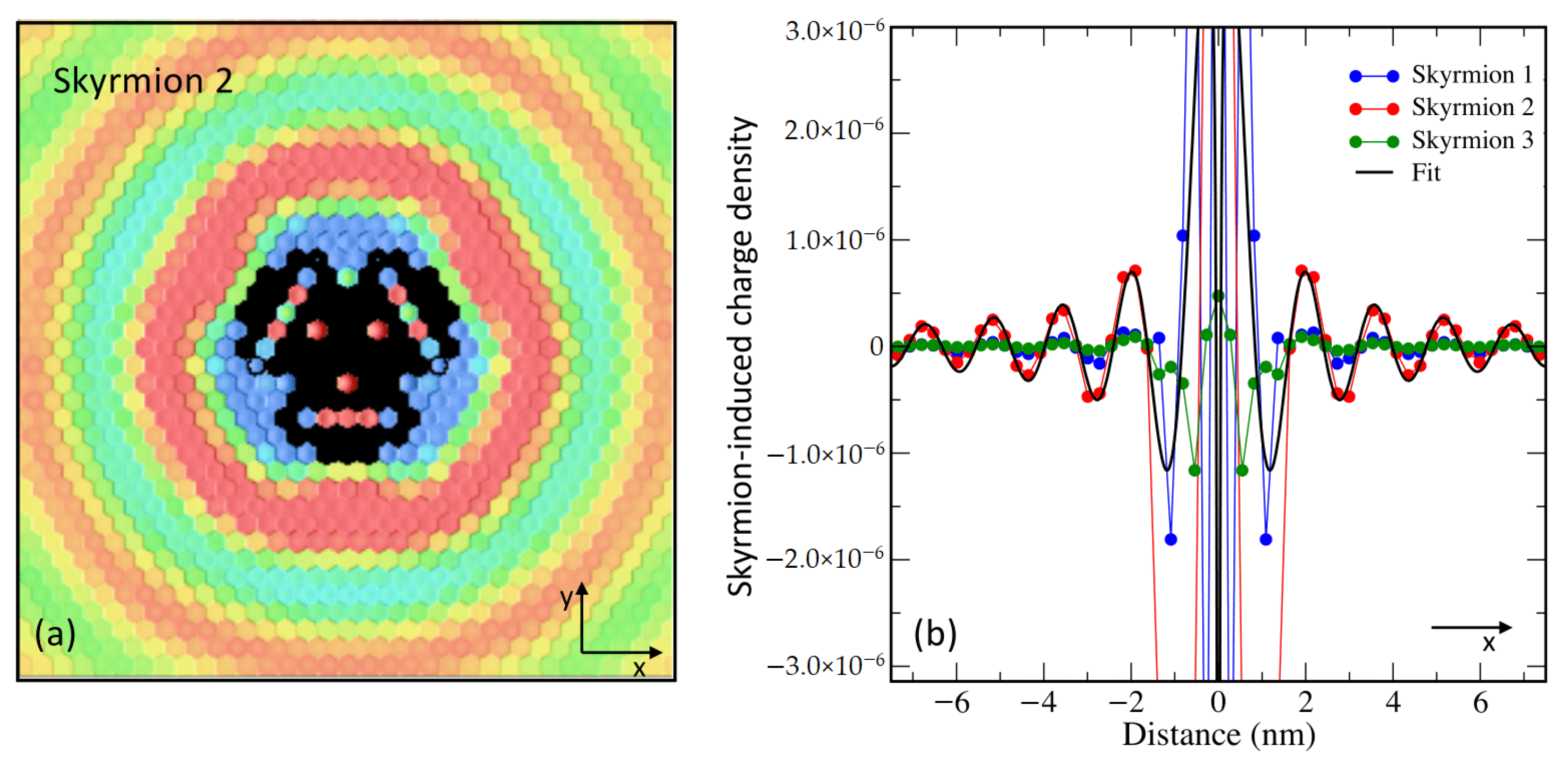
3.2. Skyrmion-Induced Friedel Oscillations Induced in PdFe Bilayer on Ir(111)
3.3. Model for Phase Shifts and Mapping to a Simple-Scattering at an Atomic Defect
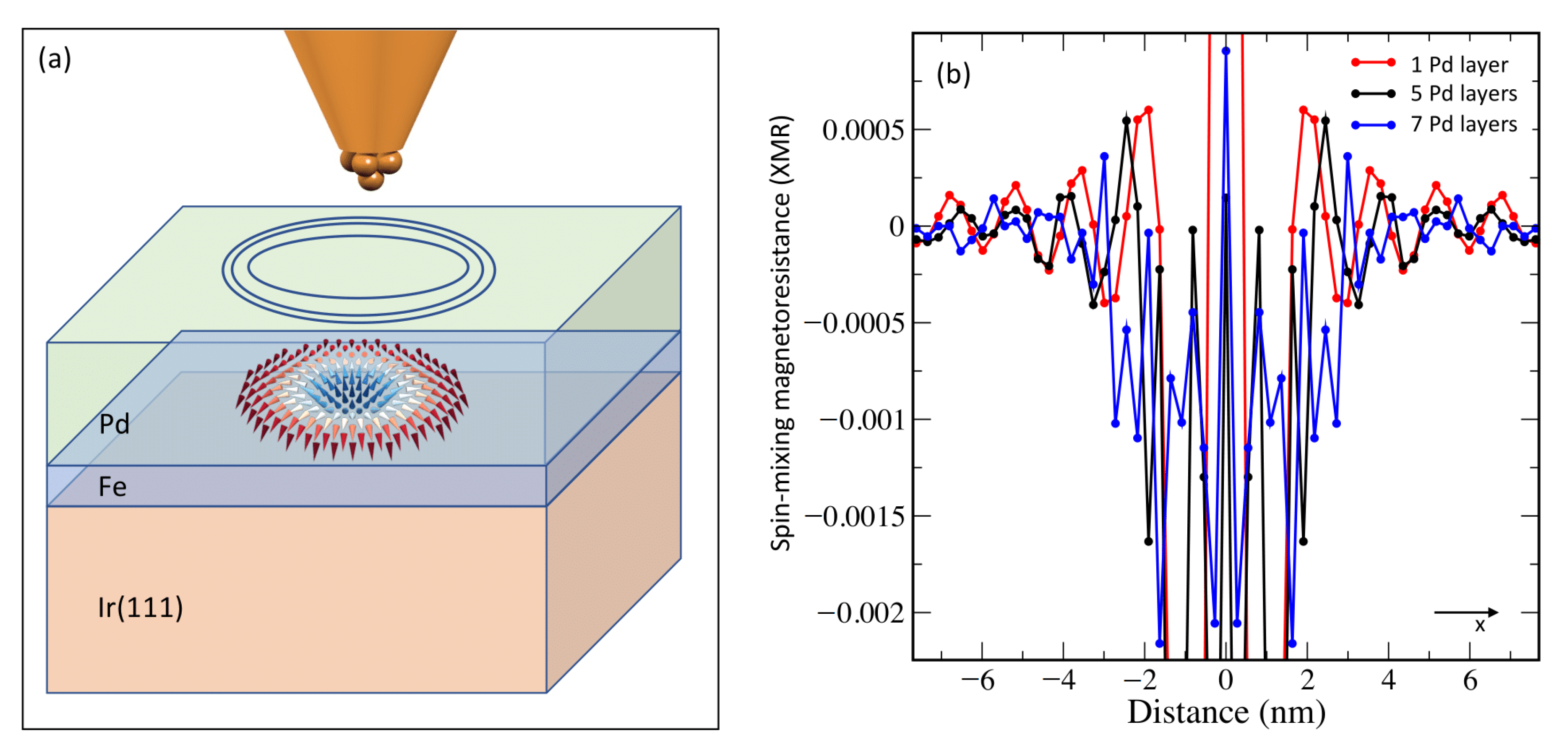
3.4. All-Electrical Detection of Buried Skyrmions via Friedel Oscillations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Multiple-Scattering Expansion for Friedel Oscillations Generated by a Noncollinear Magnetic State
References
- Crommie, M.F.; Lutz, C.P.; Eigler, D.M. Imaging standing waves in a two-dimensional electron gas. Nature 1993, 363, 524–527. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Avouris, P. Direct observation of standing wave formation at surface steps using scanning tunneling spectroscopy. Phys. Rev. Lett. 1993, 71, 1071–1074. [Google Scholar] [CrossRef]
- Crommie, M.F.; Lutz, C.P.; Eigler, D.M. Confinement of Electrons to Quantum Corrals on a Metal Surface. Science 1993, 262, 218–220. [Google Scholar] [CrossRef] [PubMed]
- Silly, F.; Pivetta, M.; Ternes, M.; Patthey, F.m.c.; Pelz, J.P.; Schneider, W.D. Creation of an Atomic Superlattice by Immersing Metallic Adatoms in a Two-Dimensional Electron Sea. Phys. Rev. Lett. 2004, 92, 016101. [Google Scholar] [CrossRef] [PubMed]
- Lounis, S.; Bringer, A.; Blügel, S. Magnetic Adatom Induced Skyrmion-Like Spin Texture in Surface Electron Waves. Phys. Rev. Lett. 2012, 108, 207202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meier, F.; Lounis, S.; Wiebe, J.; Zhou, L.; Heers, S.; Mavropoulos, P.; Dederichs, P.H.; Blügel, S.; Wiesendanger, R. Spin polarization of platinum (111) induced by the proximity to cobalt nanostripes. Phys. Rev. B 2011, 83, 075407. [Google Scholar] [CrossRef] [Green Version]
- Weismann, A.; Wenderoth, M.; Lounis, S.; Zahn, P.; Quaas, N.; Ulbrich, R.G.; Dederichs, P.H.; Blügel, S. Seeing the Fermi Surface in Real Space by Nanoscale Electron Focusing. Science 2009, 323, 1190–1193. [Google Scholar] [CrossRef] [Green Version]
- Lounis, S.; Zahn, P.; Weismann, A.; Wenderoth, M.; Ulbrich, R.G.; Mertig, I.; Dederichs, P.H.; Blügel, S. Theory of real space imaging of Fermi surface parts. Phys. Rev. B 2011, 83, 035427. [Google Scholar] [CrossRef] [Green Version]
- Prüser, H.; Wenderoth, M.; Dargel, P.E.; Weismann, A.; Peters, R.; Pruschke, T.; Ulbrich, R.G. Long-range Kondo signature of a single magnetic impurity. Nat. Phys. 2011, 7, 203–206. [Google Scholar] [CrossRef] [Green Version]
- Prüser, H.; Wenderoth, M.; Weismann, A.; Ulbrich, R.G. Mapping Itinerant Electrons around Kondo Impurities. Phys. Rev. Lett. 2012, 108, 166604. [Google Scholar] [CrossRef] [Green Version]
- Avotina, Y.S.; Kolesnichenko, Y.A.; Otte, A.F.; van Ruitenbeek, J.M. Signature of Fermi-surface anisotropy in point contact conductance in the presence of defects. Phys. Rev. B 2006, 74, 085411. [Google Scholar] [CrossRef] [Green Version]
- Bouhassoune, M.; Zimmermann, B.; Mavropoulos, P.; Wortmann, D.; Dederichs, P.H.; Blügel, S.; Lounis, S. Quantum well states and amplified spin-dependent Friedel oscillations in thin films. Nat. Commun. 2014, 5, 5558. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Rózsa, L.; Schreyer, D.; Simon, E.; Wiesendanger, R. Long-range focusing of magnetic bound states in superconducting lanthanum. Nat. Commun. 2020, 11, 4573. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Wiebe, J.; Lounis, S.; Vedmedenko, E.; Meier, F.; Blügel, S.; Dederichs, P.H.; Wiesendanger, R. Strength and directionality of surface Ruderman–Kittel–Kasuya–Yosida interaction mapped on the atomic scale. Nat. Phys. 2010, 6, 187–191. [Google Scholar] [CrossRef]
- Khajetoorians, A.A.; Wiebe, J.; Chilian, B.; Lounis, S.; Blügel, S.; Wiesendanger, R. Atom-by-atom engineering and magnetometry of tailored nanomagnets. Nat. Phys. 2012, 8, 497–503. [Google Scholar] [CrossRef]
- Ngo, A.T.; Rodriguez-Laguna, J.; Ulloa, S.E.; Kim, E.H. Quantum Manipulation via Atomic-Scale Magnetoelectric Effects. Nano Lett. 2012, 12, 13–16. [Google Scholar] [CrossRef] [Green Version]
- Prüser, H.; Dargel, P.E.; Bouhassoune, M.; Ulbrich, R.G.; Pruschke, T.; Lounis, S.; Wenderoth, M. Interplay between the Kondo effect and the Ruderman–Kittel–Kasuya–Yosida interaction. Nat. Commun. 2014, 5, 5417. [Google Scholar] [CrossRef]
- Khajetoorians, A.A.; Steinbrecher, M.; Ternes, M.; Bouhassoune, M.; dos Santos Dias, M.; Lounis, S.; Wiebe, J.; Wiesendanger, R. Tailoring the chiral magnetic interaction between two individual atoms. Nat. Commun. 2016, 7, 10620. [Google Scholar] [CrossRef] [Green Version]
- Bouaziz, J.; Ibañez Azpiroz, J.; Guimarães, F.S.M.; Lounis, S. Zero-point magnetic exchange interactions. Phys. Rev. Res. 2020, 2, 043357. [Google Scholar] [CrossRef]
- Stepanyuk, V.S.; Negulyaev, N.N.; Niebergall, L.; Bruno, P. Effect of quantum confinement of surface electrons on adatom–adatom interactions. New J. Phys. 2007, 9, 388. [Google Scholar] [CrossRef]
- Brovko, O.O.; Ignatiev, P.A.; Stepanyuk, V.S.; Bruno, P. Tailoring Exchange Interactions in Engineered Nanostructures: An Ab Initio Study. Phys. Rev. Lett. 2008, 101, 036809. [Google Scholar] [CrossRef] [Green Version]
- Bogdanov, A.N.; Yablonskii, D. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Zh. Eksp. Teor. Fiz 1989, 95, 178. [Google Scholar]
- Rössler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [Green Version]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotech. 2013, 8, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef] [PubMed]
- Sampaio, J.; Cros, V.; Rohart, S.; Thiaville, A.; Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 2013, 8, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Ezawa, M. A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry. Nat. Commun. 2014, 5, 4652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crum, D.M.; Bouhassoune, M.; Bouaziz, J.; Schweflinghaus, B.; Blügel, S.; Lounis, S. Perpendicular reading of single confined magnetic skyrmions. Nat. Commun. 2015, 6, 8541. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef] [Green Version]
- Yu, G.; Upadhyaya, P.; Li, X.; Li, W.; Kim, S.K.; Fan, Y.; Wong, K.L.; Tserkovnyak, Y.; Amiri, P.K.; Wang, K.L. Room-temperature creation and spin-orbit torque manipulation of skyrmions in thin films with engineered asymmetry. Nano Lett. 2016, 16, 1981–1988. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sanchez, F.; Sampaio, J.; Reyren, N.; Cros, V.; Kim, J. A skyrmion-based spin-torque nano-oscillator. New J. Phys. 2016, 18, 075011. [Google Scholar] [CrossRef]
- Xia, H.; Jin, C.; Song, C.; Wang, J.; Wang, J.; Liu, Q. Control and manipulation of antiferromagnetic skyrmions in racetrack. J. Phys. Appl. Phys. 2017, 50, 505005. [Google Scholar] [CrossRef]
- Fernandes, I.L.; Bouhassoune, M.; Lounis, S. Defect-implantation for the all-electrical detection of non-collinear spin-textures. Nat. Commun. 2020, 11, 1–9. [Google Scholar]
- Li, S.; Kang, W.; Zhang, X.; Nie, T.; Zhou, Y.; Wang, K.L.; Zhao, W. Magnetic skyrmions for unconventional computing. Mater. Horiz. 2021. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic Domain-Wall Racetrack Memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Zhao, X.; Rybakov, F.N.; Borisov, A.B.; Wang, S.; Tang, J.; Jin, C.; Wang, C.; Wei, W.; Kiselev, N.S.; et al. Interaction of Individual Skyrmions in a Nanostructured Cubic Chiral Magnet. Phys. Rev. Lett. 2018, 120, 197203. [Google Scholar] [CrossRef] [Green Version]
- Rózsa, L.; Deák, A.; Simon, E.; Yanes, R.; Udvardi, L.; Szunyogh, L.; Nowak, U. Skyrmions with Attractive Interactions in an Ultrathin Magnetic Film. Phys. Rev. Lett. 2016, 117, 157205. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, I.L.; Chico, J.; Lounis, S. Impurity-dependent gyrotropic motion, deflection and pinning of current-driven ultrasmall skyrmions in PdFe/Ir(111) surface. J. Phys. Condens. Matter 2020, 32, 425802. [Google Scholar] [CrossRef]
- Arjana, I.G.; Lima Fernandes, I.; Chico, J.; Lounis, S. Sub-nanoscale atom-by-atom crafting of skyrmion-defect interaction profiles. Sci. Rep. 2020, 10, 14655. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, W.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based synaptic devices. Nanotechnology 2017, 28, 08LT02. [Google Scholar] [CrossRef]
- Song, K.M.; Jeong, J.S.; Pan, B.; Zhang, X.; Xia, J.; Cha, S.; Park, T.E.; Kim, K.; Finizio, S.; Raabe, J.; et al. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 2020, 3, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based artificial neuron device. Nanotechnology 2017, 28, 31LT01. [Google Scholar] [CrossRef]
- Chen, X.; Kang, W.; Zhu, D.; Zhang, X.; Lei, N.; Zhang, Y.; Zhou, Y.; Zhao, W. A compact skyrmionic leaky–integrate–fire spiking neuron device. Nanoscale 2018, 10, 6139–6146. [Google Scholar] [CrossRef] [PubMed]
- Prychynenko, D.; Sitte, M.; Litzius, K.; Krüger, B.; Bourianoff, G.; Kläui, M.; Sinova, J.; Everschor-Sitte, K. Magnetic Skyrmion as a Nonlinear Resistive Element: A Potential Building Block for Reservoir Computing. Phys. Rev. Appl. 2018, 9, 014034. [Google Scholar] [CrossRef] [Green Version]
- Bourianoff, G.; Pinna, D.; Sitte, M.; Everschor-Sitte, K. Potential implementation of reservoir computing models based on magnetic skyrmions. AIP Adv. 2018, 8, 055602. [Google Scholar] [CrossRef] [Green Version]
- Pinna, D.; Abreu Araujo, F.; Kim, J.V.; Cros, V.; Querlioz, D.; Bessiere, P.; Droulez, J.; Grollier, J. Skyrmion Gas Manipulation for Probabilistic Computing. Phys. Rev. Appl. 2018, 9, 064018. [Google Scholar] [CrossRef] [Green Version]
- Zázvorka, J.; Jakobs, F.; Heinze, D.; Keil, N.; Kromin, S.; Jaiswal, S.; Litzius, K.; Jakob, G.; Virnau, P.; Pinna, D.; et al. Thermal skyrmion diffusion used in a reshuffler device. Nat. Nanotechnol. 2019, 14, 658–661. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Kang, W.; Zhang, Y.; Zhao, W. Thermal Brownian Motion of Skyrmion for True Random Number Generation. IEEE Trans. Electron Devices 2020, 67, 2553–2558. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Zheng, Q.; Zhu, Q.; Liu, X.; Chen, S.; Jin, C.; Liu, Q.; Jia, C.; Xue, D. Current-induced magnetic skyrmions oscillator. New J. Phys. 2015, 17, 023061. [Google Scholar] [CrossRef]
- Finocchio, G.; Ricci, M.; Tomasello, R.; Giordano, A.; Lanuzza, M.; Puliafito, V.; Burrascano, P.; Azzerboni, B.; Carpentieri, M. Skyrmion based microwave detectors and harvesting. Appl. Phys. Lett. 2015, 107, 262401. [Google Scholar] [CrossRef] [Green Version]
- Stróżecka, A.; Eiguren, A.; Pascual, J.I. Quasiparticle Interference around a Magnetic Impurity on a Surface with Strong Spin-Orbit Coupling. Phys. Rev. Lett. 2011, 107, 186805. [Google Scholar] [CrossRef]
- Denisov, K.S.; Rozhansky, I.V.; Averkiev, N.S.; Lähderanta, E. Chiral spin ordering of electron gas in solids with broken time reversal symmetry. Sci. Rep. 2019, 9, 10817. [Google Scholar]
- Wang, C.Z.; Xu, H.Y.; Lai, Y.C. Scattering of Dirac electrons from a skyrmion: Emergence of robust skew scattering. Phys. Rev. Res. 2020, 2, 013247. [Google Scholar] [CrossRef] [Green Version]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and Deleting Single Magnetic Skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romming, N.; Kubetzka, A.; Hanneken, C.; von Bergmann, K.; Wiesendanger, R. Field-Dependent Size and Shape of Single Magnetic Skyrmions. Phys. Rev. Lett. 2015, 114, 177203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solid 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Bouhassoune, M.; Fernandes, I.L.; Blügel, S.; Lounis, S. Unoccupied surface and interface states in Pd thin films deposited on Fe/Ir(111) surface. New J. Phys. 2019, 21, 063015. [Google Scholar] [CrossRef]
- Hanneken, C.; Otte, F.; Kubetzka, A.; Dupé, B.; Romming, N.; Von Bergmann, K.; Wiesendanger, R.; Heinze, S. Electrical detection of magnetic skyrmions by tunnelling non-collinear magnetoresistance. Nat. Nanotechnol. 2015, 10, 1039. [Google Scholar] [CrossRef]
- Bauer, D.S.G. Development of a Relativistic Full-Potential First-Principles Multiple Scattering Green Function Method Applied to Complex Magnetic Textures of Nano Structures at Surfaces. Ph.D. Thesis, RWTH-Aachen, Aachen, Germany, 2013. [Google Scholar]
- Papanikolaou, N.; Zeller, R.; Dederichs, P.H. Conceptual improvements of the KKR method. J. Phys. Condens. Matter 2002, 14, 2799. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Dupé, B.; Hoffmann, M.; Paillard, C.; Heinze, S. Tailoring magnetic skyrmions in ultra-thin transition metal films. Nat. Commun. 2014, 5, 4030. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Moliner, F.; Velasco, V. Theory of incomplete crystals, surfaces, defects, interfaces and layered structures. Prog. Surf. Sci. 1986, 21, 93–162. [Google Scholar] [CrossRef]
- Szunyogh, L.; Újfalussy, B.; Weinberger, P.; Kollár, J. Self-consistent localized KKR scheme for surfaces and interfaces. Phys. Rev. B 1994, 49, 2721–2729. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D.R. Theory and Application for the Scanning Tunneling Microscope. Phys. Rev. Lett. 1983, 50, 1998–2001. [Google Scholar] [CrossRef]
- Palotás, K.; Rózsa, L.; Simon, E.; Szunyogh, L. High-resolution tunneling spin transport characteristics of topologically distinct magnetic skyrmionic textures from theoretical calculations. J. Magn. Magn. Mater. 2021, 519, 167440. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouhassoune, M.; Lounis, S. Friedel Oscillations Induced by Magnetic Skyrmions: From Scattering Properties to All-Electrical Detection. Nanomaterials 2021, 11, 194. https://doi.org/10.3390/nano11010194
Bouhassoune M, Lounis S. Friedel Oscillations Induced by Magnetic Skyrmions: From Scattering Properties to All-Electrical Detection. Nanomaterials. 2021; 11(1):194. https://doi.org/10.3390/nano11010194
Chicago/Turabian StyleBouhassoune, Mohammed, and Samir Lounis. 2021. "Friedel Oscillations Induced by Magnetic Skyrmions: From Scattering Properties to All-Electrical Detection" Nanomaterials 11, no. 1: 194. https://doi.org/10.3390/nano11010194
APA StyleBouhassoune, M., & Lounis, S. (2021). Friedel Oscillations Induced by Magnetic Skyrmions: From Scattering Properties to All-Electrical Detection. Nanomaterials, 11(1), 194. https://doi.org/10.3390/nano11010194




