Investigations of Shape, Material and Excitation Wavelength Effects on Field Enhancement in SERS Advanced Tips
Abstract
1. Introduction
- The signal is produced by the sum of a large number of molecules.
- The resolution is limited to Abbe limit, which is half the wavelength of the incident light.
- The aperture type—using a fiber whose hollow core acts as an aperture for the light;
- The apertureless type—that uses a sharp tip. Near-field scanning optical microscopy (NSOM) is the general term for STM, AFM and even SFM-TERS. While ANSOM (Aperture NSOM) is mainly for fiber-type tips or cantilever tips with a hole at the tip end.
- TERS can be used in scanning probe microscopy (SPM).
- TERS can also be coupled to a scanning tunneling microscope (STM-TERS). In such a case, the enhancement will be produced by the gap mode plasmon between the metallic probe and the metallic substrate [27].
- Raman microscope coupled with atomic force microscope (AFM-TERS), which is widely used in live bio samples [28].
- Shear force microscopy based TERS system (SFM-TERS).
- Near-field scanning optical microscopy (NSOM) based TERS system (NSOM-TERS). Raman signals are collected through the same fiber that delivers the excitation light.
2. Numerical Method: The Finite Element Method (FEM) for PDEs
2.1. Best Known Methods (BKM) Choice and Usage
2.2. Mesh Shapes and Sizes
2.3. Boundary Conditions and Symmetries
3. Analytical Method: Models and Properties of Metallic Nano-Particles
3.1. Analytical Method: Models and Properties of Metallic Nano-Particles
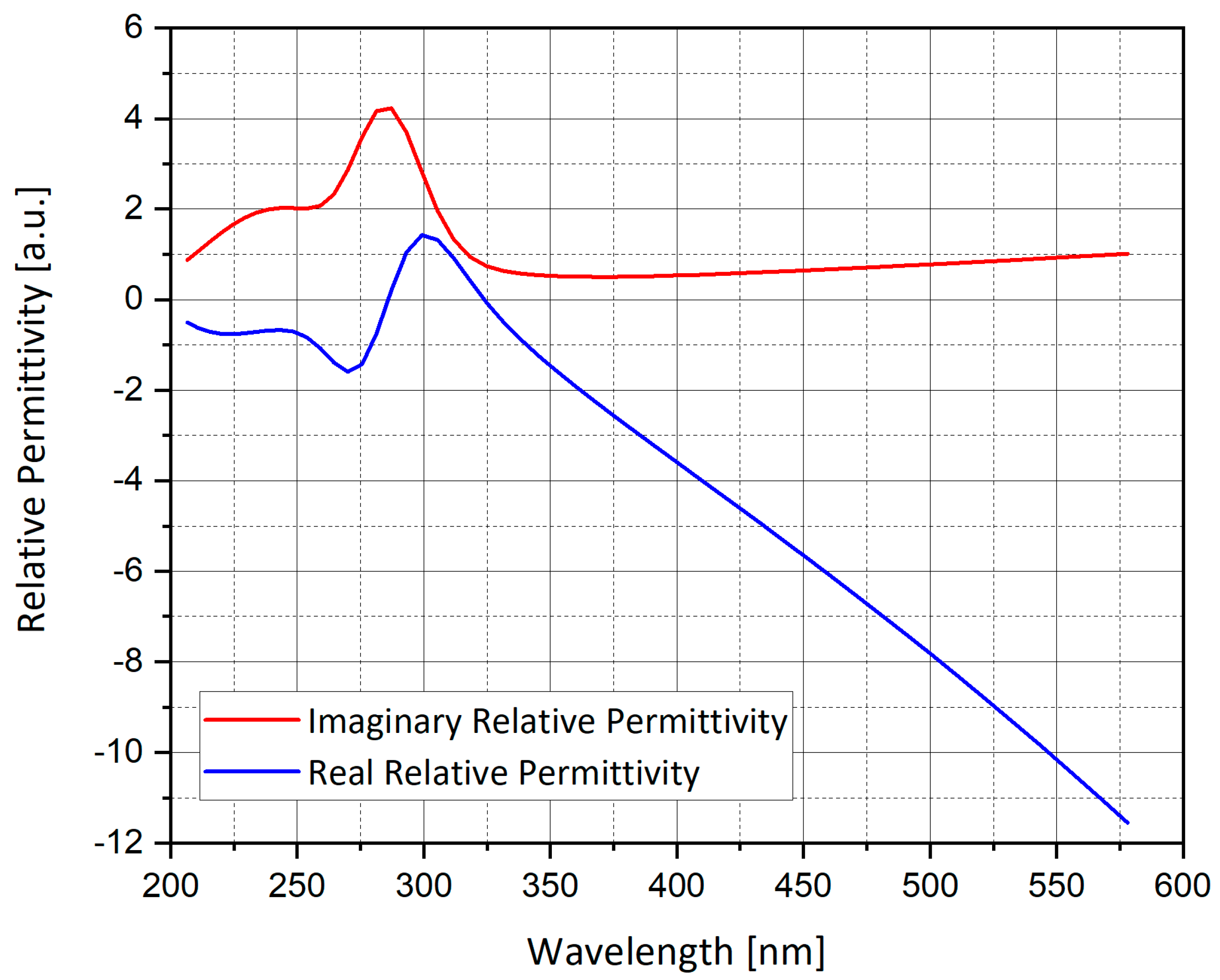
3.2. Electrostatic Approximation and Mie Theory for Metallic Sphere
- is the corrected polarization by Mie theory;
- is the ESA approximation polarization;
- is the wavenumber in the medium;
- is the size of the radius of the sphere.
- The resonant behavior of the individual nano-particle can be studied in terms of quasi-static approximation; therefore, the size of a nano-particle must be smaller than the wavelength of the light source [42]. The electromagnetic field is approximately constant over the particle volume for small nano-particles.
- The nano-particle macroscopic electromagnetic behavior can be related to its polarizability only if the considered particle is homogeneous, and the surrounding material is a homogeneous, isotropic, and non-absorbing medium.
3.3. Analytical Models of Prolate Spheroid Nano-Particles
4. Simulation Results
4.1. Field Enhancement Factor (FFF)
4.2. Parameters, Operators and Variables
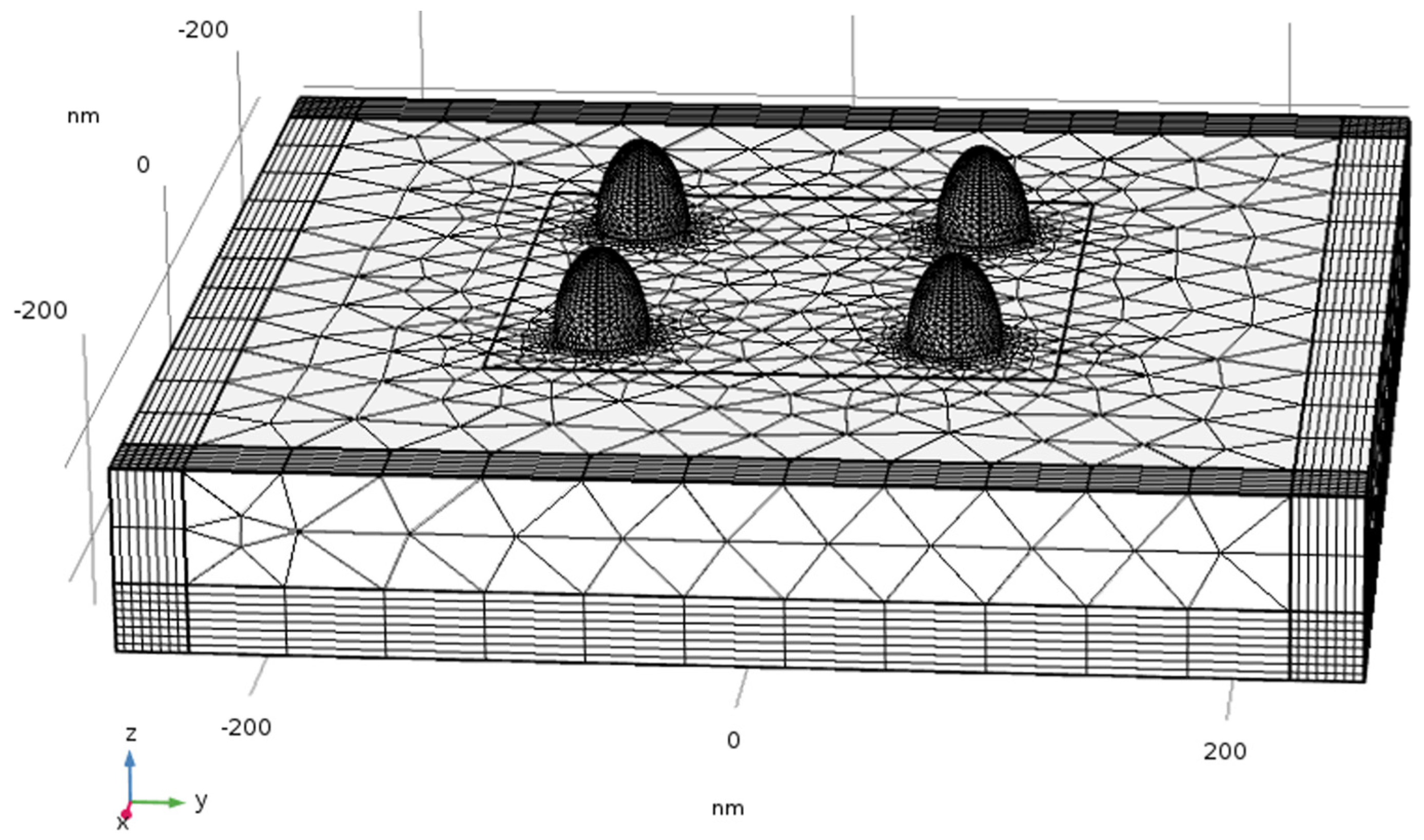
4.3. Geometric Structures, Physics Definitions, Materials and Mesh
4.4. Solvers and Studies
4.5. Hemi-Sphere Geometry Results
4.6. Cavity Geometry Results
4.7. Hemi-Spheroid Geometry Results
4.8. Nano-Cone Geometry Results
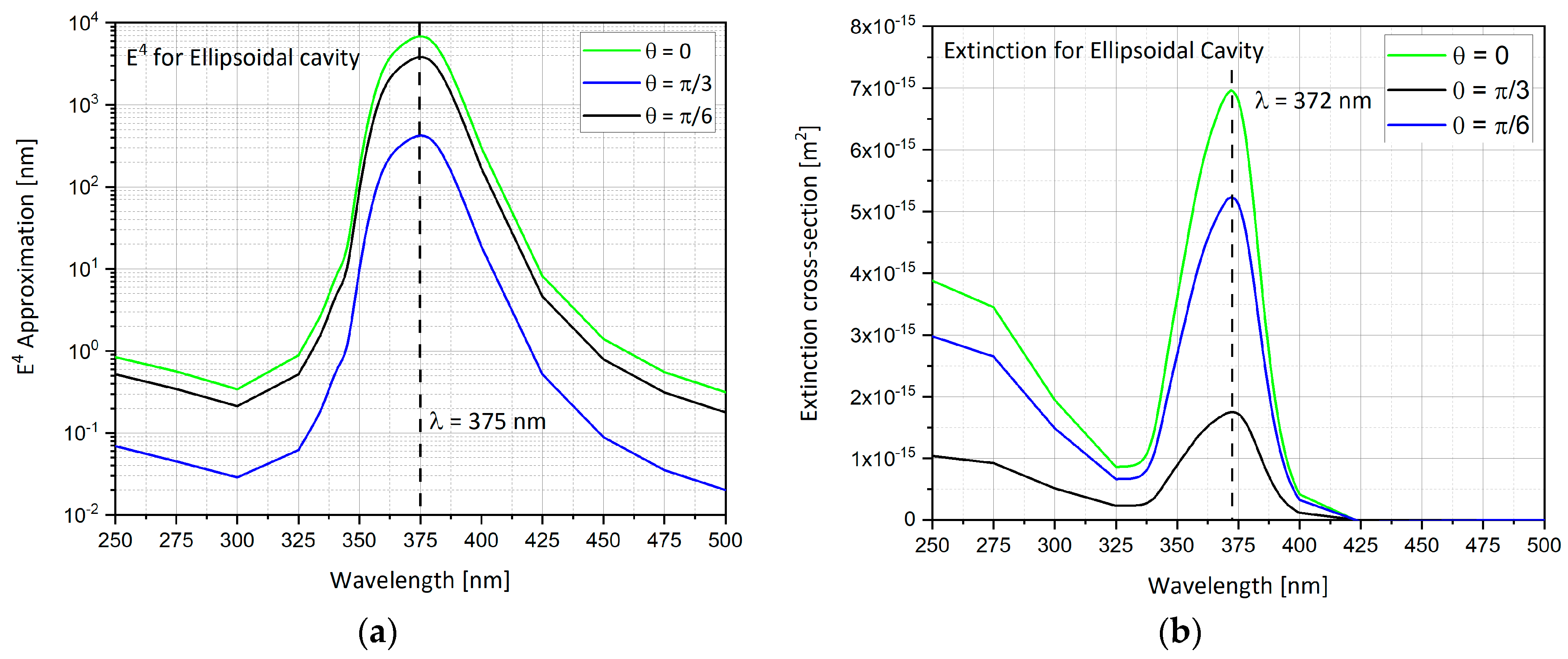
4.9. Ellipsoidal Cavity Geometry Results
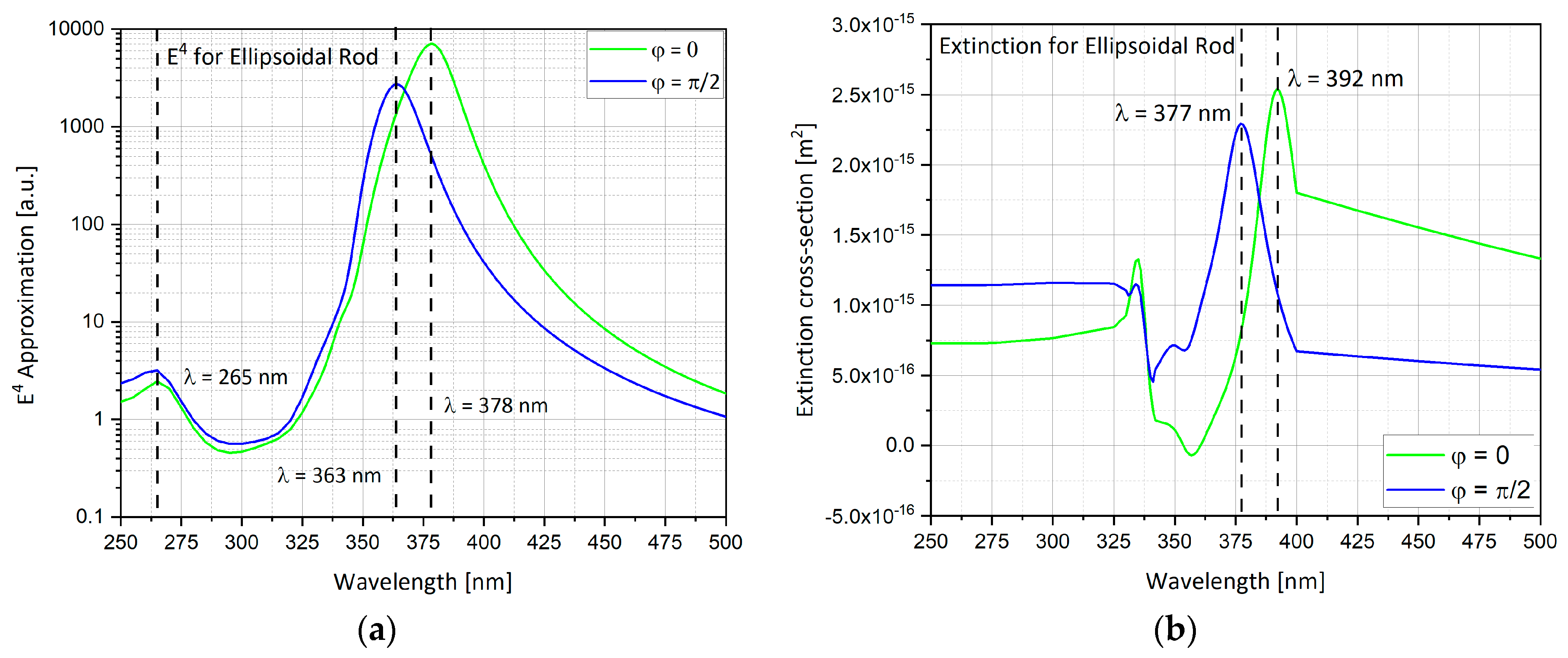
4.10. Ellipsoidal Rod Geometry Results
4.11. Double Nano-Cone Geometry Results
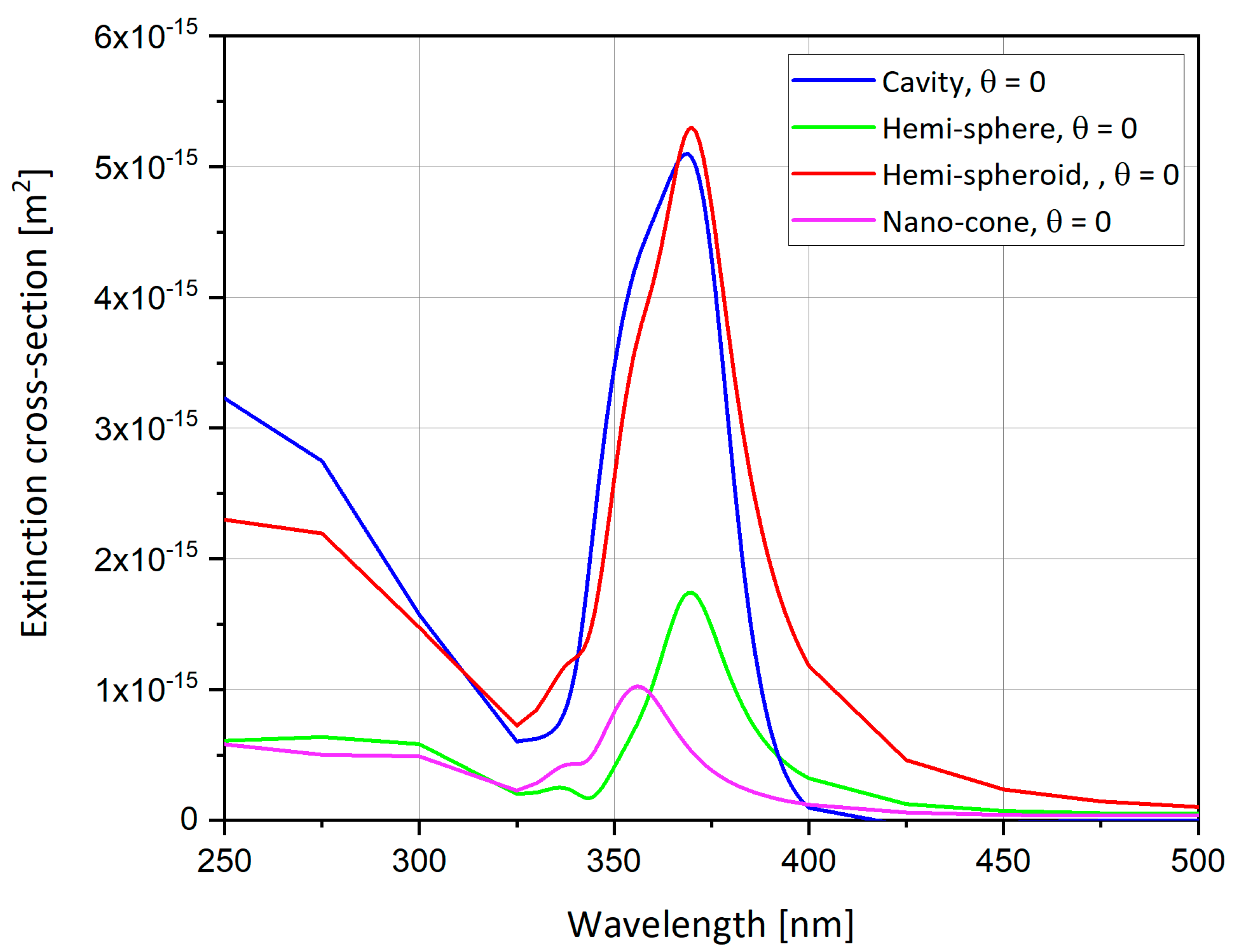
4.12. Results Comparison between Different Nano-Particles Geometries
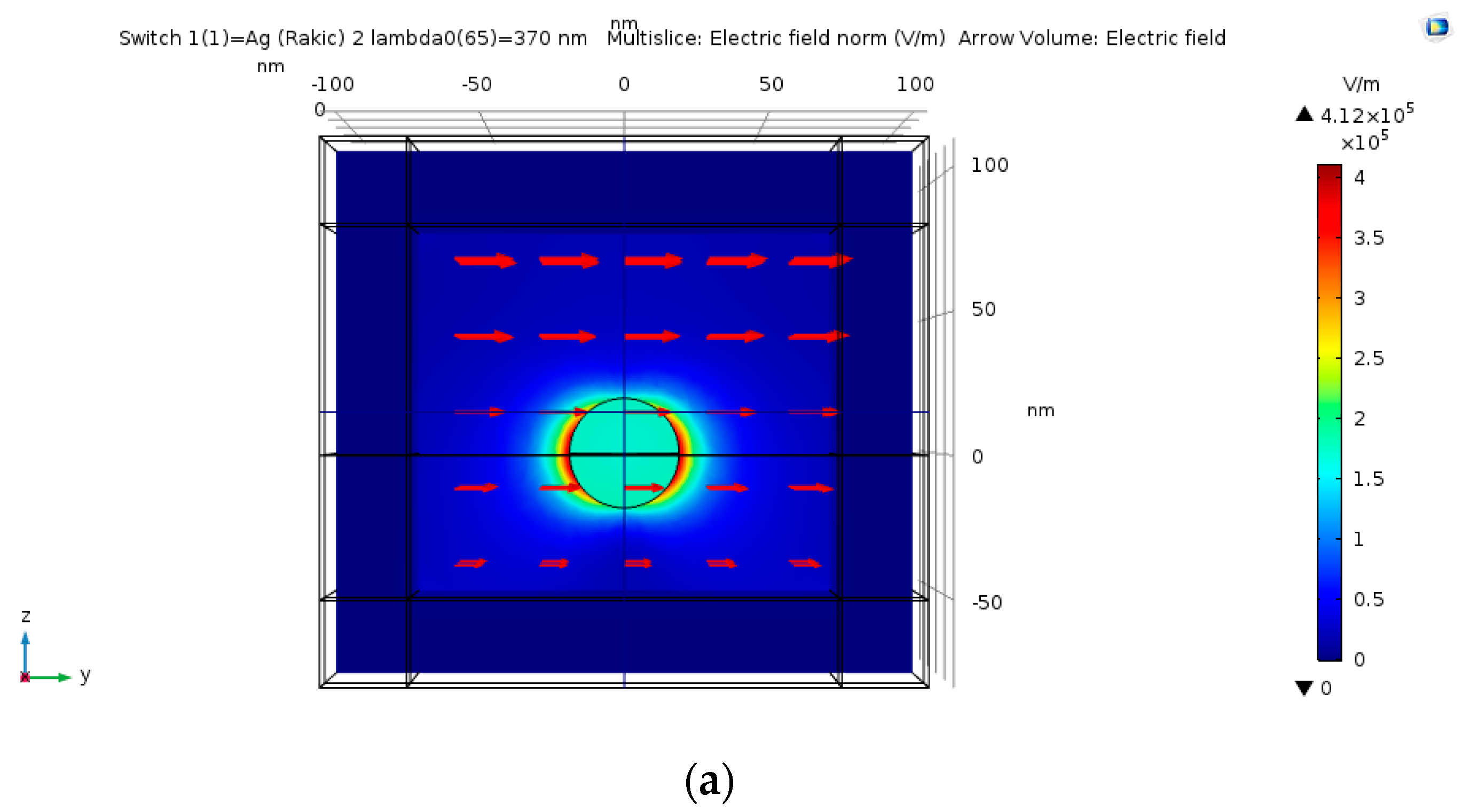
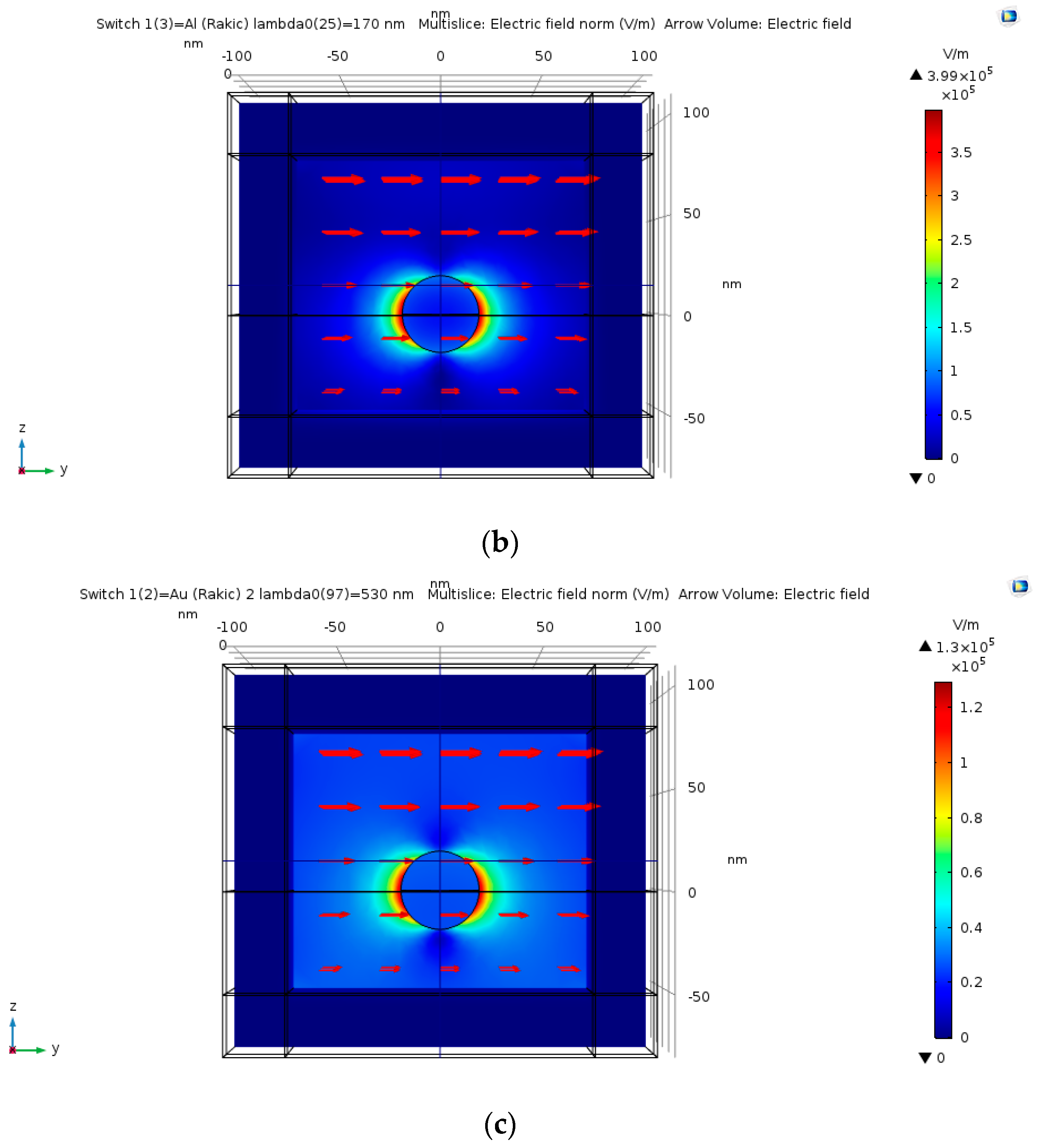
4.13. Silver vs. Gold vs. Aluminum
4.14. Nano-Shells Tuning
4.15. Multiple Nanostructures Mutual Influence
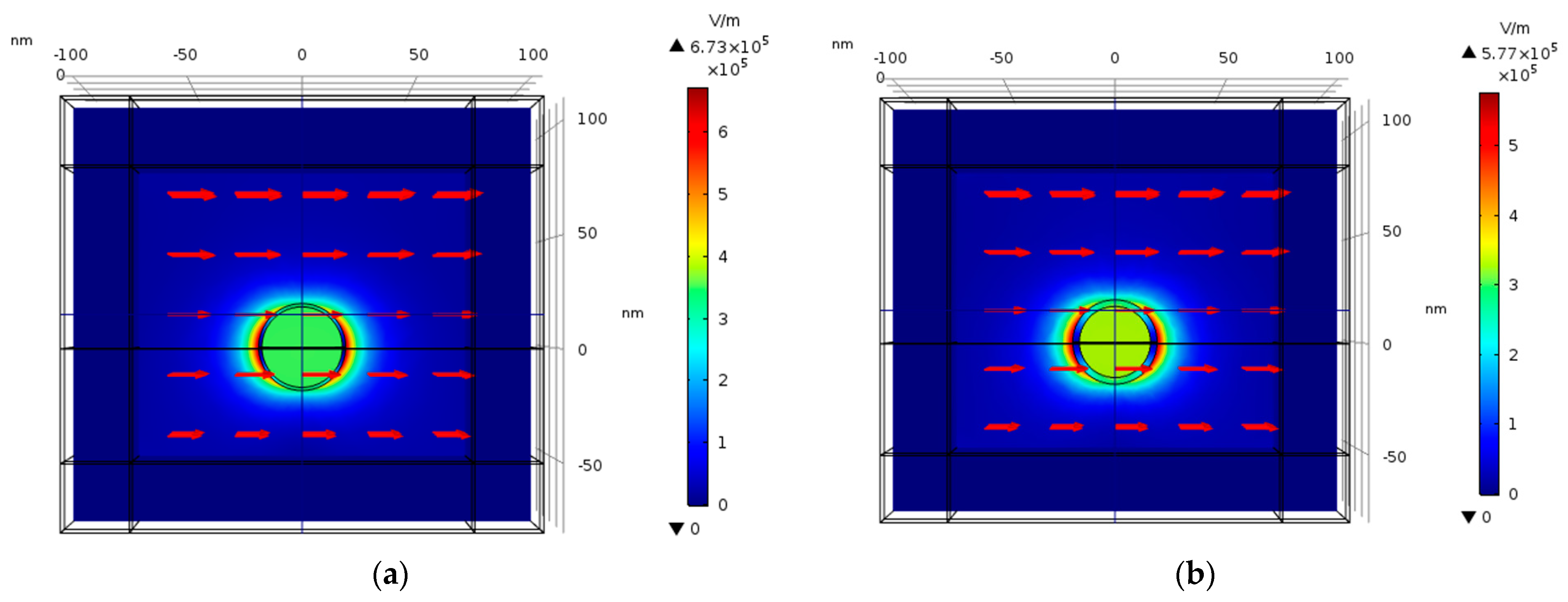
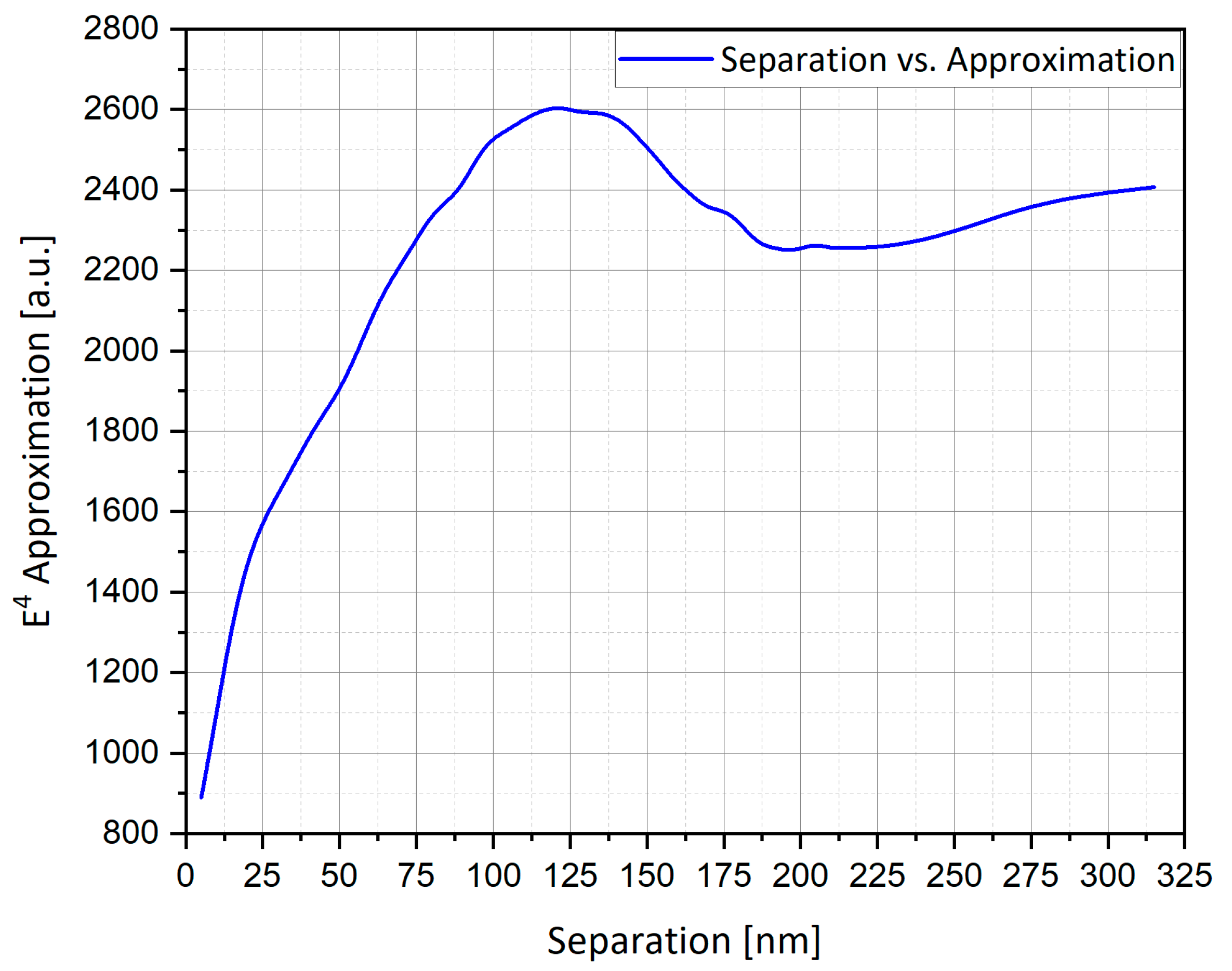
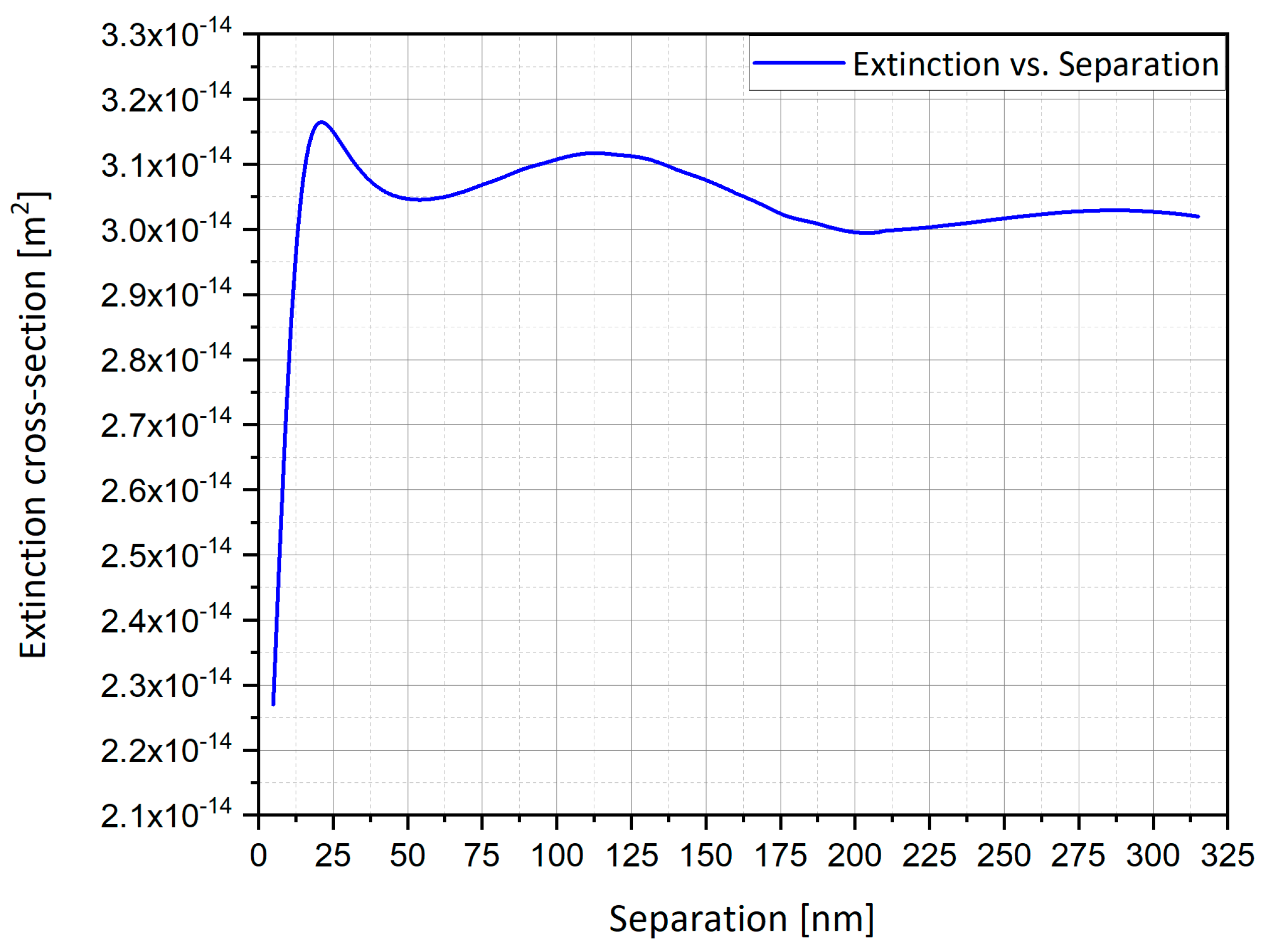
4.15.1. The Influence of Separation between Nanostructures
4.15.2. The Comparison between Preliminary Results for the Optimal Separation
5. Preliminary Experimental Results
Protrusions and Cavities Arrays Fabrication and Structural Characterization
6. Discussion
6.1. The Nano-Particles Geometry
6.2. Particles Material and Nano-Shells Tuning
6.3. SERS/TERS Nano-Particles Separation
7. Conclusions
8. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Etchegoin, P.; LeRu, E. Principles of Surface Enhanced Raman Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Opilik, L.; Schmid, T.; Zenobi, R. Modern Raman Imaging: Vibrational Spectroscopy on the Micrometer and Nanometer Scales. Ann. Rev. Anal. Chem. 2013, 6, 379–398. [Google Scholar] [CrossRef] [PubMed]
- Machida, H.; Sugahara, T.; Hirasawa, I. Preparation of dispersed metal nanoparticles in the aqueous solution of metal carboxylate and the tetra-n-butylammonium carboxylate. J. Cryst. Growth 2019, 514, 14–20. [Google Scholar] [CrossRef]
- Fleischmann, M.; Hendra, P.J.; McQuillan, A.J. Raman Spectra of Pyridine Adsorbed at a Silver Electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Jeanmaire, D.L.; Van Duyne, R.P. Surface Raman Electrochemistry Part I. Heterocyclic, Aromatic and Aliphatic Amines Adsorbed on the Anodized Silver Electrode. J. Electroanal. Chem. 1977, 84, 1–20. [Google Scholar] [CrossRef]
- Camden, J.; Dieringer, J.; Wang, Y.; Masiello, D.; Marks, L.; Schatz, G.; Van Duyne, R. Probing the Structure of Single-Molecule Surface-Enhanced Raman Scattering Hot Spots. J. Am. Chem. Soc. 2008, 130, 12616–12617. [Google Scholar] [CrossRef]
- Grant, A.M.; Creighton, J.A. Anomalously Intense Raman Spectra of Pyridine at a Silver Electrode. J. Am. Chem. Soc. 1977, 99, 5215–5217. [Google Scholar]
- Tsuneda, T.; Iwasa, T.; Taketsugu, T. Roles of silver nanoclusters in surface-enhanced Raman spectroscopy. J. Chem. Phys. 2019, 151, 094102. [Google Scholar] [CrossRef]
- Lombardi, J.; Birke, R. A Unified Approach to Surface-Enhanced Raman Spectroscopy. J. Phys. Chem. C 2008, 112, 5605–5617. [Google Scholar] [CrossRef]
- Ritchie, R.H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Mock, J.J.; Barbic, M.; Smith, D.R.; Schultz, D.A.; Schultz, S. Shape effects in plasmon resonance of individual colloidal silver nanoparticles. J. Chem. Phys. 2002, 116, 6755–6759. [Google Scholar] [CrossRef]
- Witlicki, E.H.; Johnsen, C.; Hansen, S.W.; Silverstein, D.W.; Bottomley, V.J.; Jeppesen, J.O.; Wong, E.W.; Jensen, L.; Flood, A.H. Molecular Logic Gates Using Surface-Enhanced Raman-Scattered Light. J. Am. Chem. Soc. 2011, 133, 7288–7291. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Mock, J.; Smith, D.; Gao, T.; Sailor, M.J. Surface-Enhanced Raman Scattering from Silver-Plated Porous Silicon. J. Phys. Chem. B 2004, 108, 11654–11659. [Google Scholar] [CrossRef]
- Talian, I.; Mogensen, K.B.; Oriňák, A.; Kaniansky, D.; Hübner, J. Surface-enhanced Raman spectroscopy on novel black silicon-based nanostructured surfaces. J. Raman Spectrosc. 2009, 40, 982–986. [Google Scholar] [CrossRef]
- Kanipe, K.N.; Chidester, P.P.F.; Stucky, G.D.; Moskovits, M. Large Format Surface-Enhanced Raman Spectroscopy Substrate Optimized for Enhancement and Uniformity. ACS NANO 2016, 10, 7566–7571. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Zhang, H.; Yu, X.; Zeng, S.; Yong, K.-T.; Ho, H.-P. Seed-mediated Plasmon-driven Regrowth of Silver Nanodecahedrons (NDs). Plasmonics 2011, 7, 167–173. [Google Scholar] [CrossRef]
- Aroca, R. Surface-Enhanced Vibrational Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bao, L.-L.; Mahurin, S.M.; Liang, C.-D.; Dai, S. Study of silver films over silica beads as a surface-enhanced Raman scattering (SERS) substrate for detection of benzoic acid. J. Raman Spectrosc. 2003, 34, 394–398. [Google Scholar] [CrossRef]
- Moskovits, M. Surface-Enhanced Raman Spectroscopy: A Brief Perspective in Surface-Enhanced Raman Scattering—Physics and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–18. [Google Scholar]
- Ayas, S. Label-Free Nanometer-Resolution Imaging of Biological Architectures through Surface Enhanced Raman Scattering. Sci. Rep. 2013, 3, 2624. [Google Scholar] [CrossRef]
- Mosier-Boss, P.A. Review of SERS Substrates for Chemical Sensing. Nanomaterials 2017, 7, 142. [Google Scholar] [CrossRef]
- Haynes, C.L.; McFarland, A.D.; Van Duyne, R.P. Surface Enhanced Raman Spectroscopy (SERS). Anal. Chem. 2005, 77, 338A–346A. [Google Scholar] [CrossRef]
- McNay, G.; Eustace, D.; Smith, W.E.; Faulds, K.; Graham, D. Surface-Enhanced Raman Scattering (SERS) and Surface-Enhanced Resonance Raman Scattering (SERRS): A Review of Applications. Appl. Spectrosc. 2011, 825–837. [Google Scholar] [CrossRef]
- Sharma, B.; Frontiera, R.R.; Henry, A.-I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Langer, J.; Jimenez de Aberasturi, D.; Aizpurua, J.; Alvarez-Puebla, R.A.; Auguié, B.; Baumberg, J.J.; Bazan, G.C.; Bell, S.E.; Boisen, A.; Brolo, A.G.; et al. Present and Future of Surface-Enhanced Raman Scattering. ACS Nano 2020, 14, 28–117. [Google Scholar] [CrossRef] [PubMed]
- Sonntag, M.D.; Pozzi, E.A.; Jiang, N.; Hersam, M.C.; Van Duyne, R.P. Recent Advances in Tip-Enhanced Raman Spectroscopy. J. Phys. Chem. Lett. 2014, 5, 3125–3130. [Google Scholar] [CrossRef] [PubMed]
- Stöckle, R.M.; Suh, Y.D.; Deckert, V.; Zenobi, R. Nanoscale chemical analysis by tip-enhanced Raman spectroscopy. Chem. Phys. Lett. 2000, 318, 131–136. [Google Scholar] [CrossRef]
- Anderson, M.S. Locally enhanced Raman spectroscopy with an atomic force microscope (AFM-TERS). Appl. Phys. Lett. 2000, 76, 3130. [Google Scholar] [CrossRef]
- Hou, J.G.; Yang, J.L.; Luo, Y.; Aizpurua, J.; Liao, Y.; Zhang, L.; Chen, L.G.; Zhang, C.; Jiang, S. Chemical mapping of a single molecule by plasmon-enhanced Raman scattering. Nature 2013, 498, 82–86. [Google Scholar]
- Lee, J.; Tallarida, N.; Chen, X.; Liu, P.; Jensen, L.; Apkarian, V.A. Tip-Enhanced Raman Spectromicroscopy of Co(II)-Tetraphenylporphyrin on Au(111): Toward the Chemists’ Microscope. ACS NANO 2017, 11, 11466–11474. [Google Scholar] [CrossRef]
- Tallarida, N.; Lee, J.; Apkarian, V.A. Tip-Enhanced Raman Spectromicroscopy on the Angstrom Scale: Bare and CO-Terminated Ag Tips. ACS NANO 2017, 11, 11393–11401. [Google Scholar] [CrossRef]
- Lee, J.; Tallarida, N.; Chen, X.; Jensen, L.; Apkarian, V.A. Microscopy with a single-molecule scanning electrometer. Sci. Adv. 2018, 4, eaat5472. [Google Scholar] [CrossRef]
- Lee, J.; Crampton, K.T.; Tallarida, N.; Apkarian, V.A. Visualizing vibrational normal modes of a single molecule with atomically confined light. Nature 2019, 568, 78–82. [Google Scholar] [CrossRef]
- He, Z.; Han, Z.; Kizer, M.; Linhardt, R.J.; Wang, X.; Sinyukov, A.M.; Wang, J.; Deckert, V.; Sokolov, A.V. Tip-Enhanced Raman Imaging of Single-Stranded DNA with Single Base Resolution. J. Am. Chem. Soc. 2019, 141, 753–757. [Google Scholar] [CrossRef] [PubMed]
- Crampton, K.T.; Lee, J.; Apkarian, V.A. Ion-Selective, Atom-Resolved Imaging of a 2D Cu2N Insulator: Field and Current Driven Tip-Enhanced Raman Spectromicroscopy Using a Molecule-Terminated Tip. ACS NANO 2019, 13, 6363–6371. [Google Scholar] [CrossRef] [PubMed]
- Pettinger, B.; Domke, K.F.; Zhang, D.; Picardi, G.; Schuster, R. Tip-enhanced Raman scattering: Influence of the tip-surface geometry on optical resonance and enhancement. Surf. Sci. 2009, 603, 1335–1341. [Google Scholar] [CrossRef]
- Thomas, S.; Wachter, G.; Lemell, C.; Burgdörfer, J.; Hommelhoff, P. Large optical field enhancement for nanotips with large opening Angles. N. J. Phys. 2015, 17, 063010. [Google Scholar] [CrossRef]
- Karsenty, A.; Mandelbaum, Y. Computer Algebra Challenges in Nanotechnology: Accurate Modeling of Nanoscale Electro-optic Devices Using Finite Elements Method. Math. Comp. Sci. 2019, 13, 117–130. [Google Scholar] [CrossRef]
- Jain, P.K.; El-Sayed, M.A. Plasmonic coupling in noble metal nanostructures. Chem. Phys. Lett. 2010, 487, 153–164. [Google Scholar] [CrossRef]
- Kessentini, S.; Barchiesi, D.; Grosges, T.; De La Chapelle, M.L. Selective and collaborative optimization methods for plasmonic: A comparison. Piers Online 2011, 7, 291–295. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Bohren, C.; Huffmann, D. Absorption and Scattering of Light by Small Particles; John Wiley: New York, NY, USA, 1998; pp. 357–381. [Google Scholar]
- Halas, N. Playing with Plasmons: Tuning the Optical Resonant Properties of Metallic Nanoshells. Mrs Bull. 2005, 30, 362–367. [Google Scholar] [CrossRef]
- Mandelbaum, Y.; Mottes, R.; Zalevsky, Z.; Zitoun, D.; Karsenty, A. Design of Surface Enhanced Raman Scattering (SERS) Nanosensor Array. Sensors 2020, 20, 5123. [Google Scholar] [CrossRef]



















| Name | Expression | Description |
|---|---|---|
| W | 150 nm, 250 nm, 450 nm | Width of physical geometry |
| t_pml | 30 nm | Perfectly Matched Layer (PML) thickness |
| h_air | 80 nm | Air domain height |
| h_subs | 50 nm | Substrate domain height |
| T | 1.433–8.303 nm | Nano-shell thickness (using Δ = 0.2, 0.4, 0.6, 0.8) |
| R | 20 nm | Nano-particle radius |
| A | 20 nm | Ellipsoid x semi axis |
| B | 20 nm | Ellipsoid y semi axis |
| C | 40 nm | Ellipsoid z semi axis |
| E | 0.866 | Eccentricity |
| Na | 1 | Air refractive index |
| Phi | 0, π/2 | Azimuthal angle of incidence |
| θ | 0, π/6, π/4, π/3 | Polar angle of incident field |
| I0 | 106 W/m2 | Intensity of incident field |
| P | I0w2cos(θ) | Port power |
| Sep | 5–315 nm | Separation between particles |
| Name | Expression | Unit | Description | Domain |
|---|---|---|---|---|
| ewfd.Ex | 0 | V/m | X direction electric field | PML Domain |
| ewfd.Ey | 0 | V/m | Y direction electric field | PML Domain |
| ewfd.Ez | 0 | V/m | Z direction electric field | PML Domain |
| E0x | -sin(phi) | Amplitude of Ex in X | Port 1,2 | |
| E0y | cos(phi) | Amplitude of Ey in Y | Port 1,2 | |
| intop_surf | Surface integral | nano-particle surface | ||
| intop_vol | Volume integral | nano-particle volume | ||
| nrelPoav | nx * ewfd2.relPoavx + ny * ewfd2.relPoavy + nz * ewfd2.relPoavz | W/m2 | Relative normal Poynting flux | Entire model |
| Sigma_sc | intop_surf(nrelPoav)/I0 | m2 | scattering cross-section | Entire model |
| Sigma_abs | intop_vol(ewfd2.Qh)/I0 | m2 | absorption cross-section | Entire model |
| Sigma_ext | Sigma_sc+ Sigma_abs | m2 | extinction cross-section | Entire model |
| Studied Shape | Checked Polar or Azimuth Angles | λ Peak Enhancement | E4 at Peak | Comments |
|---|---|---|---|---|
| Hemi-sphere | θ = 0, π/6, π/4, π/3 | λ = 368 nm | 2460 | ● Largest extinction cross-section at θ = 0 |
| Spheroidal cavity | θ = 0, π/6, π/4, π/3 | λ = 372 nm | 1865 | ● Largest extinction cross-section at θ = 0. ● Easiest shape using Focused Ion Beam (FIB). |
| Hemi-spheroid | θ = 0, π/6, π/4, π/3 | λ = 368 nm | 7310 | ● Largest extinction cross-section at θ = 0. ● Eccentricity of 0.866. ● Highest field enhancement. |
| Nano-cone | θ = 0, π/6, π/4, π/3 | λ = 357nm | 208 | ● Largest extinction cross-section at θ = 0. ● Nano-cone surface area = hemi-sphere’s area. |
| Ellipsoidal cavity | θ = 0, π/6, π/3 | λ = 375nm | 6832 | ● Largest extinction cross-section at θ = 0. ● Easiest feasible shape using FIB. ● Highest extinction cross-section. |
| Ellipsoidal rod | λ = 378nm | 7038 | ● Largest peak at = 0. ● Sensitive to electric field polarization | |
| Double nano-cone | λ = 375nm | 5446 | ● Largest peak at = ● Sensitive to electric field polarization |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandelbaum, Y.; Mottes, R.; Zalevsky, Z.; Zitoun, D.; Karsenty, A. Investigations of Shape, Material and Excitation Wavelength Effects on Field Enhancement in SERS Advanced Tips. Nanomaterials 2021, 11, 237. https://doi.org/10.3390/nano11010237
Mandelbaum Y, Mottes R, Zalevsky Z, Zitoun D, Karsenty A. Investigations of Shape, Material and Excitation Wavelength Effects on Field Enhancement in SERS Advanced Tips. Nanomaterials. 2021; 11(1):237. https://doi.org/10.3390/nano11010237
Chicago/Turabian StyleMandelbaum, Yaakov, Raz Mottes, Zeev Zalevsky, David Zitoun, and Avi Karsenty. 2021. "Investigations of Shape, Material and Excitation Wavelength Effects on Field Enhancement in SERS Advanced Tips" Nanomaterials 11, no. 1: 237. https://doi.org/10.3390/nano11010237
APA StyleMandelbaum, Y., Mottes, R., Zalevsky, Z., Zitoun, D., & Karsenty, A. (2021). Investigations of Shape, Material and Excitation Wavelength Effects on Field Enhancement in SERS Advanced Tips. Nanomaterials, 11(1), 237. https://doi.org/10.3390/nano11010237








