Thermodynamics of the Vapor–Liquid–Solid Growth of Ternary III–V Nanowires in the Presence of Silicon
Abstract
:1. Introduction
2. Model
3. Results and Discussion
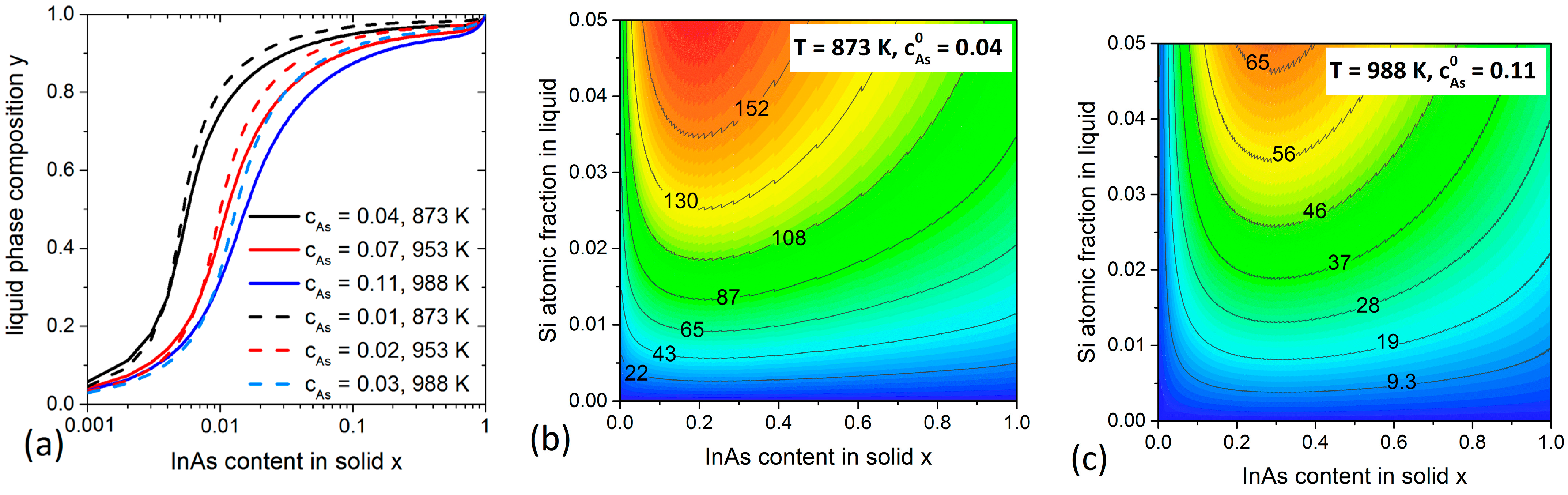
3.1. InGaAs System
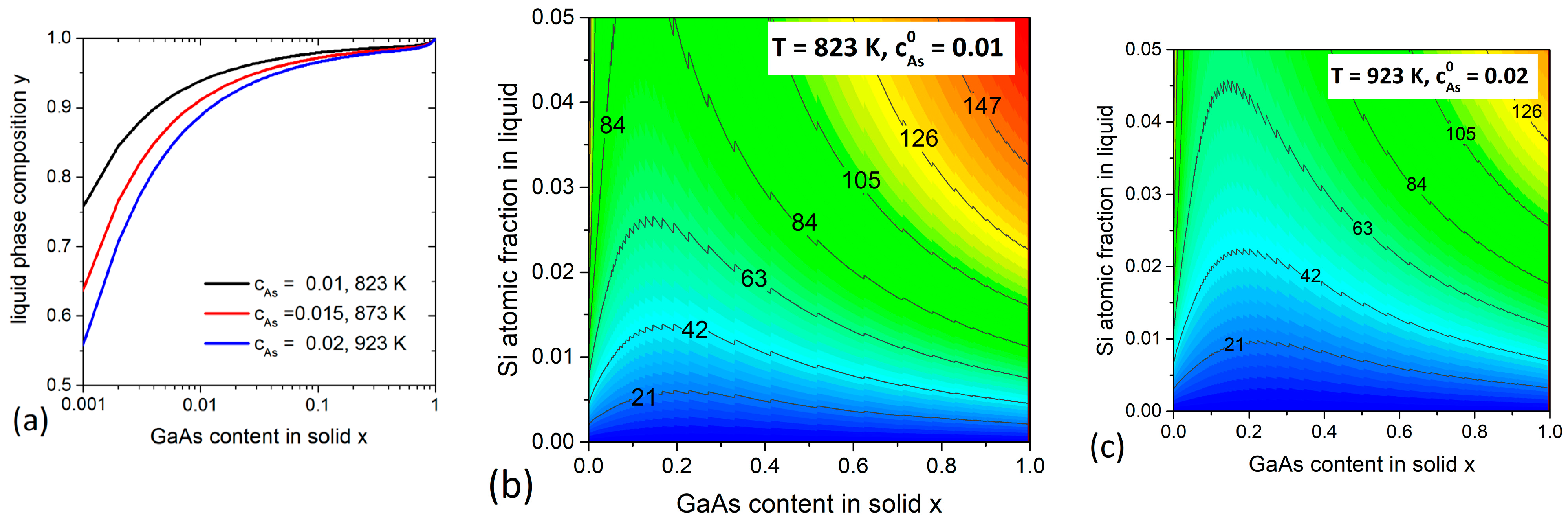
3.2. AlGaAs System
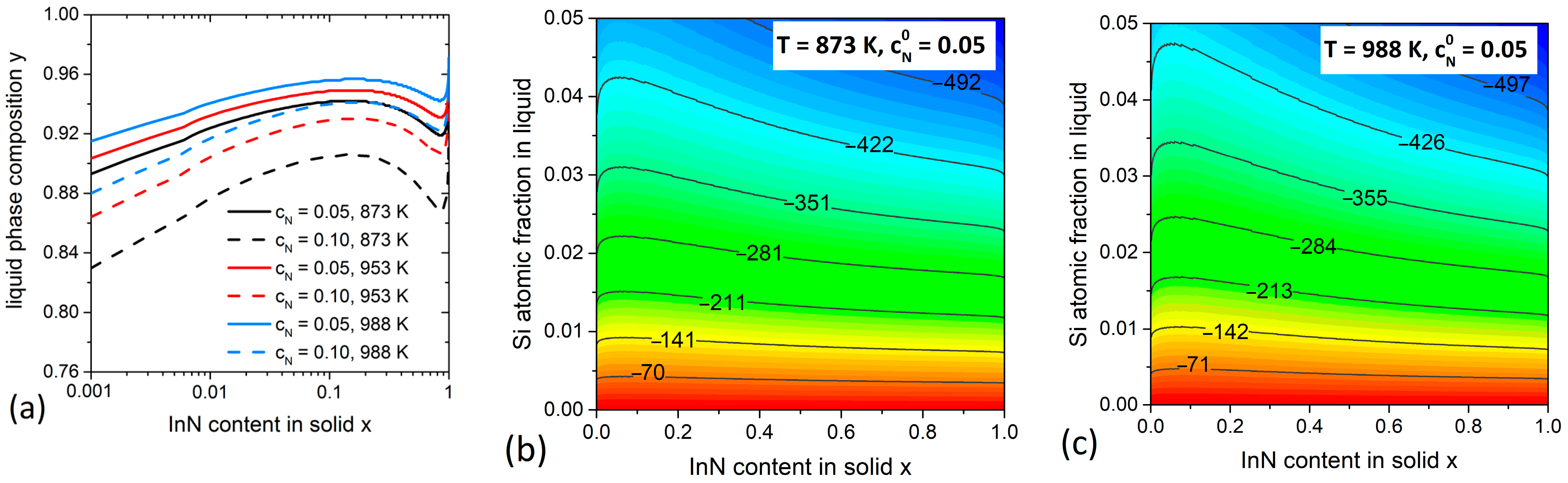
3.3. InGaN System
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adachi, S. III–V Ternary and Quaternary Compounds. In Springer Handbook of Electronic and Photonic Materials; Kasap, S., Capper, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Geum, D.M.; Kim, S.; Kim, S.K.; Kang, S.; Kyhm, J.; Song, J.; Choi, W.J.; Yoon, E. GaAs and near-infrared InGaAs for multicolor photodetectors by using high-throughput epitaxial lift-off toward high-resolution imaging systems. Sci. Rep. 2019, 9, 18661. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Itzler, M.A.; Zbinden, H.; Pan, J.-W. Advances in InGaAs/InP single-photon detector systems for quantum communication. Sci. Appl. 2015, 4, e286. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Gong, H.; Fang, J.; Shao, X.; Tang, H.; Huang, S.; Li, T.; Huang, Z. The development of InGaAs Short Wavelength Infrared Focal Plane Arrays with high performance. Infrared Phys. Technol. 2017, 80, 112–119. [Google Scholar] [CrossRef]
- Baek, S.H.; Lee, H.J.; Lee, S.N. High-performance flat-type InGaN-based light-emitting diodes with local breakdown conductive channel. Sci. Rep. 2019, 9, 13654. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.F.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nat. Commun. 2020, 11, 1331. [Google Scholar] [CrossRef]
- Jones, C.M.; Teng, C.H.; Yan, Q.; Ku, P.C.; Kioupakis, E. Impact of carrier localization on recombination in InGaN quantum wells and the efficiency of nitride light-emitting diodes: Insights from theory and numerical simulations. Appl. Phys. Lett. 2017, 111, 113501. [Google Scholar] [CrossRef]
- Lin, C.; Li, A.Z. The effect of strain on the miscibility gap in Ga-In-Sb ternary alloy. J. Cryst. Growth 1999, 203, 511–515. [Google Scholar] [CrossRef]
- Mohamad, R.; Béré, A.; Chen, J.; Ruterana, P. Investigation of strain effects on phase diagrams in the ternary nitride alloys (InAlN, AlGaN, InGaN). Phys. Status Solidi A 2017, 214, 1600752. [Google Scholar] [CrossRef]
- Xiang, H.J.; Wei, S.H.; Da Silva, J.L.F.; Li, J. Strain relaxation and band-gap tunability in ternary nanowires. Phys. Rev. B 2008, 78, 193301. [Google Scholar] [CrossRef]
- Glas, F. Critical dimensions for the plastic relaxation of strained axial heterostructures in free-standing nanowires. Phys. Rev. B 2006, 74, 121302(R). [Google Scholar] [CrossRef]
- Kuykendall, T.; Ulrich, P.; Aloni, S.; Yang, P. Complete composition tunability of InGaN nanowires using a combinatorial approach. Nat. Mater. 2007, 6, 951–956. [Google Scholar] [CrossRef] [PubMed]
- Ebaid, M.; Kang, J.H.; Yoo, Y.S.; Lim, S.H.; Cho, Y.H.; Ryu, S.W. Vertically aligned InGaN nanowires with engineered axial In composition for highly efficient visible light emission. Sci. Rep. 2015, 5, 17003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, M.D.; Alhodaib, A.; Craig, A.P.; Robson, A.; Aziz, A.; Krier, A.; Svensson, J.; Wernersson, L.-E.; Sanchez, A.M.; Marshall, A.R.J. Low leakage-current InAsSb nanowire photodetectors on silicon. Nano Lett. 2016, 16, 182–187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dimakis, E.; Jahn, U.; Ramsteiner, M.; Tahraoui, A.; Grandal, J.; Kong, X.; Marquardt, O.; Trampert, A.; Riechert, H.; Geelhaar, L. Coaxial multishell (In,Ga)As/GaAs nanowires for near-infrared emission on Si substrates. Nano Lett. 2014, 14, 2604–2609. [Google Scholar] [CrossRef] [PubMed]
- Stehr, J.E.; Dobrovolsky, A.; Sukrittanon, S.; Kuang, Y.; Tu, C.W.; Chen, W.M.; Buyanova, I.A. Optimizing GaNP Coaxial Nanowires for Efficient Light Emission by Controlling Formation of Surface and Interfacial Defects. Nano Lett. 2015, 15, 242–247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Svensson, C.P.T.; Mårtensson, T.; Trägårdh, J.; Larsson, C.; Rask, M.; Hessman, D.; Samuelson, L.; Ohlsson, J. Monolithic GaAs/InGaP nanowire light emitting diodes on silicon. Nanotechnology 2008, 19, 305201. [Google Scholar] [CrossRef]
- Wagner, R.S.; Ellis, W.C. Vapor-liquid-solid mechanism of singe crystal growth. Appl. Phys. Lett. 1964, 4, 89. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Hijazi, H.; Goktas, N.I.; LaPierre, R.R. Be, Te, and Si doping of GaAs nanowires: Theory and experiment. J. Phys. Chem. C 2020, 124, 17299–17307. [Google Scholar] [CrossRef]
- Dayeh, S.A.; Chena, R.; Roa, Y.G.; Sim, J. Progress in doping semiconductor nanowires during growth. Mater. Sci. Semicond. Process. 2017, 62, 135–155. [Google Scholar] [CrossRef] [Green Version]
- Hijazi, H.; Monier, G.; Gil, E.; Trassoudaine, A.; Bougerol, C.; Leroux, C.; Castelluci, D.; Robert-Goumet, C.; Hoggan, P.; André, Y.; et al. Si doping of vapor-liquid-solid GaAs nanowires: N-type or p-type? Nano Lett. 2019, 19, 4498–4504. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Hijazi, H. Effect of arsenic depletion on the silicon doping of vapor-liquid-solid GaAs nanowires. Phys. Stat. Sol. RRL 2020, 14, 2000129. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Hijazi, H. Oscillations of As Concentration and Electron-to-Hole Ratio in Si-Doped GaAs Nanowires. Nanomaterials 2020, 10, 833. [Google Scholar] [CrossRef] [PubMed]
- Hijazi, H.; Leroy, F.; Monier, G.; Grégoire, G.; Gil, E.; Trassoudaine, A.; Dubrovskii, V.G.; Castelluci, D.; Goktas, N.I.; LaPierre, R.R.; et al. Dynamics of Gold Droplet Formation on SiO2/Si(111) Surface. J. Phys. Chem. C 2020, 124, 11946–11951. [Google Scholar] [CrossRef]
- Hiraki, A.; Lugujjo, E.; Mayer, J.W. Formation of Silicon Oxide over Gold Layers on Silicon Substrates. J. Appl. Phys. 1972, 43, 3643. [Google Scholar] [CrossRef]
- Dallaporta, H.; Liehr, M.; Lewis, J.E. Silicon Dioxide Defects Induced by Metal Impurities. Phys. Rev. B Condens. Matter Mater. Phys. 1990, 41, 5075–5083. [Google Scholar] [CrossRef]
- Glas, F. Comparison of Modeling Strategies for the Growth of Heterostructures in III–V Nanowires. Cryst. Growth Des. 2017, 17, 4785–4794. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Koryakin, A.A.; Sibirev, N.V. Understanding the composition of ternary III–V nanowires and axial nanowire heterostructures in nucleation-limited regime. Mat. Design 2017, 132, 400–408. [Google Scholar] [CrossRef]
- Hijazi, H.; Dubrovskii, V.G.; Monier, G.; Gil, E.; Leroux, C.; Avit, G.; Trassoudaine, A.; Bougerol, C.; Castellucci, D.; Robert-Goumet, C.; et al. Influence of silicon on the nucleation rate of GaAs nanowires on Si substrates. J. Phys. Chem. C 2018, 122, 19230–19235. [Google Scholar] [CrossRef]
- Hijazi, H.; Zeghouane, M.; Bassani, F.; Gentile, P.; Salem, B.; Dubrovskii, V.G. Impact of droplet composition on the nucleation rate and morphology of vapor-liquid-solid GeSn nanowires. Nanotechnology 2020, 31, 405602. [Google Scholar] [CrossRef]
- Ansara, I.; Chatillon, C.; Lukas, H.L.; Nishizawa, T.; Ohtani, H.; Ishida, K.; Hillert, M.; Sundman, B.; Argent, B.B.; Watson, A.; et al. A binary database for III–V compound semiconductor systems. CALPHAD 1994, 18, 177. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. CALPHAD 1991, 15, 317. [Google Scholar] [CrossRef]
- Glas, F. Chemical Potentials for Au-Assisted Vapor-Liquid-Solid Growth of III–V Nanowires. J. Appl. Phys. 2010, 108, 073506. [Google Scholar] [CrossRef]
- Grecenkov, J.; Dubrovskii, V.G.; Ghasemi, M.; Johansson, J. Quaternary chemical potentials for gold-catalyzed growth of ternary InGaAs nanowires. Cryst. Growth Des. 2016, 16, 4526. [Google Scholar]
- Kumagai, Y.; Takemoto, K.; Hasegawac, T.; Koukitua, A.; Seki, H. Thermodynamics on tri-halide vapor-phase epitaxy of GaN and using and J. Cryst. Growth 2001, 231, 57. [Google Scholar] [CrossRef]
- Johansson, J.; Ghasemi, M. Composition of Gold Alloy Seeded InGaAs Nanowires in the Nucleation Limited Regime. Cryst. Growth Des. 2017, 17, 1630–1635. [Google Scholar] [CrossRef]
- Koblmüller, G.; Abstreiter, G. Growth and properties of InGaAs nanowires on silicon. Phys. Status Solidi RRL 2018, 8, 11–30. [Google Scholar] [CrossRef]
- Glas, F.; Dubrovskii, V.G. Energetics and kinetics of monolayer formation in vapor-liquid-solid nanowire growth. Phys. Rev. Mater. 2020, 4, 083401. [Google Scholar] [CrossRef]
- Roche, E.; André, Y.; Avit, G.; Bougerol, C.; Castelluci, D.; Réveret, F.; Gil, E.; Médard, F.; Leymarie, J.; Jean, T.; et al. Circumventing the miscibility gap in InGaN nanowires emitting from blue to red. Nanotechnology 2018, 29, 465602. [Google Scholar] [CrossRef]
- Zeghouane, M.; Avit, G.; André, Y.; Bougerol, C.; Yoann, R.; Ferret, P.; Castelluci, D.; Gil, E.; Dubrovskii, V.G.; Amano, H.; et al. Compositional control of homogeneous InGaN nanowires with the In content up to 90%. Nanotechnology 2018, 30, 044001. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hijazi, H.; Zeghouane, M.; Dubrovskii, V.G. Thermodynamics of the Vapor–Liquid–Solid Growth of Ternary III–V Nanowires in the Presence of Silicon. Nanomaterials 2021, 11, 83. https://doi.org/10.3390/nano11010083
Hijazi H, Zeghouane M, Dubrovskii VG. Thermodynamics of the Vapor–Liquid–Solid Growth of Ternary III–V Nanowires in the Presence of Silicon. Nanomaterials. 2021; 11(1):83. https://doi.org/10.3390/nano11010083
Chicago/Turabian StyleHijazi, Hadi, Mohammed Zeghouane, and Vladimir G. Dubrovskii. 2021. "Thermodynamics of the Vapor–Liquid–Solid Growth of Ternary III–V Nanowires in the Presence of Silicon" Nanomaterials 11, no. 1: 83. https://doi.org/10.3390/nano11010083
APA StyleHijazi, H., Zeghouane, M., & Dubrovskii, V. G. (2021). Thermodynamics of the Vapor–Liquid–Solid Growth of Ternary III–V Nanowires in the Presence of Silicon. Nanomaterials, 11(1), 83. https://doi.org/10.3390/nano11010083






