Grand Canonical Monte Carlo Simulations to Determine the Optimal Interlayer Distance of a Graphene Slit-Shaped Pore for Adsorption of Methane, Hydrogen and their Equimolar Mixture
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
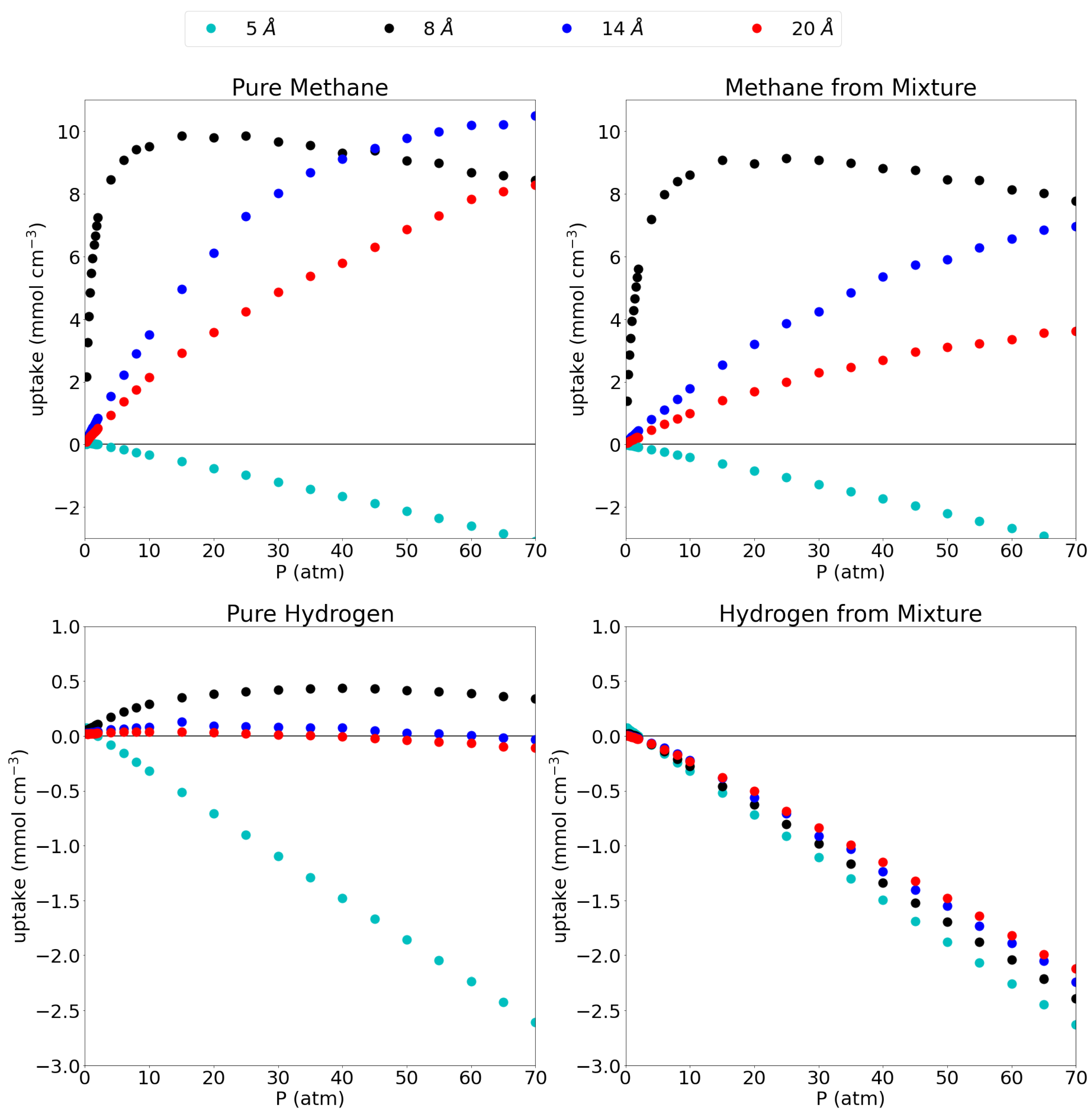
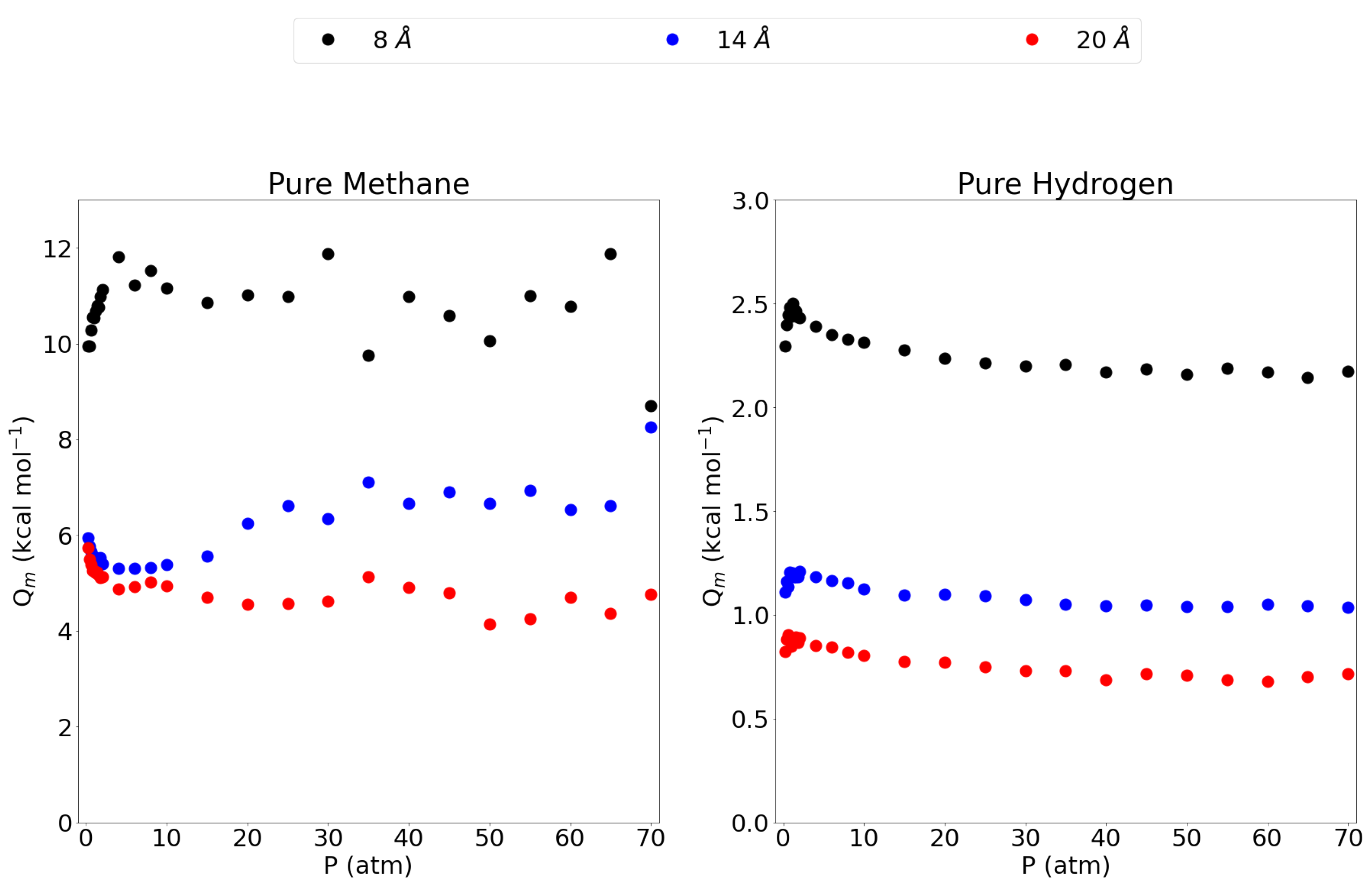
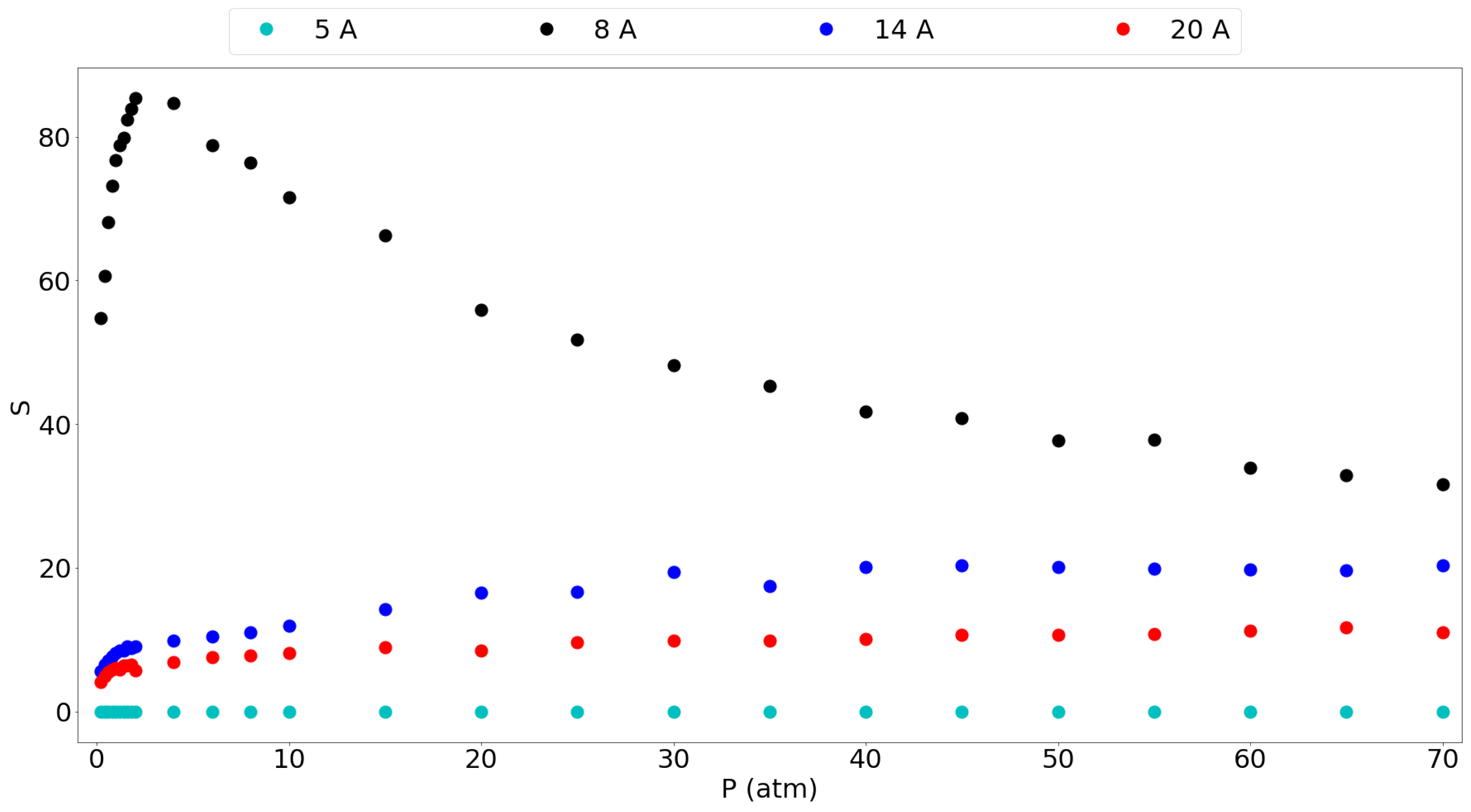
3.1. Adsorption Behavior
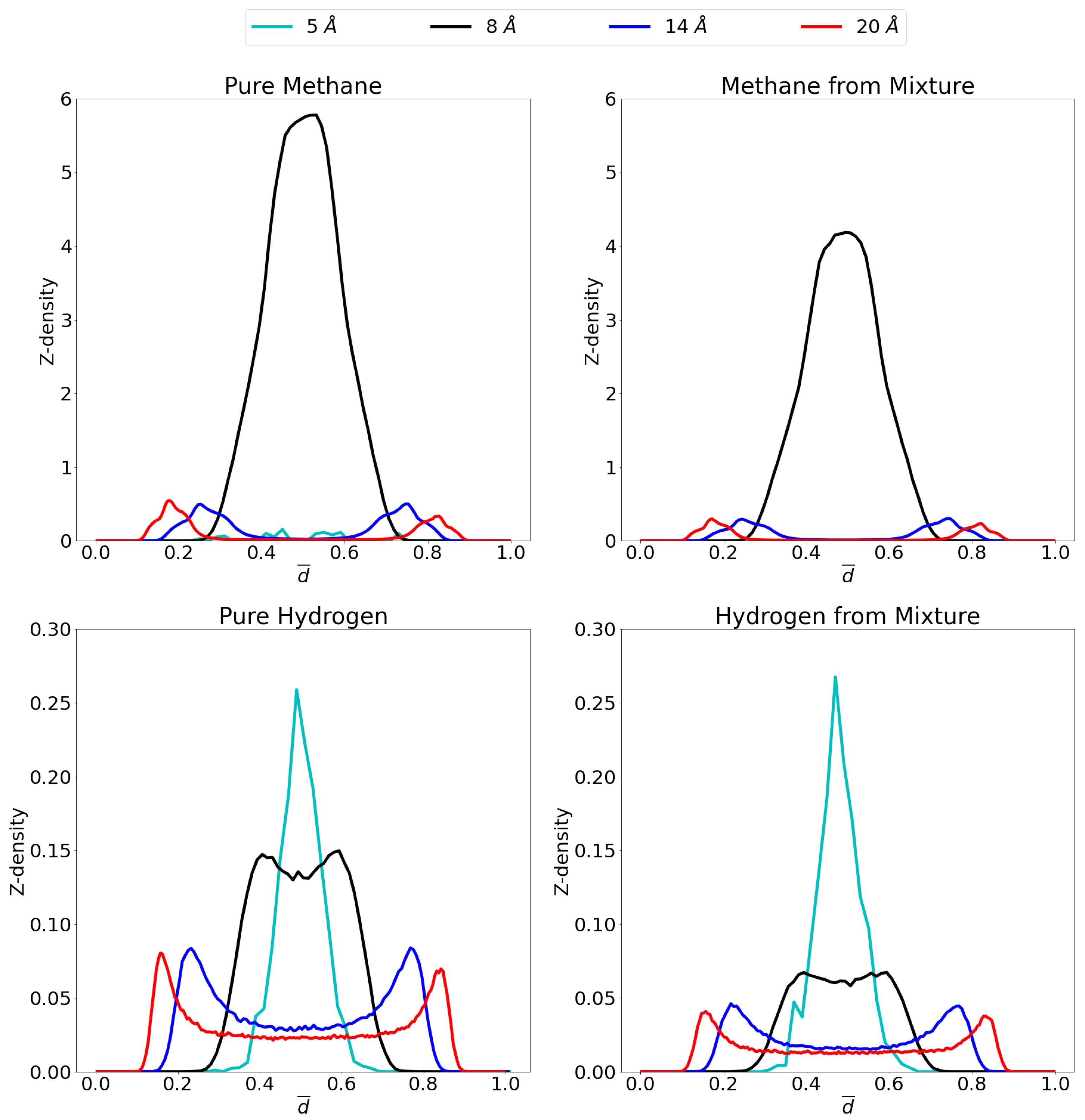
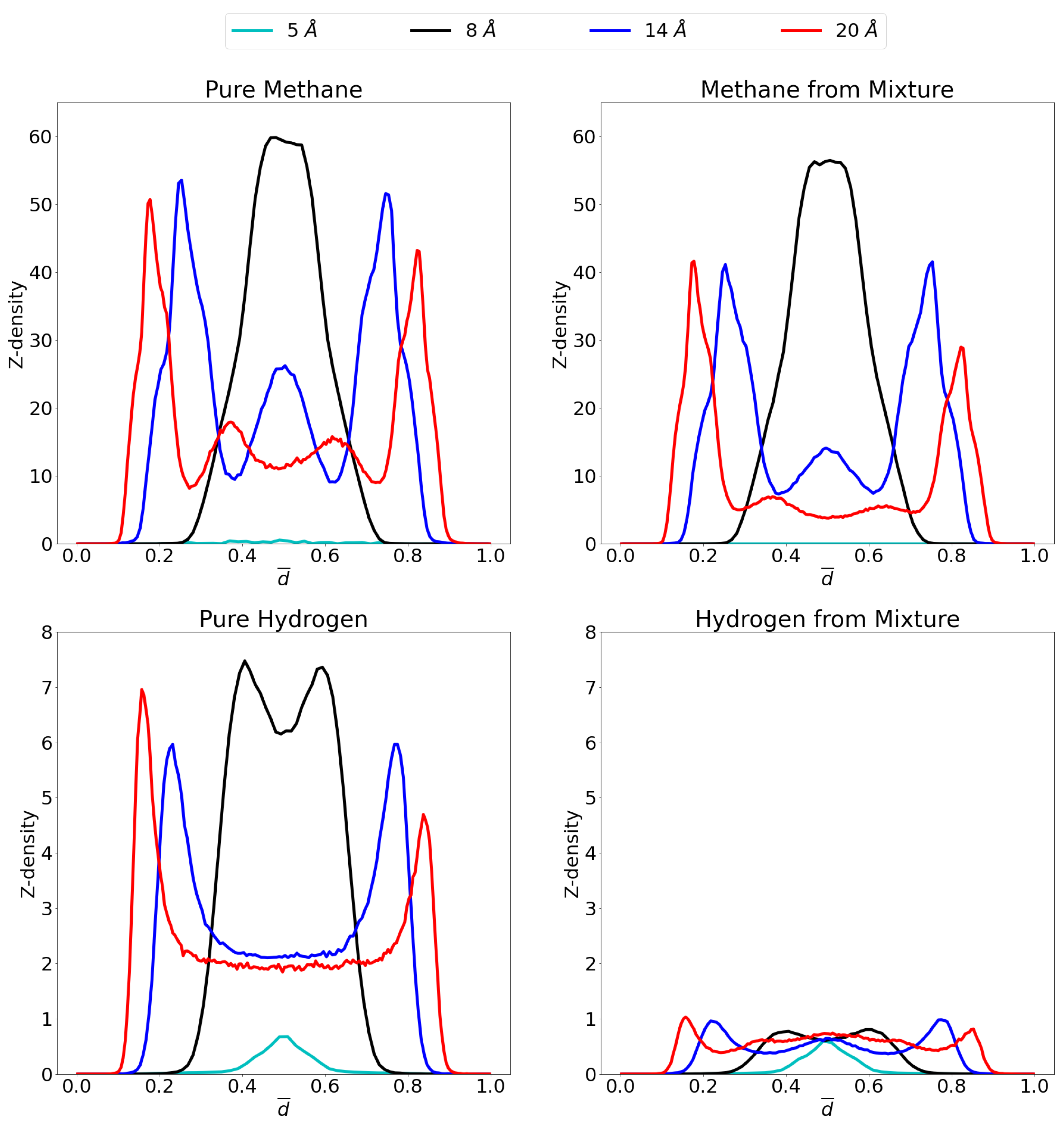
3.2. Molecular Picture
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morris, R.E.; Wheatley, P.S. Gas Storage in Nanoporous Materials. Angew. Chem. Int. Ed. 2008, 47, 4966–4981. [Google Scholar] [CrossRef]
- Choi, P.S.; Jeong, J.M.; Choi, Y.K.; Kim, M.S.; Shin, G.J.; Park, S.J. A review: Methane capture by nanoporous carbon materials for automobiles. Carbon Lett. 2016, 17, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Afgan, N.H.; Pilavachi, P.A.; Carvalho, M.G. Multi-criteria evaluation of natural gas resources. Energy Policy 2007, 35, 704–713. [Google Scholar] [CrossRef]
- Sazali, N. Emerging technologies by hydrogen: A review. Int. J. Hydrogen Energy 2020, 45, 18753–18771. [Google Scholar] [CrossRef]
- Momirlan, M.; Veziroglu, T. The properties of hydrogen as fuel tomorrow in sustainable energy system for a cleaner planet. Int. J. Hydrogen Energy 2005, 30, 795–802. [Google Scholar] [CrossRef]
- Johnston, B.; Mayo, M.C.; Khare, A. Hydrogen: The energy source for the 21st century. Technovation 2005, 25, 569–585. [Google Scholar] [CrossRef]
- Elyassi, M.; Rashidi, A.; Hantehzadeh, M.R.; Elahi, S.M. Preparation of different graphene nanostructures for hydrogen adsorption. Surf. Interface Anal. 2017, 49, 230–237. [Google Scholar] [CrossRef]
- Delgado, J.A.; Águeda, V.I.; Uguina, M.A.; Sotelo, J.L.; Brea, P.; Grande, C.A. Adsorption and Diffusion of H2, CO, CH4, and CO2 in BPL Activated Carbon and 13X Zeolite: Evaluation of Performance in Pressure Swing Adsorption Hydrogen Purification by Simulation. Ind. Eng. Chem. Res. 2014, 53, 15414–15426. [Google Scholar] [CrossRef]
- Kim, J.; Maiti, A.; Lin, L.C.; Stolaroff, J.K.; Smit, B.; Aines, R.D. New materials for methane capture from dilute and medium-concentration sources. Nat. Commun. 2013, 4, 1694. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Bhatia, S.K. Optimization of Slitlike Carbon Nanopores for Storage of hythane Fuel at Ambient Temperatures. J. Phys. Chem. B 2006, 110, 23770–23776. [Google Scholar] [CrossRef]
- Kumar, K.V.; Müller, E.A.; Rodríguez-Reinoso, F. Effect of Pore Morphology on the Adsorption of Methane/Hydrogen Mixtures on Carbon Micropores. J. Phys. Chem. C 2012, 116, 11820–11829. [Google Scholar] [CrossRef]
- Fischer, M.; Hoffmann, F.; Fröba, M. Metal–organic frameworks and related materials for hydrogen purification: Interplay of pore size and pore wall polarity. RSC Adv. 2012, 2, 4382. [Google Scholar] [CrossRef]
- Getman, R.B.; Bae, Y.S.; Wilmer, C.E.; Snurr, R.Q. Review and Analysis of Molecular Simulations of Methane, Hydrogen, and Acetylene Storage in Metal–Organic Frameworks. Chem. Rev. 2012, 112, 703–723. [Google Scholar] [CrossRef]
- Blanco, A.G.; de Oliveira, J.A.; López, R.; Moreno-Piraján, J.; Giraldo, L.; Zgrablich, G.; Sapag, K. A study of the pore size distribution for activated carbon monoliths and their relationship with the storage of methane and hydrogen. Colloids Surf. A Physicochem. Eng. Asp. 2010, 357, 74–83. [Google Scholar] [CrossRef]
- Morales-Cas, A.M.; Moya, C.; Coto, B.; Vega, L.F.; Calleja, G. Adsorption of Hydrogen and Methane Mixtures on Carbon Cylindrical Cavities. J. Phys. Chem. C 2007, 111, 6473–6480. [Google Scholar] [CrossRef]
- Raghavan, B.; Gupta, T. H 2 /CH 4 Gas Separation by Variation in Pore Geometry of Nanoporous Graphene. J. Phys. Chem. C 2017, 121, 1904–1909. [Google Scholar] [CrossRef]
- Düren, T.; Sarkisov, L.; Yaghi, O.M.; Snurr, R.Q. Design of New Materials for Methane Storage. Langmuir 2004, 20, 2683–2689. [Google Scholar] [CrossRef] [PubMed]
- Khakpay, A.; Rahmani, F.; Nouranian, S.; Scovazzo, P. Molecular Insights on the CH4/CO2 Separation in Nanoporous Graphene and Graphene Oxide Separation Platforms: Adsorbents versus Membranes. J. Phys. Chem. C 2017, 121, 12308–12320. [Google Scholar] [CrossRef]
- Tonel, M.Z.; Lara, I.V.; Zanella, I.; Fagan, S.B. The influence of the concentration and adsorption sites of different chemical groups on graphene through first principles simulations. Phys. Chem. Chem. Phys. 2017, 19, 27374–27383. [Google Scholar] [CrossRef]
- Terrones, H.; Lv, R.; Terrones, M.; Dresselhaus, M.S. The role of defects and doping in 2D graphene sheets and 1D nanoribbons. Rep. Prog. Phys. 2012, 75, 062501. [Google Scholar] [CrossRef]
- Lin, K.; Yuan, Q.; Zhao, Y.P. Using graphene to simplify the adsorption of methane on shale in MD simulations. Comput. Mater. Sci. 2017, 133, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Szczęśniak, B.; Choma, J.; Jaroniec, M. Gas adsorption properties of graphene-based materials. Adv. Colloid Interface Sci. 2017, 243, 46–59. [Google Scholar] [CrossRef]
- Mert, H.; Deniz, C.U.; Baykasoglu, C. Monte Carlo simulations of hydrogen adsorption in fullerene pillared graphene nanocomposites. Mol. Simul. 2020, 46, 650–659. [Google Scholar] [CrossRef]
- Vasanth Kumar, K.; Rodríguez-Reinoso, F. Co-adsorption of N2 in the presence of CH4 within carbon nanospaces: Evidence from molecular simulations. Nanotechnology 2013, 24, 035401. [Google Scholar] [CrossRef] [PubMed]
- Mosher, K.; He, J.; Liu, Y.; Rupp, E.; Wilcox, J. Molecular simulation of methane adsorption in micro- and mesoporous carbons with applications to coal and gas shale systems. Int. J. Coal Geol. 2013, 109–110, 36–44. [Google Scholar] [CrossRef]
- Becker, T.M.; Heinen, J.; Dubbeldam, D.; Lin, L.C.; Vlugt, T.J.H. Polarizable Force Fields for CO2 and CH4 Adsorption in M-MOF-74. J. Phys. Chem. C 2017, 121, 4659–4673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucena, S.M.; Frutuoso, L.F.; Silvino, P.F.; Azevedo, D.C.; Toso, J.; Zgrablich, G.; Cavalcante, C.L. Molecular simulation of collection of methane isotherms in carbon material using all-atom and united atom models. Colloids Surf. A Physicochem. Eng. Asp. 2010, 357, 53–60. [Google Scholar] [CrossRef]
- Liu, L.; Nicholson, D.; Bhatia, S.K. Adsorption of CH4 and CH4/CO2 mixtures in carbon nanotubes and disordered carbons: A molecular simulation study. Chem. Eng. Sci. 2015, 121, 268–278. [Google Scholar] [CrossRef] [Green Version]
- Vandenbrande, S.; Verstraelen, T.; Gutiérrez-Sevillano, J.J.; Waroquier, M.; Van Speybroeck, V. Methane Adsorption in Zr-Based MOFs: Comparison and Critical Evaluation of Force Fields. J. Phys. Chem. C 2017, 121, 25309–25322. [Google Scholar] [CrossRef]
- Pirani, F.; Alberti, M.; Castro, A.; Moix Teixidor, M.; Cappelletti, D. Atom–bond pairwise additive representation for intermolecular potential energy surfaces. Chem. Phys. Lett. 2004, 394, 37–44. [Google Scholar] [CrossRef]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard–Jones model: A simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc. 1981, 103, 335–340. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Vekeman, J.; Cuesta, I.G.; Faginas-Lago, N.; Wilson, J.; Sánchez-Marín, J.; Sánchez de Merás, A. Potential models for the simulation of methane adsorption on graphene: Development and CCSD(T) benchmarks. Phys. Chem. Chem. Phys. 2018, 20, 25518–25530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vekeman, J.; Faginas-Lago, N.; Cuesta, I.G.; Sánchez-Marín, J.; Sánchez De Merás, A. Nitrogen Gas on Graphene: Pairwise Interaction Potentials; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 10964, pp. 563–578. [Google Scholar] [CrossRef]
- Wilson, J.; Faginas-Lago, N.; Vekeman, J.; Cuesta, I.G.; Sánchez-Marín, J.; Sánchez de Merás, A. Modeling the Interaction of Carbon Monoxide with Flexible Graphene: From Coupled Cluster Calculations to Molecular-Dynamics Simulations. ChemPhysChem 2018, 19, 774–783. [Google Scholar] [CrossRef] [PubMed]
- Yeamin, M.B.; Faginas-Lago, N.; Alberti, M.; Cuesta, I.G.; Sánchez-Marín, J.; Sánchez de Merás, A.M.J. Multi-scale theoretical investigation of molecular hydrogen adsorption over graphene: Coronene as a case study. RSC Adv. 2014, 4, 54447–54453. [Google Scholar] [CrossRef]
- Vekeman, J.; Faginas-Lago, N.; Lombardi, A.; Sánchez de Merás, A.; García Cuesta, I.; Rosi, M. Molecular Dynamics of CH4/N2 Mixtures on a Flexible Graphene Layer: Adsorption and Selectivity Case Study. Front. Chem. 2019, 7, 1–13. [Google Scholar] [CrossRef]
- Vekeman, J.; Sánchez-Marín, J.; Sánchez de Merás, A.; Garcia Cuesta, I.; Faginas-Lago, N. Flexibility in the Graphene Sheet: The Influence on Gas Adsorption from Molecular Dynamics Studies. J. Phys. Chem. C 2019, 123, 28035–28047. [Google Scholar] [CrossRef]
- Patt, A.; Simon, J.M.; Picaud, S.; Salazar, J.M. A Grand Canonical Monte Carlo Study of the N2, CO, and Mixed N2 –CO Clathrate Hydrates. J. Phys. Chem. C 2018, 122, 18432–18444. [Google Scholar] [CrossRef]
- Bahamon, D.; Carro, L.; Guri, S.; Vega, L.F. Computational study of ibuprofen removal from water by adsorption in realistic activated carbons. J. Colloid Interface Sci. 2017, 498, 323–334. [Google Scholar] [CrossRef]
- Tesson, S.; Firoozabadi, A. Methane Adsorption and Self-Diffusion in Shale Kerogen and Slit Nanopores by Molecular Simulations. J. Phys. Chem. C 2018, 122, 23528–23542. [Google Scholar] [CrossRef]
- Bahamon, D.; Vega, L.F. Systematic evaluation of materials for post-combustion CO2 capture in a Temperature Swing Adsorption process. Chem. Eng. J. 2016, 284, 438–447. [Google Scholar] [CrossRef]
- Vega, L.F.; Bahamon, D. Comparative Study of MOFs and Zeolites For CO2 Capture and Separation at Process Conditions. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Lammps. Available online: http://lammps.sandia.gov (accessed on 15 August 2021).
- Dundar, E.; Boulet, P.; Wexler, C.; Firlej, L.; Llewellyn, P.; Kuchta, B. Heterogeneous melting of methane confined in nano-pores. J. Chem. Phys. 2016, 145, 144704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cristancho, D.; Akkutlu, I.Y.; Criscenti, L.J.; Wang, Y. Gas Storage in Model Kerogen Pores with Surface Heterogeneities. In Proceedings of the SPE Europec featured at 78th EAGE Conference and Exhibition, Vienna, Austria, 30 May–2 June 2016. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the Thermodynamics of Solutions. V. An Equation of State. Fugacities of Gaseous Solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Zhu, Z.; Zheng, Q. Methane adsorption on the graphene sheets, activated carbon and carbon black. Appl. Therm. Eng. 2016, 108, 605–613. [Google Scholar] [CrossRef]
- Mohammad, A.K.; Sabeeh, N.S. Comparative study for adsorption of hydrogen-methane mixtures on activated carbon and 5A molecular sieve. Braz. J. Chem. Eng. 2018, 35, 795–804. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.V.; de Castro, M.C.; Martinez-Escandell, M.; Molina-Sabio, M.; Rodriguez-Reinoso, F. Heat of adsorption and binding affinity for hydrogen on pitch-based activated carbons. Chem. Eng. J. 2011, 168, 972–978. [Google Scholar] [CrossRef]
- Delavar, M.; Ghoreyshi, A.A.; Jahanshahi, M.; Nabian, N. Comparative experimental study of methane adsorption on multi-walled carbon nanotubes and granular activated carbons. J. Exp. Nanosci. 2014, 9, 310–328. [Google Scholar] [CrossRef]
- Nicholson, D.; Parsonage, N. Computer Simulation and the Statistical Mechanics of Adsorption; Academic Press: London, UK, 1982. [Google Scholar]
- Faginas Lago, N.; Huarte Larrañaga, F.; Alberti, M. On the suitability of the ILJ function to match different formulations of the electrostatic potential for water-water interactions. Eur. Phys. J. D 2009, 55, 75–85. [Google Scholar] [CrossRef]
- Chen, J.J.; Li, W.W.; Li, X.L.; Yu, H.Q. Improving Biogas Separation and Methane Storage with Multilayer Graphene Nanostructure via Layer Spacing Optimization and Lithium Doping: A Molecular Simulation Investigation. Environ. Sci. Technol. 2012, 46, 10341–10348. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, W.; Pham, T.; Forrest, K.A.; Liu, W.; He, Y.; Wu, H.; Yildirim, T.; Chen, B.; Space, B.; et al. Fine Tuning of MOF-505 Analogues To Reduce Low-Pressure Methane Uptake and Enhance Methane Working Capacity. Angew. Chem. 2017, 129, 11584–11588. [Google Scholar] [CrossRef]
- Korman, K.J.; Decker, G.E.; Dworzak, M.R.; Deegan, M.M.; Antonio, A.M.; Taggart, G.A.; Bloch, E.D. Using Low-Pressure Methane Adsorption Isotherms for Higher-Throughput Screening of Methane Storage Materials. ACS Appl. Mater. Interfaces 2020, 12, 40318–40327. [Google Scholar] [CrossRef] [PubMed]
- Abdulsalam, J.; Mulopo, J.; Bada, S.O.; Oboirien, B. Equilibria and Isosteric Heat of Adsorption of Methane on Activated Carbons Derived from South African Coal Discards. ACS Omega 2020, 5, 32530–32539. [Google Scholar] [CrossRef] [PubMed]
- Rzepka, M.; Lamp, P.; de la Casa-Lillo, M.A. Physisorption of Hydrogen on Microporous Carbon and Carbon Nanotubes. J. Phys. Chem. B 1998, 102, 10894–10898. [Google Scholar] [CrossRef] [Green Version]
- Kuchta, B.; Firlej, L.; Cepel, R.; Pfeifer, P.; Wexler, C. Structural and energetic factors in designing a nanoporous sorbent for hydrogen storage. Colloids Surf. A Physicochem. Eng. Asp. 2010, 357, 61–66. [Google Scholar] [CrossRef]
- Kuchta, B.; Firlej, L.; Pfeifer, P.; Wexler, C. Numerical estimation of hydrogen storage limits in carbon-based nanospaces. Carbon 2010, 48, 223–231. [Google Scholar] [CrossRef]
- Bénard, P.; Chahine, R. Storage of hydrogen by physisorption on carbon and nanostructured materials. Scr. Mater. 2007, 56, 803–808. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Chen, Z.; Wu, K.; Zhang, L. Effects of an adsorbent accessible volume on methane adsorption on shale. Comput. Methods Appl. Mech. Eng. 2020, 370, 113222. [Google Scholar] [CrossRef]
- Collins, S.P.; Perim, E.; Daff, T.D.; Skaf, M.S.; Galvão, D.S.; Woo, T.K. Idealized Carbon-Based Materials Exhibiting Record Deliverable Capacities for Vehicular Methane Storage. J. Phys. Chem. C 2019, 123, 1050–1058. [Google Scholar] [CrossRef] [Green Version]
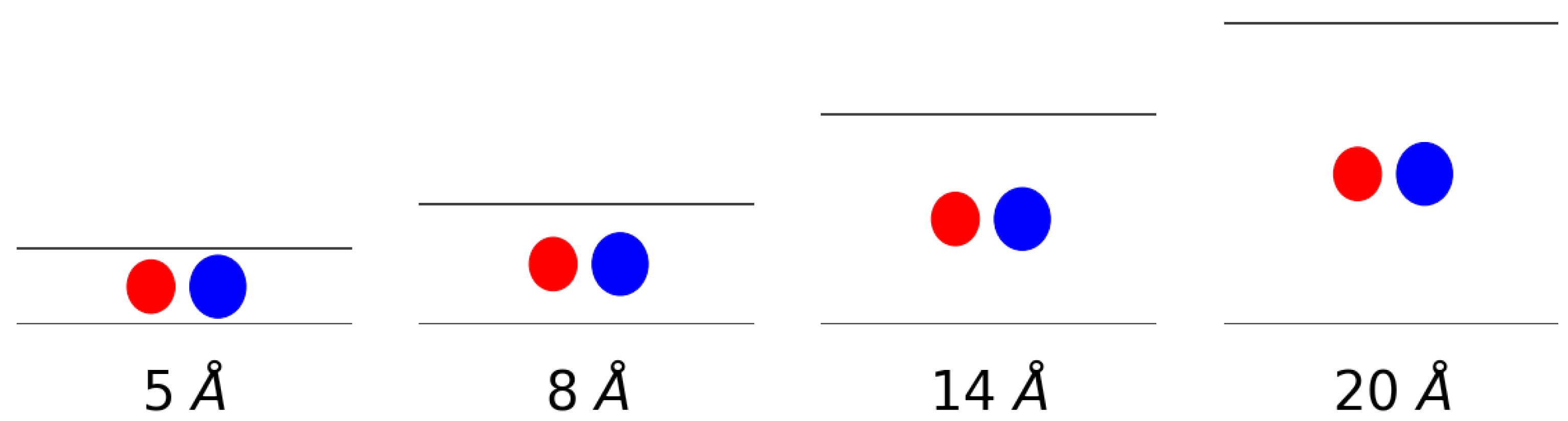

| System | (kcal mol) | r (Å) | Ref. | |
|---|---|---|---|---|
| CH-CH | 0.421 | 4.169 | 8.216 | [34] |
| CH-H | 0.180 | 3.816 | 5.618 | This work |
| H-H | 0.091 | 3.552 | 5.618 | [37] |
| C-CH | 0.210 | 3.938 | 8.185 | [34] |
| C-H | 0.088 | 3.527 | 6.813 | [37] |
| Pore Size (Å) | Pure CH | Pure H | CH Mixt. | H Mixt. |
|---|---|---|---|---|
| 5 | 0.08 (0.08) | 0.08 (0.13) | 0.00 (0.00) | 0.08 (0.11) |
| 8 | 5.50 (11.61) | 0.12 (3.08) | 3.98 (10.93) | 0.05 (0.35) |
| 14 | 0.50 (13.66) | 0.07 (2.70) | 0.29 (10.11) | 0.04 (0.50) |
| 20 | 0.34 (11.44) | 0.06 (2.63) | 0.19 (6.78) | 0.03 (0.62) |
| Pore | Pure CH | Pure H | CH Mixt. | H Mixt. | ||||
|---|---|---|---|---|---|---|---|---|
| 8 Å | 11.405 | 0.909 | 7.833 | 0.009 | 11.023 | 0.536 | 0.405 | 0.048 |
| 14Å | 22.470 | 0.023 | 13.094 | 0.004 | 24.420 | 0.010 | 0.716 | 0.029 |
| 20 Å | 31.178 | 0.008 | 18.170 | 0.002 | 19.898 | 0.007 | 0.989 | 0.020 |
| Pore Size (Å) | Pure CH | Pure H | CH Mixt. | H Mixt. |
|---|---|---|---|---|
| 5 | 0.04 (−3.08) | 0.04 ) | ) | 0.04 (−2.63) |
| 8 | 5.46 (8.44) | 0.08 (0.34) | 3.93 (7.77) | 0.01 (−2.39) |
| 14 | 0.46 (10.50) | 0.03 (−0.03) | 0.25 (6.95) | −0.00 2.24) |
| 20 | 0.29 (8.27) | 0.02 (−0.11) | 0.15 (3.61) | −0.01 (−2.12) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vekeman, J.; Bahamon, D.; García Cuesta, I.; Faginas-Lago, N.; Sánchez-Marín, J.; Sánchez de Merás, A.; Vega, L.F. Grand Canonical Monte Carlo Simulations to Determine the Optimal Interlayer Distance of a Graphene Slit-Shaped Pore for Adsorption of Methane, Hydrogen and their Equimolar Mixture. Nanomaterials 2021, 11, 2534. https://doi.org/10.3390/nano11102534
Vekeman J, Bahamon D, García Cuesta I, Faginas-Lago N, Sánchez-Marín J, Sánchez de Merás A, Vega LF. Grand Canonical Monte Carlo Simulations to Determine the Optimal Interlayer Distance of a Graphene Slit-Shaped Pore for Adsorption of Methane, Hydrogen and their Equimolar Mixture. Nanomaterials. 2021; 11(10):2534. https://doi.org/10.3390/nano11102534
Chicago/Turabian StyleVekeman, Jelle, Daniel Bahamon, Inmaculada García Cuesta, Noelia Faginas-Lago, José Sánchez-Marín, Alfredo Sánchez de Merás, and Lourdes F. Vega. 2021. "Grand Canonical Monte Carlo Simulations to Determine the Optimal Interlayer Distance of a Graphene Slit-Shaped Pore for Adsorption of Methane, Hydrogen and their Equimolar Mixture" Nanomaterials 11, no. 10: 2534. https://doi.org/10.3390/nano11102534
APA StyleVekeman, J., Bahamon, D., García Cuesta, I., Faginas-Lago, N., Sánchez-Marín, J., Sánchez de Merás, A., & Vega, L. F. (2021). Grand Canonical Monte Carlo Simulations to Determine the Optimal Interlayer Distance of a Graphene Slit-Shaped Pore for Adsorption of Methane, Hydrogen and their Equimolar Mixture. Nanomaterials, 11(10), 2534. https://doi.org/10.3390/nano11102534






