A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature
Abstract
:1. Introduction
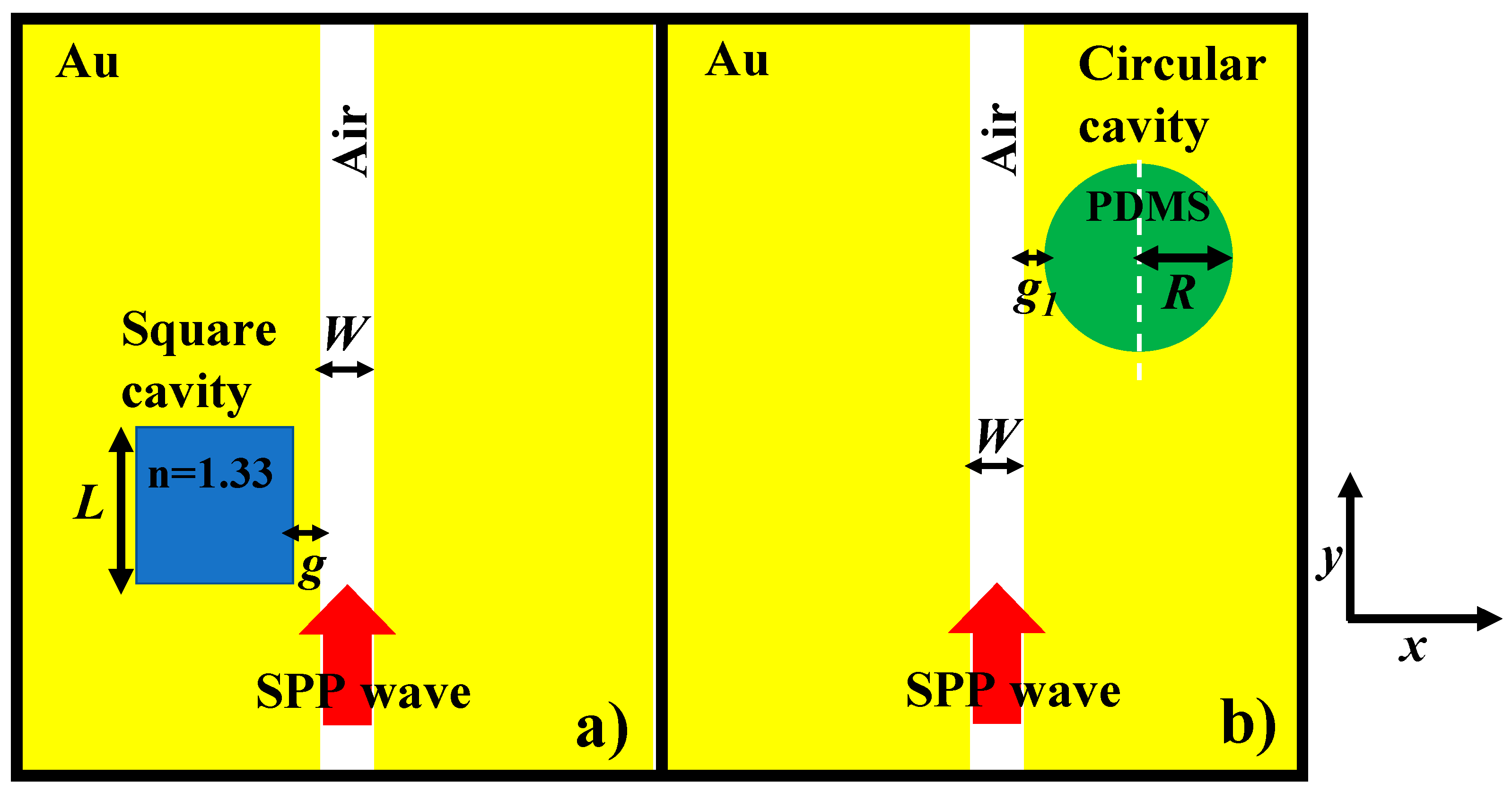
2. Single-Purpose Device Model and Simultaneous Parameters
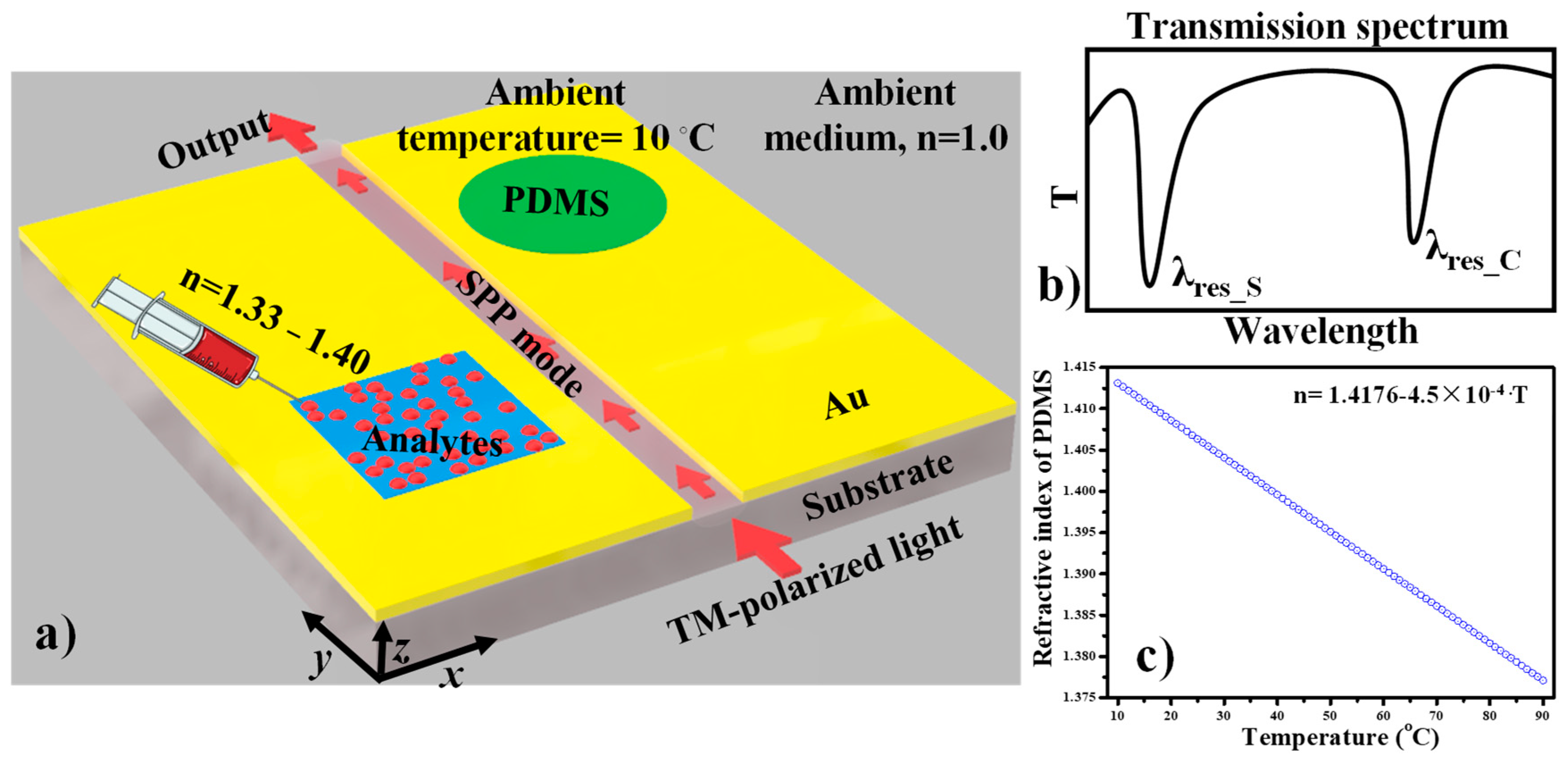
3. Dual-Purpose Sensor Design
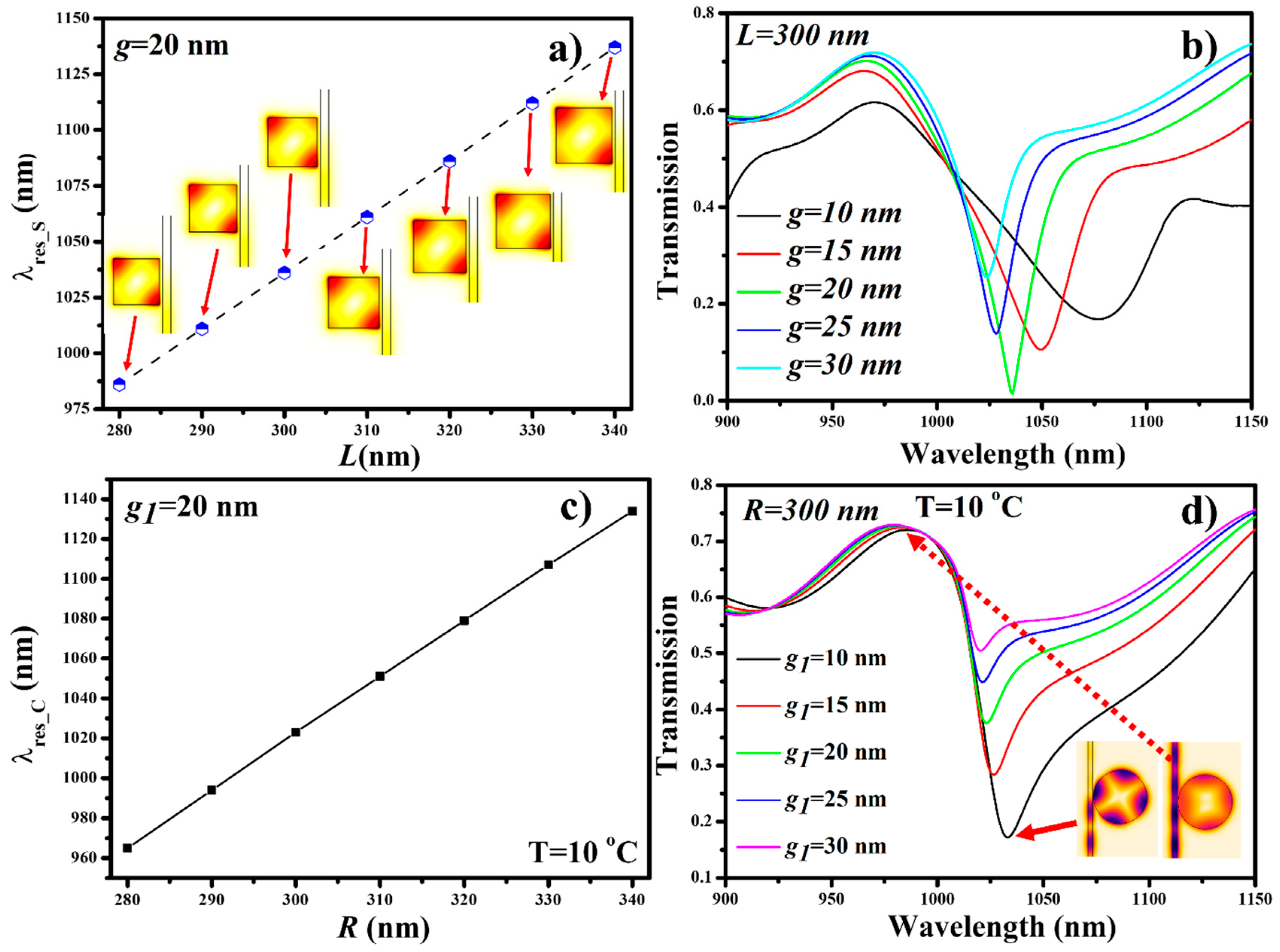
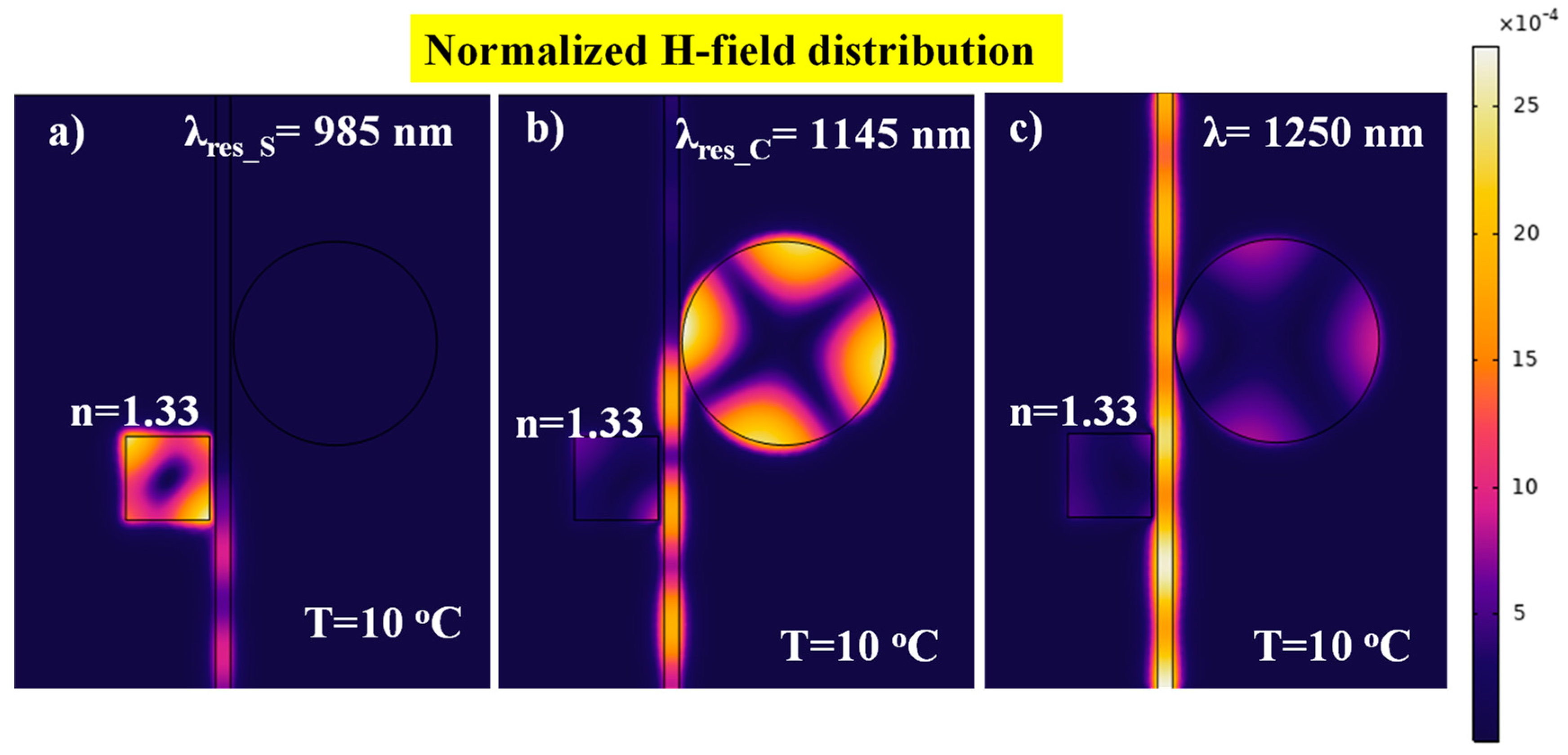
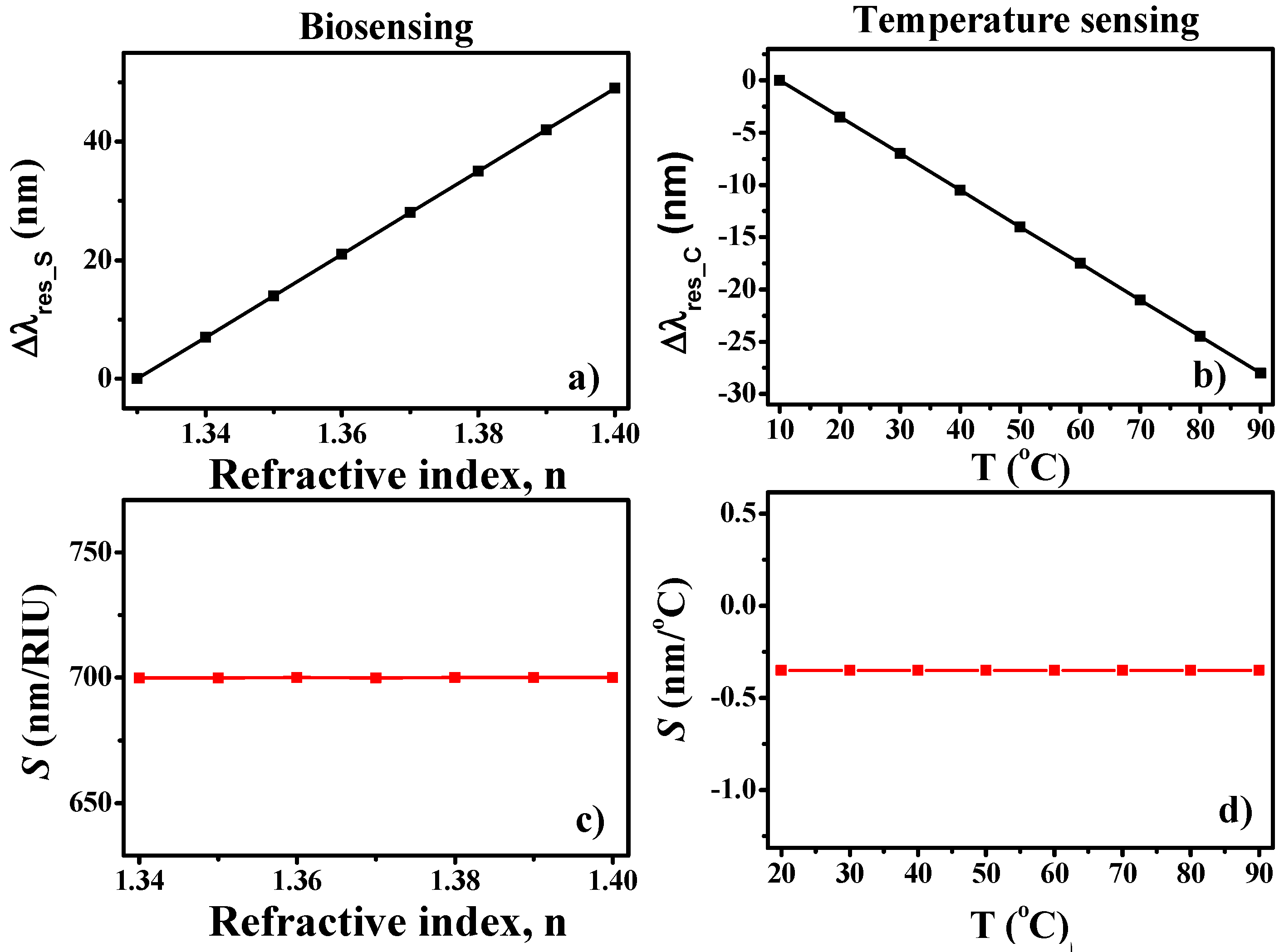
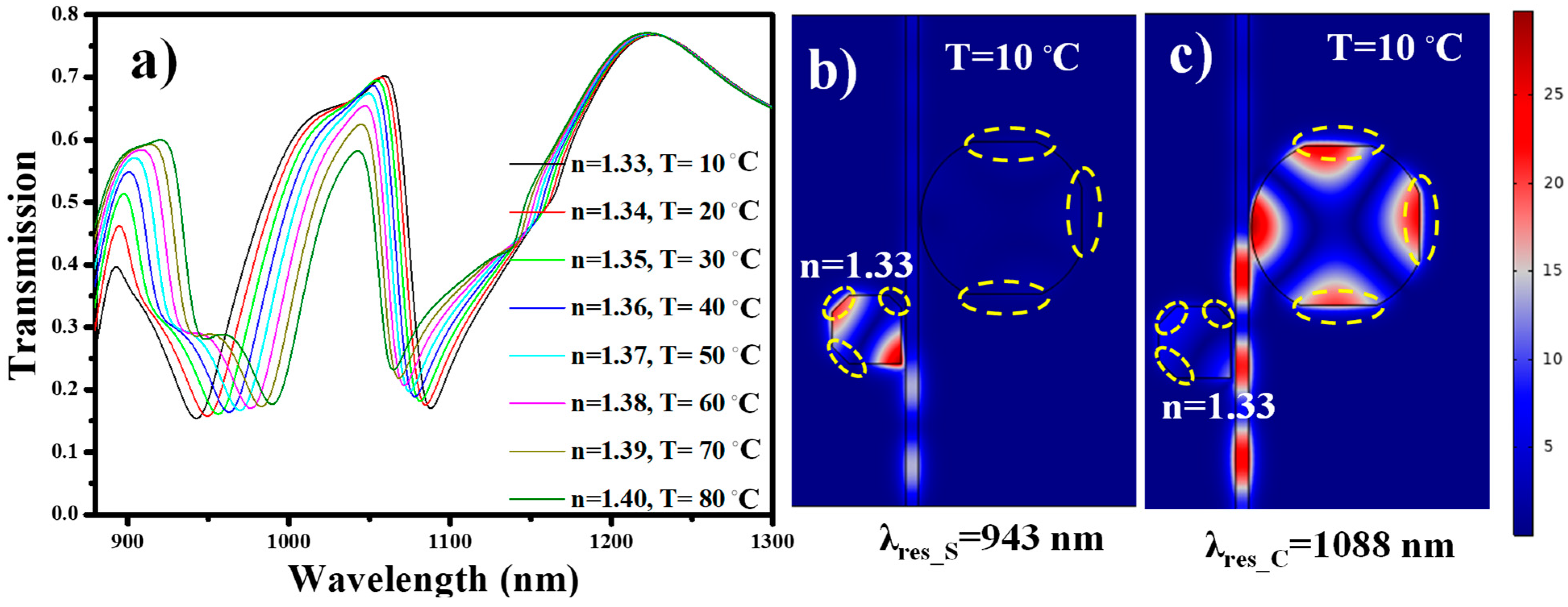
4. Modes of Operation, Results, and Discussion
5. Fabrication Inaccuracies Influence Analysis
5.1. Under-Etching Influence
5.2. Over-Etching
6. Limiting Factors
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Plasmonics: A necessity in the field of sensing—A review (invited). Fiber Integr. Opt. 2021, 40, 14–47. [Google Scholar] [CrossRef]
- Sakai, H.; Okahisa, S.; Nakayama, Y.; Nakayama, K.; Fukuhara, M.; Kimura, Y.; Ishii, Y.; Fukuda, M. Plasmonic and electronic device-based integrated circuits and their characteristics. Solid State Electron. 2016, 125, 240–246. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Xu, W. Surface plasmon polaritons: Physics and applications. J. Phys. D Appl. Phys. 2012, 45, 113001. [Google Scholar] [CrossRef]
- Butt, M.A. Numerical investigation of a small footprint plasmonic Bragg grating structure with a high extinction ratio. Photonics Lett. Pol. 2020, 12, 82–84. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Ultra-short lossless plasmonic power splitter design based on metal-insulator-metal waveguide. Laser Phys. 2019, 30, 016201. [Google Scholar] [CrossRef]
- Chao, C.-T.; Chau, Y.-F.C.; Huang, H.; Kumara, N.; Kooh, M.; Lim, C.; Chiang, H.-P. Highly sensitive and tunable plasmonic sensor based on a nanoring resonator with silver nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef] [PubMed]
- Masson, J.-F. Portable and field-deployed surface plasmon resonance and plasmonic sensors. Analyst 2020, 145, 3776–3800. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L. Nanoblocks embedded in L-shaped nanocavity of a plasmonic sensor for best sensor performance. Opt. Appl. 2021, 51, 109–120. [Google Scholar]
- Zhu, J.; Lou, J. Ultrasensitive and multifunction plasmonic temperature sensor with ethanol-sealed asymmetric ellipse resonators. Molecules 2018, 23, 2700. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Lou, J. High-sensitivity Fano resonance temperature sensor in MIM waveguides coupled with a polymethylsiloxane-sealed semi-square ring resonator. Results Phys. 2020, 18, 103183. [Google Scholar] [CrossRef]
- Tian, M.; Lu, P.; Chen, L.; Liu, D.; Lv, C. All-optical switching in MIM waveguide resonator with an outer portion smooth bend structure containing nonlinear optical materials. Opt. Commun. 2012, 285, 4562–4566. [Google Scholar] [CrossRef]
- Shibayama, J.; Kawai, H.; Yamauchi, J.; Nakano, H. Analysis of a 3D MIM waveguide-based plasmonic demultiplexer using the TRC-FDTD method. Opt. Commun. 2019, 452, 360–365. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Chao, C.-T.C.; Chaing, H.-P. Ultra-broad bandgap metal-insulator-metal waveguide filter with symmetric stubs and defects. Results Phys. 2020, 17, 103116. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Highly sensitive refractive index sensor based on plasmonic Bow Tie configuration. Photonic Sens. 2020, 10, 223–232. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, C. Optical refractive index sensor with Fano resonance based on original MIM waveguide structure. Results Phys. 2021, 21, 103858. [Google Scholar]
- Wang, Y.; Gao, B.; Zhang, K.; Yuan, K.; Wan, Y.; Xie, Z.; Xu, X.; Zhang, H.; Song, Q.; Yao, L.; et al. Refractive index sensor based on leaky resonant scattering of single semiconductor nanowire. ACS Photon. 2017, 4, 688–694. [Google Scholar] [CrossRef]
- Teng, C.; Yu, F.; Ding, Y.; Zheng, J. Refractive index sensor based on multi-mode plastic optical fiber with long period grating. Proc. SPIE 2017, 10231, 102311M. [Google Scholar]
- Xu, D.-X.; Vachon, M.; Densmore, A.; Ma, R.; Janz, S.; Delâge, A.; Lapointe, J.; Cheben, P.; Schmid, J.H.; Post, E.; et al. Real-time cancellation of temperature induced resonance shifts in SOI wire waveguide ring resonator label-free biosensor arrays. Opt. Express 2010, 18, 22867–22879. [Google Scholar] [CrossRef]
- Talebifard, S.; Schmidt, S.; Shi, W.; Wu, W.; Jaeger, N.A.F.; Kwok, E.; Ratner, D.M.; Chrostowski, L. Optimized sensitivity of silicon-on-insulator (SOI) strip waveguide resonator sensor. Biomed. Opt. Express 2017, 8, 500–511. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A.; Kazmierczak, A.; Piramidowicz, R. Plasmonic sensor based on metal-insulator-metal waveguide square ring cavity filled with functional material for the detection of CO2 gas. Opt. Express 2021, 29, 16584. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y. One-dimensional plasmonic sensors. Front. Phys. 2020, 8, 312. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Highly integrated plasmonic sensor design for the simultaneous detection of multiple analytes. Curr. Appl. Phys. 2020, 20, 1274–1280. [Google Scholar] [CrossRef]
- Kong, Y.; Wei, Q.; Liu, C.; Wang, S. Nanoscale temperature sensor based on Fano resonance in metal-insulator-metal waveguide. Opt. Commun. 2017, 384, 85–88. [Google Scholar] [CrossRef]
- Rahmatiyar, M.; Afsahi, M. Design of a refractive index plasmonic sensor based on a ring resonator coupled to a MIM waveguide containing tapered defects. Plasmonics 2020, 15, 2169–2176. [Google Scholar] [CrossRef]
- Yang, X.; Hua, E.; Wang, M.; Wang, Y.; Wen, F.; Yan, S. Fano resonance in a MIM waveguide with two triangle stubs coupled with a split-ring nanocavity for sensing application. Sensors 2019, 19, 4972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Cui, M. Refractive index sensor based on the symmetric MIM waveguide structure. J. Electron. Mater. 2019, 48, 1005–1010. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Z.; Yan, S. Tunable Fano resonance in asymmetric MIM waveguide structure. Sensors 2017, 17, 1494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, Y.; Huang, Y.; Xu, W.; Zhao, W.; He, C. A plasmonic temperature-sensing structure based on dual laterally side-coupled hexagonal cavities. Sensors 2016, 16, 706. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Zhang, H.; Sun, L.; Li, J.; Yu, C. Temperature tunable Fano resonance based on ring resonator side coupled with a MIM waveguide. Opt. Laser Technol. 2019, 116, 293–299. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, J.; Lu, P.; Tian, M.; Xu, J.; Liu, D. A single-mode fiber sensor based on core-offset inter-modal interferometer. Opt. Commun. 2014, 320, 33–37. [Google Scholar] [CrossRef]
- Srivastava, T.; Das, R.; Jha, R. Highly sensitive plasmonic temperature sensor based on Photonic Crystal surface plasmon waveguide. Plasmonics 2013, 8, 515–521. [Google Scholar] [CrossRef]
- Lotters, J.C.; Olthuis, W.; Veltink, P.H.; Bergveld, P. The mechanical properties of the rubber elastic polymer polydimethylsiloxane for sensor applications. J. Micromechanics Microengineering 1997, 7, 145. [Google Scholar] [CrossRef]
- Shi, H.; Yan, S.; Yang, X.; Wu, X.; Wu, W.; Hua, E. A nanosensor based on a metal-insulator-metal bus waveguide with a stub coupled with a racetrack ring resonator. Micromachines 2021, 12, 495. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Chen, F.; Zhang, H.; Sun, L.; Yu, C. Sensor based on multiple Fano resonances in MIM waveguide resonator system with silver nanorod-defect. Optik 2021, 229, 166237. [Google Scholar] [CrossRef]
- Bahri, H.; Mouetsi, S.; Hocini, A.; Salah, H.B. A highly sensitive sensor using MIM waveguide coupled with a rectangular cavity with Fano resonance. Opt. Quantum Electron. 2021, 53, 332. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Refractive index sensor based on concentric triple racetrack resonators side-coupled to metal-insulator-metal waveguide for glucose sensing. J. Opt. Soc. Am. B 2019, 36, 2834–2842. [Google Scholar] [CrossRef]
- Huang, B.; Meng, H.; Wang, Q.; Wang, H.; Zhang, X.; Yu, W.; Tan, C.; Huang, X.; Wang, F. Plasmonic-induced transparency and slow-light effect based on stub waveguide with nanodisk resonator. Plasmonics 2016, 11, 543–550. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Nanodots decorated MIM semi-ring resonator cavity for biochemical sensing. Photonics Nanostructures Fundam. Appl. 2020, 42, 100836. [Google Scholar] [CrossRef]
- Manfrinato, V.R.; Zhang, L.; Dong, S.; Duan, H.; Hobbs, R.G.; Stach, E.A.; Berggren, K.K. Resolution limits of electron-beam lithography toward the atomic scale. Nano Lett. 2013, 13, 1555–1558. [Google Scholar] [CrossRef]
- Sia, P.D. Overview of Drude-Lorentz type models and their applications. Nanoscale Syst. Math. Model. Theory Appl. 2014, 3, 1–13. [Google Scholar]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Metal-insulator-metal nano square ring resonator for gas sensing applications. Waves Random Complex Media 2021, 31, 146–156. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Plasmonic sensors based on Metal-insulator-metal waveguides for refractive index sensing applications: A brief review. Phys. E 2020, 117, 113798. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, L.; Liu, Z.; Zhang, Y.; Zhang, Y. Surface-plasmon-resonance-based optical-fiber temperature sensor with high sensitivity and high figure of merit. Opt. Lett. 2017, 42, 2948–2951. [Google Scholar] [CrossRef] [PubMed]
- Haslacher, H.; Szekeres, T.; Gerner, M.; Ponweiser, E.; Repl, M.; Wagner, O.F.; Perkmann, T. The effect of storage temperature fluctuations on the stability of biochemical analytes in blood serum. Clin. Chem. Lab. Med. 2017, 55, 974–983. [Google Scholar] [CrossRef] [PubMed]
- Wartell, R.M.; Benight, A.S. Thermal denaturation of DNA molecules: A comparison of theory with experiment. Phys. Rep. 1985, 126, 67–107. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A.; Kaźmierczak, A.; Piramidowicz, R. A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature. Nanomaterials 2021, 11, 2551. https://doi.org/10.3390/nano11102551
Kazanskiy NL, Khonina SN, Butt MA, Kaźmierczak A, Piramidowicz R. A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature. Nanomaterials. 2021; 11(10):2551. https://doi.org/10.3390/nano11102551
Chicago/Turabian StyleKazanskiy, Nikolay L., Svetlana N. Khonina, Muhammad A. Butt, Andrzej Kaźmierczak, and Ryszard Piramidowicz. 2021. "A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature" Nanomaterials 11, no. 10: 2551. https://doi.org/10.3390/nano11102551
APA StyleKazanskiy, N. L., Khonina, S. N., Butt, M. A., Kaźmierczak, A., & Piramidowicz, R. (2021). A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature. Nanomaterials, 11(10), 2551. https://doi.org/10.3390/nano11102551









